Methods to Calculate Entropy Generation
Abstract
1. Introduction
1.1. Local Equilibrium
1.2. States, Paths and Path (Line) Integrals
- Thermodynamics often involves changes in variables between two states. Variables include a set of the independent thermodynamic state variables Z chosen and measured for a particular system, and state dependent system properties which are functions of the states of Z. The Z characterize a system’s thermodynamic state and can include temperature T, pressure P, and number of moles N, among others. Changes in system properties such as energy E, entropy S, temperature T and use the exact differential d; are path independent, wherein changes in properties over an irreversible path (irr) are identical to changes in properties over a reversible path (rev), e.g., dE = dEirr = dErev; and the line integral depends only on the property values at the beginning and end states (o and f). This is the thermodynamic state principle.
- Path-dependent variables such as work W, heat transfer entropy generation and depend on what occurs along the path between states o and f, and use the inexact differential such that must be accumulated over all instants of time t along the (assumed known) transformation path between times and . The path-dependent parameters will depend on a set of variables = {Z} assumed to be time dependent, observable, and measurable. The Z characterize the thermodynamic state, whereas the characterize any active irreversible dissipative processes. Via a suitable numerical integration such as the trapezoid rule, with the = {Z(t), } measured as points = {Z, suitably spaced at time instants < in accord with the sampling theorem [14], the increments can be accumulated into the line integral .
- Exact differentials , state functions of the independent state variables Z(t), if intractable, can be numerically integrated over the (ideal) reversible path per methods of the prior paragraph. The reversible path must transit states o to f in quasi-equilibrium and be continuous and maximally smooth over time, which can be approximated by linear functions with slope determined by the end states, for example, if , components of Z(t) with slope where and must be measured or known at the beginning and final times and . With this, the line integral , where sum index Z denotes a sum over all the components of Z, and dE/dZ must be evaluated at each time instant < along the reversible path.
- For reversible processes with initial and final states and , satisfies the reversible path approximations of item 3.
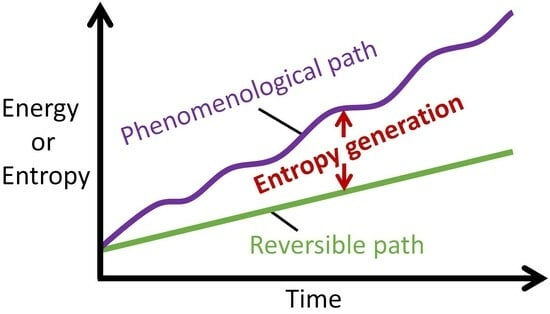
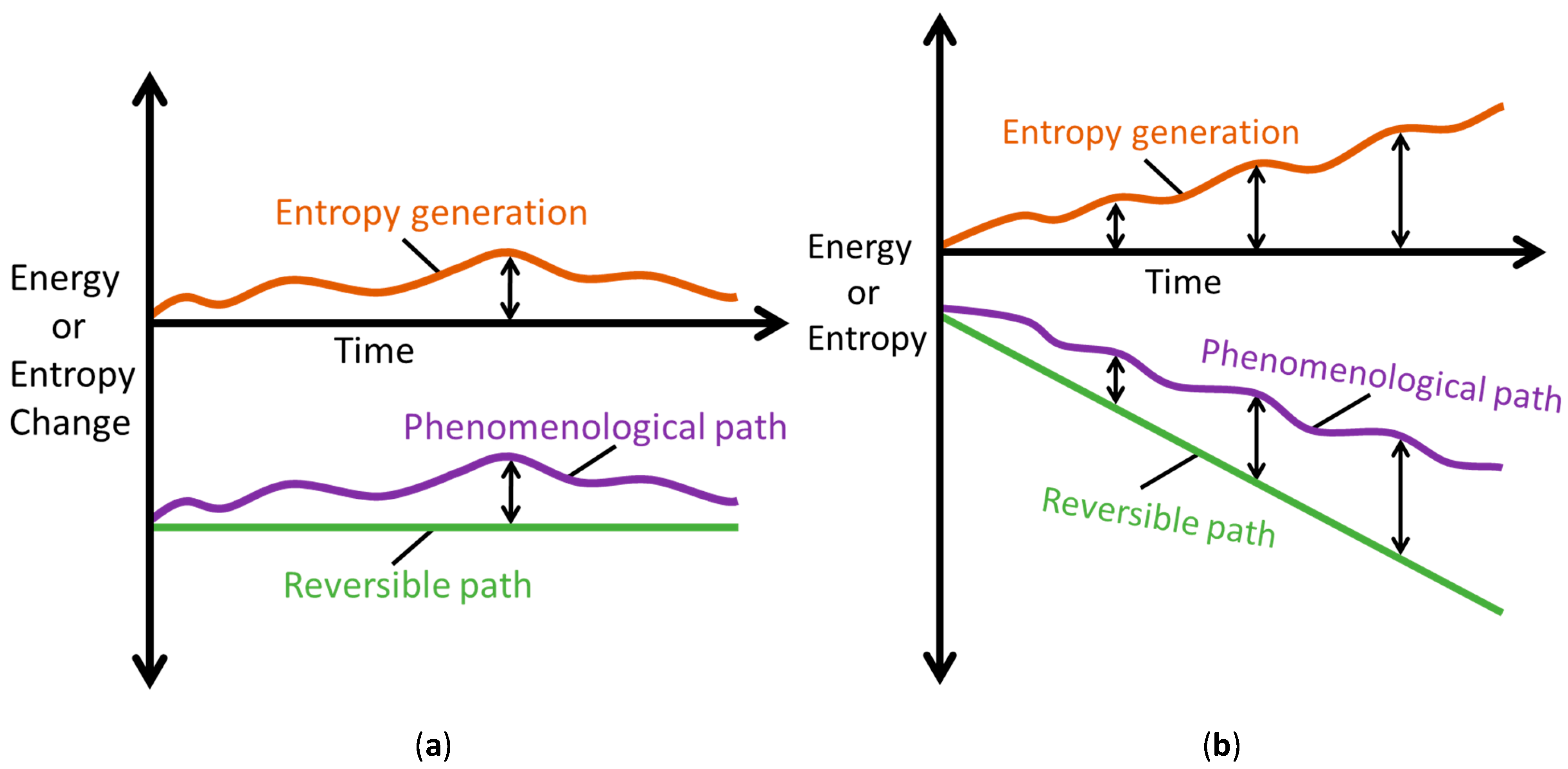
- A phenomenological path (phen) through the thermodynamic state space enclosing = {Z} defined in item 2 includes nonzero . A reversible path (rev) in the reversible subspace {Z} of [15] involves only the thermodynamic states Zrev, not the . The projection of the set of points = {Z, that comprise an irreversible phenomenological path onto the reversible subspace is the set of points { [15]. The system inputs, active mechanisms and dynamics are determined by the phenomenological path.
2. Irreversible Thermodynamics and Entropy Generation
2.1. Combining Internal Energy and Entropy Balances
2.2. Entropy Generation of Various System Classes via Thermodynamic Potentials
- : evaluated via the expressions of the middle equalities of Equations (5) and (8) at points over the irreversible phenomenological path defined in items 2 and 5 of Section 1.2, where salient quantities can be measured.
- : evaluated as an exact differential over a reversible path between the beginning and final values of the irreversible path for , as discussed in list items 3, 4 and 5 of Section 1.2. Here, the independent states in the parentheses of Equations (5) and (8) are linear in time, as per items 3 and 4 of Section 1.2.
2.3. Phenomenological Entropy Generation Theorem
2.4. Phenomenological Entropy Generation Functions for Various System Classes
2.4.1. Thermal Systems: Internal Energy and Enthalpy
2.4.2. Boundary-Loaded (Work-Capable) Systems: Helmholtz Potential
2.4.3. Internally Reactive Systems and Energy Storage Systems: Gibbs Potential
2.5. Generalized Material Properties, Entropy Content S, Internal Free Energy Dissipation “–SdT”
2.6. Stress vs. Strength Sign Conventions
2.7. Helmholtz-Gibbs Coupling
2.8. Rates
2.9. Open Systems: Pumps, Compressors, Fuel Cells, etc.
3. Evaluating Total Entropy Generation and Path (Line) Integrals
4. Sample (Phenomenological) Entropy Generation Calculations
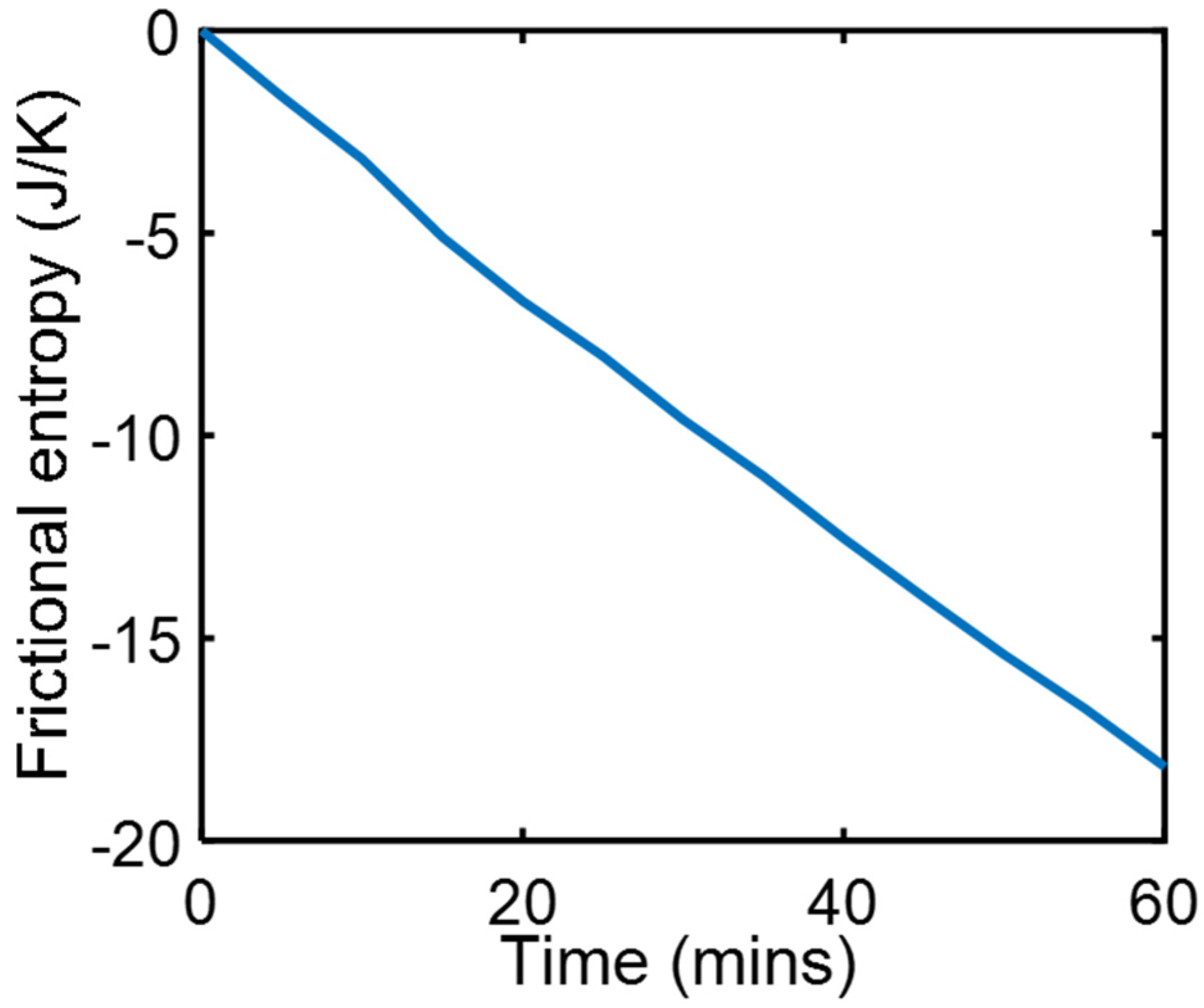
4.1. Friction Sliding of Copper against Steel at Steady Speed—(Steady State)
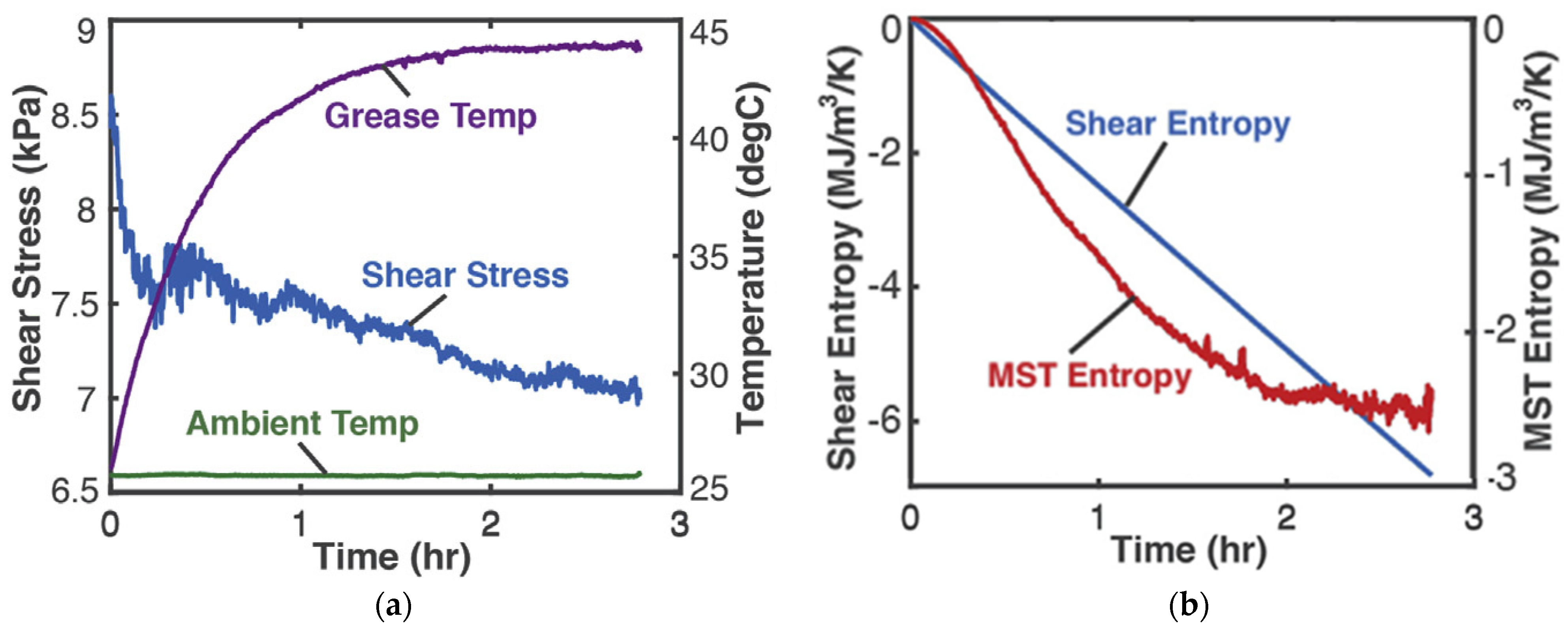
4.2. Mechanical Shearing of Grease—Shear Stress and Shear Strain (Helmholtz Potential)
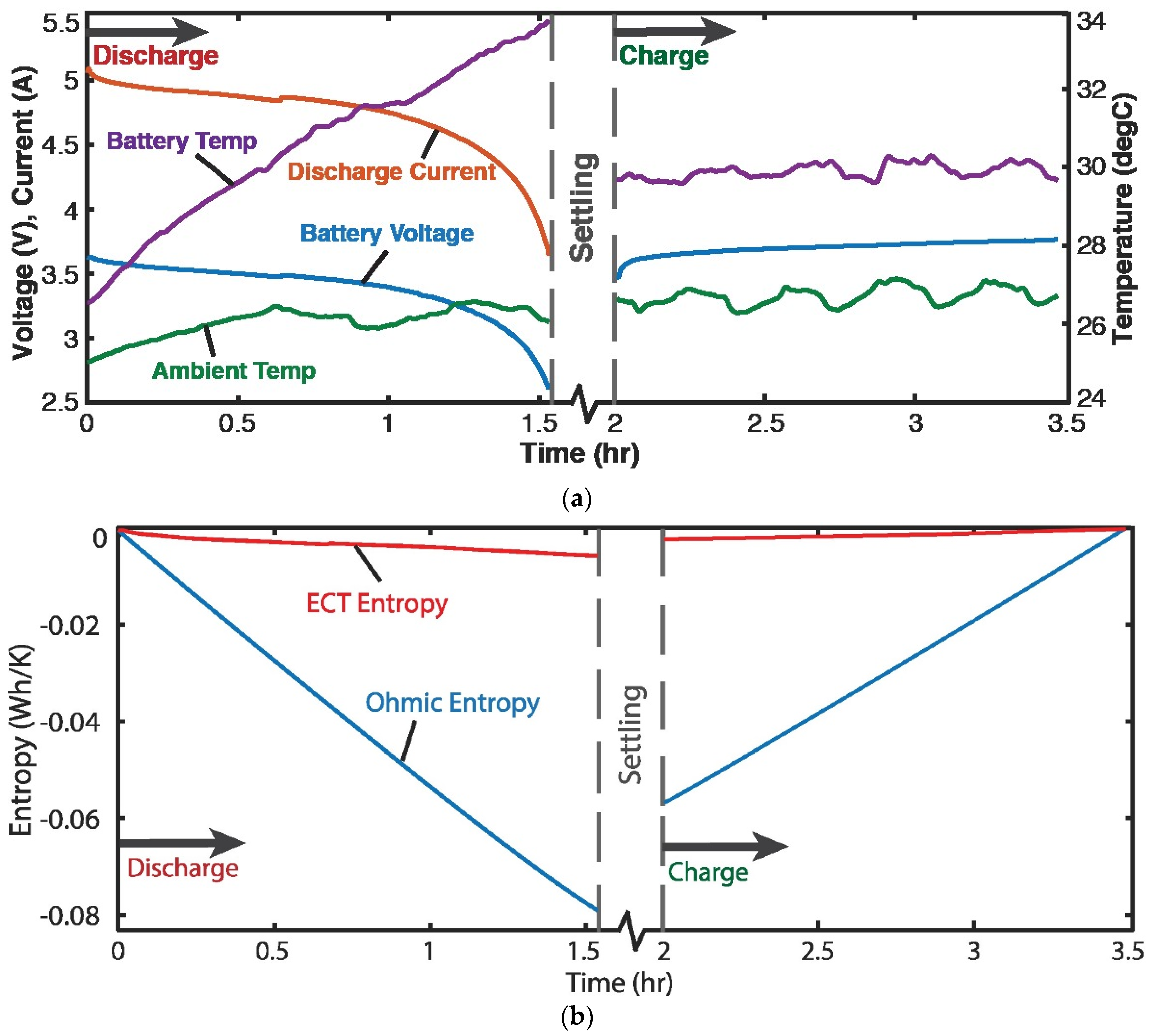
4.3. Discharge of Lithium-Ion Battery—Voltage and Charge (Helmholtz-Gibbs Coupling)
4.4. Fatigue of Metals—Stress and Strain (Helmholtz Potential)
4.5. Pump Flow—Pressure and Flow Rate (Internal Energy)
5. Discussion
5.1. Phenomenology
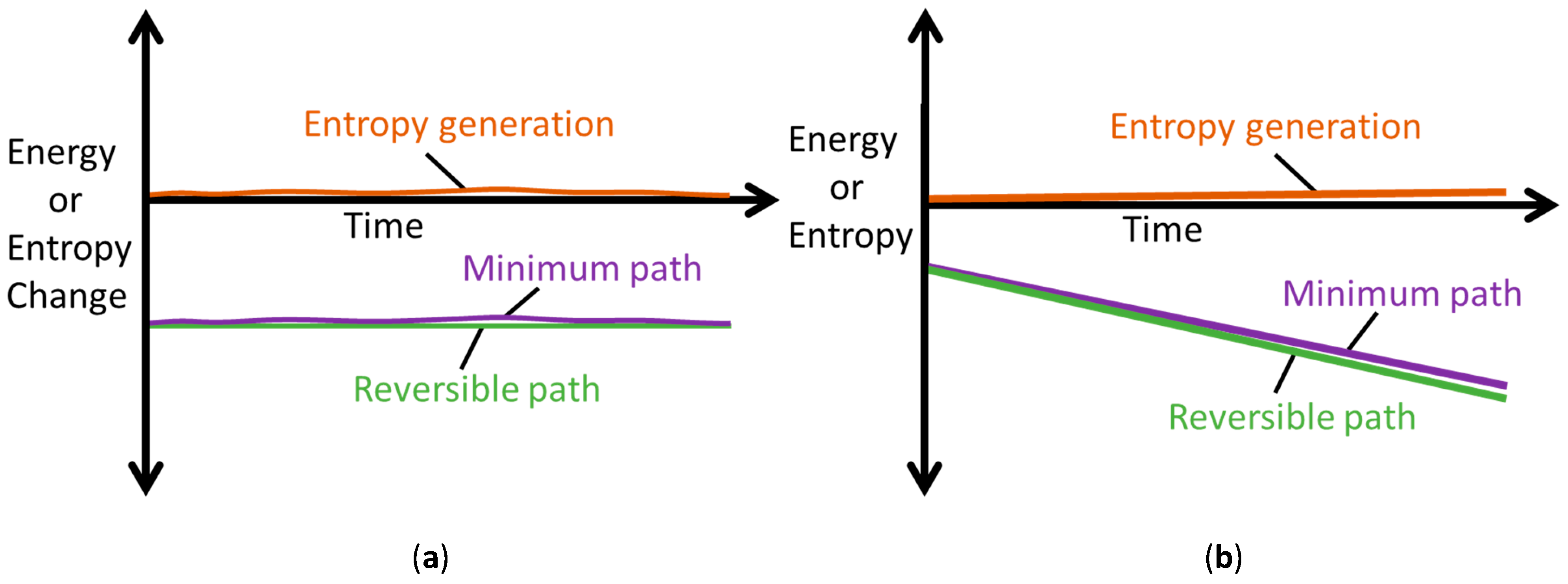
5.2. Steady vs. Unsteady Systems: Minimum Entropy Generation (MEG) vs. MicroStructuroThermal (MST) Entropy
5.3. Dissipation Factor and Entropic Efficiency
5.4. Thermal vs. Non-Thermal Systems—Internal Energy and Enthalpy vs. the Free Energies
6. Summary and Conclusions
- a combination of the thermodynamic potentials and the irreversible form of the TdS equation yields the irreversible Massieu functions;
- steady-state systems generate entropy at a minimum rate which, for a boundary-loaded, internally reactive open system, is the sum of boundary work/load entropy and compositional change entropy rates;
- for unsteady non-thermal systems, a microstructurothermal MST entropy is included to characterize the accompanying instantaneous transients during system transformation;
- phenomenological entropy generation is the sum of boundary work/load entropy , compositional change entropy and microstructurothermal MST entropy (ElectroChemicoThermal ECT entropy for electrochemical systems);
- entropy generation is the difference between phenomenological and reversible entropies at every instant, named the Phenomenological Entropy Generation (PEG) Theorem;
- along the phenomenological path, thermodynamic and other states germane to evaluating and are observable (measurable), permitting evaluation of entropy generation ;
- entropy generation is always non-negative in accordance with the second law, while its constituent terms and are directional, negative for a loaded system and positive for an energized system. This implies during load application/work output or active species decomposition, and during energization/work input or active species formation, in accordance with experience and thermodynamic laws. In plain words, measurable energy obtained from a real system is always less than the theoretical maximum/reversible energy, and measurable energy added to a real system is always more than the minimum/reversible energy. (Modulus signs indicate magnitudes only).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | Name | Unit |
| A | Helmholtz free energy | J |
| B | magnetic field | T |
| C | Heat capacity | J/K |
| F | Faraday’s constant | C/mol |
| G | Gibbs free energy | J |
| I | discharge/charge current or rate | A |
| m | mass | kg |
| n’ | number of charge species | |
| M | magnetic dipole moment | J/T |
| N, Nk | number of moles of substance | mol |
| P | pressure | Pa |
| q | charge | Ah |
| Q | heat | J |
| R | gas constant | J/mol·K |
| S | entropy or entropy content | J/K (Wh/K) |
| entropy generation function | J/K (Wh/K) | |
| S’ | entropy generation or production | J/K (Wh/K) |
| t | time | sec |
| T | temperature | °C or K |
| U | internal energy | J |
| v | voltage | V |
| V | volume | m3 |
| W | work | J |
| Z | thermodynamic state variable | |
| Symbols | ||
| μ | chemical potential | |
| ζ | phenomenological variable | |
| ρ | density | |
| Subscripts & acronyms | ||
| 0 | initial | |
| c | specific heat capacity | |
| d | diffusion | |
| e | flow | |
| f | final | |
| ECT, VT | Electro-Chemico-Thermal | |
| MST, μT | Micro-Structuro-Thermal | |
| rev | reversible | |
| irr | irreversible | |
| phen | phenomenological | |
| DEG | Degradation-Entropy Generation | |
| PEG | Phenomenological Entropy Generation | |
| NLGI | National Lubricating Grease Institute |
Appendix A. Generalized Material Properties from First Principles
Appendix A.1. Heat Capacities and
Appendix A.2. Isothermal Loadability κT and Load Modulus E’
Appendix A.3. Thermal Displacement Coefficient α and Thermal Force (Strength) Coefficient β
Appendix A.4. Isothermal Chemical Resistances and
Appendix A.5. Thermal Chemico-Transport Decay Coefficients and
Appendix A.6. Gibbs Properties vs. Helmholtz Properties
| Category | Gibbs-Based | Helmholtz-Based |
|---|---|---|
| Thermal | Constant-Force Heat Capacity | Constant-Displacement Heat Capacity |
| Thermo-mechanical | Thermal Displacement Coefficient | Thermal Force Coefficient |
| E’ | ||
| Mechanical | Isothermal Loadability | Load Modulus |
| Chemical | Isothermal Constant-Force Chemical Resistance | Isothermal Constant-Displacement Chemical Resistance |
| Thermo-chemical | Constant- Force Thermal Decay Coefficient | Constant-Displacement Thermal Decay Coefficient |
| Property | Physical Interpretation |
|---|---|
| Heat Capacity | Material’s ability to withstand heat without an increase in temperature. |
| Thermal Displacement/Force Coefficient | Impact of temperature on displacement/force. Physical response to temperature change. |
| Load Modulus | Physical response to non-thermal load. |
| Chemical Resistance | Resistance to chemical conversion of reactive species. |
| Thermal Decay Coefficient | Chemical response to temperature change. |
References
- Clapeyron, B.E. Memoir sur la puissance motrice de la chaleur. J. De L’école R. Polytech. 1834, 23, 153–190. [Google Scholar]
- Massieu, F. Sur les Fonctions caractéristiques des divers fluides. CR Acad. Sci. Paris 1869, 69, 858–862. [Google Scholar]
- Rayleigh, J.W.S.B. The Theory of Sound; Macmillan: New York, NY, USA, 1896; Volume 2. [Google Scholar]
- Onsager, L. Reciprocal Relations in Irreversible Processes. Phys. Rev. 1931, 37, 183–196. [Google Scholar] [CrossRef]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Thomas, C.C., Ed.; Cambridge University Press: Cambridge, UK, 1955. [Google Scholar]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications Inc.: New York, NY, USA, 2011. [Google Scholar]
- Osara, J.; Bryant, M. A Thermodynamic Model for Lithium-Ion Battery Degradation: Application of the Degradation-Entropy Generation Theorem. Inventions 2019, 4, 23. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Thermodynamics of grease degradation. Tribol. Int. 2019, 137, 433–445. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Thermodynamics of fatigue: Degradation-entropy generation methodology for system and process characterization and failure analysis. Entropy 2019, 21, 685. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Thermodynamics of Lead-Acid Battery Degradation: Application of the Degradation-Entropy Generation Methodology. J. Electrochem. Soc. 2019, 166, A4188–A4210. [Google Scholar] [CrossRef]
- Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the thermodynamics of degradation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1998. [Google Scholar]
- de Groot, S.R. Thermodynamics of Irreversible Processes; North-Holland Publishing Company: Amsterdam, The Netherlands, 1951. [Google Scholar] [CrossRef]
- Taub, H.; Schilling, D.L. Principles of Communication Systems; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Muschik, W. Fundamentals of Non-Equilibrium Thermodynamics. In Non-Equilibrium Thermodynamics with Applications to Solids; Muschik, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 1–67. [Google Scholar]
- Callen, H.B. Thermodynamics and An Introduction to Thermostatistics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1985. [Google Scholar]
- Gibbs, J.W. The Collected Works of J. Willard Gibbs...: Thermodynamics; Longmans, Green and Company: London, UK, 1928; Volume 1. [Google Scholar]
- Pauli, W. Thermodynamics and The Kinetic Theory of Gases; Pauli Lectures on Physics Vol 3 Dover Books; Courier Corporation: Honolulu, HI, USA, 1973. [Google Scholar]
- Osara, J.A. Thermodynamics of manufacturing processes—The workpiece and the machinery. Inventions 2019, 4, 28. [Google Scholar] [CrossRef]
- Bove, R.; Ubertini, S. (Eds.) Modeling Solid Oxide Fuel Cells Methods, Procedures and Techniques; Spinger: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Osara, J.A.; Chatra, S.; Lugt, P.M. Grease Material Properties from First Principles Thermodynamics. Lubr. Sci. 2023, 36, 36–50. [Google Scholar] [CrossRef]
- Doelling, K.L.; Ling, F.F.; Bryant, M.D.; Heilman, B.P. An Experimental Study on the Correlation between Wear and Entropy Flow in Machinery Components. J. Appl. Phys. 2000, 88, 2999–3003. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Morrow, J.D. Cyclic Plastic Strain Energy and Fatigue of Metals. In Internal Friction, Damping, and Cyclic Plasticity; ASTM International: West Conshohocken, PA, USA, 1965. [Google Scholar]
- Rincon, J.; Osara, J.A.; Bryant, M.D.; Fernandez, B. Shannon’s Machine Capacity & Degradation-Entropy Generation Methodologies for Failure Detection: Practical Applications to Motor-Pump Systems; Turbomachinery & Pump Symposia: Houston, TX, USA, 2021. [Google Scholar]
- Balian, R. François Massieu and the thermodynamic potentials. Comptes Rendus Phys. 2017, 18, 526–530. [Google Scholar] [CrossRef]
- Burghardt, M.D.; Harbach, J.A. Engineering Thermodynamics, 4th ed.; HarperCollinsCollege Publishers: New York, NY, USA, 1993. [Google Scholar]
- Bejan, A. The Method of Entropy Generation Minimization. In Energy and the Environment; Sage Publications: Thousand Oaks, CA, USA, 1990; pp. 11–22. [Google Scholar]
- Pal, R. Demystification of the Gouy-Stodola theorem of thermodynamics for closed systems. Int. J. Mech. Eng. Educ. 2017, 45, 142–153. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics, 5th ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Çengel, Y.A.; Boles, M.A. Thermodynamics—An Engineering Approach; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; John Wiley & Sons Inc.: New York, NY, USA, 1977. [Google Scholar]

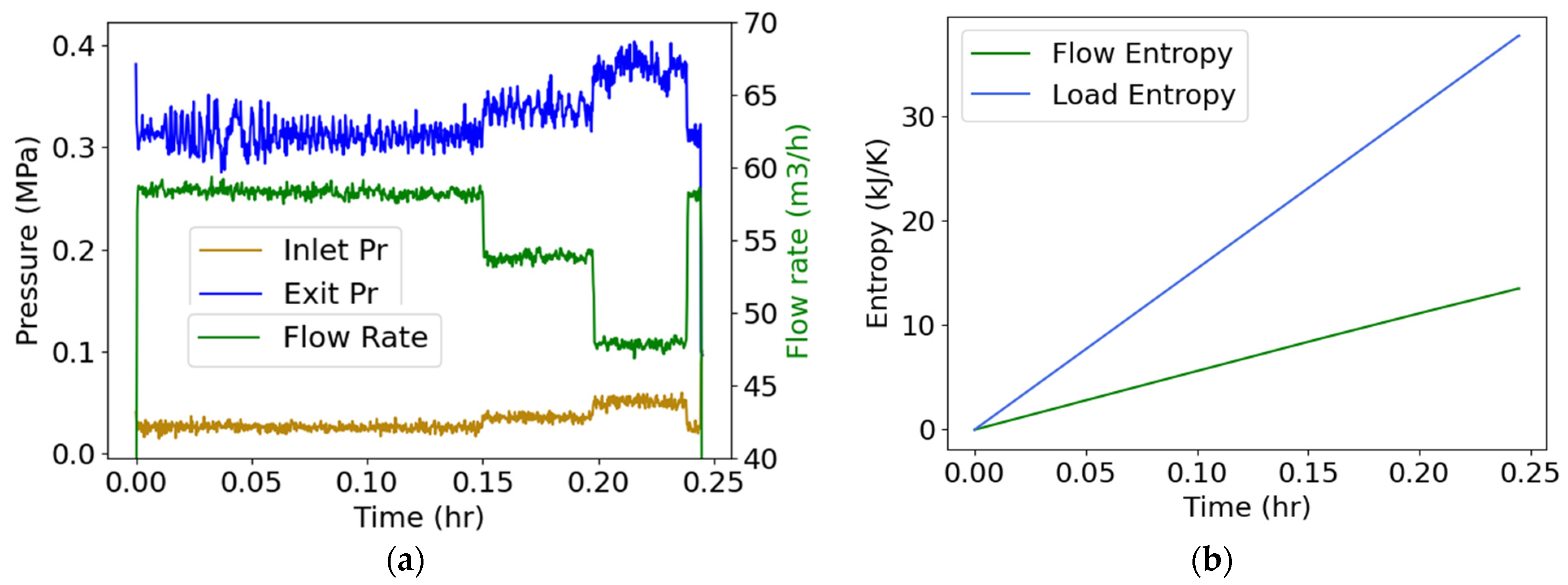
| Category | Phenomenological Entropy Generation | Example |
|---|---|---|
| Open Internal Energy | Equation (10a) (for a non-reacting system) | Compressor (with temperature rise and boundary work): |
(Rate form in Equation (19)) | ||
| Thermal Enthalpy | Equation (10b) (for a closed system) | Combustion systems without boundary work: |
| Boundary-Loaded Helmholtz potential | Equation (10c) | Mechanical loading, e.g., shearing without oxidation: |
| Reactive/Energy Gibbs potential | Equation (10d) | Electrochemical energy systems, e.g., batteries: |
| Via Gibbs-Helmholtz coupling: | ||
| Via Gibbs-Duhem formulation: | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osara, J.A.; Bryant, M.D. Methods to Calculate Entropy Generation. Entropy 2024, 26, 237. https://doi.org/10.3390/e26030237
Osara JA, Bryant MD. Methods to Calculate Entropy Generation. Entropy. 2024; 26(3):237. https://doi.org/10.3390/e26030237
Chicago/Turabian StyleOsara, Jude A., and Michael D. Bryant. 2024. "Methods to Calculate Entropy Generation" Entropy 26, no. 3: 237. https://doi.org/10.3390/e26030237
APA StyleOsara, J. A., & Bryant, M. D. (2024). Methods to Calculate Entropy Generation. Entropy, 26(3), 237. https://doi.org/10.3390/e26030237