Thermodynamic Derivation of the Reciprocal Relation of Thermoelectricity
Abstract
1. Introduction
2. Reciprocal Relations in Equilibrium Thermodynamics
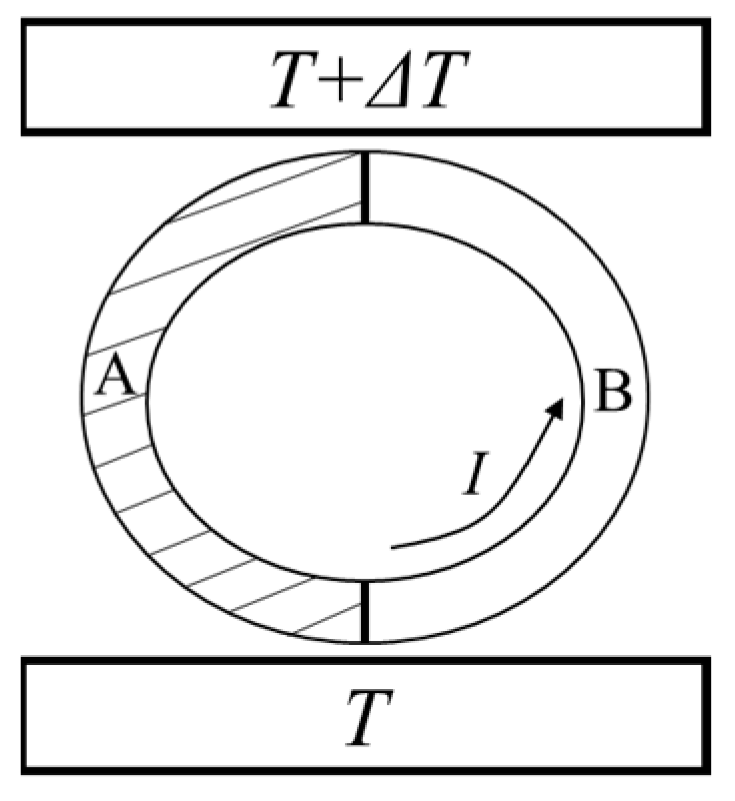
3. Thermodynamic Derivation of the Kelvin Relation
4. Thermodynamic Derivation of Onsager Reciprocal Relations for Transient Processes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seebeck, T.J. Ueber den Magnetismus der Galvenischen Kette; Technical Report; Royal Prussian Academy of Science: Berlin, Germany, 1821. [Google Scholar]
- Peltier, J.C.A. Nouvelles experiences sur la caloricite des courants electrique. Ann. Chim. Phys. 1834, 56, 371–386. [Google Scholar]
- Thomson, W. On the Mechanical Theory of Thermo-electric Currents. Trans. R. Soc. Edinb. Earth Sci. 1851, 3, 91–98. [Google Scholar] [CrossRef]
- Miller, D.G. Thermodynamics of irreversible processes. The experimental verification of the Onsager reciprocal relations. Chem. Rev. 1960, 60, 15. [Google Scholar] [CrossRef]
- Apertet, Y.; Goupil, C. On the fundamental aspect of the first Kelvin’s relation in thermoelectricity. Int. J. Therm. Sci. 2016, 104, 225. [Google Scholar] [CrossRef][Green Version]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 22265. [Google Scholar] [CrossRef]
- Miller, D.G. The origins of Onsager’s key role in the development of linear irreversible thermodynamics. J. Stat. Phys. 1995, 78, 563–573. [Google Scholar] [CrossRef]
- Callen, H.B. The Application of Onsager’s Reciprocal Relations to Thermoelectric, Thermomagnetic, and Galvanomagnetic Effects. Phys. Rev. 1948, 73, 1349–1358. [Google Scholar] [CrossRef]
- Brostow, W.; Granowski, G.; Hnatchuk, N.; Sharp, J.; White, J.B. Thermoelectric phenomena. J. Mater. Educ. 2014, 36, 175–185. [Google Scholar]
- Callen, H.B. On the Theory of Irreversible Processes. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1947. [Google Scholar]
- Vining, C.B. The thermoelectric process. MRS Online Proc. Libr. (OPL) 1997, 478, 3–13. [Google Scholar] [CrossRef]
- Goupil, C.; Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G.J. Thermodynamics of thermoelectric phenomena and applications. Entropy 2011, 13, 1481. [Google Scholar] [CrossRef]
- Hua, Y.C.; Xue, T.W.; Guo, Z.Y. Reversible reciprocal relation of thermoelectricity. Phys. Rev. E 2021, 103, 012107. [Google Scholar] [CrossRef] [PubMed]
- Domenicali, C.A. Irreversible thermodynamics of thermoelectricity. Rev. Mod. Phys. 1954, 26, 237. [Google Scholar] [CrossRef]
- Thomson, W. On the dynamical theory of heat—Part VI. Thermoelectric currents. Lon. Edinb. Dubl. Phil. Mag. J. Sci. 1856, 11, 379–388. [Google Scholar] [CrossRef]
- Lippmann, G. Über die Analogie zwischen absoluter Temperatur und elektrischem Potential. Ann. Der Phys. 1907, 328, 994–996. [Google Scholar] [CrossRef]
- Xue, T.W.; Guo, Z.Y. Thermoelectric Cycle and the Second Law of Thermodynamics. Entropy 2023, 25, 155. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M. Simulation of Thermoelectric Devices; Technischen Universität Wien: Vienna, Austria, 2007. [Google Scholar]
- Goddard, J.D. Thermoelectricity: Thomson vs. Onsager, with advice from Maxwell. Phys. Fluids 2021, 33, 127123. [Google Scholar] [CrossRef]
- De Groot, S.R. Thermodynamics of Irreversible Processes; North-Holland: Amsterdam, The Netherlands, 1951. [Google Scholar]
- Dong, Y. Clarification of Onsager reciprocal relations based on thermomass theory. Phys. Rev. E 2012, 86, 062101. [Google Scholar] [CrossRef] [PubMed]
- Brenner, H. Onsager reciprocity as a consequence of Maxwell reciprocity for “equidiffuse” fluids. Int. J. Eng. Sci. 2010, 48, 1043–1065. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, T.-W.; Guo, Z.-Y. Thermodynamic Derivation of the Reciprocal Relation of Thermoelectricity. Entropy 2024, 26, 202. https://doi.org/10.3390/e26030202
Xue T-W, Guo Z-Y. Thermodynamic Derivation of the Reciprocal Relation of Thermoelectricity. Entropy. 2024; 26(3):202. https://doi.org/10.3390/e26030202
Chicago/Turabian StyleXue, Ti-Wei, and Zeng-Yuan Guo. 2024. "Thermodynamic Derivation of the Reciprocal Relation of Thermoelectricity" Entropy 26, no. 3: 202. https://doi.org/10.3390/e26030202
APA StyleXue, T.-W., & Guo, Z.-Y. (2024). Thermodynamic Derivation of the Reciprocal Relation of Thermoelectricity. Entropy, 26(3), 202. https://doi.org/10.3390/e26030202







