Sample Augmentation Using Enhanced Auxiliary Classifier Generative Adversarial Network by Transformer for Railway Freight Train Wheelset Bearing Fault Diagnosis
Abstract
1. Introduction
- (1)
- To eliminate the cumbersome loop structure of convolutional layers; transformer networks replace CNNs in the generator and discriminator.
- (2)
- To avoid vanishing gradients, exploding gradients, and overfitting issues, the Wasserstein distance is introduced into the new cross-entropy loss function, ensuring stability.
- (3)
- To prevent the overlap of discrimination and classification tasks in the ACGAN discriminator, the classifier is separated from the discriminator as an independent component.
2. Basic Theory
2.1. Auxiliary Classifier Generative Adversarial Networks
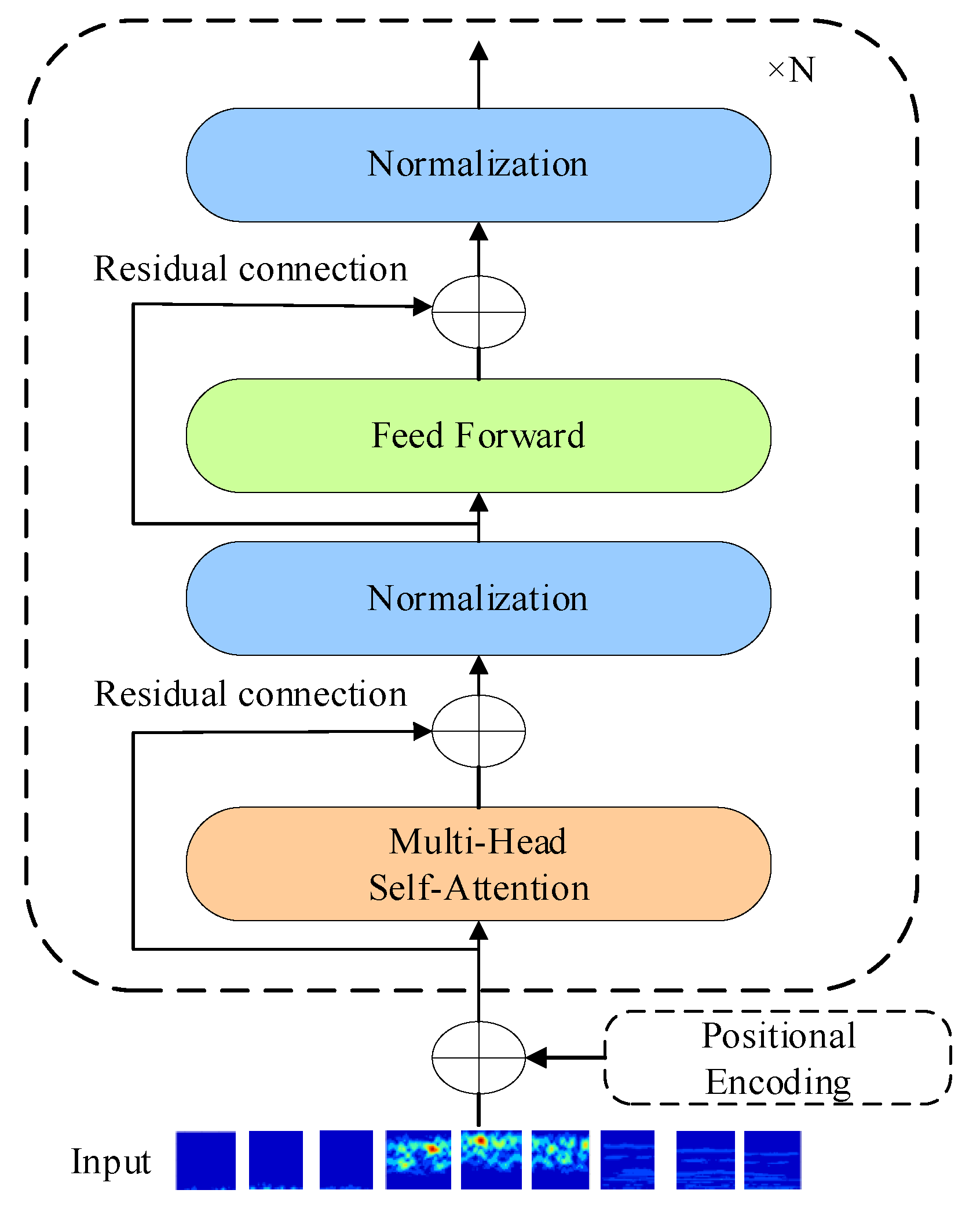
2.2. Transformer Encoder
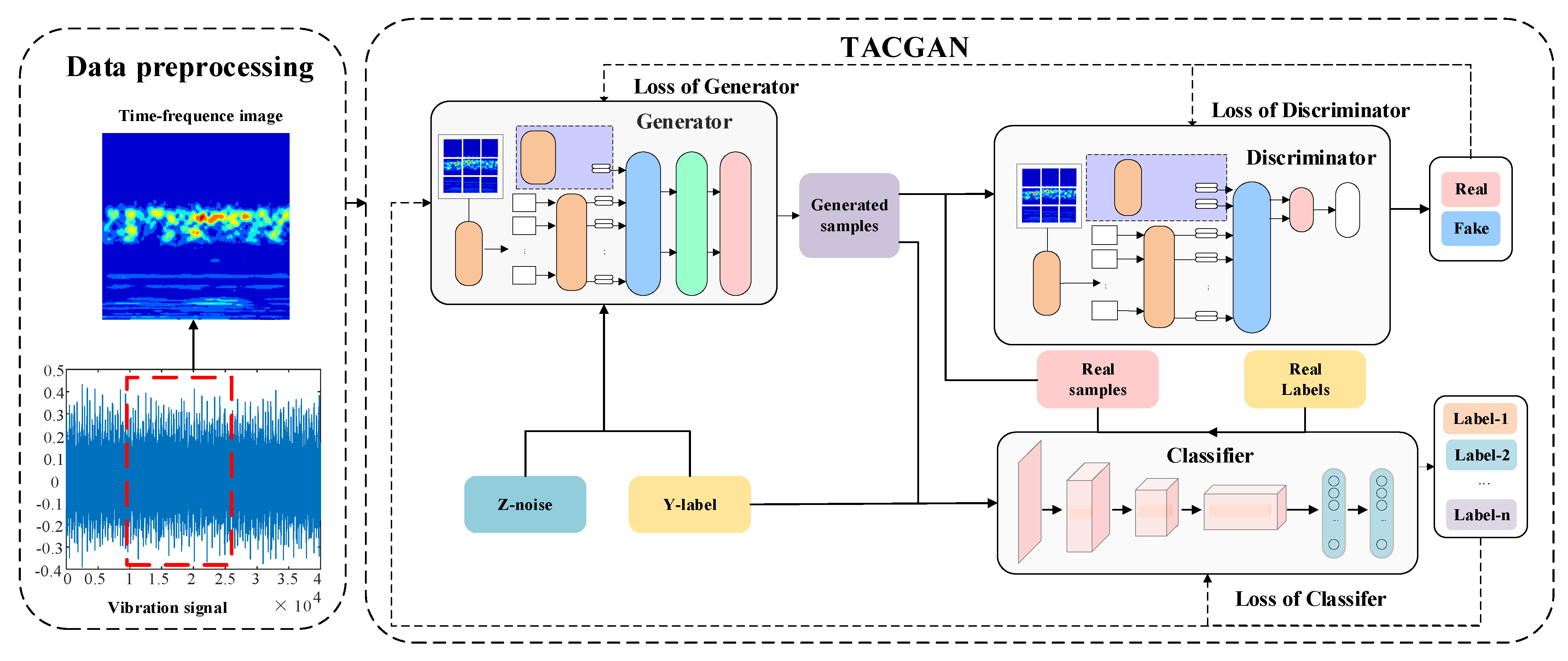
3. Proposed Framework
3.1. TACGAN Generator
3.2. TACGAN Discriminator
3.3. TACGAN Classifier
3.4. Loss Function of TACGAN
| Algorithm 1: The training algorithm of the TACGAN |
| Wheelset bearing fault diagnosis with the proposed model |
| the Inputed labeled samples X = {(xj, aj)}; |
| 1: Initialize model parameters: |
| 2: For j = 1 to N do: |
| 3: For i = 1 to 5 do: |
| 4: Extract a batch real datas{x}, Construct the noise with the label information{a, y}; |
| 5: Calculate G(a, cf); |
| 6: LD = Ereal[D(x) − Efalse[D(G(a, cf))]]; |
| 7: End For |
| 8: Extract a batch real datas{x, y}, Construct the noise with the label information{a, y}; |
| 9: Calculate G(a, cf); |
| 10: LrC = Ereal[−logP(c = cr|x)]; LfC = Efalse[−logP(c = cr|x)]; |
| 11: LG = Efalse[D(G(a, cf))] + λLfC; |
| 12: θC←Adam(LC); |
| 13: θG←RMSProp(LG); |
| 14: End For |
4. Experimental Verification
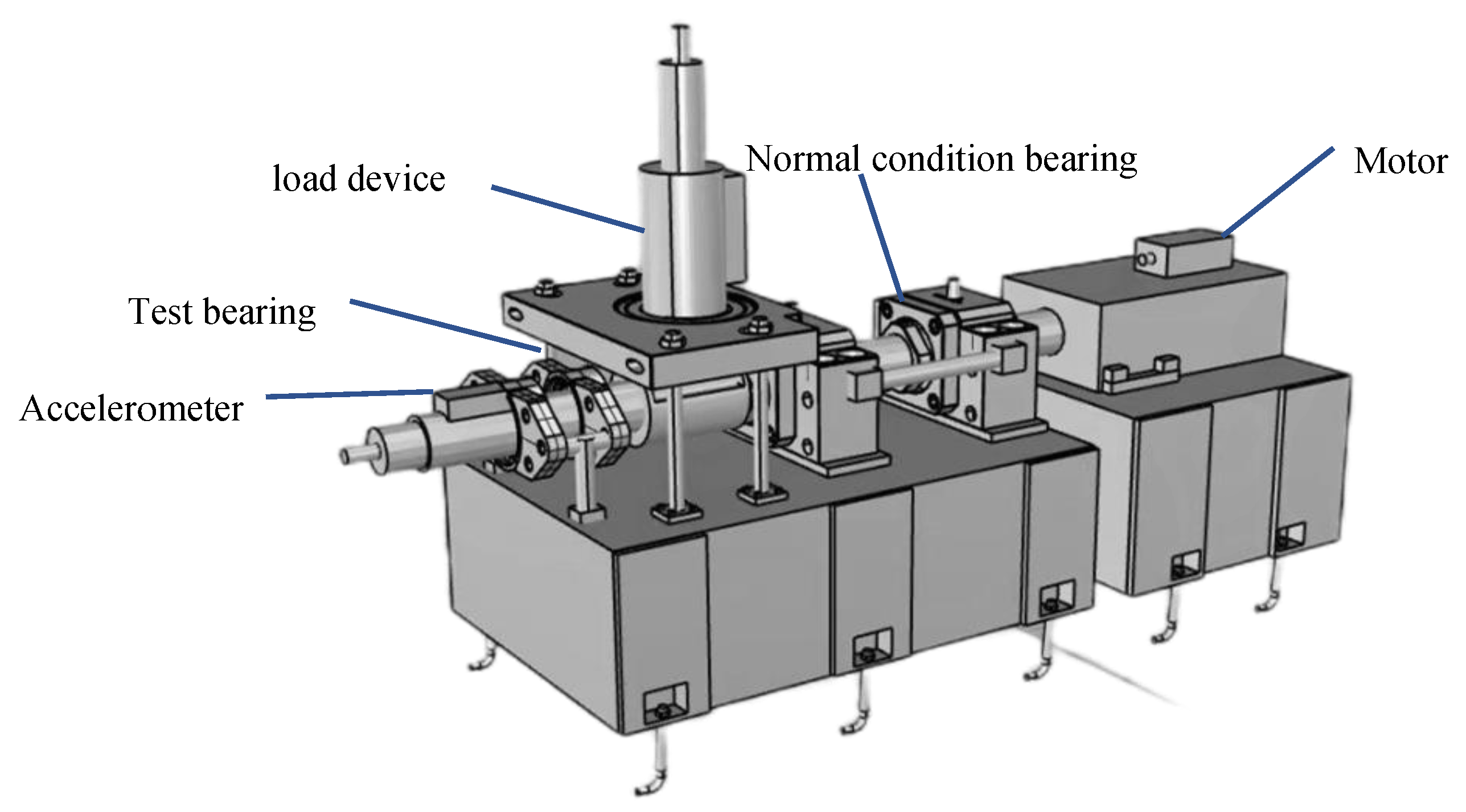
4.1. Datasets
4.2. Sample Generation and Fault Diagnosis
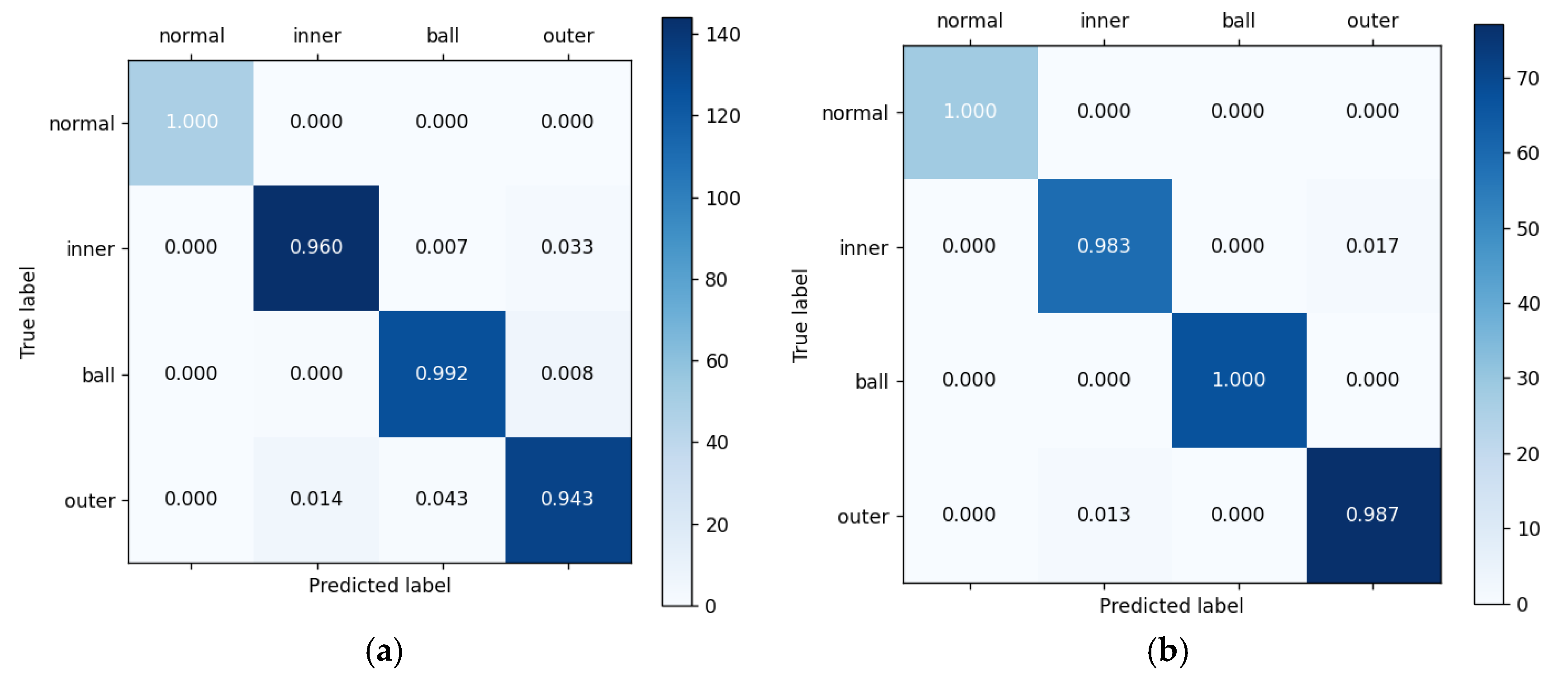
4.2.1. Performance of TACGAN
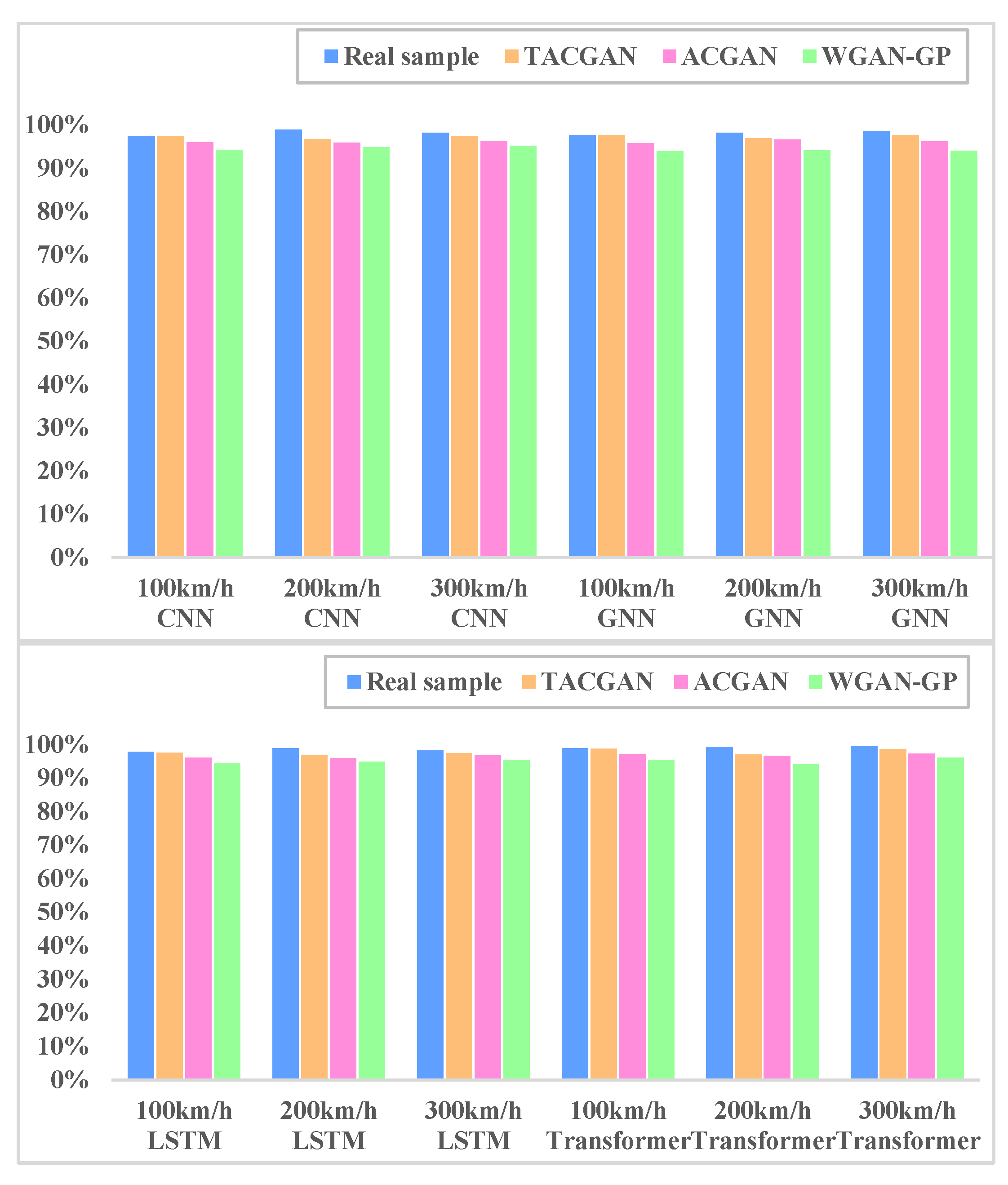
4.2.2. Comparison and Analysis of Sample Generation Effect
5. Conclusions
- (1)
- By employing a transformer network, the TACGAN bypasses the need for complex recursive structures. This approach allows for the direct extraction of both global and local features from input feature maps, thereby streamlining the model architecture and boosting computational efficiency.
- (2)
- The TACGAN effectively learns and replicates the distribution of real samples within a high-dimensional space. This results in generated samples that closely mirror the properties of actual data, which is particularly advantageous when addressing diverse and intricate fault types.
- (3)
- Testing has demonstrated that the TACGAN achieves an impressive 99% accuracy in augmenting wheelset bearing data. The fault samples produced by the TACGAN significantly enhance the dataset, improving the overall robustness and reliability of fault diagnosis systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, Z.; Li, X.; Liu, S.; Ma, Z. A recursive multi-head graph attention residual network for high-speed train wheelset bearing fault diagnosis. Meas. Sci. Technol. 2023, 34, 065108. [Google Scholar] [CrossRef]
- Fu, W.; Jiang, X.; Li, B. Rolling bearing fault diagnosis based on 2D time-frequency images and data augmentation technique. Meas. Sci. Technol. 2023, 34, 045005. [Google Scholar] [CrossRef]
- Xin, G.; Li, Z.; Jia, L. Fault diagnosis of wheelset bearings in high-speed trains using logarithmic short-time continuous wavelet transformand modified self-calibrated residual network. IEEE Trans. Ind. Inform. 2021, 18, 7285–7295. [Google Scholar] [CrossRef]
- Yang, S.; Gu, X.; Liu, Y. A general multi-objective optimized wavelet filter and its applications in fault diagnosis of wheelset bearings. Mech. Syst. Signal Process. 2020, 145, 106914. [Google Scholar] [CrossRef]
- Yi, C.; Li, Y.; Huo, X. A promising new tool for fault diagnosis of railway wheelset bearings: SSO-based Kurtogram. ISA Trans. 2022, 128, 498–512. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Fan, F.; Zhou, K. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X. Research on test bench bearing fault diagnosis of improved EEMD based on improved adaptive resonance technology. Measurement 2021, 185, 109986. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Online fault diagnosis for industrial processes with Bayesian network-based probabilistic ensemble learning strategy. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1922–1932. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J. Hierarchical discriminating sparse coding for weak fault feature extraction of rolling bearings. Reliab. Eng. Syst. Saf. 2019, 184, 41–54. [Google Scholar] [CrossRef]
- Wang, D.; Guo, Q.; Song, Y. Application of multiscale learning neural network based on CNN in bearing fault diagnosis. J. Signal Process. Syst. 2019, 91, 1205–1217. [Google Scholar] [CrossRef]
- An, Z.; Li, S.; Wang, J. A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network. ISA Trans. 2020, 100, 155–170. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Jiang, Q.; Shen, Y. Application of recurrent neural network to mechanical fault diagnosis: A review. J. Mech. Sci. Technol. 2022, 36, 527–542. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, T.; Huang, X. Fault diagnosis of rotating machinery based on recurrent neural networks. Measurement 2021, 171, 108774. [Google Scholar] [CrossRef]
- Pham, M.T.; Kim, J.M.; Kim, C.H. Rolling bearing fault diagnosis based on improved GAN and 2-D representation of acoustic emission signals. IEEE Access 2022, 10, 78056–78069. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H.; Wu, Z. Adaptive variational autoencoding generative adversarial networks for rolling bearing fault diagnosis. Adv. Eng. Inform. 2023, 56, 102027. [Google Scholar] [CrossRef]
- An, Y.; Zhang, K.; Liu, Q. Rolling bearing fault diagnosis method base on periodic sparse attention and LSTM. IEEE Sens. J. 2022, 22, 12044–12053. [Google Scholar] [CrossRef]
- Fu, G.; Wei, Q.; Yang, Y. Bearing fault diagnosis based on CNN-BiLSTM and residual module. Meas. Sci. Technol. 2023, 34, 125050. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Broad convolutional neural network based industrial process fault diagnosis with incremental learning capability. IEEE Trans. Ind. Electron. 2019, 67, 5081–5091. [Google Scholar] [CrossRef]
- Daldal, N.; Cömert, Z.; Polat, K. Automatic determination of digital modulation types with different noises using convolutional neural network based on time–frequency information. Appl. Soft Comput. 2020, 86, 105834. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Xie, J. Conditional GAN and 2-D CNN for bearing fault diagnosis with small samples. IEEE Trans. Instrum. Meas. 2021, 70, 3525712. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, J.; Du, W. Bearing fault diagnosis method based on adaptive maximum cyclostationarity blind deconvolution. Mech. Syst. Signal Process. 2022, 162, 108018. [Google Scholar] [CrossRef]
- Xiong, J.; Liu, M.; Li, C. A bearing Fault Diagnosis Method Based on Improved Mutual Dimensionless and Deep Learning. IEEE Sens. J. 2023, 23, 18338–18348. [Google Scholar] [CrossRef]
- Song, X.; Cong, Y.; Song, Y. A bearing fault diagnosis model based on CNN with wide convolution kernels. J. Ambient. Intell. Humaniz. Comput. 2021, 13, 4041–4056. [Google Scholar] [CrossRef]
- Erol, B.; Gurbuz, S.Z.; Amin, M.G. Motion classification using kinematically sifted acgan-synthesized radar micro-doppler signatures. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3197–3213. [Google Scholar] [CrossRef]
- Li, W.; Zhong, X.; Shao, H. Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inform. 2022, 52, 101552. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Q.; Gu, Y. Remaining useful life prediction of bearings based on self-attention mechanism, multi-scale dilated causal convolution, and temporal convolution network. Meas. Sci. Technol. 2023, 34, 045107. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, H.; Wang, C. MW-ACGAN: Generating multiscale high-resolution SAR images for ship detection. Sensors 2020, 20, 6673. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, N.; Wang, Z. CFFsBD: A candidate fault frequencies-based blind deconvolution for rolling element bearings fault feature enhancement. IEEE Trans. Instrum. Meas. 2023, 72, 3506412. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, Z.; Ping, S. TRA-ACGAN: A motor bearing fault diagnosis model based on an auxiliary classifier generative adversarial network and transformer network. ISA Trans. 2024, 149, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Dixit, S.; Verma, N.K.; Ghosh, A.K. Intelligent fault diagnosis of rotary machines: Conditional auxiliary classifier GAN coupled with meta learning using limited data. IEEE Trans. Instrum. Meas. 2021, 70, 3517811. [Google Scholar] [CrossRef]
- Du, X.; Jia, L.; Haq, I.U. Fault diagnosis based on SPBO-SDAE and transformer neural network for rotating machinery. Measurement 2022, 188, 110545. [Google Scholar] [CrossRef]
- Ding, Y.; Jia, M.; Miao, Q. A novel time–frequency Transformer based on self–attention mechanism and its application in fault diagnosis of rolling bearings. Mech. Syst. Signal Process. 2022, 168, 108616. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Z.; Zhang, J. A novel fault diagnosis method of rolling bearings combining convolutional neural network and transformer. Electronics 2023, 12, 1838. [Google Scholar] [CrossRef]
- Wu, H.; Triebe, M.J.; Sutherland, J.W. A transformer-based approach for novel fault detection and fault classification/diagnosis in manufacturing: A rotary system application. J. Manuf. Syst. 2023, 67, 439–452. [Google Scholar] [CrossRef]
- Jin, Y.; Hou, L.; Chen, Y. A time series transformer based method for the rotating machinery fault diagnosis. Neurocomputing 2022, 494, 379–395. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Xing, Z. Transformer fault diagnosis based on improved deep coupled dense convolutional neural network. Electr. Power Syst. Res. 2022, 209, 107969. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, J.; Chen, Z. Diagnosisformer: An efficient rolling bearing fault diagnosis method based on improved Transformer. Eng. Appl. Artif. Intell. 2023, 124, 106507. [Google Scholar] [CrossRef]
- Fang, H.; An, J.; Liu, H. A lightweight transformer with strong robustness application in portable bearing fault diagnosis. IEEE Sens. J. 2023, 23, 9649–9657. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, X.; Gao, X. ICoT-GAN: Integrated convolutional transformer GAN for rolling bearings fault diagnosis under limited data condition. IEEE Trans. Instrum. Meas. 2023, 72, 3515114. [Google Scholar] [CrossRef]
- Ma, Z.; Yuan, Z.; Li, X. Multirotational Speed Data Augmentation and Data Repair of High-speed Train Wheelset Bearings using Graph Speed Classifier GAN. IEEE Sens. J. 2023, 23, 30984–30997. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, D. An Auxiliary Classifier Generative Adversarial Network based Fault Diagnosis for Analog Circuit. IEEE Access 2023, 11, 86824–86833. [Google Scholar] [CrossRef]
- Hu, H.; Ma, X.; Shang, Y. A novel method for transformer fault diagnosis based on refined deep residual shrinkage network. IET Electr. Power Appl. 2022, 16, 206–223. [Google Scholar] [CrossRef]
- Liang, P.; Yu, Z.; Wang, B. Fault transfer diagnosis of rolling bearings across multiple working conditions via subdomain adaptation and improved vision transformer network. Adv. Eng. Inform. 2023, 57, 102075. [Google Scholar] [CrossRef]
- Tang, X.; Xu, Z.; Wang, Z. A novel fault diagnosis method of rolling bearing based on integrated vision transformer model. Sensors 2022, 22, 3878. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Liu, J.; Chen, H. Intelligent diagnosis using continuous wavelet transform and gauss convolutional deep belief network. IEEE Trans. Reliab. 2022, 72, 692–702. [Google Scholar] [CrossRef]
- Miao, Z.; Xia, Y.; Zhou, F. Fault diagnosis of wheeled robot based on prior knowledge and spatial-temporal difference graph convolutional network. IEEE Trans. Ind. Inform. 2022, 19, 7055–7065. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, W.; Shao, M. Separation and Extraction of Compound-Fault Signal Based on Multi-Constraint Non-Negative Matrix Factorization. Entropy 2024, 26, 583. [Google Scholar] [CrossRef]
- Mao, Y.; Xin, J.; Zang, L. Fault Diagnosis Method for Rolling Bearings Based on Grey Relation Degree. Entropy 2024, 26, 222. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Wang, W.; Kong, D. Fault diagnosis of rotating machinery using kernel neighborhood preserving embedding and a modified sparse bayesian classification model. Entropy 2023, 25, 1549. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Khatibi, M.M.; Ashory, M.R. Refined composite multiscale fuzzy dispersion entropy and its applications to bearing fault diagnosis. Entropy 2023, 25, 1494. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Ren, Z. A novel weak fault diagnosis method for rolling bearings based on LSTM considering quasi-periodicity. Knowl.-Based Syst. 2021, 231, 107413. [Google Scholar] [CrossRef]









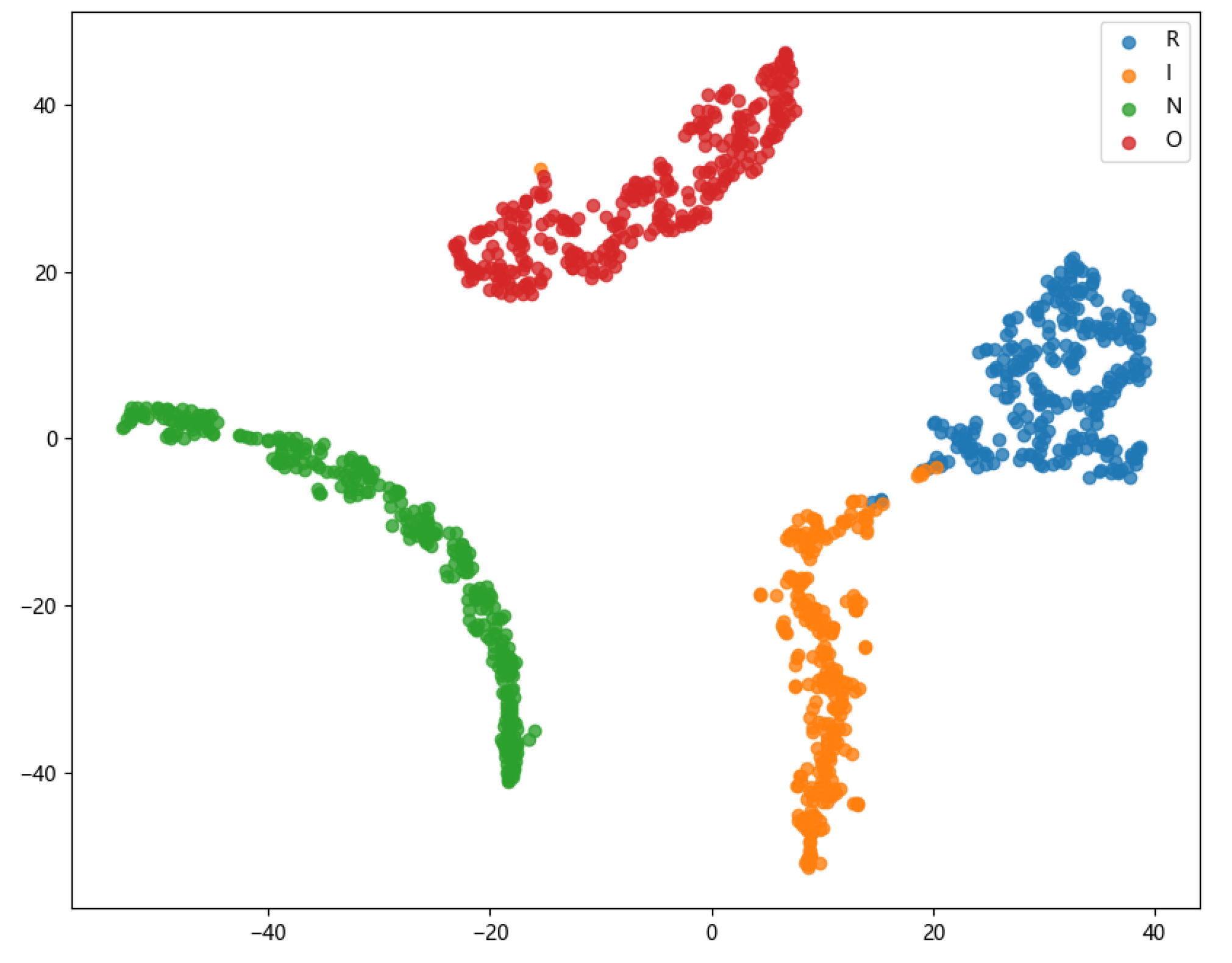

| Parameters | Value |
|---|---|
| Encoder Stacking Depth, N | 5 |
| Number of MSA Heads, h | 4 |
| Hidden Dimension of MLP, dMLP | 256 |
| Embedding Dimension, d | 64 |
| Batch Size | 32 |
| Token Sequence Length, G | 65 |
| Token Sequence Length, D | 66 |
| Networks | Layers | Parameter Setting | Operation/Activation |
|---|---|---|---|
| Classifier | Conv2D | 3 × 3 × 32 | BN + pooling/ReLu |
| Conv2D | 3 × 3 × 64 | BN + pooling/ReLu | |
| Conv2D | 3 × 3 × 128 | BN + pooling/ReLu | |
| Conv2D | 3 × 3 × 256 | BN + pooling/ReLu | |
| Dense | 256 | None/ReLu | |
| Dense | 128 | None/ReLu | |
| Dense | Class number | None/Softmax |
| Model Number | Pitch Diameter D/mm | Roller Diameter D/mm | Contact Angle φ/° | Number of Rolling Elements |
|---|---|---|---|---|
| 197,726 | 176.29 | 24.76 | 8.83 | 20 |
| Fault Type | Speed Condition/km/h | Sample Size |
|---|---|---|
| N | 100/200/300 | 2000/2000/2000 |
| I | 100/200/300 | 2000/2000/2000 |
| O | 100/200/300 | 2000/2000/2000 |
| R | 100/200/300 | 2000/2000/2000 |
| Model | Accuracy (Real Samples) | Accuracy (TACGAN) | Accuracy (ACGAN) | Accuracy (WGAN-GP) |
|---|---|---|---|---|
| CNN | 97.46% | 97.33 | 97.06 | 97.25 |
| GNN | 97.72% | 97.68% | 95.84% | 93.93% |
| LSTM | 97.82% | 97.56% | 96.12% | 94.38% |
| Transformer | 98.86% | 98.83% | 97.13% | 95.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Li, J.; Yuan, Z.; Mu, T.; Ma, Z.; Liu, S. Sample Augmentation Using Enhanced Auxiliary Classifier Generative Adversarial Network by Transformer for Railway Freight Train Wheelset Bearing Fault Diagnosis. Entropy 2024, 26, 1113. https://doi.org/10.3390/e26121113
Zhao J, Li J, Yuan Z, Mu T, Ma Z, Liu S. Sample Augmentation Using Enhanced Auxiliary Classifier Generative Adversarial Network by Transformer for Railway Freight Train Wheelset Bearing Fault Diagnosis. Entropy. 2024; 26(12):1113. https://doi.org/10.3390/e26121113
Chicago/Turabian StyleZhao, Jing, Junfeng Li, Zonghao Yuan, Tianming Mu, Zengqiang Ma, and Suyan Liu. 2024. "Sample Augmentation Using Enhanced Auxiliary Classifier Generative Adversarial Network by Transformer for Railway Freight Train Wheelset Bearing Fault Diagnosis" Entropy 26, no. 12: 1113. https://doi.org/10.3390/e26121113
APA StyleZhao, J., Li, J., Yuan, Z., Mu, T., Ma, Z., & Liu, S. (2024). Sample Augmentation Using Enhanced Auxiliary Classifier Generative Adversarial Network by Transformer for Railway Freight Train Wheelset Bearing Fault Diagnosis. Entropy, 26(12), 1113. https://doi.org/10.3390/e26121113





