Tethered Balloon Cluster Deployments and Optimization for Emergency Communication Networks
Abstract
1. Introduction
2. Related Works
3. System Model and Problem Formulation
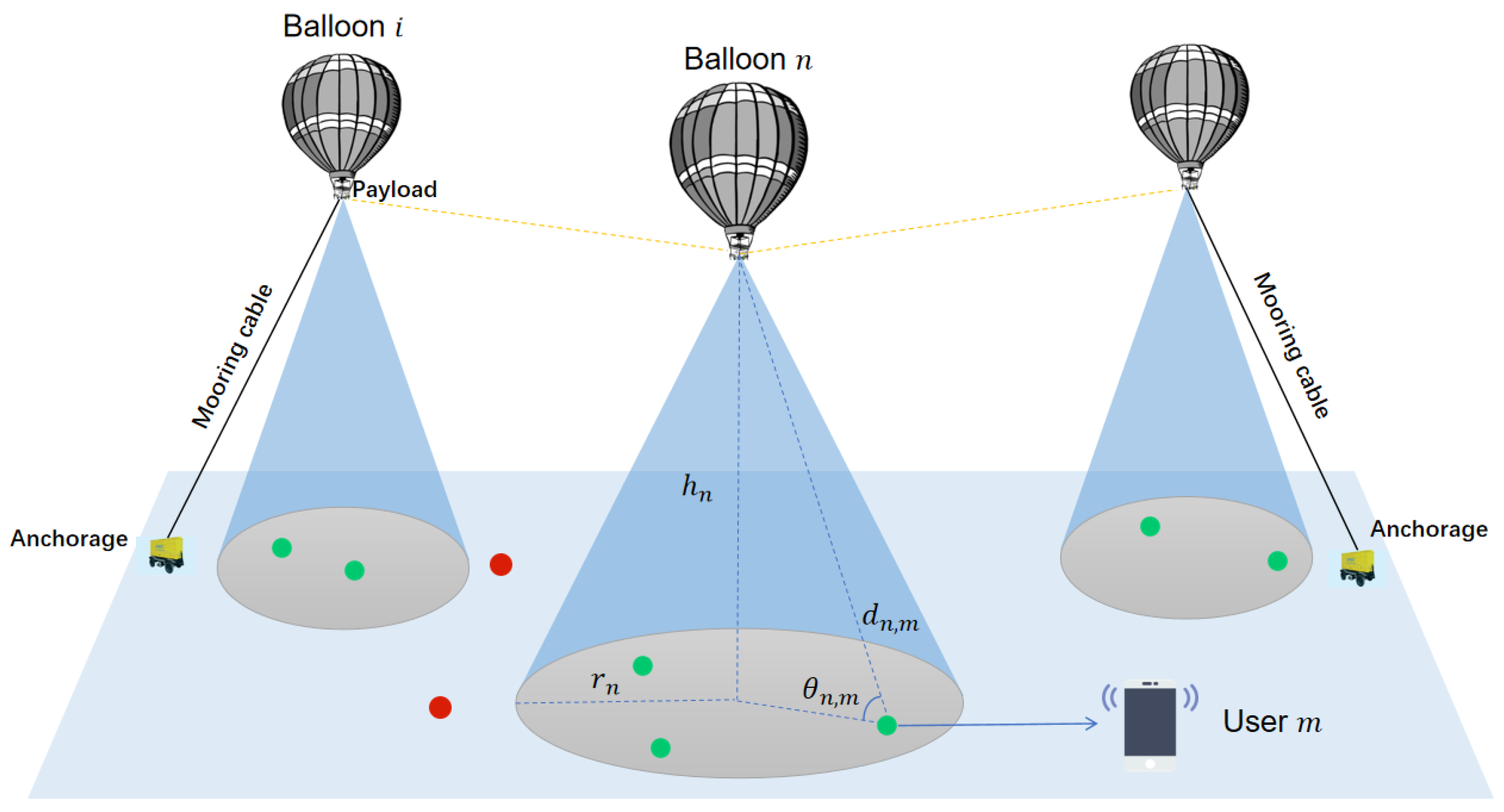
3.1. Geometrical Model
3.2. Mobility Model
3.3. Channel Model
3.3.1. Air-to-Air Channel Model
3.3.2. Air-to-Ground Channel Model
3.4. Objective Function
4. Methodology
| Algorithm 1: MOPSO for Balloon Deployment Optimization |
 |
| Algorithm 2: SA for balloons deployment locations |
 |
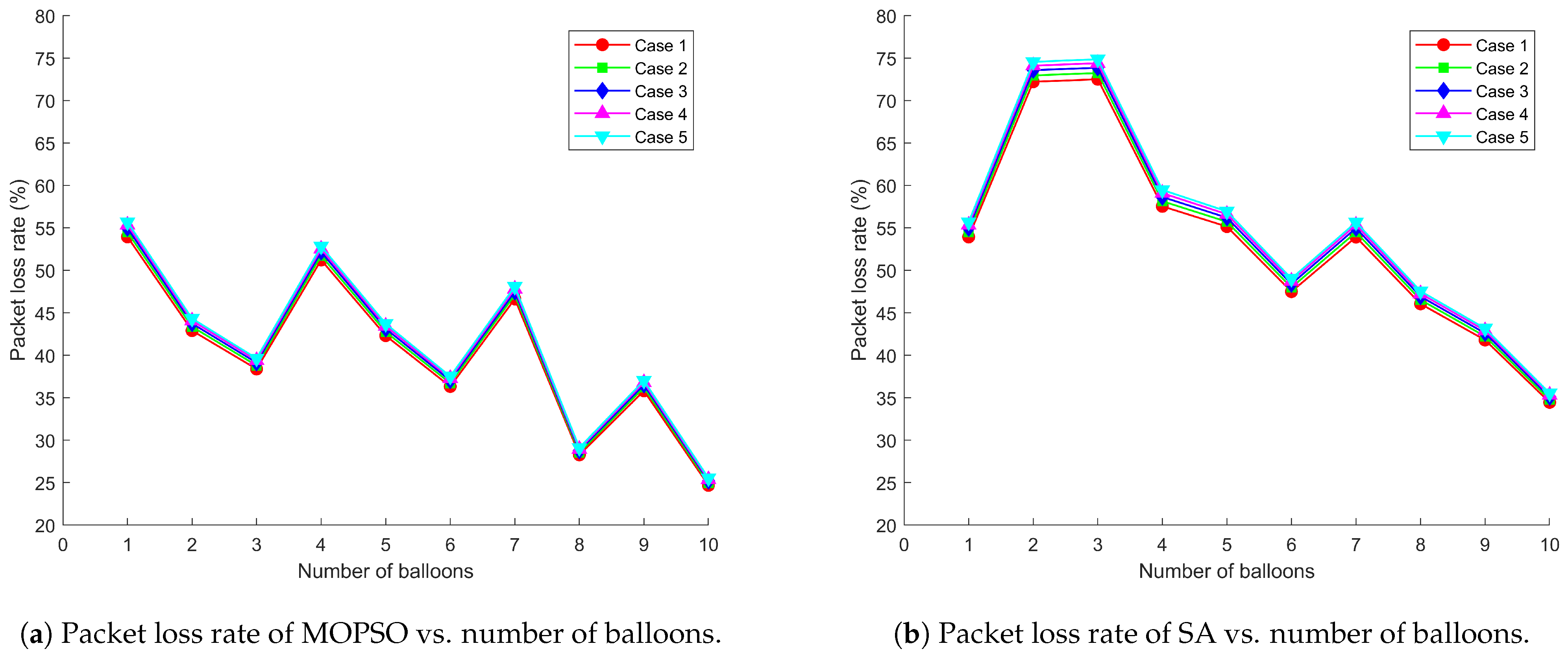
5. Simulation Validations and Discussion
5.1. Simulation Setup
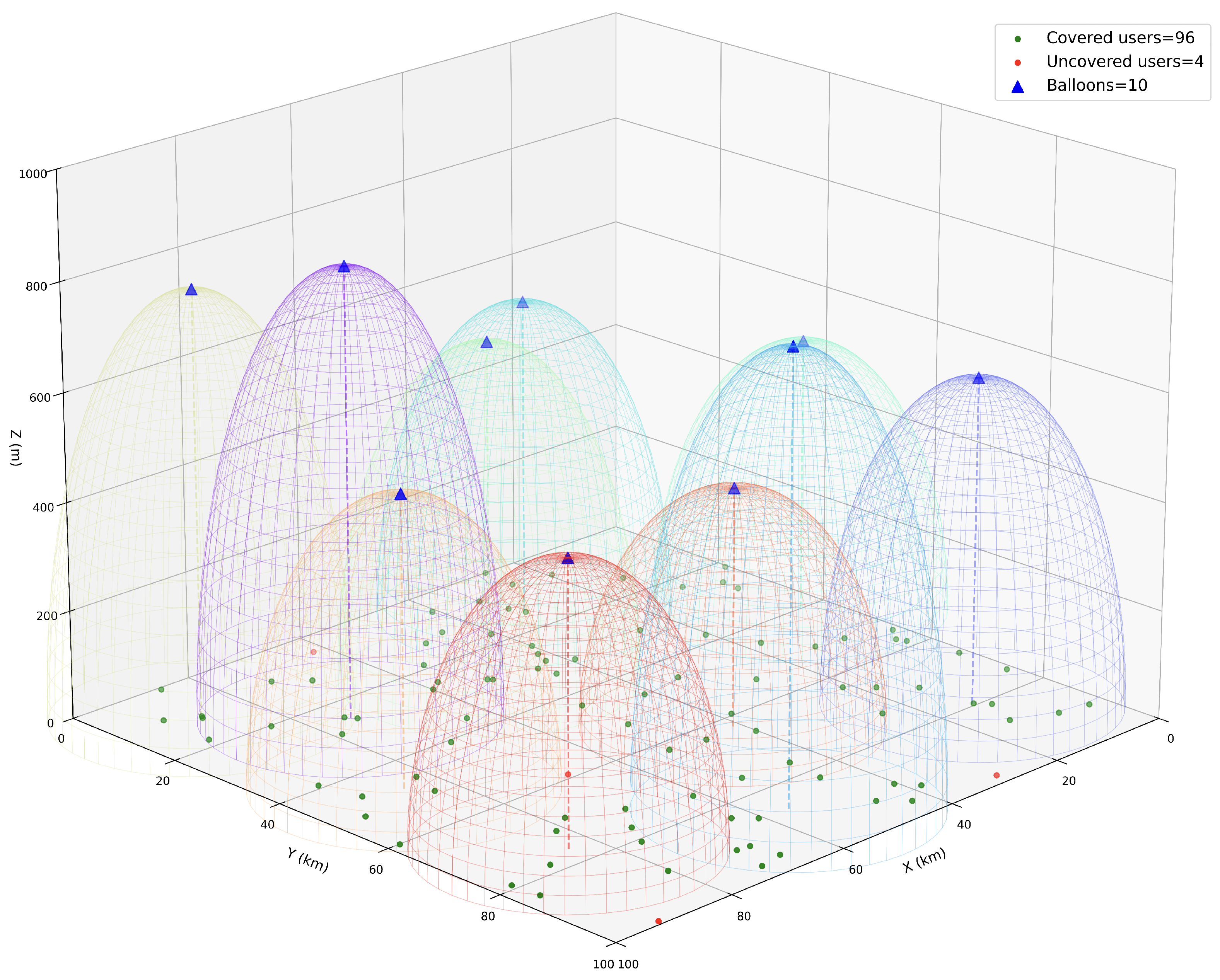
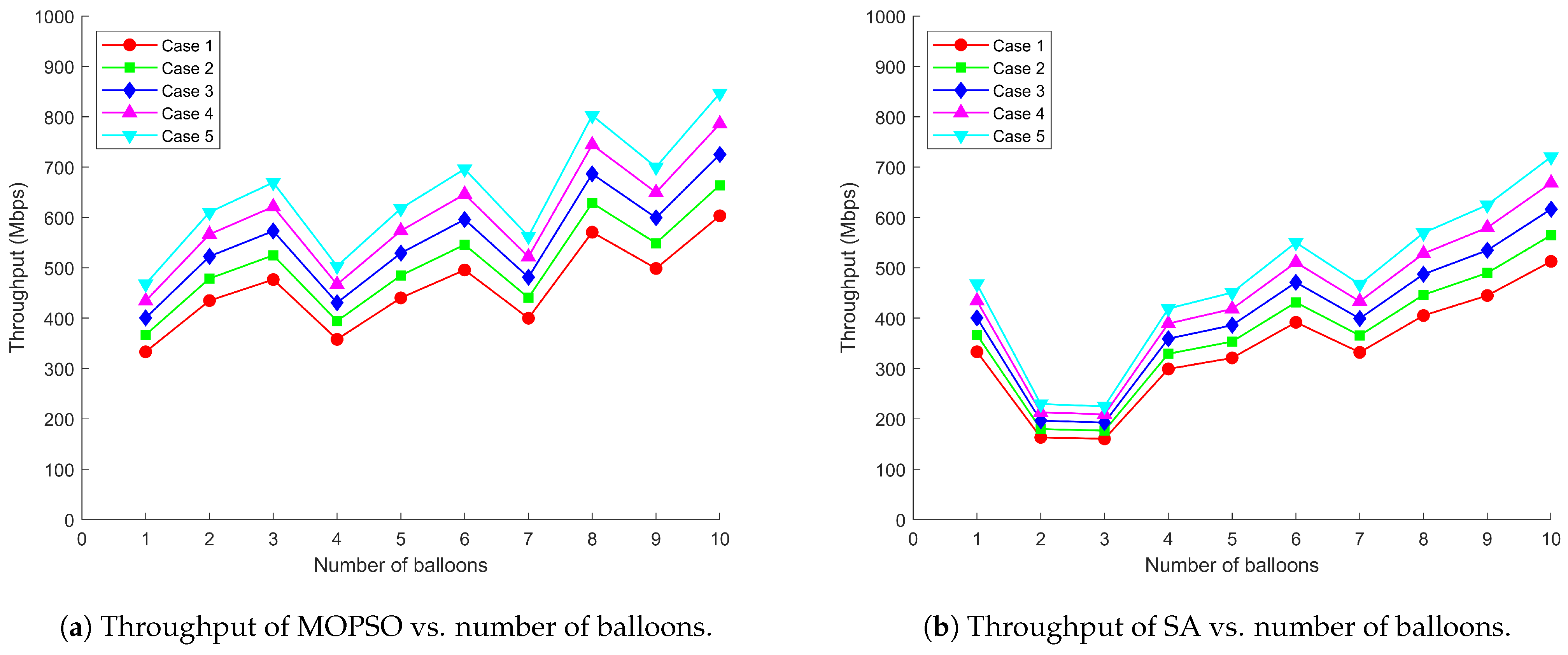
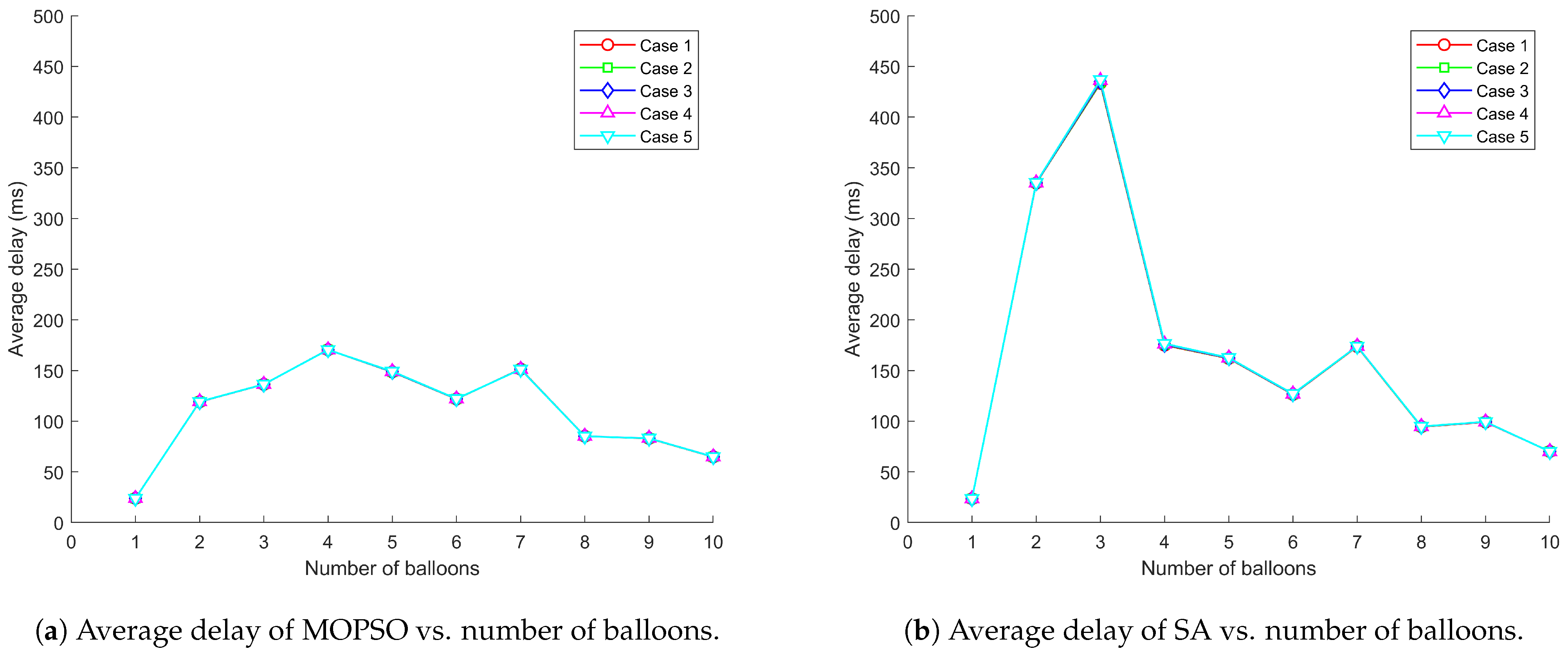
5.2. Simulation Results
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alsamhi, S.H.; Almalki, F.A.; Ma, O.; Ansari, M.S.; Angelides, M.C. Performance optimization of tethered balloon technology for public safety and emergency communications. Telecommun. Syst. 2020, 75, 235–244. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Yen, N.; Guo, S.; Cheng, Z. Big data analytics for emergency communication networks: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 1758–1778. [Google Scholar] [CrossRef]
- Jiang, S. Networking in oceans: A survey. ACM Comput. Surv. 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Ansari, M.S.; Ma, O.; Almalki, F.; Gupta, S.K. Tethered balloon technology in design solutions for rescue and relief team emergency communication services. Disaster Med. Public Health Prep. 2019, 13, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S. Best-Effort Networking Systems. In Proceedings of the Future of Information and Communication Conference, Berlin, Germany, 4–5 April 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 94–109. [Google Scholar] [CrossRef]
- Teixeira, F.B.; Campos, R.; Ricardo, M. Height optimization in aerial networks for enhanced broadband communications at sea. IEEE Access 2020, 8, 28311–28323. [Google Scholar] [CrossRef]
- Zhou, Y.; Tong, F.; Yang, X. Research on co-channel interference cancellation for underwater acoustic mimo communications. Remote Sens. 2022, 14, 5049. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Feng, J.; Jiang, X. Path Planning and Optimization of a UAV-Based Relay Communication System with Co-channel Interference. In Proceedings of the China Aeronautical Science and Technology Conference, Wuzhen, China, 6–8 September 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 241–252. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Ansari, M.S.; Rajput, N.S. Disaster coverage predication for the emerging tethered balloon technology: Capability for preparedness, detection, mitigation, and response. Disaster Med. Public Health Prep. 2018, 12, 222–231. [Google Scholar] [CrossRef] [PubMed]
- Sudheesh, P.; Mozaffari, M.; Magarini, M.; Saad, W.; Muthuchidambaranathan, P. Sum-rate analysis for high altitude platform (HAP) drones with tethered balloon relay. IEEE Commun. Lett. 2017, 22, 1240–1243. [Google Scholar] [CrossRef]
- Masroor, R.; Naeem, M.; Akram, T.; Almasoud, A.M.; Ejaz, W. Optimal stratified placement of balloons and UAVs to support users’ coverage. Internet Things 2023, 23, 100865. [Google Scholar] [CrossRef]
- Khaleefa, S.; Alsamhi, S.; Rajput, N. Tethered balloon technology for telecommunication, coverage and path loss. In Proceedings of the 2014 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, 1–2 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, H. Resource Allocation and Placement for Tethered Flying Platform-Aided IAB Network: Distributed DQN Approach. In Proceedings of the 2024 IEEE 21st Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 6–9 January 2024; pp. 1096–1097. [Google Scholar] [CrossRef]
- Alzidaneen, A.; Alsharoa, A.; Alouini, M.S. Resource and placement optimization for multiple UAVs using backhaul tethered balloons. IEEE Wirel. Commun. Lett. 2019, 9, 543–547. [Google Scholar] [CrossRef]
- Li, Y.; Xie, D.; Li, H.; He, W. Tethered balloon communication technology provides mobile communication network coverage for complex terrain environments. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 1513–1517. [Google Scholar] [CrossRef]
- Bushnaq, O.M.; Kishk, M.A.; Celik, A.; Alouini, M.S.; Al-Naffouri, T.Y. Optimal deployment of tethered drones for maximum cellular coverage in user clusters. IEEE Trans. Wirel. Commun. 2020, 20, 2092–2108. [Google Scholar] [CrossRef]
- Tuan, L.M.; Son, L.H.; Long, H.V.; Priya, L.R.; Soundar, K.R.; Robinson, Y.H.; Kumar, R. ITFDS: Channel-aware integrated time and frequency-based downlink LTE scheduling in MANET. Sensors 2020, 20, 3394. [Google Scholar] [CrossRef] [PubMed]
- Anand, M.; Sasikala, T. Efficient energy optimization in mobile ad hoc network (MANET) using better-quality AODV protocol. Clust. Comput. 2019, 22, 12681–12687. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Zhang, Y.; Huang, T.; Jiang, Y. Arithmetic optimization AOMDV routing protocol for FANETs. Sensors 2023, 23, 7550. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, L.; Zhu, L.; Zhang, T.; Xiao, Z.; Xia, X.G. 3D deployment of multiple UAV-mounted base stations for UAV communications. IEEE Trans. Commun. 2021, 69, 2473–2488. [Google Scholar] [CrossRef]
- Amponis, G.; Lagkas, T.; Argyriou, V.; Moscholios, I.; Zevgara, M.; Ouzounidis, S.; Sarigiannidis, P. Anchored self-similar 3D Gauss-Markov mobility model for ad hoc routing scenarios. IET Netw. 2023, 12, 250–259. [Google Scholar] [CrossRef]
- Korneev, D.; Leonov, A.; Litvinov, G. Estimation of mini-UAVs network parameters for search and rescue operation scenario with Gauss-Markov mobility model. In Proceedings of the 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO), Minsk, Belarus, 4–5 July 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Andryeyev, O.; Onus, U.; Casas, V.; Mitschele-Thiel, A. Experimental validation of air-to-ground propagation models for low-altitude platforms. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 29–31 May 2019; pp. 591–595. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, H.; Wu, W.; Wei, J. Deployment algorithms for UAV airborne networks toward on-demand coverage. IEEE J. Sel. Areas Commun. 2018, 36, 2015–2031. [Google Scholar] [CrossRef]
- Zhang, M.A.; Zhang, T. MOPSO Based Optimal Resources Scheduling for Multi-base Station Cooperative System. In Proceedings of the International Conference on Autonomous Unmanned Systems, Changsha, China, 24–26 September 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 2327–2335. [Google Scholar] [CrossRef]
- Jamalzadeh, M.; Maadani, M.; Mahdavi, M. EC-MOPSO: An edge computing-assisted hybrid cluster and MOPSO-based routing protocol for the Internet of Vehicles. Ann. Telecommun. 2022, 77, 491–503. [Google Scholar] [CrossRef]


| Reference | Model | Objective Function | Methodology |
|---|---|---|---|
| [1] | Not specified. | Throughput, delay. | Not specified. |
| [4] | Not specified. | Quality of service (QoS). | Not specified. |
| [9] | Okumura-Hata model. | Coverage. | Not specified. |
| [10] | Rician channel model. | Maximization of sum rate. | Interference alignment technique. |
| [11] | Multi-layer placement model. | Minimize the number of balloons and maximize user connections. | Greedy algorithm and optimal algorithm. |
| [12] | Hata model. | Path loss, coverage area, and received signal strength. | Not specified. |
| [13] | Markov decision problem (MDP). | Maximization of total rate. | Resource allocation and placement control joint optimization scheme. |
| [14] | Ricean fading, free-space path loss (FSPL), and air-to-ground (ATG) channel model. | Maximize end-to-end throughput. | Joint layout and resource allocation algorithm. |
| [15] | Longley–Rice model. | Coverage. | Triangulation method. |
| [16] | Rayleigh fading, Nakagami-m fading, FSPL, and ATG model. | Maximize coverage probability. | Stochastic geometry tools and user association policy. |
| Our contribution | Gauss–Markov mobility model, FSPL, and ATG channel model. | Maximize target coverage and system energy efficiency. | MOPSO (Swarm intelligence optimizing multiple objectives). |
| Symbol | Definition | Value |
|---|---|---|
| Simulation area | 100 km × 100 km | |
| Minimum and maximum heights of balloons | 400–1000 m | |
| N | Number of balloons | 1–10 |
| M | Number of users | 100 |
| SINR threshold | 8 dB | |
| Carrier frequency | 2.4 GHz | |
| B | Total bandwidth | 100 MHz |
| c | The speed of light | 3 × 108 m/s |
| Minimum and maximum transmit power | 60–100 W | |
| Additional path loss under LoS | 1 dB | |
| Additional path loss under NLoS | 20 dB | |
| a | Environmental impact factor | 9.6 |
| b | Environmental impact factor | 0.2 |
| Minimum distance between adjacent balloons | 500 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, M.; Feng, Z.; Jiang, S.; Zhou, W. Tethered Balloon Cluster Deployments and Optimization for Emergency Communication Networks. Entropy 2024, 26, 1071. https://doi.org/10.3390/e26121071
Guan M, Feng Z, Jiang S, Zhou W. Tethered Balloon Cluster Deployments and Optimization for Emergency Communication Networks. Entropy. 2024; 26(12):1071. https://doi.org/10.3390/e26121071
Chicago/Turabian StyleGuan, Mingyu, Zhongxiao Feng, Shengming Jiang, and Weiming Zhou. 2024. "Tethered Balloon Cluster Deployments and Optimization for Emergency Communication Networks" Entropy 26, no. 12: 1071. https://doi.org/10.3390/e26121071
APA StyleGuan, M., Feng, Z., Jiang, S., & Zhou, W. (2024). Tethered Balloon Cluster Deployments and Optimization for Emergency Communication Networks. Entropy, 26(12), 1071. https://doi.org/10.3390/e26121071






