Exploring the Trade-Off in the Variational Information Bottleneck for Regression with a Single Training Run
Abstract
1. Introduction
1.1. Information Bottleneck
1.2. Methods of IB
1.3. Effects and Applications of IB in DNNs
1.4. Efficient Exploration
1.5. Contributions and the Structure of This Paper
2. Related Work
2.1. Theory of IB
2.2. Variational Autoencoders
3. Analysis of VIB in Regression Tasks
3.1. Variational Information Bottleneck
3.2. Model Settings for Analysis
3.3. The Optimal Solution
- for all .
- for all .
- , where by orthogonal diagonalization and R is an arbitrary orthogonal matrix.
- .
4. Methods
4.1. FVIB-R
- ;
- ;
- , where by orthogonal diagonalization;
- .
4.2. Relation to FVIB
5. Experiments
5.1. Experimental Setup
5.1.1. Real Dataset
5.1.2. Synthetic Dataset
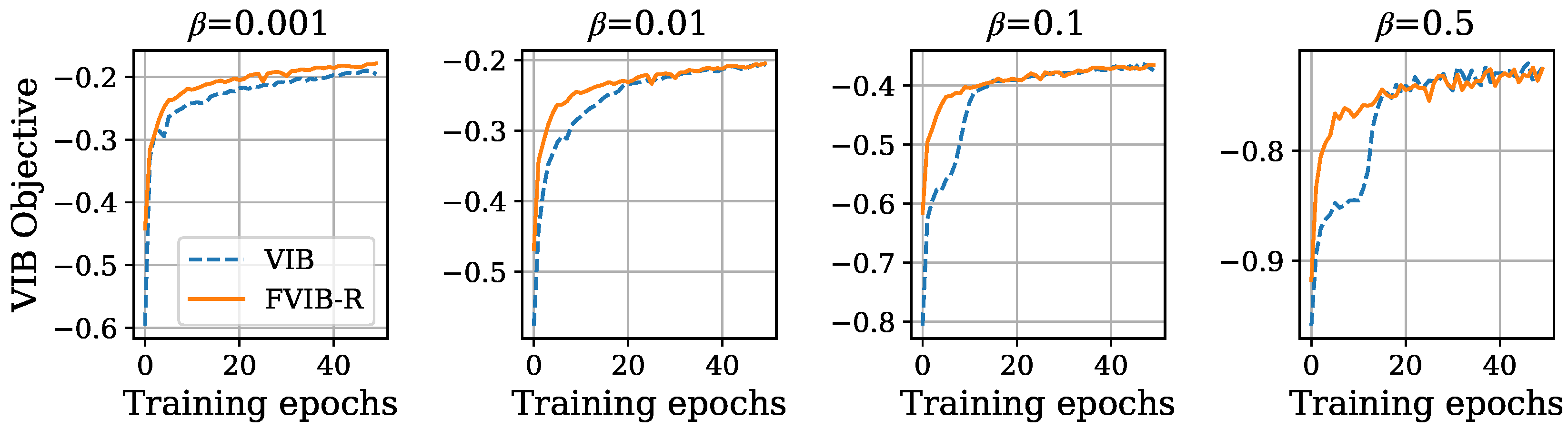
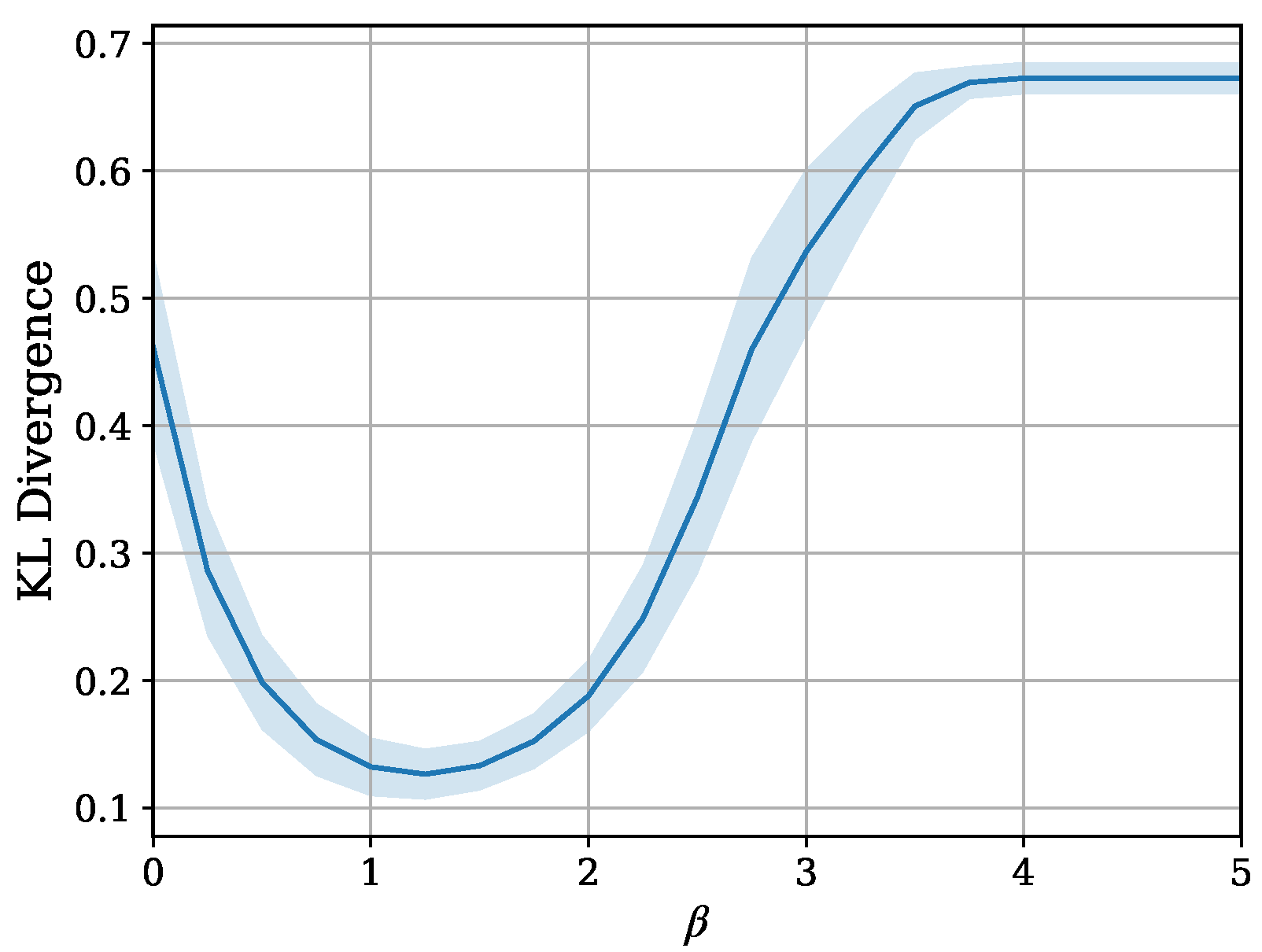
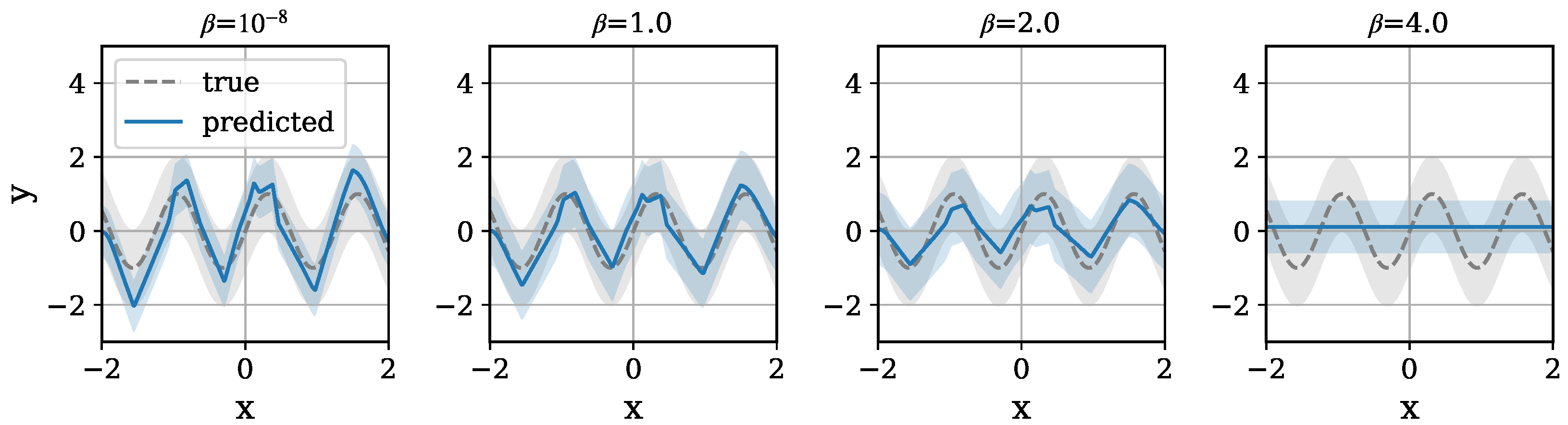
5.2. Results and Discussion
6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Lemma 1
Appendix A.2. Proof of Theorem 1
Appendix A.3. Proof of Theorem 2
References
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar]
- Lemaréchal, C. Lagrangian relaxation. In Computational Combinatorial Optimization: Optimal or Provably Near-Optimal Solutions; Springer: Berlin/Heidelberg, Germany, 2001; pp. 112–156. [Google Scholar]
- Gilad-Bachrach, R.; Navot, A.; Tishby, N. An information theoretic tradeoff between complexity and accuracy. In Proceedings of the Learning Theory and Kernel Machines: 16th Annual Conference on Learning Theory and 7th Kernel Workshop, COLT/Kernel 2003, Washington, DC, USA, 24–27 August 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 595–609. [Google Scholar]
- Chechik, G.; Globerson, A.; Tishby, N.; Weiss, Y. Information bottleneck for Gaussian variables. Adv. Neural Inf. Process. Syst. 2003, 16, 165–188. [Google Scholar]
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep variational information bottleneck. arXiv 2016, arXiv:1612.00410. [Google Scholar]
- Kolchinsky, A.; Tracey, B.D.; Wolpert, D.H. Nonlinear information bottleneck. Entropy 2019, 21, 1181. [Google Scholar] [CrossRef]
- Ma, W.D.K.; Lewis, J.; Kleijn, W.B. The HSIC bottleneck: Deep learning without back-propagation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5085–5092. [Google Scholar]
- Yu, X.; Yu, S.; Príncipe, J.C. Deep deterministic information bottleneck with matrix-based entropy functional. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; IEEE: lPiscataway, NJ, USA, 2021; pp. 3160–3164. [Google Scholar]
- Pan, Z.; Niu, L.; Zhang, J.; Zhang, L. Disentangled information bottleneck. In Proceedings of the AAAI Conference on Artificial Intelligence, virtual, 2–9 February 2021; Volume 35, pp. 9285–9293. [Google Scholar]
- Yu, S.; Yu, X.; Løkse, S.; Jenssen, R.; Principe, J.C. Cauchy-Schwarz Divergence Information Bottleneck for Regression. arXiv 2024, arXiv:2404.17951. [Google Scholar]
- Strouse, D.; Schwab, D.J. The deterministic information bottleneck. Neural Comput. 2017, 29, 1611–1630. [Google Scholar] [CrossRef] [PubMed]
- Fischer, I. The conditional entropy bottleneck. Entropy 2020, 22, 999. [Google Scholar] [CrossRef] [PubMed]
- Piran, Z.; Shwartz-Ziv, R.; Tishby, N. The dual information bottleneck. arXiv 2020, arXiv:2006.04641. [Google Scholar]
- Wang, Z.; Huang, S.L.; Kuruoglu, E.E.; Sun, J.; Chen, X.; Zheng, Y. Pac-bayes information bottleneck. arXiv 2021, arXiv:2109.14509. [Google Scholar]
- An, S.; Jammalamadaka, N.; Chong, E. Maximum entropy information bottleneck for uncertainty-aware stochastic embedding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 3809–3818. [Google Scholar]
- Kawaguchi, K.; Deng, Z.; Ji, X.; Huang, J. How Does Information Bottleneck Help Deep Learning? Int. Conf. Mach. Learn. 2023, 202, 16049–16096. [Google Scholar]
- Shamir, O.; Sabato, S.; Tishby, N. Learning and generalization with the information bottleneck. Theor. Comput. Sci. 2010, 411, 2696–2711. [Google Scholar] [CrossRef]
- Achille, A.; Soatto, S. Information dropout: Learning optimal representations through noisy computation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2897–2905. [Google Scholar] [CrossRef]
- Alemi, A.A.; Fischer, I.; Dillon, J.V. Uncertainty in the variational information bottleneck. arXiv 2018, arXiv:1807.00906. [Google Scholar]
- Ahuja, K.; Caballero, E.; Zhang, D.; Gagnon-Audet, J.C.; Bengio, Y.; Mitliagkas, I.; Rish, I. Invariance principle meets information bottleneck for out-of-distribution generalization. Adv. Neural Inf. Process. Syst. 2021, 34, 3438–3450. [Google Scholar]
- Li, B.; Shen, Y.; Wang, Y.; Zhu, W.; Li, D.; Keutzer, K.; Zhao, H. Invariant information bottleneck for domain generalization. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 7399–7407. [Google Scholar]
- Ngampruetikorn, V.; Schwab, D.J. Information bottleneck theory of high-dimensional regression: Relevancy, efficiency and optimality. Adv. Neural Inf. Process. Syst. 2022, 35, 9784–9796. [Google Scholar]
- Guo, L.; Wu, H.; Wang, Y.; Zhou, W.; Zhou, T. IB-UQ: Information bottleneck based uncertainty quantification for neural function regression and neural operator learning. J. Comput. Phys. 2024, 510, 113089. [Google Scholar] [CrossRef]
- Yang, H.; Sun, Z.; Xu, H.; Chen, X. Revisiting Counterfactual Regression through the Lens of Gromov-Wasserstein Information Bottleneck. arXiv 2024, arXiv:2405.15505. [Google Scholar]
- Yan, X.; Lou, Z.; Hu, S.; Ye, Y. Multi-task information bottleneck co-clustering for unsupervised cross-view human action categorization. ACM Trans. Knowl. Discov. Data (TKDD) 2020, 14, 1–23. [Google Scholar] [CrossRef]
- Hu, S.; Wang, R.; Ye, Y. Interactive information bottleneck for high-dimensional co-occurrence data clustering. Appl. Soft Comput. 2021, 111, 107837. [Google Scholar] [CrossRef]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the 2015 IEEE Information Theory Workshop (itw), Jerusalem, Israel, 26 April–1 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the black box of deep neural networks via information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. J. Stat. Mech. Theory Exp. 2019, 2019, 124020. [Google Scholar] [CrossRef]
- Wu, T.; Fischer, I.; Chuang, I.L.; Tegmark, M. Learnability for the information bottleneck. In Proceedings of the Uncertainty in Artificial Intelligence, Virtual, 3–6 August 2020; pp. 1050–1060. [Google Scholar]
- Rodríguez Gálvez, B.; Thobaben, R.; Skoglund, M. The convex information bottleneck lagrangian. Entropy 2020, 22, 98. [Google Scholar] [CrossRef]
- Kudo, S.; Ono, N.; Kanaya, S.; Huang, M. Flexible Variational Information Bottleneck: Achieving Diverse Compression with a Single Training. arXiv 2024, arXiv:2402.01238. [Google Scholar]
- Wu, T.; Fischer, I. Phase transitions for the information bottleneck in representation learning. arXiv 2020, arXiv:2001.01878. [Google Scholar]
- Kolchinsky, A.; Tracey, B.D.; Van Kuyk, S. Caveats for information bottleneck in deterministic scenarios. arXiv 2018, arXiv:1808.07593. [Google Scholar]
- Amjad, R.A.; Geiger, B.C. Learning Representations for Neural Network-Based Classification Using the Information Bottleneck Principle. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2225–2239. [Google Scholar] [CrossRef] [PubMed]
- Alabdulmohsin, I. An information-theoretic route from generalization in expectation to generalization in probability. In Proceedings of the ARTIFICIAL Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 92–100. [Google Scholar]
- Nachum, I.; Yehudayoff, A. Average-case information complexity of learning. In Proceedings of the Algorithmic Learning Theory, Chicago, IL, USA, 22–24 March 2019; pp. 633–646. [Google Scholar]
- Negrea, J.; Haghifam, M.; Dziugaite, G.K.; Khisti, A.; Roy, D.M. Information-theoretic generalization bounds for SGLD via data-dependent estimates. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Bu, Y.; Zou, S.; Veeravalli, V.V. Tightening mutual information-based bounds on generalization error. IEEE J. Sel. Areas Inf. Theory 2020, 1, 121–130. [Google Scholar] [CrossRef]
- Steinke, T.; Zakynthinou, L. Reasoning about generalization via conditional mutual information. In Proceedings of the Conference on Learning Theory, Graz, Austria, 9–12 July 2020; pp. 3437–3452. [Google Scholar]
- Haghifam, M.; Negrea, J.; Khisti, A.; Roy, D.M.; Dziugaite, G.K. Sharpened generalization bounds based on conditional mutual information and an application to noisy, iterative algorithms. Adv. Neural Inf. Process. Syst. 2020, 33, 9925–9935. [Google Scholar]
- Neu, G.; Dziugaite, G.K.; Haghifam, M.; Roy, D.M. Information-theoretic generalization bounds for stochastic gradient descent. In Proceedings of the Conference on Learning Theory, Boulder, CO, USA, 15–19 August 2021; pp. 3526–3545. [Google Scholar]
- Aminian, G.; Bu, Y.; Toni, L.; Rodrigues, M.; Wornell, G. An exact characterization of the generalization error for the Gibbs algorithm. Adv. Neural Inf. Process. Syst. 2021, 34, 8106–8118. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. beta-vae: Learning basic visual concepts with a constrained variational framework. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Alemi, A.; Poole, B.; Fischer, I.; Dillon, J.; Saurous, R.A.; Murphy, K. Fixing a broken ELBO. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 159–168. [Google Scholar]
- Tschannen, M.; Bachem, O.; Lucic, M. Recent advances in autoencoder-based representation learning. arXiv 2018, arXiv:1812.05069. [Google Scholar]
- Lucas, J.; Tucker, G.; Grosse, R.B.; Norouzi, M. Don’t blame the elbo! A linear vae perspective on posterior collapse. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Kumar, A.; Poole, B. On Implicit Regularization in β-VAEs. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5480–5490. [Google Scholar]
- Sicks, R.; Korn, R.; Schwaar, S. A Generalised Linear Model Framework for β-Variational Autoencoders based on Exponential Dispersion Families. J. Mach. Learn. Res. 2021, 22, 1–41. [Google Scholar]
- Poole, B.; Ozair, S.; Van Den Oord, A.; Alemi, A.; Tucker, G. On variational bounds of mutual information. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 5171–5180. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Pace, R.K.; Barry, R. Sparse spatial autoregressions. Stat. Probab. Lett. 1997, 33, 291–297. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Thames, Q.; Karpur, A.; Norris, W.; Xia, F.; Panait, L.; Weyand, T.; Sim, J. Nutrition5k: Towards automatic nutritional understanding of generic food. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8903–8911. [Google Scholar]
- Parinayok, S.; Yamakata, Y.; Aizawa, K. Open-vocabulary segmentation approach for transformer-based food nutrient estimation. In Proceedings of the ACM Multimedia Asia 2023, New York, NY, USA, 6–8 December 2023. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Series B Stat. Methodol. 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]





| California Housing Prices | Nutrition5k | Synthetic Dataset | |
|---|---|---|---|
| Feature extractor | |||
| [53] | |||
| in non-FVIB-R models | 32 | 256 | − |
| # Epochs | {50, 100, 150, 200} | {50, 100, 150, 200} | 200 |
| Learning rate | {, } | {, } | |
| Optimizer | Adam [54] | Adam | Adam |
| California Housing Prices | Nutrition5k | |||
|---|---|---|---|---|
| Method | MSE | # Parameters | MSE | # Parameters |
| FVIB-R | 0.1910 | 0.0881 | ||
| VIB | 0.1979 | 0.0805 | ||
| sq-VIB | 0.1786 | 0.0893 | ||
| NIB | 0.1816 | 0.1549 | ||
| sq-NIB | 0.1790 | 0.1431 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudo, S.; Ono, N.; Kanaya, S.; Huang, M. Exploring the Trade-Off in the Variational Information Bottleneck for Regression with a Single Training Run. Entropy 2024, 26, 1043. https://doi.org/10.3390/e26121043
Kudo S, Ono N, Kanaya S, Huang M. Exploring the Trade-Off in the Variational Information Bottleneck for Regression with a Single Training Run. Entropy. 2024; 26(12):1043. https://doi.org/10.3390/e26121043
Chicago/Turabian StyleKudo, Sota, Naoaki Ono, Shigehiko Kanaya, and Ming Huang. 2024. "Exploring the Trade-Off in the Variational Information Bottleneck for Regression with a Single Training Run" Entropy 26, no. 12: 1043. https://doi.org/10.3390/e26121043
APA StyleKudo, S., Ono, N., Kanaya, S., & Huang, M. (2024). Exploring the Trade-Off in the Variational Information Bottleneck for Regression with a Single Training Run. Entropy, 26(12), 1043. https://doi.org/10.3390/e26121043







