Abstract
We analyze the generalization properties of batch reinforcement learning (batch RL) with value function approximation from an information-theoretic perspective. We derive generalization bounds for batch RL using (conditional) mutual information. In addition, we demonstrate how to establish a connection between certain structural assumptions on the value function space and conditional mutual information. As a by-product, we derive a high-probability generalization bound via conditional mutual information, which was left open and may be of independent interest.
1. Introduction
Generalization is a fundamental concept in statistical machine learning. It measures how well a learning system performs on unseen data after being trained on a finite dataset. Effective generalization ensures that the learning approach captures the essential patterns in the data. Generalization in supervised learning has been studied for several decades. However, in reinforcement learning (RL), agnostic learning is generally infeasible and realizability is not a sufficient condition for efficient learning. Consequently, the study of generalization in RL poses more challenges.
In this work, we focus on batch reinforcement learning (batch RL), a branch of reinforcement learning where the agent learns a policy from a fixed dataset of previously collected experiences. This setting is favorable when online interaction is expensive, dangerous, or impractical. Batch RL, despite being a special case of supervised learning, still presents distinct challenges due to the complex temporal structures inherent in the data.
Originating from the work of [1,2], an information-theoretic framework has been developed to bound the generalization error of learning algorithms using the mutual information between the input dataset and the output hypothesis. This methodology formalizes the intuition that overfitted learning algorithms are less likely to generalize effectively. Unlike traditional approaches such as VC-dimension and Rademacher complexity, this information-theoretic framework offers the significant advantage of capturing all dependencies on the data distribution, hypothesis space, and learning algorithm. Given that reinforcement learning is a learning paradigm in which all the aforementioned aspects differ significantly from those in supervised learning, we believe this novel approach will provide us with more profound insights.
2. Preliminaries
2.1. Batch Reinforcement Learning with Function Approximation
An episodic Markov decision process (MDP) is defined by . We use to denote the set of the probability distribution over the set . is specified by a finite state space , a finite action space , transition functions at step , reward function at step h, and H is the number of steps in each episode. We assume the reward is bounded, i.e., (For rewards in simply rescales these bounds.), . See Figure 1 for a graphical illustration.
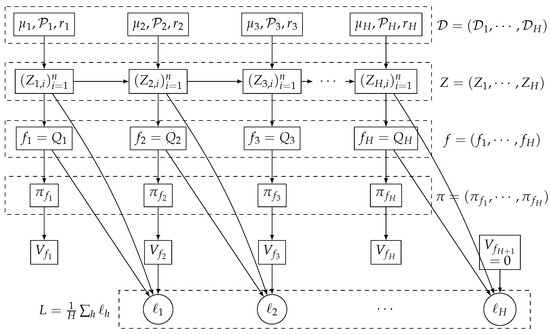
Figure 1.
Directed graph representing the training process in Batch RL under episodic MDP.
Let , where is the action distribution for policy at state s and step h. Given a policy , the value function at step h is defined as
The action-value function at step h is defined as
The Bellman operators and project functions forward by one step through the following dynamics:
Now, we denote the dataset , where , , and for a fixed h. We also denote , where . We consider batch RL with value function approximation. The learner is given a function class to approximate the optimal Q-value function. Denote . As no reward is collected in the step, we set . For each , define , where . Next, we introduce the Bellman error and its empirical version.
Definition 1
(Bellman error). Under data distribution μ, we define the Bellman error of function as
Definition 2
(Mean squared empirical Bellman error (MSBE)). Given a dataset , we define the Mean squared empirical Bellman error (MSBE) of function as
where .
For convenience, we denote .
Bellman error is used in RL as a surrogate loss function to minimize the difference between the estimated value function and the true value function under a policy. The Bellman error serves as a proxy for the optimality gap, which is the difference between the current value function and the optimal value function. Under the concentrability assumption, minimizing the Bellman error is able to reduce the optimality gap.
Lemma 1
(Bellman error to value suboptimality [3]). If there exists a constant C, such that for any policy π
then for any , we have
We note that is a biased estimate of . A common solution is to use the double sampling method, where for each state and action in the sample, at least two next states are generated [3,4,5], and define the unbiased MSBE as:
Note that , , and double sampling does not increase the sample size, except that it requires an additional generated . Therefore, the results presented in this paper can be easily extended to the double sampling setting.
2.2. Generalization Bounds
Definition 3
(Expected generalization bounds). Given a dataset and an algorithm , let denote the training loss and let denote the true loss. The expected generalization error is defined as
Definition 4
(High-probability generalization bounds). Given a dataset , and an algorithm , let denote the training loss and let denote the true loss. Given a failure probability δ and an error tolerance η, the high-probability generalization error is defined as
2.3. Mutual Information
First, we define the KL-divergence of two distributions.
Definition 5
(KL-Divergence [6]). Let be two distributions over the space Ω and suppose is absolutely continuous with respect to . The Kullback–Leibler (KL) divergence from to is
where and denote the probability mass/density functions of and on X, respectively.
Based on KL-divergence, we can define mutual information and conditional mutual information as follows.
Definition 6
([6]). Let X, Y, and Z be arbitrary random variables, and let denote the Kullback–Leibler (KL) divergence. The mutual information between X and Y is defined as:
The conditional mutual information is defined as:
Next, we introduce Rényi’s -Divergence, which is a generalization of KL-divergence. Rényi’s -Divergence has found many applications, such as hypothesis testing, differential privacy, several statistical inference, and coding problems [7,8,9,10].
Definition 7
(Rényi’s -Divergence [11]). Let , be two probability spaces. Let be a positive real different from 1. Consider a measure μ, such that and (such a measure always exists, e.g., ) and denote with the densities of with respect to μ. The α–divergence of from is defined as follows:
Note that the above definition is independent of the chosen measure . With the definition of Rényi’s -divergence, we are ready to state the definitions of -mutual information and -conditional mutual information.
Definition 8
(-mutual information [7]). Let be two random variables jointly distributed according to . Let be any probability measure over . For , the α-mutual information between X and Y is defined as follows:
Definition 9
(Conditional -mutual information). Let be three random variables jointly distributed according to . Let be any probability measure over . For , a conditional α-mutual information of order α between X and Y given Z is defined as follows:
3. Generalization Bounds via Mutual Information
Mutual information bounds provide a direct link between the generalization error and the amount of information shared between the training data and the learned hypothesis. This offers a clear information-theoretic understanding of how overfitting can be controlled by reducing the dependency on the training data. Mutual information bounds are applicable to a wide range of learning algorithms and settings, including those with unbounded loss functions and complex hypothesis spaces. Moreover, the use of mutual information can simplify the analysis of generalization compared with traditional methods, particularly in cases where those traditional measures are difficult to compute. See Appendix A for related work.
Theorem 1
([2]). Let be a distribution on Z. Let be a randomized algorithm. Let be a loss function, which is σ-subgaussian with respect to Z. Let be the empirical risk. Then
The above theorem provides a bound on the expected generalization error. High-probability generalization bounds can be obtained using the -mutual information. Note that the -mutual information shares many properties with standard mutual information.
Proposition 1
([7]). For discrete random variables X and Y, the following holds:
- (i)
- Data Processing Inequality: given , if the Markov chain holds.
- (ii)
- (iii)
- (iv)
- with equality iff X and Y are independent.
Theorem 2
([11]). Let be a distribution on Z. Let be a randomized algorithm. Let be a loss function which is σ-subgaussian with respect to Z. Let be the empirical risk. Given and fix , if the number of samples n satisfies
then, we have
The mutual information bound can be infinite in some cases and thus be vacuous. To address this, the conditional mutual information (CMI) approach was introduced. CMI bounds normalize the information content for each data point, preventing the problem of infinite information content, particularly in continuous data distributions. This makes CMI a more robust and applicable method in scenarios where mutual information would otherwise be unbounded.
Definition 10.
Let consist of samples drawn independently from . Let be uniformly random and independent from Z and the randomness of . Define , such that is the sample in Z—that is, is the subset of Z indexed by U. The conditional mutual information of with respect to is defined as
Theorem 3
([12]). Let be a distribution on Z. Let be a randomized algorithm. Let be a function, such that for all and given . Let be uniformly random. Then
Another advantage of the CMI bounds is that they can be derived from various concepts such as VC-dimension, compression schemes, stability, and differential privacy, offering a unified framework for generalization analysis. However, because CMI is defined as an expectation, i.e., , the above theorem does not provide a high-probability bound. Modifying this framework to ensure high-probability guarantees was left as future work in [12]. In the following, we use conditional -mutual information to address this issue.
Theorem 4.
Let be uniformly random. Given a dataset consists of samples. Let be a randomized algorithm. Let be a loss function which is σ-subgaussian with respect to Z. Let be the empirical risk. Given and fix , if the number of samples n satisfies
then, we have
Proof.
Let be a probability space, and let be the set of conditional probability measures , such that . Given and , let . We first prove that for a fixed ,
Using the Radon–Nikodym derivative of with respect to the product measure , we have
where is the indicator function of the event E. Next, we introduce three sets of exponents , and , such that
By applying Hölder’s inequality three times to separate the different components of the expectation, we derive
By setting and ,
Since and , we have . As , tends to the essential supremum
As , we have
Thus, Equation (2) holds by combining all of the inequalities.
Now, let and . Consider the event
where denotes the empirical risk defined as the average of n loss functions, and each loss function is -subgaussian. We can express , the fibers of E, with respect to Z and X, as
For any fixed Z and X, the random variable Y remains independent of Z and X under any . Now, using Hoeffding’s inequality, for every X and Z,
Therefore, from Equations (2) and (3),
Lastly, by setting
we obtain the desired conclusion. □
4. Information-Theoretic Generalization Bounds for Batch RL
We now provide expected and high-probability generalization bounds for batch RL. The generalization bounds are derived from mutual information between the training data and the learned hypothesis. As mutual information bounds consider the data, algorithm, and hypothesis space comprehensively, they support the design of efficient learning algorithms and fine-grained theoretical analysis.
Theorem 5.
Given that dataset consists of samples, for any batch RL algorithm with output , the expected generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by
Proof.
We first recall the Donsker—Varadhan variational representation ([13]) of the KL-divergence between any two probability measures and on a common measurable space
where the supremum is over all measurable functions , such that .
Let be be a dataset where . Let be the output of some batch RL algorithm . Let and be the independent copies of and . Let
Now, we have
As and for any h, it follows that
Thus, we obtain
By optimizing the above inequality over and , respectively, we derive
and thus,
Finally, we observe that
□
The above result suggests that reducing the mutual information between the dataset and the learned function at each step h can improve the generalization performance. Note that when the input domain is infinite, mutual information can become unbounded. To address this limitation, an approach based on conditional mutual information was introduced [12]. CMI bounds not only address the issue by normalizing the information content of each data point, but also establish connections with various other generalization concepts, as we will discuss in the next section. We now present a generalization bound using conditional mutual information.
Theorem 6.
Let be uniformly random. Given that dataset consists of samples, for any batch RL algorithm with output , the expected generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by
Proof.
Let be uniformly random. Let be a dataset where each consists of samples. Define . Let be the output of some batch RL algorithm . Let , and . Note that . We define the disintegrated mutual information
Note that . The rest of the proof is analogous to Theorem 5. We have
As and for any h, it follows that
Thus, we obtain
By optimizing the above inequality over and , respectively, we derive
and thus,
Finally, we conclude that
□
Note that our setting is identical to that in [3], i.e., batch RL with value function approximation for episodic MDPs. They established a bound of the order , where represents the Rademacher complexity of the function space . In contrast, our result yields an error bound of the order . As demonstrated in the subsequent section, under structural assumptions like a finite pseudo-dimension or effective dimension d, this bound can be refined to .
Next, we proceed to derive the high-probability version of these generalization bounds using -mutual information.
Theorem 7.
Given a dataset consists of samples, for any batch RL algorithm with output , if
then, the generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by
with a probability of at least .
Proof.
Let be a dataset where . Let be the output of some batch RL algorithm . Let
As for every f, it is -sub-Gaussian. By Theorem 2, we have
with probability at least for
As we have n samples at each , we require
The claim is now followed by the union bound by setting . □
Recall that conditional mutual information is defined as an expectation over the KL divergence. Thus, all prior works using the CMI framework have only provided bounds on the expected generalization error. We wish to establish generalization bounds with high-probability guarantees similar to Theorem 7.
Theorem 8.
Let be uniformly random. Given that dataset consists of samples, for any batch RL algorithm with output , if
then, the generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by
with probability at least .
Proof.
By substituting Theorem 2 with Theorem 4 in the proof of Theorem 7, the proof is thereby obtained. □
5. Value Functions Under Structural Assumptions
Due to the challenges stemming from large state-action spaces, long horizons, and the temporal nature of data, there is increasing interest in identifying structural assumptions for RL with value function approximation. These works include, but are not limited to, Bellman rank [14], Witness rank [15], and Eluder dimension [16]. These structural conditions aim to develop a unified theory of generalization in RL. In this section, we demonstrate that if a function class satisfies certain structural conditions reflecting a manageable complexity, the mutual information can be effectively upper bounded.
Definition 11
(Covering number). The covering number of a function class under metric , denoted as , is the minimum integer n, such that there exists a subset with , and for any , there exists , such that .
Lemma 2.
For discrete random variables , and Z, we have .
Proof.
Denote the conditional entropy of X given Z.
□
Theorem 9.
Suppose the function class has a covering number of . Let be uniformly random. Given that dataset Z consists of samples, for any batch RL algorithm with output , the expected generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by
Proof.
Let . We first define an oracle algorithm capable of outputting a function , such that
Note that is only used for theoretical analysis. Observe that
Thus,
Bounding is similar. Now, we have
As and , we have
By Theorem 6,
Therefore,
□
Structural assumptions on the function space typically entail a finite covering number. Next, we consider the simplest case: the pseudo-dimension. The pseudo-dimension is a complexity measure of real-valued function classes, analogous to the VC dimension used for binary classification. Although the value function space may be infinite, it remains learnable if it has a finite pseudo-dimension.
Definition 12
(VC-Dimension [17]). Given hypothesis class , its VC-dimension is defined as the maximal cardinality of a set that satisfies (or X is shattered by ), where is the restriction of to X, namely .
Definition 13
(Pseudo dimension [18]). Suppose is a feature space. Given hypothesis class , its pseudo dimension is defined as , where .
Lemma 3
(Bounding covering number by pseudo dimension [19]). Given hypothesis class with , we have
Corollary 1.
Suppose the function class has a finite pseudo dimension . For any batch RL algorithm with n training samples, the expected generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by .
Proof.
As and , we have . The claim follows from Theorem 9 by setting . □
A prior study on finite sample guarantees for minimizing the Bellman error, using pseudo-dimension, demonstrated a sample complexity with a dependence of [5]. In contrast, our sample complexity exhibits a dependence of on the pseudo-dimension.
Now, we introduce another complexity measure known as the effective dimension [20], which has a similar covering number to the pseudo-dimension. The effective dimension quantifies how the function class responds to data, indicating the minimum number of samples required to learn effectively.
Definition 14
(-effective dimension of a set [20]). The ϵ-effective dimension of a set is the minimum integer , such that
Definition 15
(-effective dimension of a function class [20]). Given a function class defined on , its ϵ-effective dimension is the minimum integer n, such that there exists a separable Hilbert space and a mapping , so that
- for every , there exists satisfying for all ,
- , where .
Definition 16
(Kernel MDPs [21]). In a kernel MDP of effective dimension d, for each step , there exist feature mappings and , where is a separable Hilbert space, so that the transition measure can be represented as the inner product of features, i.e.,
Besides, the reward function is linear in ϕ, i.e.,
for some . Here, ϕ is known to the learner while ψ and are unknown. Moreover, a kernel MDP satisfies the following regularization conditions: for all h
- and for all .
- for any function .
- for all h, where .
Kernel MDPs are extensions of the traditional MDPs where the transition dynamics and rewards are represented in a Reproducing Kernel Hilbert Space (RKHS). In this setup, the value functions or Q-functions are approximated using kernel methods, allowing the model to capture more complex dependencies in the data compared to linear models. To learn kernel MDPs, it is necessary to construct a function class .
Lemma 4
(Bounding covering number by effective dimension [21]). Let be a kernel MDP of effective dimension d, then
Corollary 2.
Suppose the function class has a finite effective dimension d. For any batch RL algorithm with n training samples, the expected generalization error for the mean squared empirical Bellman error (MSBE) loss is upper bounded by .
We showed that when a function class contains infinitely many elements, a finite covering number can be used to upper bound the generalization error. Just as the VC-dimension imposes a finite cardinality, various concepts in real-valued function classes, such as pseudo-dimension and effective dimension, result in a finite covering number, thereby ensuring efficient learning.
6. Discussion
In this paper, we analyzed the generalization property of batch reinforcement learning within the framework of information theory. We established generalization bounds using both conditional and unconditional mutual information. Besides, we demonstrated how to leverage the structure of the function space to guarantee generalization. Due to the merits of the information-theoretic approach, there are several appealing future research directions.
The first interesting avenue is to extend the results to the online setting. It is noteworthy that in on-policy learning, the inputs (e.g., the reward and the next state), are influenced by the output (e.g., the policy or the model), which highlights a significant disparity compared to off-policy and supervised learning. In supervised learning, a small mutual information between the input and the output indicates that the model is not overfitting. In on-policy learning, analyzing the mutual information between the input and the output can be more complicated and insightful. For example, in model-based reinforcement learning, where the model is a part of the output, a small mutual information might indicate that the learned model focuses more on the goal of maximizing the cumulative reward rather than solely capturing the transition dynamics. How to learn an effective model beyond merely fitting the transition is the central theme in decision-aware model-based reinforcement learning [22,23,24,25,26,27,28].
As in the supervised learning setting, where various algorithms such as Stochastic Gradient Descent (SGD) [29] and Stochastic Gradient Langevin Dynamics (SGLD) have been studied [30], a promising future direction is to analyze information-theoretic generalization bounds for specific reinforcement learning algorithms such as stochastic policy gradient methods.
In addition, the information-theoretic approach has the potential to unify various concepts related to generalization, such as differential privacy and stability [12,31]. It would be interesting to explore how these notions in reinforcement learning can be leveraged to guarantee generalization.
Analyzing generalization for reinforcement learning is inherently more challenging than in supervised learning [32,33,34]. Therefore, we hope that the information-theoretic approach will provide more insights into understanding the generalization of reinforcement learning.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No data were created or analyzed in this theoretical study. Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Related Work
Appendix A.1. Batch Reinforcement Learning
A body of literature focuses on finite sample guarantees for batch reinforcement learning with function approximation [35,36,37,38,39,40]. Common assumptions in batch RL, such as concentrability, realizability, and completeness, have also been examined in more recent studies [41,42,43]. The most relevant work to ours [3] investigates the generalization performance of batch RL under the same setting using Rademacher complexities.
Appendix A.2. Structural Conditions for Efficient RL
Analogous to complexity measures in supervised learning, several structural conditions have been studied to enable efficient reinforcement learning, including Bellman rank [14], Witness rank [15], Eluder dimension [16], Bellman Eluder dimension [21], and more [20,37,44]. Identifying structural conditions and classifying RL problems clarifies the limits of what can be learned and guides the design of efficient algorithms.
Appendix A.3. Information-Theoretic Study of Generalization
The information-theoretic approach was initially introduced by [1,2] and subsequently refined to derive tighter bounds [45,46,47]. Besides, various other information-theoretic bounds have been proposed, leveraging concepts such as conditional mutual information [12], f-divergence [11], the Wasserstein distance [48,49], and more [50,51]. Some studies have focused on analyzing specific algorithms [29,30,52,53,54,55] while others have examined particular settings such as deep learning [56], iterative semi-supervised learning [57], transfer learning [58], and meta-learning [59,60]. There are also works attempting to provide a unified framework for generalization from an information-theoretic perspective [31,61,62].
References
- Russo, D.; Zou, J. Controlling bias in adaptive data analysis using information theory. In Proceedings of the Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 1232–1240. [Google Scholar]
- Xu, A.; Raginsky, M. Information-theoretic analysis of generalization capability of learning algorithms. Adv. Neural Inf. Process. Syst. 2017, 30, 2521–2530. [Google Scholar]
- Duan, Y.; Jin, C.; Li, Z. Risk bounds and rademacher complexity in batch reinforcement learning. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 2892–2902. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. Robotica 1999, 17, 229–235. [Google Scholar] [CrossRef]
- Antos, A.; Szepesvári, C.; Munos, R. Learning near-optimal policies with Bellman-residual minimization based fitted policy iteration and a single sample path. Mach. Learn. 2008, 71, 89–129. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Verdú, S. α-mutual information. In Proceedings of the 2015 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 1–6 February 2015; pp. 1–6. [Google Scholar]
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Csiszár, I. Generalized cutoff rates and Rényi’s information measures. IEEE Trans. Inf. Theory 1995, 41, 26–34. [Google Scholar] [CrossRef]
- Mironov, I. Rényi differential privacy. In Proceedings of the 2017 IEEE 30th Computer Security Foundations Symposium (CSF), Santa Barbara, CA, USA, 21–25 August 2017; pp. 263–275. [Google Scholar]
- Esposito, A.R.; Gastpar, M.; Issa, I. Generalization error bounds via Rényi-, f-divergences and maximal leakage. IEEE Trans. Inf. Theory 2021, 67, 4986–5004. [Google Scholar] [CrossRef]
- Steinke, T.; Zakynthinou, L. Reasoning about generalization via conditional mutual information. In Proceedings of the Conference on Learning Theory, Graz, Austria, 9–12 July 2020; pp. 3437–3452. [Google Scholar]
- Boucheron, S.; Lugosi, G.; Massart, P. Concentration Inequalities: A Nonasymptotic Theory of Independence; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Jiang, N.; Krishnamurthy, A.; Agarwal, A.; Langford, J.; Schapire, R.E. Contextual decision processes with low bellman rank are pac-learnable. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1704–1713. [Google Scholar]
- Sun, W.; Jiang, N.; Krishnamurthy, A.; Agarwal, A.; Langford, J. Model-based rl in contextual decision processes: Pac bounds and exponential improvements over model-free approaches. In Proceedings of the Conference on Learning Theory, Phoenix, AZ, USA, 25–28 June 2019; pp. 2898–2933. [Google Scholar]
- Wang, R.; Salakhutdinov, R.R.; Yang, L. Reinforcement learning with general value function approximation: Provably efficient approach via bounded eluder dimension. Adv. Neural Inf. Process. Syst. 2020, 33, 6123–6135. [Google Scholar]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Haussler, D. Decision theoretic generalizations of the PAC model for neural net and other learning applications. Inf. Comput. 1992, 100, 78–150. [Google Scholar] [CrossRef]
- Haussler, D. Sphere packing numbers for subsets of the Boolean n-cube with bounded Vapnik-Chervonenkis dimension. J. Comb. Theory Ser. A 1995, 69, 217–232. [Google Scholar] [CrossRef]
- Du, S.; Kakade, S.; Lee, J.; Lovett, S.; Mahajan, G.; Sun, W.; Wang, R. Bilinear classes: A structural framework for provable generalization in rl. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 2826–2836. [Google Scholar]
- Jin, C.; Liu, Q.; Miryoosefi, S. Bellman eluder dimension: New rich classes of rl problems, and sample-efficient algorithms. Adv. Neural Inf. Process. Syst. 2021, 34, 13406–13418. [Google Scholar]
- Wei, R.; Lambert, N.; McDonald, A.; Garcia, A.; Calandra, R. A Unified View on Solving Objective Mismatch in Model-Based Reinforcement Learning. arXiv 2023, arXiv:2310.06253. [Google Scholar]
- Farahmand, A.M.; Barreto, A.; Nikovski, D. Value-aware loss function for model-based reinforcement learning. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1486–1494. [Google Scholar]
- Farahmand, A.M. Iterative value-aware model learning. Adv. Neural Inf. Process. Syst. 2018, 31, 9090–9101. [Google Scholar]
- Abachi, R. Policy-Aware Model Learning for Policy Gradient Methods; University of Toronto (Canada): Toronto, ON, Canada, 2020. [Google Scholar]
- Janner, M.; Fu, J.; Zhang, M.; Levine, S. When to trust your model: Model-based policy optimization. Adv. Neural Inf. Process. Syst. 2018, 32, 12519–12530. [Google Scholar]
- Ji, T.; Luo, Y.; Sun, F.; Jing, M.; He, F.; Huang, W. When to update your model: Constrained model-based reinforcement learning. Adv. Neural Inf. Process. Syst. 2022, 35, 23150–23163. [Google Scholar]
- Wang, X.; Zheng, R.; Sun, Y.; Jia, R.; Wongkamjan, W.; Xu, H.; Huang, F. Coplanner: Plan to roll out conservatively but to explore optimistically for model-based RL. arXiv 2023, arXiv:2310.07220. [Google Scholar]
- Neu, G.; Dziugaite, G.K.; Haghifam, M.; Roy, D.M. Information-theoretic generalization bounds for stochastic gradient descent. In Proceedings of the Conference on Learning Theory, Boulder, CO, USA, 15–19 August 2021; pp. 3526–3545. [Google Scholar]
- Negrea, J.; Haghifam, M.; Dziugaite, G.K.; Khisti, A.; Roy, D.M. Information-theoretic generalization bounds for SGLD via data-dependent estimates. Adv. Neural Inf. Process. Syst. 2019, 32, 11015–11025. [Google Scholar]
- Haghifam, M.; Dziugaite, G.K.; Moran, S.; Roy, D. Towards a unified information-theoretic framework for generalization. Adv. Neural Inf. Process. Syst. 2021, 34, 26370–26381. [Google Scholar]
- Du, S.S.; Kakade, S.M.; Wang, R.; Yang, L.F. Is a good representation sufficient for sample efficient reinforcement learning? arXiv 2019, arXiv:1910.03016. [Google Scholar]
- Weisz, G.; Amortila, P.; Szepesvári, C. Exponential lower bounds for planning in mdps with linearly-realizable optimal action-value functions. In Proceedings of the Algorithmic Learning Theory, Virtual, 16–19 March 2021; pp. 1237–1264. [Google Scholar]
- Wang, Y.; Wang, R.; Kakade, S. An exponential lower bound for linearly realizable mdp with constant suboptimality gap. Adv. Neural Inf. Process. Syst. 2021, 34, 9521–9533. [Google Scholar]
- Munos, R.; Szepesvári, C. Finite-Time Bounds for Fitted Value Iteration. J. Mach. Learn. Res. 2008, 9, 815–857. [Google Scholar]
- Farahmand, A.; Ghavamzadeh, M.; Mannor, S.; Szepesvári, C. Regularized policy iteration. Adv. Neural Inf. Process. Syst. 2008, 21, 441–448. [Google Scholar]
- Zanette, A.; Lazaric, A.; Kochenderfer, M.; Brunskill, E. Learning near optimal policies with low inherent bellman error. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 10978–10989. [Google Scholar]
- Lazaric, A.; Ghavamzadeh, M.; Munos, R. Finite-sample analysis of least-squares policy iteration. J. Mach. Learn. Res. 2012, 13, 3041–3074. [Google Scholar]
- Farahm, A.M.; Ghavamzadeh, M.; Szepesvári, C.; Mannor, S. Regularized policy iteration with nonparametric function spaces. J. Mach. Learn. Res. 2016, 17, 1–66. [Google Scholar]
- Le, H.; Voloshin, C.; Yue, Y. Batch policy learning under constraints. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 3703–3712. [Google Scholar]
- Chen, J.; Jiang, N. Information-theoretic considerations in batch reinforcement learning. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 1042–1051. [Google Scholar]
- Wang, R.; Foster, D.P.; Kakade, S.M. What are the statistical limits of offline RL with linear function approximation? arXiv 2020, arXiv:2010.11895. [Google Scholar]
- Xie, T.; Jiang, N. Batch value-function approximation with only realizability. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 11404–11413. [Google Scholar]
- Foster, D.J.; Kakade, S.M.; Qian, J.; Rakhlin, A. The statistical complexity of interactive decision making. arXiv 2021, arXiv:2112.13487. [Google Scholar]
- Asadi, A.; Abbe, E.; Verdú, S. Chaining mutual information and tightening generalization bounds. Adv. Neural Inf. Process. Syst. 2018, 31, 7245–7254. [Google Scholar]
- Hafez-Kolahi, H.; Golgooni, Z.; Kasaei, S.; Soleymani, M. Conditioning and processing: Techniques to improve information-theoretic generalization bounds. Adv. Neural Inf. Process. Syst. 2020, 33, 16457–16467. [Google Scholar]
- Bu, Y.; Zou, S.; Veeravalli, V.V. Tightening mutual information-based bounds on generalization error. IEEE J. Sel. Areas Inf. Theory 2020, 1, 121–130. [Google Scholar] [CrossRef]
- Lopez, A.T.; Jog, V. Generalization error bounds using Wasserstein distances. In Proceedings of the 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018; pp. 1–5. [Google Scholar]
- Wang, H.; Diaz, M.; Santos Filho, J.C.S.; Calmon, F.P. An information-theoretic view of generalization via Wasserstein distance. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 577–581. [Google Scholar]
- Aminian, G.; Toni, L.; Rodrigues, M.R. Information-theoretic bounds on the moments of the generalization error of learning algorithms. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Virtual, 12–20 July 2021; pp. 682–687. [Google Scholar]
- Aminian, G.; Masiha, S.; Toni, L.; Rodrigues, M.R. Learning algorithm generalization error bounds via auxiliary distributions. IEEE J. Sel. Areas Inf. Theory 2024, 5, 273–284. [Google Scholar] [CrossRef]
- Pensia, A.; Jog, V.; Loh, P.L. Generalization error bounds for noisy, iterative algorithms. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 546–550. [Google Scholar]
- Haghifam, M.; Negrea, J.; Khisti, A.; Roy, D.M.; Dziugaite, G.K. Sharpened generalization bounds based on conditional mutual information and an application to noisy, iterative algorithms. Adv. Neural Inf. Process. Syst. 2020, 33, 9925–9935. [Google Scholar]
- Harutyunyan, H.; Raginsky, M.; Ver Steeg, G.; Galstyan, A. Information-theoretic generalization bounds for black-box learning algorithms. Adv. Neural Inf. Process. Syst. 2021, 34, 24670–24682. [Google Scholar]
- Wang, H.; Gao, R.; Calmon, F.P. Generalization bounds for noisy iterative algorithms using properties of additive noise channels. J. Mach. Learn. Res. 2023, 24, 1–43. [Google Scholar]
- He, H.; Yu, C.L.; Goldfeld, Z. Information-Theoretic Generalization Bounds for Deep Neural Networks. arXiv 2024, arXiv:2404.03176. [Google Scholar]
- He, H.; Hanshu, Y.; Tan, V. Information-theoretic generalization bounds for iterative semi-supervised learning. In Proceedings of the The Tenth International Conference on Learning Representations, Virtual, 25 April 2022. [Google Scholar]
- Wu, X.; Manton, J.H.; Aickelin, U.; Zhu, J. On the generalization for transfer learning: An information-theoretic analysis. IEEE Trans. Inf. Theory 2024, 70, 7089–7124. [Google Scholar] [CrossRef]
- Jose, S.T.; Simeone, O. Information-theoretic generalization bounds for meta-learning and applications. Entropy 2021, 23, 126. [Google Scholar] [CrossRef]
- Chen, Q.; Shui, C.; Marchand, M. Generalization bounds for meta-learning: An information-theoretic analysis. Adv. Neural Inf. Process. Syst. 2021, 34, 25878–25890. [Google Scholar]
- Chu, Y.; Raginsky, M. A unified framework for information-theoretic generalization bounds. Adv. Neural Inf. Process. Syst. 2023, 36, 79260–79278. [Google Scholar]
- Alabdulmohsin, I. Towards a unified theory of learning and information. Entropy 2020, 22, 438. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).