Abstract
Uncertainty, time delays, and jumps often coexist in dynamic game problems due to the complexity of the environment. To address such issues, we can utilize uncertain delay differential equations with jumps to depict the dynamic changes in differential game problems that involve uncertain noise, delays, and jumps. In this paper, we first examine a linear quadratic differential game optimistic value problem within an uncertain environment characterized by jumps and delays. By applying the transform, we convert the infinite-dimensional problem into a finite-dimensional one. We then demonstrate that the condition for the existence of a Nash equilibrium strategy is equivalent to the existence of solutions to two cross-coupled matrix Riccati equations. Furthermore, we explore the saddle point equilibrium strategy of the linear quadratic differential game optimistic value model and derive the corresponding saddle point equilibrium solution. Finally, we apply our results to solve a carbon emission reduction game problem.
1. Introduction
The uncertainty of experts’ experience, particularly in relation to belief degrees [1] as expressed by experts, is a significant factor when dealing with phenomena that are indeterminate. This uncertainty can have profound implications on decision making and modeling processes, especially when the phenomena in question do not have clear, definitive outcomes. In addressing such indeterminate scenarios, incorporating a measure of this uncertainty becomes essential for more accurate analysis and predictions. To effectively capture the dynamics of phenomena that are uncertain in nature, particularly with respect to varying belief degrees, Liu [2] introduced a novel mathematical framework known as the uncertain differential equation, which is grounded in what is now called the Liu process. This process provided a structured way to model the uncertainty inherent in these phenomena. Subsequent research [3] expanded upon Liu’s initial proposal, exploring and deepening the understanding of the properties and behaviors of the Liu process, and allowing for more robust applications by uncertain differential systems driven by it. Uncertain differential equations (UDEs) and stochastic differential equations (SDEs) both deal with differential systems that exhibit some degree of randomness or uncertainty. However, they differ in their mathematical formulation and interpretation. SDEs utilize probability theory and Brownian motion to model randomness, effectively capturing the intrinsic variability and unpredictability inherent in certain phenomena. In contrast, UDEs utilize uncertainty theory, which is based on a non-additivity measure called belief degree, to describe systems with inherent indeterminacy that cannot be fully characterized by probabilistic methods. This distinction makes UDEs particularly suitable for situations where traditional probabilistic models may be inadequate or inappropriate.
In later studies, uncertain delay differential equations emerged as a significant area of interest. These equations, which incorporate time delays into uncertain systems, offered a more nuanced approach to modeling scenarios where the effects of a current state are delayed and manifest over time. This complexity attracted attention for its realism in capturing delayed responses in uncertain environments. In uncertain delay differential equations, “delay” signifies that the rate of change of the dependent variable at any time depends not only on its current value but also on a prior state. The delay represents processes where present dynamics are influenced by past states, a crucial feature for modeling temporal dependencies in control systems. Research on uncertain delay differential equations concentrated on four main aspects: solution existence, solution uniqueness, system stability under uncertainty and delays, and potential applications. Understanding these characteristics was vital to establishing whether solutions were reliable, how they evolved, and how systems could be controlled to achieve desired outcomes in the presence of uncertainty and delays. Addressing these phenomena, Barbacioru [4] utilized uncertainty functional differential equations to model volatility in financial markets, particularly for dynamic systems influenced by past states. Ge et al. [5] established existence and uniqueness theorems for uncertain delay differential equations under specific conditions, forming a theoretical foundation that ensured meaningful and interpretable solutions. Building on prior work, Wang et al. [6,7] introduced concepts such as stability in measure, mean, and p-th moment to describe the stability of uncertain delay differential equations, while Jia et al. [8] focused on stability in distribution. In this context, stability indicates whether the system remains predictable and well behaved over time, even with uncertainty. Their contributions included stability theorems that clarified conditions for system integrity despite fluctuating degrees of uncertainty. Chen, Zhu [9], and Jiang [10] investigated optimal control in uncertain systems with time delays, excluding sudden jumps. They employed expected value criteria, a common method where decisions are based on the weighted average of possible outcomes. Their research sought optimal control strategies to minimize risks and maximize desired outcomes, even in the face of uncertainty and delays.
It is widely recognized that uncertain processes can be subject to sudden, unpredictable changes brought on by emergencies or crises. These events can include economic downturns, pandemics, natural disasters like earthquakes, or geopolitical events such as wars. Such unexpected occurrences can drastically alter the behavior of a system, introducing a new layer of complexity and requiring models that can accommodate these sudden shifts. In response to the need for models that could account for abrupt changes in uncertain systems, Deng et al. [11] introduced the concept of V-jumps. These jumps represent significant, discrete changes in the state of the system that occur unpredictably. The V-jumps framework has since been widely adopted as an effective tool for describing the evolution of phenomena that experience sudden shifts in response to emergencies or other unforeseen events. Furthering the theoretical foundation of V-jumps, Deng et al. [12] provided mathematical proof of the existence and uniqueness of solutions to uncertain differential equations that incorporate V-jumps. This result was crucial because it ensured that the models used to describe systems with jumps could produce reliable and consistent outcomes, even when dealing with abrupt changes in system behavior. Following the development of uncertain differential equations with V-jumps, these mathematical models became widely adopted in the field of optimal control, particularly in situations where sudden, unpredictable changes, or jumps, occur within a system. The application of V-jumps allowed for more realistic and nuanced modeling of systems that are prone to abrupt shifts in state, making them especially useful in optimizing control strategies under uncertain conditions. One notable example of this application is found in the work of Deng [13,14,15], who explored uncertain optimal control models incorporating jumps. Deng also extended this investigation to linear quadratic models with jumps, all under the expected value evaluation criteria. These models were designed to minimize the cost or maximize the efficiency of control in systems where both linear dynamics and sudden jumps played significant roles, with the expected value approach providing a means of balancing the trade offs between different outcomes. Further extending the reach of uncertain jump models, Chen et al. [16] studied the optimal control of uncertain uncertain dynamic systems with jumps, applying their findings to practical scenarios such as advertising models. This work demonstrated the usefulness of such models in optimizing strategies for dynamic, unpredictable environments like the advertising market, where shifts in consumer behavior or market conditions can cause sudden changes in outcomes. In general terms, the expected value model is an effective measurement tool when assessing uncertain systems. By using the concept of a weighted average, this model provides a pragmatic way to account for various possible outcomes, assigning each one a belief degree and calculating the expected or average result. This approach works particularly well in situations where the range of possible outcomes is not extreme, and where a balanced, middle-ground prediction is appropriate for decision making. However, in cases where data polarization, meaning the outcomes are highly skewed or concentrated around extreme values, becomes a significant factor, or when other unique characteristics of uncertain variables must be considered, the optimistic value model offers a more suitable alternative. Unlike the expected value model, which seeks a middle ground, the optimistic value model focuses on the most favorable outcomes, making it more appropriate when decision makers prioritize the best case scenarios in uncertain environments. In contrast to the expected value approach, Deng and Chen [17,18], along with Deng et al. [19], conducted extensive research into optimistic value models within the context of uncertain optimal control with jumps. Their work aimed to explore how optimal control strategies could be devised when the focus shifts from an average, balanced outcome to a more optimistic outlook, prioritizing the potential for the best possible results despite the presence of uncertainties and sudden jumps in the system.
Building on the foundation of uncertain optimal control, Sun et al. [20] and Li et al. [21] expanded their research to address differential game problems under uncertainty, focusing specifically on the optimistic value criterion. Their study examined a counter-terror economic game model in an uncertain setting, though without the added complexity of jumps or delays. This work aimed to apply the optimistic value criterion in game theory, enabling strategic decision making in scenarios dominated by uncertainty. Jia et al. [22,23] subsequently broadened the scope by investigating uncertain differential games involving multiple factors and, notably, uncertain jumps in a multidimensional context. Their research offered significant insights into modeling and control of strategic interactions where multiple dimensions and abrupt changes introduce further unpredictability. In the realm of uncertain stochastic jump systems, Jia and Liu [24] explored a hybrid differential game system with V-n jumps, a form of sudden shift in the system. They introduced equilibrium strategies such as saddle point equilibria, indicating states where neither player can unilaterally gain an advantage. This theoretical advancement was applied to a practical case of an advertising duopoly game, where two firms compete in a market marked by stochastic elements and sudden shifts. Chen et al. [25] further advanced the field by analyzing optimal control and zero-sum games in systems characterized by multifactor uncertainty, where each factor could experience sudden jumps. Their research tackled these challenges, presenting strategies to optimize outcomes in highly unpredictable conditions. Besides their work on differential games, Jia et al. [26] contributed to the mathematical foundation by proving theorems on the existence and uniqueness of solutions for uncertain delay differential equations with jumps, ensuring that these models are mathematically robust under specified conditions. Real-world differential game problems are often characterized by combinations of uncertainty, time delays, and abrupt events. This complex setting requires adaptive models that account for uncertain, delayed, and sudden occurrences. To address these complex game problems, we will employ uncertain delay differential equations with jumps. These equations capture the dynamics of differential games influenced by Liu noises, time delays, and abrupt changes, all under the optimistic value criterion. This approach enables a focus on favorable outcomes in a highly uncertain environment, allowing for more strategic and optimistic decision making.
The contributions of this paper are: (1) to obtain the Nash equilibrium of an uncertain delay linear quadratic differential game optimistic value model with a jump; (2) to obtain the saddle equilibrium of an uncertain delay linear quadratic differential game optimistic value model with a jump. According to different optimization purposes, the expected value and optimistic value are different evaluation criterion. The results [9] of the expected model for uncertain control systems cannot be directly used for an optimistic value model. Compared with the models in Ref. [9], we extend the results to the uncertain delay linear quadratic differential game optimistic value model with a jump. Compared with the models in Ref. [20], we introduce jump factors and delays, and extend the model to the multidimensional case. In addition, we also consider Nash equilibrium solutions, and the optimistic value models in our paper are more complex and more practical due to the existences of jumps and delays; and (3) to apply the model to solve a carbon emission reduction game problem.
The structure of this paper is organized as follows. Section 2 will collect some preliminary results including the -optimistic value, Liu process, V-jump process, and so on, which are essential for our analysis. In Section 3, we pose a linear quadratic differential game optimistic value problem under an uncertain jump and delay environment. By transform, the infinite dimension problem is transformed into a finite dimension; then, we obtain the existence condition of the Nash equilibrium strategy that is equivalent to the existence solution of two cross-coupled matrix Riccati equations. Section 4 is devoted to the study of the saddle point equilibrium problem of the uncertain delay linear quadratic differential game optimistic value model with a jump. The application is given to show the validity of the obtained results in Section 5.
2. Preliminaries
In this section, we review some preliminaries including the -optimistic value, Liu process, V-jump process, and so on.
Definition 1
([4]). Let ξ be an uncertain variable, be an uncertain measure, and the confidence level Then, is called the β-optimistic value to ξ; and is called the β-pessimistic value to ξ.
Definition 2
([4]). An uncertain process is a Liu process with respect to time t if it satisfies the following:
- (a)
- and almost all sample paths are Lipschitz continuous;
- (b)
- is in independent increments and stationary;
- (c)
- Every increment is a normal uncertain variable with expected value 0 and variance , and its uncertainty distribution is
Remark 1.
Liu [27] challenged the widely accepted presumption of Ito’s calculus in 2013, and believed that Liu’s calculus is a potential tool for the stock market. For example, Liu et al. [28] considered the real Alibaba stock prices from 1 January 2019 to 30 June 2020. Ye et al. [29] considered USD–CNY exchange rates from 1 October 2019 to 30 June 2021. The experiments showed that the residuals are far from frequency stability, and should not be regarded as random variables, but rather as uncertain variables. At the same time, the uncertain differential equations driven by the Liu process were very suitable for simulating these two real cases.
The definition of V-jump uncertain process is as follow:
Definition 3
([11]). A V-jump uncertain process with parameters and for is defined if
- (i)
- (ii)
- has stationary and independent increments;
- (iii)
- For any given time every increment is a Z jump uncertain variable for , whose uncertainty distribution is
Definition 4
([12]). Suppose that is an uncertain Liu process with respect to time t, is an uncertain V-jump process with respect to time t, and , and ν are some given functions about and t. Then,
is called an uncertain differential equation with a V-jump.
Deng et al. [19] presented the following general multidimensional uncertain optimal control model with V-n jumps:
where is an n-dimensional state vector with the initial condition at time t, is the decision vector of dimension m (represents the control function of time s and state ) in a domain the objective function, and is the terminal reward function. In addition, is a column-vector function about s, , and , and are two matrix functions about s, , and , and , , where are independent Liu processes, are independent V-n jumps processes, and and for any are independent, and the final time is fixed or free.
Definition 5
([19]). Suppose is a V-jump process with parameters and , and let . Then, the β-optimistic value and β-pessimistic value are defined for any belief degree
and
respectively.
Lemma 1
([19]). If exists and is twice differentiable on Then, we have
where is the partial derivatives of the function in t. is the gradient of in τ represents the transpose, and and are the 1-norm for vectors, that is, and for respectively. are defined the same as Equation (1), and denote respectively, and
- (1)
- if (all terms are nonnegative), then or or ;
- (2)
- if (all terms are negative), then or or .
Lemma 2.
Suppose is a Liu process and is a V-jump process, and let be a continuously differentiable function. Then, is an uncertain process and
Similar to the proof of Theorem 4 of Ref. [3], Lemma 2 can be easily obtained.
3. Main Results
Real-world differential game problems are often characterized by combinations of uncertainty, time delays, and abrupt events. This complex setting requires adaptive models that account for uncertain, delayed, and sudden occurrences. To address these complex game problems, we consider the following linear uncertain delay differential systems with V-n jumps. We separately outline the system’s dynamics, constraints, and objectives for each player in the Nash equilibrium framework.
where the matrices , and are appropriate size matrix functions, state that started at time , d represents the delay, and is a constant. where are independent Liu processes. where are independent V-jump processes. The feasible strategies of the two players are: and ; is the feasible strategy set of player 1 and is the feasible strategy set of player 2. For a given confidence level the two players seek their respective optimal feasible strategies to maximize the following cost functions under the constraint of the state Equation (3), namely
where are appropriate size matrix functions, are the symmetric nonnegative definite matrix, and are the symmetric positive definite matrix. Actually, the cost functions change with the initial time t and the initial state change. Thus, we denote
where are the given initial functions and represents the space of all continuous functions on taking values in R.
The so-called Nash equilibrium problem is to find the feasible control strategies and under the system state (3)–(5) constraints such that
We note that the value functions and in (4) and (5) were defined in an infinite-dimensional space, so it is very difficult to solve it directly. We will transform the problem into a finite-dimensional space by constructing a new state. For this purpose, we use the same method as Ref. [9]. For Questions (3)–(7), we denote that
Assumption 1.
Given the feasible strategy pairs and , if follows , there exists an operator such that
where and present the Jacobi matrices of in x and in respectively.
Let For we denote , and where is a differentiable function. Then, the new state process
Define
by
by
and by
If the functions , , , , and by transform, then a finite-dimensional model can be obtained.
Assumption 2.
There are functions
such that for all and it holds that
Theorem 1.
If , , hold in an uncertain delay linear quadratic differential game model with jumps (3), then the Nash equilibrium strategies are
and the optimal value of (3) with initial value is
where , and and satisfy the following Riccati equation.
where
- (1)
- if , then or or ;
- (2)
- if , then or or .
See Appendix A for the proof process.
4. A Linear Quadratic Game Model Under Uncertain Jump and Delay Environment
In two-person uncertain Nash differential games, when the sum of the two players’ cost function is zero, i.e., , the game degenerates to a two-person zero-sum uncertain differential game problem. In this section, we consider the saddle point problem of a linear quadratic two-person zero-sum game model under an uncertain jump and delay environment. The uncertain jump and delay dynamic system is as follows:
In the above equation, , are the control functions or decision functions. The admissible control sets are defined by , which is a measurable function, where and are nonempty closed sets. , , and are defined the same as in Model (3). For any and some given confidence level we choose the objective function as follows:
where is the continuous function of state and control, and is the continuous function of terminal reward. If there exists a pair satisfying
then the pair are called the saddle point of the zero-sum uncertain differential game.
We take as follows.
where are appropriate size matrix functions, and is the symmetric nonnegative definite matrix, and are the symmetric positive definite matrix.
Theorem 2.
For the saddle equilibrium problem (17), if , , hold and is the solution of the following Riccati differential Equation (20), then the control strategy pair of (21) are the equilibrium solutions of problem (17), and the equilibrium value is
and
where ,
- (1)
- if , then or or ;
- (2)
- if , then or or ..
Proof.
Remark 2.
Comparing with the model in Ref. [20], we introduce jump factors and delays, and extend the model to the multidimensional case. In order to obtain , we need to judge the sign of , which undoubtedly increases the difficulty of solving the problem. Further, when we know the positive or negative of , then this problem is easier to solve. Therefore, we consider a necessary and sufficient condition for the existence of the saddle point of a special one-dimensional model that can be used in later application.
In the above model, , , , , , are continuous bounded functions, and and are the given constants. represents the equilibrium reward obtainable in .
We note that the value functions in (23) were defined in an infinite-dimensional space, so we will use the idea of Section 3 to transform the problem into a finite-dimensional space by constructing a new state For this purpose, we adopt the above Assumption 1 again. For Questions (22) and (23), we denote that
Define by
by
and by
If the functions , , and , F as well as h depend on through only, then the problem could be reduced to a finite-dimensional problem.
Assumption 3.
There are functions
such that for all it holds that
Now, we can transform the infinite-dimensional saddle point equilibrium problems into finite-dimensional saddle point equilibrium problems by For define Then, for the saddle equilibrium problem of the one-dimensional case of the objective function (18) and model (22) is equivalent to solving (27)–(29).
Theorem 3.
If , , and hold in Model (22), then a necessary and sufficient condition for the equilibrium solutions to Problem (22) is
where , and satisfies:
where or or ;
The equilibrium value is
See Appendix A for the proof process.
5. Carbon Emission Reduction Problem
Delays and jumps are ubiquitous in economic and management issues, such as in consumption and carbon emission reduction. We will analyze a carbon emission reduction economic game model under an uncertain jump and delay environment. The problem is crucial for addressing global climate change and is widely studied in environmental economics, policy design, and sustainability sciences. A carbon emission reduction game problem involves modeling the strategic interactions between different players, such as countries, companies, or industries, who aim to reduce carbon emissions while balancing their economic interests. The problem typically focuses on how these players can optimize their strategies to achieve emission reduction targets, considering costs and regulatory policies. In the following carbon emission reduction model, represents the carbon-emitting resources stock of carbon-emitting enterprises, which not only represents the assets owned by carbon-emitting enterprises, but also includes a comprehensive quantified value of electricity, coal, oil, and natural gas. It is a widely recognized fact that the provision of essential energy resources such as electricity, coal, oil, and natural gas can experience delays. These delays may stem from a variety of causes including logistical challenges, infrastructure limitations, regulatory hurdles, and unpredictable events such as natural disasters or geopolitical conflicts. Thus, the assets are not only related to the time but also affected by at time and indicates the assets of the time period , are a constant. The growth rate of is a linear function of , , carbon emissions, and government input measures. Moreover, despite the fact that governments and enterprises from various countries are actively taking measures to reduce carbon emissions, address global climate change, and promote sustainable development, the reality is often cruel. Certain groups or individuals, motivated by varied interests such as political gain, economic advantage, or other benefits, secretly endorse practices that increase carbon emissions. The influence of this part of “funding behind” cannot be ignored and therefore must be taken into account in analytical frameworks. However, their behavior is secretive and therefore not easily detected, and we cannot obtain sufficiently detailed data on their behavior. In this context, the expertise of criminal psychology professionals or specialists in carbon emission mitigation, particularly those focused on carbon policy, becomes invaluable. Their knowledge and experience are essential for evaluating the impact of this “funding behind” on the resources of carbon-emitting enterprises. In dealing with expert opinions, we adopt the uncertainty theory as a powerful tool, and consider that the carbon-emitting event itself is an emergency, so we describe the influence of “funding behind” as an uncertain jump process. In addition, considering the harmfulness and destructiveness of carbon-emitting enterprises, the average evaluation criterion of expected value is inappropriate for modeling the carbon emission reduction economic because it often ignores the interests of the majority of people. For the carbon emission reduction economic model, we believe that the optimistic value model is a relatively more appropriate choice because a certain confidence level (here, the confidence level is the success rate of the decision) can be selected, which also takes into account the interests of the majority. Thus, the model in a limited time horizon is as follows:
where
where is the frequency of corporate carbon emissions and is government input measures. The performance index represents the economic losses caused by carbon emissions, and and , , and are the given positive constants. Let then, it is obvious that holds, and that Assumption 1 holds. It is easy to see that Assumption 3 holds. Using Theorem 3, we can write the Riccati equation:
and we obtain
where owing to , then or or .
The equilibrium strategy is obtained as follows:
The equilibrium values are given as follows:
and
where , and . In order to explain the problem clearly, we take the following parameters:
We let , then and . We take , and then we obtain the equilibrium value of different belief degree Meanwhile, we give the dynamic change curve of the equilibrium strategy and equilibrium value of different belief degree According to Ref. [20], the equilibrium value without state delays and V-jumps process is
By taking the same parameters, we give the equilibrium value of various belief degrees without state delays and the V-jumps process as the comparison.
To study the influence of parametric errors on the carbon emission reduction model, let us take the parameter as an example. Based on the equilibrium value and error curves analysis, we firstly performed a sensitivity analysis; we perturbed the parameter by 10% to examine the effect of this change on the equilibrium values both with and without delays. The results indicate that the equilibrium values are highly sensitive to changes in , especially in the lower range, where the variation is more pronounced.The analysis shows that in the “no delay” case, the equilibrium values exhibit more dramatic fluctuations in response to changes in compared to the “with delays” case. The sensitivity curves demonstrate that the model reacts differently to parameter perturbations depending on whether state delays are included or not.
Then, we performed an error propagation analysis to assess the impact of parameter uncertainty (e.g., ± 5%) on the equilibrium values. The results display the error bounds (upper and lower limits) for both the “no delay” and “with delays” cases.The “no delay” scenario shows larger error bounds compared to the “with delays” case, indicating greater sensitivity to parameter errors. In contrast, the “with delays” model exhibits more robustness to parameter errors, with smaller variations in equilibrium values.
Figure 1a illustrates the smooth equilibrium values for both the “no delay” and “with delays” scenarios as functions of . As increases, the equilibrium values decrease in both cases, but the decline is sharper in the “no delay” case. The graph also presents the comparison between the original equilibrium values and those after a 10% perturbation in . The perturbed curves deviate more noticeably from the original in the “no delay” case, indicating higher sensitivity to parameter changes. Figure 1b displays the equilibrium values with a ±5% parameter error. The error bounds are plotted as smooth curves above and below the original equilibrium values. In the “no delay” scenario, the error bounds are wider, reflecting a higher sensitivity to parameter uncertainty. In contrast, the “with delays” scenario has narrower error bounds, indicating more stability and resistance to parameter error.
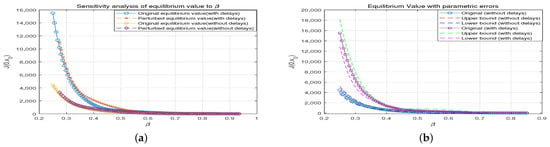
Figure 1.
The equilibrium value. (a) Sensitivity analysis of equilibrium value. (b) Equilibrium value with parametric errors.
Through sensitivity and error propagation analysis, it is evident that the “no delay” model is more sensitive to parameter changes and errors compared to the “with delays” model. This suggests that the “with delays” model demonstrates better robustness in the face of parameter uncertainties. The influence of on the equilibrium values is particularly significant in the lower range. The error analysis reveals that parameter errors can have a substantial impact on model predictions, especially in the “no delay” case.
Next, we present Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, which intuitively illustrate the equilibrium strategy values and the equilibrium values.
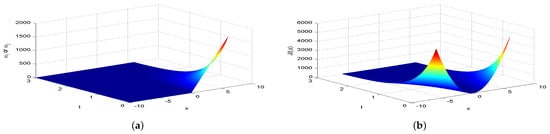
Figure 2.
The equilibrium strategy value (a) and the equilibrium value (b) when .
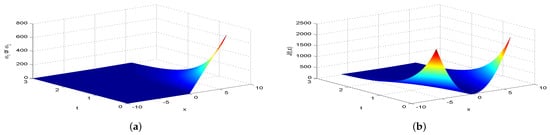
Figure 3.
The equilibrium strategy value (a) and the equilibrium value (b) when .
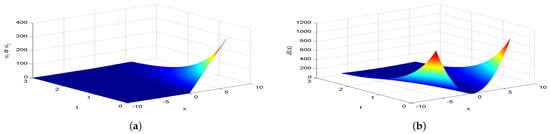
Figure 4.
The equilibrium strategy value (a) and the equilibrium value (b) when .
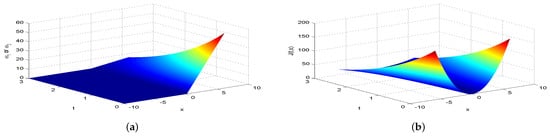
Figure 5.
The equilibrium strategy value (a) and the equilibrium value (b) when .
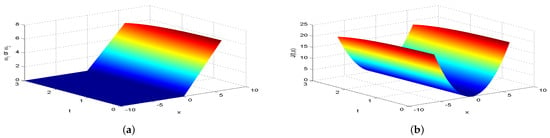
Figure 6.
The equilibrium strategy value (a) and the equilibrium value (b) when .
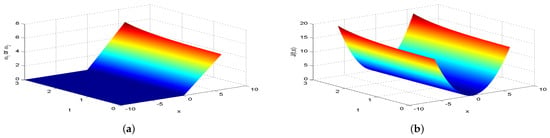
Figure 7.
The equilibrium strategy value (a) and the equilibrium value (b) when .
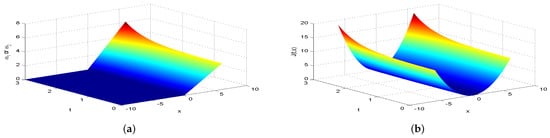
Figure 8.
The equilibrium strategy value (a) and the equilibrium value (b) when .
Table 1 shows that the belief degree represents the confidence level in reducing economic losses caused by carbon emissions. For instance, if carbon-emitting enterprises require an initial start-up fund of 10 million, they should prepare million dollars considering delays. From Table 1, we observe that the equilibrium value when , resulting in government losses of million. When , the equilibrium value is , and the government losses are million. At , the equilibrium value is , with corresponding government losses of million. When , the equilibrium value drops to , and the losses are million. At , the equilibrium value further decreases to , with losses of million. For , the equilibrium value is , and the losses are million. Finally, at , the equilibrium value is , resulting in the smallest government losses of million. This analysis reveals that both the government and carbon-emitting enterprises incur significant costs to achieve their objectives. It is also evident that due to the influence of jumps and delays, economic losses from terrorism are lower when and higher when . Among the given belief degrees, results in the least economic loss, and generally, higher values correlate with lower economic losses . Additionally, the presence of jumps and delays increases the equilibrium value compared to scenarios without these factors when . This means that economic losses rise due to jumps and delays, aligning with the real-world dynamics and the objective laws of counter-terrorism economic issues. From Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, we can intuitively observe the dynamic variation curves of the equilibrium strategy and the equilibrium value at different confidence levels . For governments, incorrect belief degrees may result in uneven resource allocation. For enterprises, mistakes in belief degrees can harm brand image and even lead to bankruptcy. Thus, improving the decision-making belief degree is crucial. Both governments and carbon-emitting enterprises must enhance the scientific and rational aspects of their decision-making processes, thoroughly considering various factors, conducting comprehensive research, and avoiding hasty decisions based on subjective assumptions. Establishing sound decision-making mechanisms and responsibility systems is also essential to ensure transparency, accountability, and support for sustainable economic and social development. In future development, governments and carbon-emitting enterprises should prioritize enhancing decision-making belief degrees by developing policies or strategies that both minimize emissions and maintain competitiveness and economic viability. Incorporating detailed economic analysis and being open to policy adjustments based on those insights will ensure that decisions are not only environmentally sound but also economically sustainable.

Table 1.
The equilibrium value of various belief degree .
6. Conclusions
This study addressed the differential game optimistic value model for uncertain delay systems with jumps. By transforming the model into a finite-dimensional framework, the research provided valuable insights into the Nash equilibrium solution specifically for uncertain delay differential game optimistic value control models that incorporate jumps. Furthermore, the study identified the saddle equilibrium solution within a linear quadratic differential game optimistic value model under conditions characterized by uncertainty, delays and sudden jumps. To illustrate these concepts in a practical context, an example of a carbon emission reduction game was presented, highlighting the implications of the theoretical findings in real-world scenarios. This example not only demonstrated the applicability of the developed models but also underscored the critical role of strategic decision making in addressing pressing environmental challenges. Looking ahead, future research could delve deeper into both theoretical and practical dimensions. On the theoretical side, exploring more complex game structures involving singular systems, switched systems, or other non-linear systems could enhance our understanding of strategic interactions in uncertain environments. Investigating alternative criteria for decision making beyond the optimistic value might also yield new insights into equilibrium concepts and stability conditions. In terms of practical applications, expanding the scope of case studies to include diverse fields such as renewable energy adoption, transportation emissions, public policy, and financial markets could demonstrate the versatility of the proposed models. Additionally, incorporating real data and advanced computational techniques could facilitate dynamic modeling, allowing for more responsive and adaptive strategies in uncertain environments.
Funding
The authors are supported by the Suqian Sci & Tech Program (Grant No. K202332) and the Startup Foundation for Newly Recruited Employees of Suqian University (Grant No. 2024XRC004).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Lemma A1.
Let be a continuously differentiable function, and given the feasible strategy pairs and , here, follows . Then, the uncertain process satisfies
Proof.
Given the feasible strategy pairs , and denoting by then, the process has the representation
Thus, Applying Lemma 2 to Equation (A1) follows.
□
Lemma A2.
Suppose that Assumptions 1 and 2 hold and is twice differentiable on Then, we have
and where is the partial derivative of the function in and is the gradient of in
- (1)
- If , then or or ;
- (2)
- if , then or or .
Proof.
Thus, In the same way, we obtain that □
Proof of Theorem 1.
Let ; then, Assumption 1 holds. Further, we have
Therefore, Assumption 2 holds if and only if:
Then, the following finite-dimensional Nash equilibrium problem can be obtained by the transformation of .
It follows from the optimality condition of Lemma A2 that:
that is,
where
where k depends on . Owing to ,
- (1)
- if , then or or ;
- (2)
- if , then or or . Let
we can obtain that
Owing to , we can guess
Then,
Thus, (A10) can be written as:
On the other hand, there is:
We denote
Considering that , we obtain
Considering that , we obtain
The proof is completed. □
For problem (27)–(29), we first give the equilibrium equation of the optimistic value model as follows:
Lemma A3.
Suppose that Assumptions 1 and 3 hold and is twice differentiable on Then, the equilibrium equation holds:
Proof.
Applying Lemma 1 to (P1) and (P2), it holds that
By (A15), it holds that
Similarly, from (A16), it holds that
Let
We note that
By (A19), we obtain
Together with (A17) and (A18), the lemma is completed. □
Proof of Theorem 3.
First, we verify the necessity. Let , then Assumption 1 holds. Further, we have
Therefore, Assumption 3 holds if and only if and , hold. Then, the following finite-dimensional saddle equilibrium problem can be obtained by the transformation of .
Since is quadratic about We guess
and
Applying the equilibrium Equations (A13) and (A14) of Lemma A3, we have
By the property of optimistic value and the assumptions , , it is easy to see Thus,
Since is strictly concave about , is strictly convex about . Thus, the equilibrium controls and satisfy
Thus, we obtain the strategy pairs
Thus, it holds that
Owing to , and , then or or .
Next, we verify the sufficient condition. We let satisfy Equation (A24). Then, it holds that
From 0 to T, integrating the above equation leads to
Substituting it into of (A21), we obtain
Obviously, the equilibrium solutions are of (A23). Then, the theorem is completed.
□
References
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin, Germany, 2010. [Google Scholar]
- Liu, B. Fuzzy process, hybrid process and uncertain process. J. Uncertain Syst. 2008, 2, 3–16. [Google Scholar]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Barbacioru, I. Uncertainty functional differential equations for finance. Surv. Math. Its Appl. 2010, 5, 275–284. [Google Scholar]
- Ge, X.; Zhu, Y. Existence and uniqueness theorem for uncertain delay differential equations. J. Comput. Inf. Syst. 2012, 8, 41–83. [Google Scholar]
- Wang, X.; Ning, Y. Stability of uncertain delay differential equations. J. Intell. Fuzzy Syst. 2017, 32, 2655–2664. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Y. A new stability analysis of uncertain delay differential equations. Math. Probl. Eng. 2019, 2019, 1257386. [Google Scholar] [CrossRef]
- Jia, L.; Sheng, Y. Stability in distribution for uncertain delay differential equation. Appl. Math. Comput. 2019, 343, 49–56. [Google Scholar] [CrossRef]
- Chen, R.; Zhu, Y. An optimal control model for uncertain systems with time-delay. J. Oper. Res. Soc. Jpn. 2013, 54, 243–256. [Google Scholar] [CrossRef]
- Jiang, Y.; Yan, Y.; Zhu, Y. Optimal control problem for uncertain linear systems with multiple input delays. J. Uncertain Syst. 2016, 4, 5. [Google Scholar] [CrossRef]
- Deng, L.; Zhu, Y. Uncertain optimal control with jump. ICIC Exp. Lett. 2012, 3, 419–424. [Google Scholar]
- Deng, L.; Zhu, Y. Existence and uniqueness theorem of solution for uncertain differential equations with jump. ICIC Exp. Lett. 2012, 6, 2693–2698. [Google Scholar]
- Deng, L. Multidimensional uncertain optimal control of linear quadratic models with jump. J. Comput. Inf. Syst. 2012, 8, 7441–7448. [Google Scholar]
- Deng, L.; Zhu, Y. An uncertain optimal control model with n jumps and application. Comput. Sci. Inf. Syst. 2012, 9, 1453–1468. [Google Scholar] [CrossRef]
- Deng, L.; Zhu, Y. Uncertain optimal control of linear quadratic models with jump. Math. Comput. Model. 2013, 57, 2432–2441. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Y.; Sheng, L. Optimal control for uncertain stochastic dynamic systems with jump and application to an advertising model. Appl. Math. Comput. 2021, 407, 126337. [Google Scholar] [CrossRef]
- Deng, L.; Zhu, Y. Optimistic value model of uncertain linear quadratic optimal control with jump. J. Adv. Comput. Intell. Intell. Inf. 2016, 20, 189–196. [Google Scholar] [CrossRef]
- Deng, L.; Chen, Y. Optimal control of uncertain systems with jump under optimistic value criterion. Eur. J. Control 2017, 38, 7–15. [Google Scholar] [CrossRef]
- Deng, L.; You, Z.; Chen, Y. Optimistic value model of multidimensional uncertain optimal control with jump. Eur. J. Control 2018, 39, 1–7. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, C.; Zhu, Y. Saddle point equilibrium under uncertain environment. Math. Methods. Appl. Sci. 2018, 41, 2063–2073. [Google Scholar] [CrossRef]
- Li, B.; Zhang, R.; Jin, T.; Shu, Y. Parametric approximate optimal control of uncertain differential game with application to counter terror. Chaos Solitons Fractals 2021, 146, 110940. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, X. Optimal control of multifactor uncertain system with jumps. Int. J. Control 2023, 96, 1272–1287. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, X. Optimistic value models of saddle point equilibrium control problems for uncertain jump systems. Optimization 2024, 1–35. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, X. Uncertain stochastic hybrid differential game system with V-n jumps:Saddle point equilibrium, strategies and application to advertising duopoly game. Chaos Solitons Fractals 2023, 171, 113490. [Google Scholar] [CrossRef]
- Chen, X.; Tian, C.; Jin, T. Optimal control and zero-sum game subject to multifactor uncertain random systems with jump. Optimization 2023, 1–42. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, X.; Li, C. Existence, uniqueness, and stability of uncertain delay differential equations with V-jump. Adv. Differ. Equ. 2020, 2020, 440. [Google Scholar] [CrossRef]
- Liu, B. Toward uncertain finance theory. J. Uncertain. Anal. Appl. 2013, 1, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, B. Residual analysis and parameter estimation of uncertain differential equations. Fuzzy Optim. Decis. Mak. 2022, 21, 513–530. [Google Scholar] [CrossRef]
- Ye, T.; Liu, B.; Li, C. Uncertain hypothesis test for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2023, 22, 195–211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).