Advanced Exergy-Based Optimization of a Polygeneration System with CO2 as Working Fluid
Abstract
1. Introduction
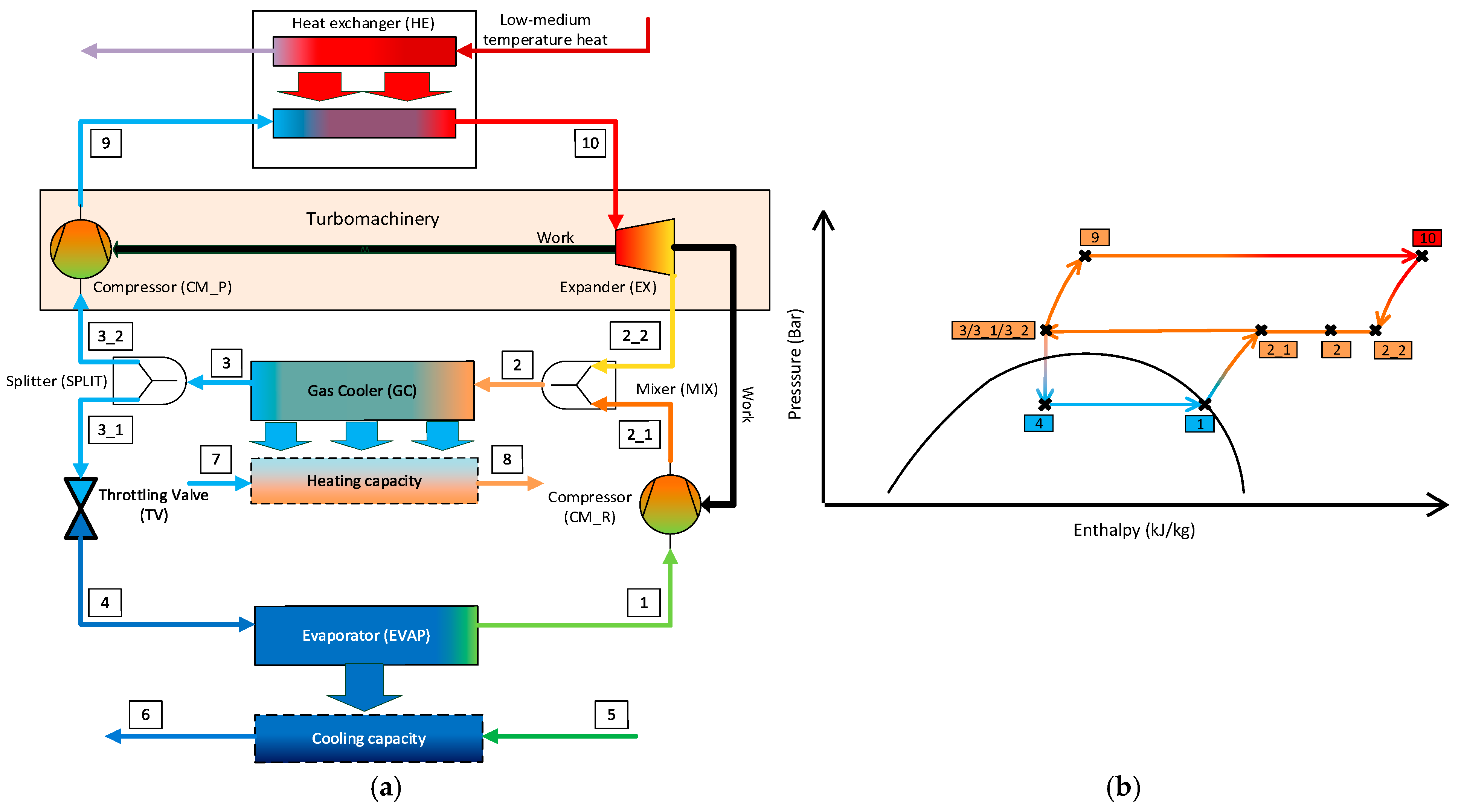
- The power cycle consists of a compressor for the power cycle (CM–P), a heat exchanger (HE), and an expander (EX). The “driving energy” is a medium-temperature heat source.
- The refrigeration cycle consists of a throttling valve (TV), an evaporator (EVAP), and a compressor for the refrigeration cycle (CM–R). The refrigeration capacity is generated within the EVAP.
2. Methodology
2.1. Advanced Exergy-Based Analysis
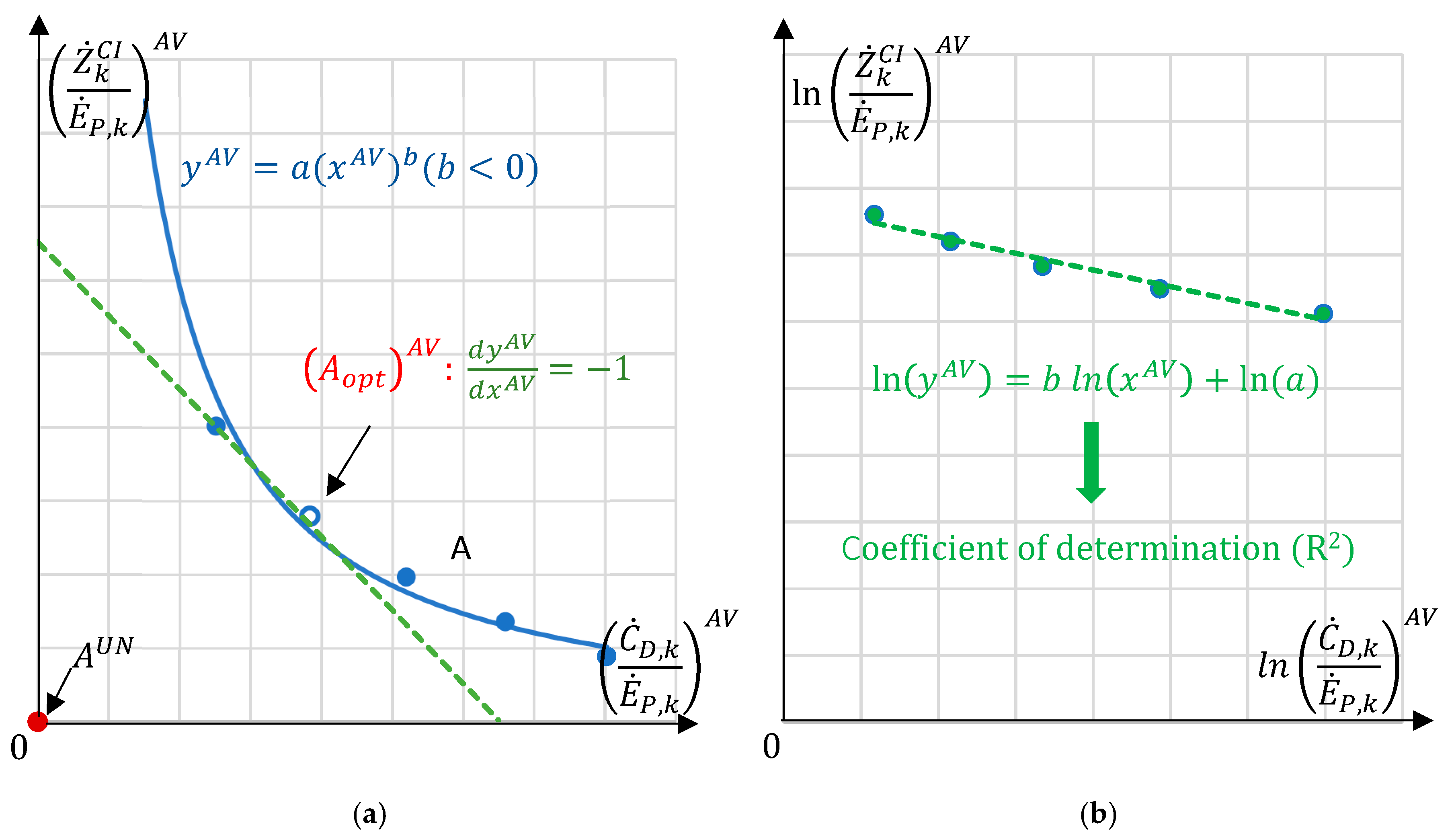
2.2. Advanced Exergy-Based Graphical Optimization
3. Results and Discussion
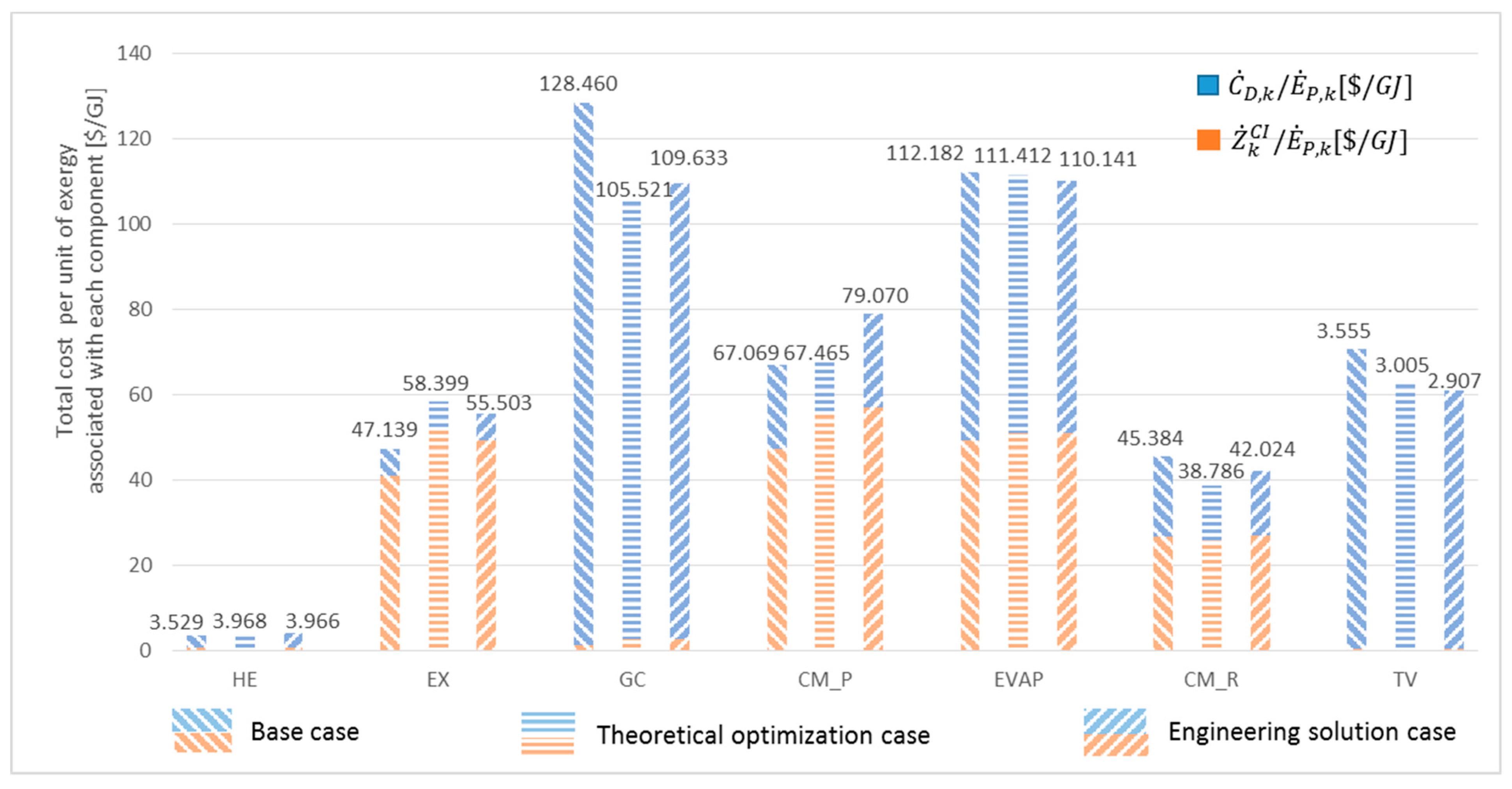
3.1. Results of Advanced Exergy-Based Analyses
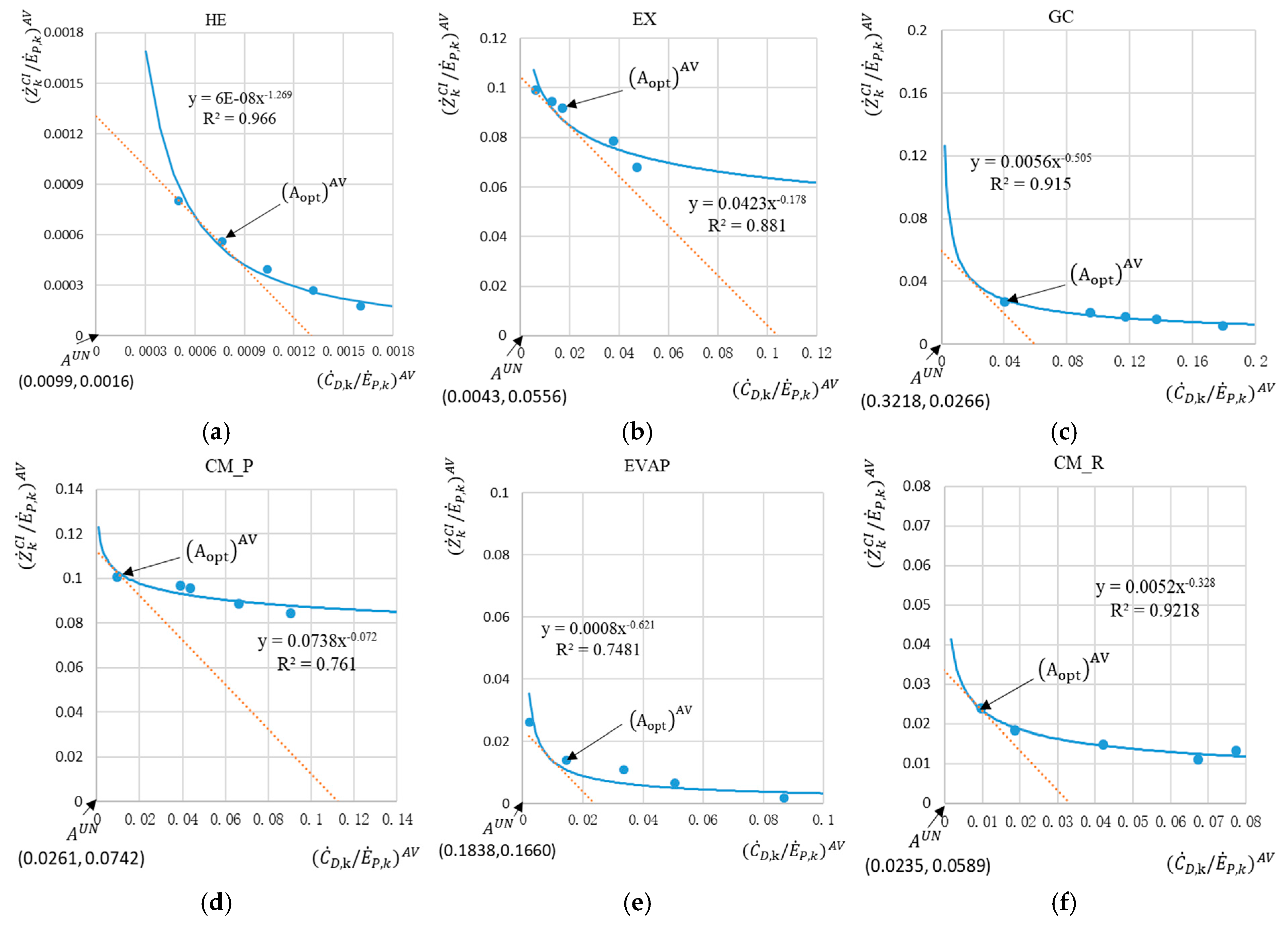
3.2. Results of Advanced Exergy-Based Graphical Optimization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| fuel cost per unit of exergy of kth component, USD/kWh | |
| product cost per unit of exergy of kth component, USD/kWh | |
| destruction cost rate associated with kth component, USD/h | |
| mechanical exergy rate of ith stream, kW | |
| thermal exergy rate of ith stream, kW | |
| fuel exergy rate of kth component, kW | |
| product exergy rate of kth component, kW, | |
| exergy destruction rate of kth component, kW | |
| avoidable exergy destruction rate of kth component, kW | |
| unavoidable exergy destruction rate of kth component, kW | |
| material factor for the calculation of purchased equipment cost, - | |
| exergoeconomic factor of kth component, % | |
| modified exergoeconomic factor of kth component, % | |
| THS | thermodynamic average temperature of the stream of matter providing the low to medium-grade heat, K |
| capital investment cost rate of kth component, USD/h | |
| avoidable capital investment cost rate of kth component, USD/h | |
| unavoidable capital investment cost rate of kth component, USD/h | |
| pinch point temperature difference, K | |
| exergetic efficiency of kth component, % | |
| modified exergetic efficiency of kth component, % | |
| isentropic efficiency, % | |
| Abbreviations | |
| CM–P | compressor in power sub-cycle |
| CM–R | compressor in refrigeration sub-cycle |
| EVAP | evaporator |
| EX | expander |
| GC | gas cooler |
| HE | heat exchanger |
| MIX | mixer |
| SPLIT | splitter |
| TV | throttling valve |
References
- IEA. World Energy Outlook 2023. Available online: https://www.iea.org/reports/world-energy-outlook-2023 (accessed on 5 August 2024).
- Liu, P.; Gerogiorgis, D.I.; Pistikopoulos, E.N. Modeling and optimization of polygeneration energy systems. Catal. Today 2007, 127, 347–359. [Google Scholar] [CrossRef]
- Chicco, G.; Mancarella, P. Trigeneration primary energy saving evaluation for energy planning and policy development. Energy Policy 2007, 35, 6132–6144. [Google Scholar] [CrossRef]
- Lorentzen, G. Revival of carbon dioxide as a refrigerant. Int. J. Refrig. 1994, 17, 292–300. [Google Scholar] [CrossRef]
- Luo, J.; Morosuk, T.; Tsatsaronis, G. Exergoeconomic investigation of a multi-generation system with CO2 as the working fluid using waste heat. Energy Convers. Manag. 2019, 197, 111882. [Google Scholar] [CrossRef]
- Tashtoush, B.; Luo, J.; Morosuk, T. Exergy-Based Optimization of a CO2 Polygeneration System: A Multi-Case Study. Energies 2024, 17, 291. [Google Scholar] [CrossRef]
- Morosuk, T.; Tsatsaronis, G. Advanced exergy-based methods used to understand and improve energy-conversion systems. Energy 2019, 169, 238–246. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Morosuk, T.V. Advanced Exergoeconomic Evaluation and its Application to Compression Refrigeration Machines. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, IMECE 2007, Seattle, WA, USA, 11–15 November 2007. IMECE2007-412202. [Google Scholar]
- Morosuk, T.; Tsatsaronis, G. Splitting physical exergy: Theory and application. Energy 2019, 167, 698–707. [Google Scholar] [CrossRef]
- Cain, J.W. Mathematics of fitting scientific data. In Molecular Life Sciences: An Encyclopedic Reference; Bell, E., Ed.; Springer: New York, NY, USA, 2014; pp. 1–7. [Google Scholar]

| Component | ||
|---|---|---|
| HE | ||
| EX | ||
| GC | ||
| CM_P | ||
| CM_R | ||
| EVAP | ||
| TV | ||
| MIX | Dissipative Component: | |
| SPLIT | - | - |
| Overall System | ||
| Component | Parameter [Unit] | “Best” Case | Base Case | “Worst” Case |
|---|---|---|---|---|
| HE | 5 | 20 | 40 | |
| EX | 98 | 90 | 70 | |
| GC | 1 | 5 | 10 | |
| CM_P | 95 | 85 | 70 | |
| EVAP | 1 | 5 | 10 | |
| CM_R | 95 | 85 | 70 |
| Component | |||||
|---|---|---|---|---|---|
| HE | 62.21 | 5.27 | 95.5 | 0.044 | 62.3 |
| EX | 1.02 | 4.49 | 94.4 | 6.967 | 95.0 |
| GC | 20.60 | 6.31 | 77.9 | 0.394 | 38.3 |
| CM_P | 1.12 | 2.56 | 90.5 | 2.333 | 87.7 |
| EVAP | 2.78 | 1.06 | 86.8 | 0.075 | 39.5 |
| CM_R | 1.93 | 4.45 | 90.3 | 0.851 | 60.1 |
| TV | 13.93 | 8.73 | 61.5 | 0.002 | 0.5 |
| MIX | 9.58 | 2.87 | - | 0.000 | 0.0 |
| Base Case | Optimization Results | Engineering Solution | Improvement Potential | |
|---|---|---|---|---|
| Operating parameters for each component | ||||
| HE | ΔT = 20 K | ΔT = 15 K | ΔT = 15 K | high |
| EX | η = 0.9 | η = 0.9 | η = 0.9 | relatively low |
| GC | ΔT = 5 K | ΔT = 2 K | ΔT = 2 K | highest (possible but difficult) |
| CM_P | η = 0.85 | η = 0.90 | η = 0.85 | relatively low |
| EVAP | ΔT = 5 K | ΔT = 4 K | ΔT = 4 K | lowest |
| CM_R | η = 0.85 | η = 0.92 | η = 0.85 | low |
| Exergetic and exergoeconomic analysis | ||||
| 16.5 | 19.1 | 18.4 | ||
| 0.00 | 0.00 | 0.00 | ||
| 6.95 | 7.14 | 7.14 | ||
| 22.21 | 17.21 | 18.21 | ||
| 0.47 | 0.31 | 0.31 | ||
| 0.82 | 0.57 | 0.58 | ||
| 0.84 | 0.86 | 0.84 | ||
| 0.83 | 0.78 | 0.76 | ||
| Relative change to the base case | ||||
| Overall exergetic efficiency | 15.4% | 11.3% | ||
| Overall average product cost | −7.1% | −8.5% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Zhu, Q.; Morosuk, T. Advanced Exergy-Based Optimization of a Polygeneration System with CO2 as Working Fluid. Entropy 2024, 26, 886. https://doi.org/10.3390/e26100886
Luo J, Zhu Q, Morosuk T. Advanced Exergy-Based Optimization of a Polygeneration System with CO2 as Working Fluid. Entropy. 2024; 26(10):886. https://doi.org/10.3390/e26100886
Chicago/Turabian StyleLuo, Jing, Qianxin Zhu, and Tatiana Morosuk. 2024. "Advanced Exergy-Based Optimization of a Polygeneration System with CO2 as Working Fluid" Entropy 26, no. 10: 886. https://doi.org/10.3390/e26100886
APA StyleLuo, J., Zhu, Q., & Morosuk, T. (2024). Advanced Exergy-Based Optimization of a Polygeneration System with CO2 as Working Fluid. Entropy, 26(10), 886. https://doi.org/10.3390/e26100886









