Quantum-Walk-Inspired Dynamic Adiabatic Local Search
Abstract
:1. Introduction
2. Background
2.1. Continuous Time Quantum Walk
2.2. Adiabatic Quantum Computing
3. Continuous Time Quantum Walk to Adiabatic Search Mapping
3.1. The Irreconcilability Issue: Constant Gap Catalyst Hamiltonian and Small Norm
3.2. Modified CTQW-Inspired Adiabatic Search
- the scaling factor of Hamiltonian ,
- , catalyst Hamiltonian
- the coefficient function of as .
4. Grover Search to Adiabatic Local Search Mapping
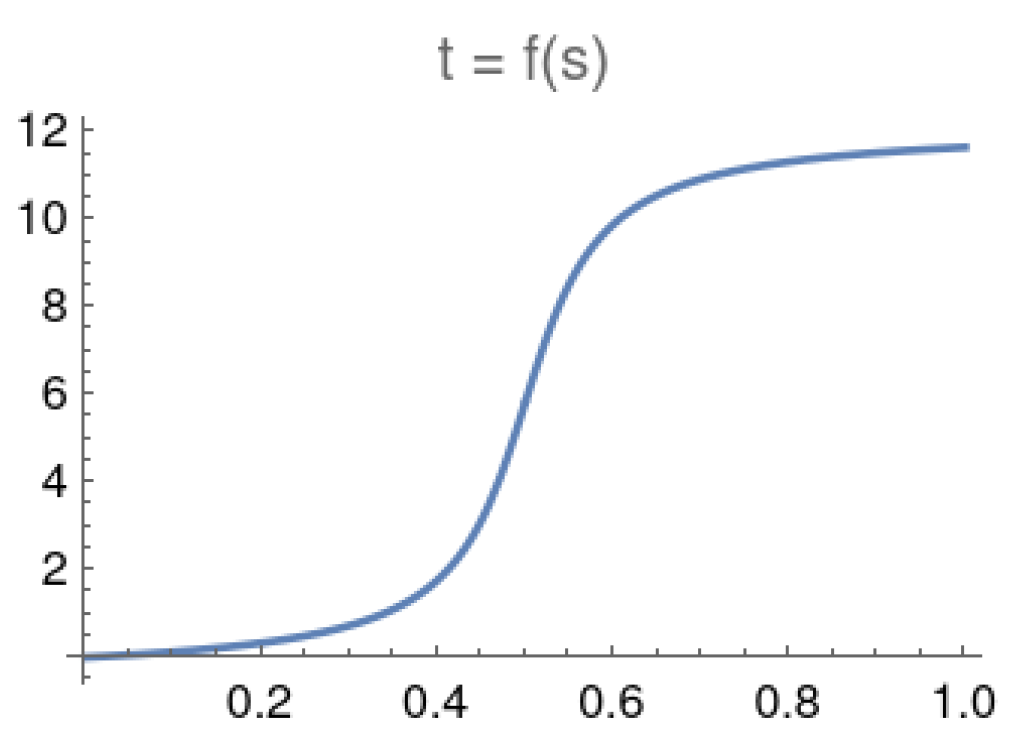
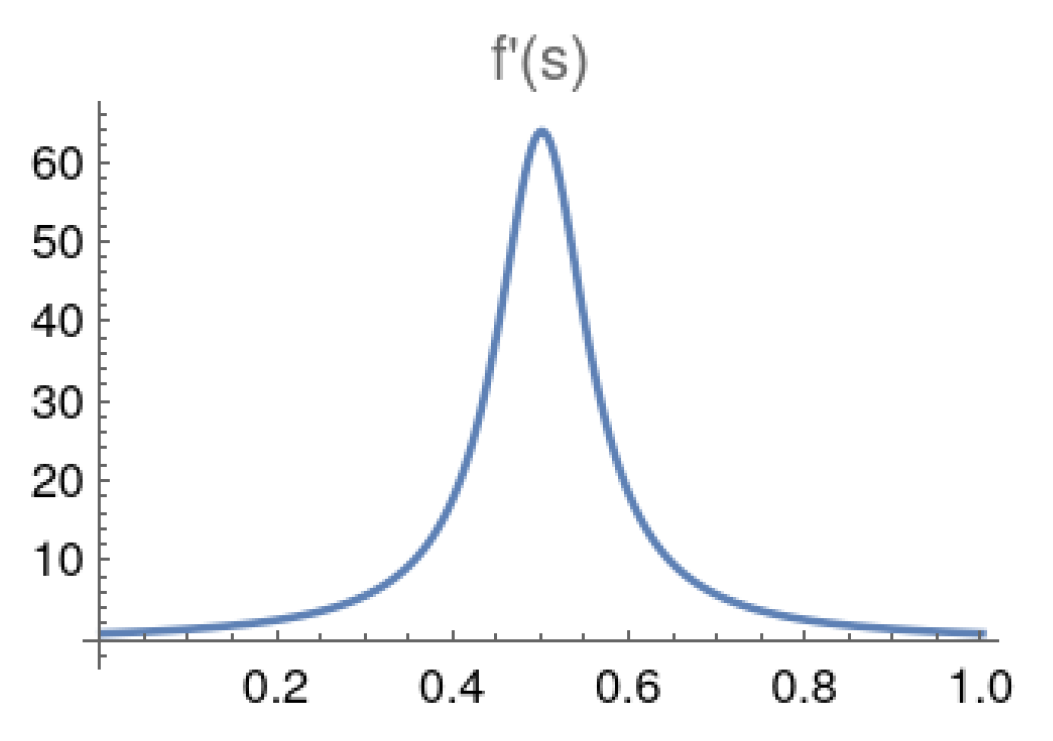
4.1. Adaptive Scheduling
4.1.1. Schedule-Dependent Gap Function
4.1.2. Determining the Sluggish Interval for the Catalyst Hamiltonian
4.1.3. Catalyst Coefficient Functions
5. Experiment and Result
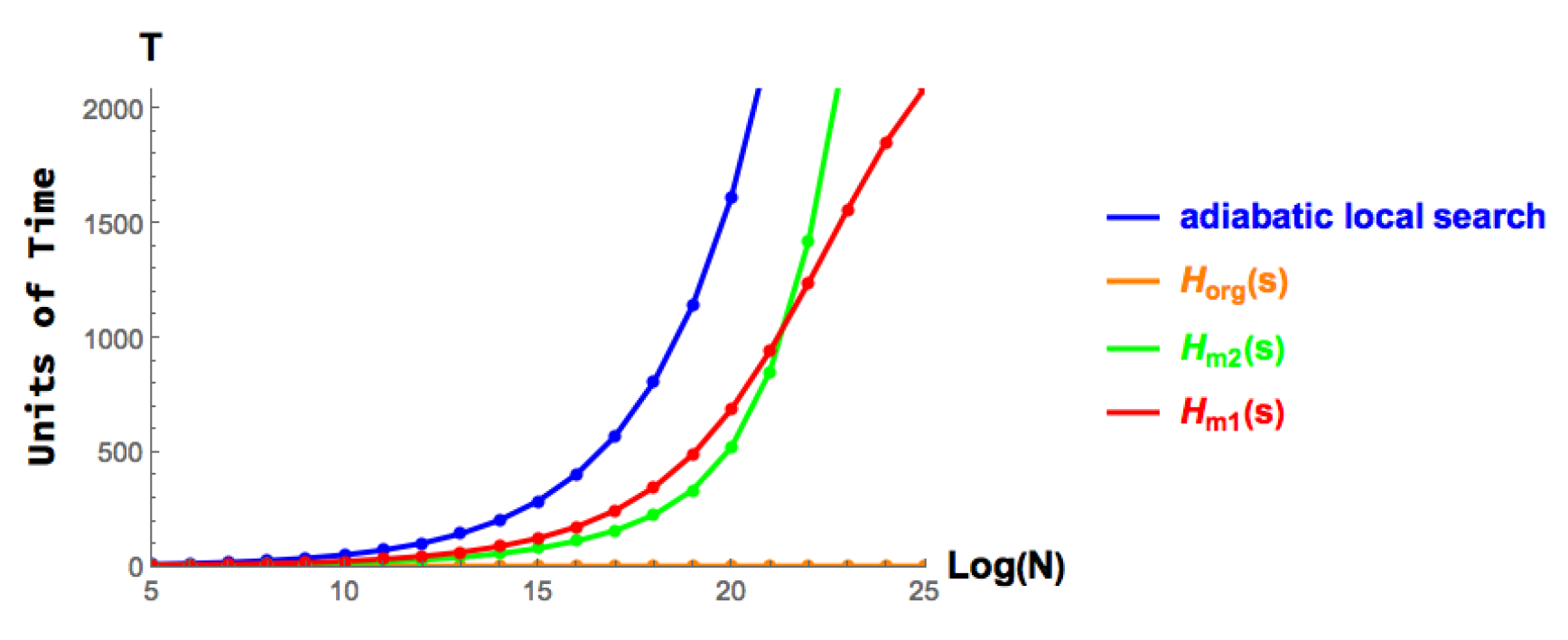
5.1. Modified CTQW-Inspired Adiabatic Search Simulation
- takes Equation (12) and drops the scaling factor as explained in Section 3.2. The adiabatic path is
- replaces the computed catalyst Hamiltonian with an ordinary Z oracle operator and keeps the magnitude M. This was used to address the constant gap irreconcilability issue. We have
- uses as the coefficient function for the catalyst Hamiltonian Z. The adiabatic path is
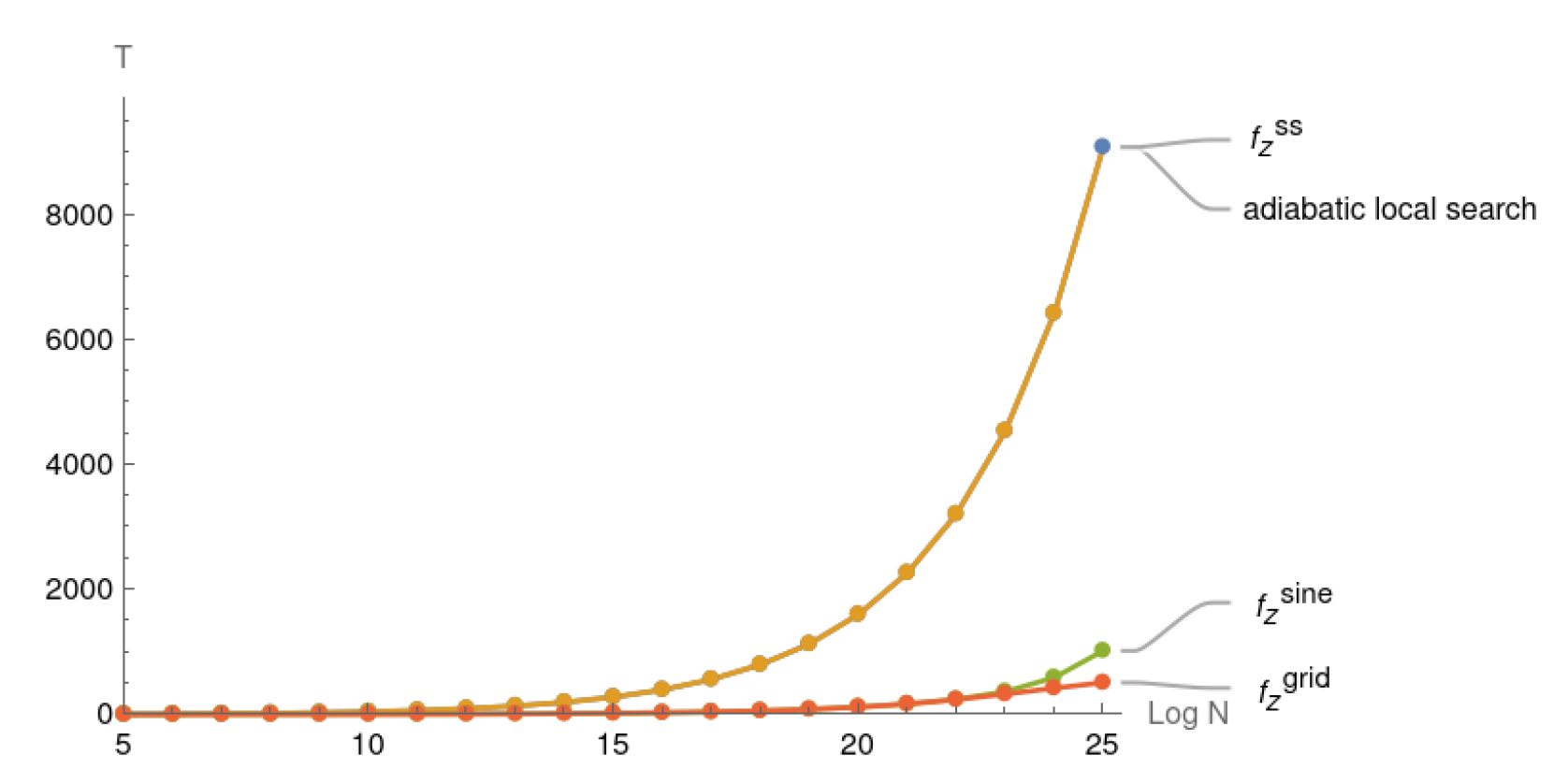
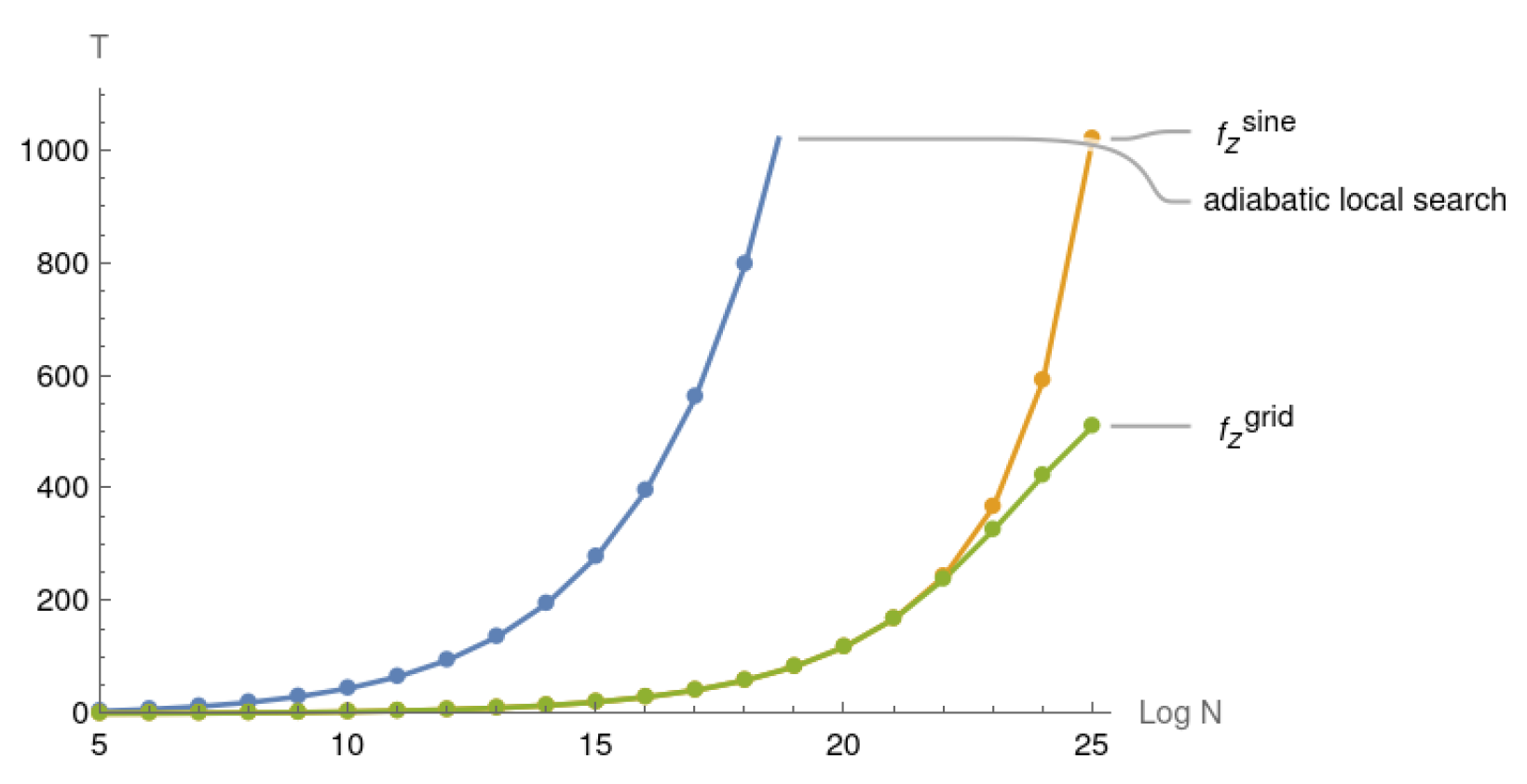
5.2. Adaptive Adiabatic Local Search Simulation with Various Coefficient Functions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Time Integration of Adiabatic Local Search
Appendix B. Energy Gap
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915. [Google Scholar] [CrossRef]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Childs, A.M. Universal computation by quantum walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef] [PubMed]
- Lovett, N.B.; Cooper, S.; Everitt, M.; Trevers, M.; Kendon, V. Universal quantum computation using the discrete-time quantum walk. Phys. Rev. A 2010, 81, 042330. [Google Scholar] [CrossRef]
- Qiang, X.; Loke, T.; Montanaro, A.; Aungskunsiri, K.; Zhou, X.; O’Brien, J.L.; Wang, J.B.; Matthews, J.C. Efficient quantum walk on a quantum processor. Nat. Commun. 2016, 7, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Caruso, F.; Chin, A.W.; Datta, A.; Huelga, S.F.; Plenio, M.B. Highly efficient energy excitation transfer in light-harvesting complexes: The fundamental role of noise-assisted transport. J. Chem. Phys. 2009, 131, 09B612. [Google Scholar] [CrossRef]
- Mohseni, M.; Rebentrost, P.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 11B603. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Bose, S. Quantum communication through an unmodulated spin chain. Phys. Rev. Lett. 2003, 91, 207901. [Google Scholar] [CrossRef]
- Kay, A. Perfect, efficient, state transfer and its application as a constructive tool. Int. J. Quantum Inf. 2010, 8, 641–676. [Google Scholar] [CrossRef]
- Omar, Y.; Moutinho, J.; Melo, A.; Coutinho, B.; Kovacs, I.; Barabasi, A. Quantum Link Prediction in Complex Networks. APS 2019, 2019, R28-003. [Google Scholar]
- Chakraborty, S.; Novo, L.; Ambainis, A.; Omar, Y. Spatial search by quantum walk is optimal for almost all graphs. Phys. Rev. Lett. 2016, 116, 100501. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W. Quantum computing. Doc. Math. 1998, 1, 1. [Google Scholar]
- Yao, A.C.C. Quantum circuit complexity. In Proceedings of the 1993 IEEE 34th Annual Foundations of Computer Science, Palo Alto, CA, USA, 3–5 November 1993; pp. 352–361. [Google Scholar]
- Jordan, S.P.; Lee, K.S.; Preskill, J. Quantum algorithms for quantum field theories. Science 2012, 336, 1130–1133. [Google Scholar] [CrossRef] [PubMed]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Sarma, S.D. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Mizel, A.; Lidar, D.A.; Mitchell, M. Simple proof of equivalence between adiabatic quantum computation and the circuit model. Phys. Rev. Lett. 2007, 99, 070502. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.F.; Hsieh, C.Y. Resonant transition-based quantum computation. Quantum Inf. Process. 2017, 16, 120. [Google Scholar] [CrossRef]
- Morimae, T.; Fujii, K. Blind topological measurement-based quantum computation. Nat. Commun. 2012, 3, 1036. [Google Scholar] [CrossRef]
- Gross, D.; Eisert, J. Novel schemes for measurement-based quantum computation. Phys. Rev. Lett. 2007, 98, 220503. [Google Scholar] [CrossRef]
- Briegel, H.J.; Browne, D.E.; Dür, W.; Raussendorf, R.; Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 2009, 5, 19–26. [Google Scholar] [CrossRef]
- Raussendorf, R.; Browne, D.E.; Briegel, H.J. Measurement-based quantum computation on cluster states. Phys. Rev. A 2003, 68, 022312. [Google Scholar] [CrossRef]
- Cutugno, M.; Giani, A.; Alsing, P.M.; Wessing, L.; Schnore, S. Quantum Computing Approaches for Mission Covering Optimization. Algorithms 2022, 15, 224. [Google Scholar] [CrossRef]
- Wong, T.G.; Meyer, D.A. Irreconcilable difference between quantum walks and adiabatic quantum computing. Phys. Rev. A 2016, 93, 062313. [Google Scholar] [CrossRef]
- Roland, J.; Cerf, N.J. Quantum search by local adiabatic evolution. Phys. Rev. A 2002, 65, 042308. [Google Scholar] [CrossRef]
- Childs, A.M.; Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 2004, 70, 022314. [Google Scholar] [CrossRef]
- Childs, A.M.; Cleve, R.; Deotto, E.; Farhi, E.; Gutmann, S.; Spielman, D.A. Exponential algorithmic speedup by a quantum walk. In Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 9–11 June 2003; pp. 59–68. [Google Scholar]
- Novo, L.; Chakraborty, S.; Mohseni, M.; Neven, H.; Omar, Y. Systematic dimensionality reduction for quantum walks: Optimal spatial search and transport on non-regular graphs. Sci. Rep. 2015, 5, 13304. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Sipser, M. Quantum computation by adiabatic evolution. arXiv 2000, arXiv:quant-ph/0001106. [Google Scholar]
- Albash, T.; Lidar, D.A. Adiabatic quantum computation. Rev. Mod. Phys. 2018, 90, 015002. [Google Scholar] [CrossRef]
- Farhi, E.; Goldston, J.; Gosset, D.; Gutmann, S.; Meyer, H.B.; Shor, P. Quantum Adiabatic Algorithms, Small Gaps, and Different Paths. Quantum Info. Comput. 2011, 11, 181–214. [Google Scholar] [CrossRef]
- Perdomo-Ortiz, A.; Venegas-Andraca, S.E.; Aspuru-Guzik, A. A study of heuristic guesses for adiabatic quantum computation. Quantum Inf. Process. 2011, 10, 33–52. [Google Scholar] [CrossRef]
- Griffiths, D.J.; Schroeter, D.F. Introduction to Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Aharonov, D.; Van Dam, W.; Kempe, J.; Landau, Z.; Lloyd, S.; Regev, O. Adiabatic quantum computation is equivalent to standard quantum computation. SIAM Rev. 2008, 50, 755–787. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiang, C.-F.; Alsing, P.M. Quantum-Walk-Inspired Dynamic Adiabatic Local Search. Entropy 2023, 25, 1287. https://doi.org/10.3390/e25091287
Chiang C-F, Alsing PM. Quantum-Walk-Inspired Dynamic Adiabatic Local Search. Entropy. 2023; 25(9):1287. https://doi.org/10.3390/e25091287
Chicago/Turabian StyleChiang, Chen-Fu, and Paul M. Alsing. 2023. "Quantum-Walk-Inspired Dynamic Adiabatic Local Search" Entropy 25, no. 9: 1287. https://doi.org/10.3390/e25091287
APA StyleChiang, C.-F., & Alsing, P. M. (2023). Quantum-Walk-Inspired Dynamic Adiabatic Local Search. Entropy, 25(9), 1287. https://doi.org/10.3390/e25091287






