Systems of Precision: Coherent Probabilities on Pre-Dynkin Systems and Coherent Previsions on Linear Subspaces †
Abstract
When posing problems in probability calculus, it should be required to indicate for which events the probabilities are assumed to exist.—Andreĭ Kolmogorov [1] (p. 52)
1. Introduction
- (a)
- A machine learning algorithm has access to a restricted subset of attributes. It cannot jointly query all attributes simultaneously. This is called “learning on partial, aggregated information” [3]. The reasons might be manifold: for privacy preservation, “not-missing-at-random” features, restricted data base access for acceleration or multi-measurement data sets.
- (b)
- Quantum physical quantities, e.g., location and impulse, are (statistically) incompatible [4].
- (c)
- First, we show that, under mild assumptions, a pair of lower and upper probabilities assign precise probabilities, i.e., lower and upper probability coincide, to events which form a pre-Dynkin system or even a Dynkin system.
- Second, we define probabilities on pre-Dynkin systems in accordance with the literature on quantum probability, in particular [19]. We argue that probabilities on pre-Dynkin systems, as well as their inner and outer extension, exhibit few desirable properties, e.g., subadditivity cannot be guaranteed. Hence, extendability, the ability to extend a probability from a pre-Dynkin system to a larger set structure, turns out to be crucial, as it implies coherence of the probability defined on the pre-Dynkin system. This observation links together the research from probabilities defined on weak set structures [6,19,20] to imprecise probabilities [2,21]. Furthermore, extendability guarantees the existence of a nicely behaving, so-called coherent extension. We finally show that the inner and outer extension of a probability defined on a pre-Dynkin system is always more pessimistic than its corresponding lower and upper coherent extension.
- Last, we develop a duality theory between pre-Dynkin systems on a predefined base measure space and their respective credal sets of probabilities. The credal sets consist of all probabilities which coincide with the pre-defined measure on a pre-Dynkin system. A so-called Galois connection links together the containment structure on the set of set systems with the containment structure on the set of credal sets.
- First, we propose a generalization of a finitely additive probability defined on a pre-Dynkin system. More concretely, we define partial expectations which correspond to expectation functionals which are only defined on a set of linear subspaces of the space of all gambles. However, on those linear subspaces, they behave like “classical” (finitely additive) expectations.
- Second, we show that under some properties, imprecise expectations are precise on a linear subspace of the linear space of gambles. (cf. Section 3)
- Third, we present a natural generalization of extendability for partial expectations, which again turns out to be equivalent to coherence of the partial expectation.
- Last, analogous to the lattice duality (A lattice is a poset with pairwise existing minimum and maximum. The duality is expressed via an antitone lattice isomorphism.) described in Section 5, we present a lattice duality for linear subsets of the space of gambles and credal sets which define coherent lower and upper previsions.
Notation and Technical Details
2. What Is a (Pre-)Dynkin System?
- (a)
- ,
- (b)
- implies
- (c)
- with implies .
- (c’)
- let , if for all with it holds then ,
2.1. Compatibility
- For the “⇒”-direction: . The fact implies .
- For the “⇐”-direction: . The fact implies . (A related result for Dynkin systems is given in [19] (5.1).) □
2.2. Probabilities on Pre-Dynkin Systems
- (a)
- Normalization: and .
- (b)
- Additivity: let and . Then, .
3. Imprecise Probabilities Are Precise on a Pre-Dynkin System
- (a)
- Normalization: .
- (b)
- Conjugacy: for .
- (c)
- Subadditivity of u: for such that , then .
- (d)
- Superadditivity of ℓ: for such that , then .
- (e)
- Continuity from below: for with such that , then,
- (e’)
- Continuity from above: for with such that , then,
4. Extending Probabilities on Pre-Dynkin Systems
4.1. Inner and Outer Extension
- (a)
- Normalization: , .
- (b)
- Conjugacy: .
- (c)
- Monotonicity: for , if , then .
4.2. Extendability and Its Equivalence to Coherence
4.2.1. Extendability, Compatibility and Contextuality
4.2.2. Extendability and Marginal Problem
4.3. Coherent Extension
4.4. Inner and Outer Extension Is More Pessimistic Than Coherent Extension
5. The Credal Set and Its Relation to Pre-Dynkin System Structure
5.1. Credal Set Function Maps from Pre-Dynkin Systems to Coherent Probabilities
5.2. The Dual Credal Set Function
5.3. Bipolar-Closed Sets
Sufficient Conditions for Bipolar-Closed Sets
5.4. Interpolation from Algebra to Trivial Pre-Dynkin System
6. A More General Perspective—The Set of Gambles with Precise Expectation
6.1. Partial Expectations Generalize Finitely Additive Probabilities on (Pre-)Dynkin Systems
- (a)
- for any and for all , then , (Partial Linearity),
- (b)
- for any and any , then , (Coherence).
6.2. System of Precision—The Space of Gambles with Precise Expectations
- (a)
- Normalization: .
- (b)
- Conjugacy: for .
- (c)
- Subadditivity of U: for , we have .
- (d)
- Superadditivity of L: for , we have .
- (e)
- Positive Homogeneity: for and , we have and .
6.3. Generalized Extendability Is Equivalent to Coherence
6.4. A Duality Theory for Previsions and Families of Linear Subspaces
- (a)
- The generalized credal set function maps to weak-closed, convex sets.
- (b)
- The generalized dual credal set function maps to a linear subspace.
- (c)
- The generalized credal set function and generalized dual credal set function form a Galois connection.
- (b)
- Let .
- Additivity
- Let . Then, for all ,i.e., .
- Homogeneity
- Let and . Then, for all ,i.e., . For homogeneity we need the easy fact that a linear prevision is not only positive homogeneous but generally homogeneous. For this consider a linear prevision and any gamble with , then .
- (c)
- The two functions constitute a Galois connection (cf. Proposition 4), . To this end, we show the left to right implication,and the right to left implication,
7. Conclusions and Open Questions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Lemmas and Proofs
Appendix A.1. Compatibility Structure
- (a)
- (b)
- For every π-system there exist such that .
Appendix A.2. Supremum of a Chain of Algebras Is an Algebra
Appendix A.3. Sufficient Conditions for Bipolar-Closed Sets
Appendix A.4. Intersection of Linear Subspaces
Appendix B. Names of Pre-Dynkin Systems and Dynkin Systems
Appendix C. Credal Sets of Pre-Dynkin System Probabilities—Credal Sets of Distorted Probabilities
- (a)
- If such that , then clearly . If such that , then . Thus, because pre-Dynkin systems are closed under complement .
- (b)
- First, we write outSince , it is easy to see that . By Proposition 5, we know that is a pre-Dynkin system. Thus, .
- (c)
- We show this set inclusion via contraposition. If has measure , then . For this we have to argue that there is a measure for every with such that .Observe that defines a normalized, monotone, submodular set function on [43] (p. 17). Furthermore, any normalized, monotone, submodular set function induces a translation equivariant, monotone, positively homogeneous and subadditive functional on all such that for all [80] (p. 260), [2] (p. 130), [43] (Proposition 5.1, Theorem 6.3). Hence, is a coherent upper prevision [2] (p. 65). Thus, Walley’s extreme point theorem applies [2] (Theorem 3.6.2 (c)). (Even though this theorem is stated in terms of coherent lower previsions, it applies to coherent upper previsions, too. The weak-compactness of the credal set , which is given by the coherence of and [2] (Theorem 3.6.1), is crucial.) For any function , in particular any with , there is a linear prevision with on dominated by such that . More concretely, for any there is a such that . If , then Lemma A6 applies and gives the desired inequality. In conclusion, there is no with measure such that . This implication finalizes the proof.
Appendix D. Dynkin Systems and Countably Additive Probability
Appendix D.1. Dynkin Systems
Appendix D.2. Technical Setup
| Polish Space | |
| Dynkin system on (Definition 1) | |
| Countably additive probability defined on (Definition 3) | |
| -algebra hull of set system | |
| Borel--algebra on | |
| Set of bounded, signed, countably additive measures on | |
| respectively | Set of countably additive probability measures on |
| -Credal set of on (Proposition A3) | |
| , | Lower respectively upper coherent -extension (Proposition A4) |
Appendix D.3. Dynkin Probability Spaces
Appendix D.4. Conditions for Extendability for Countably Additive Probabilities
Appendix D.5. Credal Set of Countably Additive Probabilities on Dynkin Systems
- Closedness
- We assumed to be equipped with the total variation distance. Hence, of a set can be identified via the convergence of sequences in Q [84] (Lemma 21.2).Suppose is a sequence of probability measures such that . This directly implies set-wise convergence,It follows that .
Appendix E. From Set Systems to Logical Structures and Back
References
- Kolmogorov, A.N. The general theory of measure and probability calculus. In Collected Works of the Mathematical Section, Communist Academy, Section for Natural and Exact Sciences; Springer: Berlin/Heidelberg, Germany, 1929; Volume 1, pp. 8–21. (In Russian). Translated to English in A.N. Shiryayev (Editor), Selected Works of A.N. Kolmogorov, Volume II Probability and Mathematical Statistics, pages 48–59, 1992 [Google Scholar]
- Walley, P. Statistical Reasoning with Imprecise Probabilities; Chapman and Hall: London, UK, 1991. [Google Scholar]
- Eban, E.; Mezuman, E.; Globerson, A. Discrete Chebyshev classifiers. In Proceedings of the International Conference on Machine Learning. PMLR, Beijing, China, 21–26 June 2014; pp. 1233–1241. [Google Scholar]
- Gudder, S.P. Stochastic Methods in Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Epstein, L.G.; Zhang, J. Subjective probabilities on subjectively unambiguous events. Econometrica 2001, 69, 265–306. [Google Scholar] [CrossRef]
- Zhang, J. Subjective ambiguity, expected utility and Choquet expected utility. Econ. Theory 2002, 20, 159–181. [Google Scholar] [CrossRef]
- Cole, E.R. Intersectionality and research in psychology. Am. Psychol. 2009, 64, 170. [Google Scholar] [CrossRef] [PubMed]
- Shields, S.A. Gender: An intersectionality perspective. Sex Roles 2008, 59, 309–311. [Google Scholar] [CrossRef]
- Weldon, S.L. Intersectionality. In Politics, Gender, and Concepts: Theory and Methodology; Goertz, G., Mazur, A.G., Eds.; Cambridge University Press: Cambridge, UK, 2008; pp. 193–218. [Google Scholar]
- Anonymous. Hypergraph. Wikipedia 2023. Available online: https://en.wikipedia.org/wiki/Hypergraph (accessed on 4 August 2023).
- Berge, C. Hypergraphs: Combinatorics of Finite Sets; North-Holland: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Anonymous. Intersectionality. Wikipedia 2023. Available online: https://en.wikipedia.org/wiki/Intersectionality (accessed on 4 August 2023).
- Hancock, A.M. Empirical intersectionality: A tale of two approaches. UC Irvine Law Rev. 2013, 3, 259–296. [Google Scholar]
- Hancock, A.M. When multiplication doesn’t equal quick addition: Examining intersectionality as a research paradigm. Perspect. Politics 2007, 5, 63–79. [Google Scholar] [CrossRef]
- Cooke, R. The anatomy of the squizzel: The role of operational definitions in representing uncertainty. Reliab. Eng. Syst. Saf. 2004, 85, 313–319. [Google Scholar] [CrossRef]
- Elstrodt, J. Maß-und Integrationstheorie; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Vitali, G. Sul problema della misura dei Gruppi di punti di una retta: Nota; Tipografia Gamberini e Parmeggiani: Bologna, Italy, 1905. [Google Scholar]
- Isaacs, Y.; Hájek, A.; Hawthorne, J. Non-measurability, imprecise credences, and imprecise chances. Mind 2022, 131, 892–916. [Google Scholar] [CrossRef]
- Gudder, S.P. Quantum probability spaces. Proc. Am. Math. Soc. 1969, 21, 296–302. [Google Scholar] [CrossRef]
- Schurz, G.; Leitgeb, H. Finitistic and frequentistic approximation of probability measures with or without σ-additivity. Stud. Log. 2008, 89, 257–283. [Google Scholar] [CrossRef]
- Augustin, T.; Coolen, F.P.; De Cooman, G.; Troffaes, M.C. Introduction to Imprecise Probabilities; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Derr, R.; Williamson, R.C. The set structure of precision. In Proceedings of the International Symposium on Imprecise Probability: Theories and Applications, Oviedo, Spain, 11–14 July 2023. [Google Scholar]
- Williams, D. Probability with Martingales; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Hildebrandt, T.H. On bounded linear functional operations. Trans. Am. Math. Soc. 1934, 36, 868–875. [Google Scholar] [CrossRef]
- Schechter, E. Handbook of Analysis and Its Foundations; Academic Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Rao, K.B.; Rao, M.B. Theory of Charges: A Study of Finitely Additive Measures; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Pták, P. Concrete quantum logics. Int. J. Theor. Phys. 2000, 39, 827–837. [Google Scholar] [CrossRef]
- von Mises, R. Grundlagen der Wahrscheinlichkeitsrechnung. Math. Z. 1919, 5, 52–99. [Google Scholar] [CrossRef]
- von Mises, R.; Geiringer, H. Mathematical Theory of Probability and Statistics; Academic Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Khrennikov, A.Y. Interpretations of Probability; Second Revised and Extended Edition; Walter de Gruyter: Berlin, Germany, 2009. [Google Scholar]
- Frohlich, C.; Derr, R.; Williamson, R.C. Towards a strictly frequentist theory of imprecise probability. In Proceedings of the International Symposium on Imprecise Probability: Theories and Applications, Oviedo, Spain, 11–14 July 2023. [Google Scholar]
- Cuadras, C.M.; Fortiana, J.; Rodriguez-Lallena, J.A. Distributions with Given Marginals and Statistical Modelling; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Gudder, S.P. An extension of classical measure theory. SIAM Rev. 1984, 26, 71–89. [Google Scholar] [CrossRef]
- Vorob’ev, N.N. Consistent families of measures and their extensions. Theory Probab. Appl. 1962, 7, 147–163. [Google Scholar] [CrossRef]
- Gudder, S.P. Generalized measure theory. Found. Phys. 1973, 3, 399–411. [Google Scholar] [CrossRef]
- Narens, L. An introduction to lattice based probability theories. J. Math. Psychol. 2016, 74, 66–81. [Google Scholar] [CrossRef]
- Khrennikov, A.Y. Contextual Approach to Quantum Formalism; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Rivas, Á. On the role of joint probability distributions of incompatible observables in Bell and Kochen–Specker Theorems. Ann. Phys. 2019, 411, 167939. [Google Scholar] [CrossRef]
- Katriňák, T.; Neubrunn, T. On certain generalized probability domains. Matematickỳ Časopis 1973, 23, 209–215. [Google Scholar]
- Šipoš, J. Subalgebras and sublogics of σ-logics. Math. Slovaca 1978, 28, 3–9. [Google Scholar]
- Brabec, J. Compatibility in orthomodular posets. Časopis pro Pěstování Matematiky 1979, 104, 149–153. [Google Scholar] [CrossRef]
- Vallander, S.S. The structure of separable Dynkin algebras. Vestn. St. Petersburg Univ. Math. 2016, 49, 219–223. [Google Scholar] [CrossRef][Green Version]
- Denneberg, D. Non-Additive Measure and Integral; Springer Science & Business Media: Berlin, Germany, 1994. [Google Scholar]
- Navara, M.; Pták, P. Considering uncertainty and dependence in Boolean, quantum and fuzzy logics. Kybernetika 1998, 34, 121–134. [Google Scholar]
- Gudder, S.P.; Zerbe, J.E. Generalized monotone convergence and Radon–Nikodym theorems. J. Math. Phys. 1981, 22, 2553–2561. [Google Scholar] [CrossRef]
- De Simone, A.; Navara, M.; Pták, P. Extending states on finite concrete logics. Int. J. Theor. Phys. 2007, 46, 2046–2052. [Google Scholar] [CrossRef]
- De Simone, A.; Pták, P. Measures on circle coarse-grained systems of sets. Positivity 2010, 14, 247–256. [Google Scholar] [CrossRef]
- Horn, A.; Tarski, A. Measures in Boolean algebras. Trans. Am. Math. Soc. 1948, 64, 467–497. [Google Scholar] [CrossRef]
- de Simone, A.; Pták, P. Extending coarse-grained measures. Bull. Pol. Acad. Sci. Math. 2006, 54, 1–11. [Google Scholar] [CrossRef]
- De Finetti, B. Theory of Probability: A Critical Introductory Treatment; John Wiley & Sons: New York, NY, USA, 1974; Reprinted in 2017. [Google Scholar]
- Troffaes, M.C.; De Cooman, G. Lower Previsions; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Delbaen, F. Coherent risk measures on general probability spaces. In Advances in Finance and Stochastics; Sandmann, K., Schönbucher, P.J., Eds.; Springer: Berlin, Gremany, 2002; pp. 1–37. [Google Scholar]
- Pelessoni, R.; Vicig, P. Imprecise previsions for risk measurement. Int. J. Uncertain. Fuzziness Based Syst. 2003, 11, 393–412. [Google Scholar] [CrossRef]
- Busch, P.; Heinosaari, T.; Schultz, J.; Stevens, N. Comparing the degrees of incompatibility inherent in probabilistic physical theories. Europhys. Lett. 2012, 103, 10002. [Google Scholar] [CrossRef]
- Xu, Z.P.; Cabello, A. Necessary and sufficient condition for contextuality from incompatibility. Phys. Rev. A 2018, 99, 020103. [Google Scholar] [CrossRef]
- Benavoli, A.; Facchini, A.; Zaffalon, M. Quantum mechanics: The Bayesian theory generalized to the space of Hermitian matrices. Phys. Rev. A 2016, 94, 042106. [Google Scholar] [CrossRef]
- Walley, P. Towards a unified theory of imprecise probability. Int. J. Approx. Reason 2000, 24, 125–148. [Google Scholar] [CrossRef]
- Kellerer, H.G. Verteilungsfunktionen mit gegebenen Marginalverteilungen. Z. Wahrscheinlichkeitstheorie Verwandte Geb. 1964, 3, 247–270. [Google Scholar] [CrossRef]
- Budroni, C.; Cabello, A.; Gühne, O.; Kleinmann, M.; Larsson, J.Å. Kochen-Specker contextuality. Rev. Mod. Phys. 2022, 94, 045007. [Google Scholar] [CrossRef]
- Maharam, D. Consistent extension of linear functionals and of probability measures. In Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability: Held at the Statistical Laboratory, University of California; University of California Press: Berkeley, CA, USA, 1972; Volume 6, pp. 127–147. [Google Scholar]
- Miranda, E.; Zaffalon, M. Compatibility, Coherence and the RIP. In Uncertainty Modelling in Data Science, SMPS2018, Proceedings of the International Conference Series on Soft Methods in Probability and Statistics, Compiègne, France, 17–21 September 2018; Advances in Intelligent Systems and Computing Book Series; Destercke, S., Denoeux, T., Gil, M.A., Grzegorzewski, P., Hryniewicz, O., Eds.; Springer: Berlin, Germany, 2018; Volume 832, pp. 166–174. [Google Scholar]
- Casanova, A.; Kohlas, J.; Zaffalon, M. Information algebras in the theory of imprecise probabilities, an extension. Int. J. Approx. Reason. 2022, 150, 311–336. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Birkhoff, G. Lattice Theory; American Mathematical Society: Providence, RI, USA, 1940. [Google Scholar]
- Rota, G.C. Twelve problems in probability no one likes to bring up. In Algebraic Combinatorics and Computer Science; Springer: Berlin, Germany, 2001; pp. 57–93. [Google Scholar]
- Khrennikov, A.Y. Bell could become the Copernicus of probability. Open Syst. Inf. Dyn. 2016, 23, 1650008. [Google Scholar] [CrossRef]
- Wirch, J.L.; Hardy, M.R. Distortion risk measures: Coherence and stochastic dominance. In Proceedings of the International Congress on Insurance: Mathematics and Economics, State College, PA, USA; 2001; pp. 15–17. [Google Scholar]
- Fröhlich, C.; Williamson, R.C. Risk measures and upper probabilities: Coherence and stratification. arXiv 2022, arXiv:2206.03183. [Google Scholar]
- Lehrer, E. Partially specified probabilities: Decisions and games. Am. Econ. J. Microecon. 2012, 4, 70–100. [Google Scholar] [CrossRef][Green Version]
- Lehrer, E. Coherent Risk Measures Induced by Partially Specified Probabilities; Technical Report; Tel Aviv University: Tel Aviv, Israe, 2007. [Google Scholar]
- De Castro, L.I.; Chateauneuf, A. Ambiguity aversion and trade. Econ. Theory 2011, 48, 243–273. [Google Scholar] [CrossRef]
- Seidenfeld, T. (Dietrich College of Humanities and Social Sciences, Carnegie Mellon University, Pittsburgh, PA, USA). Personal Communication at ISIPTA, 2023.
- Ovchinnikov, P.G. Measures on finite concrete logics. Proc. Am. Math. Soc. 1999, 127, 1957–1966. [Google Scholar] [CrossRef]
- Godowski, R. Varieties of orthomodular lattices with a strongly full set of states. Demonstr. Math. 1981, 14, 725–734. [Google Scholar] [CrossRef]
- Suppes, P. The probabilistic argument for a non-classical logic of quantum mechanics. Philos. Sci. 1966, 33, 14–21. [Google Scholar] [CrossRef]
- Pták, P. Some nearly Boolean orthomodular posets. Proc. Am. Math. Soc. 1998, 126, 2039–2046. [Google Scholar] [CrossRef][Green Version]
- Jun, S.J.; Pinkse, J.; Xu, H. Tighter bounds in triangular systems. J. Econom. 2011, 161, 122–128. [Google Scholar] [CrossRef]
- Chow, Y.S.; Teicher, H. Probability Theory: Independence, Interchangeability, Martingales, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Rubshtein, B.Z.A.; Grabarnik, G.Y.; Muratov, M.A.; Pashkova, Y.S. Foundations of Symmetric Spaces of Measurable Functions; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Huber, P.J. Robust Statistics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Kadane, J.B.; Schervish, M.J.; Seidenfeld, T.; Goel, P.K.; Zellner, A. Statistical implications of finitely additive probability. In Bayesian Inference and Decision Techniques; Elsevier Science Publisher: Amsterdam, The Netherlands, 1986; pp. 69–76, Reprinted in Rethinking the Foundations of Statistics, pages 211–232, 1999. [Google Scholar]
- Chichilnisky, G. The foundations of probability with black swans. J. Probab. Stat. 2010, 2010, 838240. [Google Scholar] [CrossRef]
- Aliprantis, C.D.; Border, K.C. Infinite Dimensional Analysis: A Hitchhiker’s Guide, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Munkres, J. Topology, 2nd ed.; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Wojtaszczyk, P. Banach Spaces for Analysts; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Stone, M.H. The theory of representations for Boolean algebras. Trans. Am. Math. Soc. 1936, 40, 37–111. [Google Scholar]
- Birkhoff, G.; von Neumann, J. The logic of quantum mechanics. Ann. Math. 1936, 37, 1–26. [Google Scholar] [CrossRef]
- Husimi, K. Studies on the foundation of quantum mechanics. I. Proc. Phys. Math. Soc. Jpn. 3rd Ser. 1937, 19, 766–789. [Google Scholar]


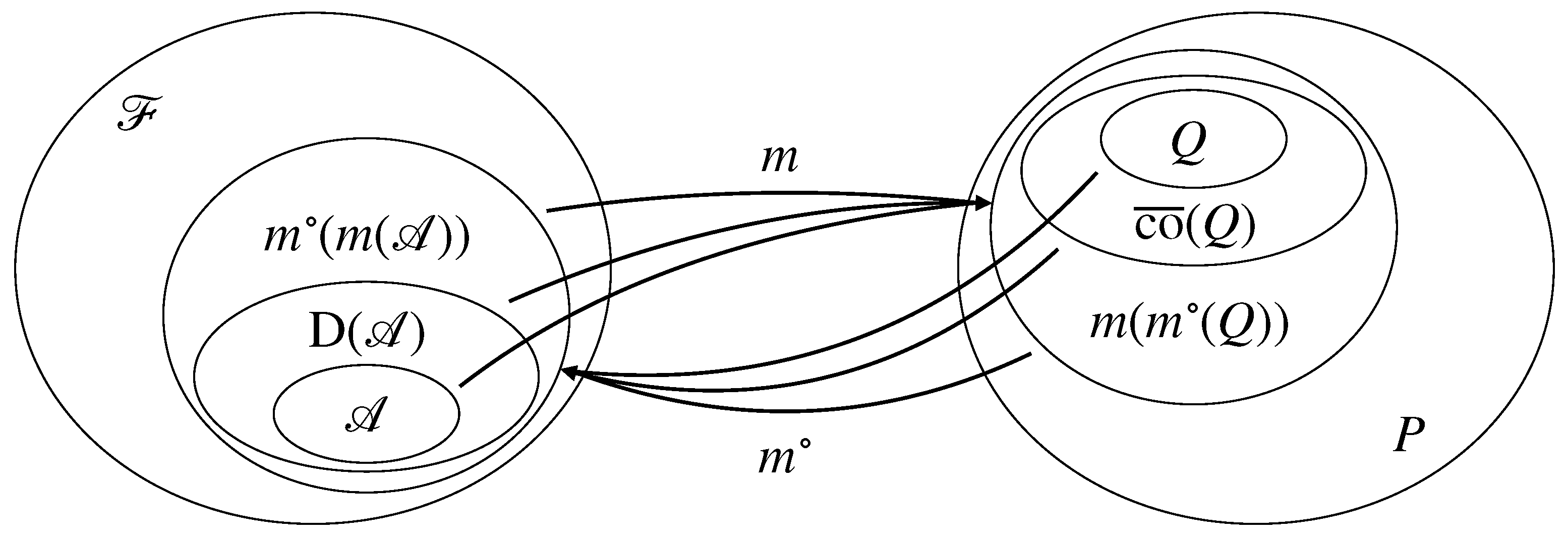
| Base set and its power set | |
| Set | |
| Pre-Dynkin system on (Definition 1) | |
| Dynkin system on (Definition 1) | |
| Pre-Dynkin hull of a set system (Definition 1) | |
| Finitely additive probability defined on (Definition 3) | |
| , | Inner respectively outer extension (Proposition 1) |
| , | Lower respectively upper coherent extension (Corollary 1) |
| Credal set of on (Corollary 1) | |
| Finitely additive probability defined on | |
| Fixed, finitely additive probability defined on | |
| Indicator function of the set | |
| Set of finitely additive probability measures on , set of linear previsions | |
| Credal set function (Definition 6) | |
| Dual credal set function (Definition 7) | |
| Convex, Weak Closure | |
| Set of real-valued, bounded functions on | |
| Set of bounded, signed, finitely additive measures on | |
| E | Partial Expectation (Definition 8) |
| Linear space of simple gambles on the set system | |
| Linear space of bounded, -measurable functions | |
| Coherent lower prevision (Definition 9) | |
| Coherent upper prevision (Definition 9) | |
| Linear prevision defined on (equivalent to above) | |
| Fixed, linear prevision defined on (equivalent to above) | |
| Generalized credal set function (Definition 11) | |
| Generalized dual credal set function (Definition 12) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derr, R.; Williamson, R.C. Systems of Precision: Coherent Probabilities on Pre-Dynkin Systems and Coherent Previsions on Linear Subspaces. Entropy 2023, 25, 1283. https://doi.org/10.3390/e25091283
Derr R, Williamson RC. Systems of Precision: Coherent Probabilities on Pre-Dynkin Systems and Coherent Previsions on Linear Subspaces. Entropy. 2023; 25(9):1283. https://doi.org/10.3390/e25091283
Chicago/Turabian StyleDerr, Rabanus, and Robert C. Williamson. 2023. "Systems of Precision: Coherent Probabilities on Pre-Dynkin Systems and Coherent Previsions on Linear Subspaces" Entropy 25, no. 9: 1283. https://doi.org/10.3390/e25091283
APA StyleDerr, R., & Williamson, R. C. (2023). Systems of Precision: Coherent Probabilities on Pre-Dynkin Systems and Coherent Previsions on Linear Subspaces. Entropy, 25(9), 1283. https://doi.org/10.3390/e25091283







