A Stochastically Optimized Two-Echelon Supply Chain Model: An Entropy Approach for Operational Risk Assessment
Abstract
1. Introduction
2. Literature Review
3. Methods
3.1. Model Concepts
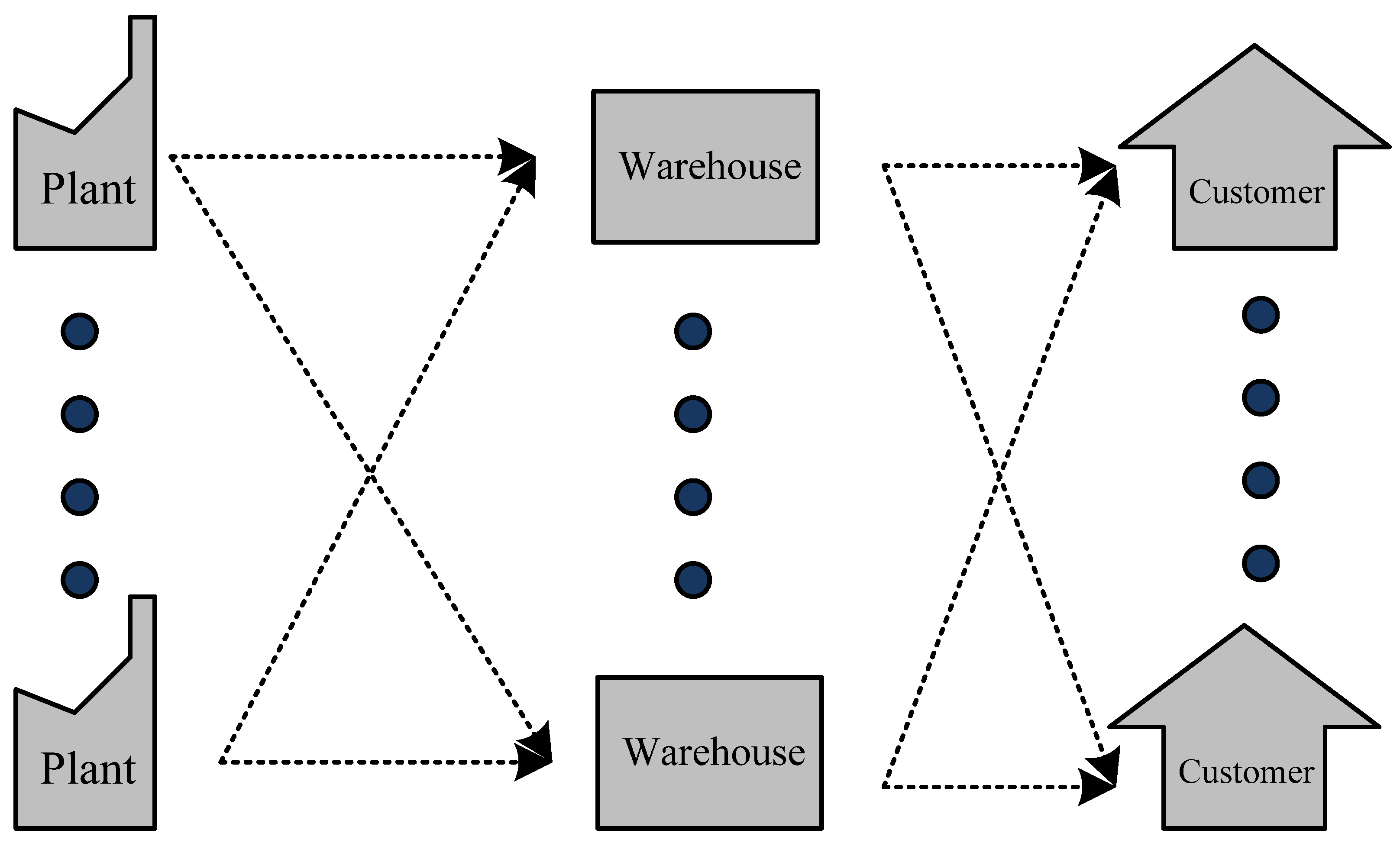
3.1.1. Supply Chain Network Framework
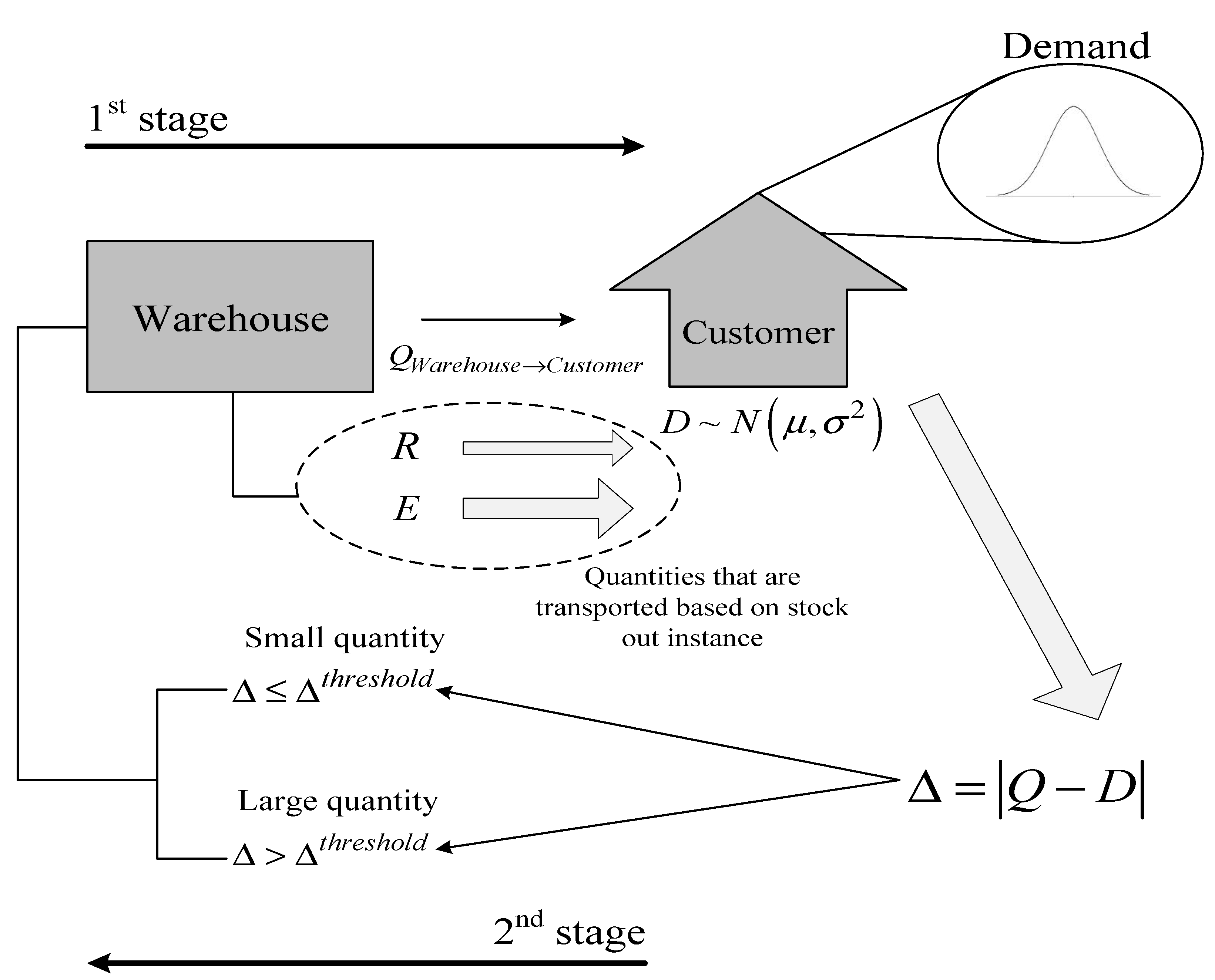
3.1.2. Deterministic Model
- 1st stage:
- ○
- Produced and transported quantities;
- ○
- Selected warehouses and capacity;
- ○
- Supply chain network;
- ○
- Demand deficit.
- 2nd stage:
- ○
- Stock out and overstocking probabilities;
- ○
- Expected lead time (ELD);
- ○
- Quantities that should be produced to cover unsatisfied demand.
3.1.3. Stochastic Model
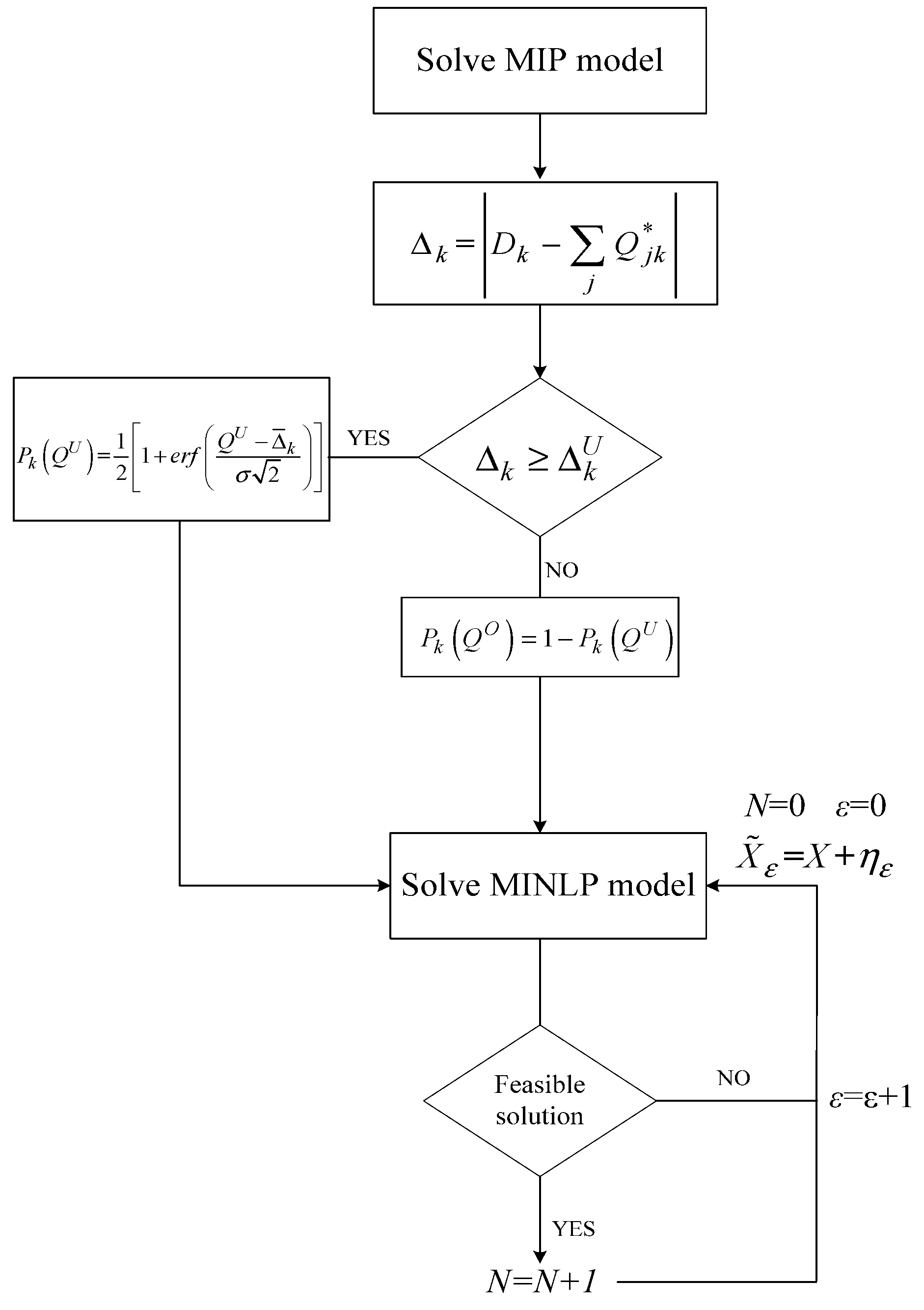
3.2. Implementation of Deterministic and Stochastic Models
Risk Assessment
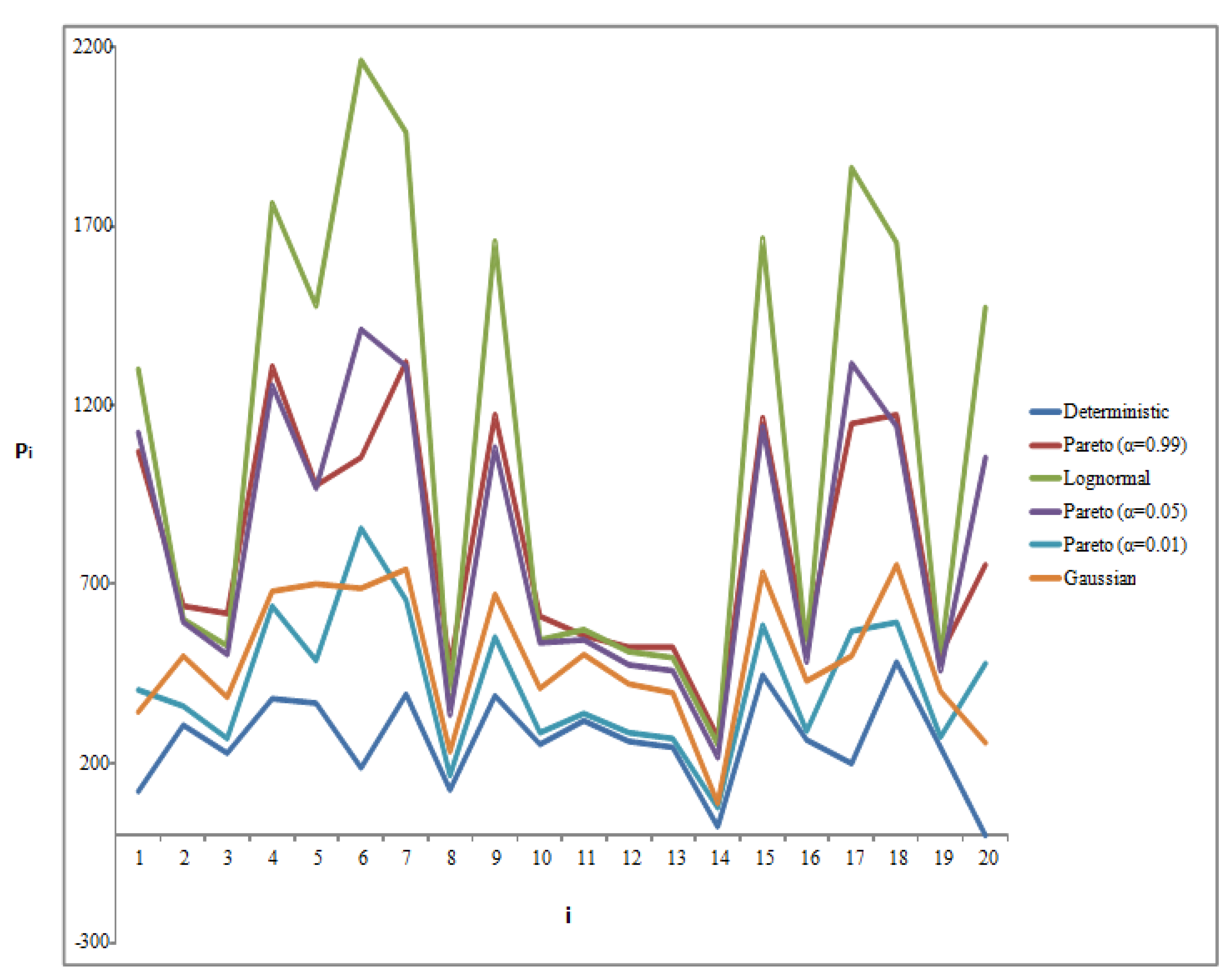
- Gaussian noise;
- Lognormal noise;
- Pareto noise for various alpha levels (α = 0.01; α = 0.5; α = 0.99).
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Index and Variable Explanation
| Index | |
| Plant | |
| Warehouse | |
| Customer | |
| Continuous Variables | |
| Total supply chain cost | |
| Transported quantities from warehouse | |
| Transported quantities from warehouse that exceed a certain level (high) | |
| with noise representation | |
| warehouse with noise representation | |
| Transported quantities from warehouse with noise representation | |
| Transported quantities from warehouse that exceed a certain level (low) | |
| Capacity of warehouse | |
| Deficit in demand satisfaction for customer k | |
| Binary Variables | |
| exists, 0 otherwise | |
| 1 if the corresponding connection between warehouse exists, 0 otherwise | |
| 1 if warehouse is selected, 0 otherwise | |
| 1 if small quantities will be delivered from warehouse j to customer k due to large demand deficit, 0 otherwise | |
| 1 if large quantities will be delivered from warehouse j to customer k due to large demand deficit, 0 otherwise | |
| , 0 otherwise | |
| , 0 otherwise | |
| Parameters | |
| Upper bounded production of plant i | |
| Lower bounded production of plant i | |
| Maximum capacity of transported quantities from plant i to warehouse j | |
| Minimum capacity of transported quantities from plant i to warehouse j | |
| Maximum capacity of transported quantities from warehouse j to customer k | |
| Minimum capacity of transported quantities from warehouse j to customer k | |
| Inventory held at warehouse j | |
| Demand of customer k | |
| Stock out quantity in customer k | |
| Maximum time for product delivery | |
| Minimum time for product delivery | |
| Coefficient relating quantity at capacity at warehouse j | |
| Production rate for quantities stored at warehouse j that will be delivered to customer k in order to cover the high deficit in demand satisfaction. | |
| Production rate for quantities stored at warehouse j that will be delivered to customer k in order to cover the low deficit in demand satisfaction. | |
| Cost Parameters | |
| Production cost of plant i | |
| Variable transportation cost of plant i to warehouse j | |
| Fixed transportation cost of plant i to warehouse j | |
| Variable transportation cost of warehouse j to customer k | |
| Fixed transportation cost of warehouse j to customer k | |
| Installation cost of warehouse j | |
| Production cost of small quantities that will be manufactured in warehouse j and will be delivered to customer k | |
| Production cost of large quantities that will be manufactured in warehouse j and will be delivered to customer k | |
Appendix B. Implementation of Stock Out Instances in the Deterministic Model
References
- Gruen, T.W.; Corsten, D.S.; Bharadwaj, S. Retail Out-of-Stocks. A Worldwide Examination of Extent, Causes, and Consumer Responses, Research Study, Atlanta; Grocery Manufacturers of America: Washington, DC, USA, 2002. [Google Scholar]
- Gruen, T.; Corsten, D. Stock-Outs Cause Walkouts. Harv. Bus. Rev. 2004, 82, 26–27. [Google Scholar]
- Govind, A.; Luke, R.; Pisa, N. Investigating stock-outs in Johannesburg’s warehouse retail liquor sector. J. Transp. Supply Chain Manag. 2017, 11, a303. [Google Scholar] [CrossRef]
- Diane, M.; Hannah, S.; Wendy, L.; Monique, U. Green, lean, and global Supply chains. Int. J. Phys. Distrib. Logist. Manag. 2010, 41, 14–41. [Google Scholar]
- Kumar, V.; Sabri, S.; Garza-Reyes, J.A.; Nadeem, S.P.; Kumari, A.; Akkaranggoon, S. The challenges of GSCM implementation in the UK manufacturing SMEs. In Proceedings of the 2018 International Conference on Production and Operations Management Society (POMS), Peradeniya, Sri Lanka, 14–16 December 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Walker, H.; Di Sisto, L.; McBain, D. Drivers and barriers to environmental supply chain management practices: Lessons from the public and private sectors. J. Purch. Supply Manag. 2008, 14, 69–85. [Google Scholar] [CrossRef]
- Bhool, R.; Narwal, M.S. An analysis of drivers affecting the implementation of green supply chain management for the Indian manufacturing industries. Int. J. Res. Eng. Technol. 2013, 2, 242–254. [Google Scholar]
- Sarkis, J. Evaluating environmentally conscious business practices. Eur. J. Oper. Res. 1998, 107, 159–174. [Google Scholar] [CrossRef]
- Welford, R.; Gouldson, A. Environmental Management & Business Strategy; Pitman Publishing Limited: London, UK, 1993. [Google Scholar]
- Davies, A.R. Clean and green? A governance analysis of waste management in New Zealand. J. Environ. Plan. Manag. 2009, 52, 157–176. [Google Scholar]
- Henriques, I.; Sadorsky, P. Environmental technical and administrative innovations in the Canadian manufacturing industry. Bus. Strategy Environ. 2007, 16, 119–132. [Google Scholar] [CrossRef]
- Baylis, R.; Connell, L.; Flynn, A. Company size, environmental regulation and ecological modernization: Further analysis at the level of the firm. Bus. Strategy Environ. 1998, 7, 285–296. [Google Scholar] [CrossRef]
- Zhu, Q.; Geng, Y.; Sarkis, J. Motivating green public procurement in China: An individual level perspective. J. Environ. Manag. 2013, 126, 85–95. [Google Scholar] [CrossRef]
- Tyagi, M.; Kumar, P.; Kumar, D. Parametric selection of alternatives to improve performance of green supply chain management system. Procedia Soc. Behav. Sci. 2015, 189, 449–457. [Google Scholar] [CrossRef]
- Boufounou, P.; Moustairas, I.; Toudas, K.; Malesios, C. ESGs and Customer Choice: Some Empirical Evidence. Circ. Econ. Sustain. 2023, 3, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Srivastav, P.; Gaur, M.K. Barriers to Implement Green Supply Chain Management in Small Scale Industry using Interpretive Structural Modeling Technique-A North Indian Perspective. Eur. J. Adv. Eng. Technol. 2015, 2, 6–13. [Google Scholar]
- Testa, F.; Iraldo, F. Shadows and lights of GSCM (Green Supply Chain Management): Determinants and effects of these practices based on a multi-national study. J. Clean. Prod. 2010, 18, 953–962. [Google Scholar] [CrossRef]
- Villanueva, R.; Garcia, L.J. Green Supply Chain Management—A competitive Advantage. In Proceedings of the International Congression on Logistics & Supply Chain (CILOG 2013), Sanfandila, Mexico, 24–25 October 2013; pp. 186–190. [Google Scholar]
- Choudhary, M.; Seth, S. Integration of green practices in supply chain environment the practices of inbound, operational, outbound and reverse logistics. Int. J. Eng. Sci. Technol. 2011, 3, 4985–4993. [Google Scholar]
- Huang, X.; Tan, B.L.; Ding, X. Green supply chain practices: An investigation of manufacturing SMEs in China. Int. J. Technol. Manag. Sustain. Dev. 2012, 11, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Frederick, H.; Elting, J. Determinants of green supply chain implementation in the food and beverage sector. Int. J. Bus. Innov. Res. 2013, 7, 164–184. [Google Scholar] [CrossRef]
- Zhu, Q.; Feng, Y.; Choi, S.B. The role of customer relational governance in environmental and economic performance improvement through green supply chain management. J. Clean. Prod. 2017, 155, 46–53. [Google Scholar] [CrossRef]
- Ninlawan, C.; Seksan, P.; Tossapol, K.; Pilada, W. The Implementation of Green Supply Chain Management Practices in Electronics Industry. In Proceedings of the International MultiConference of Engineers and Computer Scientists 2010, Hong Kong, China, 17–19 March 2010; Volume III. [Google Scholar]
- Luthra, S.; Garg, D.; Haleem, A. The impacts of critical success factors for implementing green supply chain management towards sustainability: An empirical investigation of Indian automobile industry. J. Clean. Prod. 2016, 121, 142–158. [Google Scholar] [CrossRef]
- Jain, V.K.; Sharma, S. Green Supply Chain Management Practices in Automobile Industry: An Empirical Study. J. Supply Chain Manag. Syst. 2012, 1, 20–26. [Google Scholar]
- Zhu, Q.; Sarkis, J.; Lai, K.-H. Green supply chain management: Pressures, practices and performance within the Chinese automobile industry. J. Clean. Prod. 2007, 15, 1041–1052. [Google Scholar] [CrossRef]
- Choi, T.; Yeung, W.; Cheng, T.C.E. Scheduling and co-ordination of multi-suppliers single-warehouse-operator single-manufacturer supply chains with variable production rates and storage costs. Int. J. Prod. Res. 2013, 51, 2593–2601. [Google Scholar] [CrossRef]
- Liu, S.; Papageorgiou, L.G. Multiobjective Optimisation of Production, Distribution and Capacity Planning of Global Supply Chains in the Process Industry. Omega 2013, 41, 369–382. [Google Scholar] [CrossRef]
- Seferlis, P.; Giannelos, N.F. A Two-Layered Optimisation-Based Control Strategy for Multi-Echelon Supply Chain Networks. Comput. Chem. Eng. 2004, 28, 799–809. [Google Scholar] [CrossRef]
- Fattahi, M.; Mahootchi, M.; Husseini, S.M. Integrated strategic and tactical supply chain planning with price-sensitive demands. Ann. Oper. Res. 2016, 242, 423–456. [Google Scholar] [CrossRef]
- Mahapatra, R.N.; Biswal, B.B.; Parida, P.K. A Modified Deterministic Model for Reverse Supply Chain in Manufacturing. J. Ind. Eng. 2013, 10, 987172. [Google Scholar] [CrossRef]
- Melo, M.T.; Nickel, S.; Saldanha da Gama, F. Dynamic Multi-Commodity Capacitated Facility Location: A Mathematical Modeling Framework for Strategic Supply Chain Planning. Comput. Oper. Res. 2006, 33, 181–208. [Google Scholar] [CrossRef]
- Yu, V.F.; Normasari, N.M.E.; Luong, H.T. Integrated Location-Production-Distribution Planning in a Multiproducts Supply Chain Network Design Model. Math. Probl. Eng. 2015, 2015, 473172. [Google Scholar] [CrossRef]
- Goh, M.; Meng, F. A Stochastic Model for Supply Chain Risk. In Supply Chain Risk and Vulnerability; Wu, T., Blackhurst, J., Eds.; Springer: London, UK, 2009. [Google Scholar]
- Kim, J.; Realff, M.J.; Lee, J.H. Optimal Design and Global Sensitivity Analysis of Biomass Supply Chain Networks for Biofuels under Uncertainty. Comput. Chem. Eng. 2011, 35, 1738–1751. [Google Scholar] [CrossRef]
- Govindan, K.; Fattahi, M.; Keyvanshokooh, E. Supply chain network design under uncertainty: A comprehensive review and future research directions. Eur. J. Oper. Res. 2017, 263, 108–141. [Google Scholar] [CrossRef]
- Bidhandi, H.M.; Mohd, R.; Yusuff, M.M.H.; Ahmad, M.; Bakar, M.R.A. Development of a New Approach for Deterministic Supply Chain Network Design. Eur. J. Oper. Res. 2009, 198, 121–128. [Google Scholar] [CrossRef]
- Tamas, M. Mismatched Strategies: The Weak Link in the Supply Chain? Supply Chain Manag. Int. J. 2000, 5, 171–175. [Google Scholar] [CrossRef]
- Salema, M.I.G.; Barbosa-Povoa, A.M.; Novais, A.Q. An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty. Eur. J. Oper. Res. 2007, 179, 1063–1077. [Google Scholar] [CrossRef]
- Santoso, T.; Ahmed, S.; Goetschalckx, M.; Shapiro, A. A Stochastic Programming Approach for Supply Chain Network Design under Uncertainty. Eur. J. Oper. Res. 2005, 167, 96–115. [Google Scholar] [CrossRef]
- Tsiakis, P.; Shah, N.; Pantelides, C.C. Design of Multi-Echelon Supply Chain Networks under Demand Uncertainty. Ind. Eng. Chem. Res. 2001, 40, 3585–3604. [Google Scholar] [CrossRef]
- Garcia-Herreros, P.; Wassick, J.; Grossmann, I.E. Design of Resilient Supply Chains with Risk of Facility Disruptions. Ind. Eng. Chem. Res. 2014, 53, 17240–17251. [Google Scholar] [CrossRef]
- Dillon, M.; Oliveira, F.; Abbasi, B. A two-stage stochastic programming model for inventory management in the blood supply chain. Int. J. Prod. Econ. 2017, 187, 27–41. [Google Scholar] [CrossRef]
- Nagar, L.; Jain, K. Supply chain planning using multi-stage stochastic programming. Supply Chain Manag. Int. J. 2008, 13, 251–256. [Google Scholar] [CrossRef]
- Razmi, J.; Moghadam, A.T.; Jolai, F. An Evaluative Continuous Time Markov Chain Model for a Three Echelon Supply Chain with Stochastic Demand and Lead Time. IFAC-PapersOnLine 2015, 48, 248–253. [Google Scholar] [CrossRef]
- Petridis, K. Optimal Design of Multi-Echelon Supply Chain Networks under Normally Distributed Demand. Ann. Oper. Res. 2015, 227, 63–91. [Google Scholar] [CrossRef]
- Garcia-Herreros, P.; Agarwal, A.; Wassick, J.M.; Grossmann, I.E. Optimizing inventory policies in process networks under uncertainty. Comput. Chem. Eng. 2016, 92, 256–272. [Google Scholar] [CrossRef]
- Kleywegt, A.J.; Shapiro, A.; Homem-de Mello, T. The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 2002, 12, 479–502. [Google Scholar] [CrossRef]
- Shapiro, A.; Homem-de Mello, T. A simulation-based approach to two-stage stochastic programming with recourse. Math. Program. 1998, 81, 301–325. [Google Scholar] [CrossRef]
- Beamon, B.M. Supply Chain Design and Analysis: Models and Methods. Int. J. Prod. Econ. 1998, 55, 281–294. [Google Scholar] [CrossRef]
- Tsao, Y.-C.; Lu, J.-C. A Supply Chain Network Design Considering Transportation Cost Discounts. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 401–414. [Google Scholar] [CrossRef]
- You, F.; Grossmann, I.E. Design of Responsive Supply Chains under Demand Uncertainty. Comput. Chem. Eng. 2008, 32, 3090–3111. [Google Scholar] [CrossRef]
- Pan, F.; Nagi, R. Robust Supply Chain Design under Uncertain Demand in Agile Manufacturing. Comput. Oper. Res. 2010, 37, 668–683. [Google Scholar] [CrossRef]
- Jindal, A.; Sangwan, K.S. Closed Loop Supply Chain Network Design and Optimisation Using Fuzzy Mixed Integer Linear Programming Model. Int. J. Prod. Res. 2014, 52, 4156–4173. [Google Scholar] [CrossRef]
- Krikke, H.; Bloemhof-Ruwaard, J.; Van Wassenhove, L.N. Design of Closed Loop Supply Chains: A Production and Return Network for Refrigerators. Erasmus Research Institute of Management (ERIM), 2001. Available online: https://flora.insead.edu/fichiersti_wp/inseadwp2001/2001-67.pdf (accessed on 12 July 2023).
- Krikke, H.; Bloemhof-Ruwaard, J.; Van Wassenhove, L.N. Concurrent Product and Closed-Loop Supply Chain Design with an Application to Refrigerators. Int. J. Prod. Res. 2003, 41, 3689–3719. [Google Scholar] [CrossRef]
- Grigoroudis, E.; Petridis, K.; Arabatzis, G. RDEA: A Recursive DEA Based Algorithm for the Optimal Design of Biomass Supply Chain Networks. Renew. Energy 2014, 71, 113–122. [Google Scholar] [CrossRef]
- Arabatzis, G.; Petridis, K.; Galatsidas, S.; Ioannou, K. A Demand Scenario Based Fuelwood Supply Chain: A Conceptual Model. Renew. Sustain. Energy Rev. 2013, 25, 687–697. [Google Scholar] [CrossRef]
- Fisher, M.L. An Applications Oriented Guide to Lagrangian Relaxation. Interfaces 1985, 15, 10–21. [Google Scholar] [CrossRef]
- Guillén-Gosálbez, G.; Grossmann, I.E. Optimal Design and Planning of Sustainable Chemical Supply Chains under Uncertainty. AIChE J. 2009, 55, 99–121. [Google Scholar] [CrossRef]
- Gebreslassie, B.H.; Yao, Y.; You, F. Design under Uncertainty of Hydrocarbon Biorefinery Supply Chains: Multiobjective Stochastic Programming Models, Decomposition Algorithm, and a Comparison between CVaR and Downside Risk. AIChE J. 2012, 58, 2155–2179. [Google Scholar] [CrossRef]
- Arabatzis, G.; Petridis, K.; Kougioulis, P. Proposing a Supply Chain Model for the Production-Distribution of Fuelwood in Greece Using Multi-Objective Programming. In E-Innovation for Sustainable Development of Rural Resources during Global Economic Crisis; IGI Global: Hershey, PA, USA, 2014; pp. 171–180. [Google Scholar]
- Wang, F.; Lai, X.; Shi, N. A Multi-Objective Optimization for Green Supply Chain Network Design. Decis. Support Syst. 2011, 51, 262–269. [Google Scholar] [CrossRef]
- Riddalls, C.E.; Bennett, S. Production-Inventory System Controller Design and Supply Chain Dynamics. Int. J. Syst. Sci. 2002, 33, 181–195. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- An, N.; Lu, J.-C.; Rosen, D.; Ruan, L. Supply-Chain Oriented Robust Parameter Design. Int. J. Prod. Res. 2007, 45, 5465–5484. [Google Scholar] [CrossRef]
- Baghalian, A.; Rezapour, S.; Farahani, R.Z. Robust Supply Chain Network Design with Service Level against Disruptions and Demand Uncertainties: A Real-Life Case. Eur. J. Oper. Res. 2013, 227, 199–215. [Google Scholar] [CrossRef]
- Acar, Y.; Kadipasaoglu, S.; Schipperijn, P. A Decision Support Framework for Global Supply Chain Modelling: An Assessment of the Impact of Demand, Supply and Lead-Time Uncertainties on Performance. Int. J. Prod. Res. 2009, 48, 3245–3268. [Google Scholar] [CrossRef]
- Smith, J.; Johnson, A.; Williams, B.; Brown, C. Stochastic Inventory Control in a Multi-Echelon Supply Chain: A Review. J. Supply Chain Manag. 2022, 45, 123–145. [Google Scholar]
- Johnson, R.; Thompson, M.; Garcia, S.; Davis, K. Supply Chain Risk Management: A Comprehensive Review. Int. J. Oper. Prod. Manag. 2021, 41, 567–591. [Google Scholar]
- Liu, Y.; Wang, Y.; Zhang, L.; Li, M. Managing Disruptions in Supply Chains: A Comprehensive Review. J. Oper. Manag. 2023, 50, 300–326. [Google Scholar]
- Ghadge, A.; Jena, S.K.; Kamble, S.; Misra, D.; Tiwari, M.K. Impact of financial risk on supply chains: A manufacturer-supplier relational perspective. Int. J. Prod. Res. 2021, 59, 7090–7105. [Google Scholar] [CrossRef]
- Bai, Q.; Meng, F. Impact of risk aversion on two-echelon supply chain systems with carbon emission reduction constraints. J. Ind. Manag. Optim. 2020, 16, 1943–1965. [Google Scholar] [CrossRef]
- Prabakaran, S.; Paternina-Arboleda, C.D. Laws of Thermodynamic Description in The Economic System. Int. J. Appl. Eng. Res. 2015, 10, 28657–28668. [Google Scholar]
- Paul, S.K.; Sarker, R.; Essam, D. Managing risk and disruption in production-inventory and supply chain systems: A review. J. Ind. Manag. Optim. 2016, 12, 1009–1029. [Google Scholar] [CrossRef]
- De Dominicis, C.; Martin, P.C. Energy spectra of certain randomly-stirred fluid. Phys. Rev. A 1979, 19, 419. [Google Scholar] [CrossRef]
- Chattopadhyay, A.K.; Bhattacharjee, J.K. Wall-bounded turbulent shear flow: Analytic result for a universal amplitude. Phys. Rev. E 2000, 63, 016306. [Google Scholar] [CrossRef]
- Spearman, M.L.; Zazanis, M.A. Push and Pull Production Systems: Issues and Comparisons. Oper. Res. 1992, 40, 521–532. [Google Scholar] [CrossRef]
- Debnath, B.; El-Hassani, R.; Chattopadhyay, A.K.; Krishna Kumar, T.; Ghosh, S.K.; Baidya, R. Time evolution of a supply chain network: Kinetic Modeling. Physics A 2022, 607, 128085. [Google Scholar] [CrossRef]
- Lee, H.L.; Padmanabhan, V.; Whang, S. Information Distortion in a Supply Chain: The Bullwhip Effect. Manag. Sci. 2004, 50, 1875–1886. [Google Scholar] [CrossRef]



| Standard Deviation (σ) | |
|---|---|
| Pareto Noise (a = 0.01) | 27.92 |
| Pareto Noise (a = 0.5) | 70.16 |
| Pareto Noise (a = 0.99) | 97.65 |
| Gaussian Noise | 29.39 |
| Lognormal Noise | 98.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petridis, K.; Dey, P.K.; Chattopadhyay, A.K.; Boufounou, P.; Toudas, K.; Malesios, C. A Stochastically Optimized Two-Echelon Supply Chain Model: An Entropy Approach for Operational Risk Assessment. Entropy 2023, 25, 1245. https://doi.org/10.3390/e25091245
Petridis K, Dey PK, Chattopadhyay AK, Boufounou P, Toudas K, Malesios C. A Stochastically Optimized Two-Echelon Supply Chain Model: An Entropy Approach for Operational Risk Assessment. Entropy. 2023; 25(9):1245. https://doi.org/10.3390/e25091245
Chicago/Turabian StylePetridis, Konstantinos, Prasanta Kumar Dey, Amit K. Chattopadhyay, Paraskevi Boufounou, Kanellos Toudas, and Chrisovalantis Malesios. 2023. "A Stochastically Optimized Two-Echelon Supply Chain Model: An Entropy Approach for Operational Risk Assessment" Entropy 25, no. 9: 1245. https://doi.org/10.3390/e25091245
APA StylePetridis, K., Dey, P. K., Chattopadhyay, A. K., Boufounou, P., Toudas, K., & Malesios, C. (2023). A Stochastically Optimized Two-Echelon Supply Chain Model: An Entropy Approach for Operational Risk Assessment. Entropy, 25(9), 1245. https://doi.org/10.3390/e25091245










