Synergetic Theory of Information Entropy Based on Failure Approach Index for Stability Analysis of Surrounding Rock System
Abstract
:1. Introduction
2. Numerical Limit Analysis Method of Plastic Shear Strain
2.1. Relationship between Two-Dimensional Plastic Shear Strain and Three-Dimensional Plastic Shear Strain
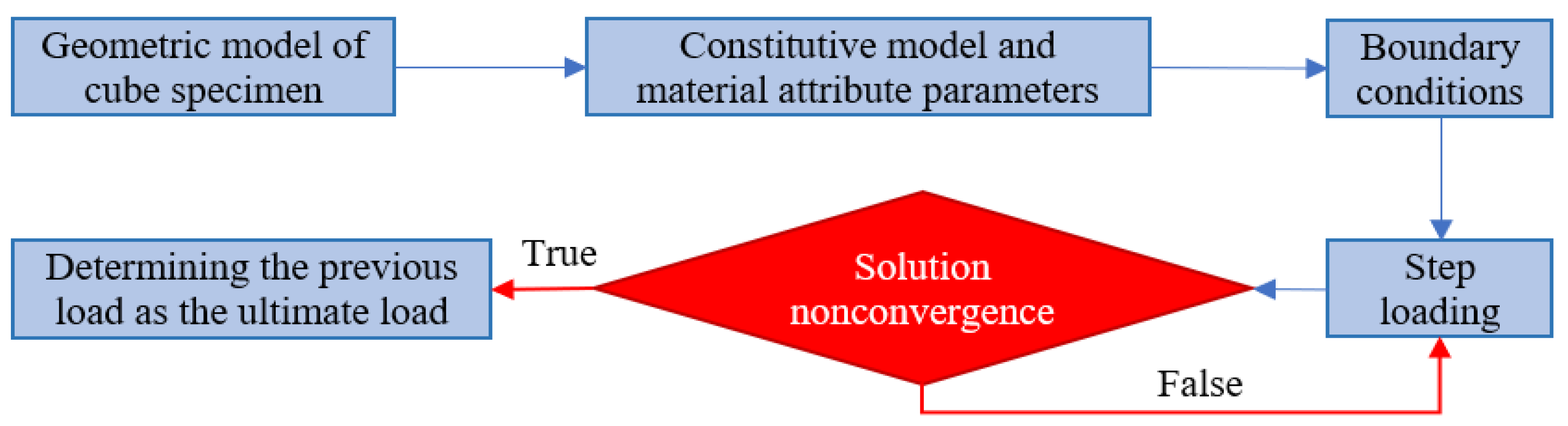
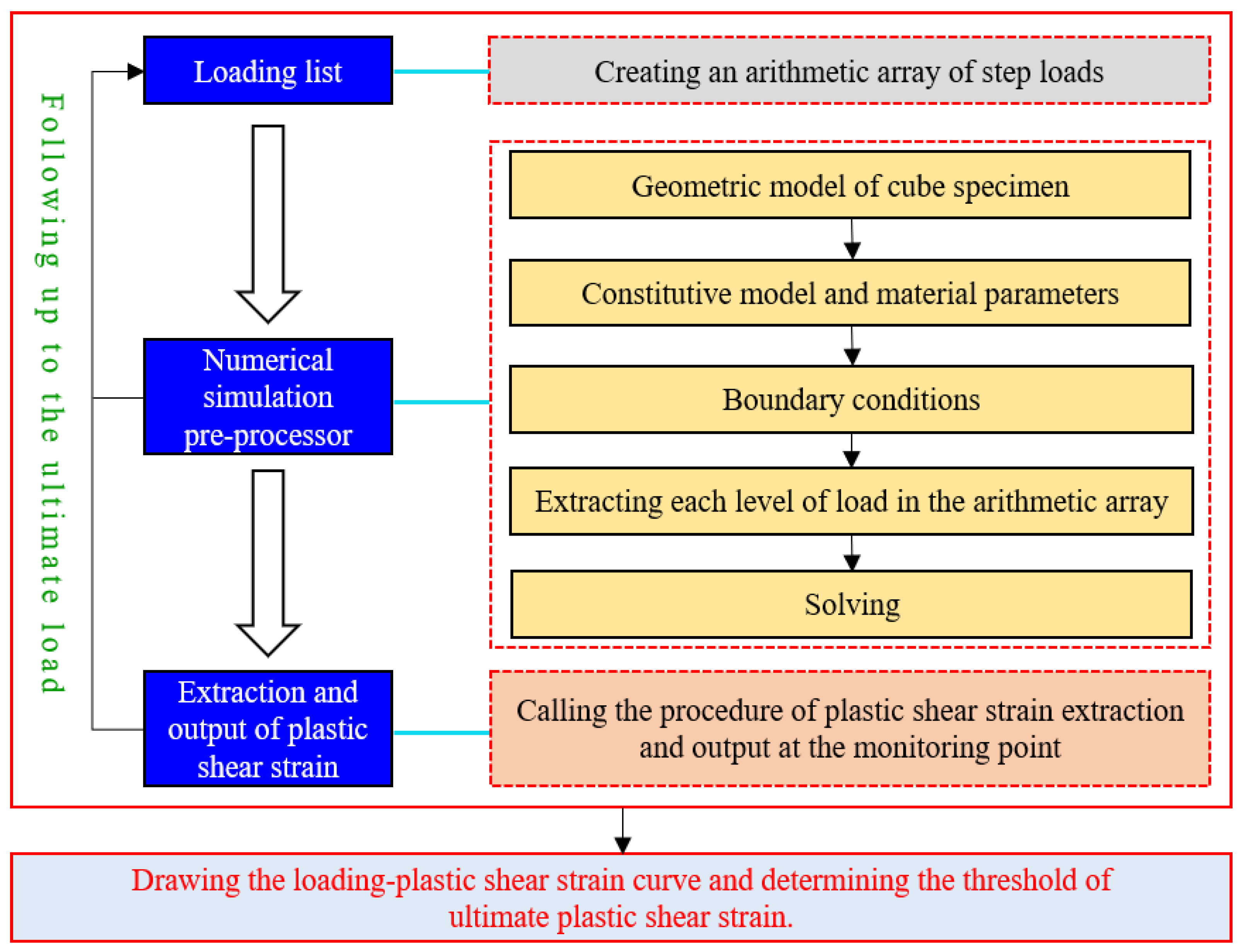
2.2. Calculation Process of the Ultimate Plastic Shear Strain
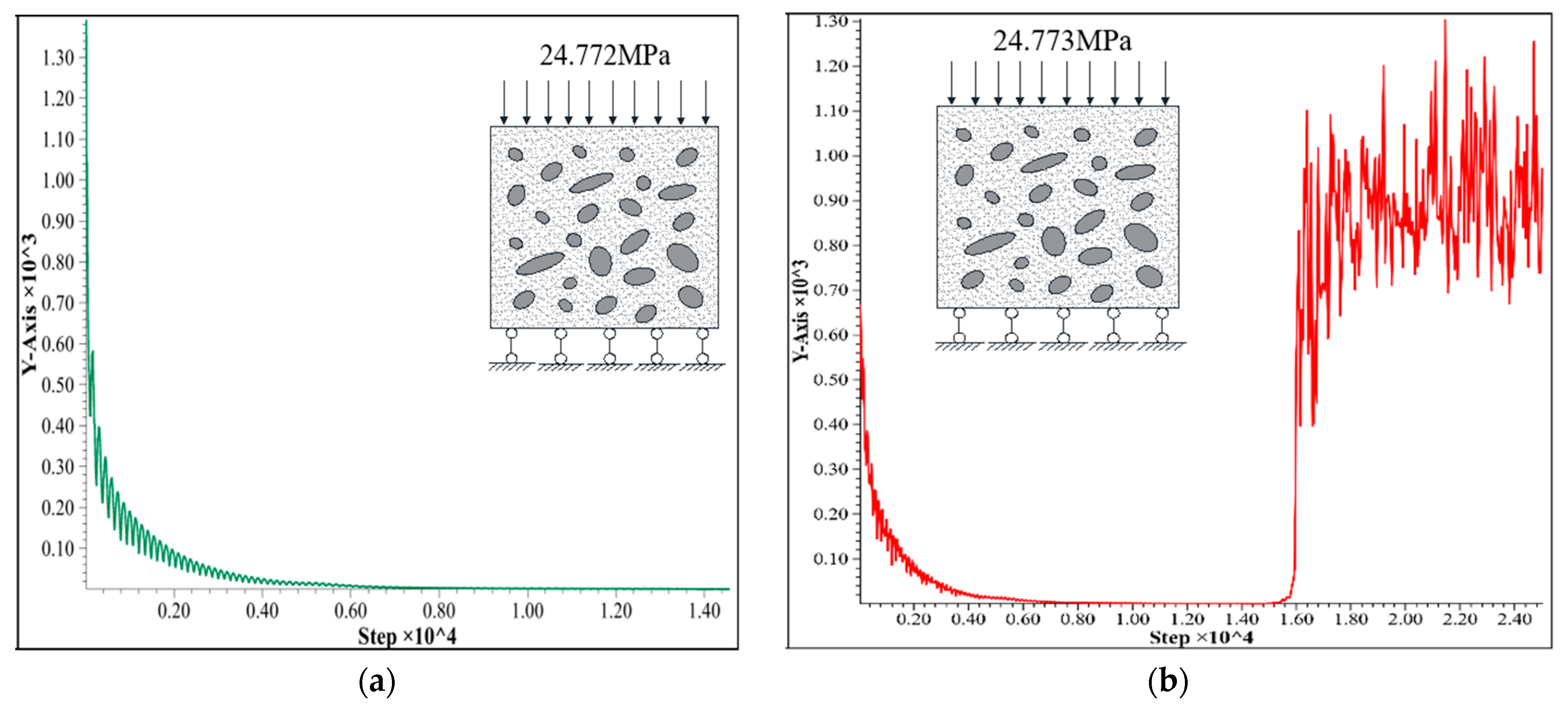
2.3. Solution and Verification of Ultimate Plastic Shear Strain
- (1)
- Carry the load to the ultimate one by using the function ‘numpy.arange( )’ in the Python computer language and forming an arithmetic array;
- (2)
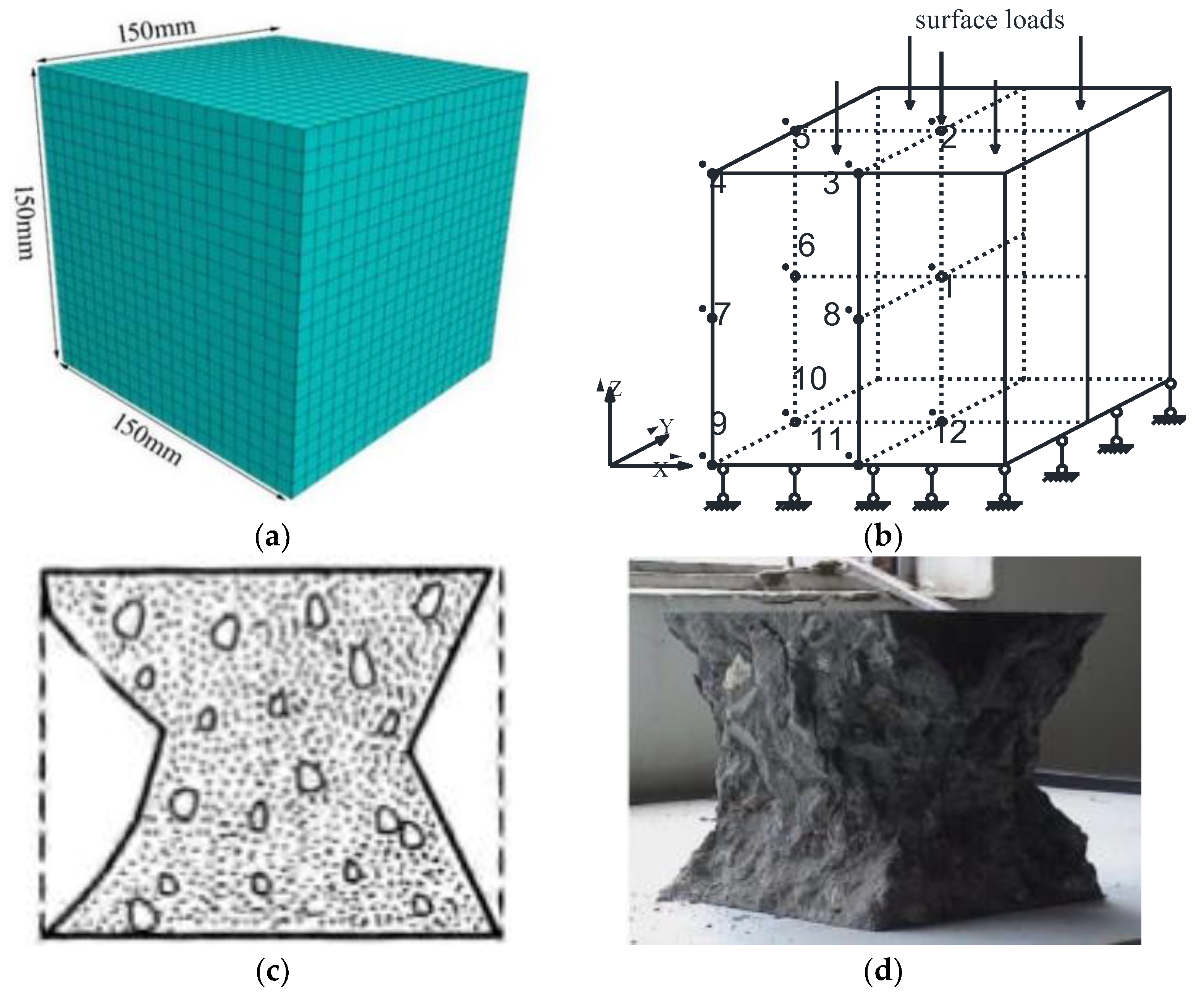
- A cube specimen model with a size of 150 mm × 150 mm × 150 mm is constructed, whose sides are divided into 20 grids;
- (3)
- Assign the strain-softened plasticity model and set the corresponding material attribute parameters (including softening parameters);
- (4)
- Apply the displacement limits in all directions at the bottom of the model and impose the uniform load at the top side;
- (5)
- Extract the load from the arithmetic array and solve it to the equilibrium state;
- (6)
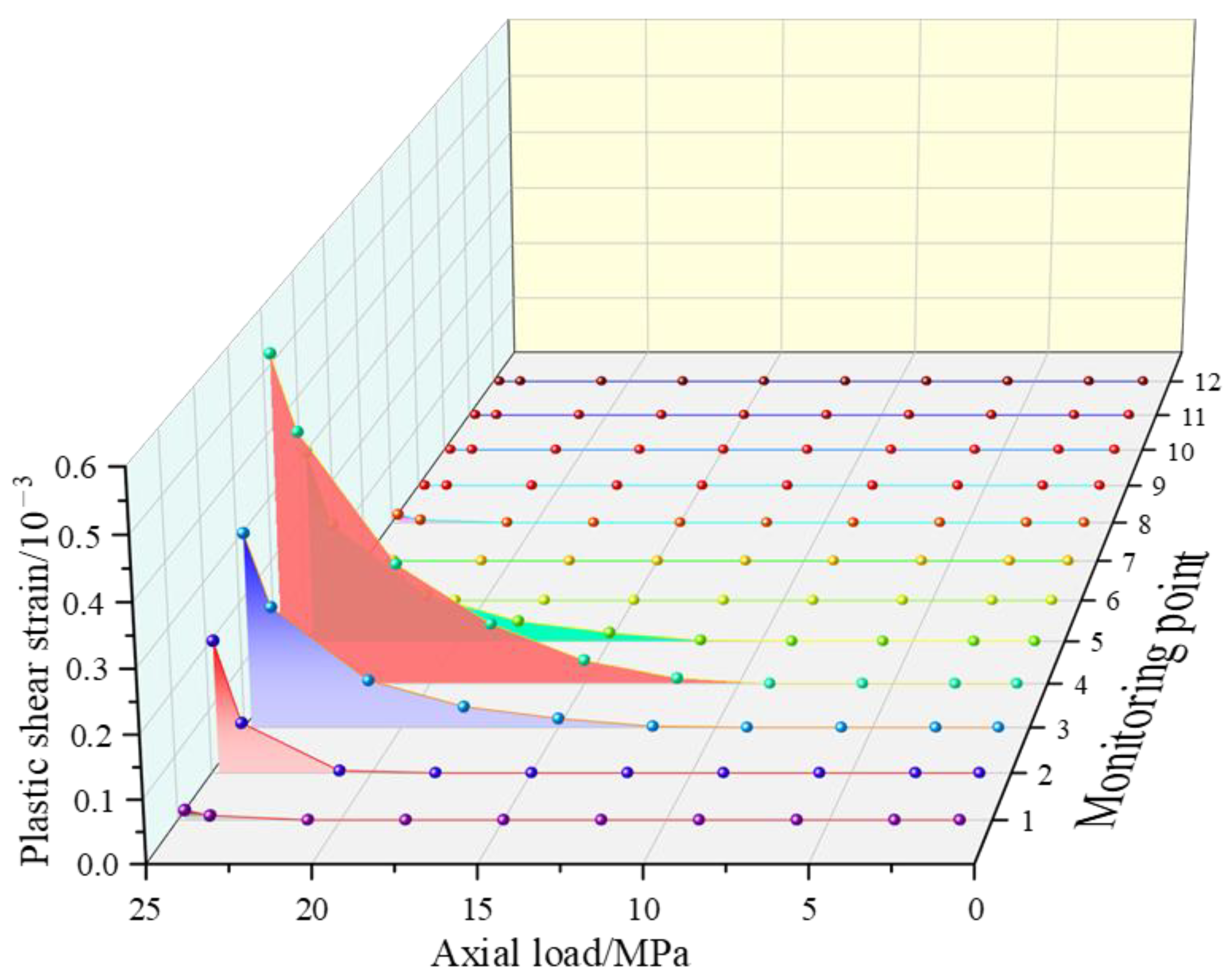
- According to the failure morphology of an ordinary concrete cube specimen, 12 key nodes (units) are set in the calculation model as monitoring points of plastic shear strain. Meanwhile, the coordinates of key nodes are loaded with the function ‘numpy.array( )’ in the Python computer language. In addition, the function ‘griddata( )’ is used to extract the plastic shear strain values of 12 key nodes under each level of load. Finally, the function ‘open( )’ is adopted to output the values of each level of load and the plastic shear strain values of 12 key nodes;
- (7)
- Repeat the steps (1–6) and cycle to the end of the ultimate load;
- (8)
- Draw the ‘axial load-plastic shear strain’ curve of 12 key nodes (elements). Under the function of the ultimate load, the maximum value of the plastic shear strain occurs at the upper part or corners of the model [22], and the damage to the upper side elements will inevitably lead to the overall failure of the specimen model. Therefore, the maximum value of the plastic shear strain is taken as the ultimate plastic shear strain of geotechnical materials.
3. Synergetic Theory of Information Entropy Based on the Failure Approach Index
3.1. Definition of the Information Entropy Based on the Failure Approach Index
3.2. Evolution Equation of Synergetic Theory of Information Entropy Based on Failure Approach Index
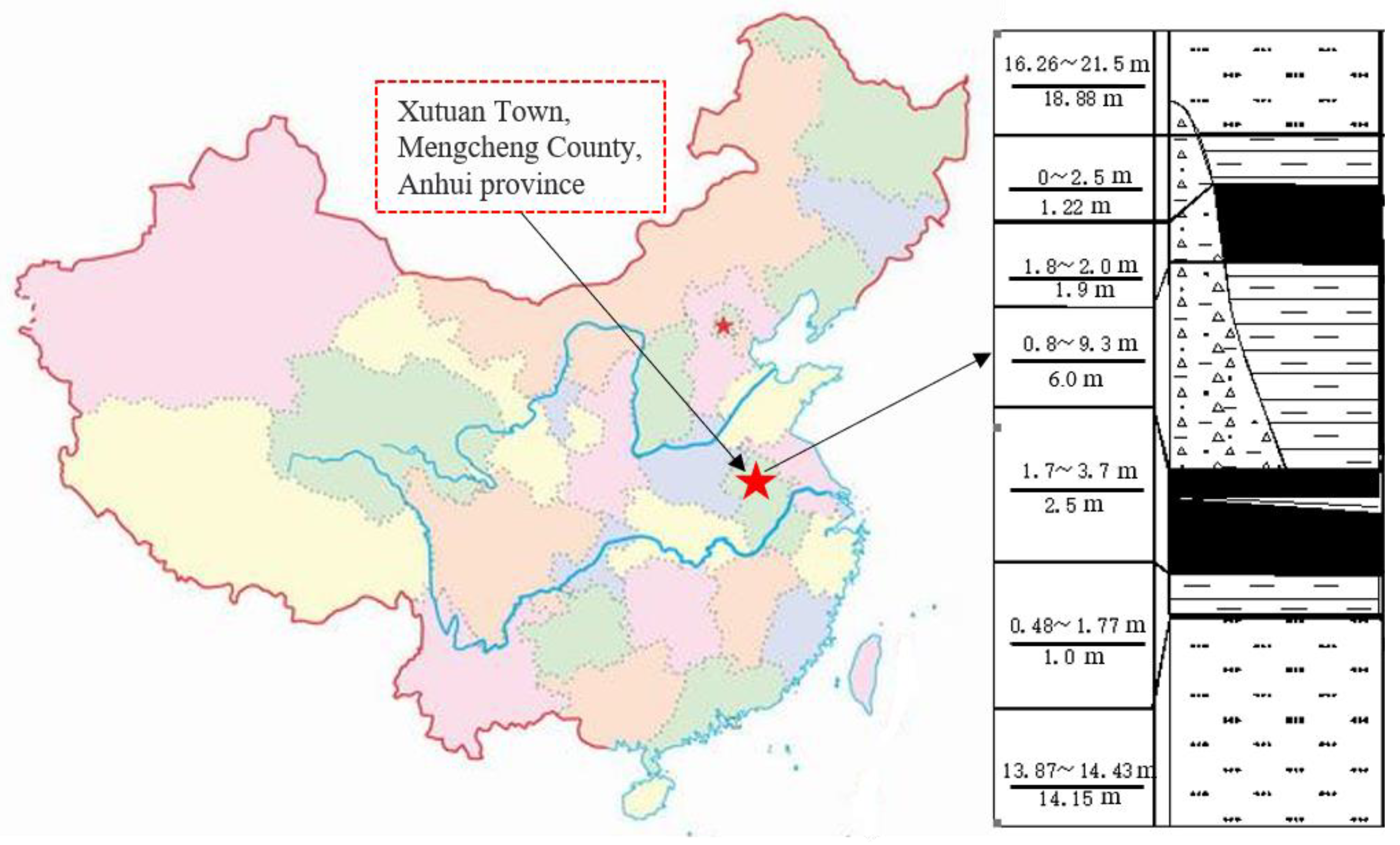
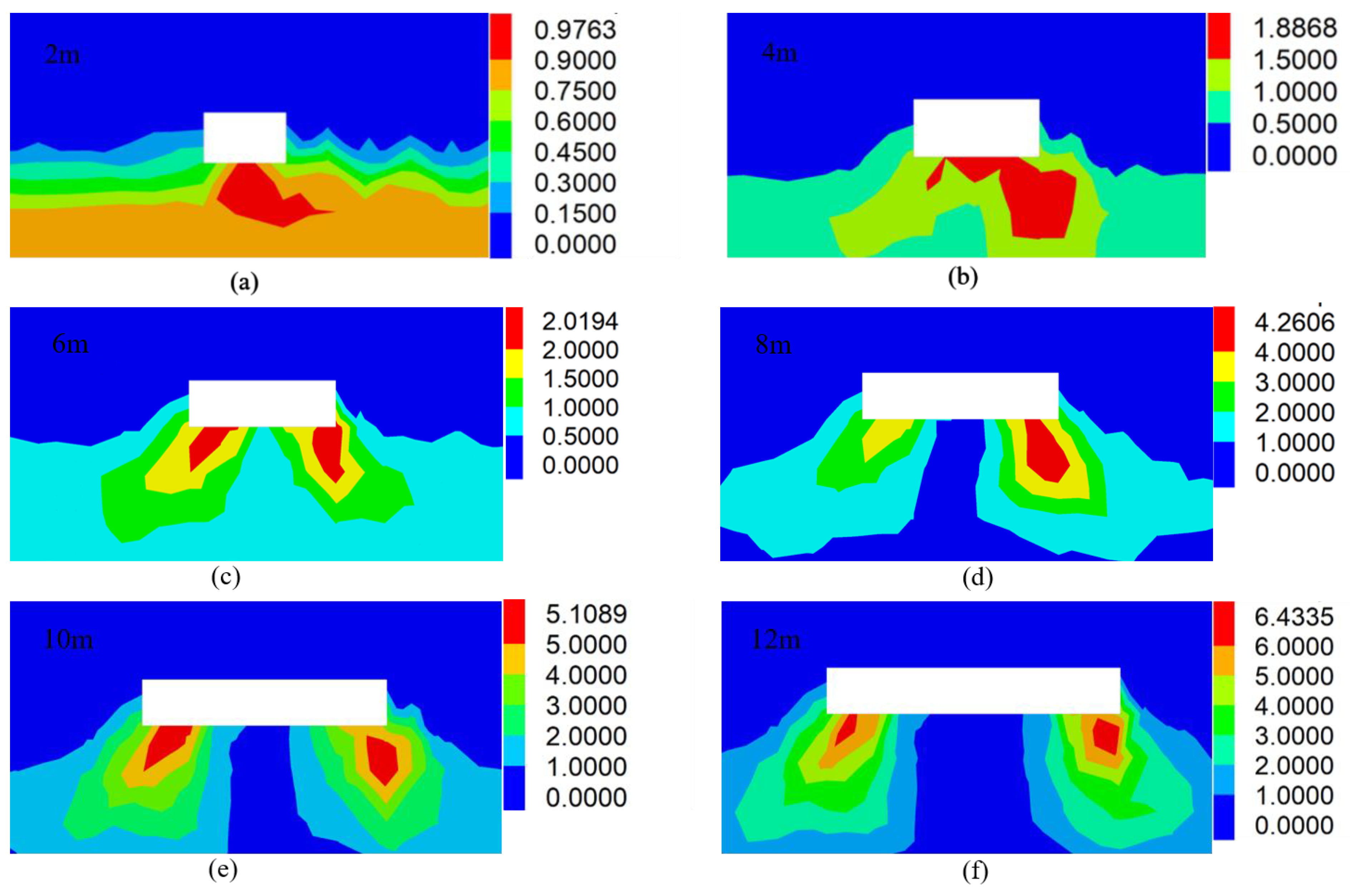
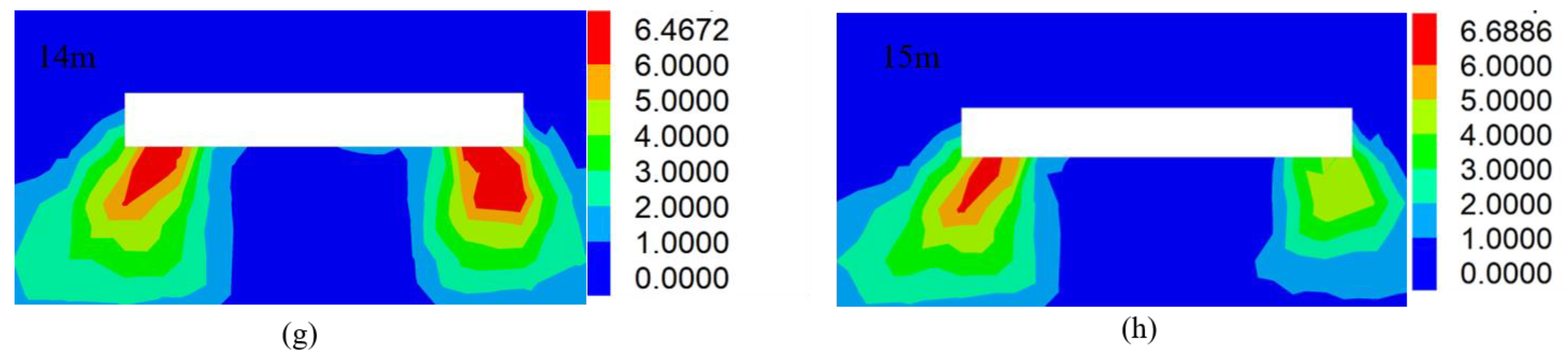
4. Stability Analysis of the Stope Floor Surrounding Rock System in a Bifurcated Coal Seam
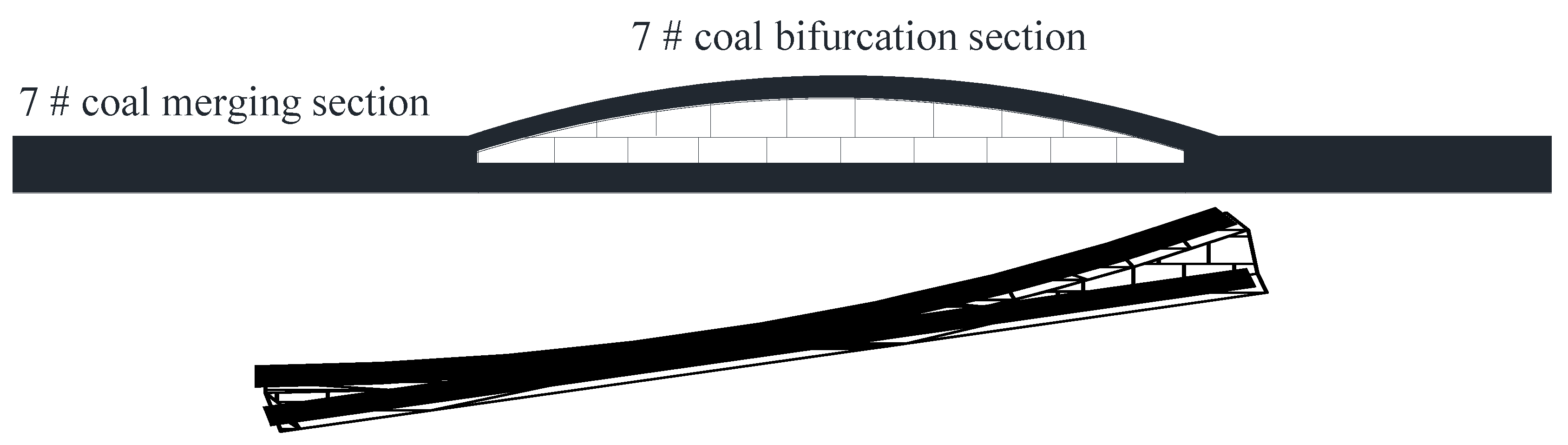
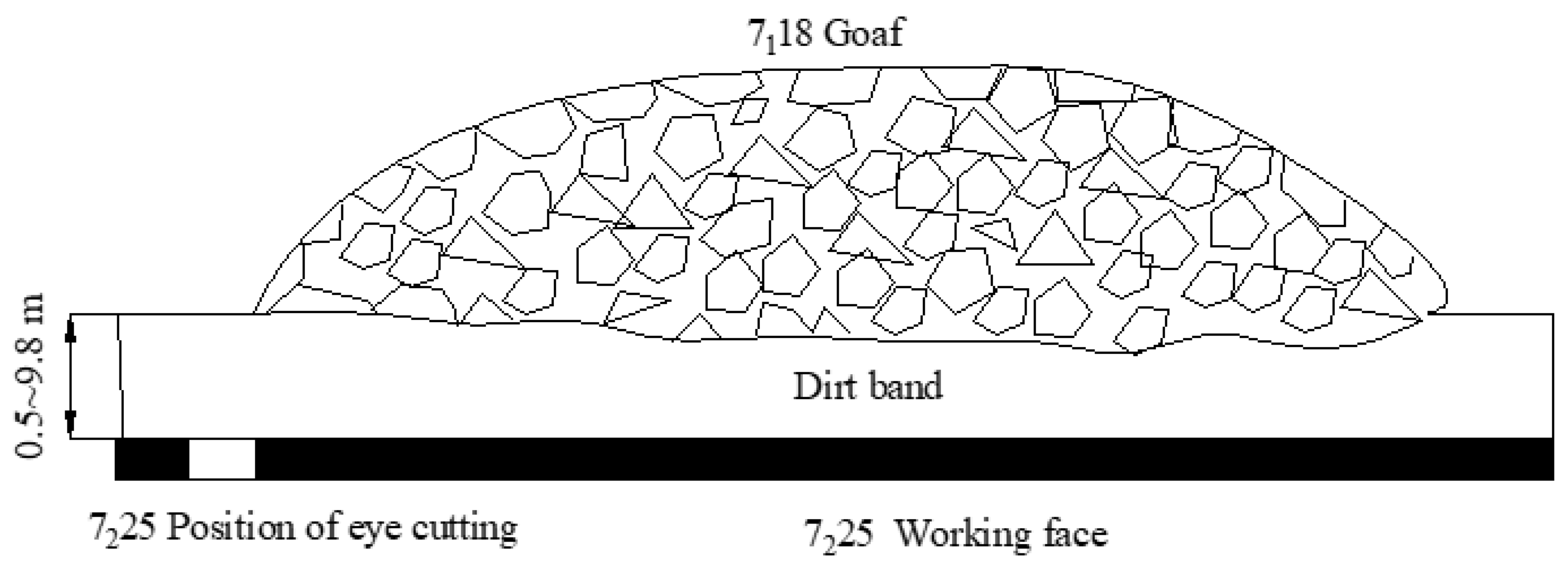
4.1. Project Overview
4.2. Stability Analysis of the Floor Surrounding Rock System of 71 Coal Seam
5. Conclusions
- (1)
- Based on the strain-softened plasticity model, the general relationship between the total two-dimensional plastic shear strain and the total three-dimensional plastic shear strain has been deduced, and the numerical limit analysis method of plastic shear strain has been proposed to obtain the threshold of the ultimate plastic shear strain, which has provided the crucial criterion for the calculation of information entropy based on the failure approach index;
- (2)
- The numerical limit analysis method was used to calculate and analyze the plastic shear strain of C25 ordinary concrete specimens, and the ultimate plastic shear strain value obtained was consistent with the result of previous studies, which verified the correctness and reliability of the numerical limit analysis method of plastic shear strain;
- (3)
- With regard to the synergetic theory of the principle of maximum information entropy, the evolution equation of the information entropy function based on the failure approach index and excavation step of the surrounding rock system in underground mining space is established. Meanwhile, the general and solution formulae and the expression of the unstable excavation step are attained, which has presented a theoretical analysis approach for the stability analysis of the surrounding rock system;
- (4)
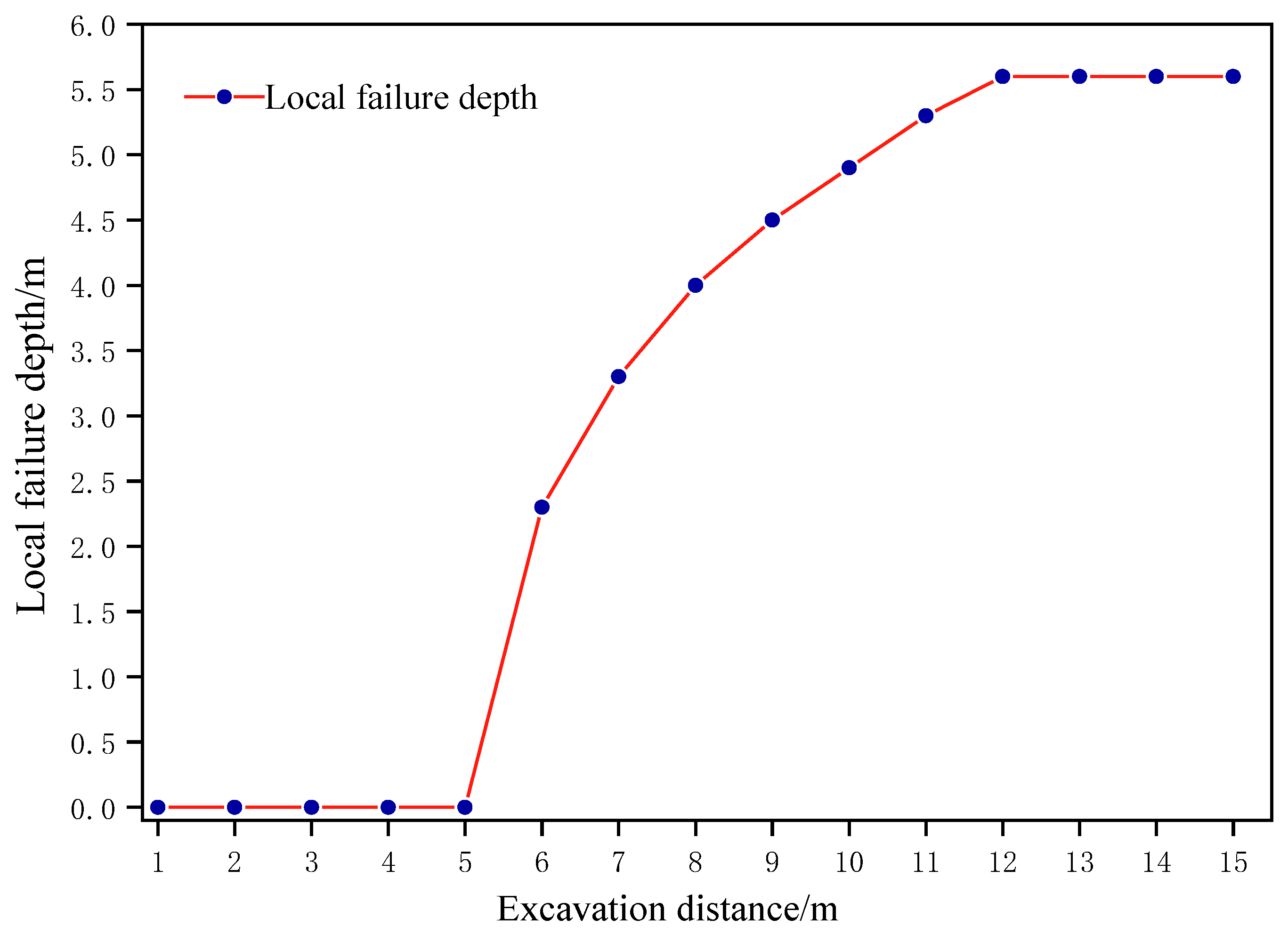
- Taking the close coal seam mining project in Xutuan Coal Mine as an example, the synergetic theory of information entropy based on the failure approach index was used to analyze whether the surrounding rock system of the 71 coal bottom plate with a layer thickness of 6 m is stable. Considering the periodic weighting of 71 coal roofs, the local damage depth of the mining floor reaches 5.6 m. In addition, the appropriate technical measures for controlling the stability of the underlying 72 coal mining roofs have been put forward to optimize the integrity of the stope roof and ensure the safety and efficiency of coal extraction.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, C.J.; Huang, D.M.; Chang, X.K.; Xi, H. Risk analysis and extension assessment for the stability of surrounding rock in deep coal roadway. Int. J. Env. Res. Pub. He. 2019, 16, 4752. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.W.; Xu, L.; Zhu, A.X.; Shan, M.Z.; Zhang, L.F.; Gu, J.F.; Shen, L. Comprehensive safety evaluation method of surrounding rock during underground cavern construction. Undergr. Space. 2019, 6, 46–61. [Google Scholar] [CrossRef]
- Su, Y.; Su, Y.H.; Zhao, M.H.; Vlachopoulos, N. Tunnel stability analysis in weak rocks using the convergence confinement method. Rock Mech. Rock Eng. 2020, 54, 559–582. [Google Scholar] [CrossRef]
- Yuan, H.P.; Cao, Z.H.; Xiong, L.J.; Li, H.Z.; Wang, Y.X. A machine learning method for engineering risk identification of goaf. Water 2022, 14, 4075. [Google Scholar] [CrossRef]
- Xu, C.H.; Ren, Q.W.; Li, R. Entropy catastrophe criterion of surrounding rock stability. Chin. J. Rock Mech. Eng. 2004, 23, 1992–1995. [Google Scholar]
- Liu, W.; Hua, Z.; Wang, R.L. Vibrational feature analysis for coal gangue caving based on information entropy of Hilbert spec trum. China Safety Sci. J. 2011, 21, 32–37. [Google Scholar] [CrossRef]
- He, H.J.; Yan, Y.M.; Qu, C.X.; Fan, Y. Study and application on stability classification of tunnel surrounding rock based on un certainty measure theory. Math. Probl. Eng. 2014, 2014, 626527. [Google Scholar] [CrossRef]
- Li, S.C.; Wu, J.; Xu, Z.H.; Li, L.P. Unascertained measure model of water and mud inrush risk evaluation in karst tunnels and its engineering application. KSCE. J. Civ. Eng. 2017, 21, 1170–1182. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, Q.; Yan, Y.J.; Wang, J.Q.; Zhao, K.; Cao, S.; Zhang, Y.J. Geological structural surface evaluation model based on unascertained measure. Geofluids 2019, 2019, 3547384. [Google Scholar] [CrossRef]
- Yang, P.; Yang, W.F.; Zhang, X.Q.; Wang, Z.R.; Yang, M.L. Dynamic evolution of overlying strata stress induced by mining and mine water disaster identification based on information entropy. J. China Coal Soc. 2021, 46, 3006–3014. [Google Scholar] [CrossRef]
- Ji, Z.X.; Jiang, P.H.; Yi, H.Y.; Zhuo, Z.; Li, C.Y.; Wu, Z.D. Application of two novel acoustic emission parameters on identifying the instability of granite. Entropy 2022, 24, 750. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.J.; Wang, J.Y.; Liu, F.; Xia, H.S. Mechanism and sensitivity analysis of collapse in large section mountain neighborhood tunnels. Front. Earth Sc-SWITZ 2022, 10, 904655. [Google Scholar] [CrossRef]
- Gao, Q.Q.; Ma, L.Q.; Liu, W.; Cao, K.W.; Khan, M.N.; Zhao, Z.Y. Appraisal of rock IR law and damage precursor: Insight infrared thermogram entropy. Infrared Phys. Techn. 2022, 127, 104443. [Google Scholar] [CrossRef]
- Zhang, C.Q.; Zhou, H.; Feng, X.T. An index for estimating the stability of brittle surrounding rock mass: FAI and its engineering application. Rock Mech. Rock Eng. 2011, 44, 401–414. [Google Scholar] [CrossRef]
- Li, P.F.; Zhao, X.G.; Guo, Z.; Ma, L.K.; Chen, L.; Wang, J. Variation of strength parameters of Beishan granite under triaxial compression. Chin. J. Rock Mech. Eng. 2017, 36, 1599–1610. [Google Scholar]
- Xiong, L.J.; Yuan, H.P.; Li, H.Z.; Wang, Y.X.; Liu, X.H.; Ye, C.X.; Wang, W.H. Evaluation method of surrounding rock stability: Failure approach index theory of strain limit analysis for engineering applications. PLoS ONE 2022, 17, e0279302. [Google Scholar] [CrossRef]
- Il’yushin, A.A. Plasticity; Gostekhizdat Publishing House: Moscow, Russia, 1948. [Google Scholar]
- Wang, W.; Chen, G.Q.; Zhu, J.; Huang, R.Q. Slope stability calculated with strength reduction method considering tensile and shear progressive failure. Chin. J. Rock Mech. Eng. 2018, 37, 2064–2074. [Google Scholar] [CrossRef]
- Zheng, Y.R. Development and application of numerical limit analysis method of geotechnical engineering. Chin. J. Rock Mech. Eng. 2012, 31, 1297–1316. [Google Scholar]
- Zheng, H. A three-dimensional rigorous method for stability analysis of landslides. Eng. Geol. 2012, 145, 30–40. [Google Scholar] [CrossRef]
- Su, Z.M.; Chen, J.X.; Zhao, D.J.; Xiang, Y.Z. Study on the numerical limit analysis method in design and application of soil tunnel. Chin. J. Undergr. Space. Eng. 2017, 13, 720–725. [Google Scholar]
- Erdi, A.; Feng, X.T.; Zheng, Y.R.; Xin, J.P. Strain analysis and numerical analysis based on limit strain for geomaterials. Chinese, J. Rock Mech. Eng. 2015, 34, 1552–1560. [Google Scholar]
- Tijani, I.A.; Wu, Y.F.; Lim, C.W. Energy balance method for modeling ultimate strain of fiber-reinforced polymer-repaired concrete. Struct. Concr. 2020, 21, 804–820. [Google Scholar] [CrossRef]
- Diego, A.D.; Arteaga, Á.; Fernández, J. Strengthening of square concrete columns with composite materials. Investigation on the FRP jacket ultimate strain. Compos. Part. B Eng. 2019, 162, 454–460. [Google Scholar] [CrossRef]
- The National Standards Compilation Group of People′s Republic of China. GB/T50010-2010 Code for Design of Concrete Structures; China Architecture and Building Press: Beijing, China, 2011. [Google Scholar]
- Bobet, A.; Einstein, H.H. Numerical modeling of fracture coalescence in a model rock material. Int. J. Fracture. 1998, 92, 22l–252. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, X.P.; Xu, X.M. Numerical simulation of failure process of rock-like materials subjected to impact loads. Int. J. Geomech. 2017, 17, 04016073. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, R.Q. Discussion on self-organized characters in the course of slope development. Chin. J. Geol. Hazard Control 1997, 8, 7–11. [Google Scholar]
- Huang, R.Q.; Xu, Q. Synergetic prediction model of slope instability. Mt. Res. 1997, 15, 7–12. [Google Scholar]
- Huang, R. Research on the Working Face of Broken Roof Control Technology under the Gob in Splitting and Merging Coal Seams; Anhui University of Science and Technology: Huainan, China, 2012. [Google Scholar]
- Zha, W.H.; Hua, X.Z.; Huang, R.; Xiong, L.J. Pre-grouting technology for broken roof of lower coal seam of splitting and merging coal. Chinese, J. Undergr. Space. Eng. 2012, 8, 1014–1020. [Google Scholar]

| Concrete | Density ρ/(kg/m3) | Elastic Modulus E/(GPa) | Poisson’s Ratio μ | Cohesion c/(MPa) | Angle of Internal Friction φ/(°) | Tensile Strength |
|---|---|---|---|---|---|---|
| C25 | 2400 | 28 | 0.2 | 3.2 | 61.4 | 1.78 |
| Lithology | Layer Thickness (m) | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Internal Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|---|
| Fine sandstone | 18.9 | 2437 | 27.55 | 0.25 | 3.56 | 35 | 3.6 |
| Mudstone | 1.2 | 2230 | 9.92 | 0.21 | 1.16 | 30 | 0.9 |
| No. 71 coal | 1.9 | 1400 | 6.50 | 0.27 | 1.25 | 28 | 0.9 |
| Mudstone | 6.0 | 2230 | 11.03 | 0.22 | 1.92 | 30 | 1.1 |
| No. 72 coal | 2.5 | 1400 | 3.80 | 0.21 | 1.46 | 28 | 0.8 |
| Fine sandstone | 15.2 | 2437 | 33.4 | 0.23 | 3.56 | 35 | 3.65 |
| Excavation Step | Information Entropy | Excavation Step | Information Entropy | Excavation Step | Information Entropy |
|---|---|---|---|---|---|
| 1 | 3.9367 | 6 | 5.0565 | 11 | 5.3842 |
| 2 | 4.3509 | 7 | 5.1201 | 12 | 5.4717 |
| 3 | 4.7005 | 8 | 5.2080 | 13 | 5.5441 |
| 4 | 4.7992 | 9 | 5.2625 | 14 | 5.5578 |
| 5 | 5.0404 | 10 | 5.3498 | 15 | 5.6858 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, L.; Yuan, H.; Liu, G.; Li, H.; Zou, Y.; Liu, X.; Li, X. Synergetic Theory of Information Entropy Based on Failure Approach Index for Stability Analysis of Surrounding Rock System. Entropy 2023, 25, 1237. https://doi.org/10.3390/e25081237
Xiong L, Yuan H, Liu G, Li H, Zou Y, Liu X, Li X. Synergetic Theory of Information Entropy Based on Failure Approach Index for Stability Analysis of Surrounding Rock System. Entropy. 2023; 25(8):1237. https://doi.org/10.3390/e25081237
Chicago/Turabian StyleXiong, Lijun, Haiping Yuan, Gaoliang Liu, Hengzhe Li, Yangyao Zou, Xiaohu Liu, and Xiaoming Li. 2023. "Synergetic Theory of Information Entropy Based on Failure Approach Index for Stability Analysis of Surrounding Rock System" Entropy 25, no. 8: 1237. https://doi.org/10.3390/e25081237
APA StyleXiong, L., Yuan, H., Liu, G., Li, H., Zou, Y., Liu, X., & Li, X. (2023). Synergetic Theory of Information Entropy Based on Failure Approach Index for Stability Analysis of Surrounding Rock System. Entropy, 25(8), 1237. https://doi.org/10.3390/e25081237






