Appendix A. SCII Strings of Non-KS MMPH Classes and Their Masters and Supermasters
Below, we give strings and coordinatizations of all MMPHs referred to in the main body of the paper. The first hyperedges in a line of a critical NBMMPH often correspond to the biggest loops in the figures.
Appendix A.1. Three-dim MMPHs
8-7 (KS “bug”) 123,34,45,567,78,81,26.
13-7 (filled 8-7) 123,394,4A5,567,7B8,8C1,2D6. 1=(0,0,1), 2=(0,1,0), 3=(1,0,0), 4=(0,1,1), 5=(1,1,−1), 6=(1,0,1), 7=(−1,2,1), 8=(2,1,0), 9=(0,1,−1), A=(2,−1,1), B=(1,−2,5), C=(1,−2,0), D=(1,0,−1)
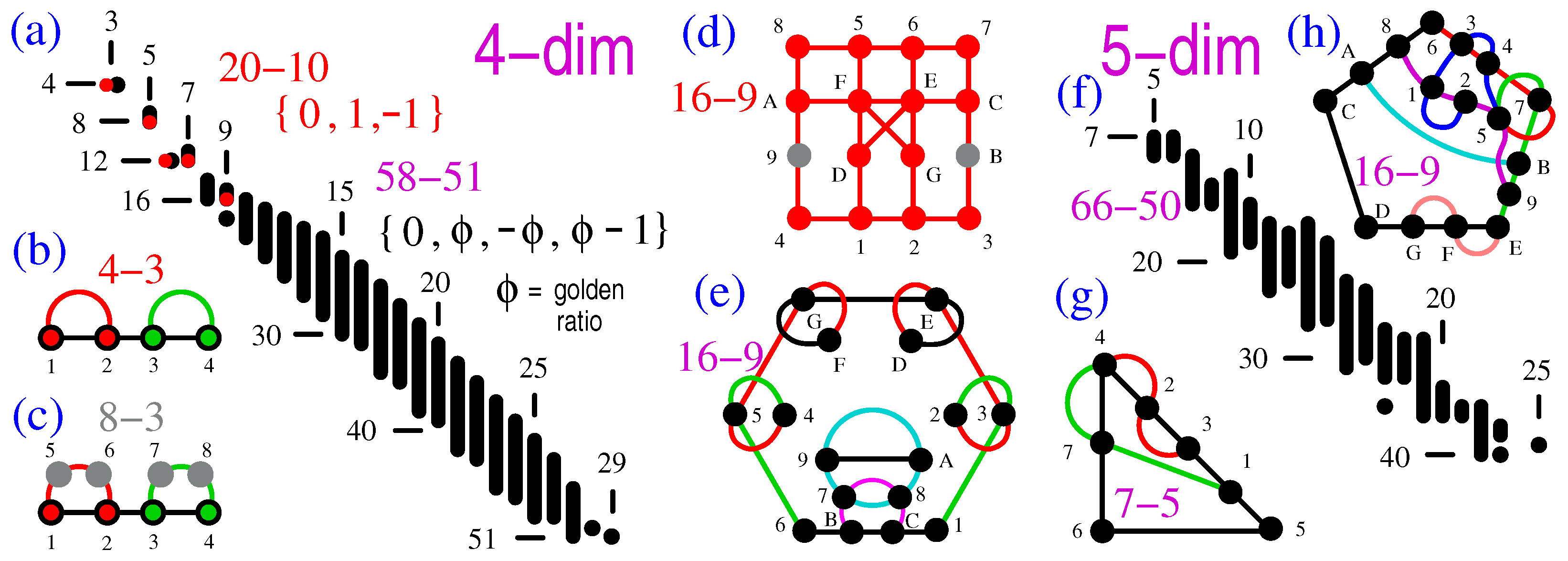
Appendix A.2. Four-dim MMPHs
4-3 12,34,1234.
8-3 (filled 4-3) 1562,3784,1234. 1=(0,0,0,1), 2=(0,0,1,0), 3=(0,1,0,0), 4=(1,0,0,0), 5=(1,1,0,0), 6=(1,−1,0,0), 7=(0,0,1,1), 8=(0,0,1,−1)
16-9 3124,49A8,8567,7BC3,DE,FG,GE62,FD51,FECA.
20-9 (filled 16-9) 1=(1,0,0,−1), 2=(0,1,1,0), 3=(1,1,−1,1), 4=(1,−1,1,1), 5=(1,0,0,1), 6=(0,1,−1,0), 7=(1,1,1,−1), 8=(−1,1,1,1), 9=(0,0,1,−1), A=(1,1,0,0), B=(0,0,1,1), C=(1,−1,0,0), D=(0,1,0,0), E=(0,0,0,1), F=(0,0,1,0), G=(1,0,0,0), H=(1,0,1,0), I=(1,0,−1,0), J=(0,1,0,1), K=(0,1,0,−1)
24-24 (Peres’ supermaster) LMNO,HIJK,DEFG,BCFG,9ADE,78EG,56DF,5678,9ABC,68JK,57HI,ACIK,9BHJ,1234,4DGO,3EFN,258M,167L,19CM,2ABL,3HKO,4IJN,34NO,12LM. 1=(0,0,0,1), 2=(0,0,1,0), 3=(1,1,0,0), 4=(1,−1,0,0), 5=(0,1,0,−1), 6=(1,0,−1,0), 7=(1,0,1,0), 8=(0,1,0,1), 9=(0,1,−1,0), A=(1,0,0,−1), B=(1,0,0,1), C=(0,1,1,0), D=(1,1,1,1), E=(1,−1,−1,1), F=(1,−1,1,−1), G=(1,1,−1,−1), H=(−1,1,1,1), I=(1,1,−1,1), J=(1,1,1,−1), K=(1,−1,1,1), L=(0,1,0,0), M=(1,0,0,0), N=(0,0,1,1), O=(0,0,1,−1)
16-9 231,1BC6,654,45GF,FGED,DE32,789A,7BC8,9A.
20-9 (filled 16-9) 2H31,1BC6,6I54,45GF,FGED,DE32,789A,7BC8,9JKA. 1=(0,0,0,), 2=(−1,0,−,0), 3=(,0,−1,0), 4=(0,,0,), 5=(0,,0,−), 6=(0,0,,0), 7=(0,0,,), 8=(0,0,,−), 9=(,−1,0,0), A=(−1,−,0,0), B=(,,0,0), C=(,−,0,0), D=(0,−1,0,−), E=(0,,0,−1), F=(,0,,0), G=(,0,−,0), H=(0,,0,0), I=(,0,0,0), J=(0,0,,−1), K=(0,0,−1,−)
60-72 (supermaster) 1234,1256,1278,129A,13BC,13DE,13FG,1HI4,1JK4,1LM4,23NO,23PQ,23RS,2TU4,2VW4,2XY4,Za34,Za56,Za78,Za9A,Z5bc,Zde6,fg34,fg56,fg78,fg9A,hi34,hi56,hi78,hi9A,ajk6,a5lm,ano6,apq6,TUBC,TUDE,TUFG,TBbo,TCmd,VWBC,VWDE,VWFG,XYBC,XYDE,XYFG,HINO,HIPQ,HIRS,HNco,HOme,JKNO,JKPQ,JKRS,LMNO,LMPQ,LMRS,UBle,UnCc,UrsC,UtCu,jkbc,INld,InOb,IvwO,IxOy,nbco,rsbo,pbcq,vwco,tbuo,xyco,lmde. 1=(0,0,0,), 2=(0,0,,0), 3=(0,,0,0), 4=(,0,0,0), 5=(,,0,0), 6=(,−,0,0), 7=(,−1,0,0), 8=(−1,−,0,0), 9=(−,−1,0,0), A=(−1,,0,0), B=(,0,,0), C=(,0,−,0), D=(−,0,−1,0), E=(−1,0,,0), F=(,0,−1,0), G=(−1,0,−,0), H=(0,,,0), I=(0,,−,0), J=(0,−1,,0), K=(0,−,−1,0), L=(0,−1,−,0), M=(0,,−1,0), N=(,0,0,), O=(,0,0,−), P=(,0,0,−1), Q=(−1,0,0,−), R=(−,0,0,−1), S=(−1,0,0,), T=(0,,0,), U=(0,,0,−), V=(0,,0,−1), W=(0,−1,0,−), X=(0,−,0,−1), Y=(0,−1,0,), Z=(0,0,,), a=(0,0,,−), b=(,−,−,), c=(,−,,−), d=(,,,−), e=(,,−,), f=(0,0,,−1), g=(0,0,−1,−), h=(0,0,−,−1), i=(0,0,−1,), j=(,,−1,−1), k=(−1,−1,−,−), l=(−,,,), m=(,−,,), n=(,,,), o=(,,−,−), p=(−,−,−1,−1), q=(−1,−1,,), r=(,−1,,−1), s=(−1,−,−1,−), t=(−,−1,−,−1), u=(−1,,−1,), v=(,−1,−1,), w=(−1,−,−,−1), x=(−,−1,−1,−), y=(−1,,,−1)
Appendix A.3. Five-dim MMPHs
7-5 41235,56,674,234,714.
16-5 (7-5 filled) 41235,589A6,6BC74,2DE34,7FG14. 1=(0,0,1,0,0), 2=(1,−1,0,0,0), 3=(1,1,0,0,0), 4=(0,0,0,0,1), 5=(0,0,0,1,0), 6=(0,1,1,0,0), 7=(1,0,0,1,0), 8=(1,0,0,0,−1), 9=(0,1,−1,0,0), A=(1,0,0,0,1), B=(1,−1,1,−1,0), C=(1,1,−1,−1,0), D=(0,0,1,1,0), E=(0,0,1,−1,0), F=(0,1,0,0,0), G=(1,0,0,−1,0)
16-9 63457,75B9E,EFGD,DC,CA86,12345,89125,AB,FGE.
26-9 (16-9 filled) 63457,75B9E,EFHGD,DIJKC,CAL86,12345,89125,AMNOB,FPQGE. 1=(1,1,1,−1,0), 2=(1,1,−1,1,0), 3=(1,−1,1,1,0), 4=(−1,1,1,1,0), 5=(0,0,0,0,1), 6=(0,0,1,−1,0), 7=(1,1,0,0,0), 8=(0,0,1,1,0), 9=(1,−1,0,0,0), A=(0,1,0,0,1), B=(0,0,1,0,0), C=(1,0,0,0,0), D=(0,1,1,0,0), E=(0,0,0,1,0), F=(1,0,0,0,1), G=(0,1,−1,0,0), H=(1,0,0,0,−1), I=(0,0,0,1,1), J=(0,1,−1,1,−1), K=(0,1,−1,−1,1), L=(0,1,0,0,−1), M=(1,1,0,−1,−1), N=(1,−1,0,−1,1), O=(1,0,0,1,0), P=(1,1,1,0,−1), Q=(−1,1,1,0,1)
105-136 (supermaster) 12345,12367,12489,12AB5,134CD,13EF5,1GH45,1GH67,1G6IJ,1GKL7,1H6MN,1HOP7,1EF89,1E8IP,1E9KN,1F8ML,1F9OJ,1ABCD,1ACJP,1ADLN,1QRST,1QUVW,1XYSZ,1XabW,1BCMK,1BDOI,1cYVd,1caeT,1fRbd,1fUeZ,1OIJP,1MKLN,234gh,23ij5,2kl45,2kl67,2k6mn,2kop7,2l6qr,2lst7,2ij89,2i8mt,2i9or,2j8qp,2j9sn,2ABgh,2Agtn,2Ahpr,2uvSw,2uxyW,2z!S",2z#$W, 2Bgoq,2Bhsm,2%!yd,2%#ew,2&v$d,2&xe",2smtn,2oqpr,’(345,’(367,’(489,’(AB5,’36)*,’3-/7, ’48:;,’4<=9,’A>?5,’@[B5,(36\],(3^_7,(48‘{,(4|}9,(A∼+15,(+2+3B5,3ijCD,3iC_*,3iD-\,3jC/],3jD^),3EFgh,3Eg_),3Eh/\,3+4+5Vw,3+4+6yT,3+7+8V",3+7+9$T,3Fg-],3Fh^*,3+A+8yZ, 3+A+9bw,3+B+5$Z,3+B+6b",3^_)*,3-/\],kl4CD,klEF5,k4C};,k4D<‘,kE+3?5,kF@∼5, l4C={,l4D|:, lE[+15,lF+2>5,GH4gh,GHij5,G4g}:,G4h=‘,Gi+3>5,Gj[∼5,+C4+5Rx,+C4+6vU,+C+7X%5,+C+Azc5, +D4+8R#,+D4+9!U,+D+4X&5,+D+Buc5,H4g<{,H4h|;,Hi@+15, Hj+2?5,+E4+8va,+E4+9Yx,+E+4zf5, +E+BQ%5,+F4+5!a,+F4+6Y#,+F+7uf5,+F+AQ&5,4|}:;,4<=‘{,+2+3>?5,@[∼+15. 1=(0,0,0,0,1), 2=(0,0,0,1,0), ’=(0,0,0,1,1), (=(0,0,0,1,−1), 3=(0,0,1,0,0), k=(0,0,1,0,1), l=(0,0,1,0,−1), G=(0,0,1,1,0), +C=(0,0,1,1,1), +D=(0,0,1,1,−1), H=(0,0,1,−1,0), +E=(0,0,1,−1,1), +F=(0,0,−1,1,1), 4=(0,1,0,0,0), i=(0,1,0,0,1), j=(0,1,0,0,−1), E=(0,1,0,1,0), +4=(0,1,0,1,1), +7=(0,1,0,1,−1), F=(0,1,0,−1,0), +A=(0,1,0,−1,1), +B=(0,−1,0,1,1), A=(0,1,1,0,0), u=(0,1,1,0,1), z=(0,1,1,0,−1), Q=(0,1,1,1,0), +2=(0,1,1,1,1), @=(0,1,1,1,−1), X=(0,1,1,−1,0), [=(0,1,1,−1,1), +3=(0,1,1,−1,−1), B=(0,1,−1,0,0), %=(0,1,−1,0,1), &=(0,−1,1,0,1), c=(0,1,−1,1,0), ∼=(0,1,−1,1,1), >=(0,1,−1,1,−1), f=(0,−1,1,1,0), ?=(0,1,−1,−1,1), +1=(0,−1,1,1,1), 5=(1,0,0,0,0), g=(1,0,0,0,1), h=(1,0,0,0,−1), C=(1,0,0,1,0), +8=(1,0,0,1,1), +5=(1,0,0,1,−1), D=(1,0,0,−1,0), +6=(1,0,0,−1,1), +9=(−1,0,0,1,1), 8=(1,0,1,0,0), !=(1,0,1,0,1), v=(1,0,1,0,−1), Y=(1,0,1,1,0), |=(1,0,1,1,1), <=(1,0,1,1,−1), R=(1,0,1,−1,0), ==(1,0,1,−1,1), }=(1,0,1,−1,−1), 9=(1,0,−1,0,0), x=(1,0,−1,0,1), #=(−1,0,1,0,1), U=(1,0,−1,1,0), ‘=(1,0,−1,1,1), :=(1,0,−1,1,−1), a=(−1,0,1,1,0), ;=(1,0,−1,−1,1), {=(−1,0,1,1,1), 6=(1,1,0,0,0), $=(1,1,0,0,1), y=(1,1,0,0,−1), b=(1,1,0,1,0), ^=(1,1,0,1,1), −=(1,1,0,1,−1), V=(1,1,0,−1,0), /=(1,1,0,−1,1), _=(1,1,0,−1,−1), e=(1,1,1,0,0), s=(1,1,1,0,1), o=(1,1,1,0,−1), O=(1,1,1,1,0), M=(−1,1,1,1,0), I=(1,−1,−1,1,0), K=(1,1,1,−1,0), q=(−1,1,1,0,1), m=(1,−1,−1,0,1), S=(1,1,−1,0,0), p=(1,1,−1,0,1), t=(1,1,−1,0,−1), L=(1,1,−1,1,0), d=(−1,1,1,0,0), J=(1,−1,1,−1,0), P=(1,1,−1,−1,0), N=(1,−1,1,1,0), n=(1,−1,1,0,−1), 7=(1,−1,0,0,0), w=(1,−1,0,0,1), "=(−1,1,0,0,1), T=(1,−1,0,1,0), \=(1,−1,0,1,1), )=(1,−1,0,1,−1), Z=(−1,1,0,1,0), *=(1,−1,0,−1,1), ]=(−1,1,0,1,1), W=(1,−1,1,0,0), r=(1,−1,1,0,1)
10-9 ([
42] Figure 5a)
17835,27846,91,97,92,8A,34,6A,5A. 31-9 (10-9 filled) 17835,27846,9BCD1,9EFG7,9HIJ2,8KLMA,3NOP4,6QRSA,5TUVA. 1=(0,0,1,0,−1), 2=(0,0,0,1,−1), 3=(0,0,0,1,0), 4=(0,0,1,0,0), 5=(0,0,1,0,1), 6=(0,0,0,1,1), 7=(0,1,0,0,0), 8=(1,0,0,0,0), 9=(0,0,1,1,1), A=(0,1,1,1,−1), B=(0,0,−1,2,−1), C=(1,2,0,0,0), D=(2,−1,0,0,0), E=(0,0,−1,−1,2), F=(1,0,1,−1,0), G=(2,0,−1,1,0), H=(0,0,2,−1,−1), I=(1,1,0,0,0), J=(1,−1,0,0,0), K=(0,0,1,−1,0), L=(0,1,0,0,1), M=(0,−1,1,1,1), N=(0,0,0,0,1), O=(−1,2,0,0,0), P=(2,1,0,0,0), Q=(0,1,1,−1,1), R=(1,1,−1,0,0), S=(2,−1,1,0,0), T=(0,1,0,−1,0), U=(2,1,−1,1,1), V=(2,−1,1,−1,−1)
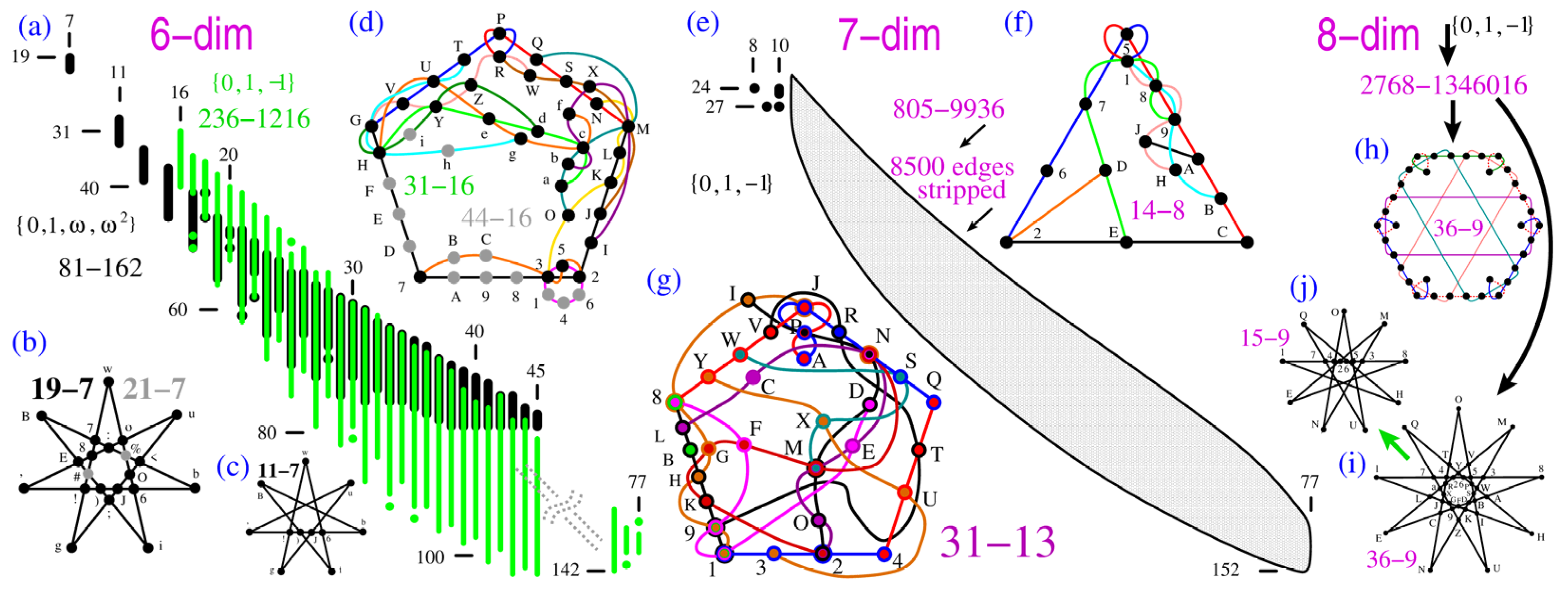
Appendix A.4. Six-dim MMPHs
19-7 7!8gw,woO6i,i;)EB,B<:b7,’!)Jb6,’o:8Eu,;<OJgu.
11-7 w!g,wi6,’!)Jb6,’u,B)i,Jgu,Bb.
21-7 (11-7, 19-7 filled) w!78#g,woOi6%,’!)Jb6,’o:8Eu,;B)i#E,;<OJgu,B<7:b%.w=(,1,1,,1,), ’=(,,,1,1,1), ;=(,1,1,,,1), !=(,1,,1,,1), B=(1,,,1,,1), <=(,1,,1,1,), o=(1,,1,1,1,), )=(,,1,1,1,), 7=(1,,,1,1,), O=(1,,,,1,1), :=(,1,1,1,,), 8=(1,,1,,,1), i=(,1,,1,1,1), J=(1,,1,1,,), #=(1,1,1,1,,), b=(1,1,1,,1,1), 6=(1,1,,1,,), g=(,,1,1,1,1), E=(1,1,,,1,), %=(,,1,1,,1), u=(1,1,,1,,1)
79-162 (81-162 stripped; %,#)) 123456,12789A,1BCD5E,1B7FGH,1ICJ9K,1I3LGM,1NODAP,1NQ4HR, 1SOJ6T,1SU8MR,1VQLET,1VUFKP,WXY45Z,WX7abA,Wcde5E,Wc7Ffg,WIdJbh,WIYifM,WjkeAP,WjQ4gl,WSkJZm,WSnaMl,WoQiEm,WonFhP,pqY89Z,pq3ab6,pcre9K,pc3Lsg,pBrDbh,pBYisH,pjte6T,pjU8gu,pNtDZm,pNnaHu,pvnLhT,pvUiKm,wxyD5Z,wx7azH,w!"e56,w!78g,wI"Lzh,wIyiK,w$keHR,w$ODgl,wVkLZ,wV&aKl,woOi6,wo&8hR,’(yDbA,’(Y4zH,’!)Jb6,’!Y8*M,’c)LzE,’cyF*K,’-kJHu,’-tDMl,’vkLA/,’v:4Kl,’otF6/,’o:8Eu,;("e9A,;(34g,;x)J9Z,;x3a*M,;B)iE,;B"F*h,;<teMR,;<OJgu,;vOiA=,;v>4hR,;VtFZ=,;V>aEu,?!reGM,?!CJsg,?qyFGZ,?qCazE,?2yisA,?2r4zh,?$:eET,?$UFg/,?-&JhT,?-UiM,?N:4Z,?N&aA/,@(deGH,@(CDfg,@X)LGZ,@XCa*K,@2)if6,@2d8*h,@<:eKP,@<QLg/,@->DhP,@-QiH=,@S:8Z=,@S>a6/,[xdJsH,[xrDfM,[X"LsA,[Xr4K,[q"Ff6,[qd8E,[<&JKm,[<nLM,[$>DEm,[$nFH=,[j>46,[j&8A=,(S"Uzm,(SynT,(VdUb,(VY&fT,(oCn9,(o3&Gm,xj)UzP,xjyQ*T,xvdU5/,xv7:fT,xorQ9/,xo3:sP,!N)nP,!N"Q*m,!vCn5=,!v7>Gm,!VrQb=,!VY>sP,X$)UbR,X$YO*T, X-"U5u,X-7tT,XorOGu,XoCtsR,q<yQbR,q<YOzP,q-"Q9l,q-3kP,qvdOGl,qvCkfR,2<yn5u,2<7tzm, 2$)n9l,2$3k*m,2Vdtsl,2Vrkfu,c-3&5=,c-7>9,cN)&fR,cNdO*,cSy>sR,cSrOz=,B<Y&5/,B<7:b,Bj)&Gl,BjCk*,BS":sl,BSrk/,I$Y>9/,I$3:b=,Ijy>Gu,IjCtz=,IN":fu,INdt/.
81-162 123456,12789A,1BCD5E,1B7FGH,1ICJ9K,1I3LGM,1NODAP,1NQ4HR,1SOJ6T,1SU8MR,1VQLET,1VUFKP,WXY45Z,WX7abA,Wcde5E,Wc7Ffg,WIdJbh,WIYifM,WjkeAP,WjQ4gl,WSkJZm,WSnaMl,WoQiEm,WonFhP,pqY89Z,pq3ab6,pcre9K,pc3Lsg,pBrDbh,pBYisH,pjte6T,pjU8gu,pNtDZm,pNnaHu,pvnLhT,pvUiKm,wxyD5Z,wx7azH,w!"e56,w!78#g,wI"Lzh,wIyi#K,w$keHR,w$ODgl,wVkLZ%,wV&aKl,woOi6%,wo&8hR,’(yDbA,’(Y4zH,’!)Jb6,’!Y8*M,’c)LzE,’cyF*K,’-kJHu,’-tDMl,’vkLA/,’v:4Kl,’otF6/,’o:8Eu,;("e9A,;(34#g,;x)J9Z,;x3a*M,;B)i#E,;B"F*h,;<teMR,;<OJgu,;vOiA=,;v>4hR,;VtFZ=,;V>aEu,?!reGM,?!CJsg,?qyFGZ,?qCazE,?2yisA,?2r4zh,?$:eET,?$UFg/,?-&JhT,?-UiM%,?N:4Z%,?N&aA/,@(deGH,@(CDfg,@X)LGZ,@XCa*K,@2)if6,@2d8*h,@<:eKP,@<QLg/,@->DhP, @-QiH=,@S:8Z=,@S>a6/,[xdJsH,[xrDfM,[X"LsA,[Xr4#K,[q"Ff6,[qd8#E,[<&JKm,[<nLM%, [$>DEm,[$nFH=,[j>46%,[j&8A=,(S"Uzm,(Syn#T,(VdUb%,(VY&fT,(oCn9%,(o3&Gm,xj)UzP,xjyQ*T, xvdU5/,xv7:fT,xorQ9/,xo3:sP,!N)n#P,!N"Q*m,!vCn5=,!v7>Gm,!VrQb=,!VY>sP,X$)UbR,X$YO*T,X-"U5u,X-7t#T,XorOGu,XoCtsR,q<yQbR,q<YOzP,q-"Q9l,q-3k#P,qvdOGl,qvCkfR,2<yn5u,2<7tzm,2$)n9l,2$3k*m,2Vdtsl,2Vrkfu,c-3&5=,c-7>9%,cN)&fR,cNdO*%,cSy>sR,cSrOz=,B<Y&5/,B<7:b%,Bj)&Gl,BjCk*%,BS":sl,BSrk#/,I$Y>9/,I$3:b=,Ijy>Gu,IjCtz=,IN":fu,INdt#/. 1=(,1,1,1,1,1), W=(,1,1,1,,),p=(,1,1,1,,), w=(,1,1,,1,),’=(,,,1,1,1), ;=(,1,1,,,1), ?=(,1,1,,1,), @=(,1,1,,,1), [=(1,,,1,1,1), (=(,1,,1,1,), x=(,,1,,1,1), !=(,1,,1,,1), X=(,,1,1,,1), q=(,,1,1,1,), 2=(1,,,,1,1), c=(,1,,,1,1), B=(1,,,1,,1), I=(1,,,1,1,), <=(,1,,1,1,), $=(,1,,1,,1), -=(1,,1,,1,1), j=(,1,,,1,1), N=(1,,1,,,1), S=(1,,1,,1,), v=(1,,1,1,,1), V=(1,,1,1,,), o=(1,,1,1,1,), )=(,,1,1,1,), "=(,1,,,1,1), y=(,,1,1,,1), d=(,1,,1,,1), r=(,1,,1,1,), C=(1,,,,1,1), Y=(,,1,,1,1), 3=(1,,,1,,1), 7=(1,,,1,1,), k=(,1,1,,,1), t=(,1,1,,1,), O=(1,,,,1,1), :=(,1,1,1,,), >=(,1,1,1,1,), &=(,1,1,1,,1), Q=(1,,,1,,1), n=(,1,1,,1,1), U=(1,,,1,1,), a=(,,,1,1,1), 8=(1,,1,,,1), 4=(1,,1,,1,), F=(1,,1,,,1), i=(,1,,1,1,1), L=(1,,1,,1,), D=(1,,1,1,,), J=(1,,1,1,,), *=(1,1,1,1,1,), z=(1,1,1,1,,1), #=(1,1,1,1,,), e=(1,,1,1,1,1), b=(1,1,1,,1,1), 5=(1,1,1,,,), 9=(1,1,1,,,), f=(1,1,1,,1,), G=(1,1,1,,,), s=(1,1,1,,,1), Z=(1,1,,1,1,1), A=(1,1,,1,,), 6=(1,1,,1,,), H=(1,1,,,1,), g=(,,1,1,1,1), M=(1,1,,,,1), E=(1,1,,,1,), K=(1,1,,,,1), h=(,,,1,1,1), ==(,,1,1,1,), %=(,,1,1,,1), l=(1,1,,1,1,), R=(1,1,,1,,), u=(1,1,,1,,1), /=(1,1,,,1,1), m=(,,1,,1,1), P=(1,1,,,1,), T=(1,1,,,,1)
31-16 237,7HG,GTUVRP,PRNQSM,MIJKL2,235,7235,3NOKLM,WXJRSM,WYZGRV,aOQbcM,YdHce,XIfbcM,fgUHce,gTUGH,YZdGH.
44-16 (master for 31-16) 123456,72389A,723B5C,7DEFGH,2IJKLM,3NOKLM,PNQRSM,PTUGRV,WXJRSM,WYZGRV,aOQbcM,aYdHce,XIfbcM,fgUHce,gTUhGH,iYZdGH. 1=(0,0,1,−1,1,0), 7=(0,0,−1,1,1,0), 2=(0,1,0,0,0,1), 3=(0,1,0,0,0,−1), P=(0,1,0,0,1,0), W=(0,1,0,0,−1,0), a=(0,1,0,1,0,0), X=(0,1,0,1,1,1), D=(0,1,0,1,−1,0), N=(0,1,0,1,−1,1), I=(0,1,0,1,−1,−1), f=(0,1,0,−1,0,0), O=(0,1,0,−1,1,1), J=(0,1,0,−1,1,−1), Q=(0,−1,0,1,1,1), E=(0,1,1,0,1,0), g=(0,1,1,1,1,0), i=(0,1,1,1,−1,0), Y=(0,1,1,−1,1,0), T=(0,1,1,−1,−1,0), Z=(0,1,−1,1,1,0), U=(0,1,−1,1,−1,0), F=(0,−1,1,1,0,0), h=(0,1,−1,−1,1,0), d=(0,−1,1,1,1,0), G=(1,0,0,0,0,1), H=(1,0,0,0,0,−1), 8=(1,0,0,1,−1,0), B=(1,0,0,−1,1,0), 4=(−1,0,0,1,1,0), 9=(1,0,1,0,1,0), b=(1,0,1,0,1,−1), c=(1,0,1,0,−1,1), 5=(1,0,1,1,0,0), R=(1,0,1,1,0,−1), K=(1,0,1,1,1,0), S=(1,0,1,−1,0,1), L=(1,0,1,−1,−1,0), M=(1,0,−1,0,0,0), 6=(1,0,−1,0,1,0), e=(1,0,−1,0,1,1), C=(−1,0,1,0,1,0), A=(−1,0,1,1,0,0), V=(−1,0,1,1,0,1)
117-116 (stripmaster of the 236-1216 supermaster) 123456,123789,1AB4CD,1AB7EF,1GHI5F,1GHJC9,1KLI8D,1KLJE6,MN8COP,MNF6QR,STE5OP,ST9DQR,UVWXYZ,UVabcd,UefgYZ,Uefabh,Uijgcd,UijWXh,UBk4XZ,UBk7ac,U3l4bd,U3l7WY,ULmIXY,ULmJbc,UHnIad,UHnJWZ,opVgYZ,opVabh,opijgh,opabqR,opYZPr,oistuv,oiwxyz,oj!"#$,oj%&’(,)*Vgcd,)*VWXh,)*efgh,)*WXqR,)*cdPr,)e-/uv,)e:;yz,)f!"<=,)f%&>?,*e@[#$,*e\]’(,*fst^_,*fwx‘{,pi@[<=,pi\]>?,pj-/^_,pj:;‘{,2|V4XZ,2|V7ac,2|3l47,2|ac}∼,2|XZ+1+2,2389u{,2356^z,2l\"+3+4,2l%[+5+6,A+7V4bd,A+7V7WY, A+7Bk47,A+7WY}∼,A+7bd+1+2,ABEFu{,ABCD^z,Ak\"+8+9,Ak%[+A+B,G+CVIXY,G+CVJbc,G+CHnIJ,G+Cbc+D+E,G+CXY+F+G,GHC9#?,GH5F<(,Gn:t+3+B,Gnw/+8+6,K+HVIad,K+HVJWZ,K+HLmIJ,K+HWZ+D+E,K+Had+F+G,KLE6#?,KL8D<(,Km:t+5+9,Kmw/+A+4,+7B@&+3+4,+7B!]+5+6,+7k89y_,+7k56‘v,|3@&+8+9,|3!]+A+B,|lEFy_,|lCD‘v,+HL-x+3+B,+HLs;+8+6,+HmC9’=,+Hm5F>$,+CH-x+5+9,+CHs;+A+4,+CnE6’=,+Cn8D>$,efab+IO,efYZQ+J,ijWX+IO,ijcdQ+J,Bkac+K+L, BkXZ+M+N,3lWY+K+L,3lbd+M+N,Lmbc+O+P,LmXY+Q+R,HnWZ+O+P,Hnad+Q+R. 1=(0,1,0,−1,0,0), M=(0,1,0,−1,1,1), S=(0,1,0,−1,1,−1), T=(0,1,0,−1,−1,1), N=(0,−1,0,1,1,1), U=(0,1,1,0,0,0), o=(0,1,1,0,1,1), )=(0,1,1,0,1,−1), *=(0,1,1,0,−1,1), p=(0,1,1,0,−1,−1), 2=(0,1,1,1,0,1), A=(0,1,1,1,0,−1), G=(0,1,1,1,1,0), K=(0,1,1,1,−1,0), +7=(0,1,1,−1,0,1), |=(0,1,1,−1,0,−1), +H=(0,1,1,−1,1,0), +C=(0,1,1,−1,−1,0), V=(0,1,−1,0,0,0), e=(0,1,−1,0,1,1), i=(0,1,−1,0,1,−1), j=(0,1,−1,0,−1,1), f=(0,−1,1,0,1,1), B=(0,1,−1,1,0,1), 3=(0,1,−1,1,0,−1), L=(0,1,−1,1,1,0), H=(0,1,−1,1,−1,0), l=(0,1,−1,−1,0,1), k=(0,−1,1,1,0,1), n=(0,1,−1,−1,1,0), m=(0,−1,1,1,1,0), I=(1,0,0,0,0,1), J=(1,0,0,0,0,−1), 4=(1,0,0,0,1,0), 7=(1,0,0,0,−1,0), g=(1,0,0,1,0,0), W=(1,0,0,1,1,1), a=(1,0,0,1,1,−1), b=(1,0,0,1,−1,1), X=(1,0,0,1,−1,−1), h=(1,0,0,−1,0,0), c=(1,0,0,−1,1,1), Y=(1,0,0,−1,1,−1), Z=(1,0,0,−1,−1,1), d=(−1,0,0,1,1,1), E=(1,0,1,0,1,1), 8=(1,0,1,0,1,−1), C=(1,0,1,0,−1,1), 5=(1,0,1,0,−1,−1), −=(1,0,1,1,0,1), s=(1,0,1,1,0,−1), @=(1,0,1,1,1,0), !=(1,0,1,1,−1,0), :=(1,0,1,−1,0,1), w=(1,0,1,−1,0,−1), \=(1,0,1,−1,1,0), %=(1,0,1,−1,−1,0), 9=(1,0,−1,0,1,1), F=(1,0,−1,0,1,−1), 6=(1,0,−1,0,−1,1), D=(−1,0,1,0,1,1), t=(1,0,−1,1,0,1), /=(1,0,−1,1,0,−1), "=(1,0,−1,1,1,0), [=(1,0,−1,1,−1,0), x=(1,0,−1,−1,0,1), ;=(−1,0,1,1,0,1), &=(1,0,−1,−1,1,0), ]=(−1,0,1,1,1,0), +A=(1,1,0,0,1,1), +5=(1,1,0,0,1,−1), +8=(1,1,0,0,−1,1), +3=(1,1,0,0,−1,−1), >=(1,1,0,1,0,1), ’=(1,1,0,1,0,−1), ‘=(1,1,0,1,1,0), y=(1,1,0,1,−1,0), <=(1,1,0,−1,0,1), #=(1,1,0,−1,0,−1), ^=(1,1,0,−1,1,0), u=(1,1,0,−1,−1,0), +Q=(1,1,1,0,0,1), +O=(1,1,1,0,0,−1), +M=(1,1,1,0,1,0), +K=(1,1,1,0,−1,0), Q=(1,1,1,1,0,0), +I=(1,1,1,−1,0,0), O=(−1,1,1,1,0,0), +F=(1,1,−1,0,0,1), +D=(1,1,−1,0,0,−1), +1=(1,1,−1,0,1,0), }=(1,1,−1,0,−1,0), P=(1,1,−1,1,0,0), +J=(1,−1,−1,1,0,0), q=(1,1,−1,−1,0,0), +L=(−1,1,1,0,1,0), +N=(1,−1,−1,0,1,0), +6=(1,−1,0,0,1,1), +B=(1,−1,0,0,1,−1), +4=(1,−1,0,0,−1,1), +9=(−1,1,0,0,1,1), (=(1,−1,0,1,0,1), ?=(1,−1,0,1,0,−1), z=(1,−1,0,1,1,0), {=(1,−1,0,1,−1,0), $=(1,−1,0,−1,0,1), ==(−1,1,0,1,0,1), v=(1,−1,0,−1,1,0), _=(−1,1,0,1,1,0), +G=(1,−1,1,0,0,1), +E=(1,−1,1,0,0,−1), +2=(1,−1,1,0,1,0), ∼=(1,−1,1,0,−1,0), r=(1,−1,1,1,0,0), +P=(−1,1,1,0,0,1), +R=(1,−1,−1,0,0,1), R=(1,−1,1,−1,0,0)
Appendix A.5. Seven-dim MMPHs
14-8 12567,189A5BC,189DE7,189HJ,189HB,2D,2EC,AJ.
31-13 1234,189DEF,189GHIJ,189KHBL,2MNDOIP,2MNEOCL,2MNGKF,QRNSAJP,QT4U,RTV9,WXMS,WYV8AJP,XY3U.
34-14 (master for 14-8 and 31-13) 1234567,189A5BC,189DE7F,189GHIJ,189KHBL,2MNDOIP,2MNEOCL,2MNGK6F,QRNSAJP,QT4U567,RTV9567,WXMS567,WYV8AJP,XY3U567. 1=(0,0,0,1,0,0,0); 2=(0,0,1,0,0,0,0); 3=(1,−1,0,0,0,0,0); 4=(1,1,0,0,0,0,0); 5=(0,0,0,0,0,0,1);6=(0,0,0,0,1,1,0); 7=(0,0,0,0,1,−1,0); 8=(0,1,−1,0,0,0,0); 9=(0,1,1,0,0,0,0); A=(0,0,0,0,1,0,0);B=(1,0,0,0,0,−1,0); C=(1,0,0,0,0,1,0); D=(1,0,0,0,1,1,−1); E=(−1,0,0,0,1,1,1); F=(1,0,0,0,0,0,1); G=(1,0,0,0,1,−1,−1);H=(1,0,0,0,1,1,1);I=(1,0,0,0,−1,0,0);J=(0,0,0,0,0,1,−1);K=(1,0,0,0,−1,1,−1); L=(0,0,0,0,1,0,−1); M=(0,1,0,1,0,0,0); N=(0,1,0,−1,0,0,0); O=(1,0,0,0,1,−1,1); P=(0,0,0,0,0,1,1); Q=(−1,1,1,1,0,0,0); R=(1,1,−1,1,0,0,0); S=(1,0,1,0,0,0,0); T=(1,−1,1,1,0,0,0); U=(0,0,1,−1,0,0,0); V=(1,0,0,−1,0,0,0); W=(1,−1,−1,1,0,0,0); X=(1,1,−1,−1,0,0,0); Y=(1,1,1,1,0,0,0)
Appendix A.6. Eight-dim MMPHs
15-9 17426538,8E,E2M,M3N,N4O,O5U,U7Q,Q6H,H1.
36-9 (master for 15-9) 17426538,8ABDF9CE,ELaR2YVM,M3WSDKZN,NCJXR4TO,OV5PSBIU,UZ9GXa7Q,QTY6PWAH,HIKFGJL1. 1=(0,0,0,0,0,0,0,1), 2=(0,0,0,0,0,0,1,0), 3=(0,0,0,0,0,1,0,0), 4=(0,0,0,0,1,0,0,0), 5=(0,0,1,1,0,0,0,0), 6=(0,0,−1,1,0,0,0,0), 7=(1,1,0,0,0,0,0,0), 8=(−1,1,0,0,0,0,0,0), 9=(0,0,0,0,0,0,1,1), A=(0,0,1,1,1,−1,0,0), B=(1,1,0,0,0,0,−1,1), C=(1,1,0,0,0,0,1,−1), D=(0,0,−1,0,1,0,0,0), E=(0,0,0,1,0,1,0,0), F=(0,0,1,−1,1,1,0,0), G=(0,0,0,1,1,0,0,0), H=(0,0,1,1,−1,1,0,0), I=(1,0,0,0,0,0,1,0), J=(0,0,−1,0,0,1,0,0), K=(−1,0,0,0,0,0,1,0), L=(0,1,0,0,0,0,0,0), M=(0,0,1,0,1,0,0,0), N=(0,0,0,1,0,0,0,0), O=(−1,1,0,0,0,0,1,1), P=(0,0,0,0,1,1,0,0), Q=(−1,1,0,0,0,0,1,−1), R=(1,0,0,0,0,0,0,1), S=(0,−1,0,0,0,0,0,1), T=(0,−1,0,0,0,0,1,0), U=(0,0,−1,1,−1,1,0,0), V=(0,0,−1,1,1,−1,0,0), W=(1,1,0,0,0,0,1,1), X=(0,0,1,0,0,1,0,0), Y=(−1,0,0,0,0,0,0,1), Z=(−1,1,0,0,0,0,−1,1), a=(0,0,−1,−1,1,1,0,0)
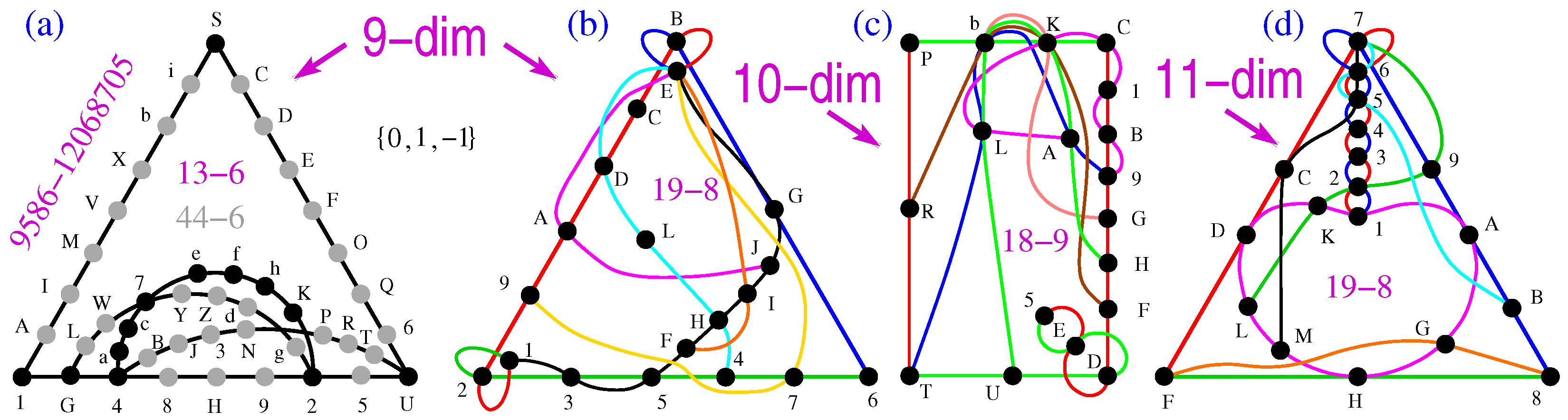
Appendix A.7. Nine-dim MMPHs
13-6 SU,1G42U,1S,472acefhK,G72,4U.
44-6 (13-6 filled) SUCDEFOQ6,1G42U8H95,1SAIMSVXbi,472acefhK,G72LWYZdg,4UBJ3NPRT. 1=(0,0,0,0,0,0,0,1,0); 2=(0,0,0,0,0,0,1,0,0); 3=(0,0,0,0,1,1,0,0,0); 4=(0,0,0,1,0,0,0,0,1); 5=(0,0,0,1,0,0,0,0,−1); 6=(0,0,0,1,0,0,−1,1,0); 7=(0,0,1,0,0,0,0,1,0); 8=(0,0,1,0,0,1,0,0,0);9=(0,0,1,0,0,−1,0,0,0); A=(0,0,1,0,−1,0,1,0,0); B=(0,0,1,0,−1,1,1,0,0); C=(0,0,−1,−1,1,1,0,1,1); D=(0,0,1,−1,−1,−1,0,1,1); H=(0,1,0,0,1,0,0,0,0); E=(0,1,0,0,1,−1,1,1,−1);F=(0,1,0,0,1,−1,−1,−1,1); G=(0,1,0,0,−1,0,0,0,0); I=(0,1,0,1,1,1,1,0,1); J=(0,1,0,−1,0,0,0,−1,1); K=(1,−1,1,1,−1,1,0,−1,−1); L=(0,1,0,−1,1,1,0,0,0); M=(0,1,0,−1,1,−1,1,0,−1);N=(0,1,−1,0,0,0,1,1,0); O=(0,1,1,1,0,1,1,0,1); P=(0,1,1,1,1,−1,1,−1,−1);Q=(0,1,1,−1,0,1,−1,0,−1); R=(0,1,−1,0,0,0,1,1,0); S=(0,−1,1,0,1,0,0,0,0); U=(1,0,0,0,0,0,0,0,0); V=(1,0,0,0,0,−1,0,0,1); W=(1,0,0,1,0,1,0,0,1); X=(1,0,0,−1,0,1,0,0,0); Y=(1,0,0,−1,0,−1,0,0,1); Z=(1,0,1,0,0,0,0,−1,−1); a=(1,1,0,0,−1,−1,0,0,0); b=(1,1,1,1,0,0,−1,0,−1);c=(1,1,1,−1,1,1,0,−1,1); d=(−1,1,1,1,1,−1,0,−1,1); e=(1,−1,−1,−1,−1,1,0,1,1);f=(1,1,−1,1,1,1,0,1,−1); g=(1,1,−1,1,1,−1,0,1,−1); h=(1,−1,0,0,1,−1,0,0,0);i=(1,−1,−1,1,0,0,1,0,−1).
19-8 1234567,129ABCDE,13FGH5IJE,GB6E,AJE,97E,LH4DE,FIE.
47-16 (master for 19-8) 123456789,12ABCDEF,13HIJ5KL,1AMCLNOPQ,1BRSETUVQ,1H4567VWX,1ICDEFYOX,1ZJ4FTUW9,1ZCDEFYP8,23abRSET,cdIeMD6f,cgaZMCLN,dghA4567,ijhBRk7f,ilbZJ4FT,jlHeSkKN. 1=(1,0,0,0,0,0,0,0,0), 2=(0,1,0,0,0,0,0,0,0), 3=(0,0,1,0,0,0,0,0,0), c=(1,1,1,1,0,0,0,0,0), d=(1,−1,1,−1,0,0,0,0,0), g=(1,−1,−1,1,0,0,0,0,0), i=(1,−1,−1,−1,0,0,0,0,0), j=(1,−1,1,1,0,0,0,0,0), l=(1,1,1,−1,0,0,0,0,0), h=(1,1,0,0,0,0,0,0,0), A=(0,0,1,1,0,0,0,0,0), B=(0,0,1,−1,0,0,0,0,0), H=(0,1,0,1,0,0,0,0,0), I=(0,1,0,−1,0,0,0,0,0), e=(1,0,−1,0,0,0,0,0,0), a=(1,0,0,−1,0,0,0,0,0), b=(1,0,0,1,0,0,0,0,0), Z=(0,1,−1,0,0,0,0,0,0), J=(0,0,0,0,1,0,0,0,0), 4=(0,0,0,0,0,1,0,0,0), 5=(0,0,0,0,0,0,1,0,0), M=(0,0,0,0,1,1,1,1,0), C=(0,0,0,0,1,−1,1,−1,0), D=(0,0,0,0,1,−1,−1,1,0), R=(0,0,0,0,1,−1,−1,−1,0), S=(0,0,0,0,1,−1,1,1,0), k=(0,0,0,0,1,1,1,−1,0), E=(0,0,0,0,1,1,0,0,0), F=(0,0,0,0,0,0,1,1,0), T=(0,0,0,0,0,0,1,−1,0), K=(0,0,0,0,0,1,0,1,0), L=(0,0,0,0,0,1,0,−1,0), N=(0,0,0,0,1,0,−1,0,0), 6=(0,0,0,0,1,0,0,−1,0), 7=(0,0,0,0,1,0,0,1,0), f=(0,0,0,0,0,1,−1,0,0), Y=(0,1,1,1,0,0,0,0,1), O=(0,1,−1,1,0,0,0,0,−1), P=(0,1,1,−1,0,0,0,0,−1), U=(0,1,1,1,0,0,0,0,−1), V=(0,1,−1,−1,0,0,0,0,−1), W=(0,1,1,−1,0,0,0,0,1), Q=(0,1,0,0,0,0,0,0,1), X=(0,0,1,0,0,0,0,0,−1), 8=(0,0,0,1,0,0,0,0,−1), :9=(0,0,0,1,0,0,0,0,1)
Appendix A.8. Ten-dim MMPHs
18-9 1BC5DEFGH9,1BCKL9A,T5DEU,TPR,TbL9A,CbKP,bKG,bKFR,bKUHA.
50-15 (master for 18-9) 12BCUVfgik,1DEJXYceoq,1DELMVWajk,1DEMNRSblm,1DEOPRTajk,1DEOQYZajk,2GHLNXZajk,2GHPQUWblm,45EFUVcdmn,46GIJSTajk,46GIUVceoq,56ABUVdeij,78ACUVfhpq,79HIUVabop,89DFUVghln. 1=(1,0,0,0,0,0,0,0,0,0), 2=(0,1,0,0,0,0,0,0,0,0), 3=(0,0,1,0,0,0,0,0,0,0), 4=(1,1,1,1,0,0,0,0,0,0), 5=(1,−1,1,−1,0,0,0,0,0,0), 6=(1,−1,−1,1,0,0,0,0,0,0), 7=(1,−1,−1,−1,0,0,0,0,0,0), 8=(1,−1,1,1,0,0,0,0,0,0), 9=(1,1,1,−1,0,0,0,0,0,0), A=(1,1,0,0,0,0,0,0,0,0), B=(0,0,1,1,0,0,0,0,0,0), C=(0,0,1,−1,0,0,0,0,0,0), D=(0,1,0,1,0,0,0,0,0,0), E=(0,1,0,−1,0,0,0,0,0,0), F=(1,0,−1,0,0,0,0,0,0,0), G=(1,0,0,−1,0,0,0,0,0,0), H=(1,0,0,1,0,0,0,0,0,0), I=(0,1,−1,0,0,0,0,0,0,0), J=(0,0,0,0,1,0,0,0,0,0), K=(0,0,0,0,0,1,0,0,0,0), L=(0,0,1,0,1,1,1,0,0,0), M=(0,0,1,0,−1,1,−1,0,0,0), N=(0,0,1,0,−1,−1,1,0,0,0), O=(0,0,1,0,−1,−1,−1,0,0,0), P=(0,0,1,0,−1,1,1,0,0,0), Q=(0,0,1,0,1,1,−1,0,0,0), R=(0,0,1,0,1,0,0,0,0,0), S=(0,0,0,0,0,1,1,0,0,0), T=(0,0,0,0,0,1,−1,0,0,0), U=(0,0,0,0,1,0,1,0,0,0), V=(0,0,0,0,1,0,−1,0,0,0), W=(0,0,1,0,0,−1,0,0,0,0), X=(0,0,1,0,0,0,−1,0,0,0), Y=(0,0,1,0,0,0,1,0,0,0), Z=(0,0,0,0,1,−1,0,0,0,0), a=(0,0,0,0,0,0,0,1,0,0), b=(0,0,0,0,0,0,0,0,1,0), c=(0,0,0,0,0,1,0,1,1,1), d=(0,0,0,0,0,1,0,−1,1,−1), e=(0,0,0,0,0,1,0,−1,−1,1), f=(0,0,0,0,0,1,0,−1,−1,−1), g=(0,0,0,0,0,1,0,−1,1,1), h=(0,0,0,0,0,1,0,1,1,−1), i=(0,0,0,0,0,1,0,1,0,0), j=(0,0,0,0,0,0,0,0,1,1), k=(0,0,0,0,0,0,0,0,1,−1), l=(0,0,0,0,0,0,0,1,0,1), m=(0,0,0,0,0,0,0,1,0,−1), n=(0,0,0,0,0,1,0,0,−1,0), o=(0,0,0,0,0,1,0,0,0,−1), p=(0,0,0,0,0,1,0,0,0,1), q=(0,0,0,0,0,0,0,1,−1,0)
Appendix A.9. Eleven-dim MMPHs
19-8 123456789AB,1234567CDF,1GHKLMDA,27KL9,567MC,567B,H8F,G8F.
50-14 (master for 19-8) 123456789AB,1234567CDEF,1GHIJKLMDAN,1GHIJKLOPQR,27STUVKL8FW,27STUVKL9QX,347YZabMDAN,567cdefMCXR,567cdefgOEW,567cdefgPBN,cdhijkJV8FW,eYlmnIUk9QX,fZoHTjmn8FW,abGShilo8FW. 1=(0,0,1,1,1,1,0,0,0,0,0), 2=(0,0,1,−1,1,−1,0,0,0,0,0), 3=(0,0,0,1,0,−1,0,0,0,0,0), 4=(0,0,1,0,−1,0,0,0,0,0,0), 5=(0,1,0,0,0,0,0,0,0,0,0), 6=(1,0,0,0,0,0,0,0,0,0,0), 7=(0,0,0,0,0,0,1,0,0,0,0), 8=(0,0,0,1,0,0,0,0,0,0,0), 9=(0,0,1,0,0,0,0,0,0,0,0), A=(0,0,0,0,0,1,0,0,0,0,0), B=(0,0,0,0,1,0,0,0,0,0,0), C=(1,−1,1,0,1,0,0,0,0,0,0), D=(1,1,0,1,0,1,0,0,0,0,0), E=(1,1,0,−1,0,−1,0,0,0,0,0), F=(−1,1,1,0,1,0,0,0,0,0,0), G=(0,1,−1,1,0,0,1,0,0,0,0), H=(1,0,1,1,0,0,0,−1,0,0,0), I=(1,0,0,0,1,1,0,1,0,0,0), J=(0,1,0,0,−1,1,−1,0,0,0,0), K=(0,0,1,0,−1,0,1,1,0,0,0), L=(0,0,0,1,0,−1,−1,1,0,0,0), M=(1,0,1,0,0,−1,1,0,0,0,0), N=(0,−1,1,0,0,1,0,1,0,0,0), O=(−1,1,0,0,0,0,1,1,0,0,0), P=(1,0,−1,−1,0,0,0,1,0,0,0), Q=(0,1,1,−1,0,0,−1,0,0,0,0), R=(1,0,0,1,−1,0,−1,0,0,0,0), S=(0,1,0,1,1,0,0,1,0,0,0), T=(1,1,0,0,0,0,1,−1,0,0,0), U=(0,1,0,0,1,−1,−1,0,0,0,0), V=(1,0,0,0,−1,−1,0,1,0,0,0), W=(1,1,0,−1,0,1,0,0,0,0,0), X=(1,−1,−1,0,1,0,0,0,0,0,0), Y=(0,0,0,0,0,0,0,0,1,0,0), Z=(0,0,0,0,0,0,0,0,0,1,0), a=(0,0,0,0,0,0,0,1,1,1,1), b=(0,0,0,0,0,0,0,1,−1,1,−1), c=(0,0,0,0,0,0,0,1,−1,−1,1), d=(0,0,0,0,0,0,0,1,−1,−1,−1), e=(0,0,0,0,0,0,0,1,−1,1,1), f=(0,0,0,0,0,0,0,1,1,1,−1), g=(0,0,0,0,0,0,0,1,1,0,0), h=(0,0,0,0,0,0,0,0,0,1,1), i=(0,0,0,0,0,0,0,0,0,1,−1), j=(0,0,0,0,0,0,0,0,1,0,1), k=(0,0,0,0,0,0,0,0,1,0,−1), l=(0,0,0,0,0,0,0,1,0,−1,0), m=(0,0,0,0,0,0,0,1,0,0,−1), n=(0,0,0,0,0,0,0,1,0,0,1), o=(0,0,0,0,0,0,0,0,1,−1,0)
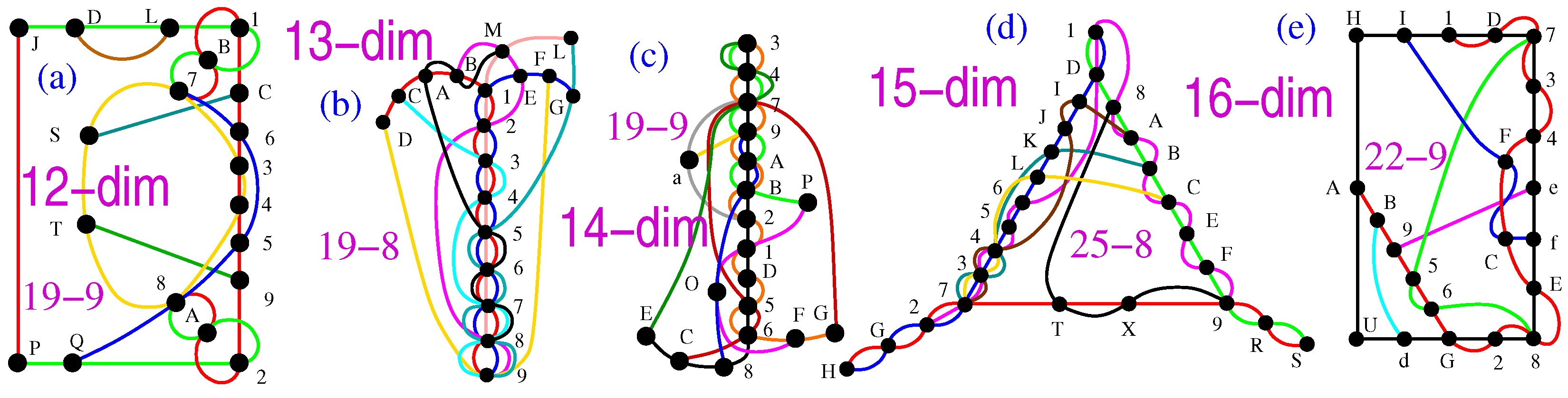
Appendix A.10. Twelve-dim MMPHs
19-9 123456789ABC,17DJBL,28PQA,PJ,3478ST,5678Q,SC,T9,DL
52-9 (master for 19-9) 123456789ABC,17DEFGHIJBKL,28MNOPHIQAKR,3478STUVWXYR,5678ZabcdWQe,ZafghiGPjJke,bSlmnFOijdoC,cTpENhmn9qYo,UVDMfglpkXqL. 1=(0,0,1,1,1,1,0,0,0,0,0,0), 2=(0,0,1,−1,1,−1,0,0,0,0,0,0), 3=(0,0,0,1,0,−1,0,0,0,0,0,0), 4=(0,0,1,0,−1,0,0,0,0,0,0,0), 5=(0,1,0,0,0,0,0,0,0,0,0,0), 6=(1,0,0,0,0,0,0,0,0,0,0,0), 7=(0,0,0,0,0,0,0,1,0,0,0,0), 8=(0,0,0,0,0,0,1,0,0,0,0,0), Z=(0,0,0,1,0,0,0,0,0,0,0,0), a=(0,0,1,0,0,0,0,0,0,0,0,0), b=(0,0,0,0,0,1,0,0,0,0,0,0), c=(0,0,0,0,1,0,0,0,0,0,0,0), S=(1,−1,1,0,1,0,0,0,0,0,0,0), T=(1,1,0,1,0,1,0,0,0,0,0,0), U=(1,1,0,−1,0,−1,0,0,0,0,0,0), V=(−1,1,1,0,1,0,0,0,0,0,0,0), D=(0,1,−1,1,0,0,1,0,0,0,0,0), M=(1,0,1,1,0,0,0,−1,0,0,0,0), f=(1,0,0,0,1,1,0,1,0,0,0,0), g=(0,1,0,0,−1,1,−1,0,0,0,0,0), l=(0,0,1,0,−1,0,1,1,0,0,0,0), p=(0,0,0,1,0,−1,−1,1,0,0,0,0), E=(1,0,1,0,0,−1,1,0,0,0,0,0), N=(0,−1,1,0,0,1,0,1,0,0,0,0), h=(−1,1,0,0,0,0,1,1,0,0,0,0), m=(1,0,−1,−1,0,0,0,1,0,0,0,0), n=(0,1,1,−1,0,0,−1,0,0,0,0,0), F=(1,0,0,1,−1,0,−1,0,0,0,0,0), O=(0,1,0,1,1,0,0,1,0,0,0,0), i=(1,1,0,0,0,0,1,−1,0,0,0,0), G=(0,1,0,0,1,−1,−1,0,0,0,0,0), P=(1,0,0,0,−1,−1,0,1,0,0,0,0), H=(1,1,0,−1,0,1,0,0,0,0,0,0), I=(1,−1,−1,0,1,0,0,0,0,0,0,0), j=(0,0,0,0,0,0,0,0,1,0,0,0), d=(0,0,0,0,0,0,0,0,0,1,0,0), J=(0,0,0,0,0,0,0,0,0,1,1,0), k=(0,0,0,0,0,0,0,0,0,1,−1,0), W=(0,0,0,0,0,0,0,0,1,0,1,0), Q=(0,0,0,0,0,0,0,0,1,0,−1,0), 9=(0,0,0,0,0,0,0,0,1,−1,0,0), e=(0,0,0,0,0,0,0,0,0,0,0,1), A=(0,0,0,0,0,0,0,0,1,1,1,1), B=(0,0,0,0,0,0,0,0,1,1,−1,−1), K=(0,0,0,0,0,0,0,0,1,−1,1,−1), X=(0,0,0,0,0,0,0,0,1,−1,−1,−1), q=(0,0,0,0,0,0,0,0,1,1,1,−1), Y=(0,0,0,0,0,0,0,0,1,1,−1,1), L=(0,0,0,0,0,0,0,0,1,0,0,1), o=(0,0,0,0,0,0,0,0,0,0,1,1), C=(0,0,0,0,0,0,0,0,0,0,1,−1), R=(0,0,0,0,0,0,0,0,0,1,0,−1)
Appendix A.11. Thirteen-dim MMPHs
19-8 123456789ABCD,123456789EFG,12345678ILM,289EBM,34789C,56789LG,5678ABM,9FD.
63-16 (master for 19-8) 123456789ABCD,123456789EFGH,12345678IJKLM,17NOPQRSTUVWM,28XYZaRS9EbBM,3478cdef9bghH,3478cdef9WhiC,3478cdefIjVkM, 5678lmno9LpGq, 5678lmnoATrBM,lmstuvQa9WpFD,lmstuvQaEKwxM,ncyz!PZv9AkLM,od"OYuz!9kgiq,od"OYuz!bUj xM,efNXsty"rJwWM. 1=(0,0,1,1,1,1,0,0,0,0,0,0,0), 2=(0,0,1,−1,1,−1,0,0,0,0,0,0,0), 3=(0,0,0,1,0,−1,0,0,0,0,0,0,0), 4=(0,0,1,0,−1,0,0,0,0,0,0,0,0), 5=(0,1,0,0,0,0,0,0,0,0,0,0,0), 6=(1,0,0,0,0,0,0,0,0,0,0,0,0), 7=(0,0,0,0,0,0,0,1,0,0,0,0,0), 8=(0,0,0,0,0,0,1,0,0,0,0,0,0), l=(0,0,0,1,0,0,0,0,0,0,0,0,0), m=(0,0,1,0,0,0,0,0,0,0,0,0,0), n=(0,0,0,0,0,1,0,0,0,0,0,0,0), o=(0,0,0,0,1,0,0,0,0,0,0,0,0), c=(1,−1,1,0,1,0,0,0,0,0,0,0,0), d=(1,1,0,1,0,1,0,0,0,0,0,0,0), e=(1,1,0,−1,0,−1,0,0,0,0,0,0,0), f=(−1,1,1,0,1,0,0,0,0,0,0,0,0), N=(0,1,−1,1,0,0,1,0,0,0,0,0,0), X=(1,0,1,1,0,0,0,−1,0,0,0,0,0), s=(1,0,0,0,1,1,0,1,0,0,0,0,0), t=(0,1,0,0,−1,1,−1,0,0,0,0,0,0), y=(0,0,1,0,−1,0,1,1,0,0,0,0,0), "=(0,0,0,1,0,−1,−1,1,0,0,0,0,0), O=(1,0,1,0,0,−1,1,0,0,0,0,0,0), Y=(0,−1,1,0,0,1,0,1,0,0,0,0,0), u=(−1,1,0,0,0,0,1,1,0,0,0,0,0), z=(1,0,−1,−1,0,0,0,1,0,0,0,0,0), !=(0,1,1,−1,0,0,−1,0,0,0,0,0,0), P=(1,0,0,1,−1,0,−1,0,0,0,0,0,0), Z=(0,1,0,1,1,0,0,1,0,0,0,0,0), v=(1,1,0,0,0,0,1,−1,0,0,0,0,0), Q=(0,1,0,0,1,−1,−1,0,0,0,0,0,0), a=(1,0,0,0,−1,−1,0,1,0,0,0,0,0), R=(1,1,0,−1,0,1,0,0,0,0,0,0,0), S=(1,−1,−1,0,1,0,0,0,0,0,0,0,0), 9=(0,0,0,0,0,0,0,0,1,0,0,0,0), A=(0,0,0,0,0,0,0,0,0,1,0,0,0), E=(0,0,0,0,0,0,0,0,0,1,1,0,0), b=(0,0,0,0,0,0,0,0,0,1,−1,0,0), T=(0,0,0,0,0,0,0,0,1,0,1,0,0), r=(0,0,0,0,0,0,0,0,1,0,−1,0,0), I=(0,0,0,0,0,0,0,0,1,−1,0,0,0), B=(0,0,0,0,0,0,0,0,0,0,0,1,0), J=(0,0,0,0,0,0,0,0,1,1,1,1,0), K=(0,0,0,0,0,0,0,0,1,1,−1,−1,0), w=(0,0,0,0,0,0,0,0,1,−1,1,−1,0), U=(0,0,0,0,0,0,0,0,1,−1,−1,−1,0), j=(0,0,0,0,0,0,0,0,1,1,1,−1,0), V=(0,0,0,0,0,0,0,0,1,1,−1,1,0), x=(0,0,0,0,0,0,0,0,1,0,0,1,0), k=(0,0,0,0,0,0,0,0,0,0,1,1,0), L=(0,0,0,0,0,0,0,0,0,0,1,−1,0), W=(0,0,0,0,0,0,0,0,0,1,0,−1,0), M=(0,0,0,0,0,0,0,0,0,0,0,0,1), p=(0,0,0,0,0,0,0,0,0,1,1,1,1), F=(0,0,0,0,0,0,0,0,0,1,−1,1,−1), G=(0,0,0,0,0,0,0,0,0,1,−1,−1,1), g=(0,0,0,0,0,0,0,0,0,1,1,−1,1), h=(0,0,0,0,0,0,0,0,0,1,1,1,−1), i=(0,0,0,0,0,0,0,0,0,1,−1,1,1), H=(0,0,0,0,0,0,0,0,0,0,0,1,1), C=(0,0,0,0,0,0,0,0,0,0,1,0,1), D=(0,0,0,0,0,0,0,0,0,0,1,0,−1), q=(0,0,0,0,0,0,0,0,0,1,0,0,−1)
Appendix A.12. Fourteen-dim MMPHs
19-9 123456789ABCDE,12345679ABFGD,1OPF,27a,347E,3479ABP,567CG,9a,O89AB.
66-15 (master for 19-9) 123456789ABCDE,12345679ABFGDH,1IJKLMNOPFQRST,27UVWXMN YZTabc,347defghijkElm,347defg9ABPHnm,347defgFijkGDH,567opqrOBPFsZt,567opqr9ABaunl,567opqrijbkCGu,opvwxyLX9iQYab,qdz!"KWyAt#Sab,re$JVx!"s%abck,fgIUvwz$Oh89AB,fgIUvwz$#R%jab. 1=(0,0,1,1,1,1,0,0,0,0,0,0,0,0), 2=(0,0,1,−1,1,−1,0,0,0,0,0,0,0,0), 3=(0,0,0,1,0,−1,0,0,0,0,0,0,0,0), 4=(0,0,1,0,−1,0,0,0,0,0,0,0,0,0), 5=(0,1,0,0,0,0,0,0,0,0,0,0,0,0), 6=(1,0,0,0,0,0,0,0,0,0,0,0,0,0), 7=(0,0,0,0,0,0,1,0,0,0,0,0,0,0), o=(0,0,0,1,0,0,0,0,0,0,0,0,0,0), p=(0,0,1,0,0,0,0,0,0,0,0,0,0,0), q=(0,0,0,0,0,1,0,0,0,0,0,0,0,0), r=(0,0,0,0,1,0,0,0,0,0,0,0,0,0), d=(1,−1,1,0,1,0,0,0,0,0,0,0,0,0), e=(1,1,0,1,0,1,0,0,0,0,0,0,0,0), f=(1,1,0,−1,0,−1,0,0,0,0,0,0,0,0), g=(−1,1,1,0,1,0,0,0,0,0,0,0,0,0), I=(0,1,−1,1,0,0,1,0,0,0,0,0,0,0), U=(1,0,1,1,0,0,0,−1,0,0,0,0,0,0), v=(1,0,0,0,1,1,0,1,0,0,0,0,0,0), w=(0,1,0,0,−1,1,−1,0,0,0,0,0,0,0), z=(0,0,1,0,−1,0,1,1,0,0,0,0,0,0), $=(0,0,0,1,0,−1,−1,1,0,0,0,0,0,0), J=(1,0,1,0,0,−1,1,0,0,0,0,0,0,0), V=(0,−1,1,0,0,1,0,1,0,0,0,0,0,0), x=(−1,1,0,0,0,0,1,1,0,0,0,0,0,0), !=(1,0,−1,−1,0,0,0,1,0,0,0,0,0,0), "=(0,1,1,−1,0,0,−1,0,0,0,0,0,0,0), K=(1,0,0,1,−1,0,−1,0,0,0,0,0,0,0), W=(0,1,0,1,1,0,0,1,0,0,0,0,0,0), y=(1,1,0,0,0,0,1,−1,0,0,0,0,0,0), L=(0,1,0,0,1,−1,−1,0,0,0,0,0,0,0), X=(1,0,0,0,−1,−1,0,1,0,0,0,0,0,0), M=(1,1,0,−1,0,1,0,0,0,0,0,0,0,0), N=(1,−1,−1,0,1,0,0,0,0,0,0,0,0,0), O=(0,0,0,0,0,0,0,0,0,0,1,0,0,0), h=(0,0,0,0,0,0,0,0,1,−1,0,0,0,0), 8=(0,0,0,0,0,0,0,0,1,1,0,0,0,0), 9=(0,0,0,0,0,0,0,0,0,0,0,0,0,1), A=(0,0,0,0,0,0,0,0,0,0,0,1,1,0), B=(0,0,0,0,0,0,0,0,0,0,0,1,−1,0), P=(0,0,0,0,0,0,0,1,0,−1,0,0,0,0), F=(0,0,0,0,0,0,0,1,0,1,0,0,0,0), i=(0,0,0,0,0,0,0,0,0,0,0,1,0,0), Q=(0,0,0,0,0,0,0,0,1,0,0,0,−1,0), Y=(0,0,0,0,0,0,0,0,1,0,0,0,1,0), s=(0,0,0,0,0,0,0,0,1,0,0,1,1,−1), Z=(0,0,0,0,0,0,0,0,1,0,0,−1,−1,−1), t=(0,0,0,0,0,0,0,0,1,0,0,0,0,1), #=(0,0,0,0,0,0,0,0,1,0,0,1,−1,−1), R=(0,0,0,0,0,0,0,0,1,0,0,1,1,1), %=(0,0,0,0,0,0,0,0,1,0,0,−1,0,0), j=(0,0,0,0,0,0,0,0,0,0,0,0,1,−1), S=(0,0,0,0,0,0,0,0,1,0,0,−1,1,−1), T=(0,0,0,0,0,0,0,0,0,0,0,1,0,−1), a=(0,0,0,0,0,0,0,0,0,1,1,0,0,0), b=(0,0,0,0,0,0,0,0,0,1,−1,0,0,0), c=(0,0,0,0,0,0,0,0,1,0,0,1,−1,1), k=(0,0,0,0,0,0,0,0,0,0,0,0,1,1), C=(0,0,0,0,0,0,0,1,−1,1,1,0,0,0), G=(0,0,0,0,0,0,0,1,−1,−1,−1,0,0,0), u=(0,0,0,0,0,0,0,1,1,0,0,0,0,0), D=(0,0,0,0,0,0,0,1,1,−1,1,0,0,0), E=(0,0,0,0,0,0,0,1,0,0,−1,0,0,0), H=(0,0,0,0,0,0,0,0,1,0,−1,0,0,0), n=(0,0,0,0,0,0,0,1,−1,1,−1,0,0,0), l=(0,0,0,0,0,0,0,1,−1,−1,1,0,0,0), m=(0,0,0,0,0,0,0,1,1,1,1,0,0,0)
Appendix A.13. Fifteen-dim MMPHs
25-8 123456789ABCDEF,1234567GHIJKLD,1RS89ABCDEF,27TRSX9GH,347CL,347BK,347AIJ,T8X9.
66-14 (master for 25-8) 123456789ABCDEF,1234567GHIJKLDM,1NOPQRS89ABCDEF,27TUVWRSX9YGHZa,347bcdeZfghiCjL,347bcdeaklBmKhi,347bcdenoApIJgl,567qrstuYpmjMEF, 567qrstvw9Yfkno,qrxyz!QW8uvwX9Y,qrxyz!QWX9YGHZa,sb"#$PV!8uvwX9Y,tc%OUz#$8uvwX9Y,deNTxy"%8uvwX9Y. 1=(0,0,1,1,1,1.0,0,0,0,0,0,0,0,0), 2=(0,0,1,−1,1,−1.0,0,0,0,0,0,0,0,0), 3=(0,0,0,1,0,−1.0,0,0,0,0,0,0,0,0), 4=(0,0,1,0,−1,0.0,0,0,0,0,0,0,0,0), 5=(0,1,0,0,0,0.0,0,0,0,0,0,0,0,0), 6=(1,0,0,0,0,0.0,0,0,0,0,0,0,0,0), 7=(0,0,0,0,0,0.1,0,0,0,0,0,0,0,0), q=(0,0,0,1,0,0.0,0,0,0,0,0,0,0,0), r=(0,0,1,0,0,0.0,0,0,0,0,0,0,0,0), s=(0,0,0,0,0,1.0,0,0,0,0,0,0,0,0), t=(0,0,0,0,1,0.0,0,0,0,0,0,0,0,0), b=(1,−1,1,0,1,0.0,0,0,0,0,0,0,0,0), c=(1,1,0,1,0,1.0,0,0,0,0,0,0,0,0), d=(1,1,0,−1,0,−1,0,0,0,0,0,0,0,0,0), e=(−1,1,1,0,1,0.0,0,0,0,0,0,0,0,0), N=(0,1,−1,1,0,0.1,0,0,0,0,0,0,0,0), T=(1,0,1,1,0,0,0,−1,0,0,0,0,0,0,0), x=(1,0,0,0,1,1.0,1,0,0,0,0,0,0,0), y=(0,1,0,0,−1,1.−1,0,0,0,0,0,0,0,0), "=(0,0,1,0,−1,0.1,1,0,0,0,0,0,0,0), %=(0,0,0,1,0,−1.−1,1,0,0,0,0,0,0,0), O=(1,0,1,0,0,−1.1,0,0,0,0,0,0,0,0), U=(0,−1,1,0,0,1.0,1,0,0,0,0,0,0,0), z=(−1,1,0,0,0,0.1,1,0,0,0,0,0,0,0), #=(1,0,−1,−1,0,0.0,1,0,0,0,0,0,0,0), $=(0,1,1,−1,0,0.−1,0,0,0,0,0,0,0,0), P=(1,0,0,1,−1,0.−1,0,0,0,0,0,0,0,0), V=(0,1,0,1,1,0.0,1,0,0,0,0,0,0,0), !=(1,1,0,0,0,0.1,−1,0,0,0,0,0,0,0), Q=(0,1,0,0,1,−1.−1,0,0,0,0,0,0,0,0), W=(1,0,0,0,−1,−1.0,1,0,0,0,0,0,0,0), R=(1,1,0,−1,0,1.0,0,0,0,0,0,0,0,0), S=(1,−1,−1,0,1,0.0,0,0,0,0,0,0,0,0), 8=(0,0,0,0,0,0.0,0,0,1,1,1,1,0,0), u=(0,0,0,0,0,0.0,0,0,1,−1,1,−1,0,0), v=(0,0,0,0,0,0.0,0,0,0,1,0,−1,0,0), w=(0,0,0,0,0,0.0,0,0,1,0,−1,0,0,0), X=(0,0,0,0,0,0.0,0,1,0,0,0,0,0,0), 9=(0,0,0,0,0,0.0,0,0,0,0,0,0,0,1), Y=(0,0,0,0,0,0.0,0,0,0,0,0,0,1,0), G=(0,0,0,0,0,0.0,0,0,0,1,0,0,0,0), H=(0,0,0,0,0,0.0,0,0,1,0,0,0,0,0), Z=(0,0,0,0,0,0.0,0,0,0,0,0,1,0,0), a=(0,0,0,0,0,0.0,0,0,0,0,1,0,0,0), f=(0,0,0,0,0,0.0,1,−1,1,0,1,0,0,0), k=(0,0,0,0,0,0.0,1,1,0,1,0,1,0,0), n=(0,0,0,0,0,0.0,1,1,0,−1,0,−1,0,0), o=(0,0,0,0,0,0.0,1,−1,−1,0,−1,0,0,0), A=(0,0,0,0,0,0.0,0,1,−1,1,0,0,1,0), p=(0,0,0,0,0,0.0,1,0,1,1,0,0,0,−1), I=(0,0,0,0,0,0.0,1,0,0,0,1,1,0,1), J=(0,0,0,0,0,0.0,0,1,0,0,−1,1,−1,0), g=(0,0,0,0,0,0.0,0,0,1,0,−1,0,1,1), l=(0,0,0,0,0,0.0,0,0,0,1,0,−1,−1,1), B=(0,0,0,0,0,0.0,1,0,1,0,0,−1,1,0), m=(0,0,0,0,0,0.0,0,1,−1,0,0,−1,0,−1), K=(0,0,0,0,0,0.0,1,−1,0,0,0,0,−1,−1), h=(0,0,0,0,0,0.0,1,0,−1,−1,0,0,0,1), i=(0,0,0,0,0,0.0,0,1,1,−1,0,0,−1,0), C=(0,0,0,0,0,0.0,1,0,0,1,−1,0,−1,0), j=(0,0,0,0,0,0.0,0,1,0,1,1,0,0,1), L=(0,0,0,0,0,0.0,1,1,0,0,0,0,1,−1), D=(0,0,0,0,0,0.0,0,1,0,0,1,−1,−1,0), M=(0,0,0,0,0,0.0,1,0,0,0,−1,−1,0,1), E=(0,0,0,0,0,0.0,1,1,0,−1,0,1,0,0), F=(0,0,0,0,0,0.0,1,−1,−1,0,1,0,0,0)
Appendix A.14. Sixteen-dim MMPHs
22-9 123456789ABCDEFG,17HID,28UdG,3478efE,5678,Bd,e9,fICF,HUA.
70-9 (master for 22-9) 123456789ABCDEFG,17HIJKLMNOPQRDST,28UVWXLMYZabScdG,3478efghijPbkElm,5678nopqrZsQtukT,novwxyKXzasBu!dm,pe"#$JWy9iY%tR&’,qf(IVx#$zOjC)lF&,ghHUvw"(ArN%)c!’. 1=(0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0), 2=(0,0,1,−1,1,−1,0,0,0,0,0,0,0,0,0,0), 3=(0,0,0,1,0,−1,0,0,0,0,0,0,0,0,0,0), 4=(0,0,1,0,−1,0,0,0,0,0,0,0,0,0,0,0), 5=(0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0), 6=(1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0), 7=(0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0), 8=(0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0), n=(0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0), o=(0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0), p=(0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0), q=(0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0), e=(1,−1,1,0,1,0,0,0,0,0,0,0,0,0,0,0), f=(1,1,0,1,0,1,0,0,0,0,0,0,0,0,0,0), g=(1,1,0,−1,0,−1,0,0,0,0,0,0,0,0,0,0), h=(−1,1,1,0,1,0,0,0,0,0,0,0,0,0,0,0), H=(0,1,−1,1,0,0,1,0,0,0,0,0,0,0,0,0), U=(1,0,1,1,0,0,0,−1,0,0,0,0,0,0,0,0), v=(1,0,0,0,1,1,0,1,0,0,0,0,0,0,0,0), w=(0,1,0,0,−1,1,−1,0,0,0,0,0,0,0,0,0), "=(0,0,1,0,−1,0,1,1,0,0,0,0,0,0,0,0), (=(0,0,0,1,0,−1,−1,1,0,0,0,0,0,0,0,0), I=(1,0,1,0,0,−1,1,0,0,0,0,0,0,0,0,0), V=(0,−1,1,0,0,1,0,1,0,0,0,0,0,0,0,0), x=(−1,1,0,0,0,0,1,1,0,0,0,0,0,0,0,0), #=(1,0,−1,−1,0,0,0,1,0,0,0,0,0,0,0,0), $=(0,1,1,−1,0,0,−1,0,0,0,0,0,0,0,0,0), J=(1,0,0,1,−1,0,−1,0,0,0,0,0,0,0,0,0), W=(0,1,0,1,1,0,0,1,0,0,0,0,0,0,0,0), y=(1,1,0,0,0,0,1,−1,0,0,0,0,0,0,0,0), K=(0,1,0,0,1,−1,−1,0,0,0,0,0,0,0,0,0), X=(1,0,0,0,−1,−1,0,1,0,0,0,0,0,0,0,0), L=(1,1,0,−1,0,1,0,0,0,0,0,0,0,0,0,0), M=(1,−1,−1,0,1,0,0,0,0,0,0,0,0,0,0,0), 9=(0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0), A=(0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0), i=(0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0), Y=(0,0,0,0,0,0,0,0,0,1,−1,0,0,0,0,0), r=(0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0), N=(0,0,0,0,0,0,0,0,1,0,−1,0,0,0,0,0), z=(0,0,0,0,0,0,0,0,1,−1,0,0,0,0,0,0), %=(0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0), O=(0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0), j=(0,0,0,0,0,0,0,0,1,1,−1,−1,0,0,0,0), P=(0,0,0,0,0,0,0,0,1,−1,1,−1,0,0,0,0), Z=(0,0,0,0,0,0,0,0,1,−1,−1,−1,0,0,0,0), a=(0,0,0,0,0,0,0,0,1,1,1,−1,0,0,0,0), s=(0,0,0,0,0,0,0,0,1,1,−1,1,0,0,0,0), b=(0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0), B=(0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0), C=(0,0,0,0,0,0,0,0,0,0,1,−1,0,0,0,0), Q=(0,0,0,0,0,0,0,0,0,1,0,−1,0,0,0,0), t=(0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0), R=(0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0), u=(0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0), k=(0,0,0,0,0,0,0,0,0,0,0,0,0,1,−1,0), D=(0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0), S=(0,0,0,0,0,0,0,0,0,0,0,0,1,0,−1,0), )=(0,0,0,0,0,0,0,0,0,0,0,0,1,−1,0,0), T=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1), c=(0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1), !=(0,0,0,0,0,0,0,0,0,0,0,0,1,1,−1,−1), d=(0,0,0,0,0,0,0,0,0,0,0,0,1,−1,1,−1), E=(0,0,0,0,0,0,0,0,0,0,0,0,1,−1,−1,−1), l=(0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,−1), F=(0,0,0,0,0,0,0,0,0,0,0,0,1,1,−1,1), m=(0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1), &=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1), ’=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,−1), G=(0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,−1)