Information Rates for Channels with Fading, Side Information and Adaptive Codewords
Abstract
1. Introduction
1.1. Block Fading
- The fading is described by a state process independent of the transmitter messages and channel noise. The subscript “H” emphasizes that the states may be hidden from the transceivers.
- Each receiver sees a state process where is a noisy function of for all i.
- Each transmitter sees a state process where is a noisy function of for all i.
1.2. CSI and In-Block Feedback
1.3. Auxiliary Models
1.4. Refined Auxiliary Models
1.5. Organization
- Proposition 1 in Section 3.1 states a known result, namely that the RHS of (6) is the maximum GMI for the AWGN auxiliary model (11) and a CSCG X.
- Lemma 1 in Section 3.2 generalizes Proposition 1 by partitioning the channel output alphabet into K subsets, . We use to establish capacity properties at high and low SNR.
- Section 4.3 treats adaptive codewords and develops structural properties of their optimal distribution.
- Lemma 2 in Section 4.4 generalizes Proposition 1 to MIMO channels and adaptive codewords. The receiver models each transmit symbol as a weighted sum of the entries of the corresponding adaptive symbol.
- Lemma 3 in Section 4.5 states that the maximum GMI for scalar channels, an AWGN auxiliary model, adaptive codewords with jointly CSCG entries, and is achieved by using a conventional codebook where each symbol is modified based on the CSIT.
- Lemma 4 in Section 4.6 extends Lemma 3 to MIMO channels, including diagonal or parallel channels.
- Theorem 1 in Section 5.1 generalizes Lemma 3 to include CSIR; we use this result several times in Section 6.
- Lemma 5 in Section 5.3 generalizes Lemmas 1 and 2 by partitioning the channel output alphabet.
- Lemma 6 in Section 6 gives a general capacity upper bound.
- Section 6.5 introduces a class of power control policies for full CSIT. Theorem 2 develops the optimal policy with an MMSE form.
- Theorem 3 in Section 6.6 provides a quadratic waterfilling expression for the GMI with partial CSIR.
- Theorem 4 in Section 9.2 generalizes Lemma 4 to MIMO block fading channels;
- Section 9.3 develops capacity expressions in terms of directed information;
- Section 9.4 specializes the capacity to fading channels with AWGN and delayed CSIR;
- Proposition 3 generalizes Proposition 2 to channels with special CSIR and CSIT.
2. Preliminaries
2.1. Basic Notation
2.2. Vectors and Matrices
2.3. Random Variables
2.4. Second-Order Statistics
2.5. MMSE and LMMSE Estimation
2.6. Entropy, Divergence, and Information
2.7. Entropy and Information Bounds
2.8. Capacity and Wideband Rates
2.9. Uniformly-Spaced Quantizer
3. Generalized Mutual Information
3.1. AWGN Forward Model with CSCG Inputs
3.2. CSIR and K-Partitions
3.3. Example: On-Off Fading
4. Channels with CSIT
4.1. Model
4.2. Capacity
4.3. Structure of the Optimal Input Distribution
4.4. Generalized Mutual Information
4.5. Optimal Codebooks for CSCG Forward Models
4.6. Forward Model GMI for MIMO Channels
5. Channels with CSIR and CSIT
5.1. Capacity and GMI
5.2. CSIT@ R
5.3. MIMO Channels and K-Partitions
6. Fading Channels with AWGN
6.1. CSIR and CSIT Models
- Full CSIT: ;
- CSIT@R: where is the quantizer of Section 2.9 with ;
- Partial CSIT: is not known exactly at the receiver.
6.2. No CSIR, No CSIT
6.3. Full CSIR, CSIT@ R
- both and decrease as increases;
- the maximal permitted by (183) is which is obtained with ;
- the maximal permitted by (184) is which is obtained with .
6.4. Full CSIR, Partial CSIT
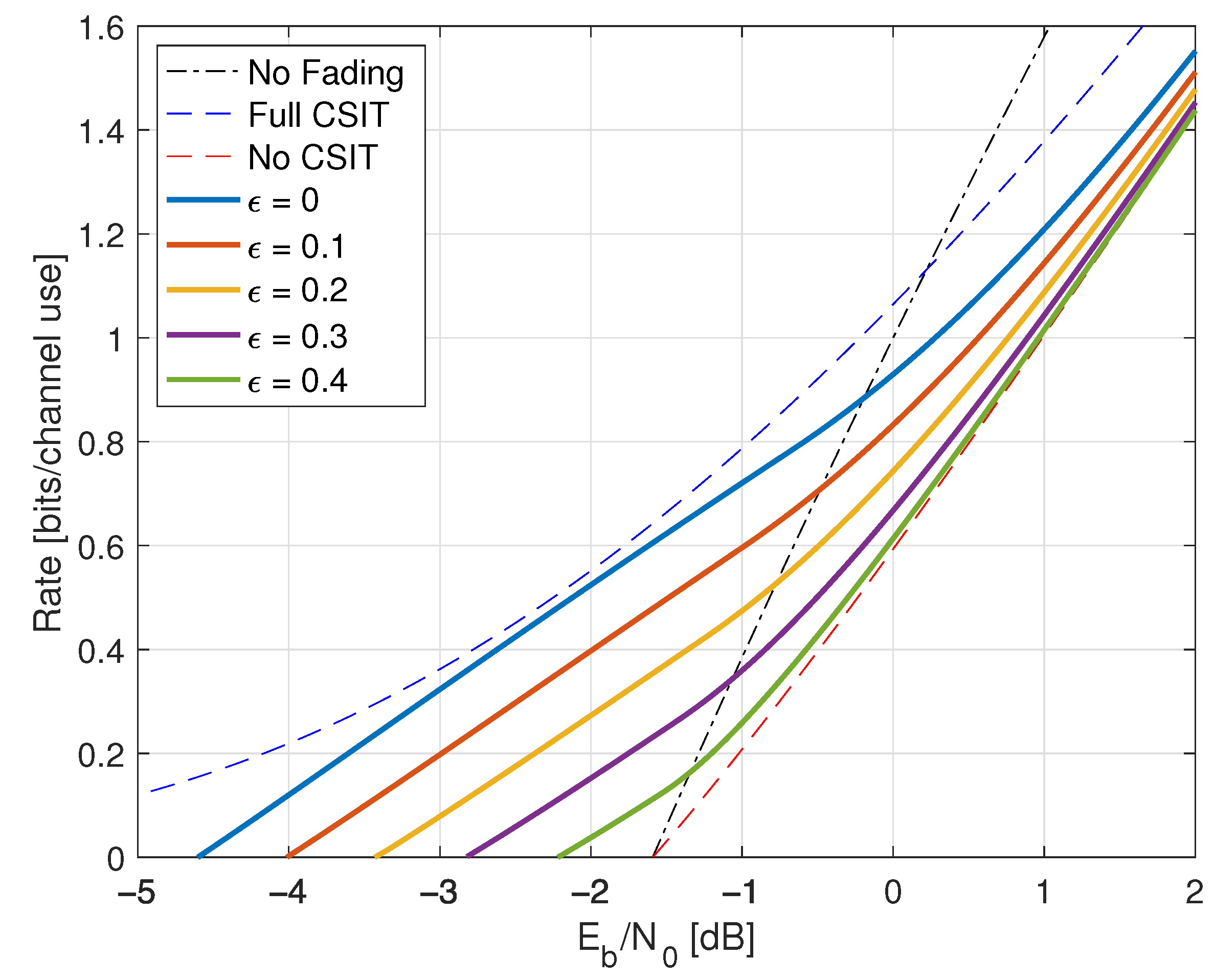
6.5. Partial CSIR, Full CSIT
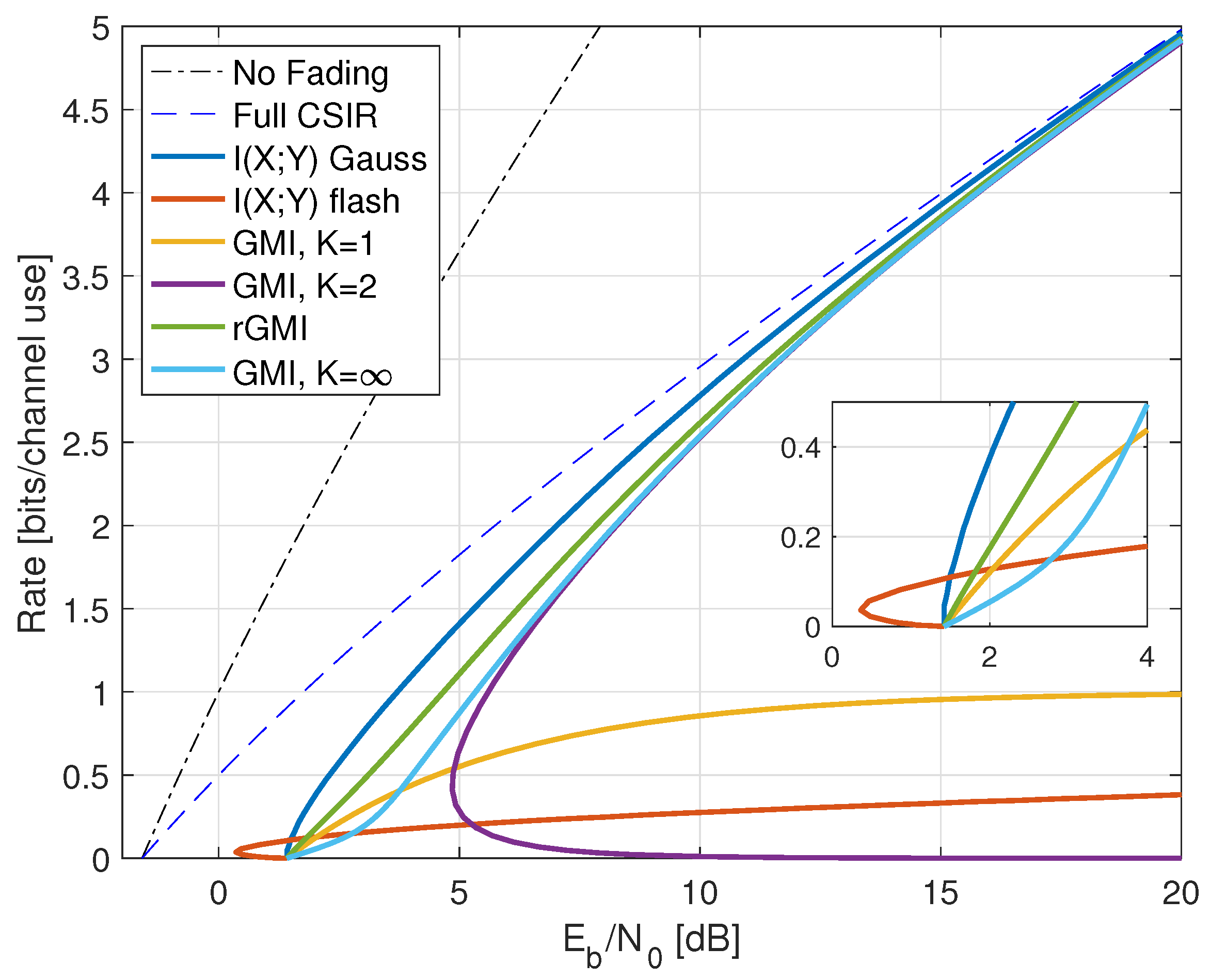
- the minimum of TCP and TCI is larger (worse) than dB unless there is no fading;
- the minimum of TMF is smaller (better) than dB unless .
- the minimum of TMF is smaller (better) than that of TCP and TCI unless there is no fading, or if the minimal is ;
- the best threshold for TMF is and the minimal is dB.
- the minimum of all policies can be better than dB by choosing ;
- the minimum of TMF is smaller (better) than that of TCP and TCI unless there is no fading or the minimal is .
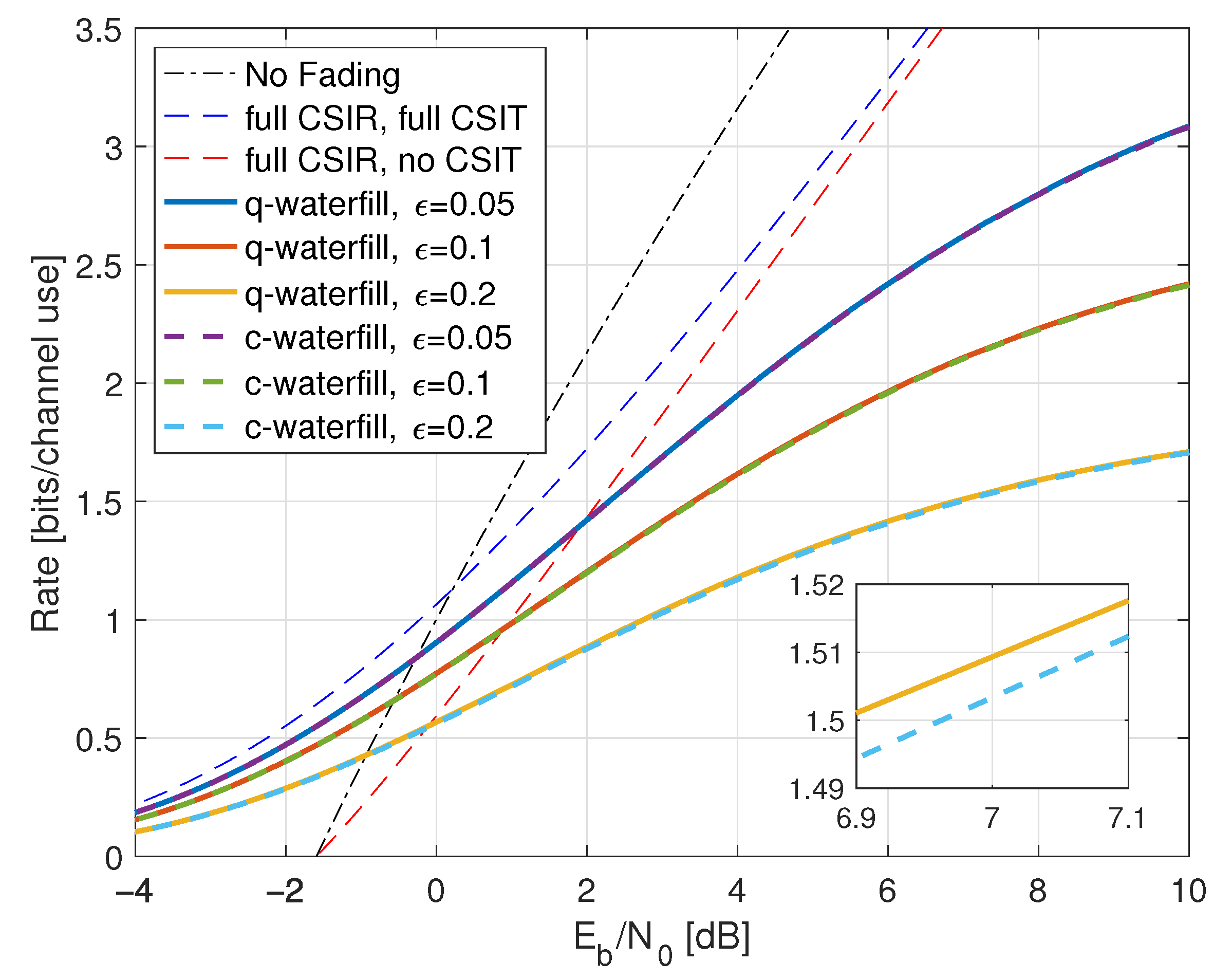
6.6. Partial CSIR, CSIT@ R
7. On-Off Fading
7.1. Full CSIR, CSIT@ R
7.2. Full CSIR, Partial CSIT
7.3. Partial CSIR, Full CSIT
7.4. Partial CSIR, CSIT@ R
8. Rayleigh Fading
8.1. No CSIR, No CSIT
8.2. Full CSIR, CSIT@ R
8.3. Full CSIR, Partial CSIT
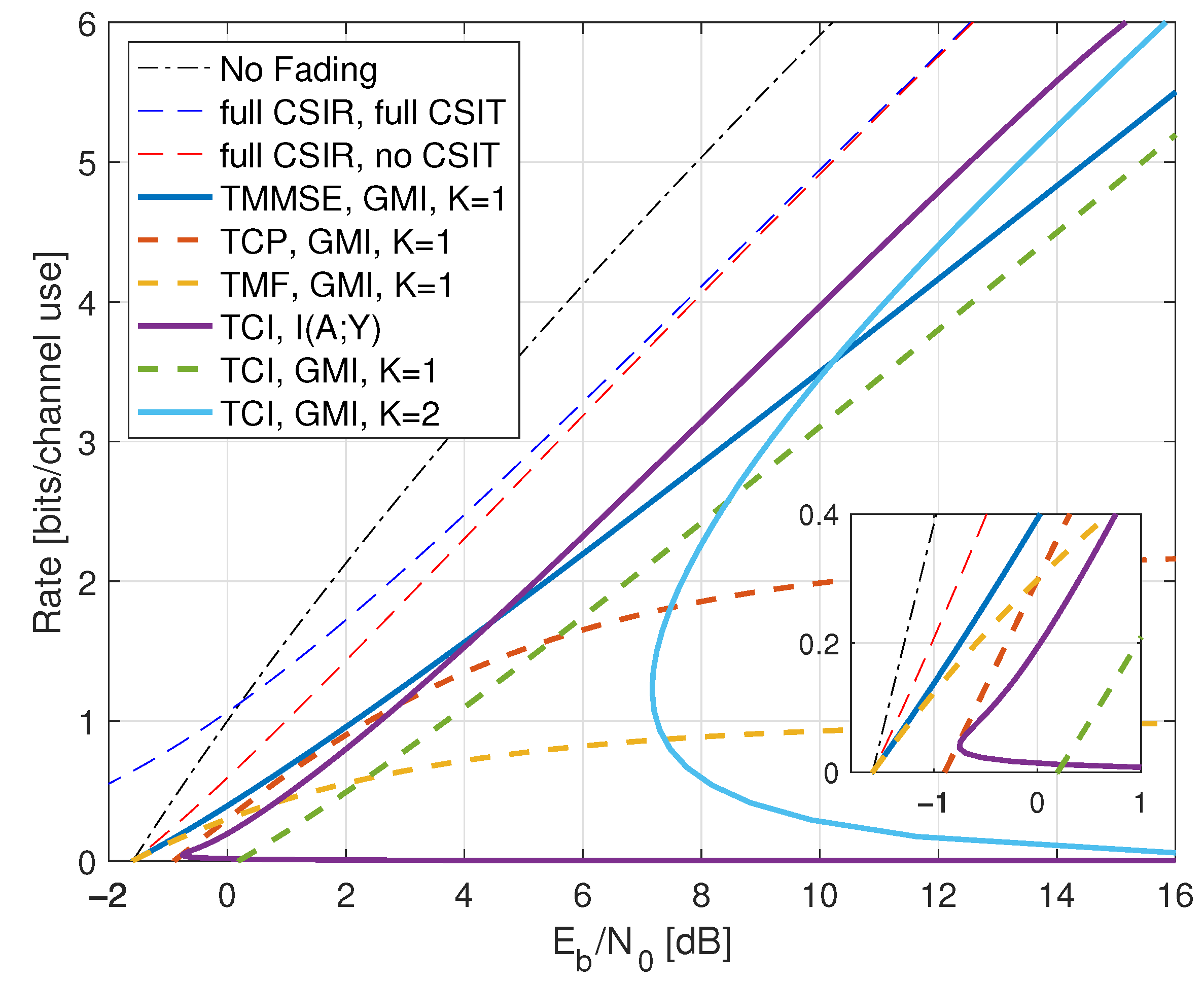
8.4. Partial CSIR, Full CSIT
- Inserting , we thus haveWe further have by using (A6) in Appendix A.2, and the high-SNR slope of the GMI matches the slope of but the additive gap to increases. The high SNR rates are shown as the curve labeled “TCI, GMI, K = 2” in Figure 10 for .
- For low SNR, we choosefor a constant . As P decreases, both t and increase and Appendix B.4 shows that
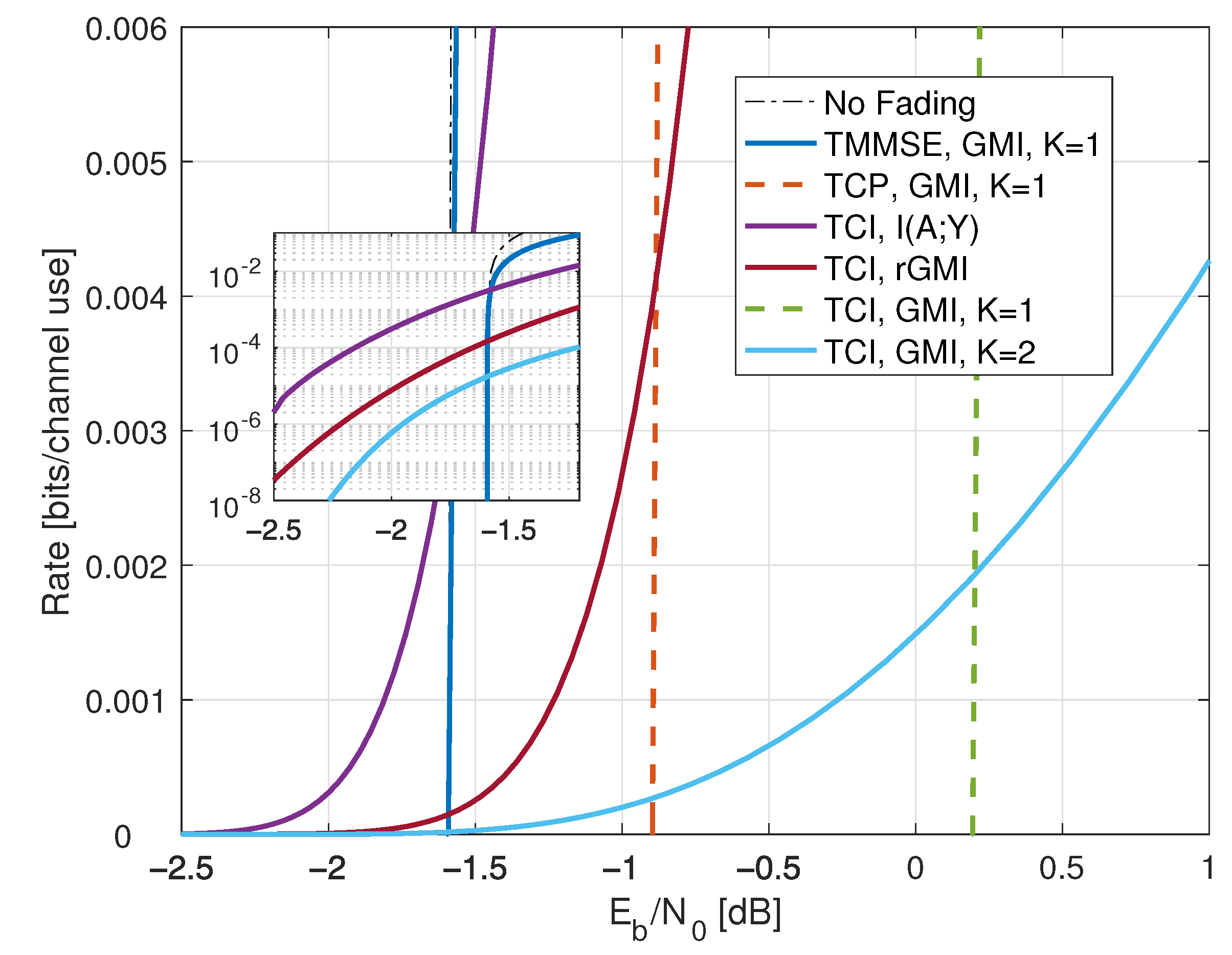
8.5. Partial CSIR, CSIT@ R
9. Channels with In-Block Feedback
9.1. Model and Capacity
9.2. GMI for Scalar Channels
9.3. CSIT@ R
9.4. Fading Channels with AWGN
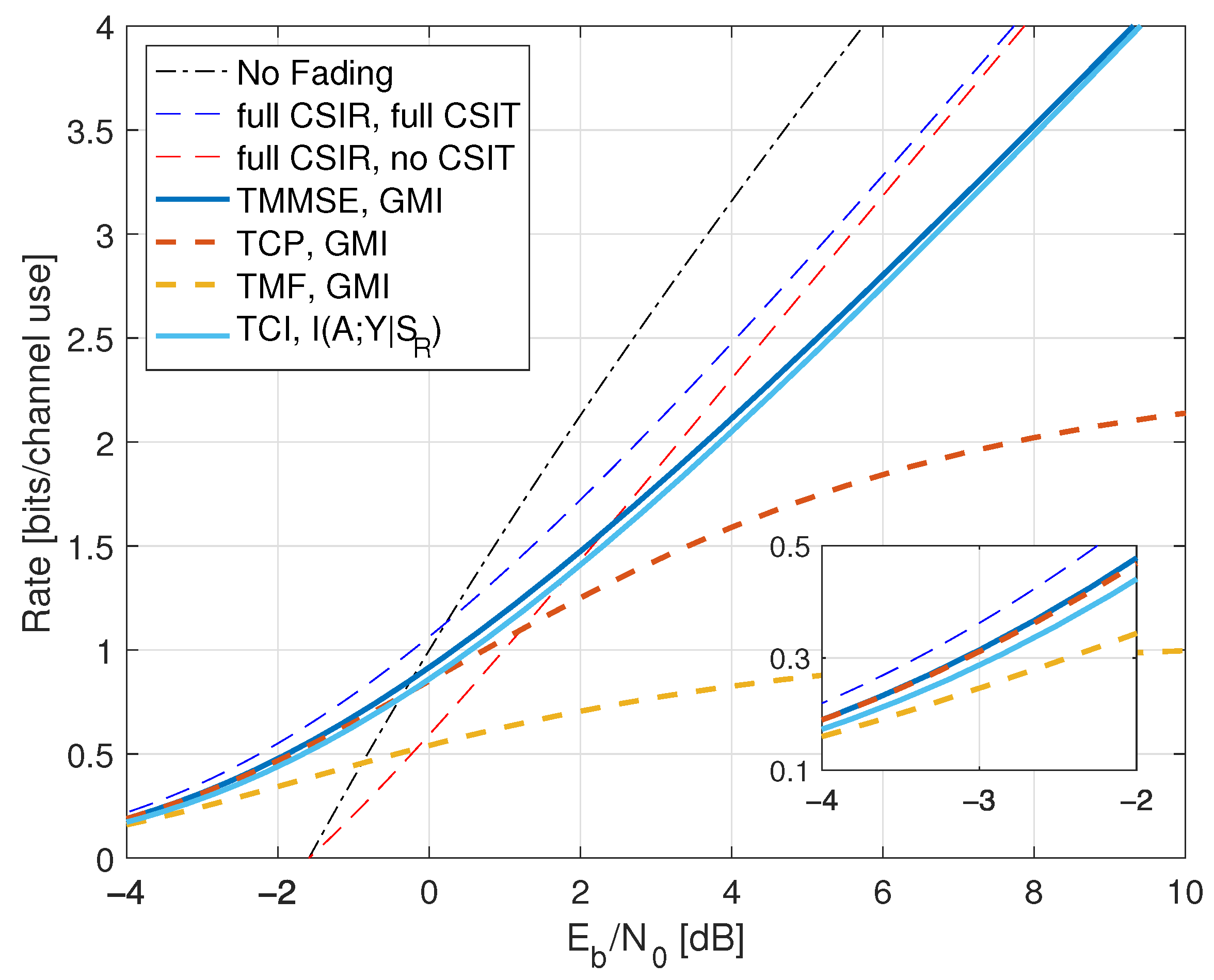
9.5. Full CSIR, Partial CSIT
9.6. On-Off Fading with Delayed CSIT
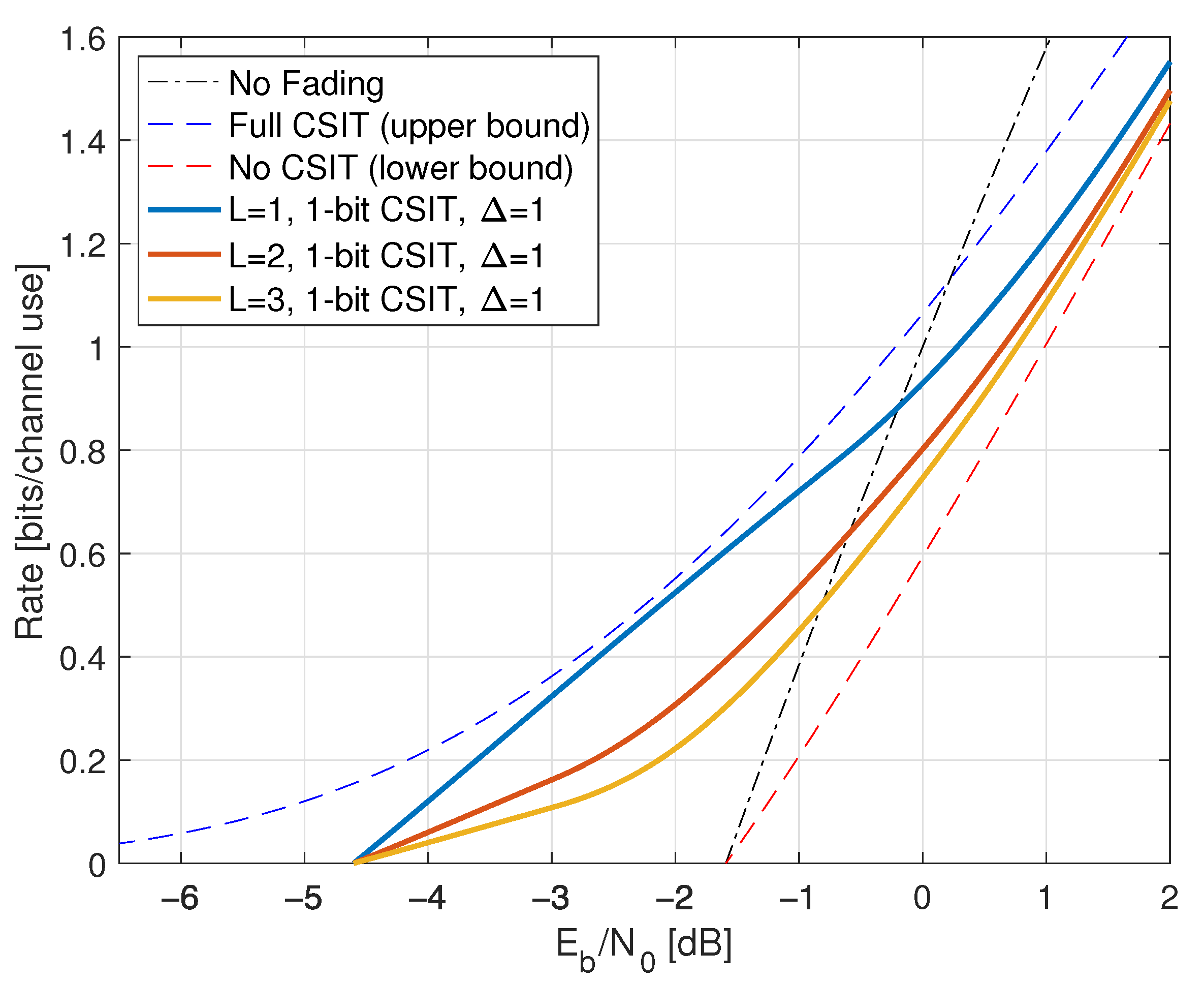
9.7. Rayleigh Fading and One-Bit Feedback
- For the CSIT (345), we study delayed feedback where for and . The delay is thus in the sense of Section 9.6.
- For the CSIT (338), we study the case , , and for . The delay is thus in the sense of Section 9.6.
10. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Special Functions
Appendix A.1. Non-Central Chi-Squared Distribution
Appendix A.2. Exponential Integral
Appendix A.3. Gamma Functions
Appendix B. Forward Model GMIs with K = 2
Appendix B.1. On-Off Fading
Appendix B.2. On-Off Fading, Partial CSIR, and Full CSIT
Appendix B.3. On-Off Fading, Partial CSIR, and CSIT@R
Appendix B.4. Rayleigh Fading, No CSIR, full CSIT, and TCI
Appendix C. Conditional Second-Order Statistics
Appendix C.1. No CSIR, No CSIT
Appendix C.2. Full CSIR, Partial CSIT
Appendix C.3. Partial CSIR, Full CSIT
Appendix C.4. Partial CSIR, CSIT@R
Appendix D. Proof of Lemma 2 and (119)
Appendix E. Proof of Lemma 3
Appendix F. Large K for Section 5.3
Appendix G. Proof of Lemma 4
References
- Ozarow, L.; Shamai, S.; Wyner, A.D. Information theoretic consideration for cellular mobile radio. IEEE Trans. Inf. Theory 1994, 43, 359–378. [Google Scholar] [CrossRef]
- Biglieri, E.; Proakis, J.; Shamai (Shitz), S. Fading channels: Information-theoretic and communications aspects. IEEE Trans. Inf. Theory 1998, 44, 2619–2692. [Google Scholar] [CrossRef]
- Love, D.J.; Heath, R.W., Jr.; Lau, V.K.N.; Gesbert, D.; Rao, B.D.; Andrews, M. An overview of limited feedback in wireless communication systems. IEEE J. Select. Areas Commun. 2008, 26, 1341–1365. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kramer, G. Information theory for cellular wireless networks. In Information Theoretic Perspectives on 5G Systems and Beyond; Cambridge University Press: Cambridge, UK, 2022; pp. 10–92. [Google Scholar] [CrossRef]
- Keshet, G.; Steinberg, Y.; Merhav, N. Channel coding in the presence of side information. Found. Trends Commun. Inf. Theory 2008, 4, 445–586. [Google Scholar] [CrossRef]
- Shannon, C.E. Channels with side information at the transmitter. IBM J. Res. Develop. 1958, 2, 289–293, Reprinted in Claude Elwood Shannon: Collected Papers; Sloane, N.J.A.,Wyner, A.D., Eds.; IEEE Press: Piscataway, NJ, USA, 1993; pp. 273–278. [Google Scholar] [CrossRef]
- Shannon, C.E. Two-way communication channels. In Proceedings of the Proc. 4th Berkeley Symp. on Mathematical Statistics and Probability; Neyman, J., Ed.; Univ. Calif. Press: Berkeley, CA, USA, 1961; Volume 1, pp. 611–644, Reprinted in Claude Elwood Shannon: Collected Papers; Sloane, N.J.A.,Wyner, A.D., Eds.; IEEE Press: Piscataway, NJ, USA, 1993; pp. 351–384. [Google Scholar]
- Blahut, R. Principles and Practice of Information Theory; Addison-Wesley: Reading, MA, USA, 1987. [Google Scholar]
- Kramer, G. Directed Information for Channels with Feedback; Vol. ETH Series in Information Processing; Hartung-Gorre Verlag: Konstanz, Germany, 1998; Volume 11. [Google Scholar] [CrossRef]
- Caire, G.; Shamai (Shitz), S. On the capacity of some channels with channel state information. IEEE Trans. Inf. Theory 1999, 45, 2007–2019. [Google Scholar] [CrossRef]
- McEliece, R.J.; Stark, W.E. Channels with block interference. IEEE Trans. Inf. Theory 1984, 30, 44–53. [Google Scholar] [CrossRef]
- Stark, W.; McEliece, R. On the capacity of channels with block memory. IEEE Trans. Inf. Theory 1988, 34, 322–324. [Google Scholar] [CrossRef]
- Wang, H.S.; Moayeri, N. Finite-state Markov channel-a useful model for radio communication channels. IEEE Trans. Vehic. Technol. 1995, 44, 163–171. [Google Scholar] [CrossRef]
- Wang, H.S.; Chang, P.C. On verifying the first-order Markovian assumption for a Rayleigh fading channel model. IEEE Trans. Vehic. Technol. 1996, 45, 353–357. [Google Scholar] [CrossRef]
- Viswanathan, H. Capacity of Markov channels with receiver CSI and delayed feedback. IEEE Trans. Inf. Theory 1999, 45, 761–771. [Google Scholar] [CrossRef]
- Zhang, Q.; Kassam, S. Finite-state Markov model for Rayleigh fading channels. IEEE Trans. Commun. 1999, 47, 1688–1692. [Google Scholar] [CrossRef]
- Tan, C.C.; Beaulieu, N.C. On first-order Markov modeling for the Rayleigh fading channel. IEEE Trans. Commun. 2000, 48, 2032–2040. [Google Scholar] [CrossRef]
- Médard, M. The effect upon channel capacity in wireless communications of perfect and imperfect knowledge of the channel. IEEE Trans. Inf. Theory 2000, 46, 933–946. [Google Scholar] [CrossRef]
- Riediger, M.; Shwedyk, E. Communication receivers based on Markov models of the fading channel. In Proceedings of the IEEE CCECE2002, Canadian Conference on Electrical and Computer Engineering, Conference Proceedings (Cat. No.02CH37373), Winnipeg, MB, Canada, 12–15 May 2002; Volume 3, pp. 1255–1260. [Google Scholar] [CrossRef]
- Agarwal, M.; Honig, M.L.; Ata, B. Adaptive training for correlated fading channels With feedback. IEEE Trans. Inf. Theory 2012, 58, 5398–5417. [Google Scholar] [CrossRef]
- Ezzine, R.; Wiese, M.; Deppe, C.; Boche, H. A rigorous proof of the capacity of MIMO Gauss-Markov Rayleigh fading channels. In Proceedings of the 2022 IEEE International Symposium on Information Theory (ISIT), Espoo, Finland, 26 June–1 July 2022; pp. 2732–2737. [Google Scholar] [CrossRef]
- Kramer, G. Information networks with in-block memory. IEEE Trans. Inf. Theory 2014, 60, 2105–2120. [Google Scholar] [CrossRef]
- Pinsker, M.S. Calculation of the rate of information production by means of stationary random processes and the capacity of stationary channel. Dokl. Akad. Nauk USSR 1956, 111, 753–756. [Google Scholar]
- Ihara, S. On the capacity of channels with additive non-Gaussian noise. Inf. Control 1978, 37, 34–39. [Google Scholar] [CrossRef]
- Pinsker, M.; Prelov, V.; Verdú, S. Sensitivity of channel capacity. IEEE Trans. Inf. Theory 1995, 41, 1877–1888. [Google Scholar] [CrossRef]
- Shamai, S. On the capacity of a twisted-wire pair: Peak-power constraint. IEEE Trans. Commun. 1990, 38, 368–378. [Google Scholar] [CrossRef]
- Kalet, I.; Shamai, S. On the capacity of a twisted-wire pair: Gaussian model. IEEE Trans. Commun. 1990, 38, 379–383. [Google Scholar] [CrossRef]
- Diggavi, S.; Cover, T. The worst additive noise under a covariance constraint. IEEE Trans. Inf. Theory 2001, 47, 3072–3081. [Google Scholar] [CrossRef]
- Klein, T.; Gallager, R. Power control for the additive white Gaussian noise channel under channel estimation errors. In Proceedings of the 2001 IEEE International Symposium on Information Theory (IEEE Cat. No.01CH37252), Washington, DC, USA, 29–29 June 2001; p. 304. [Google Scholar] [CrossRef]
- Bhashyam, S.; Sabharwal, A.; Aazhang, B. Feedback gain in multiple antenna systems. IEEE Trans. Commun. 2002, 50, 785–798. [Google Scholar] [CrossRef]
- Hassibi, B.; Hochwald, B. How much training is needed in multiple-antenna wireless links? IEEE Trans. Inf. Theory 2003, 49, 951–963. [Google Scholar] [CrossRef]
- Yoo, T.; Goldsmith, A. Capacity and power allocation for fading MIMO channels with channel estimation error. IEEE Trans. Inf. Theory 2006, 52, 2203–2214. [Google Scholar] [CrossRef]
- Agarwal, M.; Honig, M.L. Wideband fading channel capacity With training and partial feedback. IEEE Trans. Inf. Theory 2010, 56, 4865–4873. [Google Scholar] [CrossRef]
- Soysal, A.; Ulukus, S. Joint channel estimation and resource allocation for MIMO systems-part I: Single-user analysis. IEEE Trans. Wireless Commun. 2010, 9, 624–631. [Google Scholar] [CrossRef]
- Marzetta, T.L.; Larsson, E.G.; Yang, H.; Ngo, H.Q. Fundamentals of Massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Li, Y.; Tao, C.; Lee Swindlehurst, A.; Mezghani, A.; Liu, L. Downlink achievable rate analysis in massive MIMO systems with one-bit DACs. IEEE Commun. Lett. 2017, 21, 1669–1672. [Google Scholar] [CrossRef]
- Caire, G. On the ergodic rate lower bounds With applications to massive MIMO. IEEE Trans. Wireless Communi. 2018, 17, 3258–3268. [Google Scholar] [CrossRef]
- Noam, Y.; Zaidel, B.M. On the two-user MISO interference channel with single-user decoding: Impact of imperfect CSIT and channel dimension reduction. IEEE Trans. Signal Proc. 2019, 67, 2608–2623. [Google Scholar] [CrossRef]
- Kaplan, G.; Shamai (Shitz), S. Information rates and error exponents of compound channels with application to antipodal signaling in a fading environment. Arch. für Elektron. Und Übertragungstechnik 1993, 47, 228–239. [Google Scholar]
- Merhav, N.; Kaplan, G.; Lapidoth, A.; Shamai Shitz, S. On information rates for mismatched decoders. IEEE Trans. Inf. Theory 1994, 40, 1953–1967. [Google Scholar] [CrossRef]
- Scarlett, J.; i Fàbregas, A.G.; Somekh-Baruch, A.; Martinez, A. Information-Theoretic Foundations of Mismatched Decoding. Found. Trends Commun. Inf. Theory 2020, 17, 149–401. [Google Scholar] [CrossRef]
- Lapidoth, A. Nearest neighbor decoding for additive non-Gaussian noise channels. IEEE Trans. Inf. Theory 1996, 42, 1520–1529. [Google Scholar] [CrossRef]
- Lapidoth, A.; Shamai, S. Fading channels: How perfect need “perfect side information” be? IEEE Trans. Inf. Theory 2002, 48, 1118–1134. [Google Scholar] [CrossRef]
- Weingarten, H.; Steinberg, Y.; Shamai, S. Gaussian codes and weighted nearest neighbor decoding in fading multiple-antenna channels. IEEE Trans. Inf. Theory 2004, 50, 1665–1686. [Google Scholar] [CrossRef]
- Asyhari, A.T.; Fàbregas, A.G.i. MIMO block-fading channels With mismatched CSI. IEEE Trans. Inf. Theory 2014, 60, 7166–7185. [Google Scholar] [CrossRef]
- Östman, J.; Lancho, A.; Durisi, G.; Sanguinetti, L. URLLC With massive MIMO: Analysis and design at finite blocklength. IEEE Trans. Wireless Commun. 2021, 20, 6387–6401. [Google Scholar] [CrossRef]
- Zhang, W. A general framework for transmission with transceiver distortion and some applications. IEEE Trans. Commun. 2012, 60, 384–399. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Shen, C.; Liang, N. A regression approach to certain information transmission problems. IEEE J. Selected Areas Commun. 2019, 37, 2517–2531. [Google Scholar] [CrossRef]
- Pang, S.; Zhang, W. Generalized nearest neighbor decoding for MIMO channels with imperfect channel state information. In Proceedings of the IEEE Inf. Theory Workshop, Kanazawa, Japan, 17–21 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W. Generalized nearest neighbor decoding. IEEE Trans. Inf. Theory 2022, 68, 5852–5865. [Google Scholar] [CrossRef]
- Nedelcu, A.S.; Steiner, F.; Kramer, G. Low-resolution precoding for multi-antenna downlink channels and OFDM. Entropy 2022, 24, 504. [Google Scholar] [CrossRef] [PubMed]
- Essiambre, R.J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. IEEE/OSA J. Lightw. Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Dar, R.; Shtaif, M.; Feder, M. New bounds on the capacity of the nonlinear fiber-optic channel. Opt. Lett. 2014, 39, 398–401. [Google Scholar] [CrossRef]
- Secondini, M.; Agrell, E.; Forestieri, E.; Marsella, D.; Camara, M.R. Nonlinearity mitigation in WDM systems: Models, strategies, and achievable rates. IEEE/OSA J. Lightw. Technol. 2019, 37, 2270–2283. [Google Scholar] [CrossRef]
- García-Gómez, F.J.; Kramer, G. Mismatched models to lower bound the capacity of optical fiber channels. IEEE/OSA J. Lightw. Technol. 2020, 38, 6779–6787. [Google Scholar] [CrossRef]
- García-Gómez, F.J.; Kramer, G. Mismatched models to lower bound the capacity of dual-polarization optical fiber channels. IEEE/OSA J. Lightw. Technol. 2021, 39, 3390–3399. [Google Scholar] [CrossRef]
- García-Gómez, F.J.; Kramer, G. Rate and power scaling of space-division multiplexing via nonlinear perturbation. J. Lightw. Technol. 2022, 40, 5077–5082. [Google Scholar] [CrossRef]
- Secondini, M.; Civelli, S.; Forestieri, E.; Khan, L.Z. New lower bounds on the capacity of optical fiber channels via optimized shaping and detection. J. Lightw. Technol. 2022, 40, 3197–3209. [Google Scholar] [CrossRef]
- Shtaif, M.; Antonelli, C.; Mecozzi, A.; Chen, X. Challenges in estimating the information capacity of the fiber-optic channel. Proc. IEEE 2022, 110, 1655–1678. [Google Scholar] [CrossRef]
- Mecozzi, A.; Shtaif, M. Information Capacity of Direct Detection Optical Transmission Systems. IEEE/OSA Trans. Lightw. Technol. 2018, 36, 689–694. [Google Scholar] [CrossRef]
- Plabst, D.; Prinz, T.; Wiegart, T.; Rahman, T.; Stojanović, N.; Calabrò, S.; Hanik, N.; Kramer, G. Achievable rates for short-reach fiber-optic channels with direct detection. IEEE/OSA J. Lightw. Technol. 2022, 40, 3602–3613. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Divsalar, D. Performance of Mismatched Receivers on Bandlimited Channels. Ph.D. Thesis, Univ. California, Los Angeles, CA, USA, 1978. [Google Scholar]
- Ozarow, L.; Wyner, A. On the capacity of the Gaussian channel with a finite number of input levels. IEEE Trans. Inf. Theory 1990, 36, 1426–1428. [Google Scholar] [CrossRef]
- Chagnon, M. Optical Communications for Short Reach. IEEE/OSA Trans. Lightw. Technol. 2019, 37, 1779–1797. [Google Scholar] [CrossRef]
- Arnold, D.; Loeliger, H.A.; Vontobel, P.; Kavcic, A.; Zeng, W. Simulation-based computation of information rates for channels with memory. IEEE Trans. Inf. Theory 2006, 52, 3498–3508. [Google Scholar] [CrossRef]
- Aboy-Faycal, I.; Lapidoth, A. On the capacity of reduced-complexity receivers for intersymbol interference channels. In Proceedings of the Convention of the Electrical and Electronic Engineers in Israel, Tel-Aviv, Israel, 11–12 April 2000; pp. 263–266. [Google Scholar] [CrossRef]
- Rusek, F.; Prlja, A. Optimal channel shortening for MIMO and ISI channels. IEEE Trans. Wireless Commun. 2012, 11, 810–818. [Google Scholar] [CrossRef]
- Hu, S.; Rusek, F. On the design of channel shortening demodulators for iterative receivers in linear vector channels. IEEE Access 2018, 6, 48339–48359. [Google Scholar] [CrossRef]
- Mezghani, A.; Nossek, J.A. Analysis of 1-bit output noncoherent fading channels in the low SNR regime. In Proceedings of the IEEE International Symposium on Information Theory, Seoul, Republic of Korea, 28 June–3 July 2009; pp. 1080–1084. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed.; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Kramer, G. Capacity results for the discrete memoryless network. IEEE Trans. Inf. Theory 2003, 49, 4–21. [Google Scholar] [CrossRef]
- Verdú, S. Spectral efficiency in the wideband regime. IEEE Trans. Inf. Theory 2002, 48, 1319–1343. [Google Scholar] [CrossRef]
- Kramer, G.; Ashikhmin, A.; van Wijngaarden, A.; Wei, X. Spectral efficiency of coded phase-shift keying for fiber-optic communication. IEEE/OSA J. Lightw. Technol. 2003, 21, 2438–2445. [Google Scholar] [CrossRef]
- Hui, J.Y.N. Fundamental Issues of Multiple Accessing. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1983. [Google Scholar]
- Scarlett, J.; Martinez, A.; Fabregas, A.G.i. Mismatched decoding: Error exponents, second-order rates and saddlepoint approximations. IEEE Trans. Inf. Theory 2014, 60, 2647–2666. [Google Scholar] [CrossRef]
- Asadi Kangarshahi, E.; Guillén i Fàbregas, A. A single-letter upper bound to the mismatch capacity. IEEE Trans. Inf. Theory 2021, 67, 2013–2033. [Google Scholar] [CrossRef]
- Lau, V.K.N.; Liu, Y.; Chen, T.A. Capacity of memoryless channels and block-fading channels with designable cardinality-constrained channel state feedback. IEEE Trans. Inf. Theory 2004, 50, 2038–2049. [Google Scholar] [CrossRef]
- Shannon, C.E. Geometrische Deutung einiger Ergebnisse bei der Berechnung der Kanalkapazität. Nachrichtentechnische Z. 1957, 10, 1–4, English version in Claude Elwood Shannon: Collected Papers; Sloane, N.J.A., Wyner, A.D., Eds.; IEEE Press: Piscataway, NJ, USA, 1993; pp. 259–264. [Google Scholar]
- Farmanbar, H.; Khandani, A.K. Precoding for the AWGN channel with discrete interference. IEEE Trans. Inf. Theory 2009, 55, 4019–4032. [Google Scholar] [CrossRef][Green Version]
- Wachsmann, U.; Fischer, R.; Huber, J. Multilevel codes: Theoretical concepts and practical design rules. IEEE Trans. Inf. Theory 1999, 45, 1361–1391. [Google Scholar] [CrossRef]
- Stolte, N. Rekursive Codes mit der Plotkin-Konstruktion und ihre Decodierung. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2002. [Google Scholar]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Seidl, M.; Schenk, A.; Stierstorfer, C.; Huber, J.B. Polar-coded modulation. IEEE Trans. Commun. 2013, 61, 4108–4119. [Google Scholar] [CrossRef]
- Honda, J.; Yamamoto, H. Polar coding Without alphabet extension for asymmetric models. IEEE Trans. Inf. Theory 2013, 59, 7829–7838. [Google Scholar] [CrossRef]
- Runge, C.; Wiegart, T.; Lentner, D.; Prinz, T. Multilevel binary polar-coded modulation achieving the capacity of asymmetric channels. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Espoo, Finland, 26 June–1 July 2022; pp. 2595–2600. [Google Scholar] [CrossRef]
- Parthasarathy, K.R. Extreme points of the convex set of joint probability distributions with fixed marginals. Proc. Math. Sci 2007, 117, 505–515. [Google Scholar] [CrossRef]
- Nadkarni, M.G.; Navada, K.G. On the number of extreme measures with fixed marginals. arXiv 2008, arXiv:math/0806.1214. [Google Scholar] [CrossRef]
- Farmanbar, H.; Gharan, S.O.; Khandani, A.K. Channel code design with causal side information at the encoder. Eur. Trans. Telecommun. 2010, 21, 337–351. [Google Scholar] [CrossRef]
- Birkhoff, G. Three observations on linear algebra. Univ. Nac. Tucumán. Revista A 1946, 5, 147–151. [Google Scholar]
- Wolfowitz, J. Coding Theorems of Information Theory, 2nd ed.; Springer: Berlin, Germany, 1964. [Google Scholar]
- Kim, T.T.; Skoglund, M. On the Expected Rate of Slowly Fading Channels With Quantized Side Information. IEEE Trans. Commun. 2007, 55, 820–829. [Google Scholar] [CrossRef]
- Rosenzweig, A.; Steinberg, Y.; Shamai, S. On channels with partial channel state information at the transmitter. IEEE Trans. Inf. Theory 2005, 51, 1817–1830. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656, Reprinted in Claude Elwood Shannon: Collected Papers; Sloane, N.J.A.,Wyner, A.D., Eds.; IEEE Press: Piscataway, NJ, USA, 1993; pp. 5–83. [Google Scholar] [CrossRef]
- Goldsmith, A.J.; Varaiya, P.P. Capacity of fading channels with channel side information. IEEE Trans. Inf. Theory 1997, 43, 1986–1992. [Google Scholar] [CrossRef]
- Abou-Faycal, I.; Trott, M.; Shamai, S. The capacity of discrete-time memoryless Rayleigh-fading channels. IEEE Trans. Inf. Theory 2001, 47, 1290–1301. [Google Scholar] [CrossRef]
- Lapidoth, A.; Moser, S.M. Capacity bounds via duality with applications to multiple-antenna systems on flat fading channels. IEEE Trans. Inf. Theory 2003, 49, 2426–2467. [Google Scholar] [CrossRef]
- Taricco, G.; Elia, M. Capacity of fading channel with no side information. Elec. Lett. 1997, 33, 1368–1370. [Google Scholar] [CrossRef]
- Marzetta, T.L.; Hochwald, B.M. Capacity of a mobile multiple-antenna communication link in Rayleigh flat fading. IEEE Trans. Inf. Theory 1999, 45, 139–157. [Google Scholar] [CrossRef]
- Zheng, L.; Tse, D. Communication on the Grassmann manifold: A geometric approach to the noncoherent multiple-antenna channel. IEEE Trans. Inf. Theory 2002, 48, 359–383. [Google Scholar] [CrossRef]
- Gursoy, M.; Poor, H.; Verdu, S. The noncoherent Rician fading channel—part I: Structure of the capacity-achieving input. IEEE Trans. Wireless Commun. 2005, 4, 2193–2206. [Google Scholar] [CrossRef]
- Chowdhury, M.; Goldsmith, A. Capacity of block Rayleigh fading channels without CSI. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1884–1888. [Google Scholar] [CrossRef]
- Goldsmith, A.J.; Médard, M. Capacity of time-varying channels with causal channel side information. IEEE Trans. Inf. Theory 2007, 53, 881–899. [Google Scholar] [CrossRef][Green Version]
- Jelinek, F. Indecomposable channels with side information at the transmitter. Inf. Control 1965, 8, 36–55. [Google Scholar] [CrossRef]
- Das, A.; Narayan, P. Capacities of time-varying multiple-access channels with side information. IEEE Trans. Inf. Theory 2002, 48, 4–25. [Google Scholar] [CrossRef]
- Van Veen, B.; Buckley, K. Beamforming: A versatile approach to spatial filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Liaskos, C.; Nie, S.; Tsioliaridou, A.; Pitsillides, A.; Ioannidis, S.; Akyildiz, I. A new wireless communication paradigm through software-controlled metasurfaces. IEEE Commun. Mag. 2018, 56, 162–169. [Google Scholar] [CrossRef]
- Renzo, M.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come. J. Wirel. Com. Netw. 2019, 2019, 129. [Google Scholar] [CrossRef]
- Thangaraj, A.; Kramer, G.; Böcherer, G. Capacity bounds for discrete-time, amplitude-constrained, additive white Gaussian noise channels. IEEE Trans. Inf. Theory 2017, 63, 4172–4182. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Channels; Akadémiai Kiadó: Budapest, Hungary, 1981. [Google Scholar]
- Cody, W.J.; Thacher, H.C., Jr. Rational Chebyshev approximations for the exponential integral E1(x). Math. Comp. 1968, 22, 641–649. [Google Scholar]
- Nantomah, K. On Some Bounds for the Exponential Integral Function. J. Nepal Mathem. Soc. 2021, 4, 28–34. [Google Scholar] [CrossRef]
- Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K.; Sharif, B.S. Solutions to integrals involving the Marcum Q-function and applications. IEEE Signal Proc. Lett. 2015, 22, 1752–1756. [Google Scholar] [CrossRef]
- Neeser, F.; Massey, J. Proper complex random processes with applications to information theory. IEEE Trans. Inf. Theory 1993, 39, 1293–1302. [Google Scholar] [CrossRef]
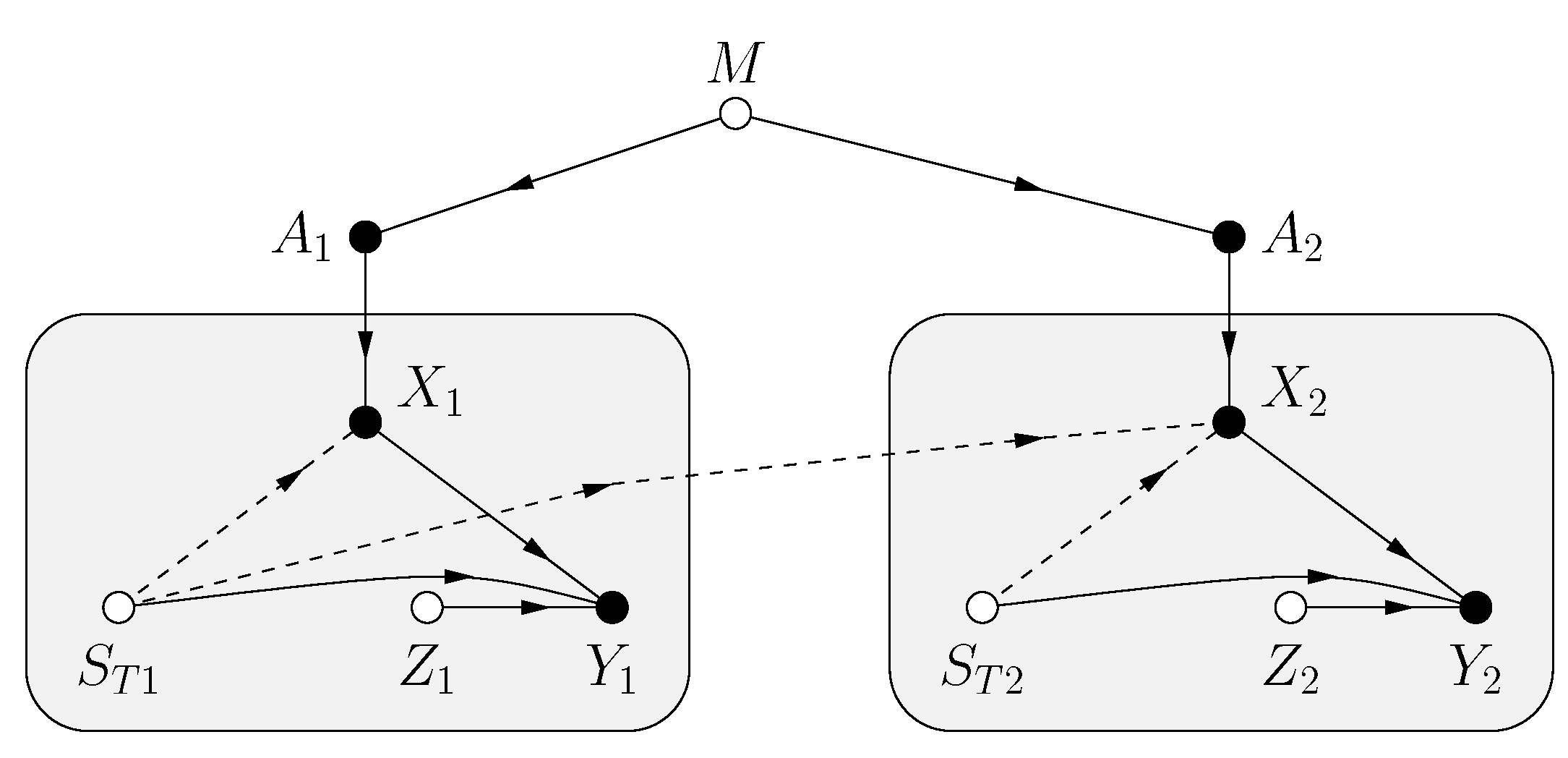
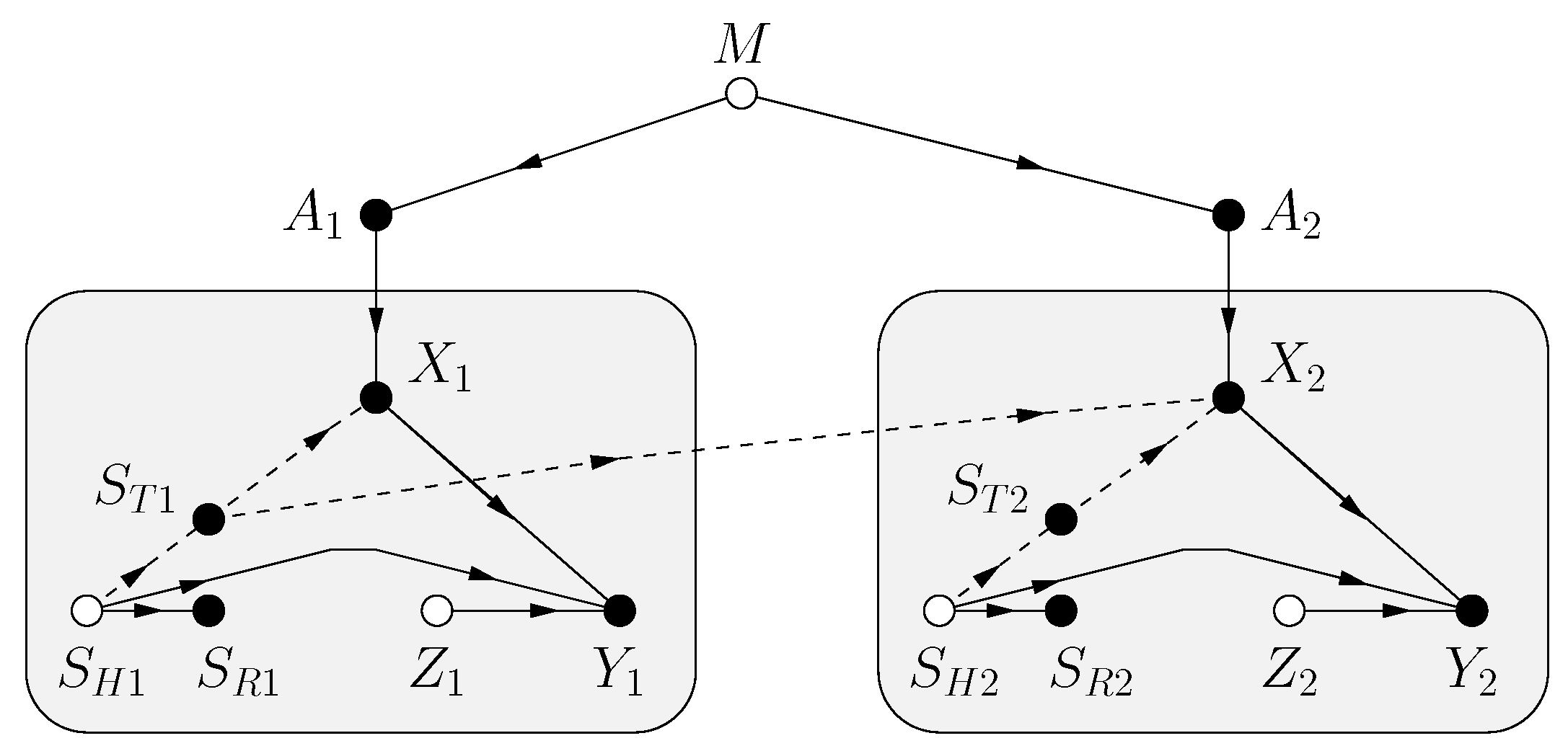
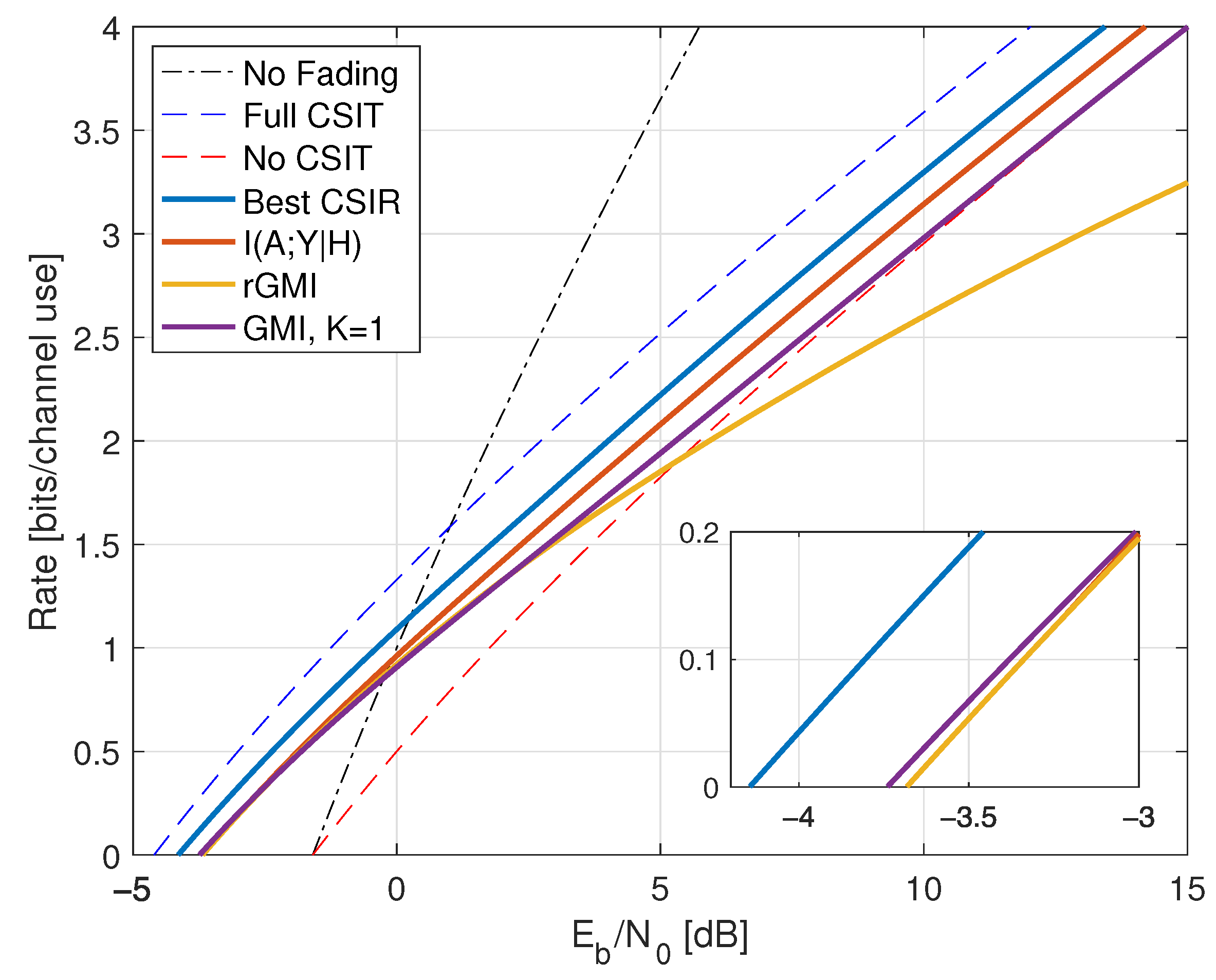
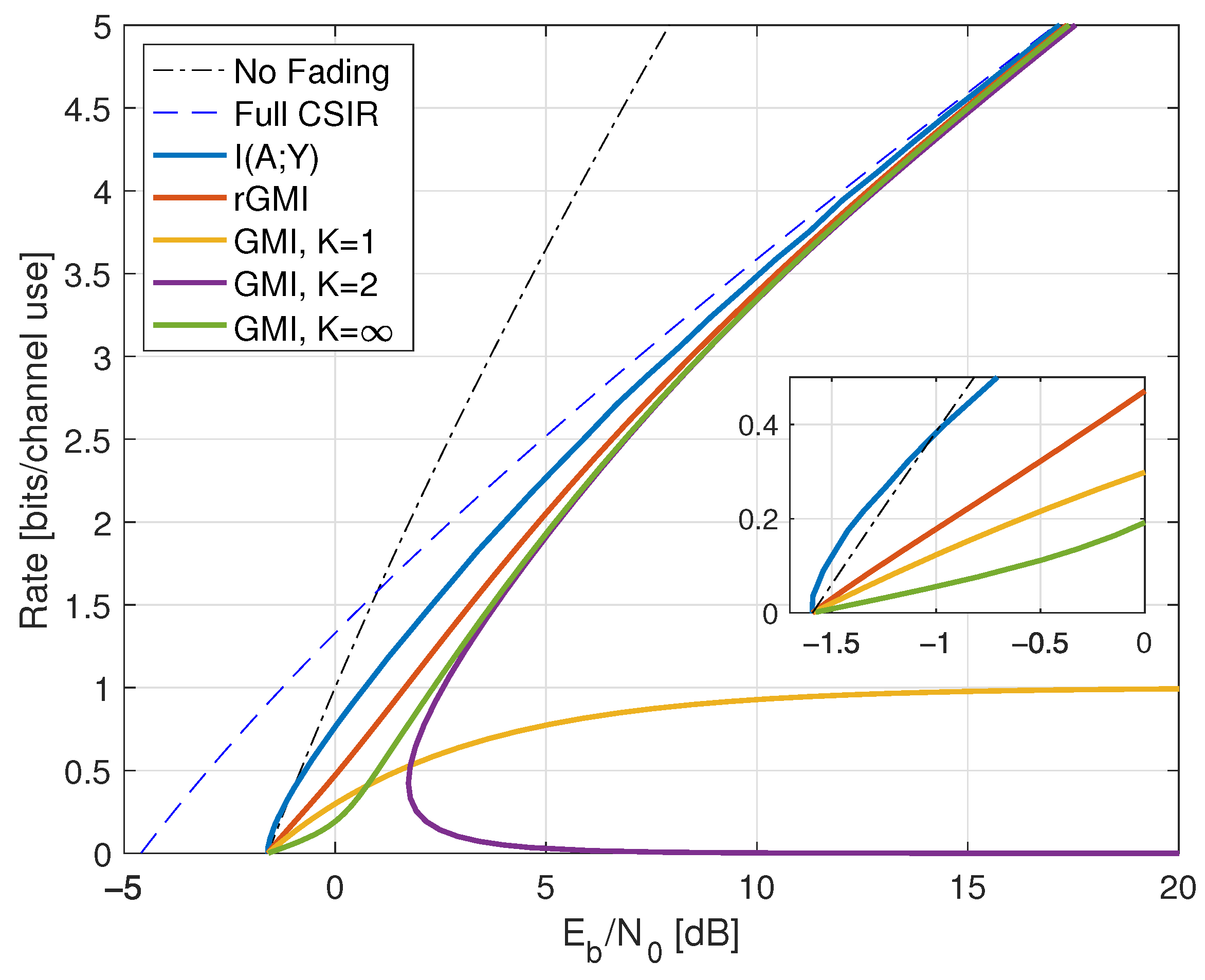
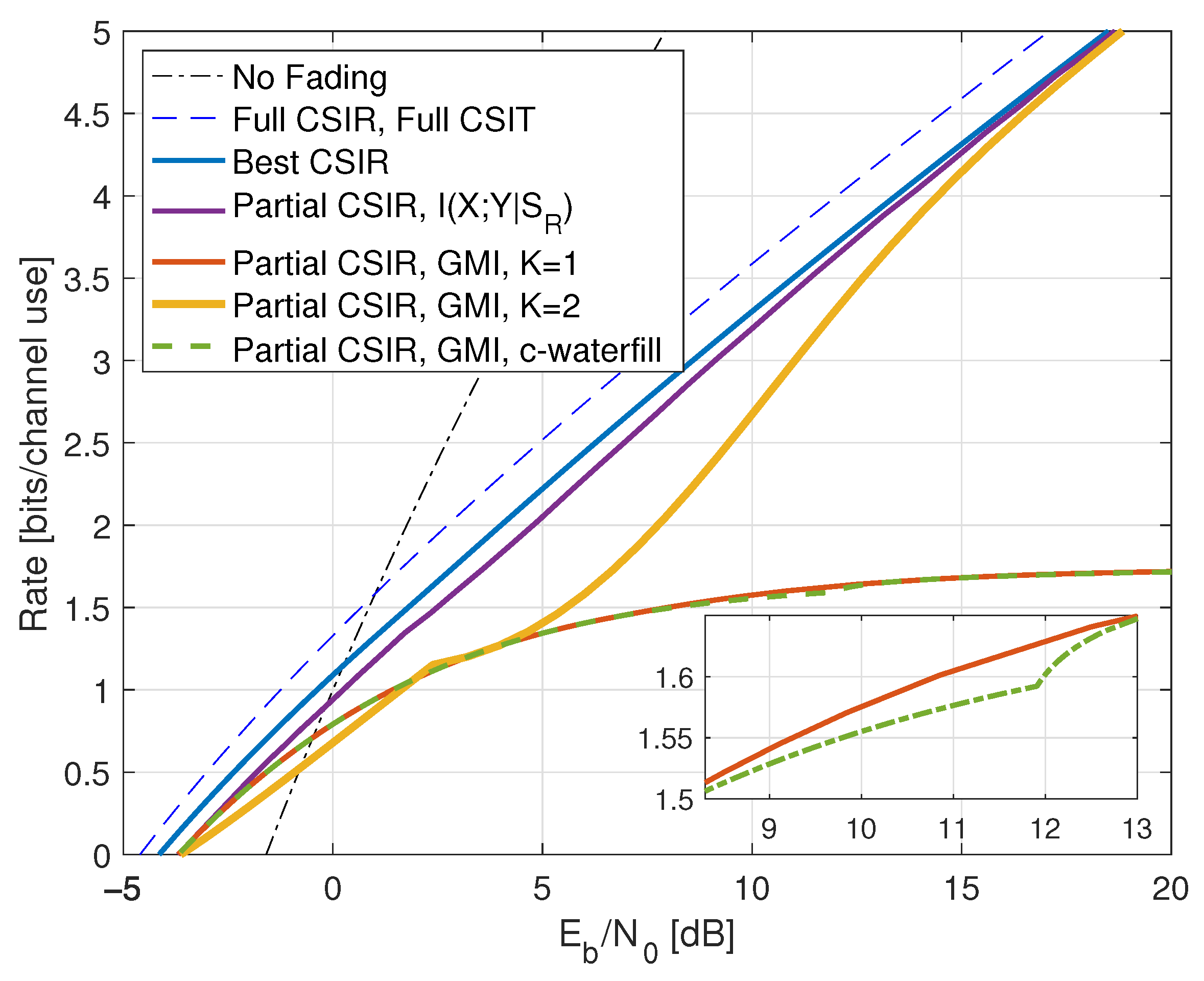
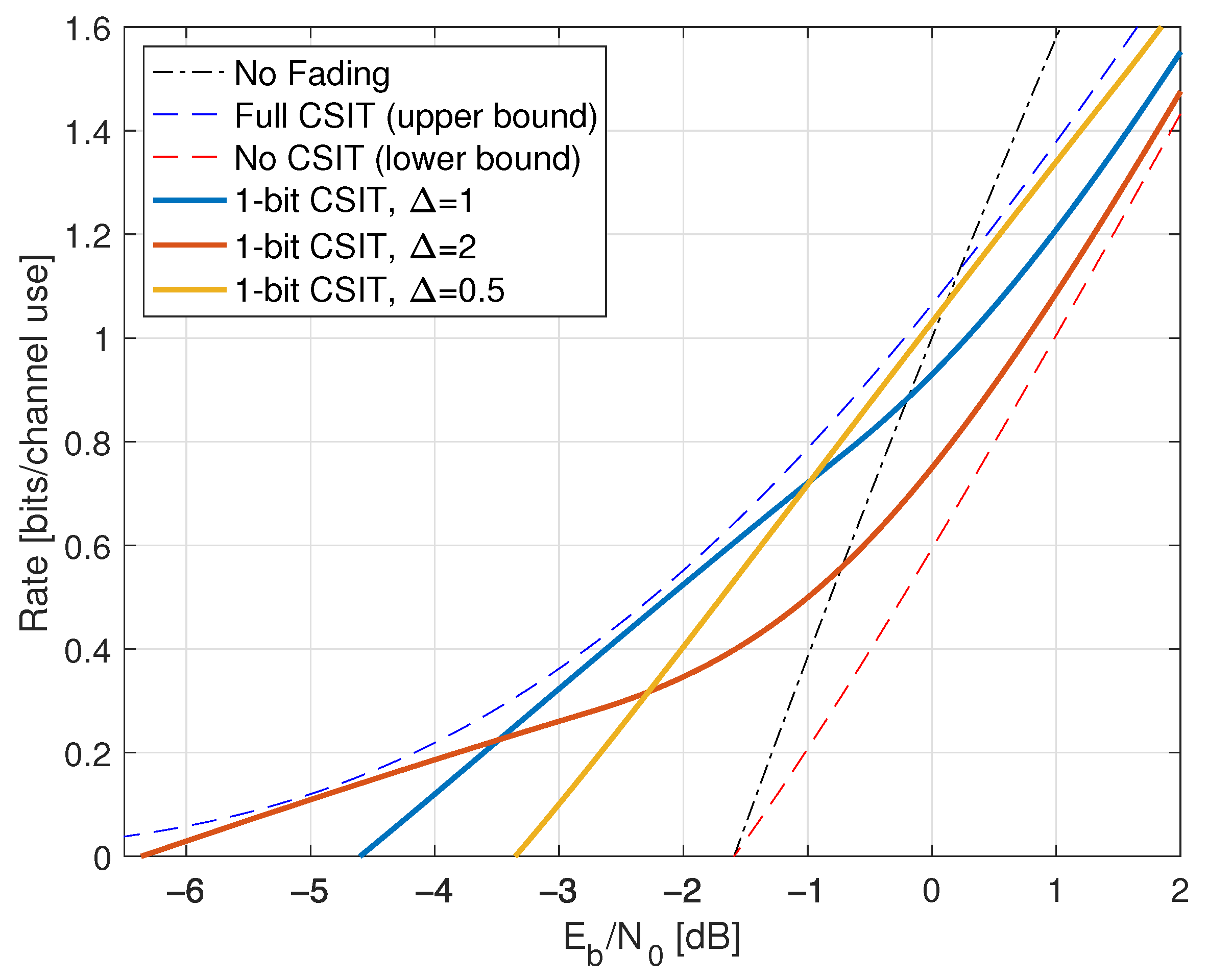



| CSIR | |||
|---|---|---|---|
| Full | Partial/No | ||
| CSIT | Full | Section 6.3 | Section 6.5 |
| @R | Section 6.3 | Section 6.6 | |
| Partial/No | Section 6.4 | Section 6.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kramer, G. Information Rates for Channels with Fading, Side Information and Adaptive Codewords. Entropy 2023, 25, 728. https://doi.org/10.3390/e25050728
Kramer G. Information Rates for Channels with Fading, Side Information and Adaptive Codewords. Entropy. 2023; 25(5):728. https://doi.org/10.3390/e25050728
Chicago/Turabian StyleKramer, Gerhard. 2023. "Information Rates for Channels with Fading, Side Information and Adaptive Codewords" Entropy 25, no. 5: 728. https://doi.org/10.3390/e25050728
APA StyleKramer, G. (2023). Information Rates for Channels with Fading, Side Information and Adaptive Codewords. Entropy, 25(5), 728. https://doi.org/10.3390/e25050728






