Uniform Error Estimates of the Finite Element Method for the Navier–Stokes Equations in
Abstract
1. Introduction
2. Functional Settings
3. Finite Element Approximation
4. Uniform Error Estimates
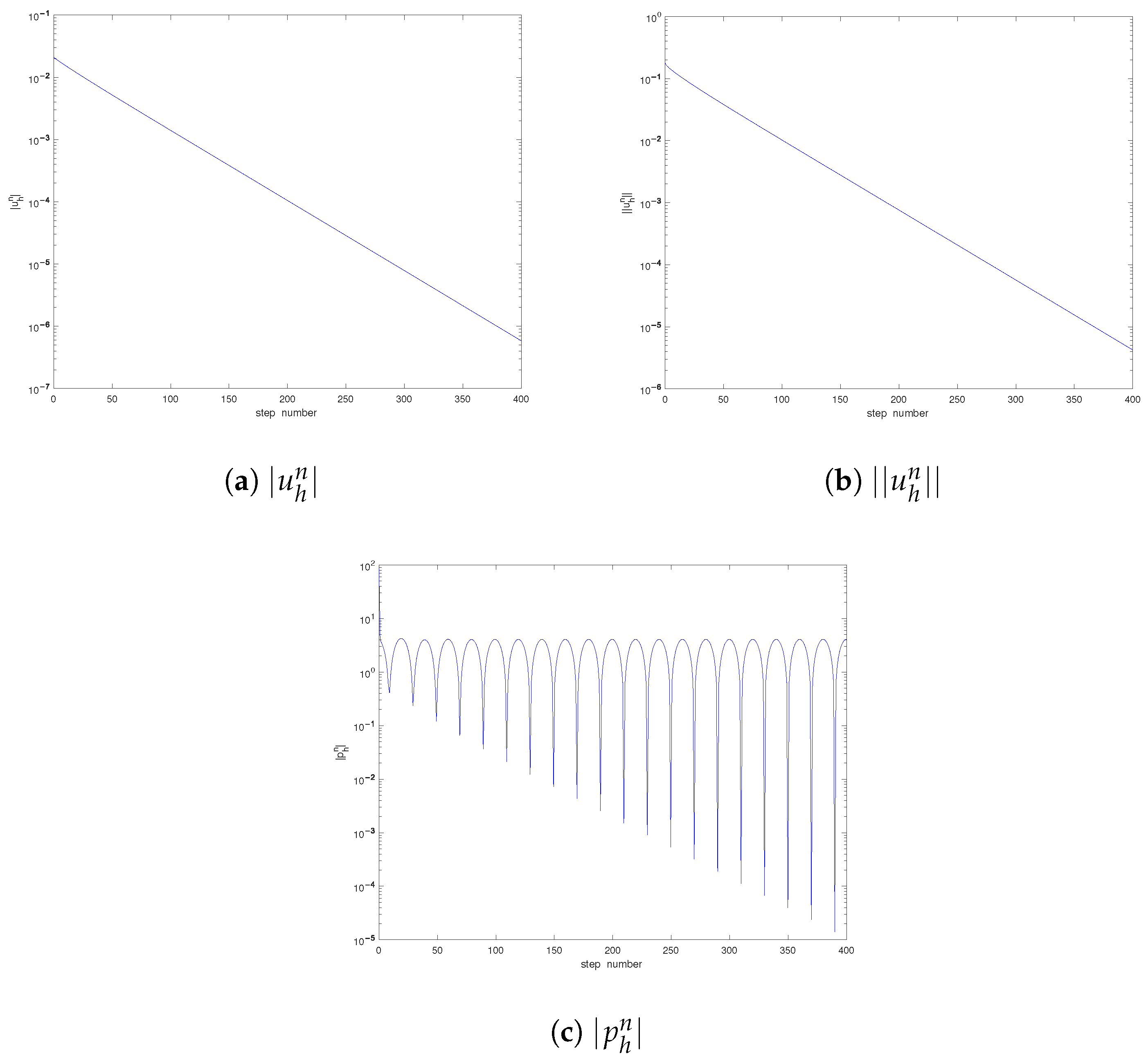
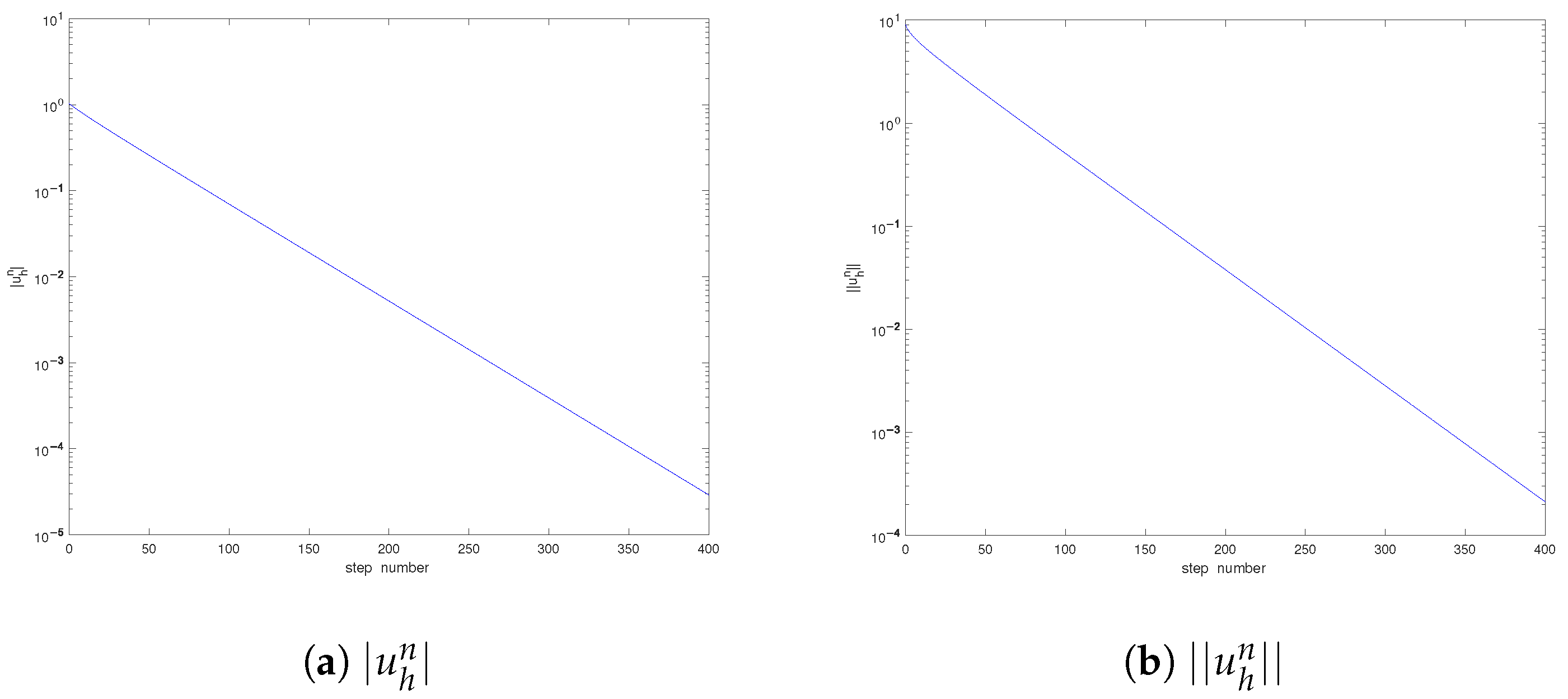
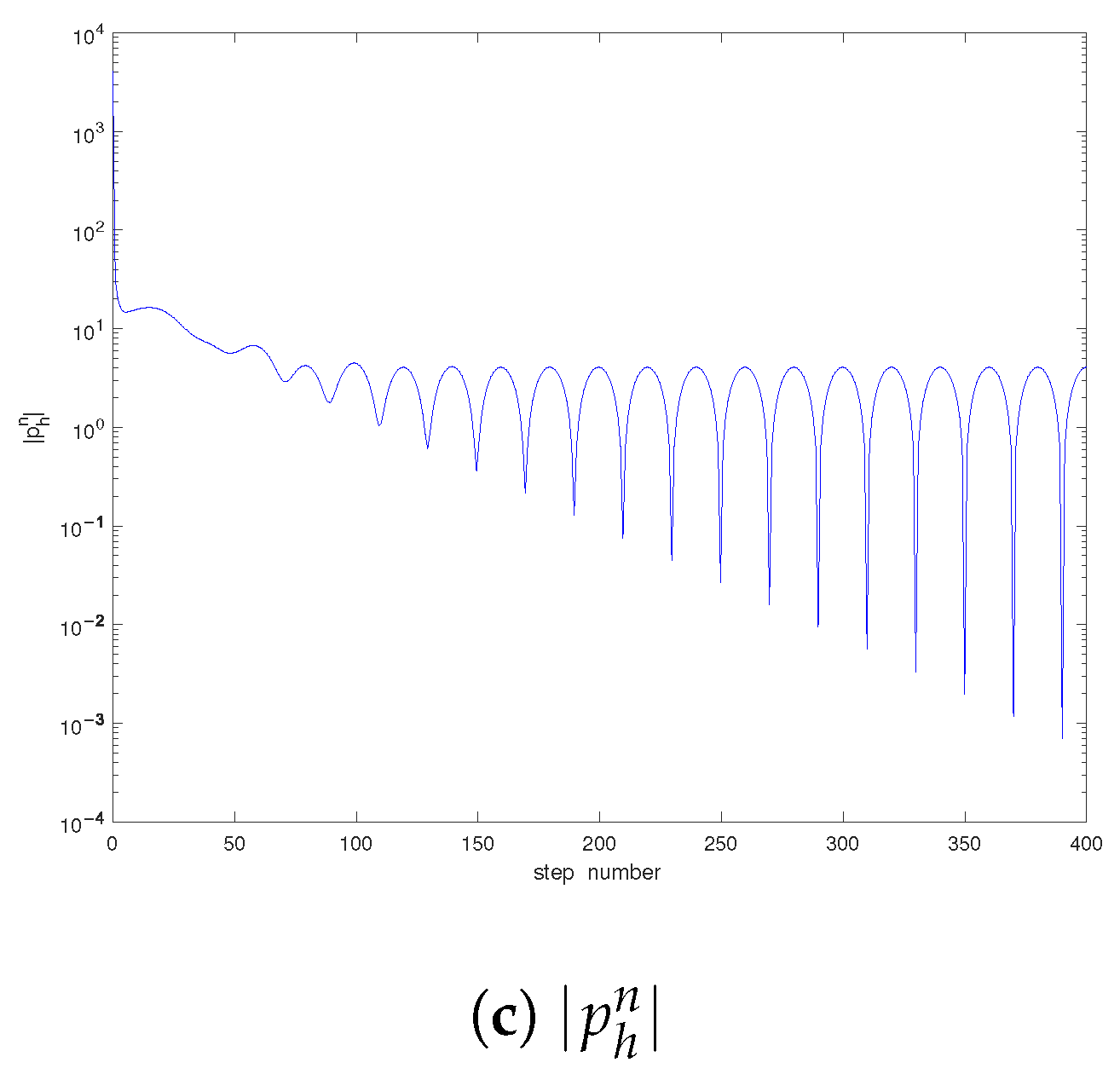
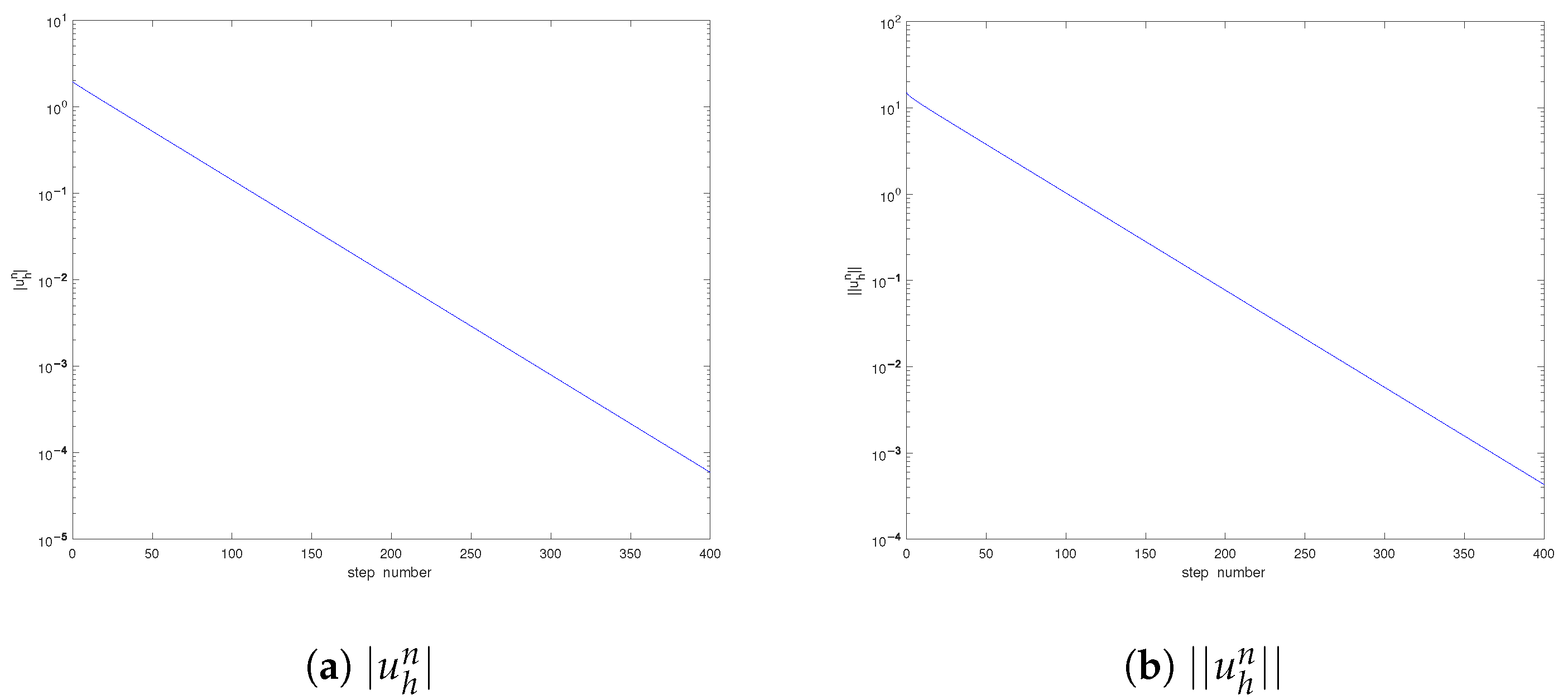
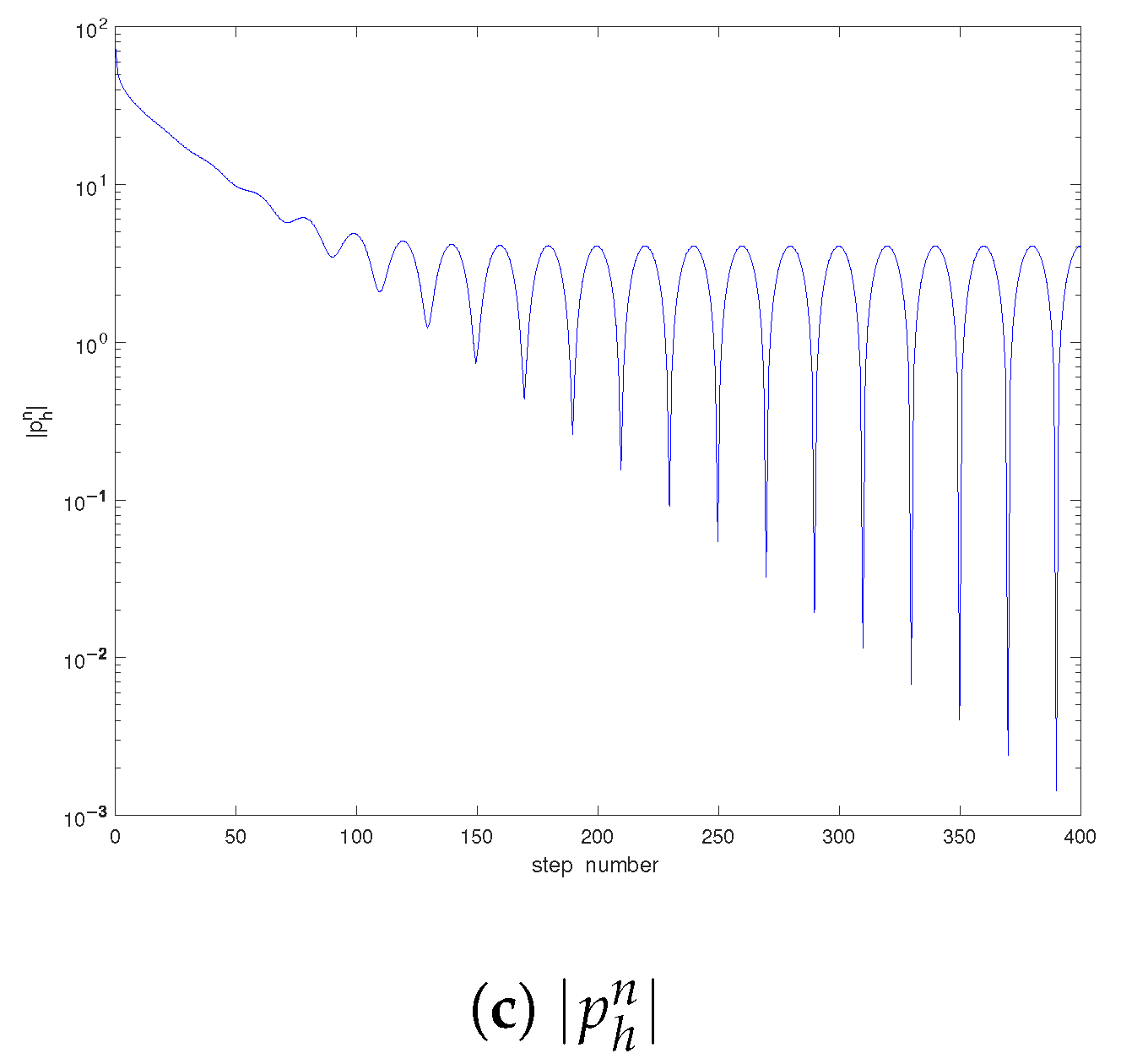
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Girault, V.; Raviart, P. Finite Element Approximation of the Navier-Stokes Equations; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Heywood, J.; Rannacher, R. Finite element approximation of the nonstationary Navier-Stokes problem. I. Regularity of solutions and second-order error estimates for spatial discretization. SIAM J. Numer. Anal. 1982, 19, 275–311. [Google Scholar] [CrossRef]
- Heywood, J.; Rannacher, R. Finite element approximation of the nonstationary Navier-Stokes problem III. Smoothing property and higher order error estimates for spatial discretization. SIAM J. Numer. Anal. 1988, 25, 489–512. [Google Scholar] [CrossRef]
- Heywood, J.; Rannacher, R. Finite-element approximation of the nonstationary Navier-Stokes problem. Part IV: Error analysis for second-order time discretization. SIAM J. Numer. Anal. 1990, 27, 353–384. [Google Scholar] [CrossRef]
- Sherwin, S.; Ainsworth, M. Unsteady Navier-Stokes solvers using hybrid spectral/hp element methods. Appl. Numer. Math. 2000, 33, 357–363. [Google Scholar] [CrossRef]
- Xie, C.; Wang, K. Viscosity explicit analysis for finite element methods of time-dependent Navier-Stokes equations. J. Comput. Appl. Math. 2021, 392, 113481. [Google Scholar] [CrossRef]
- Xie, C.; Wang, K. Uniform finite element error estimates with power-type asymptotic constants for unsteady Navier-Stokes equations. Entropy 2022, 24, 948. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.; Süli, E. Approximation of the global attractor for the incompressible Navier-Stokes equations. IMA J. Numer. Anal. 2000, 20, 633–667. [Google Scholar] [CrossRef]
- Chen, H.; Ewing, R.; Lazarov, R. Superconvergence of mixed finite element methods for parabolic problems with nonsmooth initial data. Numer. Math. 1998, 78, 495–521. [Google Scholar] [CrossRef]
- Luskin, M.; Rannacher, R. On the smoothing property of the Galerkin method for parabolic equations. SIAM J. Numer. Anal. 1982, 19, 93–113. [Google Scholar] [CrossRef]
- He, Y. The Euler implicit/explicit scheme for the 2D time-dependent Navier-Stokes equations with smooth or non-smooth initial data. Math. Comput. 2008, 77, 2097–2124. [Google Scholar] [CrossRef]
- He, Y. Stability and error analysis for spectral Galerkin method for the Navier-Stokes equations with L2 initial data. Numer. Methods Part. Diff. Equ. 2008, 24, 79–103. [Google Scholar] [CrossRef]
- He, Y.; Huang, P.; Feng, X. H2-stability of the first order fully discrete schemes for the time-dependent Navier-Stokes equations. J. Sci. Comput. 2015, 62, 230–264. [Google Scholar] [CrossRef]
- He, Y.; Huang, P.; Li, J. H2-stability of some second order fully discrete schemes for the Navier-Stokes equations. Discret. Contin. Dyn. Sys. Ser. B 2019, 24, 2745–2780. [Google Scholar]
- Zhang, T.; Qian, Y. Stability analysis of several first order schemes for the Oldroyd model with smooth and nonsmooth initial data. Numer. Methods Partial Differ. Equ. 2018, 34, 2180–2216. [Google Scholar] [CrossRef]
- Yang, J.; Liang, H.; Zhang, T. The Crank-Nicolson/explicit scheme for the natural convection equations with nonsmooth initial data. Adv. Appl. Math. Mech. 2020, 12, 1481–1519. [Google Scholar]
- Jin, J.; Zhang, T.; Li, J. H2-stability of the first order Galerkin method for the Boussinesq equations with smooth and non-smooth initial data. Comput. Math. Appl. 2018, 75, 248–288. [Google Scholar] [CrossRef]
- Ju, N. On the global stability of a temporal discretization scheme for the Navier-Stokes equations. IMA J. Numer. Anal. 2022, 22, 577–597. [Google Scholar] [CrossRef]
- Tone, F.; Wirosoetisno, D. On the long-time stability of the implicit Euler scheme for the two-dimensional Navier-Stokes equations. SIAM J. Numer. Anal. 2006, 44, 29–40. [Google Scholar] [CrossRef]
- Temam, R. Navier-Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2001. [Google Scholar]
- Lions, J.; Prodi, G. Un théorème d’ existence et d’unicité dans les équations de Navier-Stokes en dimension 2. C. R. Acad. Sci. 1959, 248, 3519–3521. [Google Scholar]
- Hodge, Z. The Finite Element Method for Elliptic Problems; SIAM: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Cox, S.; Matthews, P. Exponential time differencing for stiff systems. J. Comput. Phys. 2002, 176, 430–455. [Google Scholar] [CrossRef]
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| 0.0000818 |
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| 0.0000591 |
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| 0.0000528 |
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
| h | Rate | Rate | Rate | |||
|---|---|---|---|---|---|---|
| − | − | − | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Wang, K.; Feng, X.
Uniform Error Estimates of the Finite Element Method for the Navier–Stokes Equations in
Ren S, Wang K, Feng X.
Uniform Error Estimates of the Finite Element Method for the Navier–Stokes Equations in
Ren, Shuyan, Kun Wang, and Xinlong Feng.
2023. "Uniform Error Estimates of the Finite Element Method for the Navier–Stokes Equations in
Ren, S., Wang, K., & Feng, X.
(2023). Uniform Error Estimates of the Finite Element Method for the Navier–Stokes Equations in






