Acoustic Emissions in Rock Deformation and Failure: New Insights from Q-Statistical Analysis
Abstract
1. Introduction and Motivations
2. Experimental Setup and Data Analysis
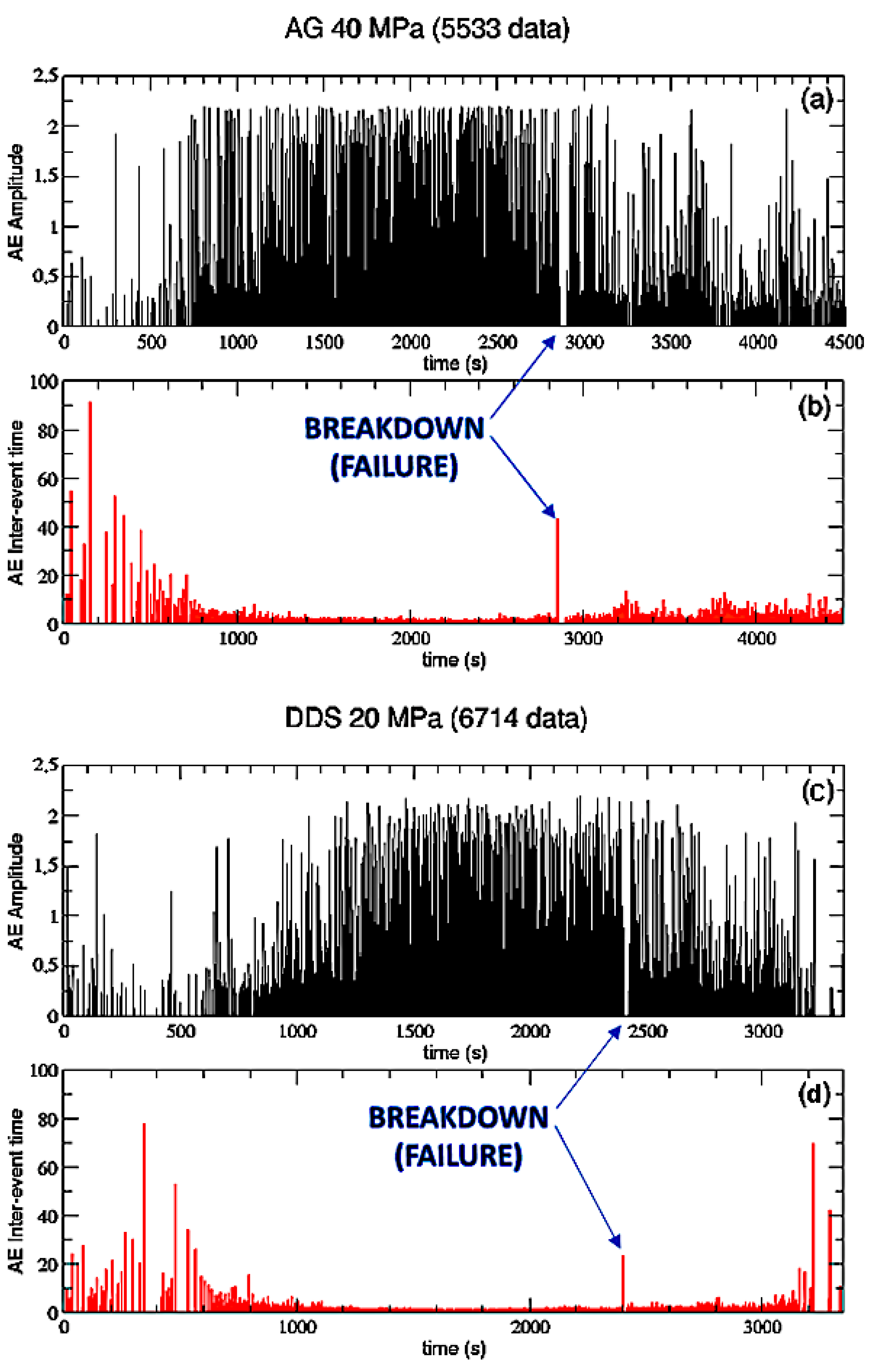
2.1. AE Amplitudes
- -
- From the beginning to 30% tB;
- -
- From 30% tB to 70% tB;
- -
- From 70% tB to breakdown;
- -
- After breakdown.
- (i)
- Events in the first time interval (within 30% tB) are always too few to give consistent distributions, regardless of the material;
- (ii)
- Distributions before and after failure are quite similar, again regardless of the material, with an initial sudden increase, a peak and a slow decrease for high amplitudes;
- (iii)
- Distributions after failure are more peaked for both AG and DDS.
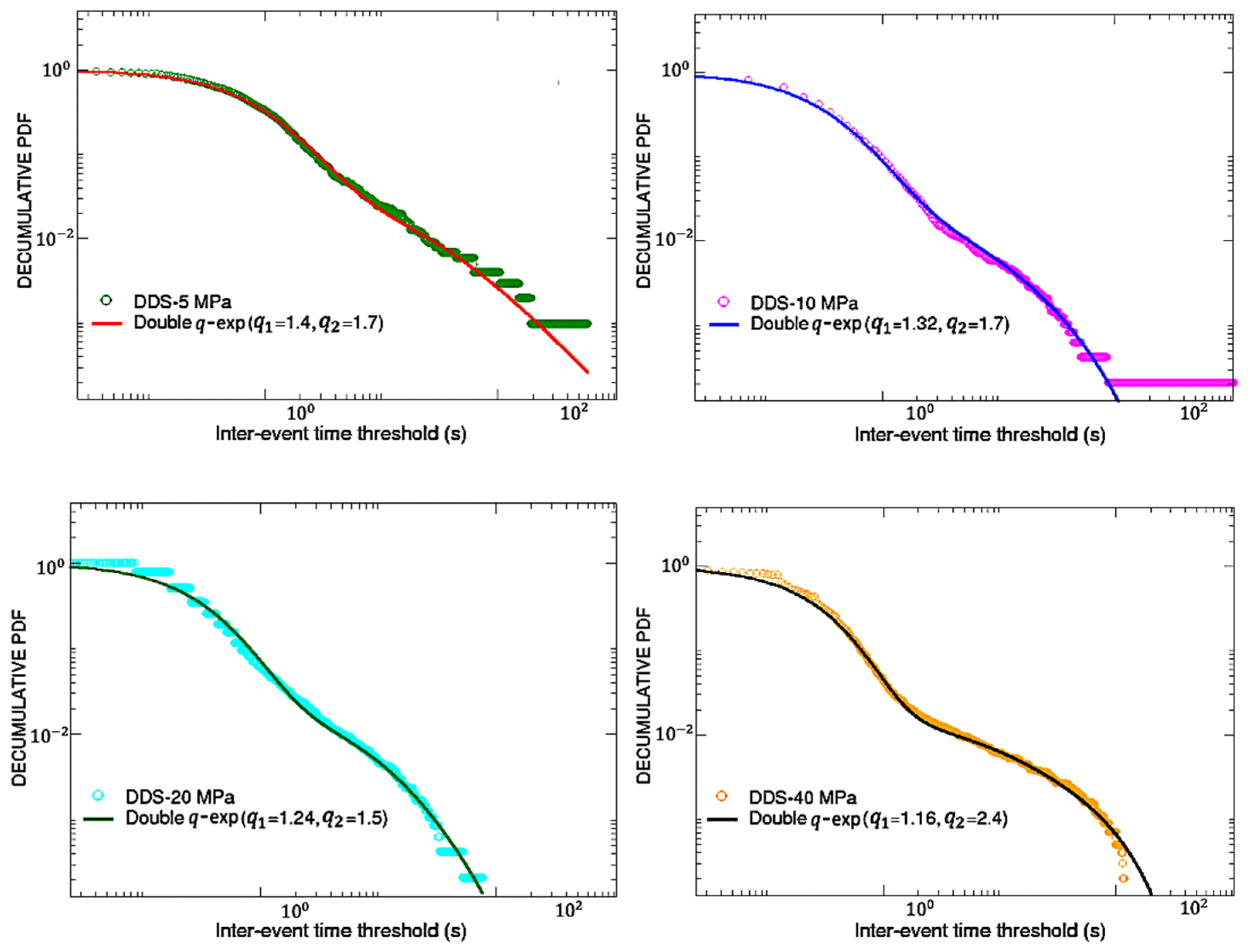
2.2. AE Inter-Event Times
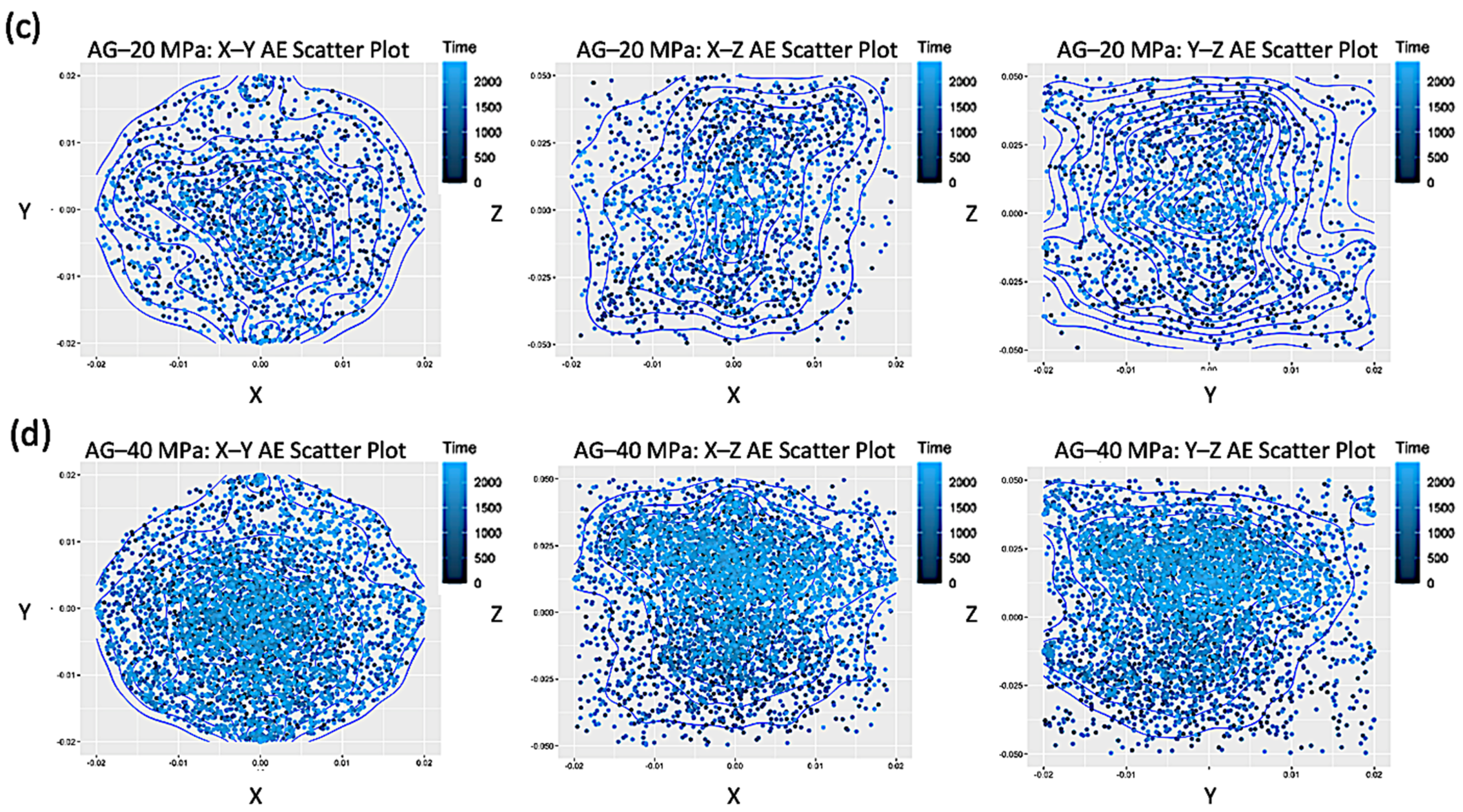
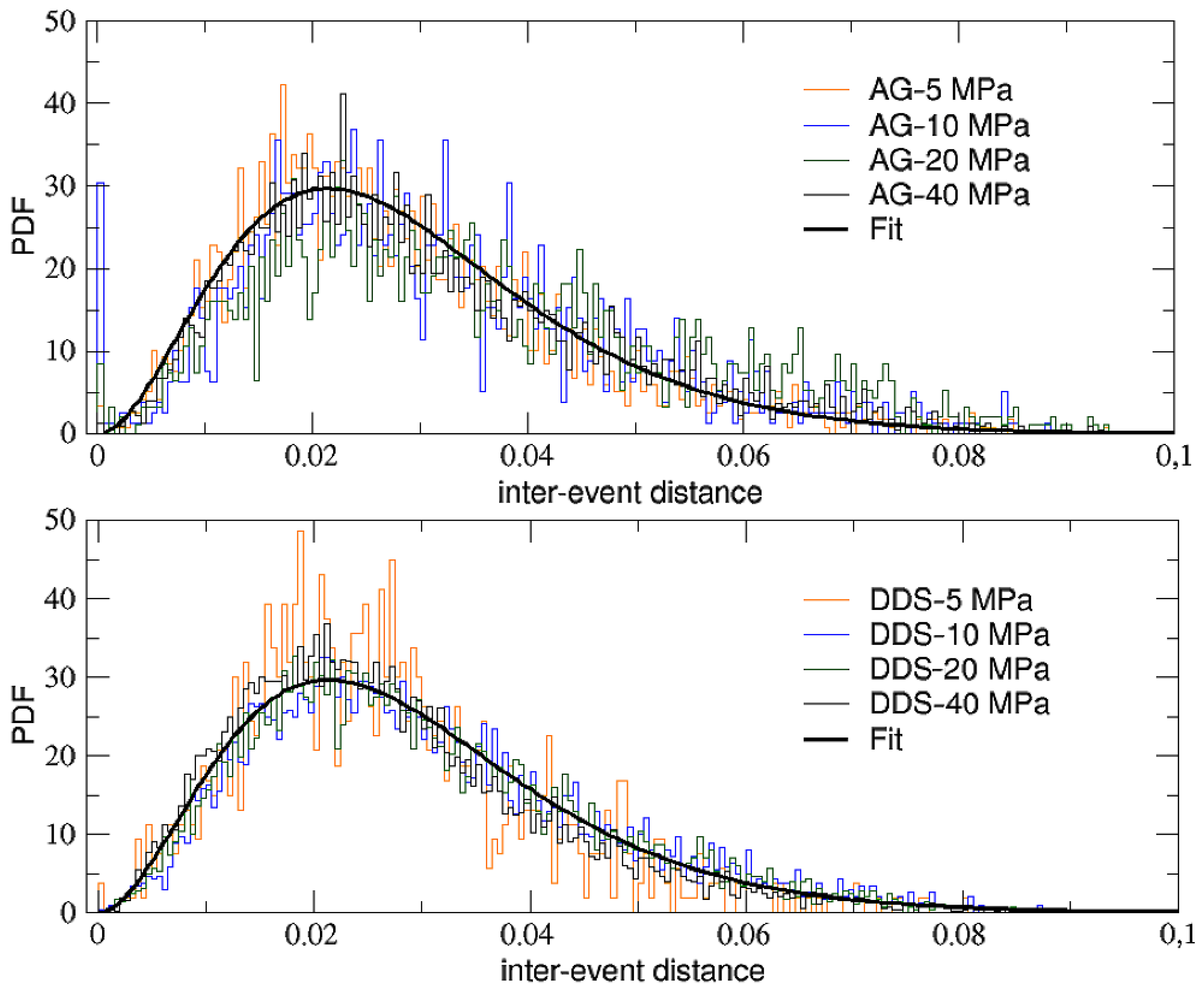
2.3. AE Positions and Inter-Event Distances
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Acoustic Emissions |
| DDS | Darley Dale Sandstone |
| AG | Alzo Granite |
| 3D | Three dimensional |
| Probability density function | |
| Lin-Lin | Linear-Linear |
| Log-Lin | Logarithmic-Linear |
| Log-Log | Logarithmic-Logarithmic |
References
- Stavrakas, I.; Triantis, D.; Kourkoulis, S.; Pasiou, E.; Dakanali, I. Acoustic Emission Analysis of Cement Mortar Specimens During Three Point Bending Tests. Lat. Am. J. Solids Struct. 2016, 13, 2283. [Google Scholar] [CrossRef]
- Stavrakas, I. Acoustic emissions and pressure stimulated currents experimental techniques used to verify Kaiser effect during compression tests of Dionysos marble. Fract. Struct. Integr. 2017, 40, 32. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Hloupis, G.; Triantis, D.; Vallianatos, F. Electrical and Acoustic Emissions in cement mortar beams subjected to mechanical loading up to fracture. Eng. Fail. Anal. 2013, 35, 454–461. [Google Scholar] [CrossRef]
- Kyriazopoulos, A.; Anastasiadis, C.; Triantis, D.; Vallianatos, F. Monitoring of Acoustic Emissions on three-point bending experiments in cement mortar beams in the light of non-extensive statistical physics. In Proceedings of the 1st International Conference of the Greek Society of Experimental Mechanics of Materials, Athens, Greece, 10–12 May 2018; p. 77. [Google Scholar]
- Greco, A.; Tsallis, C.; Rapisarda, A.; Pluchino, A.; Fichera, G.; Contrafatto, L. Acoustic emissions in compression of building materials: Q-statistics enables the anticipation of the breakdown point. Eur. Phys. J. Speéc. Top. 2020, 229, 841–849. [Google Scholar] [CrossRef]
- Triantis, D.; Loukidis, A.; Stavrakas, I.; Pasiou, E.D.; Kourkoulis, S.K. Attenuation of the Acoustic Activity in Cement Beams under Constant Bending Load Closely Approaching the Fracture Load. Foundations 2022, 2, 590–606. [Google Scholar] [CrossRef]
- Loukidis, A.; Stavrakas, I.; Triantis, D. Non-Extensive Statistical Mechanics in Acoustic Emissions: Detection of Upcoming Fracture in Rock Materials. Appl. Sci. 2023, 13, 3249. [Google Scholar] [CrossRef]
- Zang, A.; Wagner, F.C.; Stanchits, S.; Dresen, G.; Andresen, R.; Haidekker, M.A. Source analysis of acoustic emissions in Aue granite cores under symmetric and asymmetric compressive loads. Geophys. J. Int. 1998, 135, 1113–1130. [Google Scholar] [CrossRef]
- Burlini, L.; Vinciguerra, S.; Di Toro, G.; DE Natale, G.; Meredith, P.; Burg, J.-P. Seismicity preceding volcanic eruptions: New experimental insights. Geology 2007, 35, 183–186. [Google Scholar] [CrossRef]
- Benson, P.M.; Thompson, B.D.; Meredith, P.G.; Vinciguerra, S.; Young, R.P. Imaging slow failure in triaxially deformed Etna basalt using 3D acoustic-emission location and X-ray computed tomography. Geophys. Res. Lett. 2007, 34, L03303. [Google Scholar] [CrossRef]
- Fazio, M.; Benson, P.; Vinciguerra, S. On the generation mechanisms of fluid-driven seismic signals related to volcano-tectonics. Geophys. Res. Lett. 2017, 44, 734–742. [Google Scholar] [CrossRef]
- Lockner, D.A.; Byerlee, J.D.; Kuksenko, V.; Ponomarev, A.; Sidorin, A. Quasi-static fault growth and shear fracture energy in granite. Nature 1991, 350, 39–42. [Google Scholar] [CrossRef]
- Hanks, T.C. Small earthquakes, tectonic forces. Science 1992, 256, 1430–1432. [Google Scholar] [CrossRef] [PubMed]
- Hatton, C.G.; Main, I.G.; Meredith, P.G. Non-universal scaling of fracture length and opening displacement. Nature 1994, 367, 160–162. [Google Scholar] [CrossRef]
- Hudson, J.A.; Kennett, B.L.N. Quantitative Seismology (two vols) K. Aki and P. G. Richards, W.H. Freeman, San Francisco 934 pp. $35.00 (£20.70 per volume). Geophys. J. Int. 1981, 64, 802–806. [Google Scholar] [CrossRef]
- King, T.; Vinciguerra, S.; Burgess, J.; Benson, P.; De Siena, L. Source Mechanisms of Laboratory Earthquakes during Fault Nucleation and Formation. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021059. [Google Scholar] [CrossRef]
- Ko, J.; Jeong, S. A Study on Rock Mass Classifications and Tunnel Support Systems in Unconsolidated Sedimentary Rock. Sustainability 2017, 9, 573. [Google Scholar] [CrossRef]
- Ma, H.; Wang, J.; Man, K.; Chen, L.; Gong, Q.; Zhao, X. Excavation of underground research laboratory ramp in granite using tunnel boring machine: Feasibility study. J. Rock Mech. Geotech. Eng. 2020, 12, 1201–1213. [Google Scholar] [CrossRef]
- Wang, M.; Zhu, Z.; Xiao, J. An Experimental Study on Deformation Fractures of Fissured Rock around Tunnels in True Triaxial Unloads. Adv. Mater. Sci. Eng. 2015, 2015, 98284. [Google Scholar] [CrossRef]
- Vrakas, A.; Dong, W.; Anagnostou, G. Elasticic deformation modulus for estimating convergence when tunnelling through squeezing ground. Geotechnique 2018, 68, 713–728. [Google Scholar] [CrossRef]
- Haimson, B.; Chang, C. A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 285–296. [Google Scholar] [CrossRef]
- Bai, Q.; Zhang, C.; Young, R.P. Using true-triaxial stress path to simulate excavation-induced rock damage: A case study. Int. J. Coal Sci. Technol. 2022, 9, 49. [Google Scholar] [CrossRef]
- Benson, P.M.; Austria, D.C.; Gehne, S.; Butcher, E.; Harnett, C.E.; Fazio, M.; Rowley, P.; Tomas, R. Laboratory simulations of fluid-induced seismicity, hydraulic fracture, and fluid flow. Géoméch. Energy Environ. 2019, 24, 100169. [Google Scholar] [CrossRef]
- Tsallis, C.; Anteneodo, C.; Borland, L.; Osorio, R. Nonextensive statistical mechanics and economics. Phys. A Stat. Mech. Its Appl. 2003, 324, 89–100. [Google Scholar] [CrossRef]
- Wong, C.; Wilk, G.; Cirto, L.; Tsallis, C. From QCD-based hard-scattering to nonextensive statistical mechanical descriptions of transverse momentum spectra in high-energy pp and pp¯ collisions. Phys. Rev. D 2015, 91, 114027. [Google Scholar] [CrossRef]
- Tsallis, C.; Tirnakli, U. Predicting COVID-19 Peaks around the World. Front. Phys. 2020, 8, 217. [Google Scholar] [CrossRef]
- Tsallis, C.; Bemski, G.; Mendes, R.S. Is re-association in folded proteins a case of nonextensivity? Phys. Lett. A 1999, 257, 93–98. [Google Scholar] [CrossRef]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann-Gibbs statistics to Tsallis statistics. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, G.; Tirnakli, U.; Borges, E.P.; Tsallis, C. Statistical characterization of the standard map. J. Stat. Mech. Theory Exp. 2017, 2017, 063403. [Google Scholar] [CrossRef]
- Ruiz, G.; Tirnakli, U.; Borges, E.; Tsallis, C. Statistical characterization of discrete conservative systems: The web map. Phys. Rev. E 2017, 96, 042158. [Google Scholar] [CrossRef]
- Bogachev, M.I.; Kayumov, A.; Bunde, A. Universal Internucleotide Statistics in Full Genomes: A Footprint of the DNA Structure and Packaging? PLoS ONE 2014, 9, e112534. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behaviour of fracture in triaxially deformed Etna basalt using acoustic emissions. Europhys. Lett. 2012, 97, 58002. [Google Scholar] [CrossRef]









| Sample | tB | tTOT | N* Events before Breakdown | Tot. N Events |
|---|---|---|---|---|
| AG-5 MPa | 2398 s | 3395 s | 2367 | 2751 |
| AG-10 MPa | 1767 s | 2445 s | 1577 | 1956 |
| AG-20 MPa | 2160 s | 2973 s | 1874 | 2367 |
| AG-40 MPa | 2857 s | 4566 s | 4419 | 5533 |
| DDS-5 MPa | 2400 s | 2540 s | 1067 | 1100 |
| DDS-10 MPa | 5808 s | 6248 s | 4802 | 5334 |
| DDS-20 MPa | 2409 s | 3348 s | 5760 | 6714 |
| DDS-40 MPa | 9710 s | 11,736 s | 10,659 | 11,696 |
| Sample | ||||||
|---|---|---|---|---|---|---|
| AG-5 MPa | 0.975 | 3.5 | 1.48 | 0.01 | 1.7 | 0.09 |
| AG-10 MPa | 0.98 | 2.0 | 1.32 | 0.02 | 2.5 | 0.19 |
| AG-20 MPa | 0.98 | 1.3 | 1.2 | 0.04 | 2.0 | 0.13 |
| AG-40 MPa | 0.983 | 2.6 | 1.16 | 0.017 | 1.4 | 0.12 |
| DDS-5 MPa | 0.975 | 1.5 | 1.4 | 0.0001 | 1.7 | 0.055 |
| DDS-10 MPa | 0.98 | 4.0 | 1.32 | 0.02 | 1.7 | 0.19 |
| DDS-20 MPa | 0.98 | 4.1 | 1.24 | 0.017 | 1.5 | 0.20 |
| DDS-40 MPa | 0.983 | 4.6 | 1.16 | 0.015 | 2.4 | 0.19 |
| Sample | |||
|---|---|---|---|
| AG-5 MPa | 1.48 | 0.76 | 2.24 |
| AG-10 MPa | 1.32 | 0.75 | 2.07 |
| AG-20 MPa | 1.2 | 0.69 | 1.89 |
| AG-40 MPa | 1.16 | 0.75 | 1.91 |
| DDS-5 MPa | 1.4 | 0.78 | 2.18 |
| DDS-10 MPa | 1.32 | 0.75 | 2.07 |
| DDS-20 MPa | 1.24 | 0.69 | 1.93 |
| DDS-40 MPa | 1.16 | 0.79 | 1.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinciguerra, S.C.; Greco, A.; Pluchino, A.; Rapisarda, A.; Tsallis, C. Acoustic Emissions in Rock Deformation and Failure: New Insights from Q-Statistical Analysis. Entropy 2023, 25, 701. https://doi.org/10.3390/e25040701
Vinciguerra SC, Greco A, Pluchino A, Rapisarda A, Tsallis C. Acoustic Emissions in Rock Deformation and Failure: New Insights from Q-Statistical Analysis. Entropy. 2023; 25(4):701. https://doi.org/10.3390/e25040701
Chicago/Turabian StyleVinciguerra, Sergio C., Annalisa Greco, Alessandro Pluchino, Andrea Rapisarda, and Constantino Tsallis. 2023. "Acoustic Emissions in Rock Deformation and Failure: New Insights from Q-Statistical Analysis" Entropy 25, no. 4: 701. https://doi.org/10.3390/e25040701
APA StyleVinciguerra, S. C., Greco, A., Pluchino, A., Rapisarda, A., & Tsallis, C. (2023). Acoustic Emissions in Rock Deformation and Failure: New Insights from Q-Statistical Analysis. Entropy, 25(4), 701. https://doi.org/10.3390/e25040701










