1. Introduction
Two-component reaction–diffusion systems often model the interaction of two chemicals, leading to the formation of non-uniform spatial patterns of chemical concentration or morphogenesis under certain conditions due to chemical reactions and spreading. Since Turing’s groundbreaking work [
1], reaction–diffusion systems have been extensively used in developmental biology modeling. For example, let
and
represent the concentration of two chemical species, which may either enhance or suppress each other depending on the context. The system of
u and
v can be modeled as follows:
where
denotes the Laplacian operator,
and
are interactions between
u and
v. The functions
and
are sums of various reaction terms that can be derived from physical or chemical principles such as mass-action laws, Michaelis–Menten kinetics, or products that represent some competition, cooperation effects. We refer the readers to ([
2], Section 2.2) for more discussions. Hence,
and
are sums of meaningful functions that represent specific mechanisms: if we are able to identify these terms and discover the explicit formulas for
and
, then we can learn more about the nature of the interactions and predict future behaviors well. This situation arises commonly in biological applications such as chemotaxis, pattern formation in developmental biology, and also the cell polarity phenomenon [
3,
4].
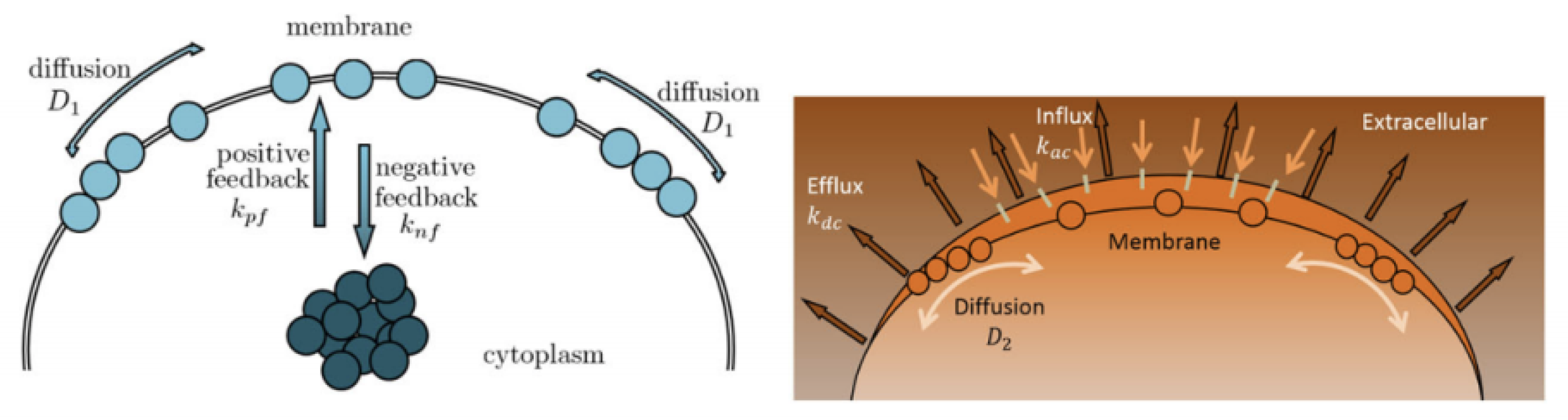
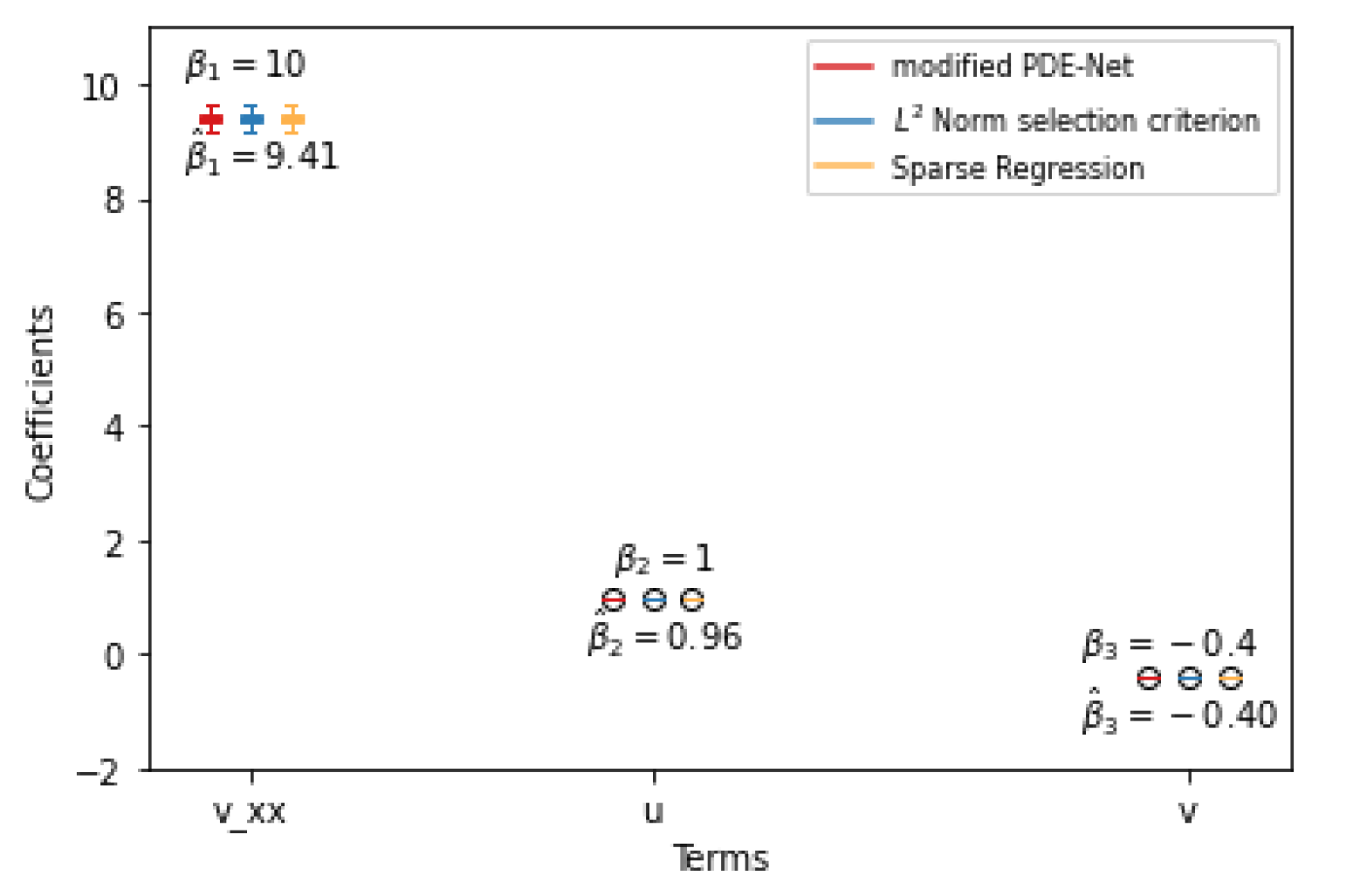
Cell polarity plays a vital role in cell growth and function for many cell types, affecting cell migration, proliferation, and differentiation. A classic example of polar growth is pollen tube growth, which is controlled by the Rho GTPase (ROP1) molecular switch. Recent studies have revealed that the localization of active ROP1 is regulated by both positive and negative feedback loops, and calcium ions play a role in ROP1’s negative feedback mechanism. Initially, ROP1 is inside the membrane. During positive feedback (rate
), some of the ROP1 enters the membrane. At the same time, negative feedback (rate
) causes some of it to return inside the membrane while the rest diffuse on the membrane (rate
). Calcium ions follow a similar process with positive rate
, negative rate
, and diffusion rate
. In [
5,
6], the following 2D reaction–diffusion system (
2) is introduced:
with suitable initial and boundary conditions being proposed to quantitatively describe such spatial and temporal connection between ROP1 and calcium ions, leading to rapid oscillations in their distributions on the cell membrane. Here,
,
, and
,
,
,
,
and
are abbreviated notations for partial derivatives with respect to the time
t or to the spatial variable
x. Moreover, the non-linear function
characterizes how calcium ions play a role in ROP1’s negative feedback loop. Specifically, the active ROP1 causes an increase in
levels, leading to a reduction in ROP1 activity and a decrease in its levels. Meanwhile, the flow of
slows down as ROP1 drops. Ref. [
6] proposed the equation
to describe such spatial–temporal patterns of calcium, where
is a positive constant. Based on this model, ref. [
6] developed a modified gradient matching procedure for parameter estimation, including
and
. However, it requires that
in (
2) is a known function. In this work, we propose to apply neural network methods to uncover the function
or more broadly, to learn interaction terms
and
in general reaction-diffusion PDEs (
1), which may contain fractional expressions (
Figure 1).
In the past decade, the artificial intelligence community has focused increasingly on neural networks, which have become crucial in many applications, especially PDEs. Deep learning-based approaches to PDEs have made substantial progress and are well-studied, both for forward and inverse problems. For forward problems with appropriate initial and boundary conditions in various domains, several methods have been developed to accurately predict dynamics (e.g., [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]). For inverse problems, there are two classes of approaches. The first class of approaches focuses on inferring coefficients from known data (e.g., [
7,
10,
12,
15,
18,
19]). An example of this is the widely known PINN (Physics-informed Neural Networks) method [
10], which uses PDEs in the loss function of neural networks to incorporate scientific knowledge. Ref. [
7] improved the efficiency of PINNs with the residual-based adaptive refinement (RAR) method and created a library of open-source codes for solving various PDEs, including those with complex geometry. However, this method is only capable of estimating coefficients for fixed known terms in PDEs, and may not work well for discovering hidden PDE models. Although [
9] extended the PINN method to find unknown dynamic systems, the nonlinear learner function remains a black-box and no explicit expressions of the discovered terms in the predicted PDE are available, making it difficult to interpret their physical meaning. The second class of approaches not only estimates coefficients, but also discovers hidden terms (e.g., [
16,
17,
20,
21,
22,
23,
24,
25,
26]). An example is the PDE-Net method [
16], which combines numerical approximations of convolutional differential operators with symbolic neural networks. PDE-Net can learn differential operators through convolution kernels, a natural method for solving PDEs that has been well-studied in [
27]. This approach is capable of recovering terms in PDE models with explicit expressions and relatively accurate coefficients, but often produces many noisy terms that lack interpretation. In order to produce parsimonious models, refs. [
25,
26] proposed to create a regression model with the response variable
, and a matrix
with a collection of spatial and polynomial derivative functions (e.g.,
):
. The estimation of differential equations by modeling the time variations of the solution is known to produce consistent estimates [
28]. In addition, the Ridge regression with hard thresholding can be used to approximate the coefficient vector
. This sparse regression-based method generally results in a PDE model with accurately predicted terms and high accuracy coefficients. However, few existing studies have focused on effectively recovering interaction terms in the fractional form (say one polynomial term divided by another polynomial term) in hidden partial differential equations, which is the focus of this paper.
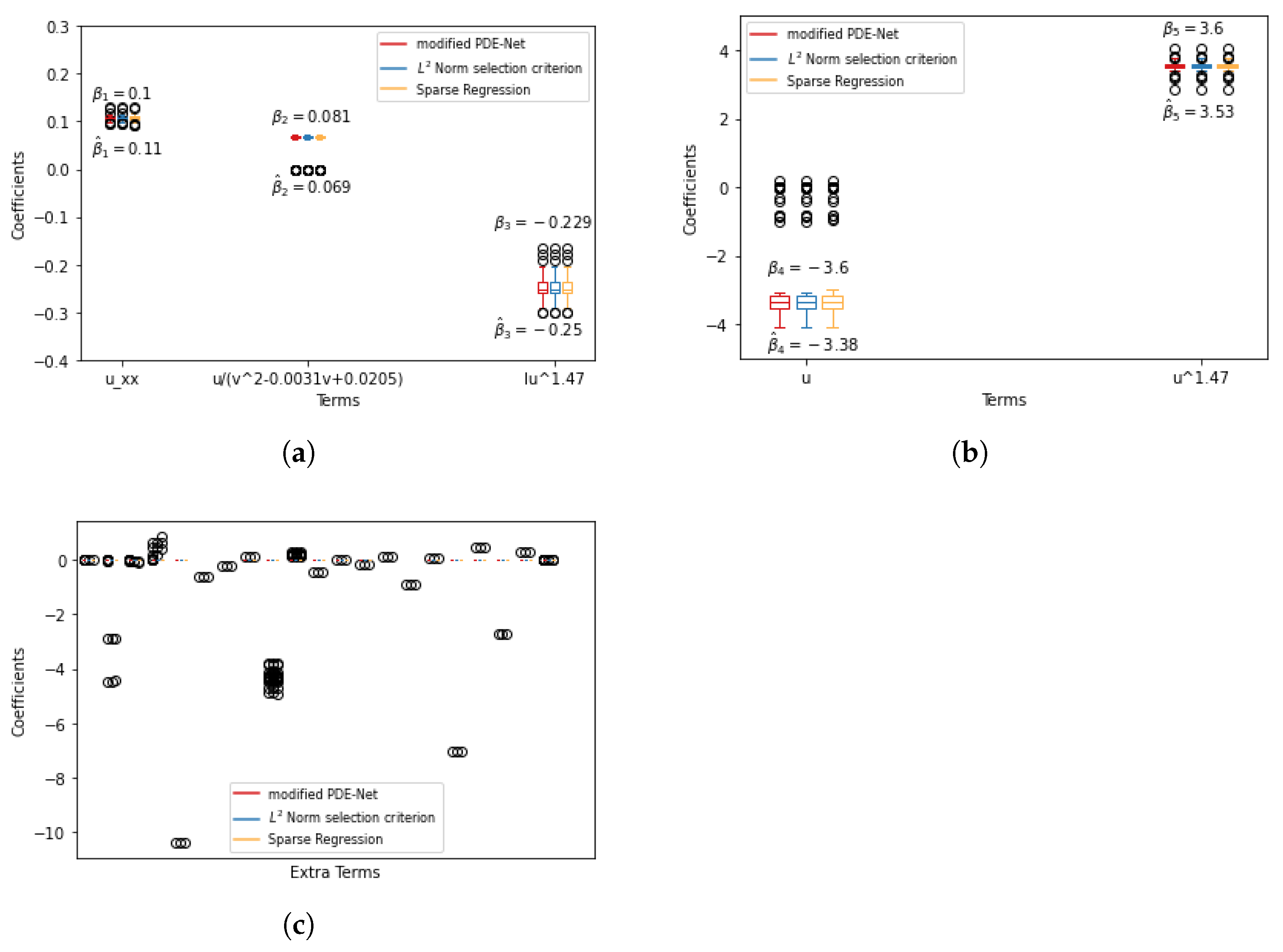
Previous methods for identifying the hidden terms in reaction–diffusion partial differential equation models have mostly focused on polynomial forms. However, as indicated in Equation (
2), the model for ROP1 and calcium ion distribution also involves fractional and integral forms, which can pose identifiability issues when combined with polynomial forms. Furthermore, we want to attain a parsimonious model, as the interpretability of the PDE model is important for biologists to comprehend biological behavior and phenomena revealed by the model.
In this paper, we utilize a combination of a modified PDE-Net method (which adds fractional and integration terms to the original PDE-Net approach), an norm term selection criterion, and an appropriate sparsity regression. This combination proves to produce meaningful and stable terms with accurate estimation of coefficients. For ease of reference to this combination, we call it Frac-PDE-Net.
The paper is organized as follows. In
Section 2, we explain the main idea and the framework of our proposed method Frac-PDE-Net. In
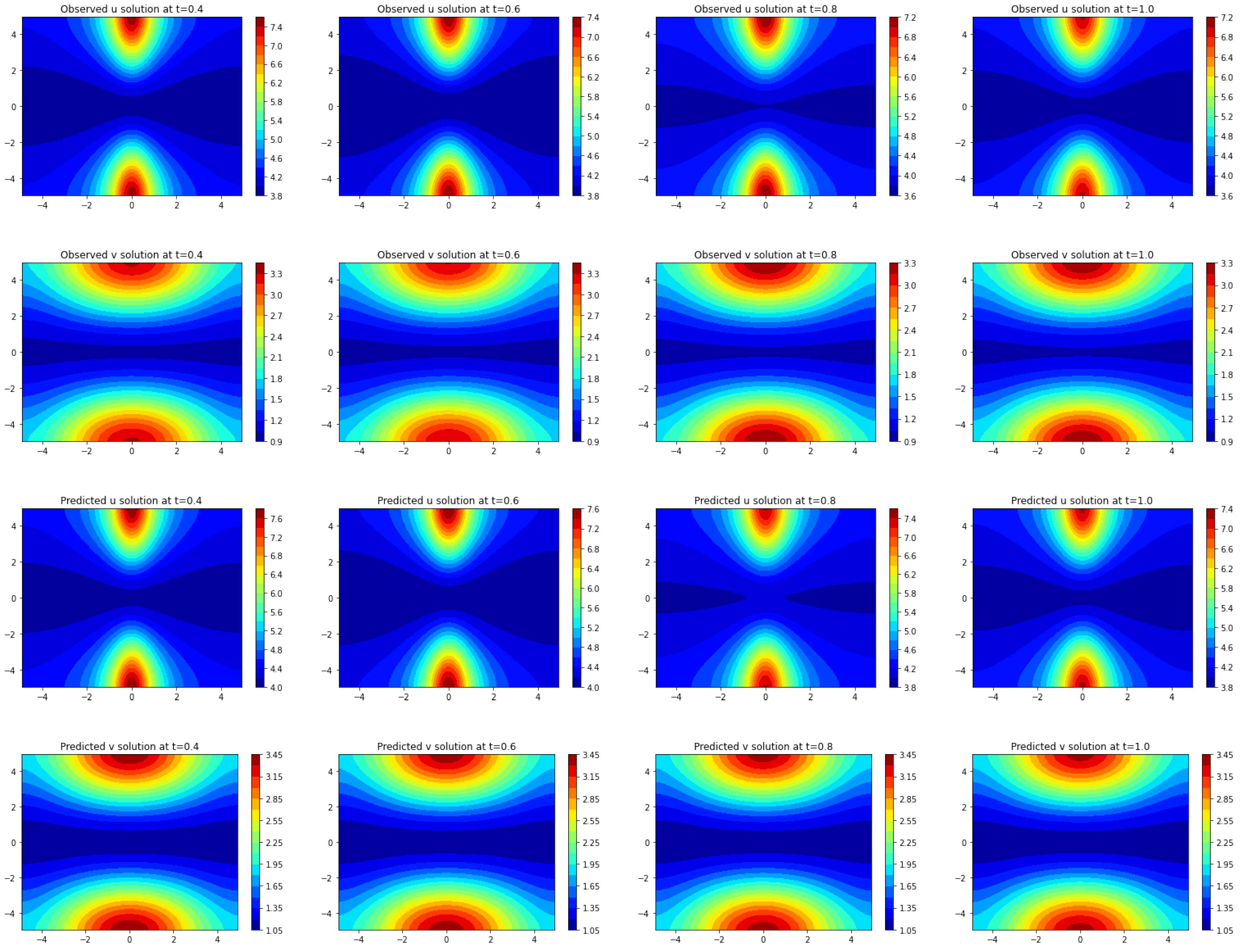
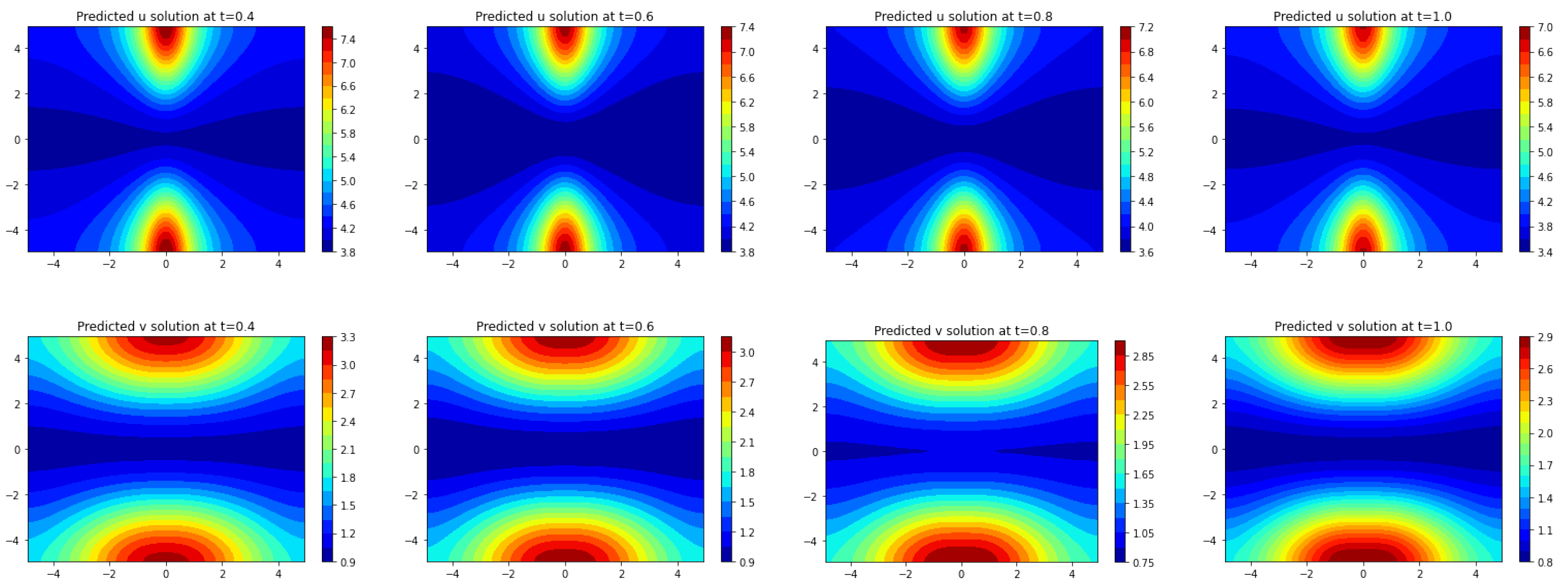
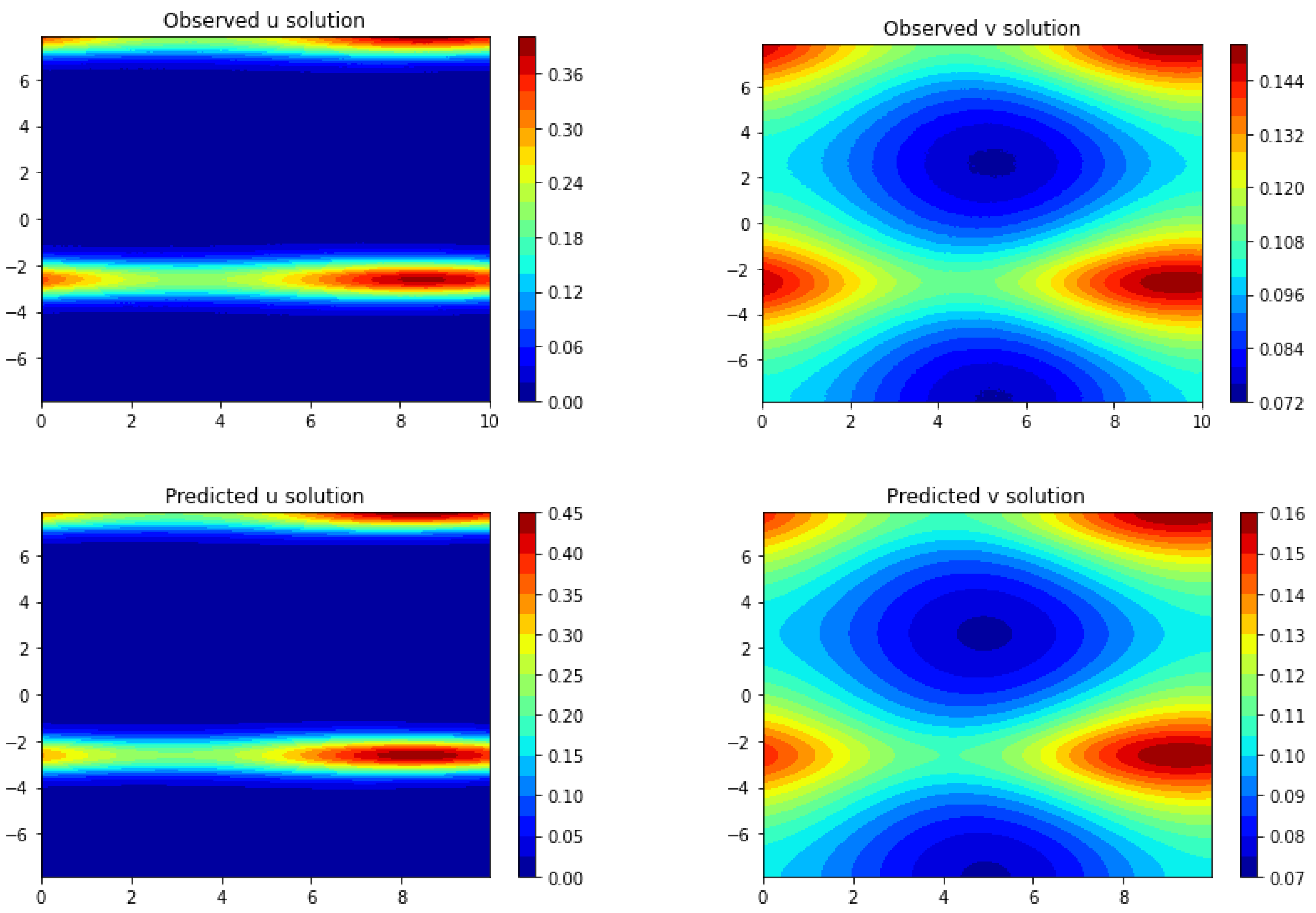
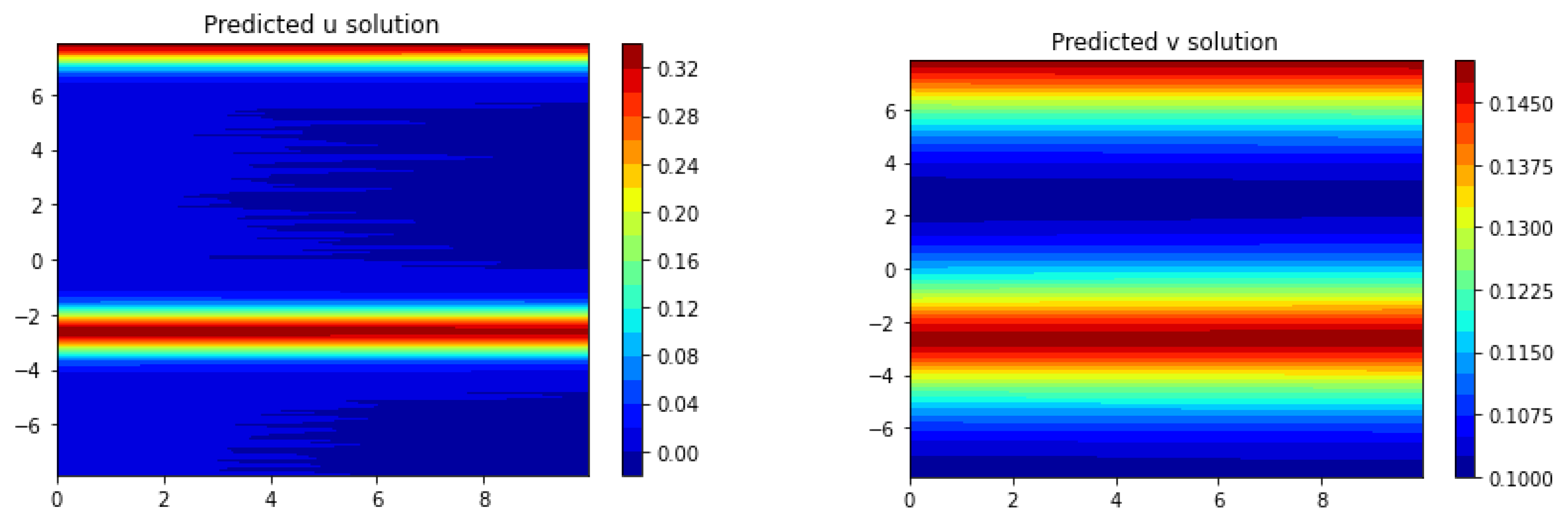
Section 3, we apply Frac-PDE-Net to discover some biological PDE models based on simulation data. Then, in
Section 4, we make some predictions to test the effectiveness of the models learned in
Section 3. Finally, we summarize our findings and present some possible future works in
Section 5.
2. Methodology
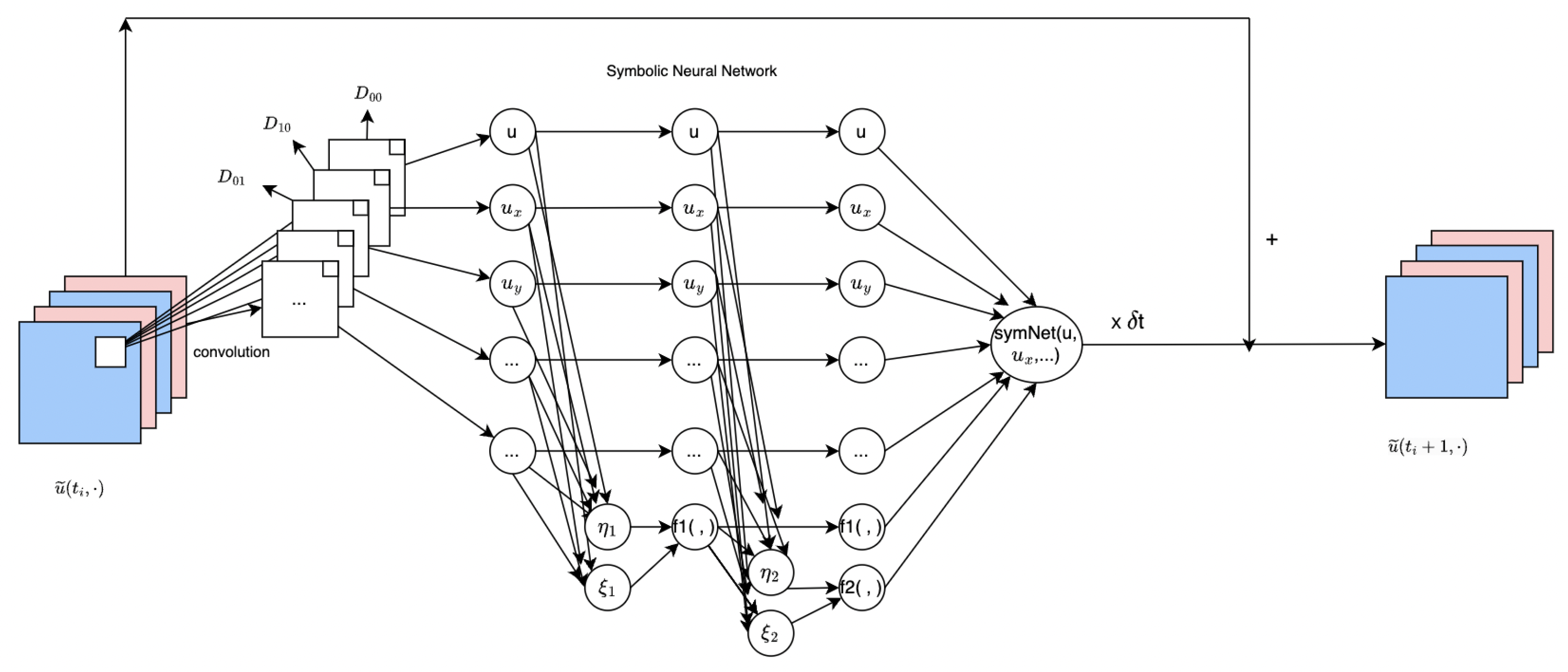
The main idea of the PDE-Net method, as described in [
16], is to use a deep convolutional neural network (CNN) to study generic nonlinear evolution partial differential equations (PDEs) as shown below:
where
is a function (scalar valued or vector valued) of the space variable
and the temporal variable
t. Its architecture is a feed-forward network that combines the forward Euler method in time with the second-order finite difference method in space through the implementation of special filters in the CNN that imitate differential operators. The network is trained to approximate the solution to the above PDEs and then the network is used to make predictions for the subsequent time steps. The authors of [
16] show that this approach is effective for solving a range of PDEs and can achieve satisfactory accuracy and computational efficiency compared to traditional numerical methods. In this paper, we follow a similar framework to PDE-Net, but with modifications on a symbolic network framework (
) to better align with biological models.
2.1. PDE-Net Review
The feed-forward network consists of several -blocks, all of which use the same parameters optimized through minimizing a loss function. For simplicity, we will only show one -block for two-dimensional PDEs, as repeating it generates multiple -blocks, and the concept can easily be extended to higher-dimensional PDEs.
Denote the space variable
in (
3) to be
since we are dealing with the two-dimensional case. Let
and
be the given initial data. For
,
denotes the predicted value of
u at time
calculated from the predicted (true) value of
at time
using the following procedure:
where SymNet is an approximation operator of
F. Here, the operators
are convolution operators with the underlying filters
, i.e.,
. These operators approximate differential operators:
For a general
filter
, where
,
By Taylor expansion,
where
In particular, if choosing
, then
As a result, the training of
q can be performed through the training of
since the moment matrix
. It is important to note that the trainable filters
M (or
q) must be carefully constrained to match differential operators.
For example, to approximate
by
, or equivalently by
for a
filter
, we may choose
where ∗ means no constraint on the corresponding entry. Generally, the fewer instances of ∗ present, the more restrictions are imposed, leading to increased accuracy. In this example of (
6), the choice of
ensures the 1st order accuracy and the choice of
guarantees the 2
nd order accuracy. More precisely, if we plug
into (
5) with
, then
which implies
. Similarly, if we plug
into (
5), then
. In PDE-Net 2.0, all moment matrices are trained as subject to partial constraints so that the accuracy is at least 2nd order.
The
network, modeled after CNNs, is employed to approximate the multivariate nonlinear response function
F. It takes a
m-dimensional vector as input and consists of
k layers. As depicted in
Figure 2, the
network has two hidden layers, where each
unit performs a dyadic multiplication and the output is added to the
th hidden layer.
The loss function for this method has three components and is defined as follows:
Here,
measures the difference between the true data and the prediction. Consider the data set
, where
n is the number of
blocks,
N is the total number of samples, and
is the number of space grids. The index
j indicates the
jth solution path with a certain initial condition of the unknown dynamics, and the index
i represents the solution at time
. Then, we define
Here,
, where
represents the real data and
denotes the predicted data. For a given threshold
s, recall the Huber’s loss function
defined as
We then define the following:
where
s are filters and
is the moment matrix of
. Using the same Huber loss function as in (
8), we define
where
s are the parameters in SymNet. The coefficients
and
in Equation (
7) serve as regularization terms to help control the magnitude of the parameters, preventing them from becoming too large and overfitting to the training data.
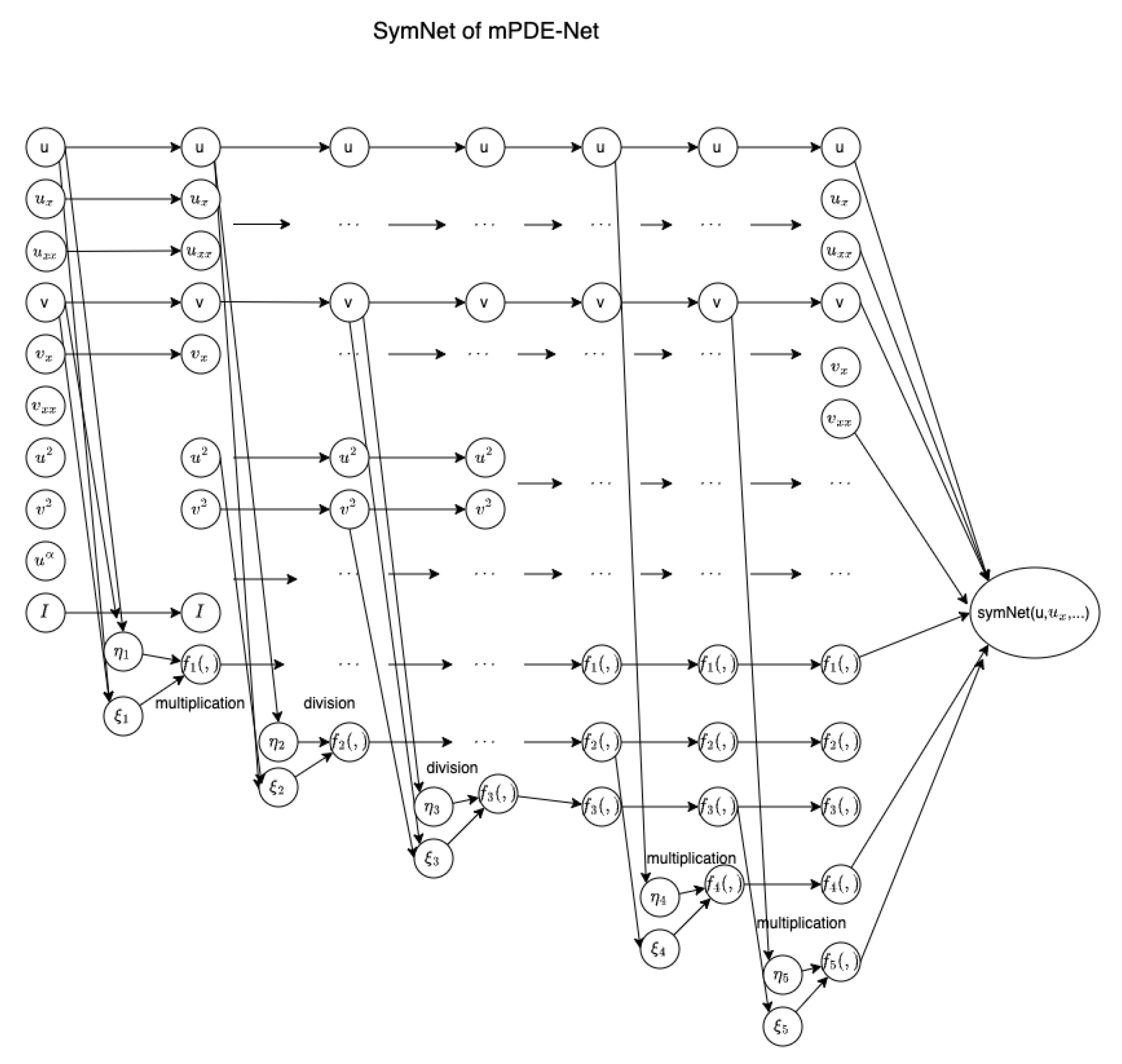
2.2. mPDE-Net (Modified PDE-Net)
In mPDE-Net, we do not include multiplications between derivatives of
u and
v, as these interactions are not commonly present in biological phenomena. Additionally, to handle interactions in fractional or integral forms, such as those in Equation (
2), mPDE-Net incorporates integral terms and division operations into
. However, there was a challenge with identifiability using mPDE-Net. For instance, consider a two-component input vector
u and
v. mPDE-Net may produce results such as
or
, where
is a small number due to noise. Although both of these terms essentially represent the same term
u, the mPDE-Net is unable to automatically identify them as such. Keeping all similar terms such as
,
and
u at the same time would result in a complex model and the real fractional term would not be effectively trained.
To address the identifiability issue, restrictions were imposed on the nonlinear interaction term
by assuming that
, where either
g or
h is linear and the other one can contain a fractional term with the order of the denominator larger than that of the numerator. For instance, the terms
and
are further decomposed as follows:
As seen, the main part of the above two terms is
u while the rest, such as
,
and
, are considered as perturbations since
is very small. This allows the mPDE-Net to identify and combine the main parts of terms, resulting in a compact model.
Figure 3 presents an example of a system involving the derivatives of
u and
v up to the second order. The symbolic neural network in this example has five hidden layers, referred to as
. The operators
are multiplication functions, i.e.,
, for
; and
are division functions, i.e.,
, for
. Additionally, a term
is included to incorporate fractional powers, such as the term
in (
2). The algorithm corresponding to this example is outlined in Algorithm 1, where
| Algorithm 1 Scheme of mPDE-Net. |
Input: , where I represents , , , , , , , , , , , Output: , . |
To further demonstrate the mPDE-Net approach, we present a concrete example. To simplify the notation, we introduce the row vector
with a 1 in the
ith component and 0 in all other components, i.e.,
where the number “1” is on the
ith position. Then, we set
According to Algorithm 1 for
,
Therefore,
Let
denote the library for PDE-Net 2.0 and
denote the library for mPDE-Net. It is clear that
and
are distinct. Typically,
only seeks to identify multiplication terms and has the form:
where
Conversely,
is engineered to learn both multiplication terms and fractional terms, subject to certain constraints. In our paper, we make the choice of
which is much larger than
. Therefore, our framework of neural networks, built upon
, is more challenging to implement than the original framework, which is based on
.
2.3. Optimizing Hyperparameters
In this section, we will explain the process of tuning hyperparameters
and
in the loss function (
7). Firstly, the range of spatial and temporal variables in the training set are defined as
and
, respectively. Then, using the finite difference method, we generate a dataset that acts as the “true data”. Additionally, we consider
M initial conditions. The time interval is determined by
, where
is the time step size for computing the “true data” and
represents the time step size for selecting the “observational data”. Typically,
is chosen to be much smaller than
. The solution corresponding to the
mth initial condition is denoted as
, where the first “·” refers to the spatial variable and the second “·” represents the temporal variable. If the solution is evaluated at the
kth time step, it is written as
, with “·” representing the spatial variable.
The M initial values from M initial conditions are divided into three separate groups, resulting in , where , , and represent the sizes of the training set, validation set, and test set, respectively. The solutions produced by these initial values are designated as follows:
Training set: ;
Validation set: ;
Testing set: .
We use the training set to train our models, the validation set to find the best parameters, and the testing set to evaluate the performance of the trained models.
Assume we divide the time range
into
K blocks, with cutting points denoted as
for
. Then, for any
and for any
, we define
where
denotes the
norm with respect to the space variable on
,
is the “true solution”, and
is the “predicted solution” by a neural network. Based on this, the training loss, validation loss and the testing loss are defined as follows:
We choose the hyperparameters
and
in the loss function (
7) using the validation sets. Let
and
, where
,
and
. We define the training number by
. We then gradually increase the time points of the training and validation sets. For instance, if K = 15 and
, the training and validation sets can be selected as follows. The performance metric is the same as the validation loss in (
10).
| Training | | Validation | | Validation Loss |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
Furthermore, we tune the hyperparameters using Hyperopt [
29], which uses Bayesian optimization to explore the hyperparameter space more efficiently than a brute-force grid search. Specifically, the mPDE-Net is nested in the objective function of Hyperopt, which will optimize the average validation loss
of models.
The selection procedure is described in Algorithm 2.
| Algorithm 2 Optimizing Hyperparameters using Hyperopt |
- 1:
Initialize the search spaces for and ; - 2:
Define the objective function (to be optimized) as the average testing loss obtained from mPDE-Net, implemented using PyTorch; - 3:
Set the optimization algorithm, specify the number of trials, and initialize the results list. - 4:
for to number of trials do - 5:
Sample a set of hyperparameters from the search spaces, evaluate the objective function with the sampled hyperparameters, and set a list called the Validation loss. - 6:
for to do - 7:
Train model of mPDE-Net on , test it on to get a validation loss, and then append the validation loss to the Validation loss. - 8:
end for - 9:
Get an average validation loss from the Validation loss, append the hyperparameters and the average validation loss to the results list, and then update the search space based on the results so far. - 10:
end for - 11:
return the hyperparameters with the minimum objective function value.
|
2.4. Frac-PDE-Net
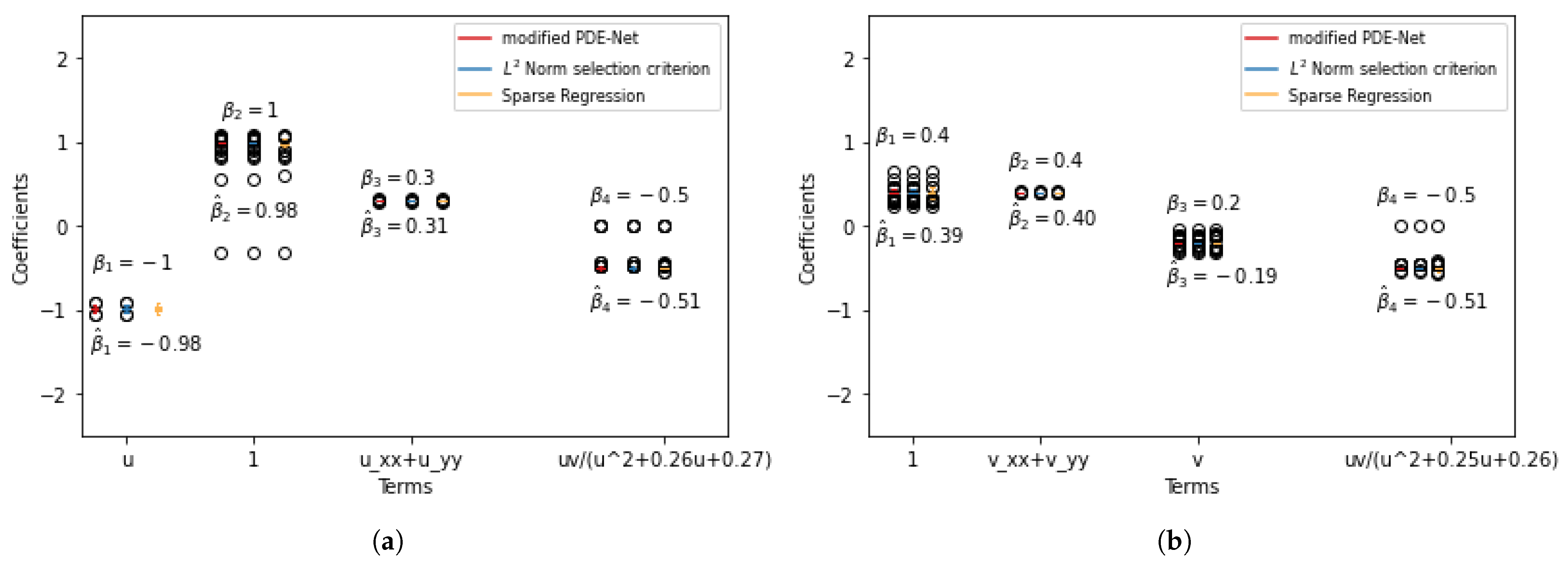
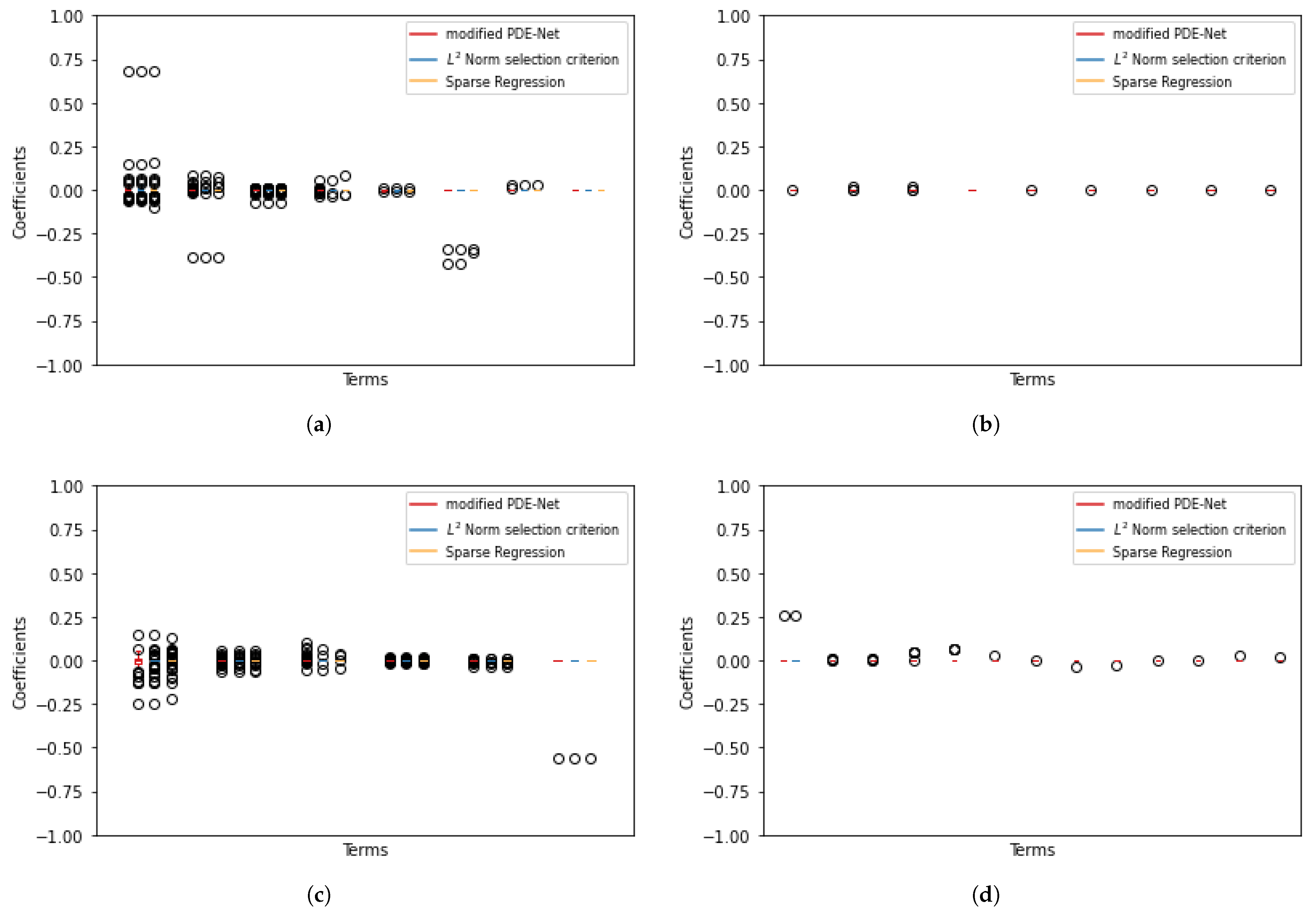
We have noted that mPDE-Net accurately fits data and recovers terms, but it may not always simplify the learned PDE, making it challenging to interpret. To address this, we implement sparsity-encouraging methods such as the Lasso approach. However, even with Lasso and hyperparameters chosen from the validation sets, the predicted equation still had redundant terms. This is likely due to correlated data and linear dependencies in the data, which prevent Lasso from fully shrinking the extra coefficients to zero. To overcome this, we employ two approaches. The first, called the norm-based term selection criterion, weakens or eliminates linear dependencies in the data. The second, called sequential threshold ridge regression (STRidge), creates concise models through strong thresholding. We will discuss these approaches in more detail below.
norm based term selection criterion. Consider the underlying PDE in the form of
where
To address the issue of excessive terms in the learned PDE, we apply the
norm based term selection criterion. This involves normalizing the columns of
to obtain
where
and adjusting the coefficients
to
,
By removing the terms in
whose adjusted coefficients
are significantly smaller than the largest one, we shorten the vector
to
. The corresponding columns in
form a new matrix
with reduced linear dependency between its columns. This results in a simplified approximation of the PDE:
Sparse regression: STRidge. After using the
norm-based term selection criterion to select terms, as discussed previously, we move on to consider sparse regression to further improve the compactness of the representation for the hidden PDE model (
13). Here, a tolerance threshold “tol” is introduced to select coefficients for sparse results. Coefficients smaller than “tol” will be discarded, and the remaining ones will be utilized until the number of terms stabilizes. The sparsity regression process is outlined in Algorithm 3. For further information, see [
25].
To summarize, the mPDE-Net approach allows us to achieve relatively accurate predictions for the function and its derivatives. We then employ an
norm-based term selection criterion and sparse regression to obtain a concise model, which we refer to as Frac-PDE-Net. Algorithm 4 summarizes this procedure.
| Algorithm 3: STRidge(, , , tol, iters) |
- 1:
▹ ridge regression - 2:
bigcoeffs= ▹ select large coefficients - 3:
▹ apply hard threshold - 4:
▹ recursive call with fewer coefficients - 5:
return
|
| Algorithm 4: Norm selection criterion+ STRidge(, , , tol, iters) |
- 1:
▹ Adjusted coefficients - 2:
bigcoeffs= ▹ Select large coefficients - 3:
- 4:
and - 5:
▹ ridge regression - 6:
bigcoeffs= ▹ select large coefficients - 7:
▹ apply hard threshold - 8:
▹ recursive call with fewer non-zero coefficients - 9:
return
|
2.5. Kolmogorov-Smirnov Test
After applying the Frac-PDE-Net procedure, a simplified, interpretable model has been created. Our next goal is to determine if this model can be further compressed. We designate Model 1 as the system learned by Frac-PDE-Net, and Model 2 as the system obtained by removing the interaction term with the smallest norm from Model 1. To determine if Model 1 and Model 2 come from the same distribution, we use the Kolmogorov–Smirnov test (K-S test).
Since our examples involve systems of two PDEs, a two-dimensional K-S test is appropriate. The time range is with time step size , giving time grids denoted as , where , and . At a fixed time , we aim to test the proximity of two samples and , which are associated with Model 1 and Model 2, respectively, at time . For each , we specify:
Hypothesis 1 (Null). The two sets and come from a common distribution.
Hypothesis 2 (Alternative). The two sets and do not come from a common distribution.
Let
and
denote null hypotheses and the corresponding p-values, respectively, for
. In this paper, we employed Bonerroni [
30], Holm [
31] and Benjamini–Hochberg (B-H) [
32] methods for multiple testing adjustment. Note that the Bonferroni method is the most conservative one among these three methods. Under the complete null hypothesis of a common distribution across all time points, no more than
of the total time points can be rejected.
5. Conclusions
Our approach, Frac-PDE-Net, builds on the symbolic approach developed in PDE-Net for addressing the discovery of realistic and interpretable PDE from data. While the neural network remains very efficient for generating and learning dictionaries of functions, typically polynomials, we have shown that if we enrich the dictionaries with large families of functions (typically uncountable), an extra-care is needed for selecting the important terms by penalization and by evaluating and testing the impact of a reaction term in the predicted solution. Quite remarkably, we can extract a sparse equation with readable terms and with good estimates of the associated parameters.
The introduction of rich families of functions, such as fractions (rational functions) is often necessary because they are well used by modelers, but also they can avoid the limitations of the approximation capacity of polynomials. Indeed, it might be necessary to have numerous terms in the expansion in order to have a correct approximation of the unknown reaction terms. As a matter of fact, we have introduced a very flexible family of fractions that avoid truncation based on powers . While we learn then the numerator and denominator coefficients in , our approach is incorporated seamlessly in the symbolic differentiable neural network framework of PDE-Net by the introduction of extra layers.
Our work is originally motivated by the discovery and estimation of reaction–diffusion PDEs, with possibly complex terms such as fractions, non-integer powers, or non-local terms (such as an integral), as it has been introduced for the pollen tube growth problem [
6]. Nevertheless, our selection approach could be used to handle other dictionaries, or in the presence of advection terms as our methodology does exploit the reaction–diffusion structure only for imposing some constraints on the dictionaries of interest, and because of the interpretability of each term in that case. As the next steps, the Frac-PDE-Net methodology can be improved by considering more advanced numerical schemes in time discretization, say implicit Euler or second-order Runge–Kutta. In that case, we expect to have a better accuracy and stability for model recovery and prediction. Another possible improvement would be to enrich the dictionaries of fractionals by replacing the current form
by more rational functions with denominators that depends both on
u and
v, say
. Finally, we put an emphasis on the fact that Frac-PDE-Net reaches a trade-off by discovering the main terms of the PDE, accurately estimating each coefficient in order to gain interpretability, while it also allows effective long-term prediction, even for unseen initial conditions.