Analysis on Cascading Failures of Directed–Undirected Interdependent Networks with Different Coupling Patterns
Abstract
1. Introduction
2. Related Works
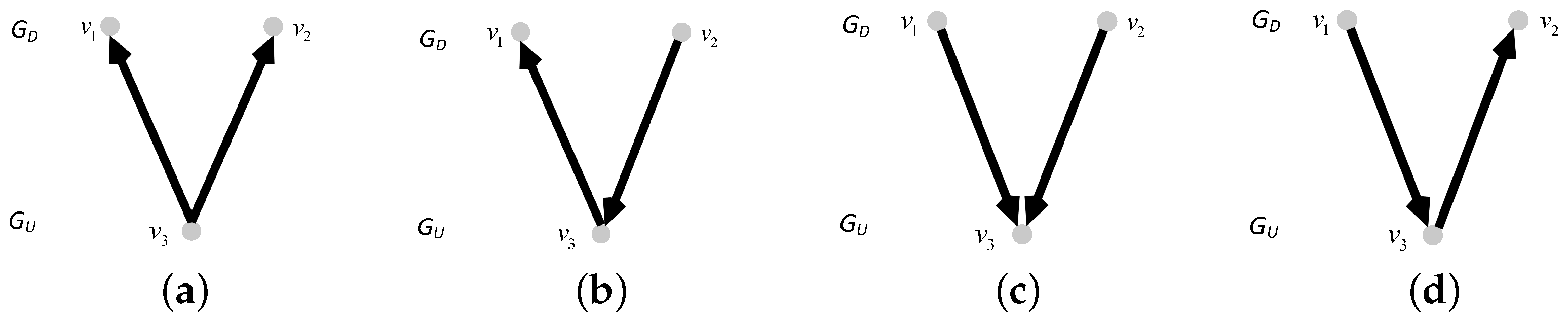
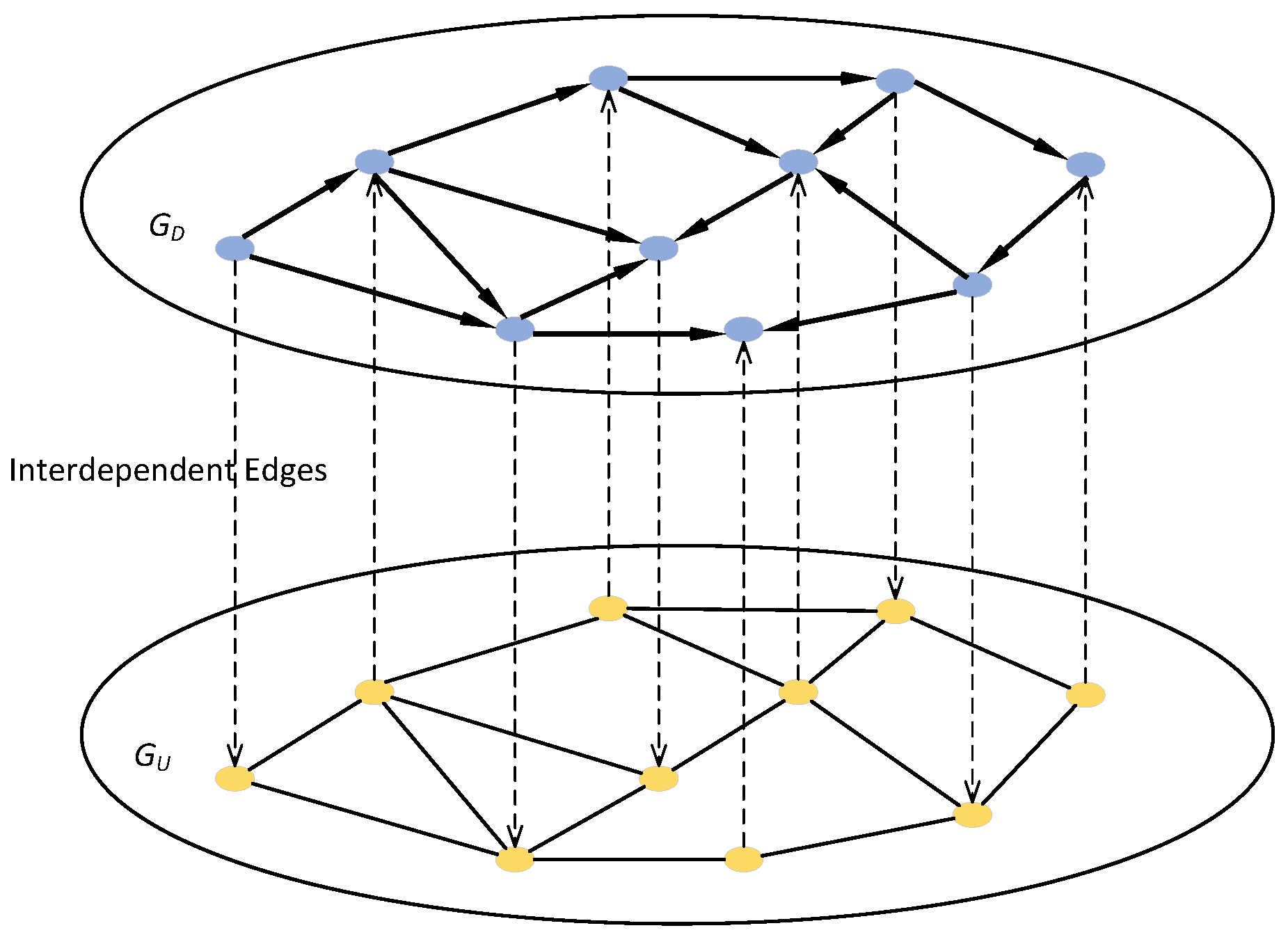
3. Theoretical Model of the Directed-Undirected Interdependent Network
4. Cascading Failure Model of Directed–Undirected Interdependent Networks
4.1. Load and Capacity
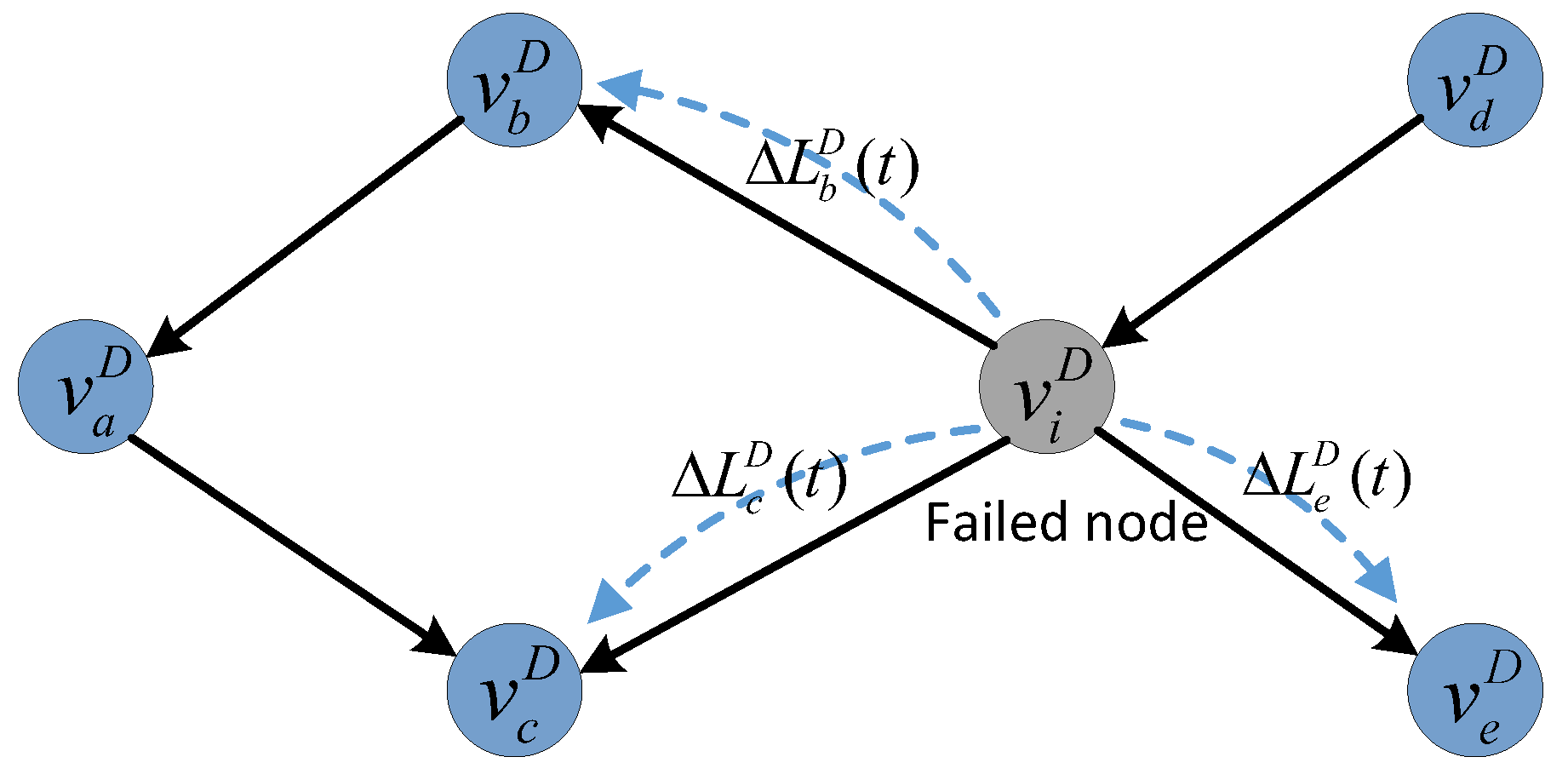
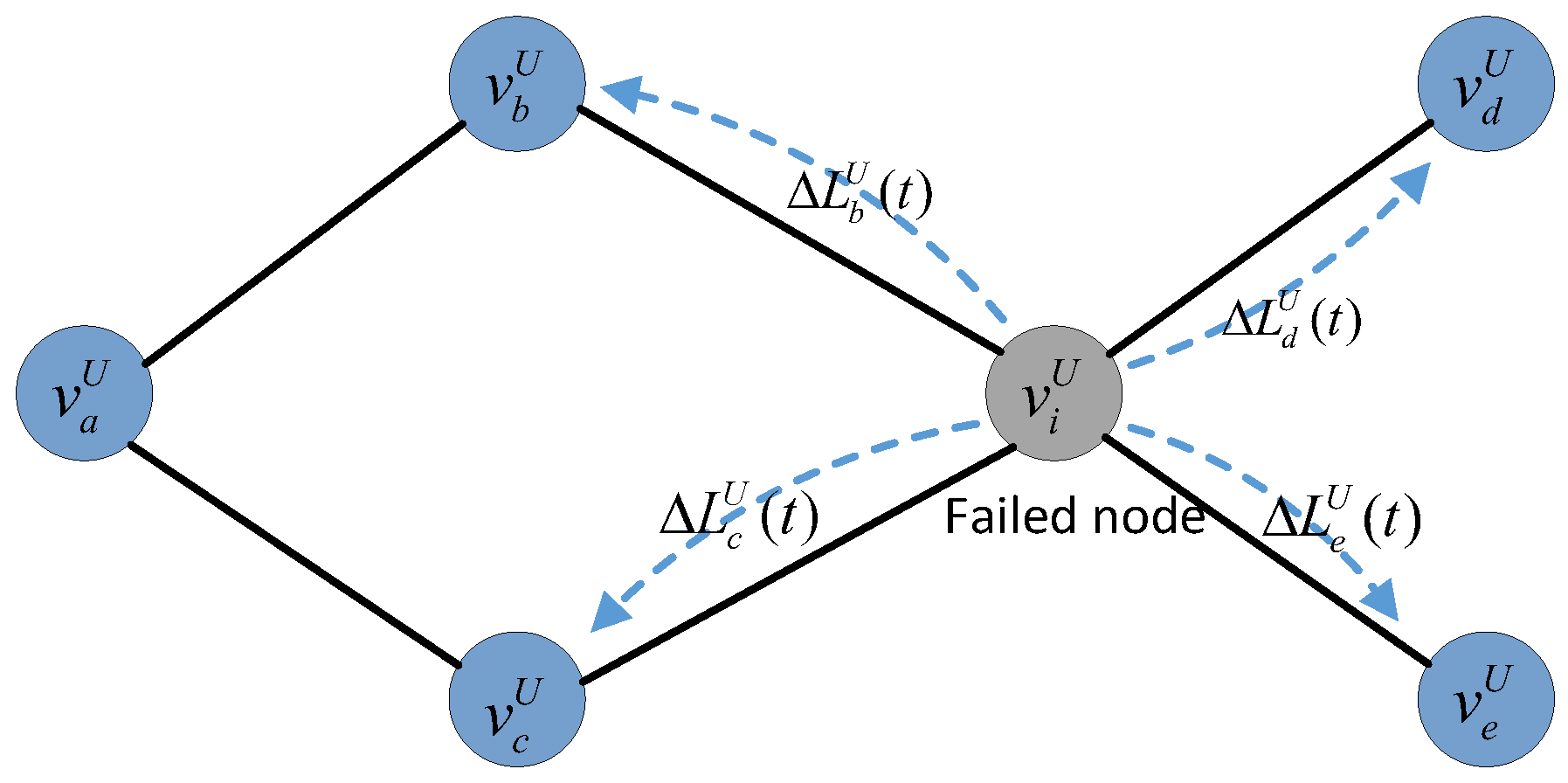
4.2. Load-Redistribution Schemes
4.3. Cascading Mechanism
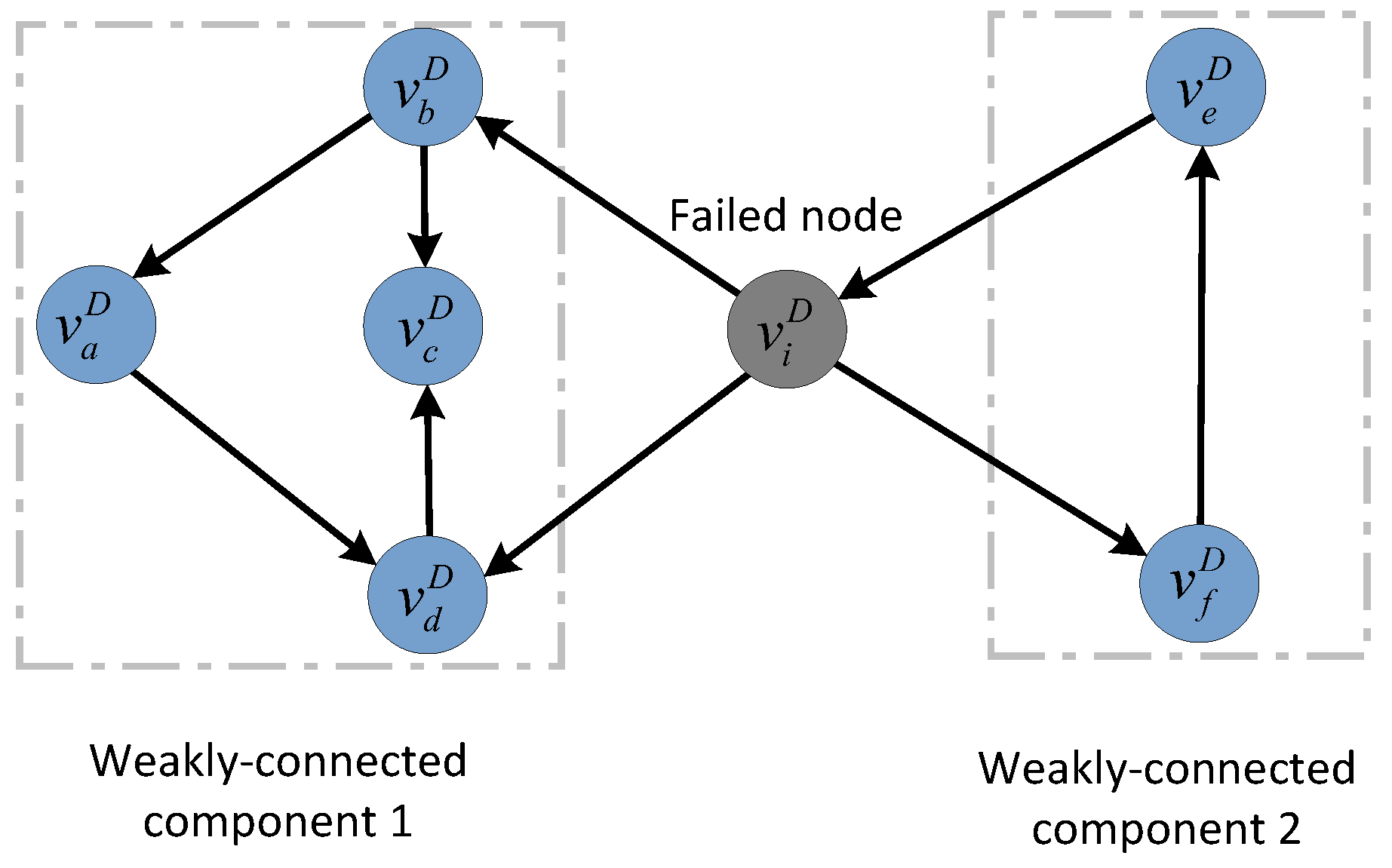
4.4. Cascading Failure Mechanism of the Directed–Undirected Interdependent Network
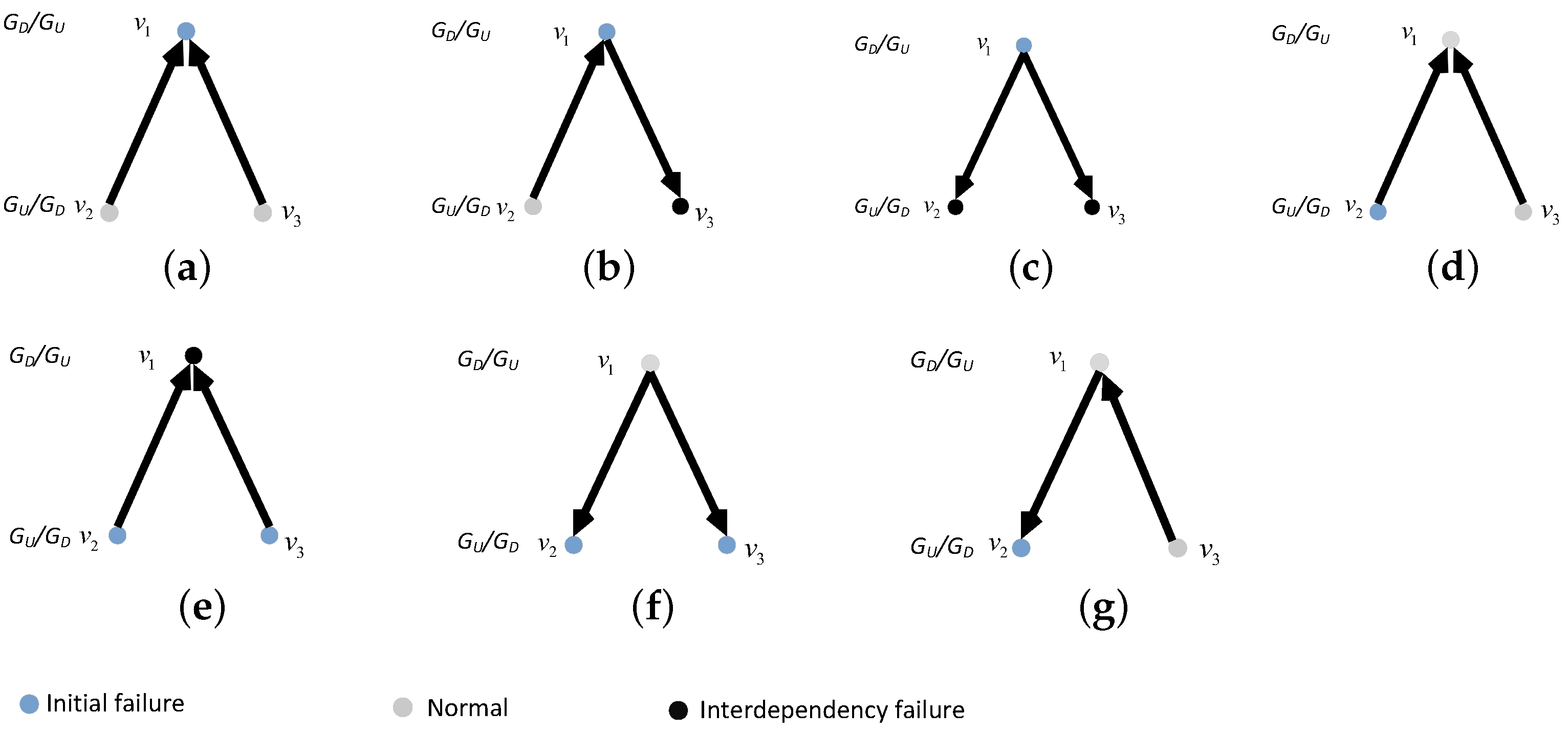
4.4.1. Initial Stage of Cascading Failure Mechanism in the Directed–Undirected Interdependent Network
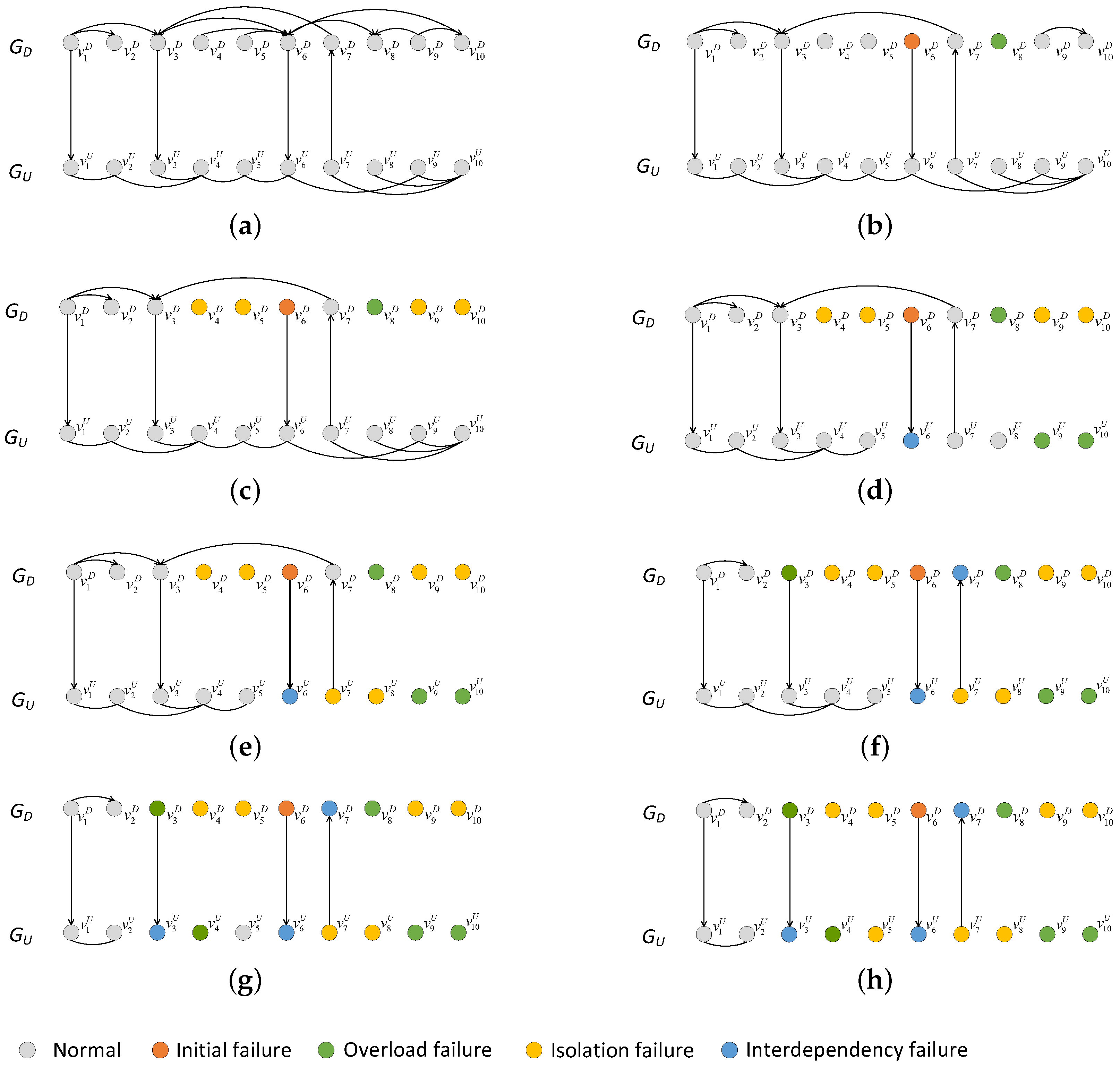
4.4.2. Example of Cascading Failure Process in a Directed–Undirected Interdependent Network
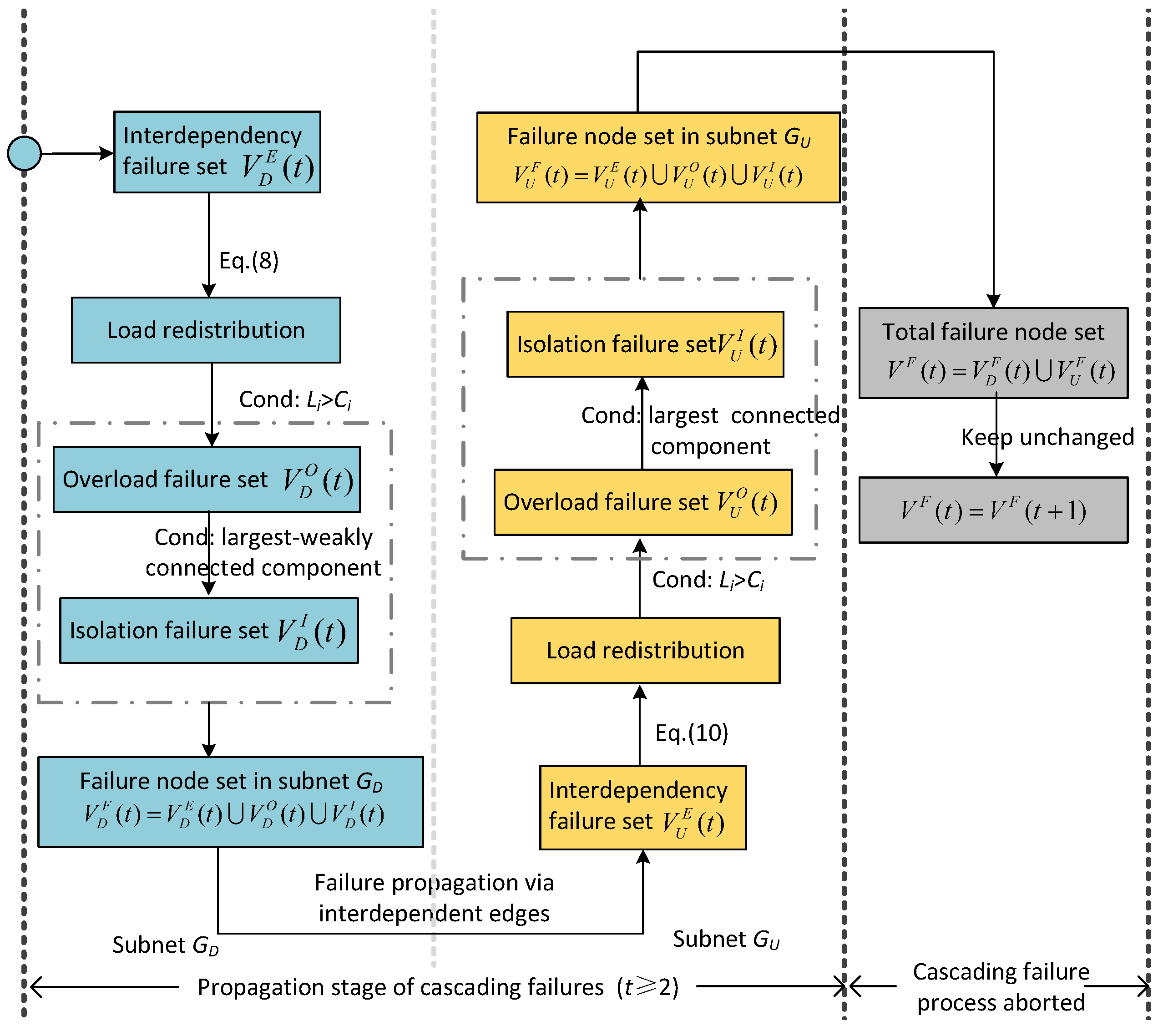
4.4.3. Time-Varying Interactive Equation of Cascading Failures
5. Simulation Results
5.1. Simulation Setup
5.2. Robustness Metrics
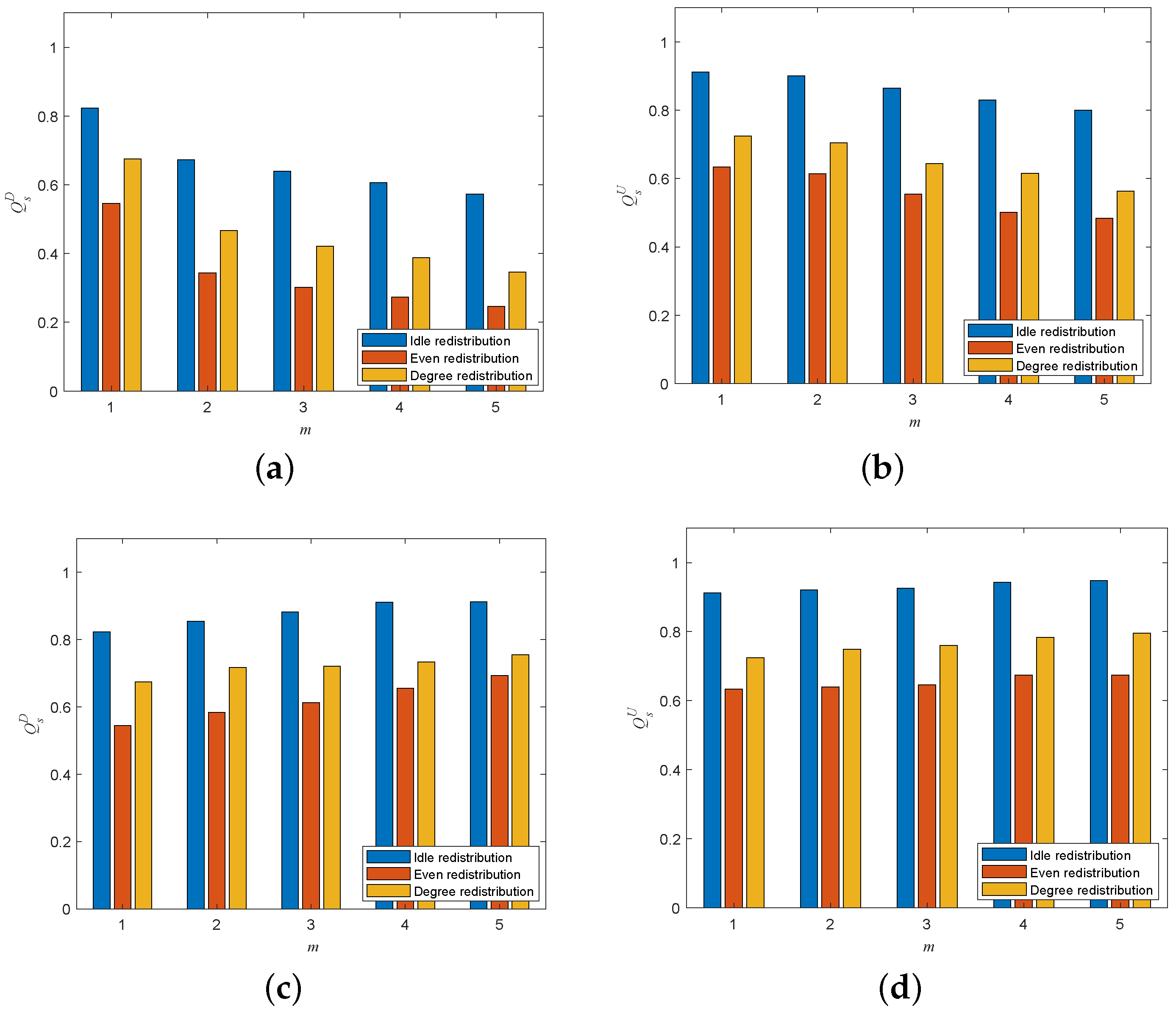
5.3. Influences of Load-Redistribution Schemes
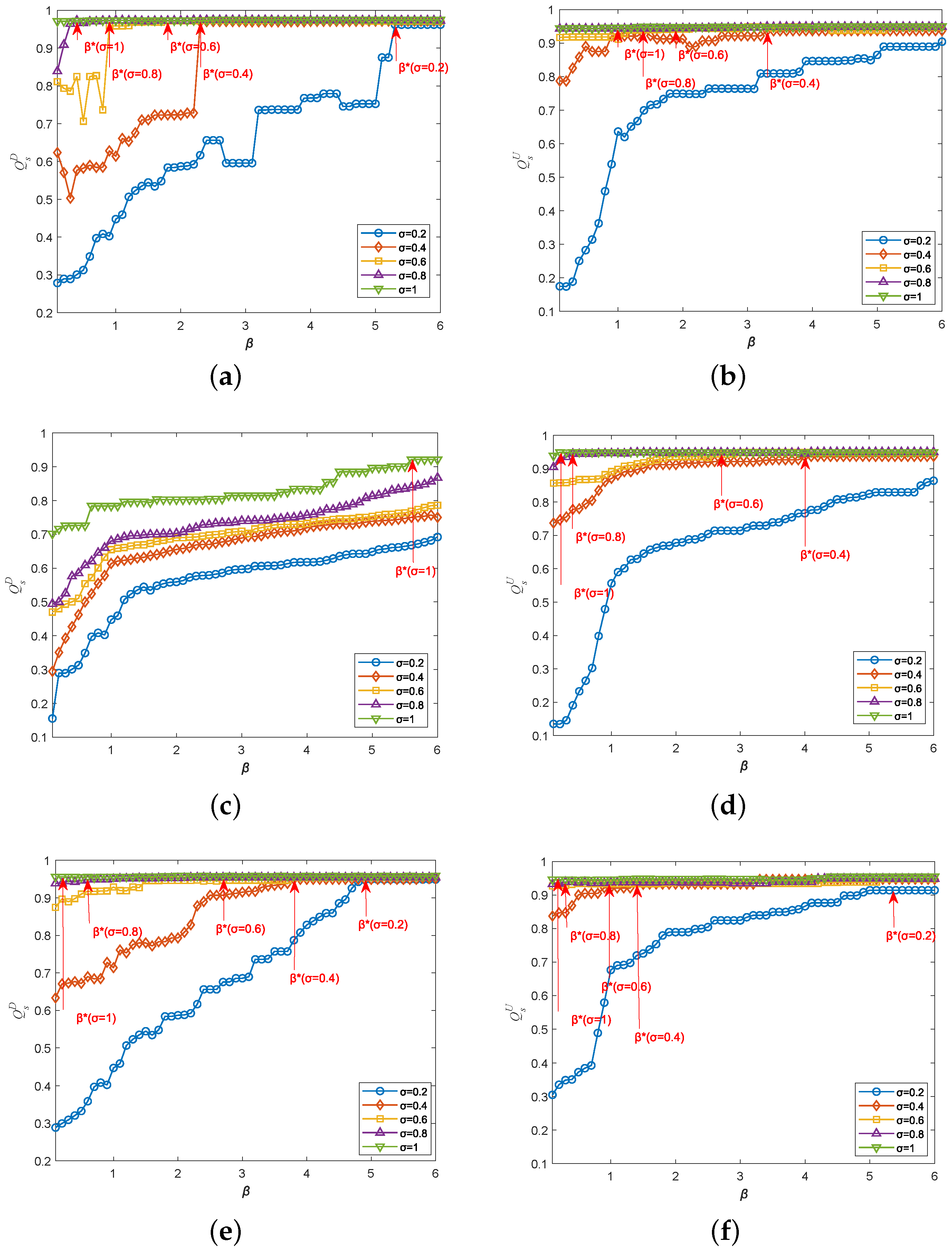
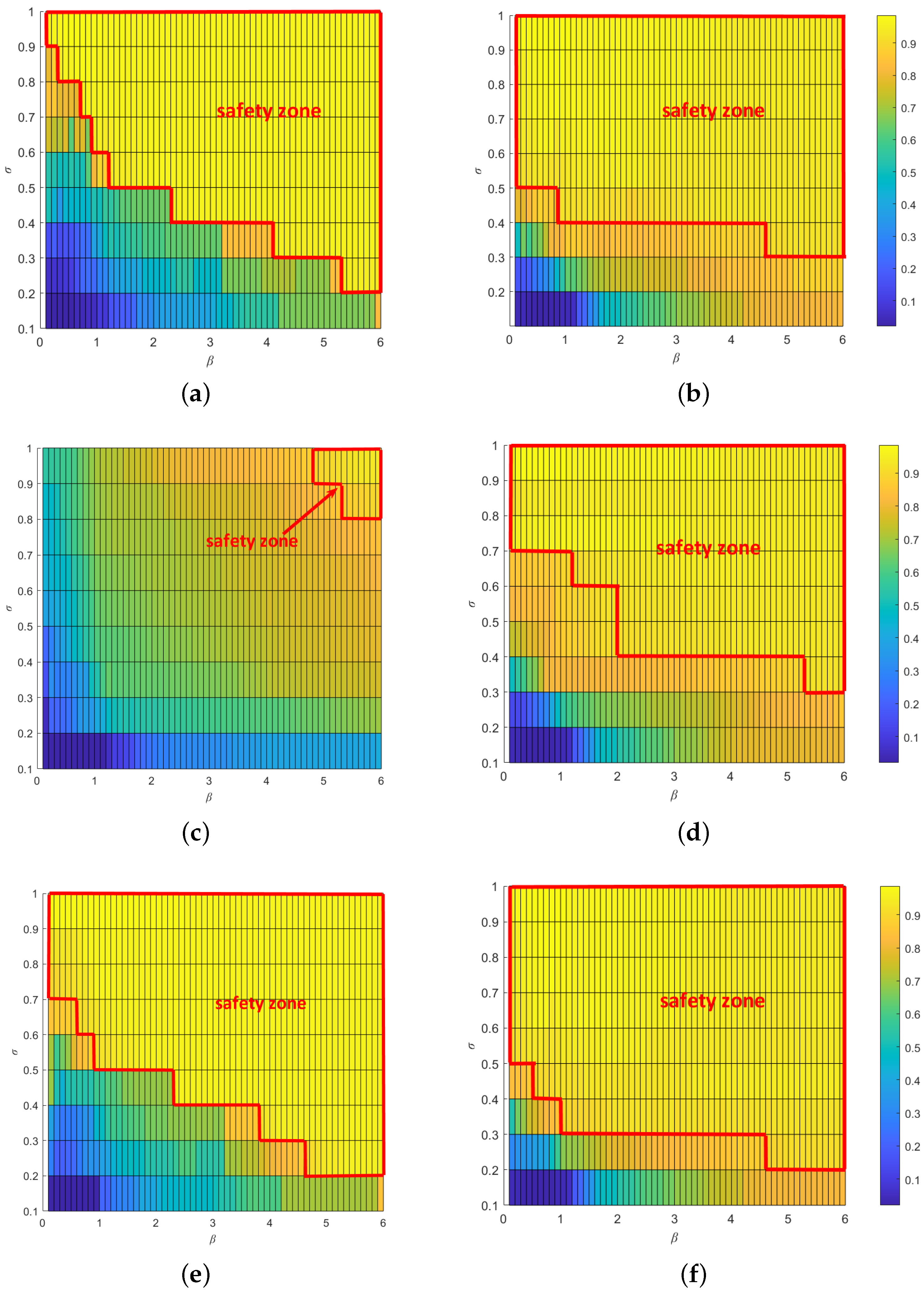
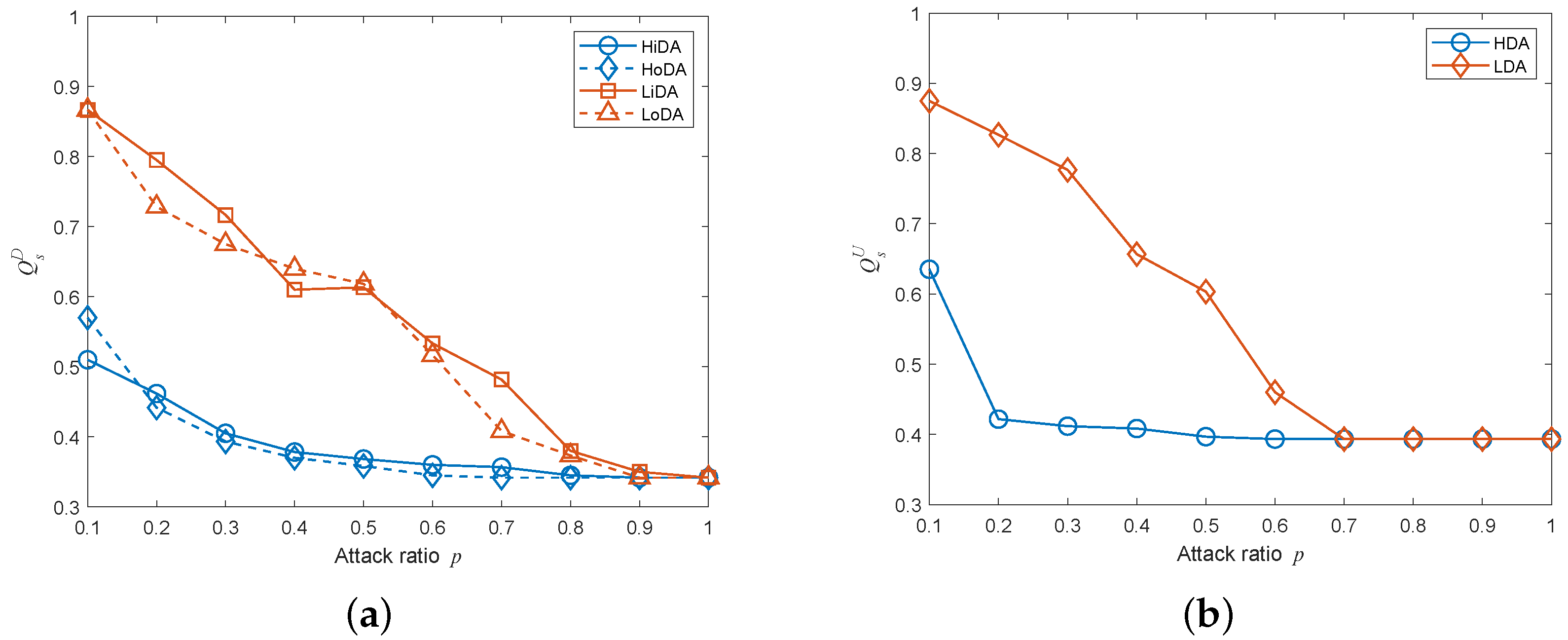
5.4. Influences of Modeling Parameters
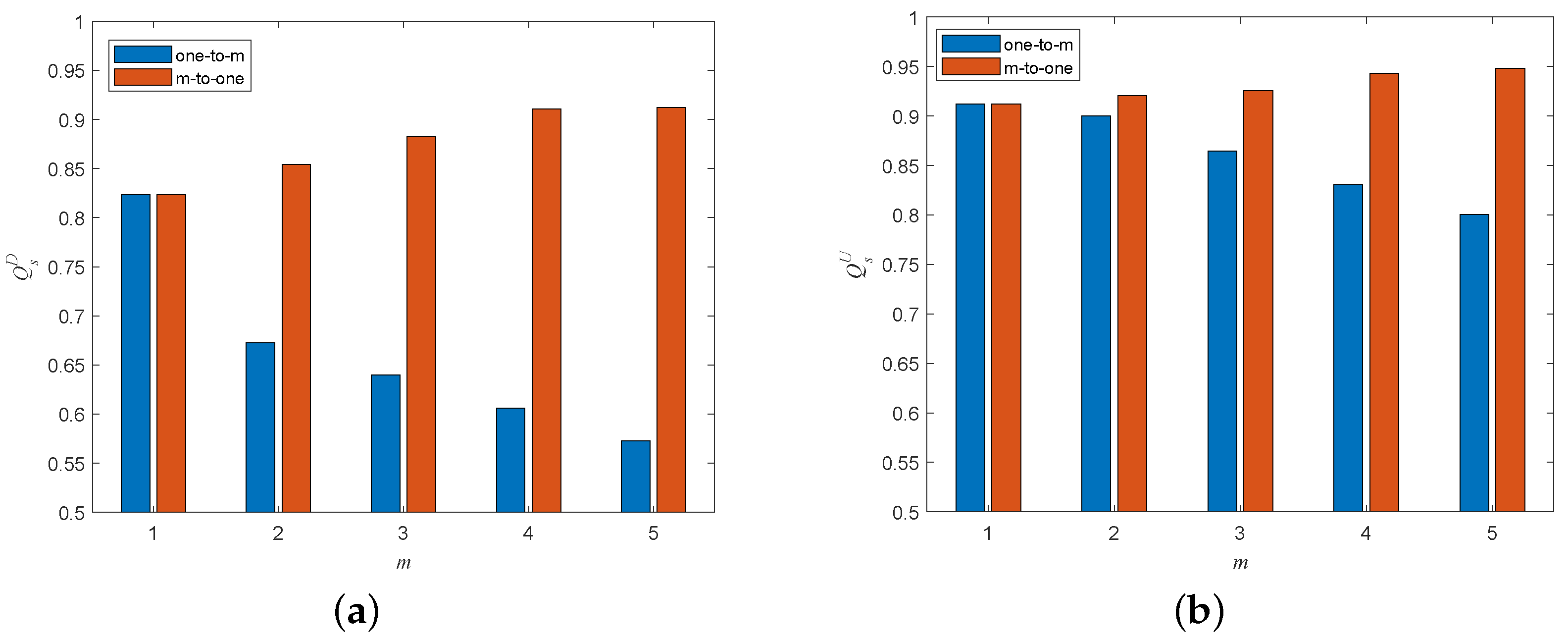
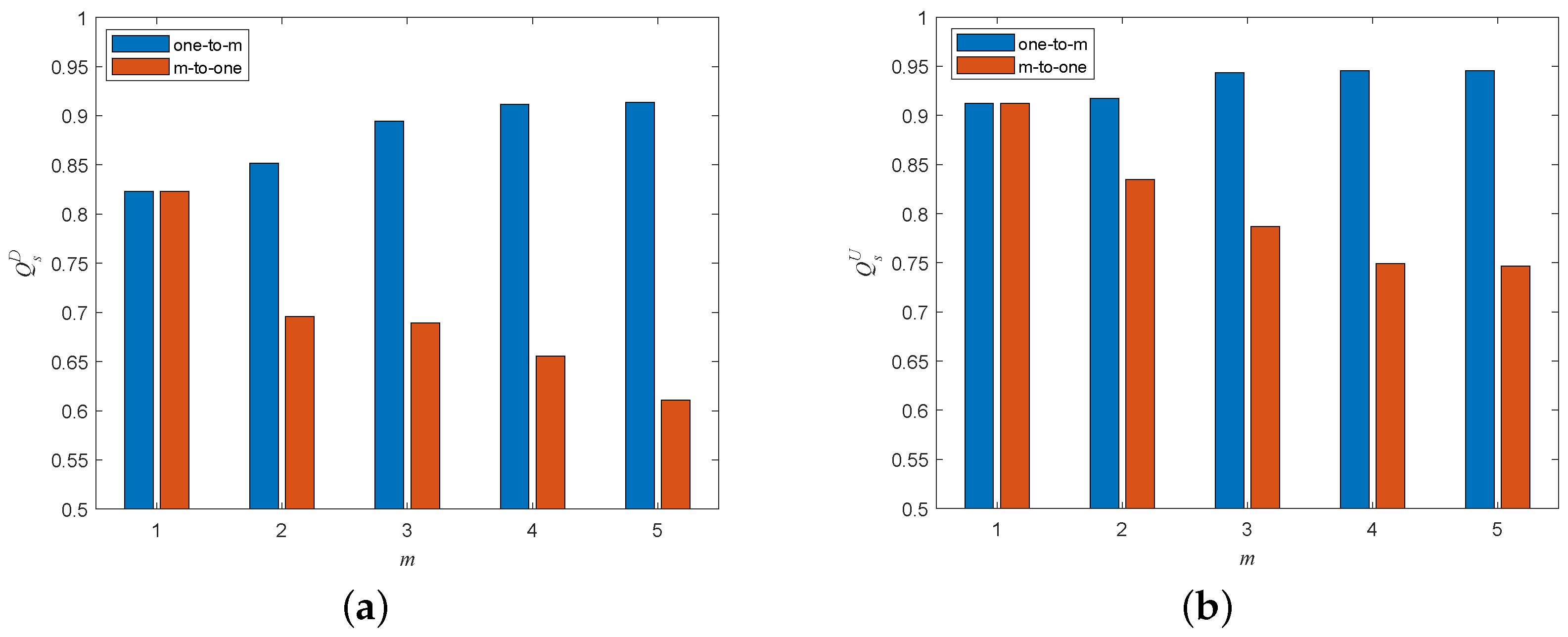
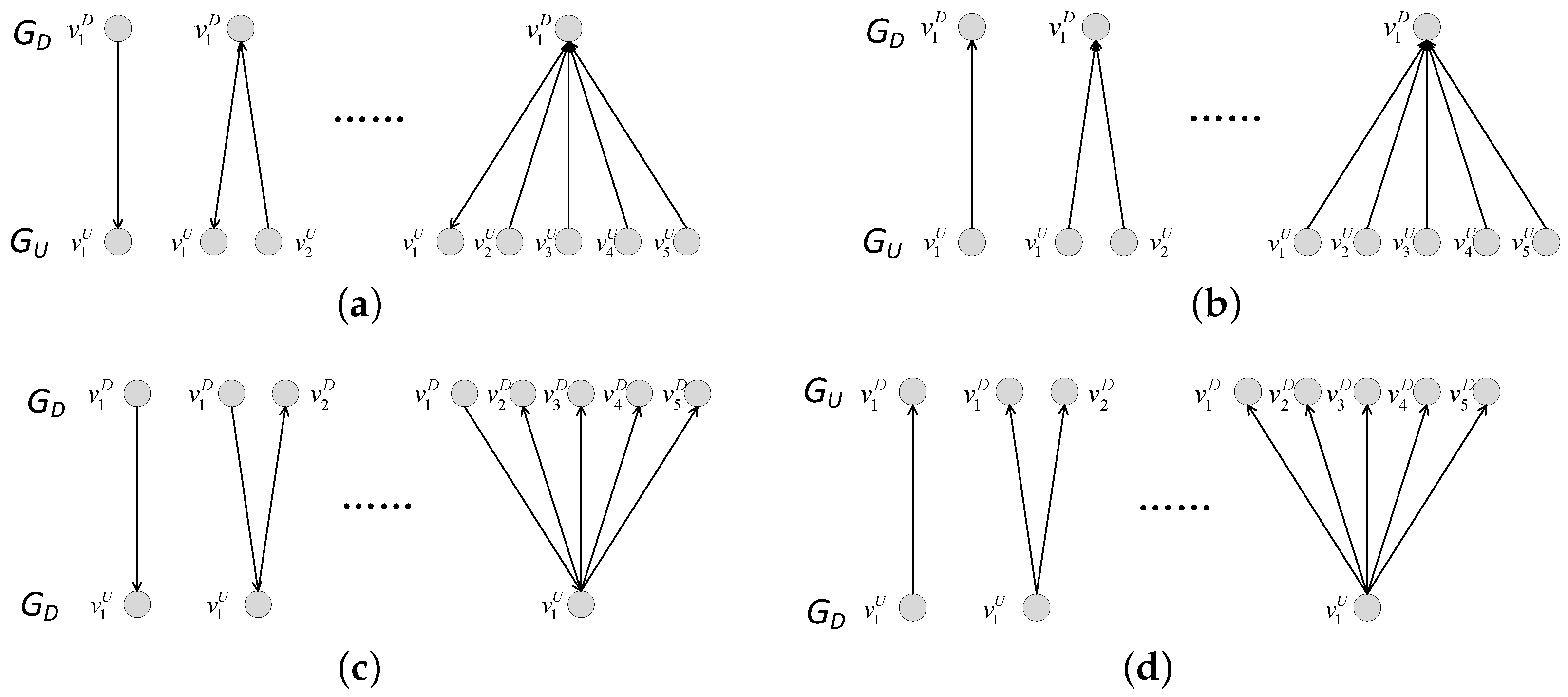
5.5. Influence of Coupling Patterns When Adding Different Interdependent Edges
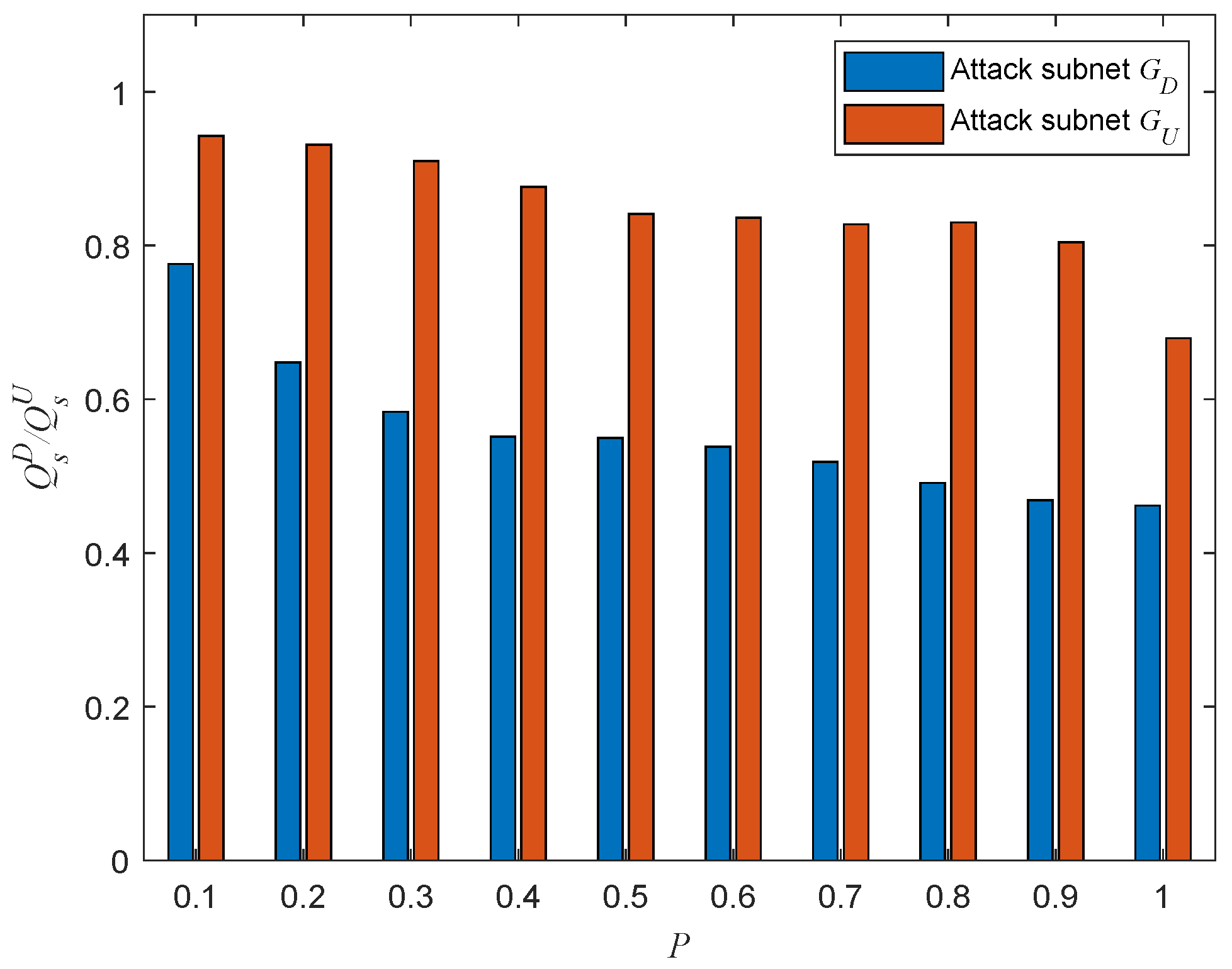
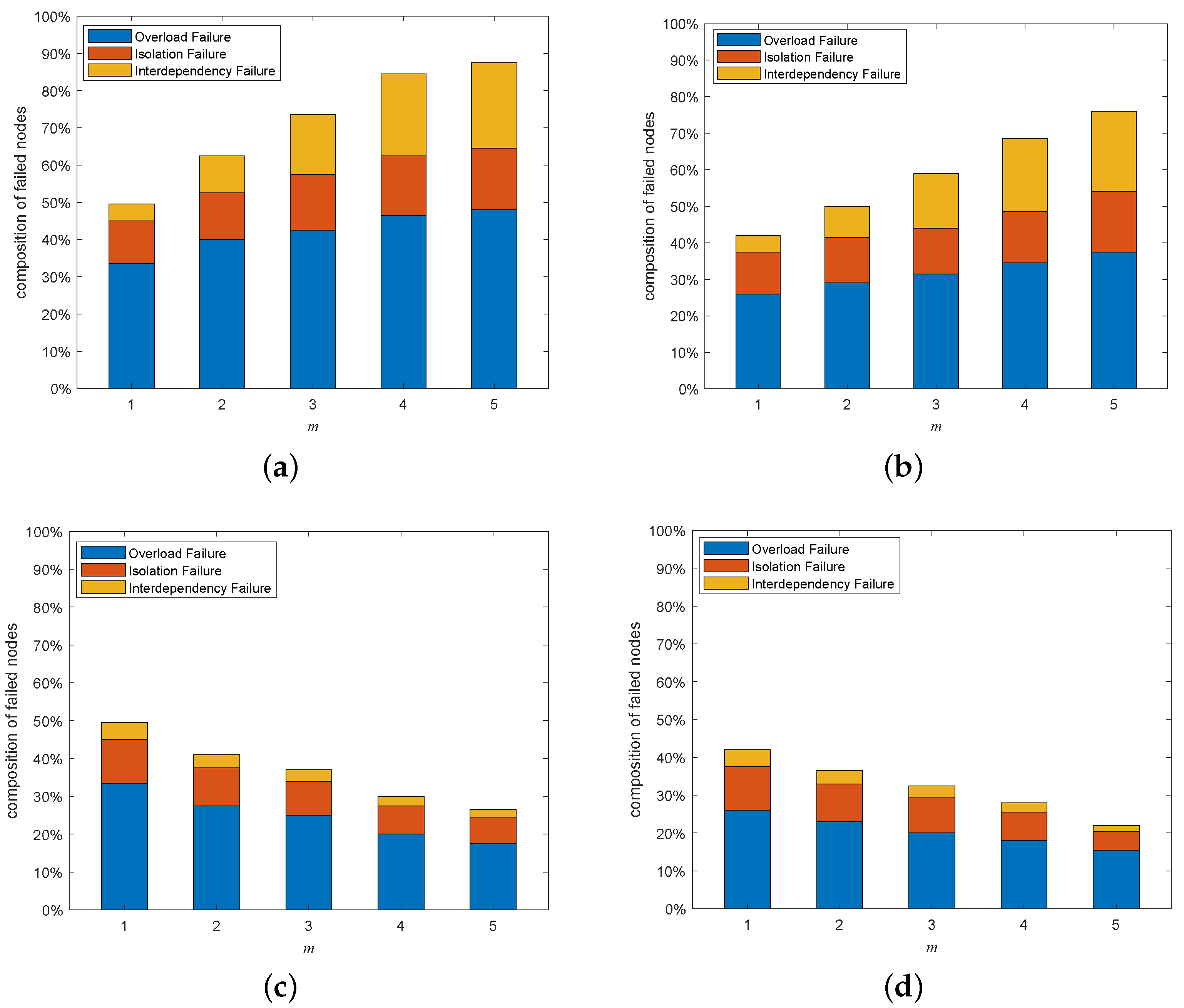
5.6. Composition Analysis on Cascading Failures
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- De Domenico, M.; Granell, C.; Porter, M.A.; Arenas, A. The physics of spreading processes in multilayer networks. Nat. Phys. 2016, 12, 901–906. [Google Scholar] [CrossRef]
- Fu, X.; Yao, H.; Yang, Y. Modeling and optimizing the cascading robustness of multisink wireless sensor networks. IEEE Trans. Reliab. 2020, 70, 121–133. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Fu, X.; Yang, Y. Modeling and analyzing cascading failures for Internet of Things. Inf. Sci. 2021, 545, 753–770. [Google Scholar] [CrossRef]
- Rosato, V.; Issacharoff, L.; Tiriticco, F.; Meloni, S.; Porcellinis, S.; Setola, R. Modelling interdependent infrastructures using interacting dynamical models. Int. J. Crit. Infrastruct. 2008, 4, 63–79. [Google Scholar] [CrossRef]
- Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. Identifying, understanding, and analyzing critical infrastructure interdependencies. IEEE Control Syst. Mag. 2001, 21, 11–25. [Google Scholar]
- Vaknin, D.; Bashan, A.; Braunstein, L.A.; Buldyrev, S.V.; Havlin, S. Cascading failures in anisotropic interdependent networks of spatial modular structures. New J. Phys. 2021, 23, 113001. [Google Scholar] [CrossRef]
- Wang, N.; Jin, Z.Y.; Zhao, J. Cascading failures of overload behaviors on interdependent networks. Phys. A Stat. Mech. Its Appl. 2021, 574, 125989. [Google Scholar] [CrossRef]
- Zio, E. Challenges in the vulnerability and risk analysis of critical infrastructures. Reliab. Eng. Syst. Saf. 2016, 152, 137–150. [Google Scholar] [CrossRef]
- Bashan, A.; Parshani, R.; Havlin, S. Percolation in networks composed of connectivity and dependency links. Phys. Rev. E 2011, 83, 051127. [Google Scholar] [CrossRef]
- Bachmann, I.; Bustos-Jiménez, J.; Bustos, B. A survey on frameworks used for robustness analysis on interdependent networks. Complexity 2020, 2020, 2363514. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, G.; Liu, L.; Hill, D.J. Cascading risk assessment in power-communication interdependent networks. Phys. A Stat. Mech. Its Appl. 2020, 540, 120496. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Zhang, N.; Song, G.; Wang, Q.; Ran, B. Effects of mutual traffic redistribution on robustness of interdependent networks to cascading failures under fluctuant load. Phys. A Stat. Mech. Its Appl. 2020, 560, 125138. [Google Scholar] [CrossRef]
- Zhou, D.; Stanley, H.E.; D’Agostino, G.; Scala, A. Assortativity decreases the robustness of interdependent networks. Phys. Rev. E 2012, 86, 066103. [Google Scholar] [CrossRef]
- Shi, X.; Long, W.; Li, Y.; Deng, D. Robustness of interdependent supply chain networks against both functional and structural cascading failures. Phys. A Stat. Mech. Its Appl. 2022, 586, 126518. [Google Scholar] [CrossRef]
- Baycik, N.O.; Sharkey, T.C.; Rainwater, C.E. Interdicting layered physical and information flow networks. IISE Trans. 2018, 50, 316–331. [Google Scholar] [CrossRef]
- Fu, X.; Pace, P.; Aloi, G.; Guerrieri, A.; Li, W.; Fortino, G. Tolerance Analysis of Cyber-Manufacturing Systems to Cascading Failures. ACM Trans. Internet Technol. 2023. [Google Scholar] [CrossRef]
- Fu, X.; Wang, Y.; Yang, Y.; Postolache, O. Analysis on cascading reliability of edge-assisted Internet of Things. Reliab. Eng. Syst. Saf. 2022, 223, 108463. [Google Scholar] [CrossRef]
- Radicchi, F. Percolation in real interdependent networks. Nat. Phys. 2015, 11, 597–602. [Google Scholar] [CrossRef]
- Gao, J.; Barzel, B.; Barabási, A.L. Universal resilience patterns in complex networks. Nature 2016, 530, 307–312. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Mu, D.; Yue, X.; Ren, H. Robustness of Cyber-Physical Supply Networks in Cascading Failures. Entropy 2021, 23, 769. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Magoua, J.J.; Li, N. Modeling cascading failure of interdependent critical infrastructure systems using HLA-based co-simulation. Autom. Constr. 2022, 133, 104008. [Google Scholar] [CrossRef]
- Yang, L.; Gu, Z.; Dang, Y.; He, P. Analysis of Vulnerability on Weighted Power Networks under Line Breakdowns. Entropy 2022, 24, 1449. [Google Scholar] [CrossRef]
- Tang, L.; Jing, K.; He, J.; Stanley, H.E. Complex interdependent supply chain networks: Cascading failure and robustness. Phys. A Stat. Mech. Its Appl. 2016, 443, 58–69. [Google Scholar] [CrossRef]
- Peng, H.; Qian, Z.; Kan, Z.; Zhao, D.; Yu, J.; Han, J. Cascading failure dynamics against intentional attack for interdependent industrial internet of things. Complexity 2021, 2021, 7181431. [Google Scholar] [CrossRef]
- Parshani, R.; Rozenblat, C.; Ietri, D.; Ducruet, C.; Havlin, S. Inter-similarity between coupled networks. EPL (Europhys. Lett.) 2011, 92, 68002. [Google Scholar] [CrossRef]
- Parshani, R.; Buldyrev, S.V.; Havlin, S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett. 2010, 105, 048701. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, F.; Yang, S.; Li, D. Restoration of interdependent network against cascading overload failure. Phys. A Stat. Mech. Its Appl. 2019, 514, 884–891. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, C.; Qian, J. Robustness of interdependent networks with different link patterns against cascading failures. Phys. A Stat. Mech. Its Appl. 2014, 393, 535–541. [Google Scholar] [CrossRef]
- Shao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Cascade of failures in coupled network systems with multiple support-dependence relations. Phys. Rev. E 2011, 83, 036116. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhou, W.; Li, R.; Cao, J.; Lin, X. Improving robustness of interdependent networks by a new coupling strategy. Phys. A Stat. Mech. Its Appl. 2018, 492, 1075–1080. [Google Scholar] [CrossRef]
- Hong, S.; Zhang, X.; Zhu, J.; Zhao, T.; Wang, B. Suppressing failure cascades in interconnected networks: Considering capacity allocation pattern and load redistribution. Mod. Phys. Lett. B 2016, 30, 1650049. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef]
- Gao, X.; Peng, M.; Chi, K.T.; Zhang, H. A stochastic model of cascading failure dynamics in cyber-physical power systems. IEEE Syst. J. 2020, 14, 4626–4637. [Google Scholar] [CrossRef]
- Yin, R.R.; Liu, B.; Liu, H.R.; Li, Y.Q. The critical load of scale-free fault-tolerant topology in wireless sensor networks for cascading failures. Phys. A Stat. Mech. Its Appl. 2014, 409, 8–16. [Google Scholar] [CrossRef]
- Li, Y.P.; Li, J.; Wang, N.; Che, X.S.; Chen, H.B.; Liu, Z.T. Optical and structural properties of co-sputtered Ge1-xCx thin films as a function of the substrate temperature. Thin Solid Films 2014, 551, 74–78. [Google Scholar] [CrossRef]
- Cai, Y.; Cao, Y.; Li, Y.; Huang, T.; Zhou, B. Cascading failure analysis considering interaction between power grids and communication networks. IEEE Trans. Smart Grid 2015, 7, 530–538. [Google Scholar] [CrossRef]






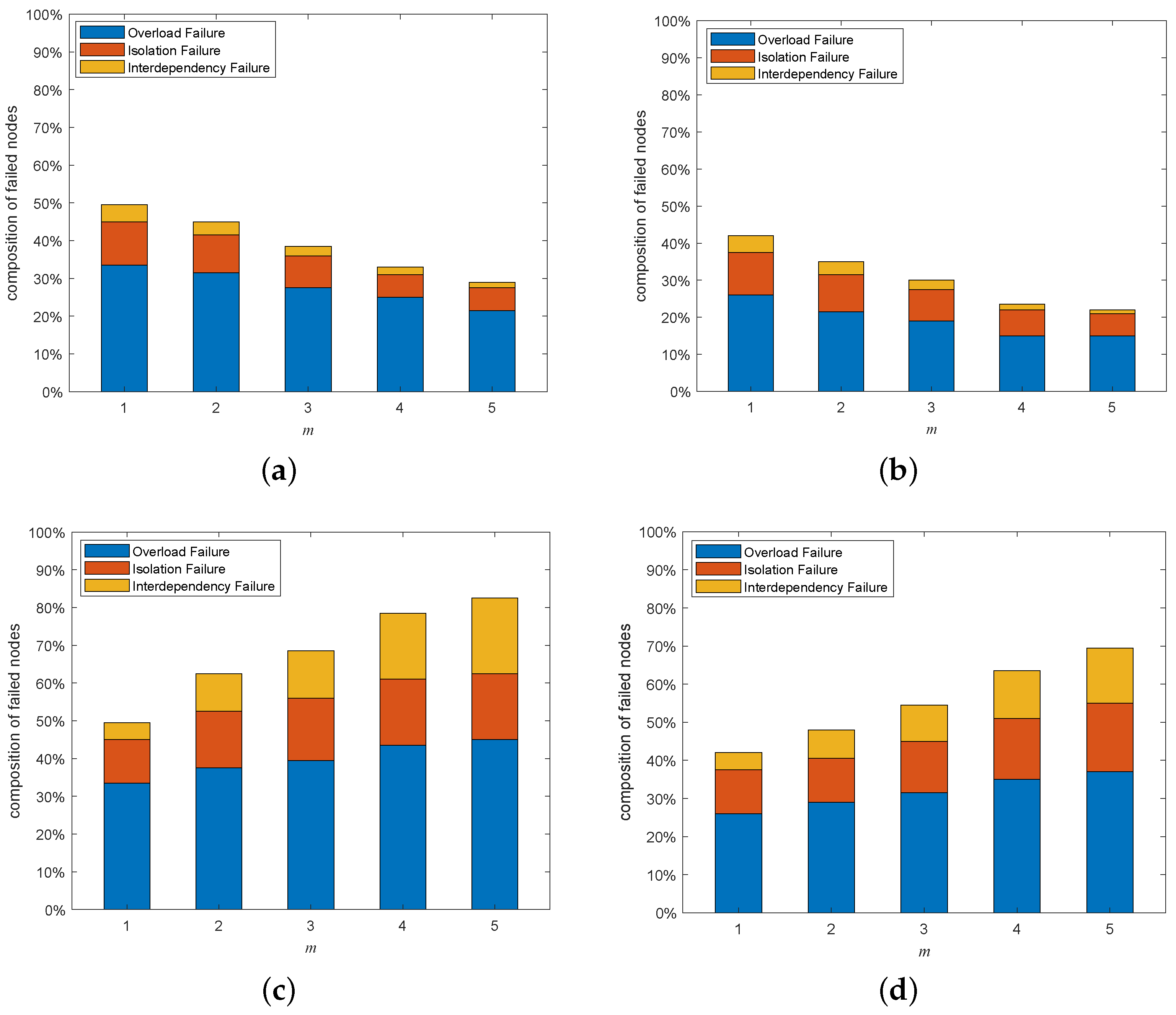
| Reference | Network Type | Coupling Pattern | Subnet Type | Interdependent Edge Type |
|---|---|---|---|---|
| [19] | Power-Information Network | one-to-one | Undirected-Undirected | Undirected |
| [20] | Power-Information Network | one-to-one | Undirected-Undirected | Undirected |
| [21] | Supply-Information Network | one-to-one | Undirected-Undirected | Undirected |
| [22] | Water-Power Network | one-to-one | Undirected-Undirected | Undirected |
| [23] | Supply-Information Network | one-to-one | Directed-Undirected | Undirected |
| [24] | IoT-Information Network | one-to-three | Undirected-Undirected | Undirected |
| [25] | Seaport-Airport- World-wide Airport Network | one-to-one | Undirected-Undirected-Undirected | Undirected |
| [26] | General Network | one-to-one | Undirected-Undirected | Undirected |
| [27] | General Network | one-to-one | Undirected-Undirected | Undirected |
| [28] | General Network | one-to-one | Undirected-Undirected | Undirected |
| [29] | General Network | one-to-one | Undirected-Undirected | Undirected |
| [30] | General Network | one-to-one | Undirected-Undirected | Undirected |
| Notation | Description |
|---|---|
| The directed subnet. | |
| The undirected subnet. | |
| The set of nodes in subnet . | |
| The set of nodes in subnet . | |
| The set of connectivity links in subnet . | |
| The set of connectivity links in subnet . | |
| A node i in directed subnet . | |
| A node i in directed subnet . | |
| Interdependent edge matrix between subnet. | |
| Node number in subnet . | |
| Node number in subnet . | |
| Number of nodes with interdependent edges in subnet . | |
| Number of nodes with interdependent edges in subnet . | |
| Proportion of nodes with interdependent edges in subnet . | |
| Proportion of nodes with interdependent edges in subnet . | |
| P | Proportion of nodes with interdependent edges in both subnet of one-to-one interdependent networks. |
| Degree of node . | |
| Degree of node . | |
| In-degree of node . | |
| Out-degree of node . | |
| Average degree of subnet . | |
| Average degree of subnet . | |
| The set of out-degree nodes of node . | |
| The set of out-degree nodes of node . | |
| p | Proportion of nodes initially removed under multi-node attack. |
| The set of the initially removed nodes in subnet . | |
| The set of overload failure nodes in subnet at time t. | |
| The set of isolation failure nodes in subnet at time t. | |
| The set of interdependency failure nodes in subnet at time t. | |
| The set of failure nodes in subnet at time t. | |
| The set of overload failure nodes in subnet at time t. | |
| The set of isolation failure nodes in subnet at time t. | |
| The set of interdependency failure nodes in subnet at time t. | |
| The set of failure nodes in subnet at time t. | |
| The set of failure nodes in directed–undirected interdependent network G at time t. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Fu, X. Analysis on Cascading Failures of Directed–Undirected Interdependent Networks with Different Coupling Patterns. Entropy 2023, 25, 471. https://doi.org/10.3390/e25030471
Xu X, Fu X. Analysis on Cascading Failures of Directed–Undirected Interdependent Networks with Different Coupling Patterns. Entropy. 2023; 25(3):471. https://doi.org/10.3390/e25030471
Chicago/Turabian StyleXu, Xiaojie, and Xiuwen Fu. 2023. "Analysis on Cascading Failures of Directed–Undirected Interdependent Networks with Different Coupling Patterns" Entropy 25, no. 3: 471. https://doi.org/10.3390/e25030471
APA StyleXu, X., & Fu, X. (2023). Analysis on Cascading Failures of Directed–Undirected Interdependent Networks with Different Coupling Patterns. Entropy, 25(3), 471. https://doi.org/10.3390/e25030471







