An Efficient Quantum Secret Sharing Scheme Based on Restricted Threshold Access Structure
Abstract
1. Introduction
2. Preliminary Knowledge
3. The Proposed Protocol
3.1. Initialization Phase
3.2. Share Distribution Phase
3.3. Detecting Eavesdropping
3.4. Measuring Information Particles
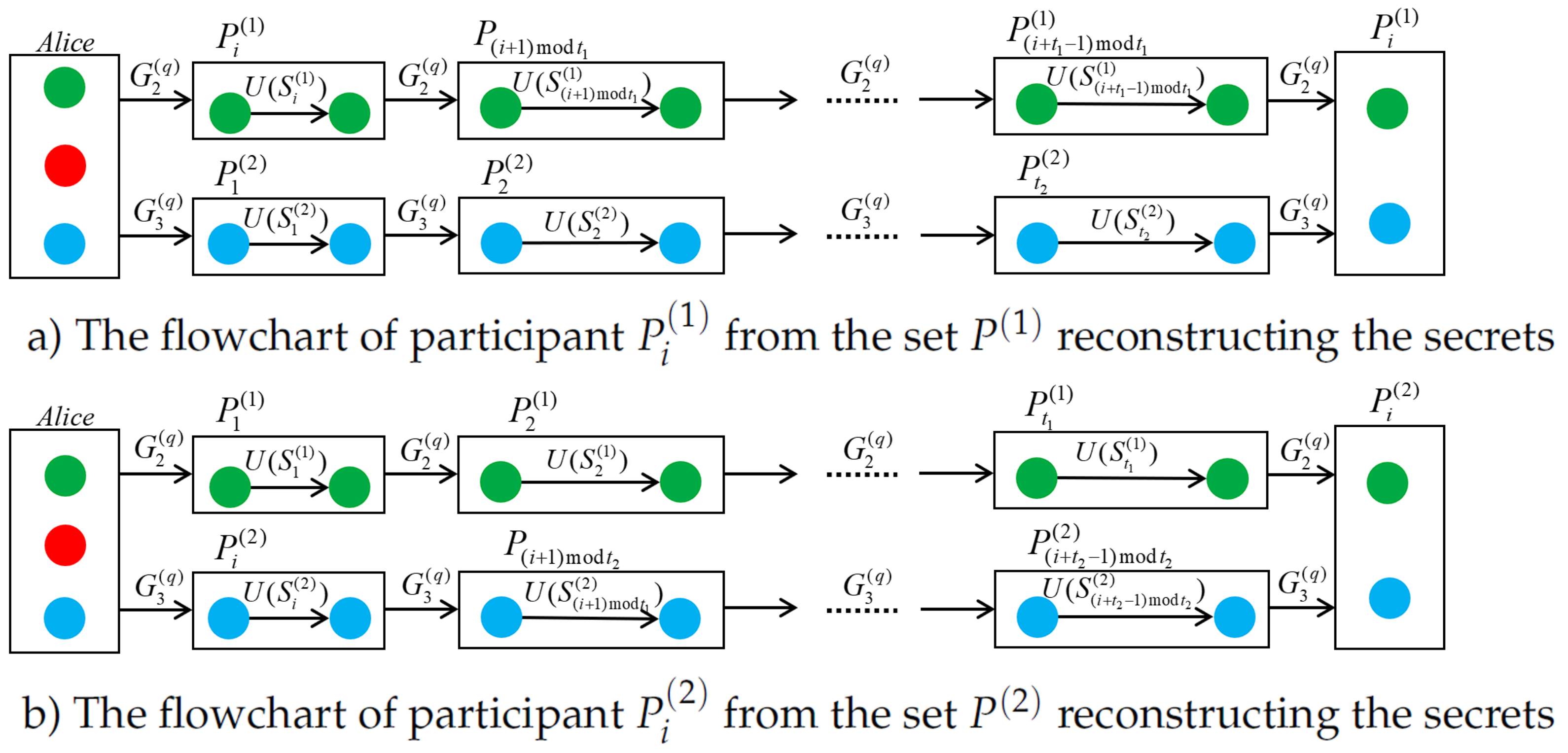
3.5. Reconstruction and Detection of Keys
4. Performance Analysis
4.1. Correctness
4.2. Security Analysis of the Protocol
4.2.1. Direct Measurement by the Attacker
4.2.2. Interception–Relaunch Attack
4.2.3. Entanglement Measurement Attack
5. Comparisons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shamir, A. How to share a secret. Commun. Acm. 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Blakley, G. Safeguarding cryptographic keys. In Proceedings of the 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; Volume 48, pp. 313–317. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–19 December 1984; pp. 175–179. [Google Scholar]
- Goldenberg, L.; Vaidman, L. Quantum cryptography based on orthogonal states. Phys. Rev. Lett. 1995, 75, 1239. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.B.; Yu, Z.W.; Hu, X.L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 2018, 98, 062323. [Google Scholar] [CrossRef]
- Cleve, R.; Gottesman, D.; Lo, H. How to share a quantum secret. Phys. Rev. Lett. 1999, 83, 648–651. [Google Scholar] [CrossRef]
- Hillery, M.; Buzek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef]
- Guo, G.P.; Guo, G.C. Quantum secret sharing without entanglement. Phys. Rev. A 2003, 310, 247–251. [Google Scholar] [CrossRef]
- Hsu, L. Quantum secret-sharing protocol based on Grover’s algorithm. Phys. Rev. A 2003, 68, 022306. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Man, Z. Multiparty quantum secret sharing. Phys. Rev. A 2005, 71, 044301. [Google Scholar] [CrossRef]
- Bai, C.M.; Li, Z.H.; Li, Y.M. Improving fidelity of quantum secret sharing in noisy environments. Eur. Phys. J. D. 2018, 72, 126. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, X.; Jia, H.; Zhang, L. A new n-party quantum secret sharing model based on multiparty entangled states. Quantum Inf. Process. 2019, 18, 81. [Google Scholar] [CrossRef]
- Sutradhar, K.; Om, H. Efficient quantum secret sharing without a trusted player. Quantum Inf. Process. 2020, 19, 73. [Google Scholar] [CrossRef]
- Chou, Y.H.; Zeng, G.J.; Chen, X.Y.; Kuo, S.Y. Multiparty weighted threshold quantum secret sharing based on the Chinese remainder theorem to share quantum information. Sci. Rep. 2021, 11, 6093. [Google Scholar] [CrossRef]
- Tavakoli, A.; Herbauts, I.; Zukowski, M.; Bourennane, M. Secret sharing with a single d-level quantum system. Phys. Rev. A 2015, 92, 030302(R). [Google Scholar] [CrossRef]
- Bai, C.M.; Li, Z.H.; Wang, J.T.; Liu, C.J.; Li, Y.M. Restricted (k, n)-threshold quantum secret sharing scheme based on local distinguishability of orthogonal multiqudit entangled states. Quantum Inf. Process. 2018, 17, 312. [Google Scholar] [CrossRef]
- Liu, L.J.; Li, Z.H.; Han, Z.W.; Zhi, D.L. A quantum secret sharing scheme with veriable function. Eur. Phys. J. D 2020, 74, 154. [Google Scholar] [CrossRef]
- Hsu, L.Y. Quantum Secret Sharing Using Product Statesm. Phys. Rev. A 2005, 71, 159. [Google Scholar] [CrossRef]
- Yang, Y.G.; Wen, Q.Y.; Zhu, F.C. An Efficient Quantum Secret Sharing Protocol with Orthogonal Product States. Sci. China Ser. G 2007, 50, 331–338. [Google Scholar] [CrossRef]
- Xu, J.; Chen, H.W.; Liu, W.J.; Liu, Z.H. An Efficient Quantum Secret Sharing Scheme Based on Orthogonal Product States. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–4. [Google Scholar]
- Gheorghiu, V.; Sanders, B.C. Accessing quantum secrets via local operations and classical communication. Phys. Rev. A 2013, 88, 022340. [Google Scholar] [CrossRef]
- Rahaman, R.; Parker, M.G. Quantum secret sharing based on local distinguishability. Phys. Rev. A 2015, 91, 022330. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Peng, H.; Yang, Y. Quantum-secret-sharing scheme based on local distinguishability of orthogonal multiqudit entangled states. Phys. Rev. A 2017, 95, 022320. [Google Scholar] [CrossRef]
- Li, M.S.; Shi, F.; Wang, Y.L. Local discrimination of generalized Bell states via commutativity. Phys. Rev. A 2022, 105, 032455. [Google Scholar] [CrossRef]
- Li, F.L.; Yan, J.Y.; Zhu, S.X. General quantum secret sharing scheme based on two-Qudit. Quantum Inf. Process. 2021, 20, 328. [Google Scholar] [CrossRef]
- Yang, Y.H.; Gao, F.; Wu, X.; Qin, S.; Zuo, H.; Wen, Q. Quantum secret sharing via local operations and classical communication. Sci. Rep. 2015, 5, 16967. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Zhu, X.; Dai, Y. (t, n) threshold quantum secret sharing using the phase shift operation. Quantum Inf. Process. 2015, 14, 2997–3004. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University: Cambridge, UK, 2002. [Google Scholar]
- Song, X.; Liu, Y.; Deng, H.; Xiao, Y. (t, n) threshold d-level quantum secret sharing. Sci. Rep. 2017, 7, 6366. [Google Scholar] [CrossRef]
- Lu, C.; Miao, F.; Meng, K.; Yu, Y. Threshold quantum secret sharing based on single qubit. Quantum Inf. Process. 2018, 17, 64. [Google Scholar] [CrossRef]
- Yan, C.H.; Li, Z.H.; Liu, L.; Lu, D.J. Cheating identifiable (k, n) threshold quantum secret sharing scheme. Quantum Inf. Process. 2022, 21, 8. [Google Scholar] [CrossRef]
- Cabello, A. Quantum key distribution in the Holevo limit. Phys. Rev. Lett. 2000, 85, 5635–5638. [Google Scholar] [CrossRef]

| Measurements of | ||||
|---|---|---|---|---|
| Alice | ||||
| RP2015 [22] | YGWQZW2015 [26] | BLWLL2018 [16] | LYZ2021 [25] | Our Scheme | |
|---|---|---|---|---|---|
| Number of participants reconstruction key | 2 | 2 | k | 1 | 1 |
| Information particle trajectories | Tree form | Tree form | Tree form | Single circle | Double circle |
| Information quantum states | GHZ state (with t particles) | GHZ state (with t particles) | GHZ state (with t particles) | Generalised Bell state (with two particles) | GHZ state (with three particles) |
| The dimension of information quantum states | 2 | k | k | k | 2 |
| Detection of quantum states | GHZ state (with t particles) | Single photon | GHZ state (with t particles) | Single photon | Three dimensions GHZ state |
| Number of measurements | |||||
| Number of unitary operations | 0 | 0 | 0 | ||
| Hash function | N | N | N | Y | Y |
| Information efficiency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, Z. An Efficient Quantum Secret Sharing Scheme Based on Restricted Threshold Access Structure. Entropy 2023, 25, 265. https://doi.org/10.3390/e25020265
Li L, Li Z. An Efficient Quantum Secret Sharing Scheme Based on Restricted Threshold Access Structure. Entropy. 2023; 25(2):265. https://doi.org/10.3390/e25020265
Chicago/Turabian StyleLi, Lei, and Zhi Li. 2023. "An Efficient Quantum Secret Sharing Scheme Based on Restricted Threshold Access Structure" Entropy 25, no. 2: 265. https://doi.org/10.3390/e25020265
APA StyleLi, L., & Li, Z. (2023). An Efficient Quantum Secret Sharing Scheme Based on Restricted Threshold Access Structure. Entropy, 25(2), 265. https://doi.org/10.3390/e25020265





