Temporal, Structural, and Functional Heterogeneities Extend Criticality and Antifragility in Random Boolean Networks
Abstract
1. Introduction
2. Methods
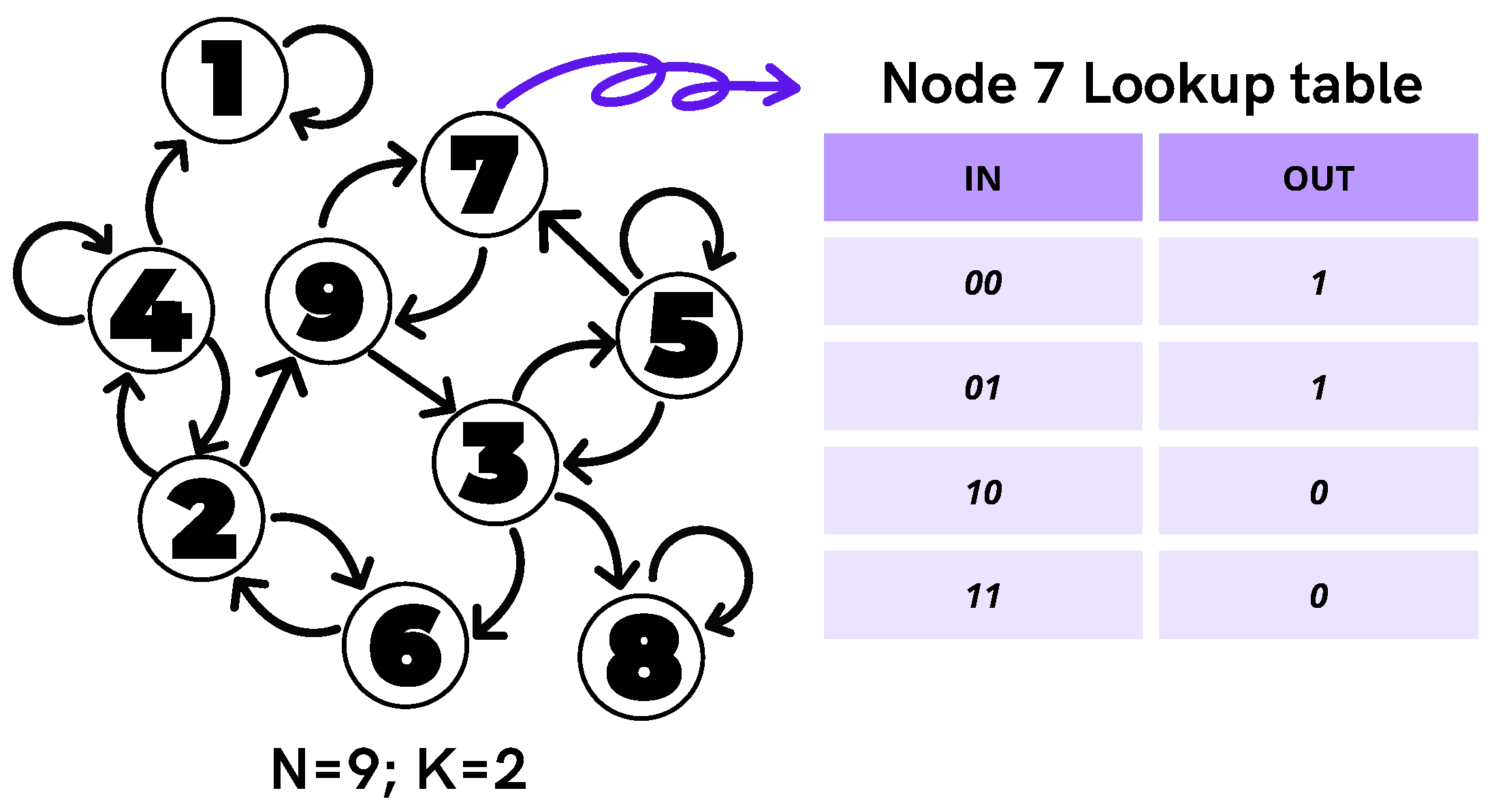
2.1. Random Boolean Networks
- Each gene is regulated by exactly K other genes.
- The K genes that regulate each node are chosen randomly using a uniform probability.
- All genes are updated synchronously, i.e., at the same timescale [47].
- Each gene is expressed (i.e., its Boolean value is 1) with probability p and is unexpressed with probability .
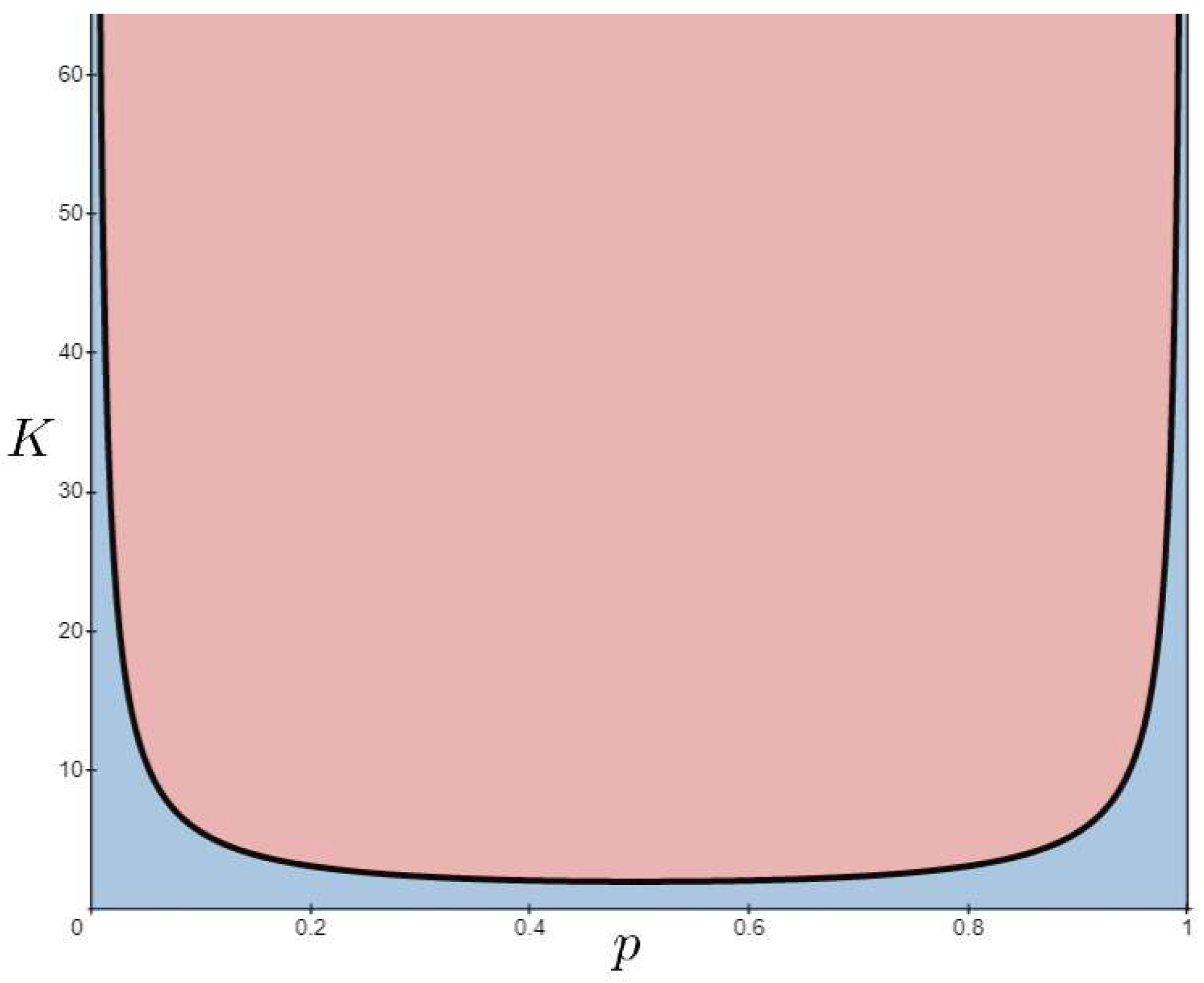
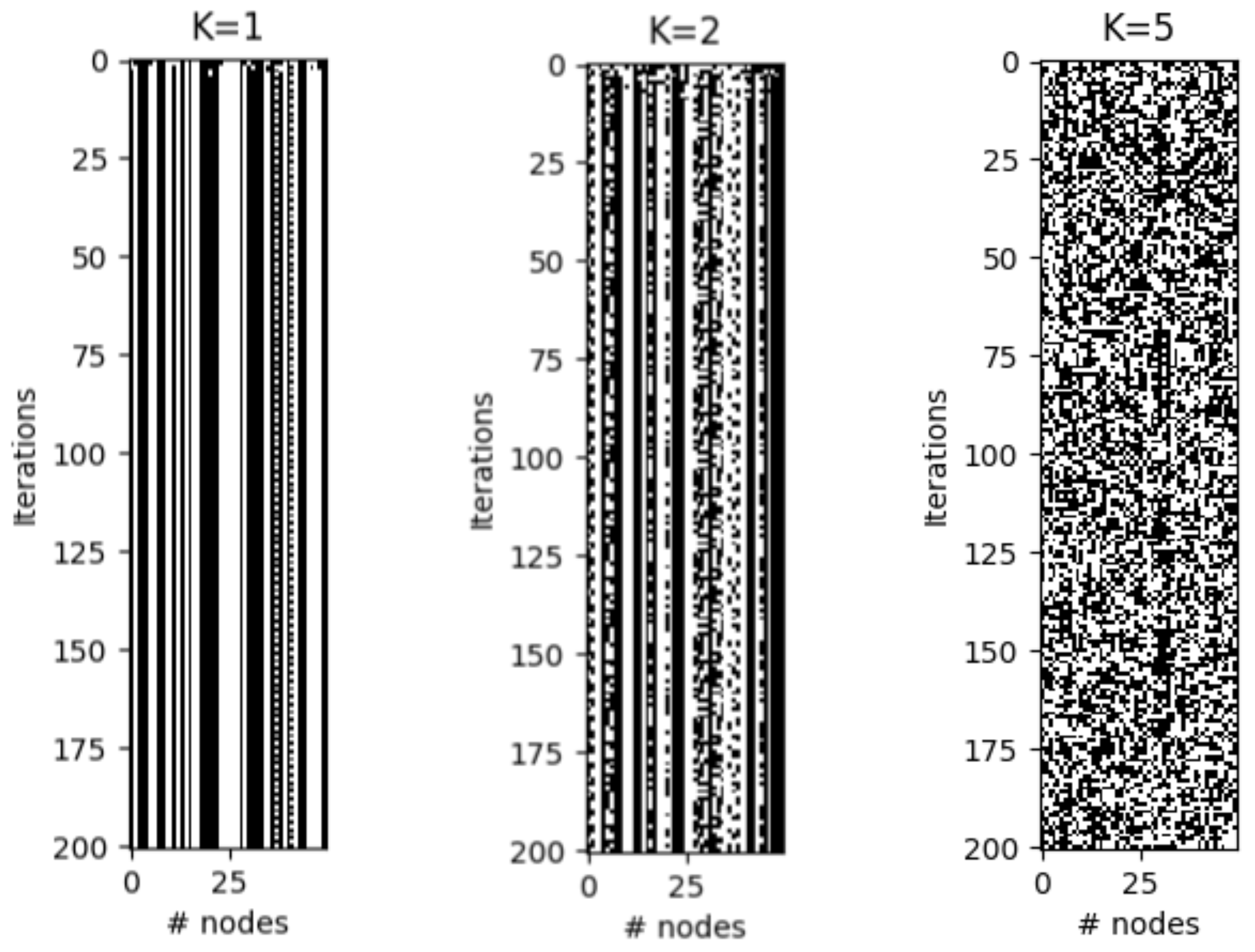
2.2. Criticality
2.3. Antifragility
3. Results and Discussion
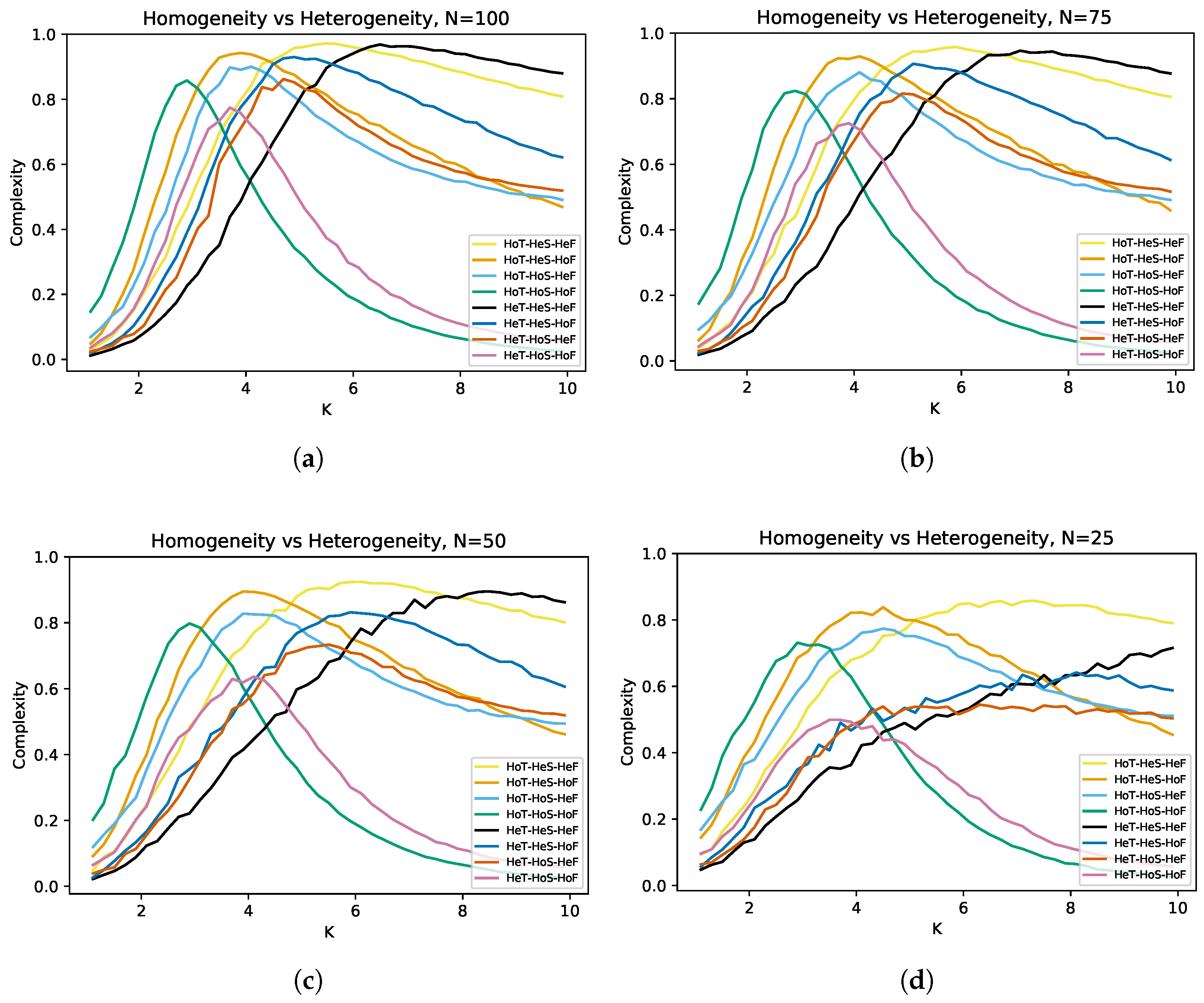
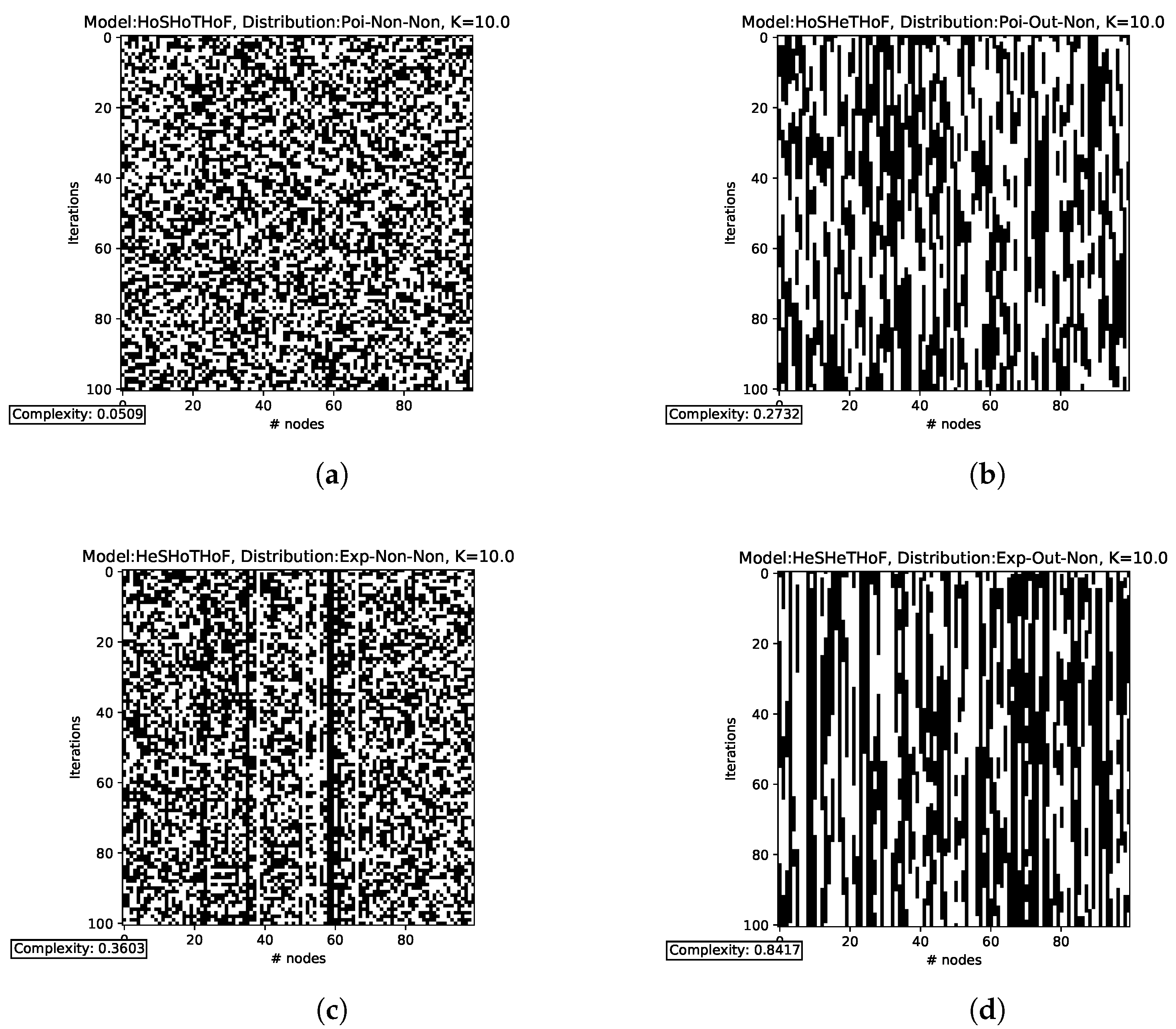
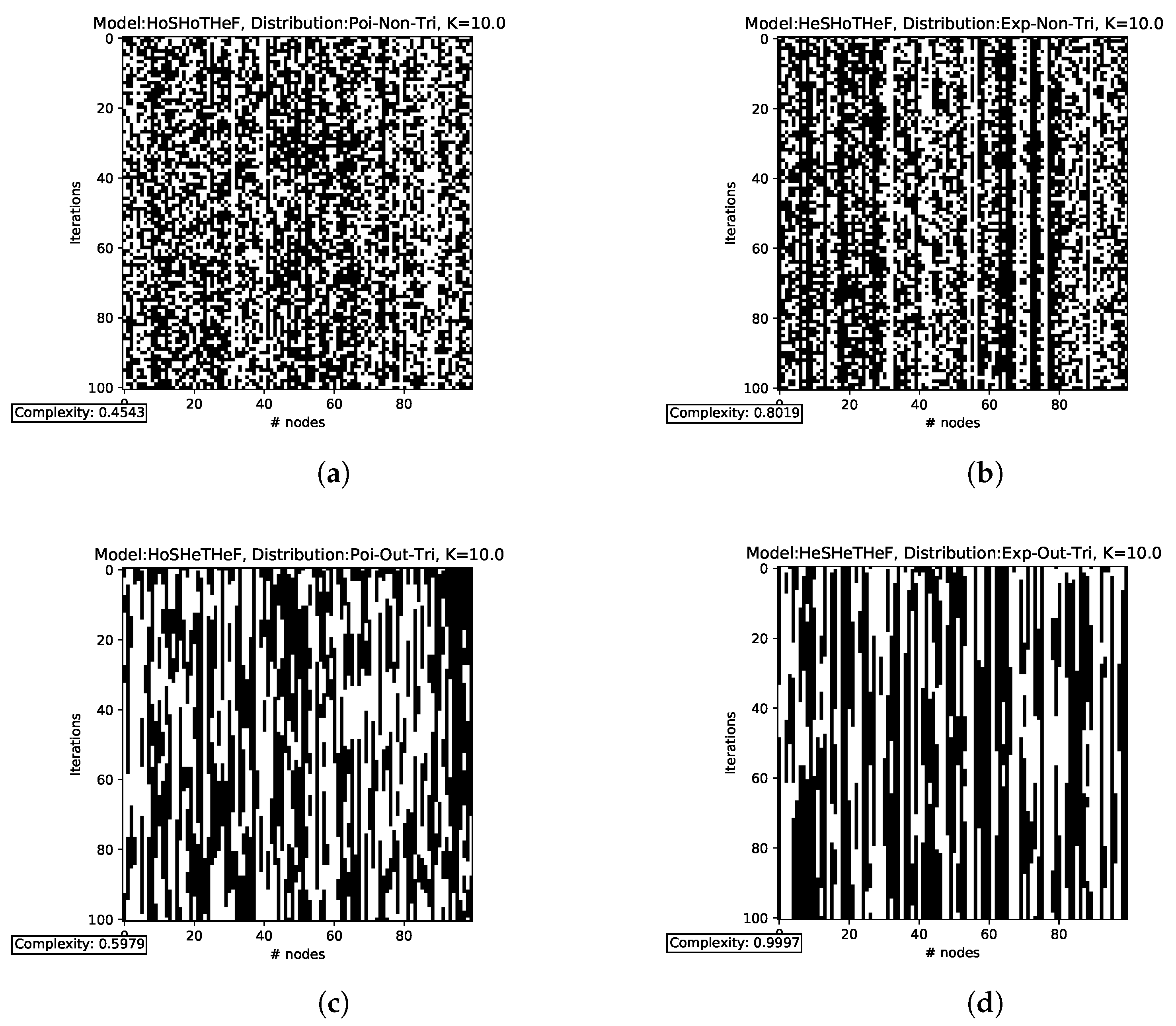
3.1. Homogeneity vs. Heterogeneity
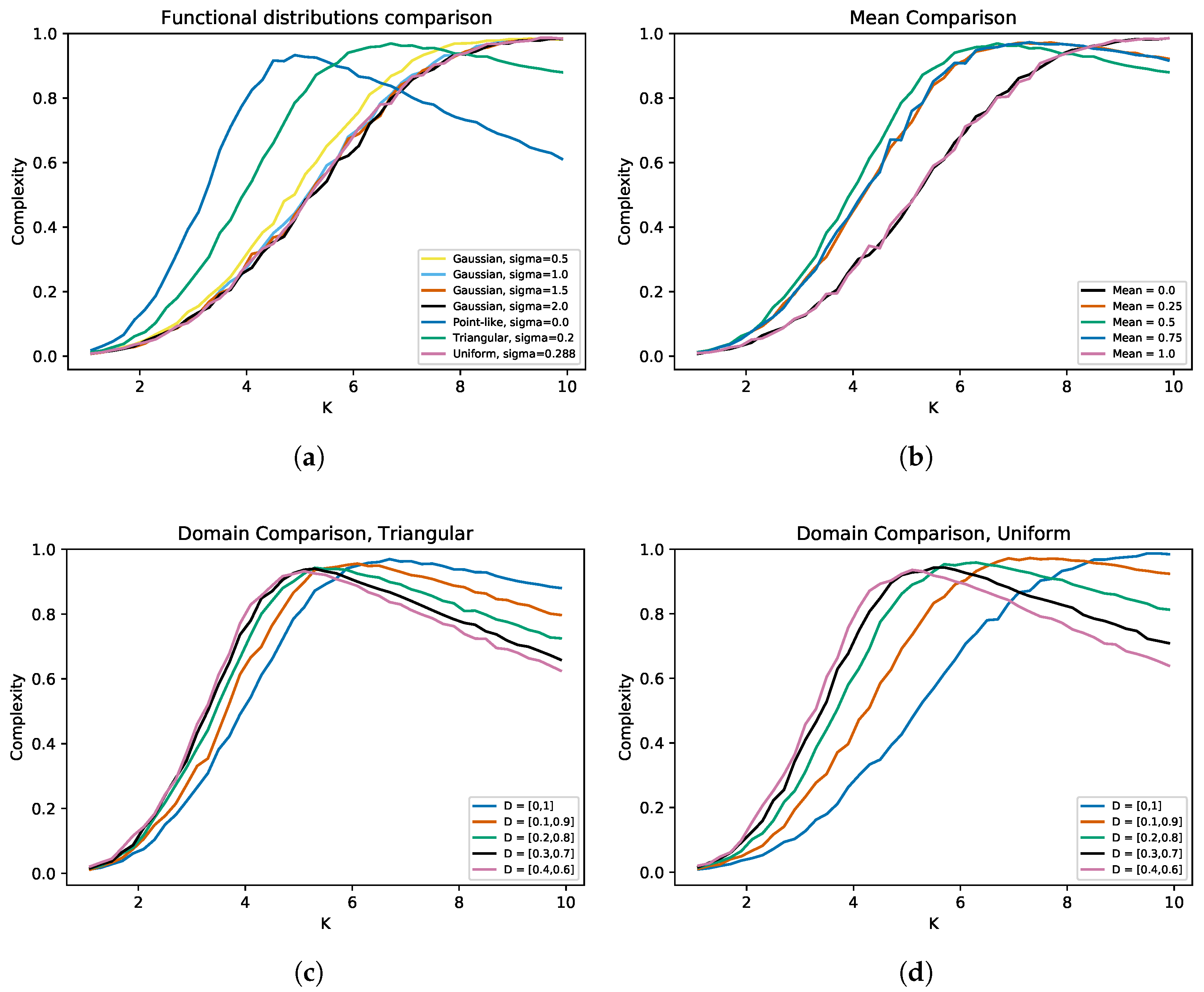
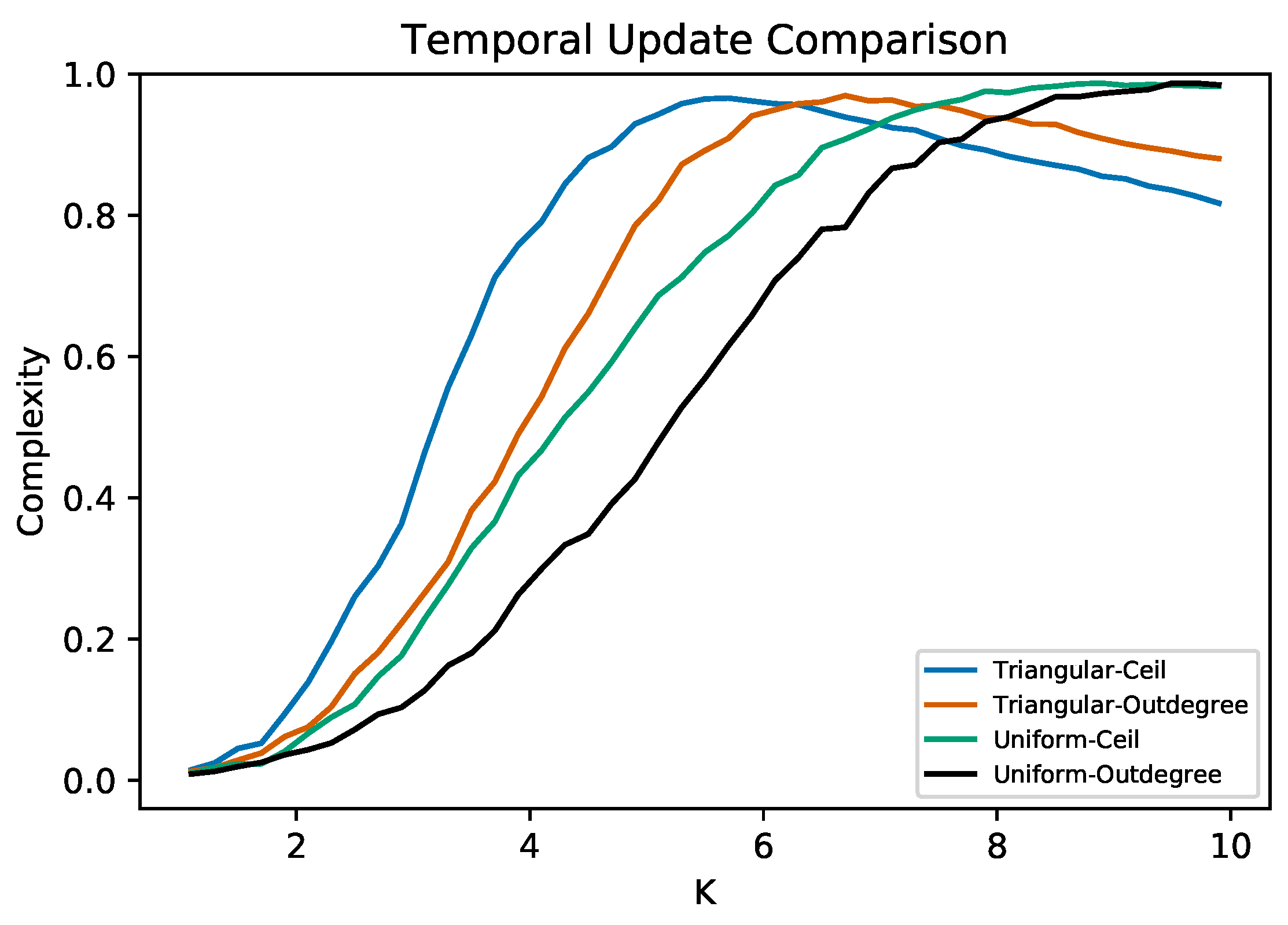
3.2. Varying Functional and Temporal Parameters
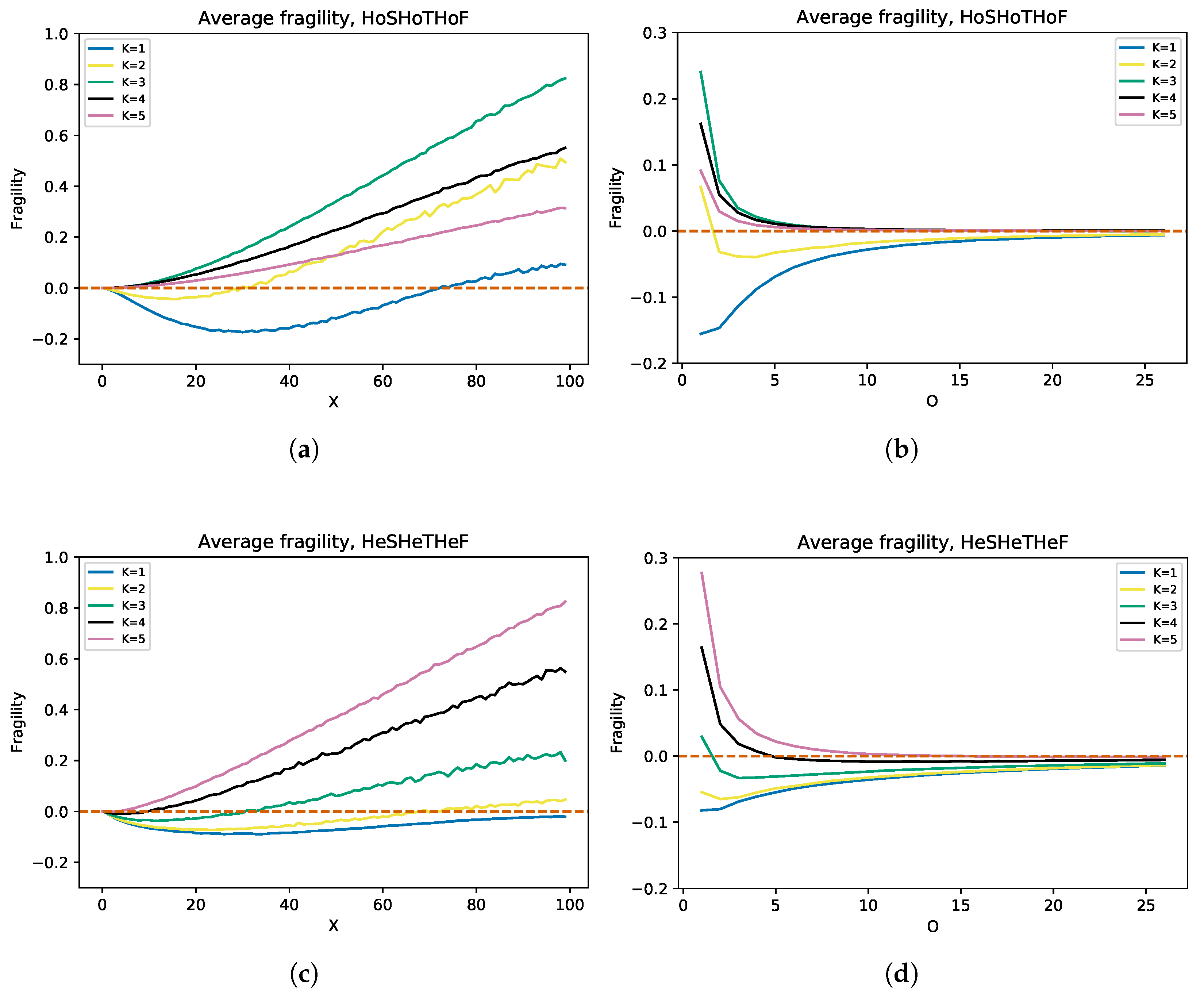
3.3. Antifragility
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RBN | Random Boolean network |
Appendix A. Code
Appendix A.1. mi_ rbn.py
Appendix A.2. complexity.py
Appendix A.3. antifragility.py
References
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Haimovici, A.; Tagliazucchi, E.; Balenzuela, P.; Chialvo, D.R. Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett. 2013, 110, 178101. [Google Scholar] [CrossRef] [PubMed]
- Setzler, M.; Marghetis, T.; Kim, M. Creative leaps in musical ecosystems: Early warning signals of critical transitions in professional jazz. In CogSci 2018. Changing/Minds. 40th Annual Cognitive Science Society Meeting, Madison WI, USA, 25–28 July 2018; Kalish, C., Rau, M., Zhu, J., Rogers, T., Eds.; pp. 2467–2472. Available online: https://cogsci.mindmodeling.org/2018/ (accessed on 1 September 2022).
- Christensen, K.; Moloney, N.R. Complexity and Criticality; World Scientific: Singapore, 2005. [Google Scholar]
- Mora, T.; Bialek, W. Are Biological Systems Poised at Criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef]
- Roli, A.; Villani, M.; Filisetti, A.; Serra, R. Dynamical Criticality: Overview and Open Questions. J. Syst. Sci. Complex. 2018, 31, 647–663. [Google Scholar] [CrossRef]
- Taleb, N.N. Antifragile: Things That Gain From Disorder; Random House: London, UK, 2012. [Google Scholar]
- Aven, T. The concept of antifragility and its implications for the practice of risk analysis. Risk Anal. 2015, 35, 476–483. [Google Scholar] [CrossRef] [PubMed]
- Danchin, A.; Binder, P.M.; Noria, S. Antifragility and tinkering in biology (and in business) flexibility provides an efficient epigenetic way to manage risk. Genes 2011, 2, 998–1016. [Google Scholar] [CrossRef]
- Abid, A.; Khemakhem, M.T.; Marzouk, S.; Jemaa, M.B.; Monteil, T.; Drira, K. Toward antifragile cloud computing infrastructures. Procedia Comput. Sci. 2014, 32, 850–855. [Google Scholar] [CrossRef]
- Jones, K.H. Engineering antifragile systems: A change in design philosophy. Procedia Comput. Sci. 2014, 32, 870–875. [Google Scholar] [CrossRef]
- Kauffman, S.A. Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Aldana-González, M.; Coppersmith, S.; Kadanoff, L.P. Boolean Dynamics with Random Couplings. In Perspectives and Problems in Nonlinear Science. A Celebratory Volume in Honor of Lawrence Sirovich; Applied Mathematical Sciences Series; Kaplan, E., Marsden, J.E., Sreenivasan, K.R., Eds.; Springer: Berlin, Germany, 2003. [Google Scholar] [CrossRef]
- Gershenson, C. Introduction to Random Boolean Networks. In Workshop and Tutorial Proceedings, Ninth International Conference on the Simulation and Synthesis of Living Systems (ALife IX), Boston, MA, USA, 12–15 September 2004; Bedau, M., Husbands, P., Hutton, T., Kumar, S., Suzuki, H., Eds.; ISAL: Boston, MA, USA, 2004; pp. 160–173. [Google Scholar] [CrossRef]
- Luque, B.; Solé, R.V. Phase Transitions in Random Networks: Simple Analytic Determination of Critical Points. Phys. Rev. E 1997, 55, 257–260. [Google Scholar] [CrossRef]
- Gershenson, C. Guiding the Self-organization of Random Boolean Networks. Theory Biosci. 2012, 131, 181–191. [Google Scholar] [CrossRef]
- von Neumann, J. The Theory of Self-Reproducing Automata; Burks, A.W., Ed.; University of Illinois Press: Champaign, IL, USA, 1966. [Google Scholar]
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Wuensche, A.; Lesser, M. The Global Dynamics of Cellular Automata; An Atlas of Basin of Attraction Fields of One-Dimensional Cellular Automata; Santa Fe Institute Studies in the Sciences of Complexity, Addison-Wesley: Reading, MA, USA, 1992. [Google Scholar]
- Griffiths, R.B. Nonanalytic Behavior Above the Critical Point in a Random Ising Ferromagnet. Phys. Rev. Lett. 1969, 23, 17–19. [Google Scholar] [CrossRef]
- Bray, A. Nature of the Griffiths phase. Phys. Rev. Lett. 1987, 59, 586. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Newman, M.; Barabási, A.L.; Watts, D.J. (Eds.) The Structure and Dynamics of Networks; Princeton Studies in Complexity, Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Munoz, M.A.; Juhász, R.; Castellano, C.; Ódor, G. Griffiths phases on complex networks. Phys. Rev. Lett. 2010, 105, 128701. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Gershenson, C.; Helbing, D. When slower is faster. Complexity 2015, 21, 9–15. [Google Scholar] [CrossRef]
- Carreón, G.; Gershenson, C.; Pineda, L.A. Improving public transportation systems with self-organization: A headway-based model and regulation of passenger alighting and boarding. PLoS ONE 2017, 12, e0190100. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M.; Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Lu, X.; Holme, P. Universal evolution patterns of degree assortativity in social networks. Soc. Netw. 2020, 63, 47–55. [Google Scholar] [CrossRef]
- Oosawa, C.; Savageau, M.A. Effects of Alternative Connectivity on Behavior of Randomly Constructed Boolean Networks. Phys. D 2002, 170, 143–161. [Google Scholar] [CrossRef]
- Aldana, M. Boolean Dynamics of Networks with Scale-Free Topology. Phys. D 2003, 185, 45–66. [Google Scholar] [CrossRef]
- Gershenson, C.; Kauffman, S.A.; Shmulevich, I. The Role of Redundancy in the Robustness of Random Boolean Networks. In Artificial Life X, Proceedings of the Tenth International Conference on the Simulation and Synthesis of Living Systems; Rocha, L.M., Yaeger, L.S., Bedau, M.A., Floreano, D., Goldstone, R.L., Vespignani, A., Eds.; MIT Press: Bloomington, IN, USA, 2006; pp. 35–42. [Google Scholar] [CrossRef]
- Sánchez-Puig, F.; Zapata, O.; Pineda, O.K.; Iñiguez, G.; Gershenson, C. Heterogeneity Extends Criticality. arXiv 2022, arXiv:2208.06439. [Google Scholar]
- Schlosser, G.; Wagner, G.P. Modularity in Development and Evolution; The University of Chicago Press: Chicago, IL, USA, 2004. [Google Scholar]
- Callebaut, W.; Rasskin-Gutman, D. Modularity: Understanding the Development and Evolution of Natural Complex Systems; Vienna Series in Theoretical Biology; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Poblanno-Balp, R.; Gershenson, C. Modular Random Boolean Networks. In Artificial Life XII Proceedings of the Twelfth International Conference on the Synthesis and Simulation of Living Systems, Odense, Denmark, 19–23 August 2010; Fellermann, H., Dörr, M., Hanczyc, M.M., Laursen, L.L., Maurer, S., Merkle, D., Monnard, P.A., Sty, K., Rasmussen, S., Eds.; MIT Press: Odense, Denmark, 2010; pp. 303–304. [Google Scholar] [CrossRef]
- Smith, C.; Pechuan, X.; Puzio, R.S.; Biro, D.; Bergman, A. Potential unsatisfiability of cyclic constraints on stochastic biological networks biases selection towards hierarchical architectures. J. R. Soc. Interface 2015, 12, 20150179. [Google Scholar] [CrossRef] [PubMed]
- Ódor, G.; Hartmann, B. Heterogeneity effects in power grid network models. Phys. Rev. E 2018, 98, 022305. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, F.; Bonachela, J.A.; López, C.; Munoz, M.A. Temporal griffiths phases. Phys. Rev. Lett. 2011, 106, 235702. [Google Scholar] [CrossRef]
- Iñiguez, G.; Pineda, C.; Gershenson, C.; Barabási, A.L. Universal dynamics of ranking. Nat. Commun. 2022, 13, 1646. [Google Scholar] [CrossRef]
- Wang, S.J.; Zhou, C. Hierarchical modular structure enhances the robustness of self-organized criticality in neural networks. New J. Phys. 2012, 14, 023005. [Google Scholar] [CrossRef]
- Moretti, P.; Muñoz, M.A. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun. 2013, 4, 1–10. [Google Scholar] [CrossRef]
- Ratnayake, P.; Weragoda, S.; Wansapura, J.; Kasthurirathna, D.; Piraveenan, M. Quantifying the Robustness of Complex Networks with Heterogeneous Nodes. Mathematics 2021, 9, 2769. [Google Scholar] [CrossRef]
- Sormunen, S.; Gross, T.; Saramäki, J. Critical drift in a neuro-inspired adaptive network. arXiv 2022, arXiv:2206.10315v1. [Google Scholar]
- Drossel, B. Random Boolean networks. In Reviews of Nonlinear Dynamics and Complexity; Schuster, H.G., Ed.; Wiley-VCH Verlag GmbH & Co: Weinheim, Germany, 2008; pp. 69–110. [Google Scholar] [CrossRef]
- Gershenson, C. Updating Schemes in Random Boolean Networks: Do They Really Matter? In Artificial Life IX Proceedings of the Ninth International Conference on the Simulation and Synthesis of Living Systems, Boston, MA, USA, 12–15 September 2004; Pollack, J., Bedau, M., Husbands, P., Ikegami, T., Watson, R.A., Eds.; MIT Press: Cambridge, MA, USA, 2004; pp. 238–243. [Google Scholar]
- Derrida, B.; Pomeau, Y. Random Networks of Automata: A Simple Annealed Approximation. Europhys. Lett. 1986, 1, 45–49. [Google Scholar] [CrossRef]
- Gershenson, C. Classification of Random Boolean Networks. In Artificial Life VIII: Proceedings of the Eight International Conference on Artificial Life, Sydney, Australia, 9–13 December 2002; Standish, R.K., Bedau, M.A., Abbass, H.A., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 1–8. [Google Scholar] [CrossRef]
- Lloyd, S. Measures of Complexity: A Non-Exhaustive List; Technical Report; Department of Mechanical Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 2001. [Google Scholar]
- Edmonds, B. Syntactic Measures of Complexity. Ph.D. Thesis, University of Manchester, Manchester, UK, 1999. [Google Scholar]
- Prokopenko, M.; Boschetti, F.; Ryan, A.J. An Information-Theoretic Primer On Complexity, Self-Organisation And Emergence. Complexity 2009, 15, 11–28. [Google Scholar] [CrossRef]
- De Domenico, M.; Camargo, C.; Gershenson, C.; Goldsmith, D.; Jeschonnek, S.; Kay, L.; Nichele, S.; Nicolás, J.; Schmickl, T.; Stella, M.; et al. Complexity Explained: A Grassroot Collaborative Initiative to Create a Set of Essential Concepts of Complex Systems. Available online: https://complexityexplained.github.io (accessed on 1 September 2022). [CrossRef]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Fernández, N.; Maldonado, C.; Gershenson, C. Information Measures of Complexity, Emergence, Self-organization, Homeostasis, and Autopoiesis. In Guided Self-Organization: Inception; Emergence, Complexity and Computation; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 9, pp. 19–51. [Google Scholar] [CrossRef]
- Santamaría-Bonfil, G.; Gershenson, C.; Fernández, N. A Package for Measuring Emergence, Self-organization, and Complexity Based on Shannon Entropy. Front. Robot. AI 2017, 4, 10. [Google Scholar] [CrossRef]
- Pineda, O.K.; Kim, H.; Gershenson, C. A Novel Antifragility Measure Based on Satisfaction and Its Application to Random and Biological Boolean Networks. Complexity 2019, 2019, 10. [Google Scholar] [CrossRef]
- Monton, B. God, fine-tuning, and the problem of old evidence. Br. J. Philos. Sci. 2006, 57, 405–424. [Google Scholar] [CrossRef]
- Solé, R.V.; Luque, B.; Kauffman, S.A. Phase Transitions in Random Networks with Multiple States; Technical Report 00-02-011; Santa Fe Institute: Santa Fe, NM, USA, 2000. [Google Scholar]
- Kosmann-Schwarzbach, Y. The Noether Theorems. In The Noether Theorems; Springer: New York, NY, USA; Dordrecht/Heidelberg, Germany; London, UK, 2011; pp. 55–64. [Google Scholar] [CrossRef]
- Luque, B.; Solé, R.V. Lyapunov exponents in random Boolean networks. Phys. A Stat. Mech. Its Appl. 2000, 284, 33–45. [Google Scholar] [CrossRef]
- Roy, M.; Pascual, M.; Franc, A. Broad scaling region in a spatial ecological system. Complexity 2003, 8, 19–27. [Google Scholar] [CrossRef]
- Zapata, O.; Gershenson, C. Random Fuzzy Networks. In Artificial Life 14: Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems, New York, NY, USA, 30 July–2 August 2014; Sayama, H., Rieffel, J., Risi, S., Doursat, R., Lipson, H., Eds.; MIT Press: Cambridge, MA, USA, 2014; pp. 427–428. [Google Scholar] [CrossRef]
- Zapata, O.; Kim, H.; Gershenson, C. k On two information-theoretic measures of random fuzzy networks. In Artificial Life Conference Proceedings; MIT Press: Cambridge, MA, USA, 2020; Volume 32, pp. 623–625. [Google Scholar] [CrossRef]
- Hoel, E.P.; Albantakis, L.; Tononi, G. Quantifying causal emergence shows that macro can beat micro. Proc. Natl. Acad. Sci. USA 2013, 110, 19790–19795. [Google Scholar] [CrossRef] [PubMed]
- Pascual, M.; Roy, M.; Laneri, K. Simple models for complex systems: Exploiting the relationship between local and global densities. Theor. Ecol. 2011, 4, 211–222. [Google Scholar] [CrossRef] [PubMed]
- Gross, T.; Sayama, H. (Eds.) Adaptive Networks: Theory, Models and Applications; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Khajehabdollahi, S.; Prosi, J.; Giannakakis, E.; Martius, G.; Levina, A. When to Be Critical? Performance and Evolvability in Different Regimes of Neural Ising Agents. Artif. Life 2022, 28, 458–478. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Díaz, A.J.; Sánchez-Puig, F.; Gershenson, C. Temporal, Structural, and Functional Heterogeneities Extend Criticality and Antifragility in Random Boolean Networks. Entropy 2023, 25, 254. https://doi.org/10.3390/e25020254
López-Díaz AJ, Sánchez-Puig F, Gershenson C. Temporal, Structural, and Functional Heterogeneities Extend Criticality and Antifragility in Random Boolean Networks. Entropy. 2023; 25(2):254. https://doi.org/10.3390/e25020254
Chicago/Turabian StyleLópez-Díaz, Amahury Jafet, Fernanda Sánchez-Puig, and Carlos Gershenson. 2023. "Temporal, Structural, and Functional Heterogeneities Extend Criticality and Antifragility in Random Boolean Networks" Entropy 25, no. 2: 254. https://doi.org/10.3390/e25020254
APA StyleLópez-Díaz, A. J., Sánchez-Puig, F., & Gershenson, C. (2023). Temporal, Structural, and Functional Heterogeneities Extend Criticality and Antifragility in Random Boolean Networks. Entropy, 25(2), 254. https://doi.org/10.3390/e25020254










