1. Introduction
Financial markets are widely recognized as typical examples of complex dynamical systems [
1]. Asset prices are created by a large number of nonlinear interactions between heterogeneous agents and complex events occurring in the external environment [
2,
3]. The properties observed in financial time series such as nonlinearity, long-range dependence [
4,
5], volatility clustering [
6], fat tails [
7,
8], asymmetry [
9], chaos [
10,
11], fractals and multifractals [
12,
13], and self-similarity [
14] have attracted the interest of many scientists from different fields. In the last three decades, physicists have studied and developed models to understand the behaviors and interactions in financial systems, establishing an interdisciplinary research field known as Econophysics [
15,
16,
17]. This term first appeared in the published article by Stanley et al. [
18] when analyzing the Dow Jones index; they found that stock returns followed a power law distribution. Since then, significant progress has been made in the field of Econophysics [
19].
The dynamics of financial markets are difficult to understand not only because of the complexity of their internal elements but also because of the many intractable external factors acting on them. A recent example of an external factor causing disruptions in global financial markets is the outbreak of the COVID-19 pandemic. At its roots, the COVID-19 crisis is not a financial or economic crisis, it is a health crisis. Nevertheless, through its effects on supply and demand conditions, it evolved rapidly to a large-scale financial and economic crisis. In March 2020, the US stock market hit the circuit breaker mechanism four times in a period of ten days. Since its inception in 1987, the breaker has only ever been triggered once, in 1997. At the same time as the US crash, stock markets in Asia and Europe plunged also. More specifically, Japan’s stock market fell by more than
, while the UK’s main index, FTSE, fell by about
on 12 March 2020. Additionally, during the pandemic period, most economies experienced exchange rate volatility and currency depreciation due to capital outflows and market sentiments. Typical examples are the Australian dollar hitting a 17-year low of
and the New Zealand dollar hitting an 11-year low of
. Furthermore, the price of gold dropped about 3.53%. It is worth noting that although gold is considered a strong safe haven for most developed markets during financial crises, there are findings showing that during the pandemic it was a weak safe haven for investors in the stock market [
20]. The impact of COVID-19 affected even the newer asset classes such as cryptocurrencies. The declines in value of the three leading cryptocurrencies (Bitcoin, Ethereum, and Litecoin) exceeded
during the pandemic period.
The exchange rate is crucial for maintaining an economy’s external stability. As exchange rate directly associates with foreign debt, capital flows, trade balance, and export competitiveness, maintaining a stable exchange rate is one of the policymakers’ major concerns. On the other hand, several researchers argue that specific characteristics of cryptocurrencies, including the independence from monetary policy and the non-correlation with traditional assets, increase their resilience during crisis periods such as the recent pandemic crisis [
21,
22,
23]. However, there is also the opposing view which argues that monetary policy has a significant impact on the price of cryptocurrencies as well as that the cryptocurrencies do not have zero correlation with other asset classes. For example, Chaoqun Ma et al. [
24] found a strong response of Bitcoin prices to unexpected monetary policy actions, while Khanh Quoc Nguyen [
25] found that S&P 500 returns significantly affected Bitcoin returns during the pandemic period. Therefore, it is concluded that understanding the pandemic’s impact and the possible changes it caused in the cryptocurrency and foreign exchange markets is crucial for both investors and risk managers as well as policymakers.
Particularly useful conclusions about the effects of COVID-19 on financial markets can be obtained by studying changes in the multifractality and complexity of financial time series during the period around the COVID-19 outbreak. In the field of Econophysics, extensive research has been conducted on these topics. For example, Mnif et al. [
26] utilized the multifractal detrended fluctuation analysis (MF-DFA) approach to investigate the degree of cryptocurrency efficiency before and after the COVID-19 outbreak using a limited time period, until 19 May 2020. Their results indicated that the pandemic outbreak positively affected the efficiency of the five cryptocurrencies that they studied. Naeem et al. [
9] examined the asymmetric efficiency of the cryptocurrencies Bitcoin, Ethereum, Litecoin, and Ripple, using 1-h data. In their analysis, the authors utilized the A-MF-DFA and their results showed that the price of cryptocurrencies exhibited significant asymmetric multifractality. Moreover, they found that uptrends showed stronger multifractality than downtrends. Additionally, applying the time-varying deficiency measure, they found that the pandemic outbreak had a negative impact on the efficiency of the cryptocurrencies that they analyzed. Kakinaka and Umeno [
27], applying the A-MF-DFA, examined the asymmetric multifractality along with the market efficiency of two main cryptocurrencies (Bitcoin, Ethereum) during the pandemic period, taking into consideration different investment horizons. Their empirical results showed that the outbreak of COVID-19 affected the efficiency of the two cryptocurrencies differently in the short- and long-term horizons. More specifically, after the outbreak of COVID-19, Bitcoin and Ethereum in the short term exhibited stronger multifractality, while in the long term exhibited weaker multifractality. In addition, they studied the asymmetric market patterns between small and large price fluctuations and between upward and downward trends. These results confirmed that the outbreak caused a significant change in the level of asymmetry in cryptocurrency markets. Aslam et al. [
28] applied the MF-DFA to study the efficiency of foreign exchange markets during the initial period of the COVID-19 pandemic. In their analysis, they used high-frequency data of six major currencies, during the period from 1 October 2019 to 31 March 2020. Before calculating the MF-DFA, they examined the inner dynamics of multifractality through seasonal and trend decomposition using loess. Their results indicated that efficiency of foreign exchange markets during the COVID-19 outbreak declined. Mensi et al. [
29] examined the effect caused by the COVID-19 crisis on the pricing efficiency and asymmetric multifractality of major asset classes (US Treasury bond, US dollar index, S&P500, Brent oil, Gold, and Bitcoin). In their article, they applied the permutation entropy on intraday data from 30 April 2019 to 13 May 2020. Their results indicated that after the outbreak of COVID-19, the efficiency of all asset classes that they studied was deteriorated, and in most cases this deterioration was significant. In addition, using the A-MF-DFA, they found evidence of asymmetric multifractality in all markets. Drożdż et al. [
30] studied the complexity of the cryptocurrency market in the period around the COVID-19 outbreak from three different perspectives. Their findings showed that throughout the time period analyzed, the returns of exchange rates were multifractal with intermittent signatures of bifractality that can be associated with the periods where the market was more volatile.
Lahmiri and Bekiros [
31] investigated the time-varying characteristics of the informational efficiency in sixteen international stock markets and forty-five cryptocurrency markets before and during the pandemic period using the approximate entropy and Largest Lyapunov Exponent. Their results indicated that cryptocurrencies exhibited more irregularity and more instability during the pandemic period compared to international stock markets. Additionally, Lahmiri and Bekiros [
32], applying Rényi entropy, analyzed the multiscale entropy function in the return time series of S&P500, Brent, WTI, Gas, Silver, Gold, Bitcoin, and VIX. Additionally, they analyzed the information sharing between these markets by estimating mutual information. Their results from Rényi entropy showed that for all market indices, disorder and randomness were more concentrated in less probable events. In addition, their results from the mutual information indicated that the information sharing network between markets has changed during the pandemic period. Wang J. and Wang X. [
33] investigated the market efficiency of the S&P 500 Index, Gold, Bitcoin, and US Dollar Index during the extreme event of the COVID-19 pandemic using a multiscale entropy-based method. Their results indicated that, at all scales, the four markets’ efficiency decreased abruptly and persistently during the period from February to March 2020. Market efficiency decreased the most in the S&P 500 Index and the least in the Bitcoin market. Additionally, their results showed that Bitcoin market efficiency was more resilient than the others during the extreme event. Fernandes et al. [
34] investigated the informational efficiency and price disorder of five main cryptocurrencies (Ethereum, Bitcoin, Cardano, XRP, and BNB) before and during the pandemic period. In their article, the authors applied the permutation entropy and Fisher information measure to construct the Shannon–Fisher causality plane in order to map the cryptocurrencies and their respective locations in a two-dimensional plane. Their results indicated that all cryptocurrencies exhibited high but slightly varying informational efficiency during both periods. Additionally, their results showed that Cardano was the most efficient cryptocurrency. Kim and Lee [
35] investigated the evolution of the complexity of the cryptocurrency market and analyzed the properties from the previous upward trend market in 2017 against the COVID-19 pandemic. In their article, the authors used three popular measures of complexity based on the nonlinear analysis: sample entropy, approximate entropy, and Lempel–Ziv complexity. They studied the market complexity/unpredictability for forty-three cryptocurrency prices. They found that sample entropy, approximate entropy, and Lempel–Ziv complexity metrics of all markets could not generalize the COVID-19 effect of the complexity due to different patterns. Nevertheless, market unpredictability increased by the ongoing health crisis. Olbryś and Majewska [
36] applied sample entropy to evaluate changes in the regularity of returns of thirty-six U.S. and European stock market indices during periods of uncertainty. Specifically, the authors studied the period of the Global Financial Crisis as well as the period of the COVID-19 pandemic. Their results showed that entropy decreased during the periods of turbulence, indicating that the regularity and predictability of stock market indices returns increased during these periods. In the field of Econophysics, the study of the complexity and multifractality of financial time series during the pandemic is a challenging topic. However, to the best of our knowledge, until now there has not been an in-depth comparative analysis of the effects of the pandemic on the complexity and fractal characteristics of the returns of two completely different currencies, such as BTC/USD and EUR/USD, that play a key role in the modern financial system.
In this article, we present a study of the temporal evolution of the multifractality and complexity of BTC/USD and EUR/USD returns for the period before and after the
announcement that declared COVID-19 a global pandemic (i.e., 11 March 2020). We chose to analyze and compare the effects of the pandemic on the two most representative currencies from the cryptocurrency and forex markets, respectively. Although these two markets are completely different from each other, they play a significant role in the modern financial system. More specifically, we applied the A-MF-DFA to investigate the temporal evolution of the asymmetric multifractal spectrum parameters
before and after the outbreak of the pandemic. Although there are numerous studies that have followed a similar approach for the study of financial time series (e.g., [
37,
38,
39]), as far as we are able to know, this is the first time that the temporal evolution of the specific parameters has been applied to BTC/USD and EUR/USD returns to study the period before and during COVID-19. At this point, it is important to mention that the analysis of the multifractal properties of financial time series has a wide contribution to the field of finance. For example, multifractality can be used to obtain better forecasts of tail risk as demonstrated by Batten et al. [
40]. In addition, we examined the temporal evolution of four popular complexity measures. Although approximate and sample entropies are quite common for financial time series analysis [
31,
35,
41], we chose to use Fuzzy entropy as it is considered as an upgraded alternative of approximate and sample entropy for evaluating the complexity, specifically for short time series contaminated by noise [
42]. In combination, we chose to use the Shannon entropy as the standard information measure and Tsallis entropy as its non-extensive generalization, very closely related to multifractality. Additionally, we used another complexity measure, Fisher information. In financial data analysis, the application of Fisher information is very widespread for the construction of the Shannon–Fisher causality plane [
34,
43]. In the present article, we chose to investigate the temporal evolution of Fisher information as we believe that it can reveal useful elements for the evolution of the complexity of the dynamical system, providing a “mirror image” of the evolution of entropies, but also presenting the key difference of its so-called “locality” property (see
Section 2.4). Our study attempts to provide a complete picture of the pandemic’s impact in terms of the dynamical change of the complexity and the fractal characteristics of the two currencies. Additionally, our results provide useful conclusions about the behavior of two very different currencies during uncertainty periods. At the same time, interesting conclusions are drawn about the impact of
announcements and the reaction of investors to external events such as the pandemic. Our findings can help both investors and risk managers, as well as policymakers, to formulate a comprehensive response to the occurrence of such external events.
3. Data and Results
The cryptocurrency market is a relatively new and emerging market, meaning that the trading mechanism is unique and makes it very different from traditional markets. More than
different cryptocurrencies are currently traded around the world with an estimated total market capitalization of over USD
billion (see, e.g.,
https://coinmarketcap.com/ (accessed on 7 December 2022)). On the other hand, the foreign exchange market is the largest financial market worldwide, with transactions amounting to trillions of US dollars daily [
70]. In this article, we focused on the analysis of the two most representative currencies of these two markets, i.e., the BTC/USD and EUR/USD. Our analyses were applied to the daily logarithmic returns (
, where
denotes the price at time
) of the BTC/USD and EUR/USD during the period from 1 May 2019 to 20 January 2021. In an announcement by the
on 11 March 2020, the outbreak of COVID-19 was declared a global pandemic. Therefore, we considered the period from 1 May 2019 to 11 March 2020 as the pre-announcement period, and the period from 12 March 2020 to 20 January 2021 as the post-announcement period. All financial time series were taken from Yahoo Finance (
http://finance.yahoo.com/ (accessed on 7 December 2022)).
In our study, we investigated the temporal evolution of complexity and fractal characteristics by using overlapping sliding windows (with window length equal to 512 samples and slide step equal to 1 sample). First, we investigated the temporal evolution of the multifractal spectrum parameters before and after the outbreak of the pandemic. Then, for the same time period, we extended our analysis by examining the temporal evolution of Fuzzy entropy, Tsallis entropy, Shannon entropy, and Fisher information.
At this point, we should mention that for the calculation of Tsallis entropy we have chosen to use the value
for the non-extensive parameter,
. On one hand, for financial time series
has been found to take values
[
3], which has been discussed within the framework of the similarities in scaling properties and universality related to observables of extreme events from different disciplines (e.g., financial crisis, earthquake, epileptic seizure, magnetic storm, solar flare) [
3,
55,
60,
61]. On the other hand, from the time series analysis point of view, the selection of the
value for the calculation of the temporal variation of Tsallis entropy practically only affects the “separation” between the lower and higher complexity parts of the analyzed time series (e.g., min to max entropy values ratio, in direct analogy to the signal to noise ratio), while for the herein analyzed time series it was found that any
value in the range
leads to approximately the same results.
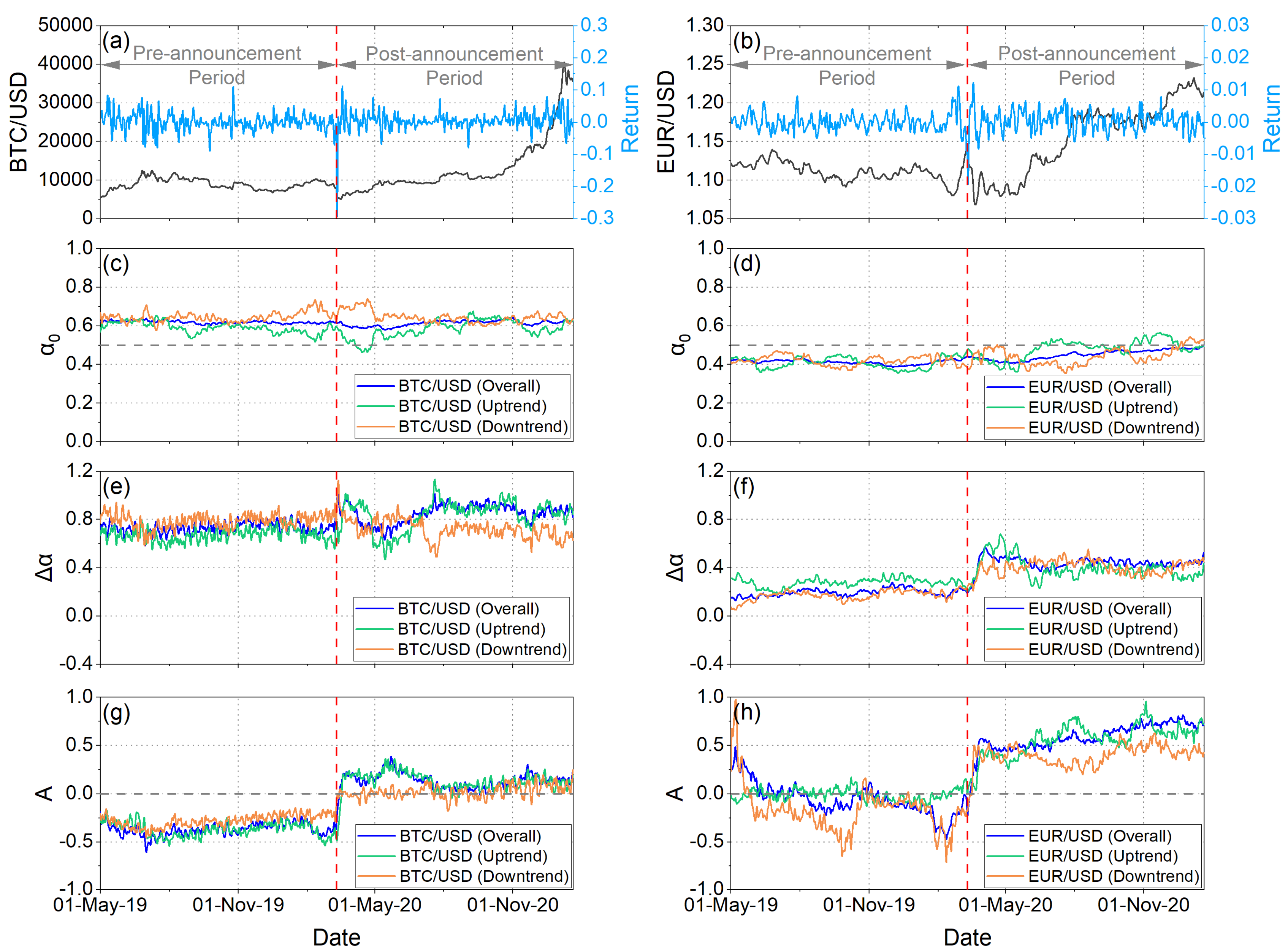
Figure 1c,d, depict the temporal evolution of
values under different market trends of the BTC/USD and EUR/USD returns, respectively. By analyzing the overall trend of the BTC/USD returns, it is observed that the values of the
fluctuate around
(
Figure 1c). These results indicate that the returns time series is characterized by long-range correlations, both before and after the onset of COVID-19. By analyzing the downtrend markets of the BTC/USD returns, it is observed that the values of the
fluctuate over
both before and after the outbreak of the pandemic, indicating persistent behavior. In the uptrend markets of the BTC/USD returns, the values of
fluctuate between
and
for almost throughout the analysis period. An exception is a short period of time after the
announcement, where
values fell below
.
Figure 1d depicts the temporal evolution of the
values of the EUR/USD returns under different market trends. In this case, we observe that for the overall trend the
values fluctuate around
during the whole pre-announcement period, while after the announcement they present a progressive increase approaching very close to
at the end of the considered analysis period. This suggests that the time series exhibit a “different” power-law correlation, such that large and small time series are more likely to alternate (anti-persistent behavior). It is worth mentioning that the downtrend
values remain at the anti-persistent side except for the very last part of the analyzed period, while the uptrend
values, although
for the whole pre-announcement period, present an alternating behavior after the
announcement, taking values
for two two-month-long periods.
Figure 1e,f illustrate the width of the multifractal spectrum under different market trends of the BTC/USD and EUR/USD returns, respectively. As already mentioned in
Section 2.1.1, the width of the multifractal spectrum
is a measure of the degree of multifractality. If a time series presents a smaller width of the multifractal spectrum, this indicates that the time series has lower heterogeneity, i.e., lower fluctuations and lower market risk [
58]. The results show that throughout the period analyzed, the width of the multifractal spectrum receives higher values for the BTC/USD returns compared to the EUR/USD returns. Therefore, it can be concluded that EUR/USD is relatively more stable than BTC/USD. In addition, we observe that after the outbreak of the pandemic, the width of the multifractal spectrum increased for both BTC/USD returns and the EUR/USD returns for the overall trend. This suggests that after the outbreak of the pandemic, both currencies reacted similarly in terms of multifractality when observed from an overall trend point of view. The degree of multifractality increased, and, therefore, the fluctuations became more intense and the market risk increased. However, in terms of asymmetric multifractality, this is not always the case. When focused on downside markets of BTC/USD, the degree of multifractality decreased after the outbreak. More interestingly, downtrend multifractality was higher than the uptrend multifractality during the period before COVID-19, but during the pandemic the uptrend multifractality became higher. These findings reveal that the incremental multifractality in BTC/USD is due to intense fluctuations and higher heterogeneity during price increases, but not during price declines. In EUR/USD, it appears that the downside markets play a more important role in increasing multifractality. Nevertheless, both market trends may have had some impact in the post-announcement period increase in multifractality. It is important to note that the increase in multifractality in BTC/USD returns during COVID-19 is consistent with the existing literature as other studies have reached the same conclusion (e.g., [
26,
27]).
Figure 1g,h depict the temporal evolution of the asymmetry parameter
values under different market trends of the BTC/USD and EUR/USD returns, respectively. In the time period before the onset of the pandemic, the asymmetry parameter
of BTC/USD returns appears to have been consistently below
, indicating relative dominance of the small fluctuations. Immediately after the date of the
announcement, there was a sharp change in the values of
in all market trends. Specifically, for both overall trend and uptrend markets, the values of
of the BTC/USD returns remain above
for the entire period after the outbreak of the pandemic. This sharp change shows a transition from a period where small fluctuations predominate (before the pandemic) to a period where large fluctuations predominate (during the pandemic). In the downtrend markets, the values of parameter
are almost at
for the entire period after the outbreak of the pandemic, indicating that the spectrum became practically symmetrical (
Figure 1g). On the other hand, the values of the asymmetry parameter
of the EUR/USD returns for the uptrend markets are almost equal to
for the whole period before the outbreak of the pandemic. This fact indicates that the spectrum is practically symmetrical. On the contrary, analyzing the overall and downward trends of the market, we observe that the values of the asymmetry parameter
are below
, almost for the entire period before the outbreak of the pandemic. Therefore, it is concluded that in the overall and downward trends of the markets, they are dominated by the small fluctuations in EUR/USD returns before the outbreak of the pandemic. Immediately after the announcement date, the values of the asymmetry parameter
of the EUR/USD returns exceeded
in all market trends. This result shows that EUR/USD returns after the outbreak of the pandemic are dominated by large fluctuations (
Figure 1h).
Figure 2c,d indicate that the effect of the announcement was, for all cases (for both BTC/USD and EUR/USD returns and for all three considered market trends), a sharp change towards right-truncation, which means that after the
announcement the multifractal structure in the time series became more insensitive to the local fluctuations with small magnitudes. On the other hand,
Figure 2e,f show that the behavior of BTC/USD and EUR/USD returns was different concerning the degree of truncation asymmetry, indicated by the so-called
. Specifically, EUR/USD returns present
quite close to 0 before the
announcement, which means that the underlying system then presented the lowest possible undulation or instability. After the
announcement, the picture changed and for all market trends an increase in the undulation or instability of the underlying system is observed. In contrast, BTC/USD returns present a general trend (although with notable fluctuations for the overall and uptrend markets) towards a decrease in the
after the
announcement, which means that a trend for the decrease in the undulation or instability of the underlying system is observed. It is noted that the downtrend market after the
announcement presents
closer to 0, as compared with the uptrend and overall markets, indicating lower undulation or instability.
Moreover, we analyzed the temporal evolution of some complexity measures.
Figure 3c,d illustrate the temporal evolution of the Fuzzy entropy of the BTC/USD and EUR/USD returns, respectively. As it has already been mentioned in
Section 2.2., smaller values of Fuzzy entropy indicate a greater chance that a set of data will be followed by similar data (regularity). Conversely, larger values of Fuzzy entropy point to a lower chance of similar data being repeated (irregularity). As we observe in
Figure 3c,d, the values of Fuzzy entropy dropped sharply in both BTC/USD and EUR/USD returns immediately after the
announcement. This fact indicates that in the pre-announcement period, both BTC/USD and EUR/USD returns were characterized by a higher degree of disorder and randomness, i.e., by higher complexity. In contrast, in the period during the pandemic, the values of Fuzzy entropy decreased, suggesting that the returns were characterized by a higher degree of order and lower complexity. Therefore, it is concluded that the pandemic led investors to behave in an “organized” (similar) way that thereby reduced the complexity of the two markets.
Corresponding results are obtained by also studying two quite popular complexity measures, i.e., the Shannon entropy (
Figure 3g,h) and Tsallis entropy (
Figure 3e,f). More specifically, the time variations of the Shannon entropy as well as the Tsallis entropy (for a given
) quantify the dynamical changes of the information content and the complexity of the system. Smaller values characterize time series with lower complexity and randomness, as well as higher information content and order. Conversely, larger values characterize time series with higher complexity, disorder and randomness, as well as lower information content. As we observe in
Figure 3e–h, during COVID-19, the values of Tsallis and Shannon entropies were reduced in both BTC/USD and EUR/USD returns, indicating that the complexity of the two markets was reduced and the information content was increased. It is important to note that all the entropy measures we applied quickly adapted to market conditions, showing a sharp decrease immediately after the
announcement, with Shannon entropy being the exception in the case of BTC/USD. Additionally, it is of particular interest that the entropy values remained at low levels throughout the pandemic period we analyzed, showing that the effects of the pandemic were not short-term. Additionally, concerning the study of Lahmiri and Bekiros [
32], although not the main finding of their analyses, it is nevertheless important to note that their results showed a decrease in Rényi entropy (and consequently a decrease in randomness) for the BTC/USD market during the pandemic compared to before.
In addition, we applied one more complexity measure, the Fisher information. Fisher information is a useful method to study non-stationary and complex time series. Fisher information is used as a measure of the degree of order of a system, behaving inversely to entropy, i.e., when the order increases, the entropy decreases, while the Fisher information increases. Moreover, unlike entropy, it is sensitive to changes in the shape of the probability distribution corresponding to the measured variable.
Figure 3i,j illustrate the temporal evolution of the Fisher information of the BTC/USD and EUR/USD returns, respectively. We observe that immediately after the
announcement, the values of Fisher information increased in both BTC/USD and EUR/USD returns, indicating an increase in the order of the two markets.
At this point, it has to be mentioned that the observed decrease in randomness after the
announcement, indicated by all the applied complexity measures, is fully compatible with the corresponding increase of multifractality. Specifically, the more random a time series is, the more unifractal its scaling is, which means that a more multifractal time series can be considered as being farther away from “randomness” [
71].
From the interpretation of our results in financial terms, useful conclusions are revealed. More specifically, in analyzing the values of
for overall trend, as we have already mentioned, we observe that the BTC/USD returns show persistent behavior, while the EUR/USD returns exhibit anti-persistent behavior almost throughout the time period we studied them (
Figure 1c,d). A persistent or anti-persistent market return series is characterized by a long memory effect. Therefore, what happens today, theoretically, will impact the future in a nonlinear fashion. For example, if a persistent market return change has been up (down) in the last period, then the changes will continue to be positive (negative) in the next period. On the other hand, anti-persistent markets are “mean-reverting.” If the market return was up (down) in the previous period, it is more likely to be down (up) in the next period [
72]. The long-memory characteristic in asset return is a fascinating topic for investors, risk managers, and scholars since appropriate return modeling is crucial for asset allocation and risk control. For example, existence of long memory in asset returns indicates that historical returns changes could be predictors of future returns changes [
73]. Then, analyzing the
and
parameters, we observe that in the post-announcement period, mainly in the case of the EUR/USD, the degree of multifractal returns increased, and, therefore, fluctuations became more intense and market risk increased (
Figure 1e,f). At the same time, we observe that in the post-announcement period, returns were dominated by large fluctuations (
Figure 1g,h). Therefore, it is concluded that in the post-announcement period, EUR/USD returns experienced intense and large fluctuations. Similar behavior is observed for the overall trend and uptrend markets of the BTC/USD returns. Regarding the downtrend markets of the BTC/USD returns, it appears that during the pandemic period there were less intense fluctuations compared to the pre-pandemic period without small or large fluctuations in returns dominating. The analysis of the truncation asymmetry degree (
Figure 2e,f), moreover, revealed that the
announcement had different impacts on BTC/USD and EUR/USD returns concerning the undulation or instability of the underlying system. For EUR/USD returns, the post-announcement period was characterized by an increase in the undulation or instability of the underlying system, whereas for BTC/USD returns, the opposite behavior was generally observed. Analyzing the complexity measures (Fuzzy entropy, Tsallis entropy, Shannon entropy, and Fisher information) (
Figure 3c–j), we observe a sharp decline in complexity (i.e., increase in the order and information content, and decrease in randomness) in the returns of both BTC/USD and EUR/USD in the post-announcement period. This fact, in financial terms, suggests that the pandemic led investors to behave in an “organized” (similar) way that thereby reduced the complexity of the two markets. In other words, after the outbreak of the pandemic, it seems that investors behaved like a herd. Therefore, it is concluded that although the fluctuations were larger and more intense after the outbreak of the pandemic, this was not carried out in a random way as investors seem to have behaved in an “organized” way; however, this behavior for BTC/USD returns was generally followed by a decrease in undulation or instability of the underlying system, while the opposite happened for EUR/USD returns.
Additionally, it is worth noting that the majority of the measures that we studied showed a strong change for both BTC/USD and EUR/USD returns immediately after the
announcement (11 March 2020), in which COVID-19 was mentioned for the first time as a pandemic. This fact indicates that the behavior of the system changed immediately after the
announcement, although the discussions about COVID-19 being a public health emergency of international concern had begun weeks before. Therefore, although many researchers accept the date of 2 January 2020 as the beginning of the COVID-19 pandemic crisis (e.g., [
74,
75,
76]), we consider the most suitable start date of the pandemic to be 11 March 2020.
4. Conclusions
The detection of dynamical complexity in time series originated from various complex systems, including the disciplines of physics, finance, and medicine, and is one of the foremost problems in science. The measurement of complexity includes nonlinear statistics methods to extract hidden patterns as well as exploring multifractality, randomness, and information flows. Hence, complexity provides important information regarding the order or disorder states of a system under scrutiny. In the field of finance, the detection of the dissimilarity of complexity between order and disorder states (e.g., before and after the occurrence of extreme events) could shed light on the mechanisms associated with investor reaction to these events.
In this article, we studied the temporal evolution of the multifractality and complexity of BTC/USD and EUR/USD returns for the period before and after the announcement that declared COVID-19 a global pandemic. In our study, we first examined the asymmetric multifractality through the analysis of the multifractal spectrum parameters as obtained by the A-MF-DFA method. Then, we extended our analysis by applying Fuzzy, Tsallis, and Shannon entropies as well as the Fisher information measure. Our results can be summarized as follows: (i) For the entire time period that we studied (i.e., before and during the pandemic), the behavior of BTC/USD returns was persistent in all trends of the market. On one hand, in the period before the outbreak of the pandemic, the behavior of EUR/USD returns was anti-persistent in all trends of the market. On the other hand, in almost the entire period after the outbreak of the pandemic, the returns of the EUR/USD exhibited anti-persistent behavior in the overall trend and downtrend markets, while the uptrend market presented an alternating behavior, including short periods of persistent dynamics. (ii) Throughout the period analyzed, the width of the multifractal spectrum received higher values for the BTC/USD returns compared to the EUR/USD returns. This implies that the multifractality of the BTC/USD returns was higher than the multifractality of the EUR/USD returns. In addition, after the outbreak of the pandemic, in the overall trend and uptrend markets, the width of the multifractal spectrum increased for both BTC/USD returns and EUR/USD returns. In the case of BTC/USD, the downtrend multifractality was higher in the pre-announcement period. In EUR/USD, it appears that the downtrend markets played an important role in increasing multifractality. Nevertheless, both market trends may have had some impact on the post-announcement period increase in multifractality. (iii) In the pre-announcement period, small fluctuations in BTC/USD returns for all market trends dominated. In contrast, in the post-announcement period, large fluctuations in BTC/USD returns for overall trend and uptrend markets dominated, while in downtrend markets the spectrum became practically symmetrical. On the other hand, although in the uptrend markets the spectrum of EUR/USD returns was almost symmetrical, the returns in the overall trend and downtrend markets were dominated by small fluctuations for almost the entire pre-announcement period. During the pandemic period, the returns of the EUR/USD were dominated by large fluctuations in all market trends. (iv) For both BTC/USD and EUR/USD returns and all market trends, a sharp change towards becoming more insensitive to the local fluctuations with small magnitudes was observed after the announcement. Nevertheless, the announcement had different impacts on BTC/USD and EUR/USD returns concerning the undulation or instability of the underlying system. For EUR/USD returns, the post-announcement period was characterized by an increase in the undulation or instability of the underlying system, whereas for BTC/USD returns, the opposite behavior was generally observed. (v) Fuzzy entropy, non-extended Tsallis entropy, Shannon entropy, and Fisher information showed a sharp decrease in the degree of complexity immediately after the announcement for both BTC/USD and EUR/USD. This fact shows that in the post-announcement period, the order and the information content of the systems increased, i.e., the randomness and complexity in the returns of the two currencies decreased. Therefore, in financial terms, we conclude that investors seem to have behaved in an “organized” way, as a herd. In addition, our analyses show that the date of the announcement (11 March 2020) could be considered as the most appropriate date for the start of the pandemic. This element could be useful in future research studies.
The main finding that is revealed from our study is that immediately after the announcement, the returns of both BTC/USD and EUR/USD presented a decrease in complexity and corresponding increase in multifractality, both indicating that they became less random compared to the pre-announcement period. Hence, it seems that although they are two such different currencies, which both play a key role in the modern financial system, they reacted in a similar way in response to the pandemic.