Computational Simulations of Fabrication of Aluminum-Based Josephson Junctions: Topological Aspects of the Barrier Structure
Abstract
1. Introduction
2. Methods
2.1. Molecular Dynamics
2.2. Voronoi Tessellation and Coordination Number
3. Results and Discussion
3.1. Distribution of Voronoi Polyhedron Atomic Volume
3.2. Distribution of Configurational Entropy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neill, C.; Roushan, P.; Kechedzhi, K.; Boixo, S.; Isakov, S.V.; Smelyanskiy, V.; Megrant, A.; Chiaro, B.; Dunsworth, A.; Arya, K.; et al. A Blueprint for Demonstrating Quantum Supremacy with Superconducting Qubits. Science 2018, 360, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Lau, J.W.Z.; Lim, K.H.; Shrotriya, H.; Kwek, L.C. NISQ Computing: Where Are We and Where Do We Go? AAPPS Bull. 2022, 32, 27. [Google Scholar] [CrossRef]
- Huang, H.-L.; Wu, D.; Fan, D.; Zhu, X. Superconducting Quantum Computing: A Review. Sci. China Inf. Sci. 2020, 63, 180501. [Google Scholar] [CrossRef]
- Kjaergaard, M.; Schwartz, M.E.; Braumüller, J.; Krantz, P.; Wang, J.; Gustavsson, S.; Oliver, W.D. Superconducting Qubits: Current State of Play. Annu. Rev. Condens. Matter Phys. 2020, 11, 369–395. [Google Scholar] [CrossRef]
- Makhlin, Y.; Schön, G.; Shnirman, A. Quantum-State Engineering with Josephson-Junction Devices. Rev. Mod. Phys. 2001, 73, 357–400. [Google Scholar] [CrossRef]
- Siddiqi, I. Engineering High-Coherence Superconducting Qubits. Nat. Rev. Mater. 2021, 6, 875–891. [Google Scholar] [CrossRef]
- Hutchings, M.D.; Hertzberg, J.B.; Liu, Y.; Bronn, N.T.; Keefe, G.A.; Brink, M.; Chow, J.M.; Plourde, B.L.T. Tunable Superconducting Qubits with Flux-Independent Coherence. Phys. Rev. Appl. 2017, 8, 044003. [Google Scholar] [CrossRef]
- de Leon, N.P.; Itoh, K.M.; Kim, D.; Mehta, K.K.; Northup, T.E.; Paik, H.; Palmer, B.S.; Samarth, N.; Sangtawesin, S.; Steuerman, D.W. Materials Challenges and Opportunities for Quantum Computing Hardware. Science 2021, 372, eabb2823. [Google Scholar] [CrossRef]
- Ostrovskii, V.Y.; Karimov, A.I.; Rybin, V.G.; Kopets, E.E.; Butusov, D.N. Comparing the Finite-Difference Schemes in the Simulation of Shunted Josephson Junctions. In Proceedings of the 2018 23rd Conference of Open Innovations Association (FRUCT), Bologna, Italy, 13–16 November 2018; pp. 300–305. [Google Scholar]
- Rettaroli, A.; Alesini, D.; Babusci, D.; Barone, C.; Buonomo, B.; Beretta, M.M.; Castellano, G.; Chiarello, F.; Di Gioacchino, D.; Felici, G.; et al. Josephson Junctions as Single Microwave Photon Counters: Simulation and Characterization. Instruments 2021, 5, 25. [Google Scholar] [CrossRef]
- Trybula, M.E.; Korzhavyi, P.A. Atomistic Simulations of Al(100) and Al(111) Surface Oxidation: Chemical and Topological Aspects of the Oxide Structure. J. Phys. Chem. C 2019, 123, 334–346. [Google Scholar] [CrossRef]
- Trybula, M.E.; Korzhavyi, P.A. Temperature Dependency of Structure and Order Evolution in 2D Confined Oxide Films Grown on Al Substrates using Reactive Molecular Dynamics. Vacuum 2021, 190, 110243. [Google Scholar] [CrossRef]
- Cyster, M.J.; Smith, J.S.; Vogt, N.; Opletal, G.; Russo, S.P.; Cole, J.H. Simulating the Fabrication of Aluminium Oxide Tunnel Junctions. NPJ Quantum Inf. 2021, 7, 12. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, J. Oxide Growth Characteristics on Al(100), (110), and (111) Surfaces: A Chemo-Mechanical Evaluation. Mater. Today Commun. 2021, 26, 102006. [Google Scholar] [CrossRef]
- Jeurgens, L.P.H.; Sloof, W.G.; Tichelaar, F.D.; Mittemeijer, E.J. Composition and Chemical State of the Ions of Aluminium-Oxide Films Formed by Thermal Oxidation of Aluminium. Surf. Sci. 2002, 506, 313–332. [Google Scholar] [CrossRef]
- Cai, N.; Zhou, G.; Müller, K.; Starr, D.E. Temperature and Pressure Dependent Mott Potentials and Their Influence on Self-Limiting Oxide Film Growth. Appl. Phys. Lett. 2012, 101, 171605. [Google Scholar] [CrossRef]
- Zeng, L.J.; Nik, S.; Greibe, T.; Krantz, P.; Wilson, C.M.; Delsinget, P.; Olsson, E. Direct Observation of the Thickness Distribution of Ultra Thin AlOx Barriers in Al/AlOx/Al Josephson Junctions. J. Phys. D Appl. Phys. 2015, 48, 395308. [Google Scholar] [CrossRef]
- Nik, S.; Krantz, P.; Zeng, L.; Greibe, T.; Pettersson, H.; Gustafsson, S.; Delsing, P.; Eva Olsson, E. Correlation between Al Grain Size, Grain Boundary Grooves and Local Variations in Oxide Barrier Thickness of Al/AlOx/Al Tunnel Junctions by Transmission Electron Microscopy. SpringerPlus 2016, 5, 1067. [Google Scholar] [CrossRef]
- Fritz, S.; Radtke, L.; Schneider, R.; Luysberg, M.; Weides, M.; Gerthsen, D. Structural and Nanochemical Properties of AlOx layers in Al/AlOx/Al-Layer Systems for Josephson Junctions. Phys. Rev. Mater. 2019, 3, 114805. [Google Scholar] [CrossRef]
- Cai, N.; Zhou, G.; Müller, K.; Starr, D.E. Effect of Oxygen Gas Pressure on the Kinetics of Alumina Film Growth during the Oxidation of Al(111) at Room Temperature. Phys. Rev. B 2011, 84, 125445. [Google Scholar] [CrossRef]
- Flötotto, D.; Wang, Z.M.; Mittemeijer, E.J. On the Structural Development during Ultrathin Amorphous Al2O3 Film Growth on Al(111) and Al(100) Surfaces by Thermal Oxidation. Surf. Sci. 2015, 633, 1–7. [Google Scholar] [CrossRef]
- Nguyen, L.; Hashimoto, T.; Zakharov, D.N.; Stach, E.A.; Rooney, A.P.; Berkels, B.; Thompson, G.E.; Haigh, S.J.; Burnett, T.L. Atomic-Scale Insights into the Oxidation of Aluminum. ACS Appl. Mater. Interfaces 2018, 10, 2230–2235. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S.; Radtke, L.; Schneider, R.; Weides, M.; Gerthsen, D. Optimization of Al/AlOx/Al-Layer Systems for Josephson Junctions from a Microstructure Point of View. J. Appl. Phys. 2019, 125, 165301. [Google Scholar] [CrossRef]
- Cooper, A.S. Precise Lattice Constants of Germanium, Aluminum, Gallium Arsenide, Uranium, Sulphur, Quartz and Sapphire. Acta Crystallogr. 1962, 15, 578–582. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Annu. Rev. Condens. Matter Phys. 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Roddatis, V.V.; Hübner, U.; Ivanov, B.I.; Il’ichev, E.; Meyer, H.-G.; Koval’chuket, M.V.; Vasiliev, A.L. The Morphology of Al-based Submicron Josephson Junction. J. Appl. Phys. 2011, 110, 123903. [Google Scholar] [CrossRef]
- Satoh, T.; Noguchi, Y.; Yamagishi, M.; Nagasawa, S.; Hinode, K.; Hidaka, M.; Maezawa, M.; Horikawa, T. Fabrication of Superconducting Qubits with Al Trilayer Josephson Junctions. IEEE Trans. Appl. Supercond. 2014, 25, 3. [Google Scholar] [CrossRef]
- Streitz, F.H.; Mintmire, J.W. Electrostatic Potentials for Metal-Oxide Surfaces and Interfaces. Phys. Rev. B 1994, 50, 11996–12003. [Google Scholar] [CrossRef]
- DuBois, T.C.; Russo, S.P.; Cole, J.H. Atomic Delocalization as a Microscopic Origin of Two-Level Defects in Josephson Junctions. New J. Phys. 2015, 17, 023017. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting Dislocations and Non-dislocation Crystal Defects from Atomistic Simulation Data. Model. Simul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Lazar, E.A.; Han, J.; Srolovitz, D.J. Topological Framework for Local Structure Analysis in Condensed Matter. Proc. Natl. Acad. Sci. USA 2015, 112, E5769–E5776. [Google Scholar] [CrossRef]
- Han, C.; Sun, H.; Hou, C.; Wang, S.; Xu, J.; Shan, Z. Revealing Temperature-Dependent Noise Sources in Aluminum Oxide Josephson Junctions Using Topological Analysis. J. Phys. Chem. C 2022, 126, 14297–14304. [Google Scholar] [CrossRef]
- Curran, J.E.; Page, J.S.; Pick, U. The Influence of Some Evaporation Parameters on the Structure and Properties of Thin Aluminium Films. Thin Solid Films 1982, 97, 259–276. [Google Scholar] [CrossRef]
- Żydek, A.; Wermiński, M.; Trybula, M.E. Description of Grain Boundary Structure and Topology in Nanocrystalline Aluminum using Voronoi Analysis and Order Parameter. Comput. Mater. Sci. 2021, 197, 110660. [Google Scholar] [CrossRef]
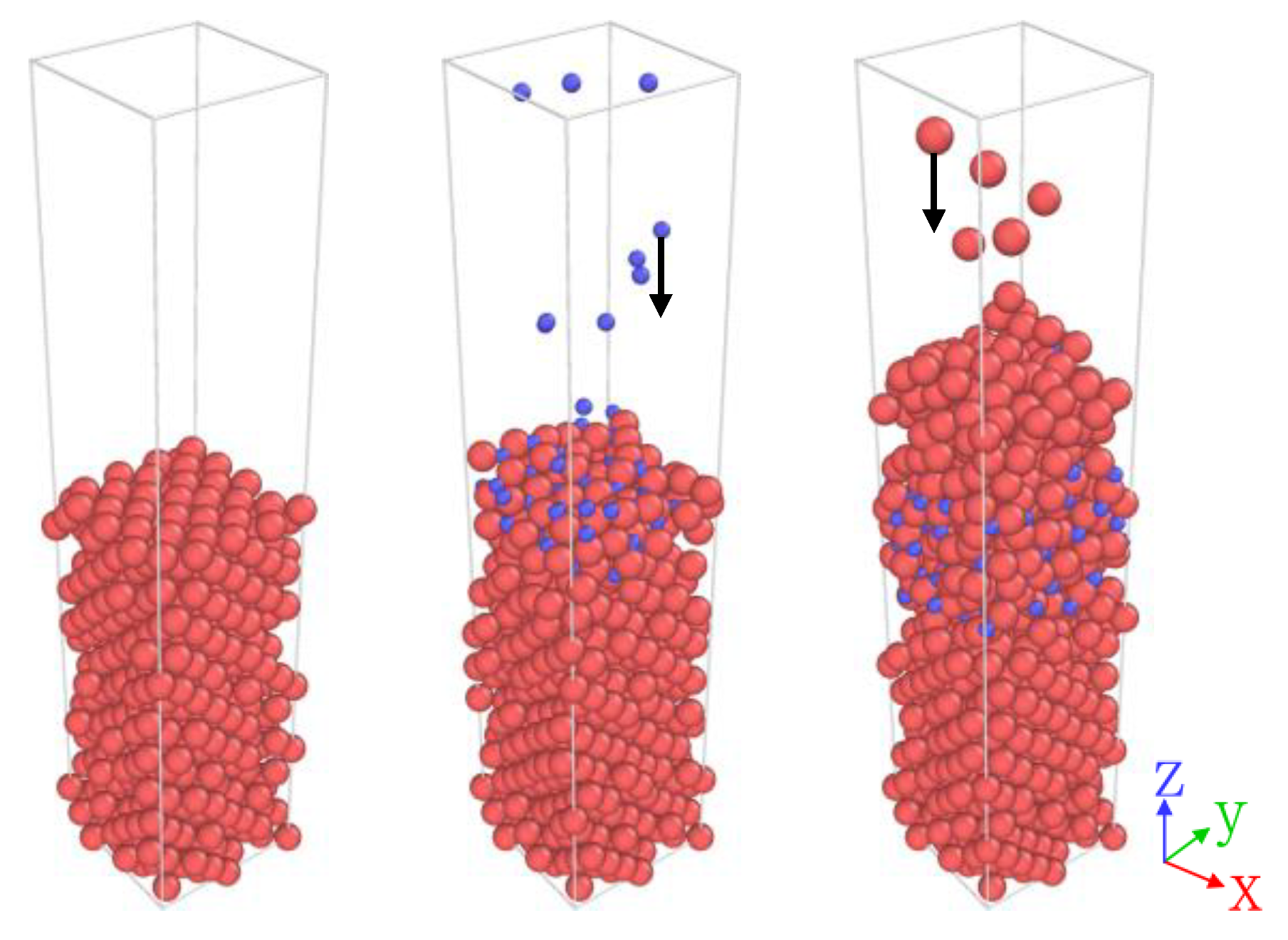

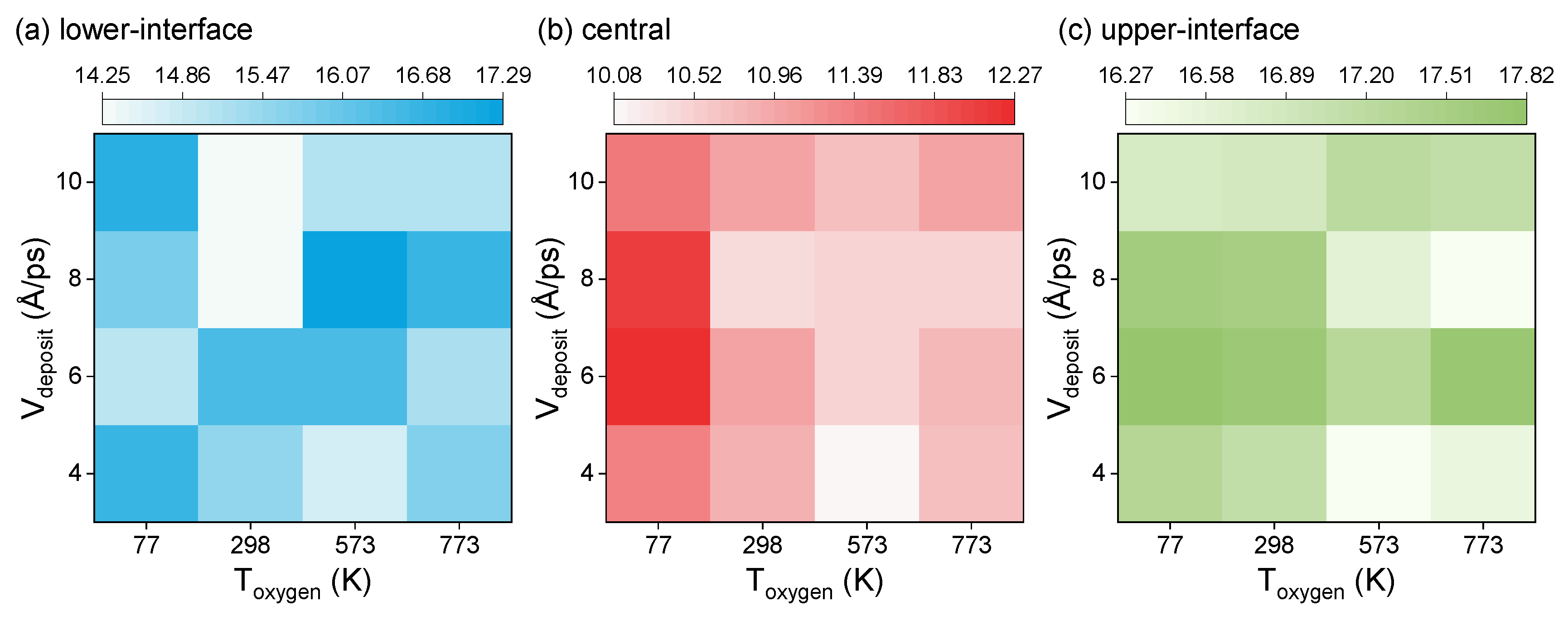
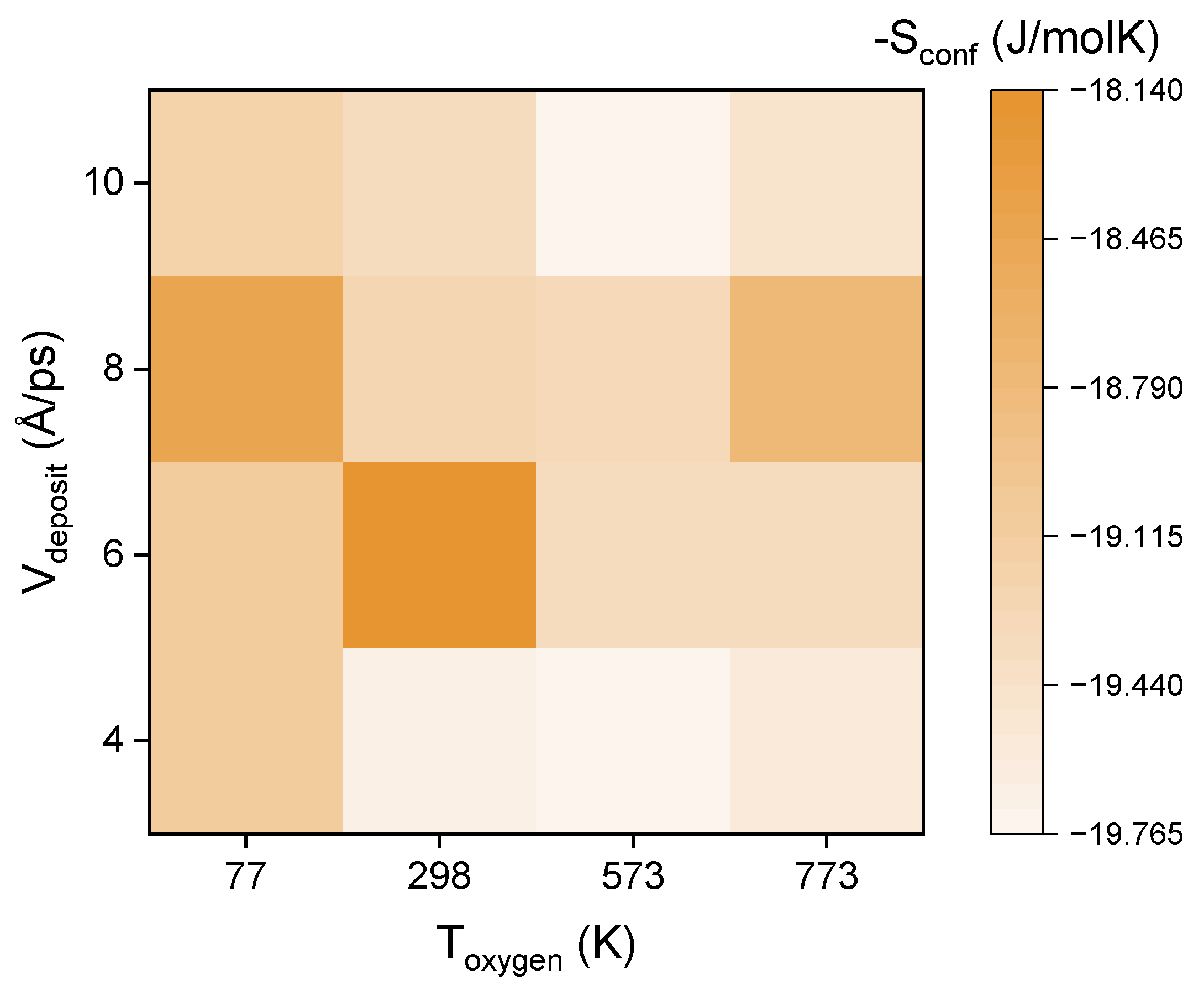
| 298 | 77 | 4 |
| 77 | 6 | |
| 77 | 8 | |
| 77 | 10 | |
| 298 | 4 | |
| 298 | 6 | |
| 298 | 8 | |
| 298 | 10 | |
| 573 | 4 | |
| 573 | 6 | |
| 573 | 8 | |
| 573 | 10 | |
| 773 | 4 | |
| 773 | 6 | |
| 773 | 8 | |
| 773 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Sun, H.; Liu, F.; Zhao, X.; Shan, Z. Computational Simulations of Fabrication of Aluminum-Based Josephson Junctions: Topological Aspects of the Barrier Structure. Entropy 2023, 25, 182. https://doi.org/10.3390/e25020182
Han C, Sun H, Liu F, Zhao X, Shan Z. Computational Simulations of Fabrication of Aluminum-Based Josephson Junctions: Topological Aspects of the Barrier Structure. Entropy. 2023; 25(2):182. https://doi.org/10.3390/e25020182
Chicago/Turabian StyleHan, Chuanbing, Huihui Sun, Fudong Liu, Xiangju Zhao, and Zheng Shan. 2023. "Computational Simulations of Fabrication of Aluminum-Based Josephson Junctions: Topological Aspects of the Barrier Structure" Entropy 25, no. 2: 182. https://doi.org/10.3390/e25020182
APA StyleHan, C., Sun, H., Liu, F., Zhao, X., & Shan, Z. (2023). Computational Simulations of Fabrication of Aluminum-Based Josephson Junctions: Topological Aspects of the Barrier Structure. Entropy, 25(2), 182. https://doi.org/10.3390/e25020182






