Design of Closed-Loop Control Schemes Based on the GA-PID and GA-RBF-PID Algorithms for Brain Dynamic Modulation
Abstract
:1. Introduction
2. Materials and Methods
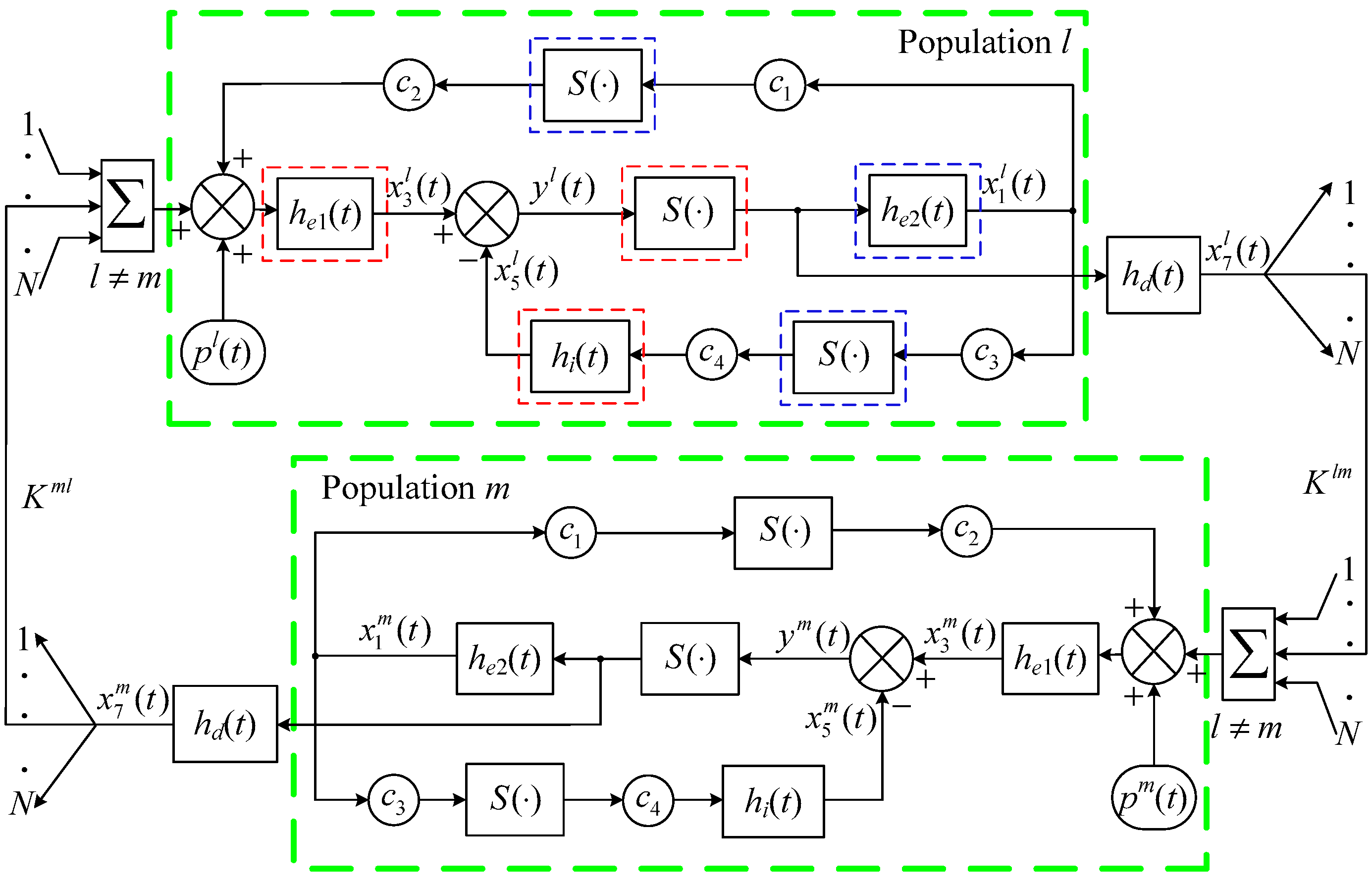
2.1. Wendling-Type Coupled Neural Mass Model
2.2. Design of Closed-Loop Control Schemes for Brain Dynamic Modulation
2.2.1. Preliminary Knowledge
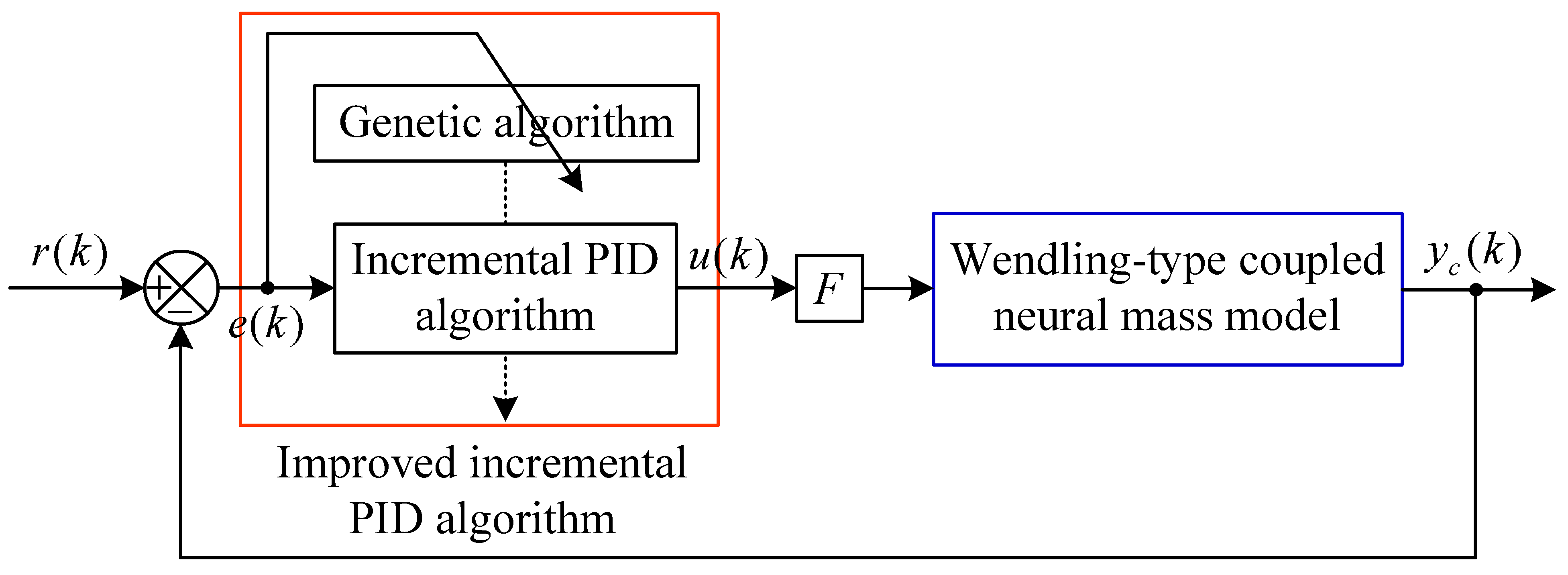
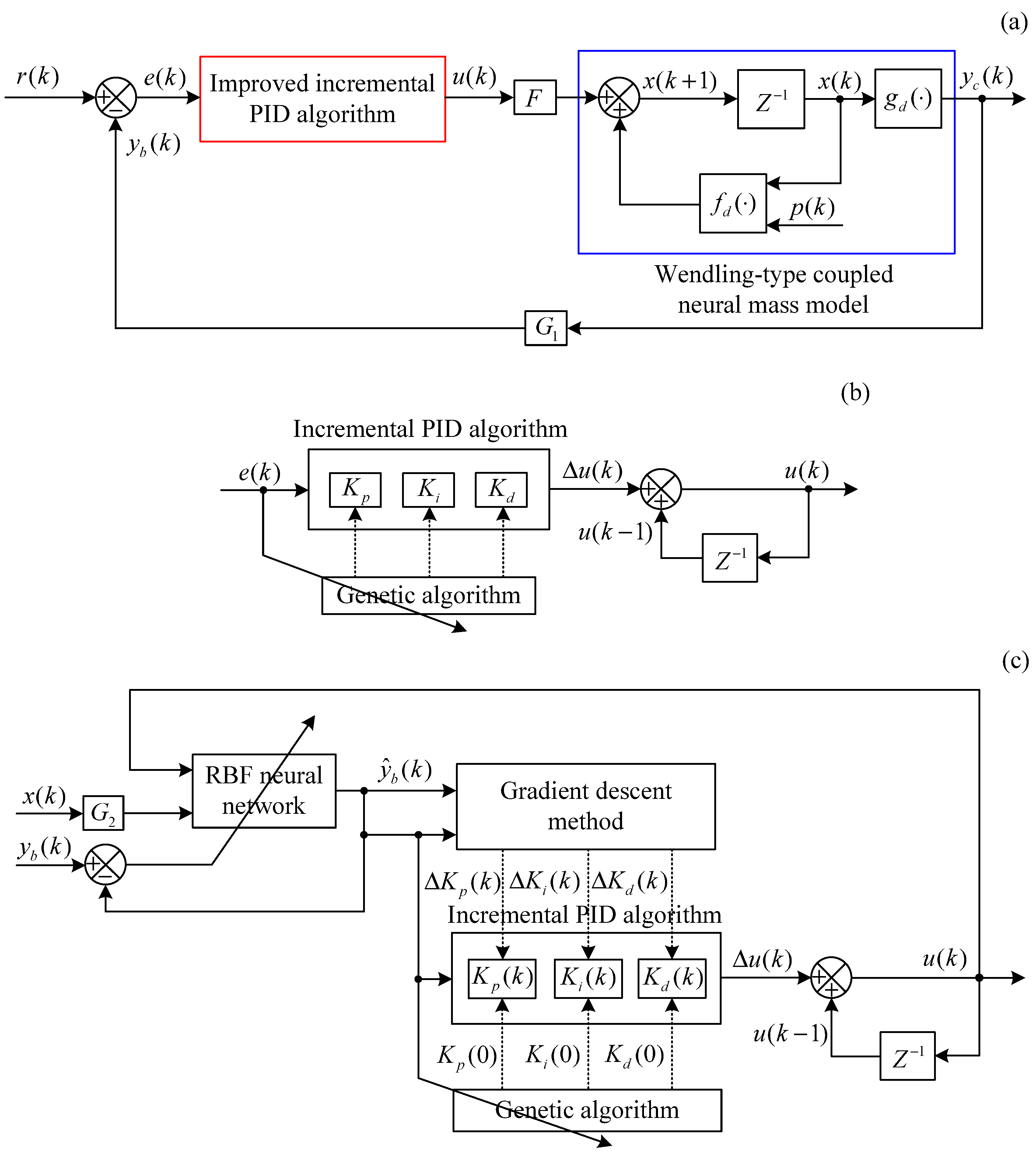
2.2.2. GA-PID Algorithm Based Closed-Loop Control Scheme
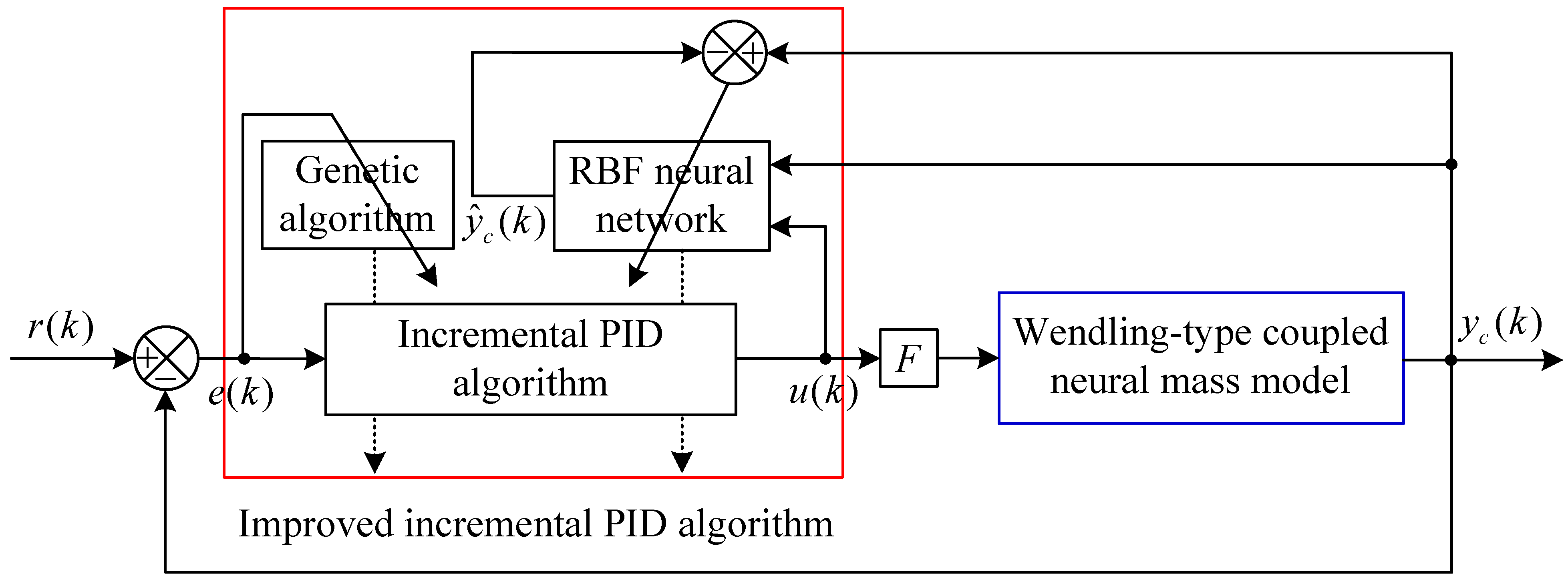
2.2.3. GA-RBF-PID Algorithm Based Closed-Loop Control Scheme
2.3. Performance Metrics
3. Results
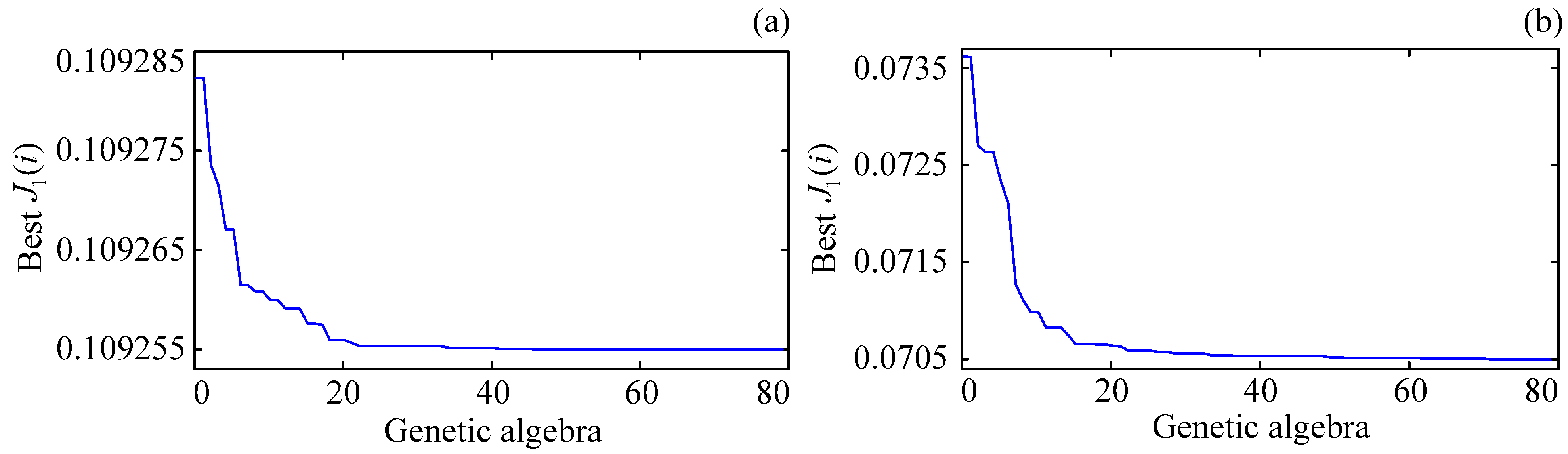
3.1. Results of GA Optimization Control Parameters
3.2. Analysis of Brain Dynamic Modulation Results
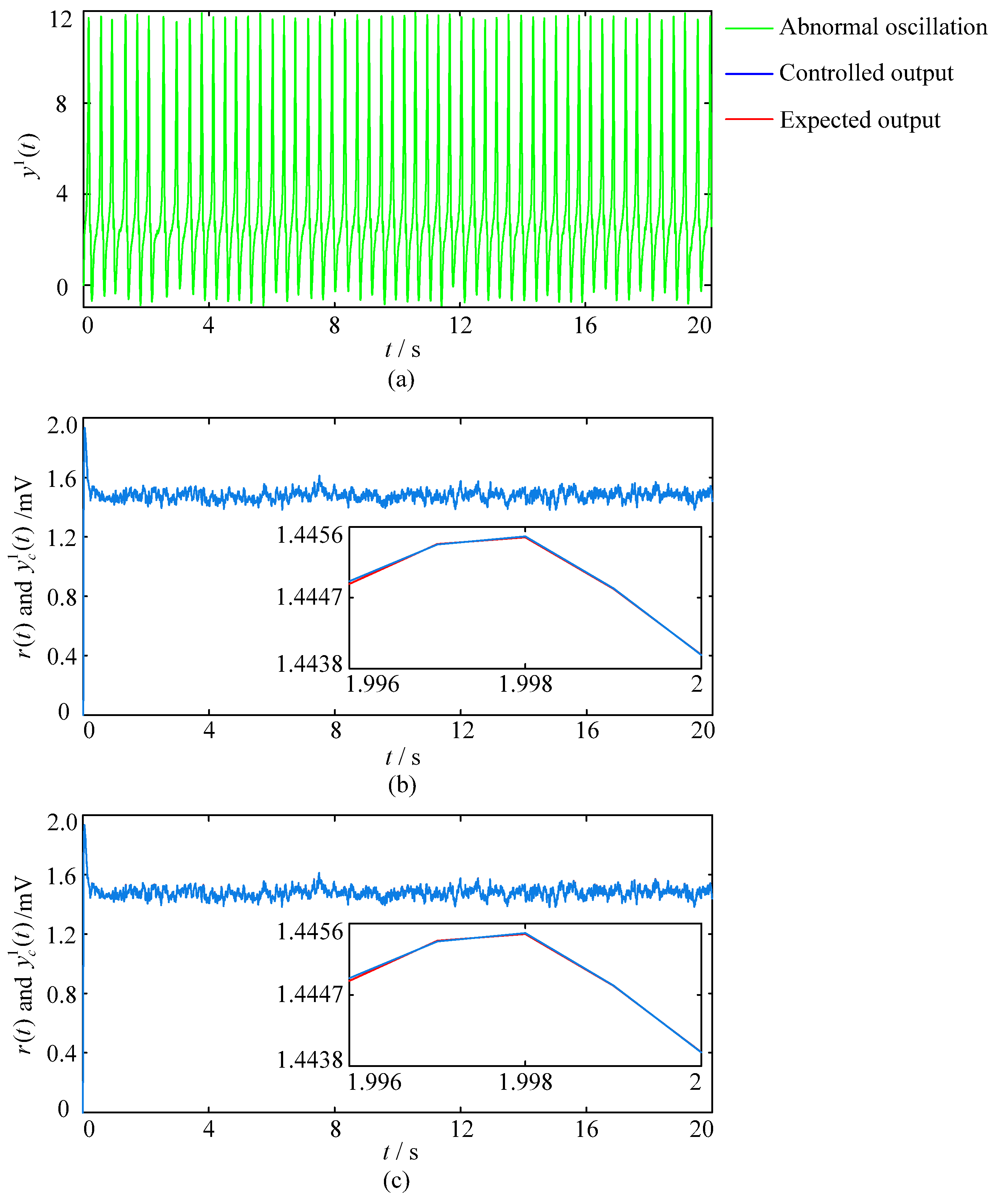
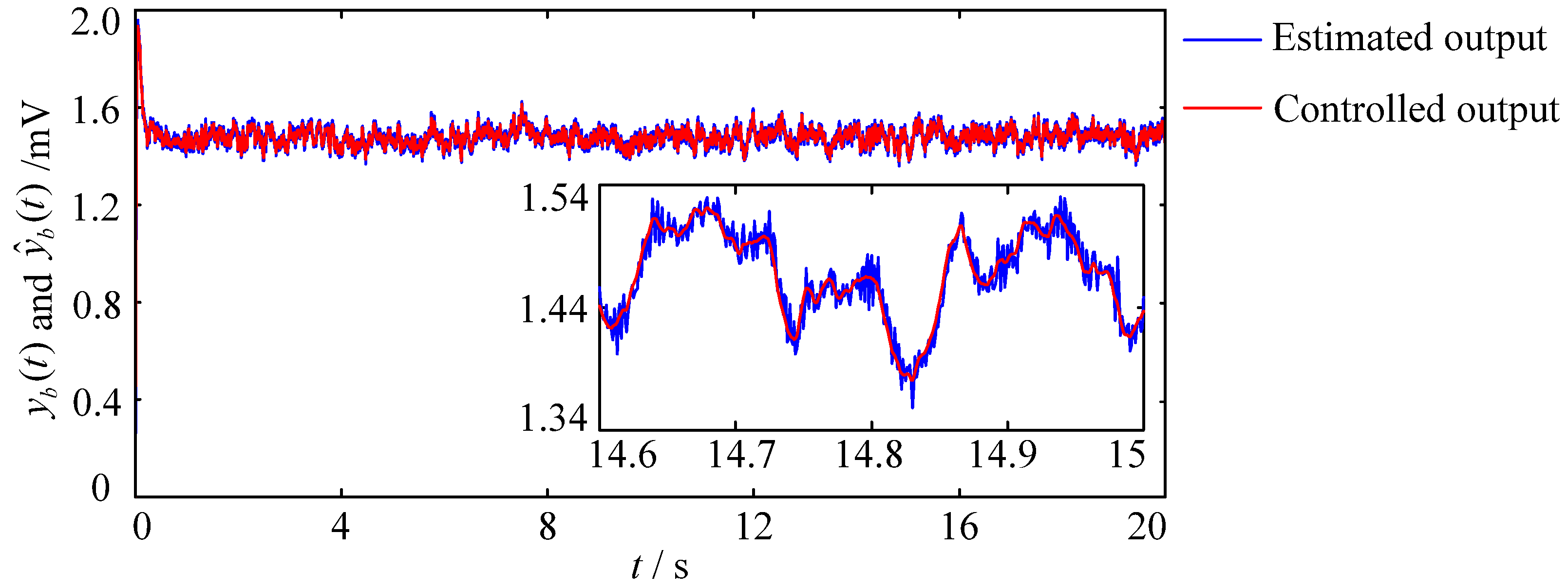
3.2.1. The Simulation Experiments with the Fixed Excitatory Gains
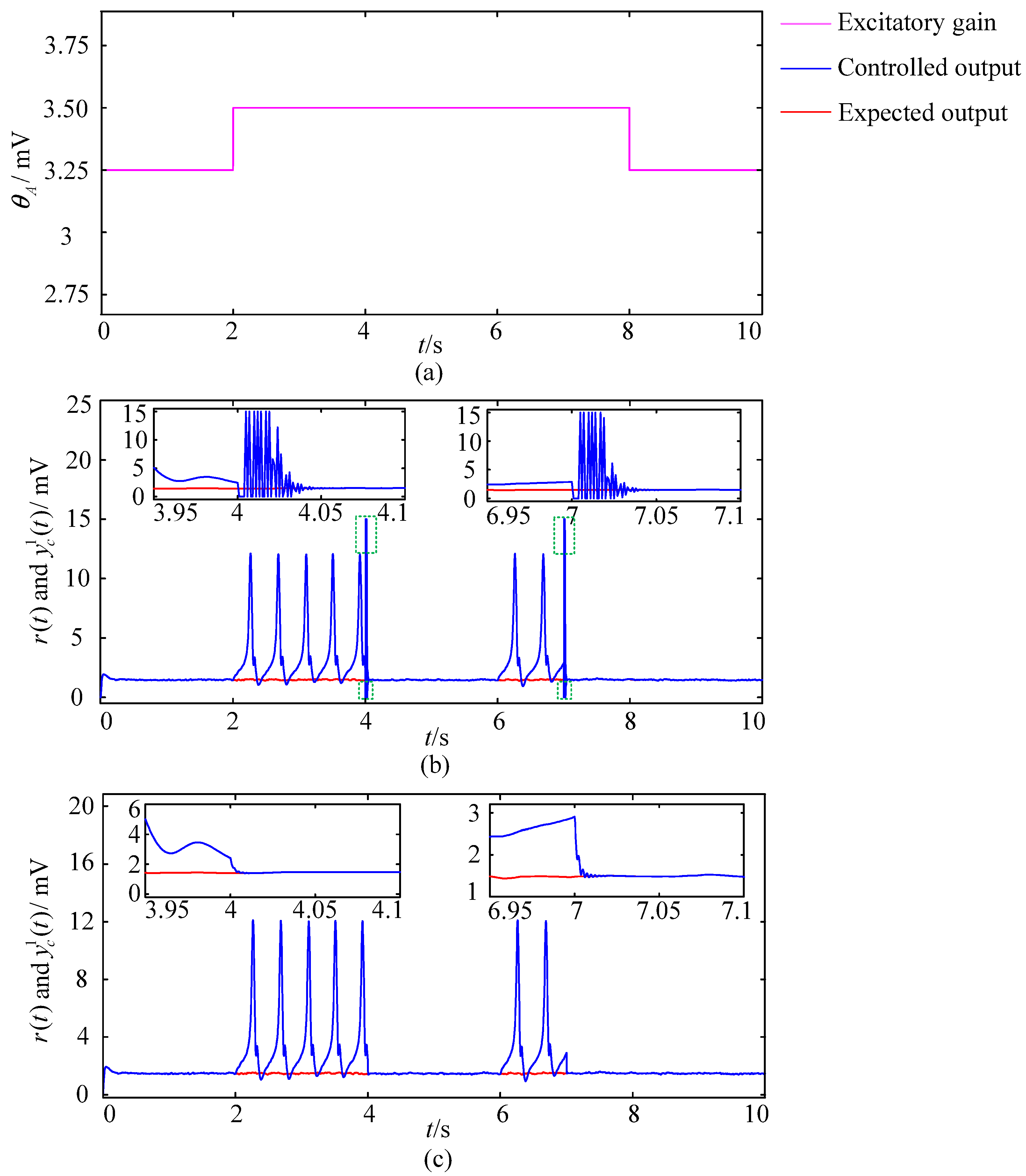
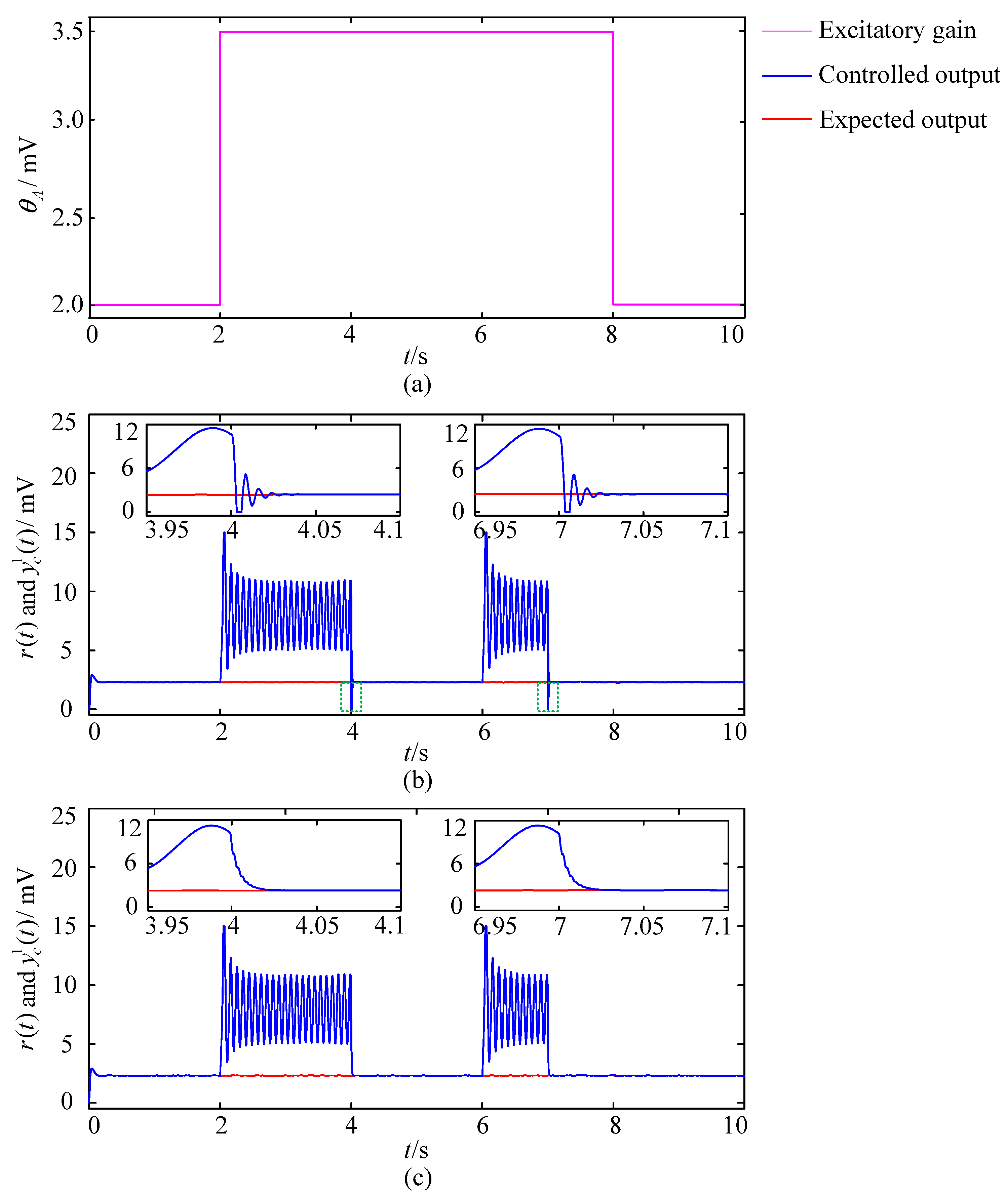
3.2.2. The Simulation Experiments with the Mutated Excitatory Gains
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wiener, N.; Schadé, J.P. Introduction to Neurocybernetics. Prog. Brain Res. 1963, 2, 1–7. [Google Scholar]
- David, O.; Friston, K.J. A Neural Mass Model for MEG/EEG: Coupling and Neuronal Dynamics. Neuroimage 2003, 20, 1743–1755. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Simple Model of Spiking Neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Wendling, F.; Bellanger, J.J.; Bartolomei, F.; Chauvel, P. Relevance of Nonlinear Lumped-Parameter Models in the Analysis of Depth-EEG Epileptic Signals. Biol. Cybern. 2000, 83, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Bi, L.Z.; Lian, J.L.; Li, H.Q. Mathematical Modeling of EEG Signals-Based Brain-Control Behavior. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1535–1543. [Google Scholar] [CrossRef]
- Jansen, B.H.; Rit, V.G. Electroencephalogram and Visual Evoked Potential Generation in a Mathematical Model of Coupled Cortical Columns. Biol. Cybern. 1995, 73, 357–366. [Google Scholar] [CrossRef]
- Wei, W.; Wei, X.F.; Zuo, M.; Yu, T.; Li, Y. Seizure Control in a Neural Mass Model by an Active Disturbance Rejection Approach. Int. J. Adv. Robot. Syst. 2019, 16, 175001201–175001213. [Google Scholar] [CrossRef]
- Yang, X.G.; Huang, M.X.; Wu, Y.Y.; Feng, S.L. Observer-Based PID Control Protocol of Positive Multi-Agent Systems. Mathematics 2023, 11, 419. [Google Scholar] [CrossRef]
- Xu, Y.W.; Shu, H.; Qin, H.C.; Wu, X.L.; Peng, J.X.; Jiang, C.; Xia, Z.P.; Wang, Y.A.; Li, X. Real-Time State of Health Estimation for Solid Oxide Fuel Cells Based on Unscented Kalman Filter. Energies 2022, 15, 2534. [Google Scholar] [CrossRef]
- Khan, M.W.; Muhammad, Y.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y.G. A New Fractional Particle Swarm Optimization with Entropy Diversity Based Velocity for Reactive Power Planning. Entropy 2020, 22, 1112. [Google Scholar] [CrossRef]
- Su, F.; Wang, J.; Deng, B.; Wei, X.L.; Chen, Y.Y.; Liu, C. Adaptive Control of Parkinson’s State Based on a Nonlinear Computational Model with Unknown Parameters. Int. J. Neural Syst. 2015, 25, 1450030. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wang, J.; Li, H.Y.; Lu, M.L.; Deng, B.; Yu, H.T.; Wei, X.L.; Fietkiewicz, C.; Loparo, K.A. Closed-Loop Modulation of the Pathological Disorders of the Basal Ganglia Network. IEEE Trans. Neural Netw. 2017, 28, 371–382. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Gao, Q. Parameter Estimation and Control for a Neural Mass Model Based on the Unscented Kalman Filter. Phys. Rev. E 2013, 88, 042905. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, H.J.; Tang, Y.G.; Gao, Q.; Chen, Z.W. Fuzzy Adaptive Unscented Kalman Filter Control of Epileptiform Spikes in a Class of Neural Mass Models. Nonlinear Dyn. 2014, 76, 1291–1299. [Google Scholar] [CrossRef]
- Shan, B.N.; Wang, J.; Deng, B.; Wei, X.L.; Yu, H.T.; Li, H.Y. UKF-Based Closed Loop Iterative Learning Control of Epileptiform Wave in a Neural Mass Model. Cogn. Neurodynam. 2015, 9, 31–40. [Google Scholar] [CrossRef]
- Shan, B.N.; Wang, J.; Deng, B.; Wei, X.L.; Yu, H.T.; Zhang, Z.; Li, H.Y. Particle Swarm Optimization Algorithm Based Parameters Estimation and Control of Epileptiform Spikes in a Neural Mass Model. Chaos 2016, 26, 073118. [Google Scholar] [CrossRef]
- Gorzelic, P.; Schiff, S.J.; Sinha, A. Model-Based Rational Feedback Controller Design for Closed-Loop Deep Brain Stimulation of Parkinson’s Disease. J. Neural Eng. 2013, 10, 026016. [Google Scholar] [CrossRef]
- Wang, J.S.; Niebur, E.; Hu, J.Y.; Li, X.L. Suppressing Epileptic Activity in a Neural Mass Model Using a Closed-Loop Proportional-Integral Controller. Sci. Rep. 2016, 6, 27344. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Chen, Y.Y.; Deng, B.; Wei, X.L.; Li, H.Y. Closed-Loop Control of the Thalamocortical Relay Neuron’s Parkinsonian State Based on Slow Variable. Int. J. Neural Syst. 2013, 23, 1350017. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, M.L.; Li, X.L.; Niebur, E. Closed-Loop Control of Epileptiform Activities in a Neural Population Model Using a Proportional-Derivative Controller. Chin. Phys. B 2015, 24, 038701. [Google Scholar] [CrossRef]
- Chen, T.P.; Chen, H. Approximation Capability to Functions of Several Variables, Nonlinear Functionals, and Operators by Radial Basis Function Neural Networks. IEEE Trans. Neural Netw. 1995, 6, 904–910. [Google Scholar] [CrossRef] [PubMed]
- Coit, D.W. Genetic Algorithms and Engineering Design. Eng. Econ. 1998, 43, 379–381. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, Y.L.; Liu, F.; Wang, J.; Li, H.Y.; Deng, B.; Fietkiewiczb, C.; Loparo, A. Neural Mass Models Describing Possible Origin of the Excessive Beta Oscillations Correlated with Parkinsonian State. J. Adv. Ceram. 2017, 88, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Sanner, R.M.; Slotine, J.J.E. Gaussian Networks for Direct Adaptive Control. IEEE Trans. Neural Netw. 1992, 3, 837–863. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.W.; Hu, H.G.; Xu, L.H.; Li, G.H. Nonlinear Adaptive PID Control for Greenhouse Environment Based on RBF Network. Sensors 2012, 12, 5328–5348. [Google Scholar] [CrossRef] [PubMed]
- Glüer, C.C.; Blake, G.; Lu, Y.; Blunt, B.A.; Jergas, M.; Genant, H.K. Accurate Assessment of Precision Errors: How to Measure the Reproducibility of Bone Densitometry Techniques. Osteoporos. Int. 1995, 5, 262–270. [Google Scholar] [CrossRef]
- Liu, X.; Feng, Z.; Wang, G.; Gao, Q. A New Method for Nonlinear Dynamic Analysis of the Multi-kinetics Neural Mass Model. IRBM 2019, 40, 183–191. [Google Scholar] [CrossRef]
- Fernandez-Ruiz, A.; Sirota, A.; Lopes-dos-Santos, V.; Dupret, D. Over and Above Frequency: Gamma Oscillations as Units of Neural Circuit Operations. Neuron 2023, 7, 926–953. [Google Scholar] [CrossRef]
- Traub, R.; Whittington, M. Cortical Oscillations in Health and Disease; Oxford University Press: Oxford, UK; New York, NY, USA, 2010. [Google Scholar]
- Alarcón, G.; Jiménez-Jiménez, D.; Valentín, A.; Martín-López, D. Characterizing EEG Cortical Dynamics and Connectivity with Responses to Single Pulse Electrical Stimulation (SPES). Int. J. Neural Syst. 2018, 28, 1750057. [Google Scholar] [CrossRef]
- Xu, S.S.; Lee, W.L.; Perera, T.; Sinclair, N.C.; Bulluss, K.J.; Mcdermott, H.J.; Thevathasan, W. Can Brain Signals and Anatomy Refine Contact Choice for Deep Brain Stimulation in Parkinson’s Diseas? J. Neurol. Neurosurg. Psychiatry 2022, 93, 1338–1341. [Google Scholar]
- Xu, Y.; Zhang, C.H.; Niebur, E.; Wang, J.S. Analytically Determining Frequency and Amplitude of Spontaneous Alpha Oscillation in Jansens Neural Mass Model Using the Describing Function Method. Chin. Phys. B 2018, 27, 048701. [Google Scholar] [CrossRef] [PubMed]
- Mina, F.; Benquet, P.; Pasnicu, A.; Biraben, A.; Wendling, F. Modulation of Epileptic Activity by Deep Brain Stimulation: A Model-Based Study of Frequency-Dependent Effects. Front. Comput. Neurosci. 2013, 7, 94. [Google Scholar] [CrossRef] [PubMed]
- Khrennikov, A. Open Systems, Quantum Probability, and Logic for Quantum-like Modeling in Biology, Cognition, and Decision-Making. Entropy 2023, 25, 886. [Google Scholar] [CrossRef] [PubMed]
- Zúñiga-Galindo, W.A.; Zambrano-Luna, B.A. Open Systems, Hierarchical Wilson–Cowan Models and Connection Matrices. Entropy 2023, 25, 949. [Google Scholar] [CrossRef]
- Ying, T.; Burkitt, A.N.; Kameneva, T. Combining the Neural Mass Model and Hodgkin-Huxley Formalism: Neuronal Dynamics Modelling. Biomed. Signal Process 2023, 79, 104026. [Google Scholar] [CrossRef]
- Zhao, L.; Zeng, W.M.; Shi, Y.H.; Nie, W.F. Dynamic Effective Connectivity Network Based on Change Points Detection. Biomed. Signal Process 2022, 72, 103274. [Google Scholar] [CrossRef]
- Eguíluz, V.M.; Chialvo, D.R.; Cecchi, G.A.; Baliki, M.; Apkarian, A.V. Scale-Free Brain Functional Networks. Phys. Rev. Lett. 2005, 94, 018102. [Google Scholar] [CrossRef]
- Micheloyannis, S.; Pachou, E.; Stam, C.J.; Breakspear, M.; Bitsios, P.; Vourkas, M.; Erimaki, S.; Zervakis, M. Small-World Networks and Disturbed Functional Connectivity in Schizophrenia. Schizophr. Res. 2006, 87, 60–66. [Google Scholar] [CrossRef]
- Stam, C.J.; Jones, B.F.; Nolte, G.; Breakspear, M.; Scheltens, P. Small-World Networks and Functional Connectivity in Alzheimer’s Disease. Cereb. Cortex. 2006, 17, 92–99. [Google Scholar] [CrossRef]
- Ponten, S.C.; Bartolomei, F.; Stam, C.J. Small-World Networks and Epilepsy: Graph Theoretical Analysis of Intracerebrally Recorded Mesial Temporal Lobe Seizures. Clin. Neurophysiol. 2007, 118, 918–927. [Google Scholar] [CrossRef]
- Deng, B.; Wang, J.; Che, Y.Q. Combined Method to Estimate Parameters of Neuron from A Heavily Noise-Corrupted Time Series of Active Potential. Chaos 2009, 19, 015105. [Google Scholar] [CrossRef] [PubMed]
- López-Cuevas, A.; Castillo-Toledo, B.; Medina-Ceja, L.; Ventura-Mejía, C. State and Parameter Estimation of A Neural Mass Model from Electrophysiological Signals During the Status Epilepticus. Neuroimage 2015, 113, 374–386. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Physiological Meaning | Standard Value |
|---|---|---|
| average gains of excitatory and inhibitory synaptic | ||
| membrane transfer and dendritic tree average time delay | ||
| average contact time between neural populations | = 33 | |
| average synaptic connections in the excitatory feedback loop | = 135, = 108 | |
| average synaptic connections in the inhibitory feedback loop | = 33.75 | |
| represents the maximum firing rate | = 2.5 | |
| r represents bending degree of the sigmoid function | r = 0.56 | |
| is the postsynaptic potential corresponding to firing rate | = 6 mV | |
| v represents the presynaptic average membrane potential | no standard value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Geng, L.; Liu, X.; Gao, Q. Design of Closed-Loop Control Schemes Based on the GA-PID and GA-RBF-PID Algorithms for Brain Dynamic Modulation. Entropy 2023, 25, 1544. https://doi.org/10.3390/e25111544
Sun C, Geng L, Liu X, Gao Q. Design of Closed-Loop Control Schemes Based on the GA-PID and GA-RBF-PID Algorithms for Brain Dynamic Modulation. Entropy. 2023; 25(11):1544. https://doi.org/10.3390/e25111544
Chicago/Turabian StyleSun, Chengxia, Lijun Geng, Xian Liu, and Qing Gao. 2023. "Design of Closed-Loop Control Schemes Based on the GA-PID and GA-RBF-PID Algorithms for Brain Dynamic Modulation" Entropy 25, no. 11: 1544. https://doi.org/10.3390/e25111544
APA StyleSun, C., Geng, L., Liu, X., & Gao, Q. (2023). Design of Closed-Loop Control Schemes Based on the GA-PID and GA-RBF-PID Algorithms for Brain Dynamic Modulation. Entropy, 25(11), 1544. https://doi.org/10.3390/e25111544





