Appendix A. Critique of the Historical Argument against a Simple Nonlinear Term
The standard argument that simple, spontaneous collapse models all involve superluminal communication is reviewed here.
Suppose that we have a source that emits a standard two-photon entangled state,
where
is a vertically linearly polarized state, and
is horizontally polarized; the first ket refers to a left-going photon and the second to a right-going one.
The photon on the left then hits a standard detection apparatus oriented to detect vertical and horizontal polarization. It is assumed that this leads to the following density matrix:
i.e., a mixed state of the projection onto states
,
,
, and
. If we define
for the photon on the left, an operator of the form
will then give
If, for example,
, this gives
This leads to evolution toward the pure
state.
On the other hand, suppose, at the last second, a person on the left changed the measurement to polarization along
instead of
H and
V. The recipe for getting the density matrix of the mixed state, in this case, is to project the state (
A1) onto these axes and then create the stochastic mixture. The projector for
acting on the states on the left is
If we act with this operator on the whole state and normalize, we obtain
which occurs with probability
. The corresponding pure-density matrix is
The
polarization is similar:
The mixed-density matrix that occurs is then
The total probability of getting a measurement of a photon with
H-polarization on the right is still the same, namely
(the sum of the two diagonal terms corresponding to a ket with a rightmost
), but there are now off-diagonal terms.
It is assumed that the non-Hermitian operator
, in this case, involves the number operator
for the 45
polarizations. The creation operator for 45
polariztion is
, which implies the number operator
. Similarly,
, and therefore
. The time dependence is then given by
with
as before, but in this case, the expectation value of
is zero since there is an equal likelihood of both polarizations. The time dependence is then given just by the
operator,
This gives
By comparing this to (
A7), we see that the action is to move the mixed-density matrix toward the density matrix for the pure
polarization state. The relative probability of detecting single photons with
H and
V polarizations is unchanged.
Therefore, the change in the count rates is different for the detector on the right, depending on what measurement setting the person on the left has chosen since in the first case above, with vertical and horizontal detection, the non-Hermitian term was found to give a change of the relative probabilities. The person on the right can, therefore, presumably detect the position of the detector on the left instantaneously, which would imply superluminal communication.
As discussed in the main text, this argument depends crucially on first creating the mixed state and then, afterward, applying the non-Hermitian operator. However, the probabilistic nature of the mixed state assumes the existence of an ensemble of trials in which multiple collapses or projections have occurred. Applying the non-Hermitian operator afterward assumes that it acts the same way, deterministically, for every one of these trials in the ensemble. However, the assumption of our model is that the non-Hermitian operator is the cause of the collapses and that it acts stochastically to give random outcomes in each trial, in accordance with the Born rule. The proper recipe, therefore, is to first form the density matrix of the pure state and then apply the non-Hermitian operator to get a collapse in one particular trial and, last, to average over many of these trials to get the final mixed-density matrix.
One must be careful when carrying this out. The approaches that use Itô calculus (for a review, see [
44]) to perform the stochastic average can also implicitly rely on improper assumptions. For example, Gisin and Percival [
45] posit the form of the Schrödinger equation (in terms of the operators used here)
where
is a (real-valued) Itô stochastic differential accounting for fluctuations. This can be rewritten as
and
. The averaged density matrix can then be constructed as
As per Itô calculus, those terms that are linear in
vanish (the mean of the random walk remains unchanged) while
(fluctuation of different states are uncorrelated, and the magnitude of the random walk increases as
). This gives us
The last three terms are exactly the Lindbladian for the operator
. It can be shown that this term gives the decay of the off-diagonal terms of the density matrix while preserving the diagonal terms, leading to a diagonal density matrix that corresponds to a mixed state. This, in turn, prevents superluminal communication of the type discussed above since the diagonal of the mixed-density matrix is always left unchanged.
This approach of Gisin and Percival requires fine-tuning in that the magnitude of the third term in (
A13) must match exactly the amplitude of the noise assumed in the fourth term. Without the third term, the Itô calculus applied to just the fourth term, as taken by Gisin and Percival, will not preserve the diagonal of the density matrix. But we argue here that such a term is not needed when physically realistic fluctuations are accounted for correctly.
Itô calculus intrinsically assumes that the fluctuations are fast compared to all other time scales; in particular, it assumes that fluctuations occur on time scales that are short compared to
. However, in our model, as discussed in
Section 5, the fluctuations are assumed to arise from physical fluctuations in the environment. As such, these have a short but nonzero persistence time, which means that one can always pick a
that is short enough such that
can be treated as constant. Therefore, one should
first take the
to derive the time evolution and, only
afterward, take the stochastic average.
For the moment, treating
as not time-varying, we can then use standard time-dependent perturbation theory in the interaction representation, as in
Section 2 (see, e.g., Ref. [
29], Chapter 4). Starting with the Schrödinger equation
the prescription of this method is to write
where
and
. Since
commutes with the Hamiltonian
, the only time-dependence of
comes from the time dependence of
, which is used in the term
, which occurs in
. The expansion of the time dependence up to the first order is then
When substituting this back into (
A18) for the second-order expansion, we then have
When taking
as being negligible compared to
t, as we did in
Section 2, we form the density matrix
Again, by keeping just the terms linear in
t, we then have
where
is the change in the state by normal Hamiltonian evolution. In other words, when taking
as an infinitesimal, the change in the density matrix due to the non-Hermitian term is
The action of the operator
on the two states
and
, for
is given by the matrix
As discussed in Ref. [
27], this maps to a one-dimensional problem corresponding to a random walk of the polar angle
on the Bloch sphere, where
; the off-diagonal components of the density matrix are not independent of the diagonal components but instead approach zero as the diagonal components approach either
or
.
We can now take the stochastic average for fluctuations in
. Since the fluctuations of
are linearly proportional to
, the Itô calculus prescribes that the average of
does not change in time. This implies that an average over many random walks will give
in accordance with the Born rule. This is an alternate derivation of the proof given in
Appendix B.
Appendix B. Proof That a Martingale Random Walk Satisfies the Born Rule
Let
be a sequence of independent and identically distributed random variables with a common symmetric, continuous probability density
that is strictly positive in an open neighborhood of the origin. Examples of such
include the Gaussian and Lorenztian distributions. We also suppose that
is a fixed constant, small enough so that
where
is a cutoff parameter that we will make use of later. For convenience of numerical implementation, we want to ensure that the step sizes are uniformly bounded. We define
to be the function
Finally, we define
. For each fixed
n,
is, thus, a continuous, symmetric random variable with mean 0 and uniformly bounded range
.
We wish to study the following stochastic finite difference equation (SFDE):
This SFDE is a random walk starting at a given
. We shall show that this model leads to the Born rule. That is, when given any initial condition
, we can assign a probability,
, of collapsing to state 1, and a probability,
, of collapsing to state
, such that
Our strategy is to first prove that we can achieve the Born rule within arbitrary precision
, and then to take the limit as
tends to 0 to recover the Born rule. The crucial observation we will make is that the stochastic process
defined by (
A28) is a martingale. The martingale property is that
where
denotes the conditional expectation. Intuitively, our best prediction of the next position of a martingale, given the history of the process, is simply the current position (martingales are like stochastic constants). In order to prove that our process is a martingale, we simply compute the conditional expectation.
First, we note that
depends only on
and not
. Moreover,
is known to us at time
n. Finally,
is independent of
. According to the properties of conditional expectation, we, therefore, have
In the last line, we have used
for every
n. Therefore, the sequence
is a martingale.
Now, we introduce
and define a stopping time
We state here and prove below that
is finite almost surely, which simply means that
. Because of this, we can make use of the optional stopping theorem, ref. [
46] which states that if a martingale
is bounded in the sense that there exists some
, such that
for all
, and if a stopping time
is finite almost surely, then
.
We have already established that
is a martingale, and we are assuming that
is finite almost surely. Thus, we only need to find a uniform bound on
to apply the optional stopping theorem. A bound is achieved as follows: for all
n,
according to the triangle inequality. Thus, the optional stopping theorem applies, and we can conclude that
With (
A33) in hand, we proceed as follows: Let
be the probability that collapse to
occurs (before collapse to
) with a tolerance of
, and let
be the probability that collapse to
occurs (before collapse to
) with a tolerance of
. Since we are assuming that
, we know that at least one of the two events
or
must occur. Moreover, for sufficiently small
, these two events are complements. Therefore, the probabilities satisfy
.
Let
if the event
occurred, and let
if the event
occurred. We have
and
, but we will also need a sufficiently large lower bound on
b, as well as a sufficiently small lower bound on
a. It turns out that, in fact,
and
. To prove this, consider the function
defined on the interval
. It is straightforward to find that the maximum value of
f on this closed interval is 1. Thus, we can estimate the position of the random walk at the stopping time
:
since, prior to the stopping time,
must be an element of
.
Now, we can expand out the expected value in (
A33):
Solving for
yields
Since we have shown that
and
, it follows that
and
; hence,
. Likewise, one finds that
Therefore, (
A29) holds.
Proof that is bounded almost surely. We wish to show that
. Choose
so that
on
and such that
. We claim that the stochastic process
defined via (
A28) exhibits arbitrarily long sequences of consecutive, equally sized steps in the direction of
. Let
K be an arbitrary natural number, and let
be the event
for
. Consider the sequence of independent events
. From our assumptions on the probability density
for
, we have
Therefore,
Since the events
are independent, the second Borel-Cantelli lemma applies, and
. We can, thus, choose an
m so that
holds almost surely. Consider now the SFDE (after reindexing, we can assume the process starts at time
)
Consider the analogous deterministic finite difference equation
It follows from the consideration of the function
f defined above and the fact that
that, for system (
A40),
for all
n. Moreover,
is monotone-increasing. Thus, the sequence converges upward to a limit,
y. Then,
, so
. Thus,
. Hence, we can find a least
, so that
, and
. Now, select
K to be large enough so that
. For every
, we have
; thus,
. Hence, (almost surely)
Appendix C. Relativistic Formalism for Nonlocal Projections
The non-unitary term (
18) has the appeal that it is a compact addition to the Schrödinger equation that allows numerical methods to be applied. It also has nonlocal effects, acting as a type of projector at equal times over all space.
As discussed in Ref. [
27], one can generalize this to other relativistic reference frames by positing that there is a favored, universal reference frame in which these projections occur, which could be the center of mass of the universe, seen in the cosmic microwave background, or some other chosen frame. In this case, we can take the many-body states of the system, defined along equal-time slices in this favored reference frame.
A many-body “state” in the laboratory rest frame at time
can be written as
where
and
are complex phase factors for a potentially infinite number of different superpositions of Fock states, and the Fock states are generated by the factor
acting at each point
in space, where
N can equal 0 or 1. This is somewhat unconventional notation, as the state created by
is not an eigenstate of the system, but the set of Fock states defined this way is a complete set of orthogonal states that can form the basis of any many-body state. This can be carried out simply by switching the roles of
and
in the standard plane-wave basis of the many-body field theory (see, e.g., Ref. [
29], Chapter 4) to give a discrete sum over
-states and a continuum of
-states created by
. In this notation, a plane-wave state with momentum
is created as
which is a superposition of Fock states, each with a single particle at one location. Here,
is a cutoff of momentum, which plays the same role as a system size cutoff
V in conventional notation, and the limit is taken of
. (It has been questioned [
47,
48] whether the limit
can be taken without causing a breakdown of the conventional many-body theory, as the finite value of
V is used to justify discrete
-states. Here we simply note that when taking
V as infinite from the start, with
finite, and, afterward, taking
, it is formally and mathematically equivalent to the conventional approach of taking
defined over an infinite range with
V being finite, and then taking the limit
, since we have just redefined the names of the conjugate variables.)
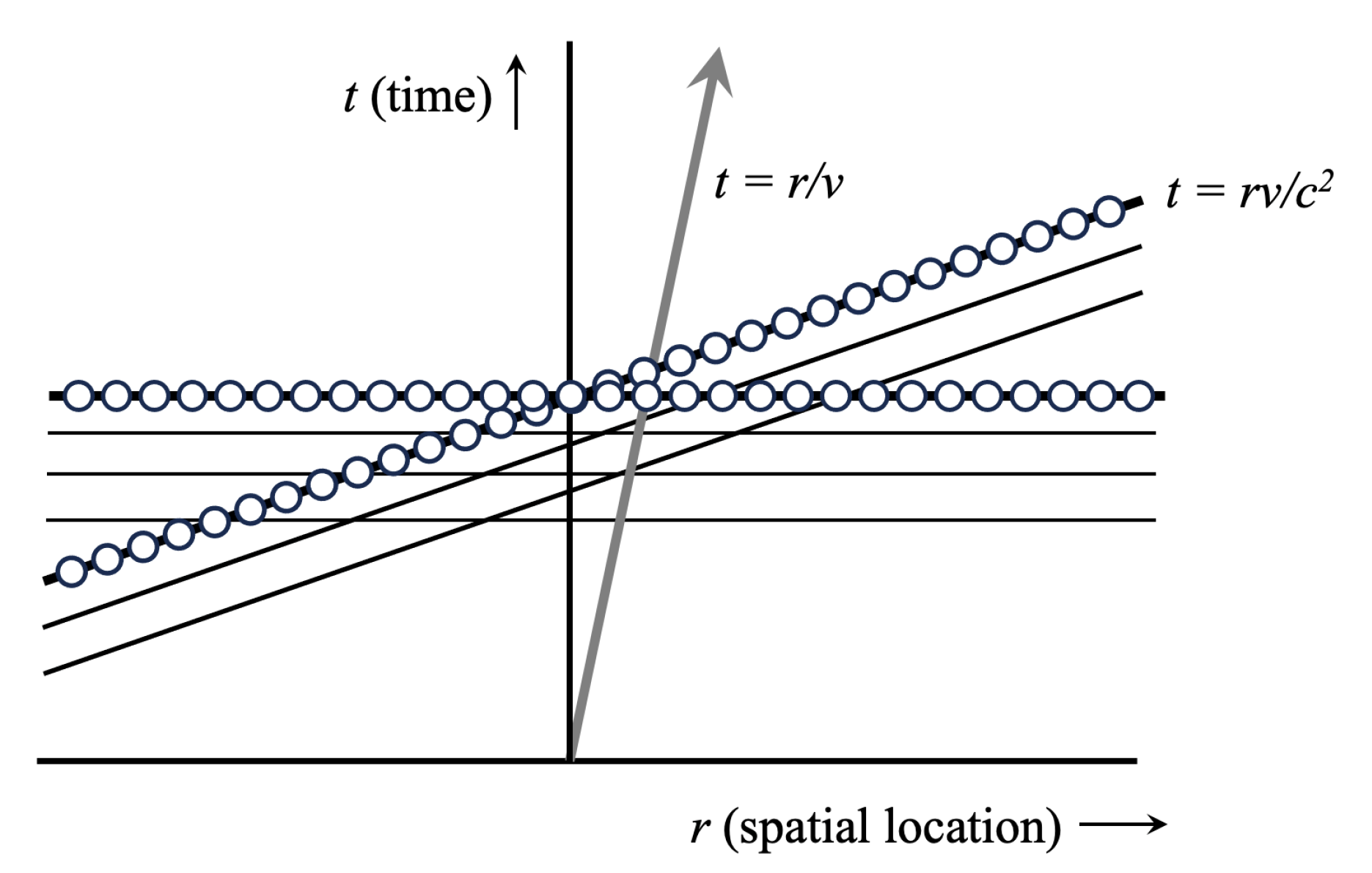
The state (
A41) can be visualized as the horizontal line in
Figure A1 with open circles, where each circle represents a local fermionic state in a continuum. It amounts to taking a slice at equal times in the overall hyperspace field. If an operator
is applied to this state, this will remove any Fock states in the overall superposition that have
.
The time-slice on which a many-body “state” is defined is somewhat arbitrary, however. We could also define a “state” as a slice of the global field at equal times in a different, chosen reference frame (e.g., the rest frame of the cosmic microwave background). If that chosen reference frame is moving at speed
v relative to the laboratory rest frame, its equal time slice will correspond and have the same form as (
A41), but in this case of the local creation operators, it will be
. This corresponds to the tilted line with open circles in
Figure A1. If an operator
is applied to this state, this will remove any Fock states in this overall superposition that have
. This implies a backwards-in-time action of a sort, but as discussed in Ref. [
27], it does not imply grandfather paradoxes.
Of course, we could just solve all problems in the chosen reference frame, in which case we do not have to worry about backwards-in-time actions. But in many cases, it may be more convenient to solve the normal Hermitian Hamiltonian dynamics in the laboratory frame and then apply the nonlocal, non-Hermitian term separately. In this case, we have a well-defined algorithm for evolving the field in time:
For a given many-body “state” along a time slice, first evolve the state using the local, Hermitian interaction Hamiltonian to take the state from time t to time . This may generate superpositions of different Fock states.
At each point of this new “state”, apply the non-Hermitian operator (
18). This will have the effect of changing the relative weights of the phase factors
,
of the overall superposition of Fock states.
With this new superposition, go on to the next time slice and start the process over.
This algorithm may seem odd, but it is well-defined, is consistent between different reference frames, and involves no random numbers other than what randomness is generated by actual fluctuations in the local environment via the
term in (
18).
Figure A1.
Horizontal line with open circles: the standard definition of a many-body state at equal times in the observer’s rest frame. The circles represent creation at multiple locations via . Tilted line with open circles: the definition of a many-body state at equal times in a universal, favored reference frame, moving at speed v relative to the rest frame of the horizontal axis (with the time axis given by the line with an arrow, ). The circles represent creation at multiple locations via .
Figure A1.
Horizontal line with open circles: the standard definition of a many-body state at equal times in the observer’s rest frame. The circles represent creation at multiple locations via . Tilted line with open circles: the definition of a many-body state at equal times in a universal, favored reference frame, moving at speed v relative to the rest frame of the horizontal axis (with the time axis given by the line with an arrow, ). The circles represent creation at multiple locations via .