Feedback Control of Quantum Correlations in a Cavity Magnomechanical System with Magnon Squeezing
Abstract
:1. Introduction
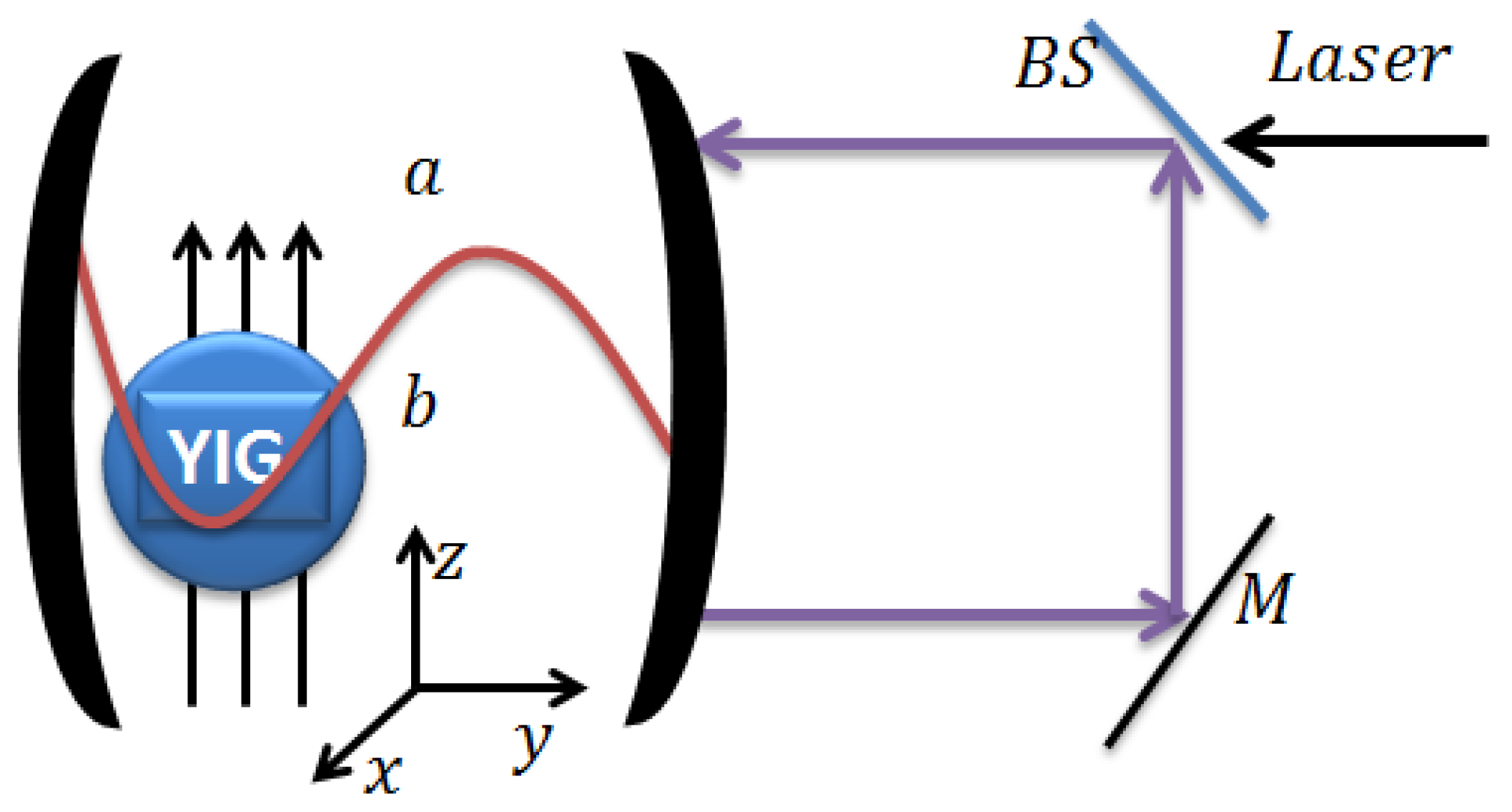
2. Model
3. Linearization of Quantum Langevin Equations
4. Entanglement, Steerability and Discord
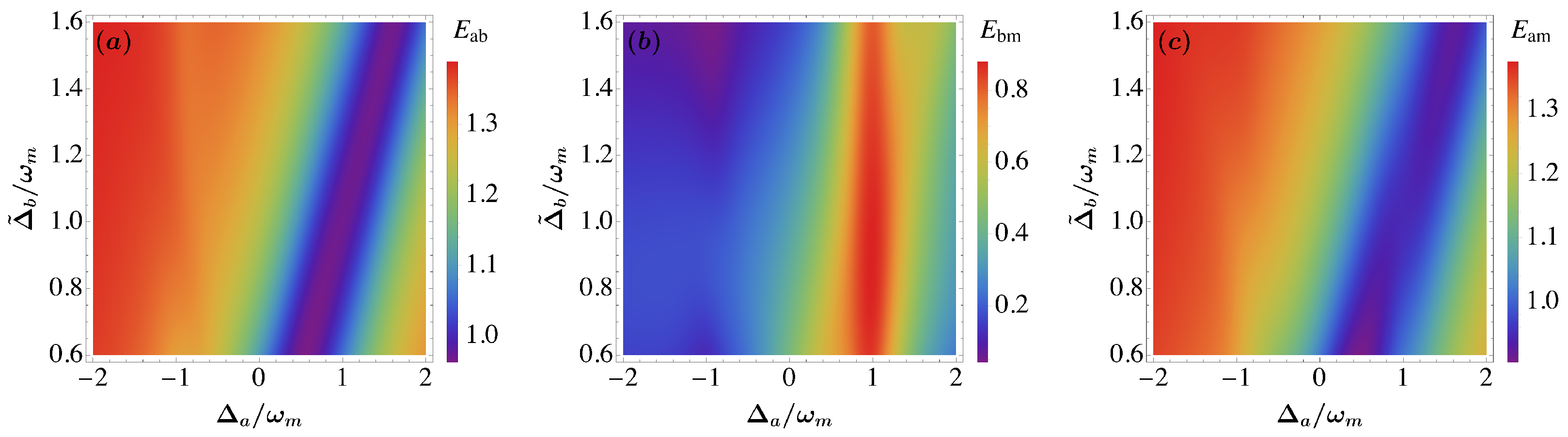
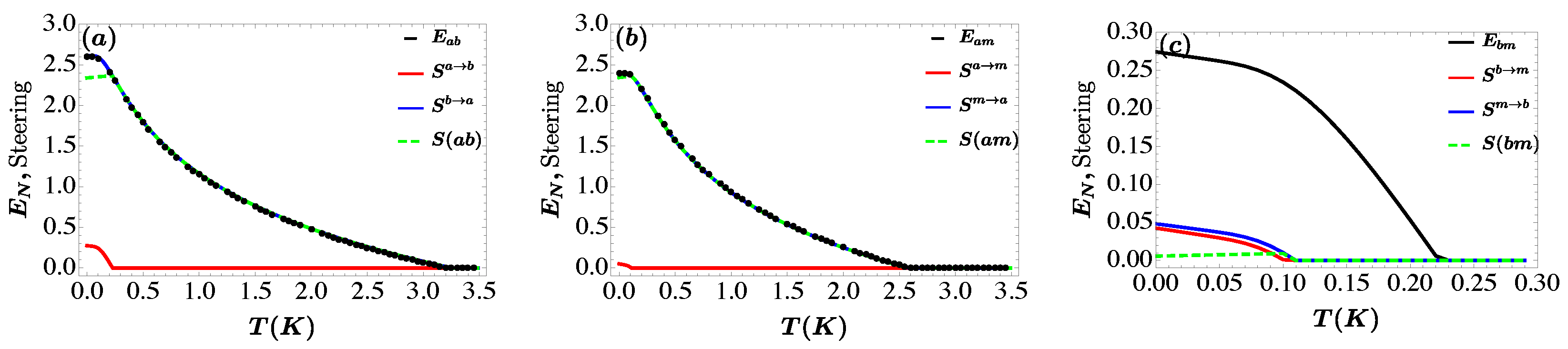
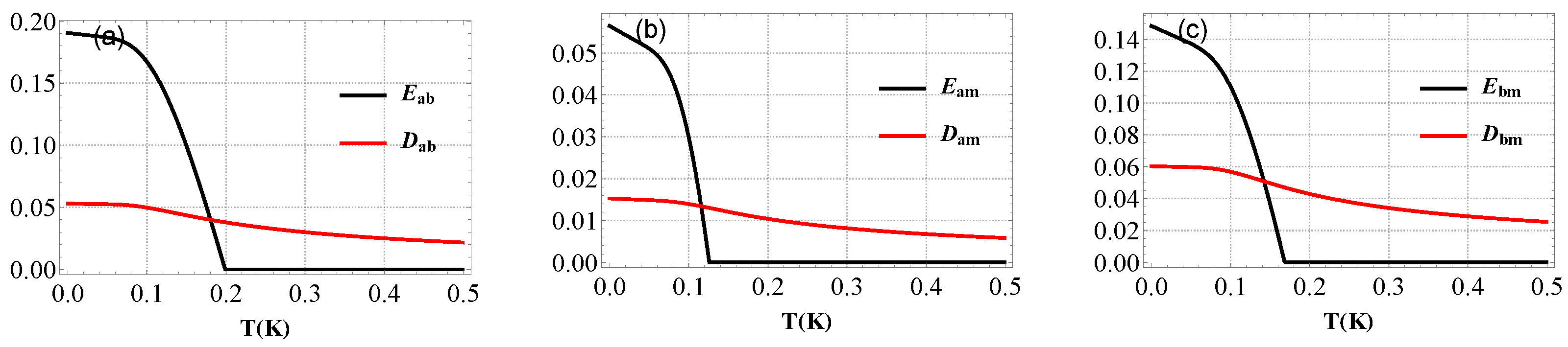
5. Results and Discusion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, K.W. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef] [PubMed]
- Scarani, V.; Iblisdir, S.; Gisin, N.; Acín, A. Quantum cloning. Rev. Mod. Phys. 2005, 77, 1225–1256. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Michalakis, S.; Nachtergaele, B. Entanglement in finitely correlated spin states. Phys. Rev. Lett. 2006, 97, 140601. [Google Scholar] [CrossRef] [PubMed]
- Szabo, J.C.; Trivedi, N. Entanglement dynamics between ising spins and a central ancilla. Phys. Rev. A 2022, 105, 052431. [Google Scholar] [CrossRef]
- Retzker, A.; Cirac, J.I.; Reznik, B. Detecting vacuum entanglement in a linear ion trap. Phys. Rev. Lett. 2005, 94, 050504. [Google Scholar] [CrossRef]
- Li, G.-X.; Wu, S.-P.; Huang, G.-M. Generation of entanglement and squeezing in the system of two ions trapped in a cavity. Phys. Rev. A 2005, 71, 063817. [Google Scholar] [CrossRef]
- Semião, F.L.S.; Furuya, K. Entanglement in the dispersive interaction of trapped ions with a quantized field. Phys. Rev. A 2007, 75, 042315. [Google Scholar] [CrossRef]
- Nicacio, F.; Furuya, K.; Semião, F.L. Motional entanglement with trapped ions and a nanomechanical resonator. Phys. Rev. A 2013, 88, 022330. [Google Scholar] [CrossRef]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565–582. [Google Scholar] [CrossRef]
- Vollbrecht, K.G.H.; Cirac, J.I. Delocalized entanglement of atoms in optical lattices. Phys. Rev. Lett. 2007, 98, 190502. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Peng, J.-X.; Asjad, M.; Mazaheri, M. Entanglement and coherence in a hybrid Laguerre–gaussian rotating cavity optomechanical system with two-level atoms. J. Phys. B Atomic Mol. Opt. Phys. 2021, 54, 215502. [Google Scholar] [CrossRef]
- Jo, H.; Song, Y.; Kim, M.; Ahn, J. Rydberg atom entanglements in the weak coupling regime. Phys. Rev. Lett. 2020, 124, 033603. [Google Scholar] [CrossRef] [PubMed]
- Asjad, M.; Shahzad, M.A.; Saif, F. Quantum degenerate fermi gas entanglement in optomechanics. Eur. Phys. D 2013, 67, 1. [Google Scholar] [CrossRef]
- Eisenberg, H.S.; Khoury, G.; Durkin, G.A.; Simon, C.; Bouwmeester, D. Quantum entanglement of a large number of photons. Phys. Rev. Lett. 2004, 93, 193901. [Google Scholar] [CrossRef]
- Manninen, J.; Asjad, M.; Ojajärvi, R.; Kuusela, P.; Massel, F. Clauser-Horne-Shimony-Holt Bell inequality test in an optomechanical device. Phys. Rev. A 2018, 98, 043831. [Google Scholar] [CrossRef]
- Teklu, B. Continuous-variable entanglement dynamics in lorentzian environment. Phys. Lett. A 2022, 432, 128022. [Google Scholar] [CrossRef]
- Salart, D.; Landry, O.; Sangouard, N.; Gisin, N.; Herrmann, H.; Sanguinetti, B.; Simon, C.; Sohler, W.; Thew, R.T.; Thomas, A.; et al. Purification of single-photon entanglement. Phys. Rev. Lett. 2010, 104, 180504. [Google Scholar] [CrossRef]
- Asjad, M.; Zippilli, S.; Tombesi, P.; Vitali, D. Large distance continuous variable communication with concatenated swaps. Phys. Scr. 2015, 90, 074055. [Google Scholar] [CrossRef]
- Wang, H.; Mariantoni, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Sank, D.; Weides, M.; Wenner, J.; et al. Deterministic entanglement of photons in two superconducting microwave resonators. Phys. Rev. Lett. 2011, 106, 060401. [Google Scholar] [CrossRef] [PubMed]
- Teklu, B.; Bina, M.; Paris, M.G.A. Noisy propagation of Gaussian states in optical media with finite bandwidth. Sci. Rep. 2022, 12, 11646. [Google Scholar] [CrossRef]
- Akram, U.; Munro, W.; Nemoto, K.; Milburn, G.J. Photon-phonon entanglement in coupled optomechanical arrays. Phys. Rev. A 2012, 86, 042306. [Google Scholar] [CrossRef]
- Teklu, B.; Byrnes, T.; Khan, F.S. Cavity-induced mirror-mirror entanglement in a single-atom Raman laser. Phys. Rev. A 2018, 97, 023829. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 1935, 31, 555–563. [Google Scholar] [CrossRef]
- Kogias, I.; Lee, A.R.; Ragy, S.; Adesso, G. Quantification of gaussian quantum steering. Phys. Rev. Lett. 2015, 114, 060403. [Google Scholar] [CrossRef] [PubMed]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277–4281. [Google Scholar] [CrossRef]
- Quintino, M.T.; Vértesi, T.; Cavalcanti, D.; Augusiak, R.; Demianowicz, M.; Acín, A.; Brunner, N. Inequivalence of entanglement, steering, and Bell nonlocality for general measurements. Phys. Rev. A 2015, 92, 032107. [Google Scholar] [CrossRef]
- Kiesewetter, S.; He, Q.Y.; Drummond, P.D.; Reid, M.D. Scalable Quantum Simulation of Pulsed Entanglement and Einstein-Podolsky-Rosen Steering in Optomechanics. Phys. Rev. A 2014, 90, 043805. [Google Scholar] [CrossRef]
- Vostrosablin, N.; Rakhubovsky, A.A.; Hoff, U.B.; Andersen, U.L.; Filip, R. Quantum Optomechanical Transducer with Ultrashort Pulses. New J. Phys. 2018, 20, 083042. [Google Scholar] [CrossRef]
- Branciard, C.; Cavalcanti, E.G.; Walborn, S.P.; Scarani, V.; Wiseman, H.M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 2012, 85, 010301. [Google Scholar] [CrossRef]
- Walk, N.; Hosseini, S.; Geng, J.; Thearle, O.; Haw, J.Y.; Armstrong, S.; Assad, S.M.; Janousek, J.; Ralph, T.C.; Symul, T.; et al. Experimental demonstration of gaussian protocols for one-sided device-independent quantum key distribution. Optica 2016, 3, 634–642. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Wang, Y.P.; You, J.Q. Theory of the magnon Kerr effect in cavity magnonics. Science China Physics. Mech. Astron. 2019, 62, 987511. [Google Scholar] [CrossRef]
- Xiong, W.; Wang, M.; Zhang, G.Q.; Chen, J. Optomechanical-interface-induced strong spin-magnon coupling. Phys. Rev. A 2023, 107, 033516. [Google Scholar] [CrossRef]
- Huebl, H. High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids. Phys. Rev. Lett. 2013, 111, 127003. [Google Scholar] [CrossRef]
- Tabuchi, Y. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 2014, 113, 083603. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Tabuchi, Y.; Gloppe, A.; Usami, K.; Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 2019, 12, 070101. [Google Scholar] [CrossRef]
- Yuan, H.; Cao, Y.; Kamra, A.; Duine, R.A.; Yan, P. Quantum magnonics: When magnon spintronics meets quantum information science. Phys. Rep. 2022, 965, 1–74. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, C.-L.; Jiang, L.; Tang, H.X. Cavity magnomechanics. Sci. Adv. 2016, 2, e1501286. [Google Scholar] [CrossRef]
- Fan, Z.-Y.; Shen, R.-C.; Wang, Y.-P.; Li, J.; You, J.Q. Optical sensing of magnons via the magnetoelastic displacement. Phys. Rev. A 2022, 105, 033507. [Google Scholar] [CrossRef]
- Harwood, A.; Brunelli, M.; Serafini, A. Cavity optomechanics assisted by optical coherent feedback. Phys. Rev. A 2021, 103, 023509. [Google Scholar] [CrossRef]
- Ernzer, M.; Aguilera, M.B.; Brunelli, M.; Schmid, G.-L.; Thomas, T.; Bruder, C.; Potts, P.P.; Treutlein, P. Optical coherent feedback control of a mechanical oscillator. arXiv 2022, arXiv:2210.07674. [Google Scholar] [CrossRef]
- Amazioug, M.; Teklu, B.; Asjad, M. Enhancement of magnon–photon–phonon entanglement in a cavity magnomechanics with coherent feedback loop. Sci. Rep. 2023, 13, 3833. [Google Scholar] [CrossRef]
- Paris, M.G.A.; Genoni, M.G.; Shammah, N.; Teklu, B. Quantifying the nonlinearity of a quantum oscillator. Phys. Rev. A 2014, 90, 012104. [Google Scholar] [CrossRef]
- Teklu, B.; Ferraro, A.; Paternostro, M.; Paris, M.G.A. Nonlinearity and nonclassicality in a nanomechanical resonator. EPJ Quantum Technol. 2015, 2, 16. [Google Scholar] [CrossRef]
- Albarelli, F.; Ferraro, A.; Paternostro, M.; Paris, M.G.A. Nonlinearity as a resource for nonclassicality in anharmonic systems. Phys. Rev. A 2016, 93, 032112. [Google Scholar] [CrossRef]
- Collett, M.J.; Walls, D.F. Squeezing spectra for nonlinear optical systems. Phys. Rev. A 1985, 32, 2887–2892. [Google Scholar] [CrossRef]
- Rebić, S.; Twamley, J.; Milburn, G.J. Giant kerr nonlinearities in circuit quantum electrodynamics. Phys. Rev. Lett. 2009, 103, 150503. [Google Scholar] [CrossRef]
- Wang, Y.P.; Zhang, G.Q.; Zhang, D.; Luo, X.Q.; Xiong, W.; Wang, S.P.; Li, T.F.; Hu, C.M.; You, J.Q. Magnon Kerr effect in a strongly coupled cavity-magnon system. Phys. Rev. B 2016, 94, 224410. [Google Scholar] [CrossRef]
- Tian, M.; Wang, M.; Zhang, G.Q.; Li, H.C.; Xiong, W. Critical Cavity-Magnon Polariton Mediated Strong Long-Distance Spin-Spin Coupling. arXiv 2023, arXiv:2304.13553. [Google Scholar]
- Liu, G.; Xiong, W.; Ying, Z.J. Switchable Superradiant Phase Transition with Kerr Magnons. arXiv 2023, arXiv:2302.07163. [Google Scholar]
- Zhang, G.Q.; Wang, Y.; Xiong, W. Detection sensitivity enhancement of magnon Kerr nonlinearity in cavity magnonics induced by coherent perfect absorption. Phys. Rev. B 2023, 107, 064417. [Google Scholar]
- Xiong, W.; Tian, M.; Zhang, G.Q.; You, J.Q. Strong long-range spin-spin coupling via a Kerr magnon interface. Phys. Rev. B 2022, 105, 245310. [Google Scholar]
- Lachance-Quirion, D.; Tabuchi, Y.; Ishino, S.; Noguchi, A.; Ishikawa, T.; Yamazaki, R.; Nakamura, Y. Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet. Sci. Adv. 2017, 3, e1603150. [Google Scholar]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar]
- Adesso, G.; Serafini, A.; Illuminati, F. Determination of continuous variable entanglement by purity measurements. Phys. Rev. Lett. 2004, 92, 087901. [Google Scholar] [PubMed]
- Giorda, P.; Paris, M.G.A. Gaussian quantum discord. Phys. Rev. Lett. 2010, 105, 020503. [Google Scholar] [PubMed]
- Amazioug, M.; Maroufi, B.; Daoud, M. Using coherent feedback loop for high quantum state transfer in optomechanics. Phys. Lett. A 2020, 384, 126705. [Google Scholar]
- Kittel, C. Interaction of spin waves and ultrasonic waves in ferromagnetic crystals. Phys. Rev. 1958, 110, 836–841. [Google Scholar]
- Wang, Y.-P.; Zhang, G.-Q.; Zhang, D.; Li, T.-F.; Hu, C.-M.; You, J.Q. Bistability of cavity magnon polaritons. Phys. Rev. Lett. 2018, 120, 057202. [Google Scholar] [PubMed]
- Li, J.; Zhu, S.-Y.; Agarwal, G.S. Magnon-photon-phonon entanglement in cavity magnomechanics. Phys. Rev. Lett. 2018, 121, 203601. [Google Scholar] [PubMed]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1995. [Google Scholar]
- Gardiner, C.W.C.W.; Zoller, P.P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics, 2nd ed.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2000. [Google Scholar]
- Giovannetti, V.; Vitali, D. Phase-noise measurement in a cavity with a movable mirror undergoing quantum brownian motion. Phys. Rev. A 2001, 63, 023812. [Google Scholar]
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288. [Google Scholar]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar]
- Amazioug, M.; Nassik, M.; Habiballah, N. Gaussian quantum discord and EPR steering in optomechanical system. Optik 2018, 158, 1186–1193. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amazioug, M.; Singh, S.; Teklu, B.; Asjad, M. Feedback Control of Quantum Correlations in a Cavity Magnomechanical System with Magnon Squeezing. Entropy 2023, 25, 1462. https://doi.org/10.3390/e25101462
Amazioug M, Singh S, Teklu B, Asjad M. Feedback Control of Quantum Correlations in a Cavity Magnomechanical System with Magnon Squeezing. Entropy. 2023; 25(10):1462. https://doi.org/10.3390/e25101462
Chicago/Turabian StyleAmazioug, Mohamed, Shailendra Singh, Berihu Teklu, and Muhammad Asjad. 2023. "Feedback Control of Quantum Correlations in a Cavity Magnomechanical System with Magnon Squeezing" Entropy 25, no. 10: 1462. https://doi.org/10.3390/e25101462
APA StyleAmazioug, M., Singh, S., Teklu, B., & Asjad, M. (2023). Feedback Control of Quantum Correlations in a Cavity Magnomechanical System with Magnon Squeezing. Entropy, 25(10), 1462. https://doi.org/10.3390/e25101462







