Soft Quantization Using Entropic Regularization
Abstract
:1. Introduction
- (i)
- Our regularization approach stabilizes and simplifies the standard quantization problem by introducing penalty terms or constraints that discourage overly complex or overfitted models, promoting better generalizations and robustness in the solutions.
- (ii)
- The influence of entropy is controlled using a parameter, , which enables us to reach the genuine optimal quantizers.
- (iii)
- Generally, parameter tuning comes with certain limitations. However, our method builds upon the framework of the well-established softmin function, which allows us to exercise parameter control without encountering any restrictions.
- (iv)
- For larger values of the regularization parameter , the optimal measure accumulates all its mass at the center of the measure.
- Applications in the Context of Quantization.
- Related Works and Contributions.
- –
- Lloyd-Max Algorithm: this algorithm, also known as Lloyd’s algorithm or the k-means algorithm, is a popular iterative algorithm for computing optimal vector quantizers. It iteratively adjusts the centroids of the quantization levels to minimize the quantization error (cf. Scheunders [13]).
- –
- Tree-Structured Vector Quantization (TSVQ): TSVQ is a hierarchical quantization method that uses a tree structure to partition the input space into regions. It recursively applies vector quantization at each level of the tree until the desired number of quantization levels is achieved (cf. Wei and Levoy [14]).
- –
- Expectation-maximization (EM) algorithm: the EM algorithm is a general-purpose optimization algorithm that can be used for optimal quantization. It is an iterative algorithm that estimates the parameters of a statistical model to maximize the likelihood of the observed data (cf. Heskes [15]).
- –
- Stochastic Optimization Methods: stochastic optimization methods such as simulated annealing, genetic algorithms, and particle swarm optimization can be used to find optimal quantization strategies by exploring the search space and iteratively improving the quantization performance (cf. Pagès et al. [16]).
- –
- Greedy vector quantization (GVQ): the greedy algorithm tries to solve this problem iteratively by adding one code word at every step until the desired number of code words is reached, each time selecting the code word that minimizes the error. GVQ is known to provide suboptimal quantization compared to other non-greedy methods such as the Lloyd-Max and Linde–Buzo–Gray algorithms. However, it has been shown to perform well when the data have a strong correlation structure. Notably, it utilizes the Wasserstein distance to measure the error of approximation (cf. Luschgy and Pagès [2]).
- Outline of the Paper.
2. Preliminaries
2.1. Distances and Divergences of Measures
2.2. The Smooth Minimum
2.3. Softmin Function
- The Derivative with respect to the Probability Measure
- The Derivative with respect to the Random Variable
3. Regularized Quantization
3.1. Approximation with Inflexible Marginal Measures
3.2. Approximation with Flexible Marginal Measure
3.3. The Relation of Soft Quantization and Entropy
4. Soft Tessellation
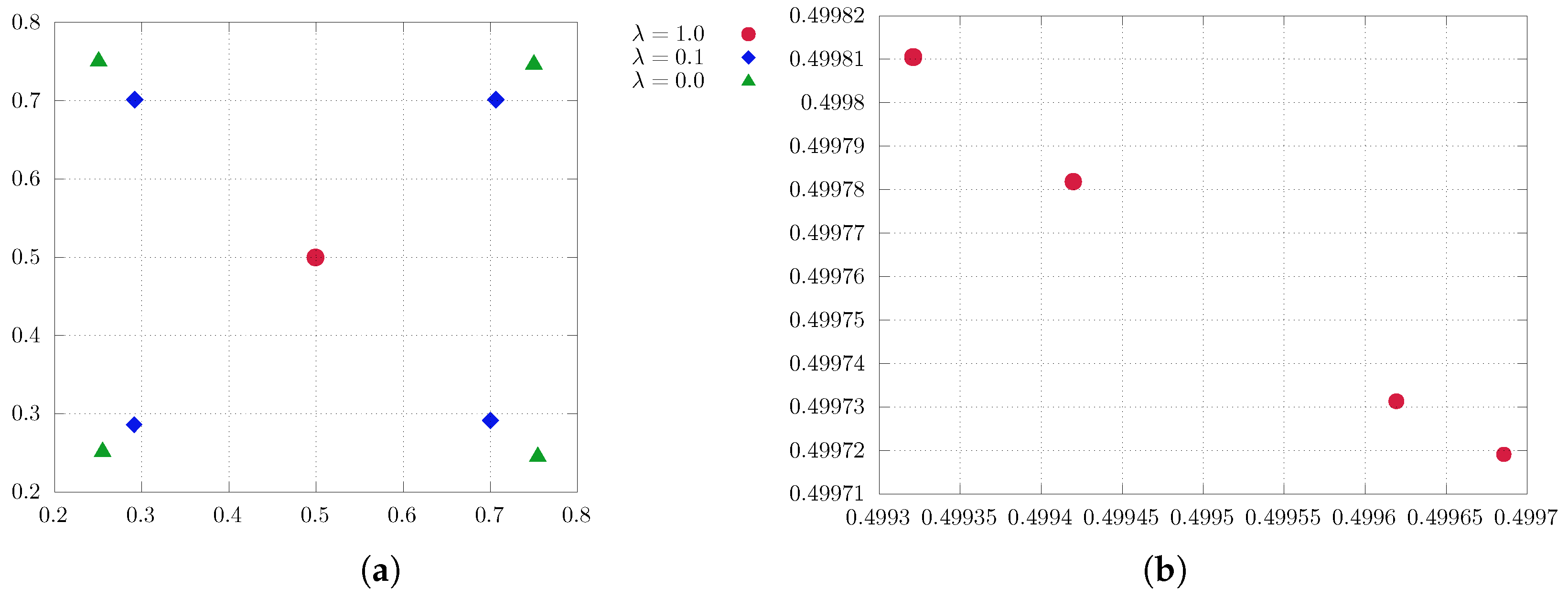
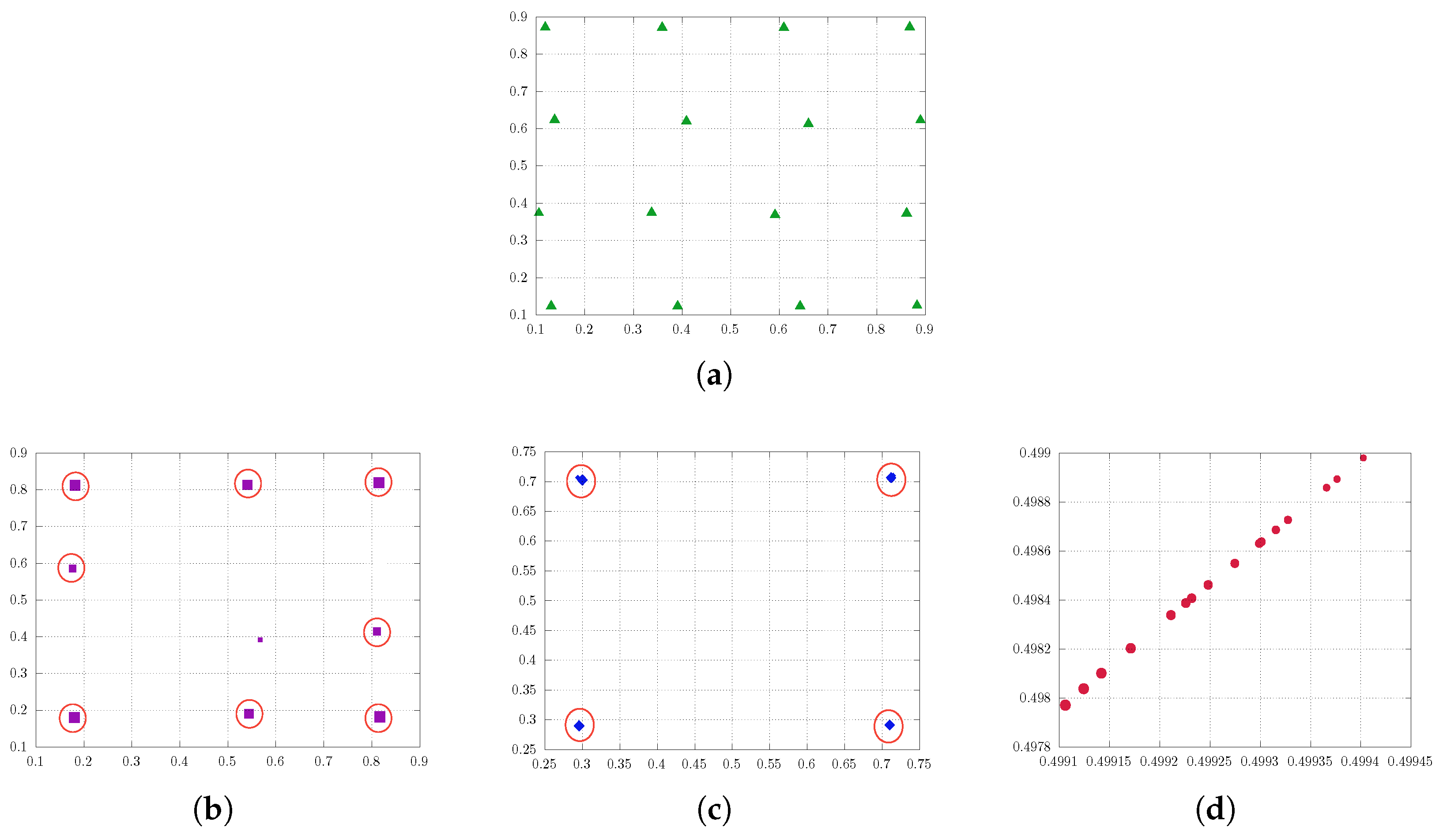
4.1. Optimal Weights
- Soft Tessellation
4.2. Optimal Locations
| Algorithm 1: Stochastic gradient algorithm to find the optimal quantizers and optimal masses |
 |
4.3. Quantization with Large Regularization Parameters
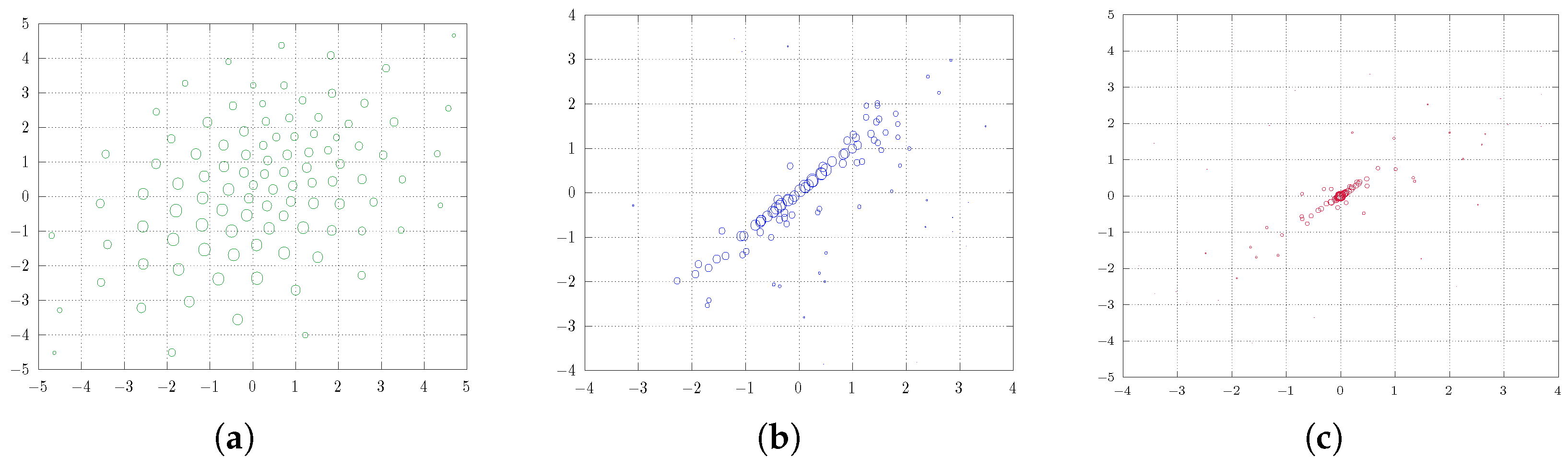
5. Numerical Illustration
5.1. One Dimension
5.2. Two Dimensions
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Hessian of the Softmin
References
- Graf, S.; Mauldin, R.D. A Classification of Disintegrations of Measures. Contemp. Math. 1989, 94, 147–158. [Google Scholar]
- Luschgy, H.; Pagès, G. Greedy vector quantization. J. Approx. Theory 2015, 198, 111–131. [Google Scholar] [CrossRef]
- El Nmeir, R.; Luschgy, H.; Pagès, G. New approach to greedy vector quantization. Bernoulli 2022, 28, 424–452. [Google Scholar] [CrossRef]
- Graf, S.; Luschgy, H. Foundations of Quantization for Probability Distributions; Lecture Notes in Mathematics; Springer: Berlin, Germany, 2000; Volume 1730. [Google Scholar] [CrossRef]
- Breuer, T.; Csiszár, I. Measuring distribution model risk. Math. Financ. 2013, 26, 395–411. [Google Scholar] [CrossRef]
- Breuer, T.; Csiszár, I. Systematic stress tests with entropic plausibility constraints. J. Bank. Financ. 2013, 37, 1552–1559. [Google Scholar] [CrossRef]
- Pichler, A.; Schlotter, R. Entropy based risk measures. Eur. J. Oper. Res. 2020, 285, 223–236. [Google Scholar] [CrossRef]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhuang, B.; Liu, L.; Tan, M.; Shen, C.; Reid, I. Training quantized neural networks with a full-precision auxiliary module. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020; pp. 1488–1497. Available online: https://openaccess.thecvf.com/content_CVPR_2020/html/Zhuang_Training_Quantized_Neural_Networks_With_a_Full-Precision_Auxiliary_Module_CVPR_2020_paper.html (accessed on 6 October 2023).
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks. Adv. Neural Inf. Process. Syst. 2016, 29. Available online: https://proceedings.neurips.cc/paper_files/paper/2016/hash/d8330f857a17c53d217014ee776bfd50-Abstract.html (accessed on 6 October 2023).
- Polino, A.; Pascanu, R.; Alistarh, D.-A. Model compression via distillation and quantization. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; Available online: https://research-explorer.ista.ac.at/record/7812 (accessed on 6 October 2023).
- Bhattacharya, K. Semi-classical description of electrostatics and quantization of electric charge. Phys. Scr. 2023, 98, 8. [Google Scholar] [CrossRef]
- Scheunders, P. A genetic Lloyd-Max image quantization algorithm. Pattern Recognit. Lett. 1996, 17, 547–556. [Google Scholar] [CrossRef]
- Wei, L.Y.; Levoy, M. Fast texture synthesis using tree-structured vector quantization. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques; 2000; pp. 479–488. Available online: https://dl.acm.org/doi/abs/10.1145/344779.345009 (accessed on 6 October 2023).
- Heskes, T. Self-organizing maps, vector quantization, and mixture modeling. IEEE Trans. Neural Netw. 2001, 12, 1299–1305. [Google Scholar] [CrossRef] [PubMed]
- Pagès, G.; Pham, H.; Printems, J. Optimal Quantization Methods and Applications to Numerical Problems in Finance. In Handbook of Computational and Numerical Methods in Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; pp. 253–297. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Volume 26. [Google Scholar]
- Ramdas, A.; García Trillos, N.; Cuturi, M. On Wasserstein two-sample testing and related families of nonparametric tests. Entropy 2017, 19, 47. [Google Scholar] [CrossRef]
- Neumayer, S.; Steidl, G. From optimal transport to discrepancy. In Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging: Mathematical Imaging and Vision; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–36. [Google Scholar] [CrossRef]
- Altschuler, J.; Bach, F.; Rudi, A.; Niles-Weed, J. Massively scalable Sinkhorn distances via the Nyström method. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’ Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Lakshmanan, R.; Pichler, A.; Potts, D. Nonequispaced Fast Fourier Transform Boost for the Sinkhorn Algorithm. Etna—Electron. Trans. Numer. Anal. 2023, 58, 289–315. [Google Scholar] [CrossRef]
- Ba, F.A.; Quellmalz, M. Accelerating the Sinkhorn algorithm for sparse multi-marginal optimal transport via fast Fourier transforms. Algorithms 2022, 15, 311. [Google Scholar] [CrossRef]
- Lakshmanan, R.; Pichler, A. Fast approximation of unbalanced optimal transport and maximum mean discrepancies. arXiv 2023, arXiv:2306.13618. [Google Scholar] [CrossRef]
- Monge, G. Mémoire sue la théorie des déblais et de remblais. Histoire de l’Académie Royale des Sciences de Paris, Avec les Mémoires de Mathématique et de Physique Pour la Même Année. 1781, pp. 666–704. Available online: https://cir.nii.ac.jp/crid/1572261550791499008 (accessed on 6 October 2023).
- Kantorovich, L. On the translocation of masses. J. Math. Sci. 2006, 133, 1381–1382. [Google Scholar] [CrossRef]
- Villani, C. Topics in Optimal Transportation; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2003; Volume 58. [Google Scholar] [CrossRef]
- Rachev, S.T.; Rüschendorf, L. Mass Transportation Problems Volume I: Theory, Volume II: Applications; Probability and Its Applications; Springer: New York, NY, USA, 1998; Volume XXV. [Google Scholar] [CrossRef]
- Rüschendorf, L. Mathematische Statistik; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Ch Pflug, G.; Pichler, A. Multistage Stochastic Optimization; Springer Series in Operations Research and Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]

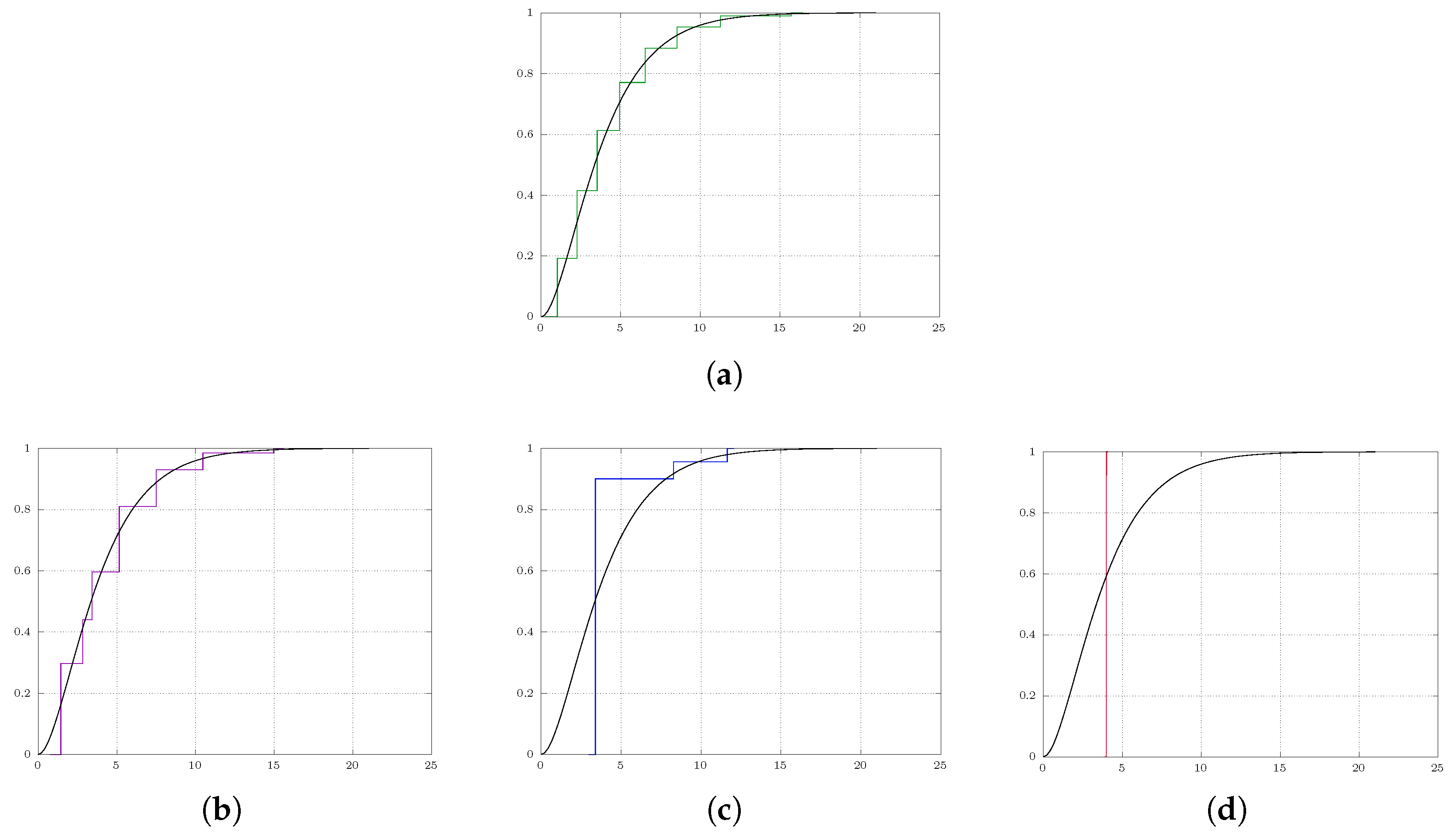
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakshmanan, R.; Pichler, A. Soft Quantization Using Entropic Regularization. Entropy 2023, 25, 1435. https://doi.org/10.3390/e25101435
Lakshmanan R, Pichler A. Soft Quantization Using Entropic Regularization. Entropy. 2023; 25(10):1435. https://doi.org/10.3390/e25101435
Chicago/Turabian StyleLakshmanan, Rajmadan, and Alois Pichler. 2023. "Soft Quantization Using Entropic Regularization" Entropy 25, no. 10: 1435. https://doi.org/10.3390/e25101435
APA StyleLakshmanan, R., & Pichler, A. (2023). Soft Quantization Using Entropic Regularization. Entropy, 25(10), 1435. https://doi.org/10.3390/e25101435





