Thermodynamics of the Ramsey Zone
Abstract
:1. Introduction
2. Model
3. Results
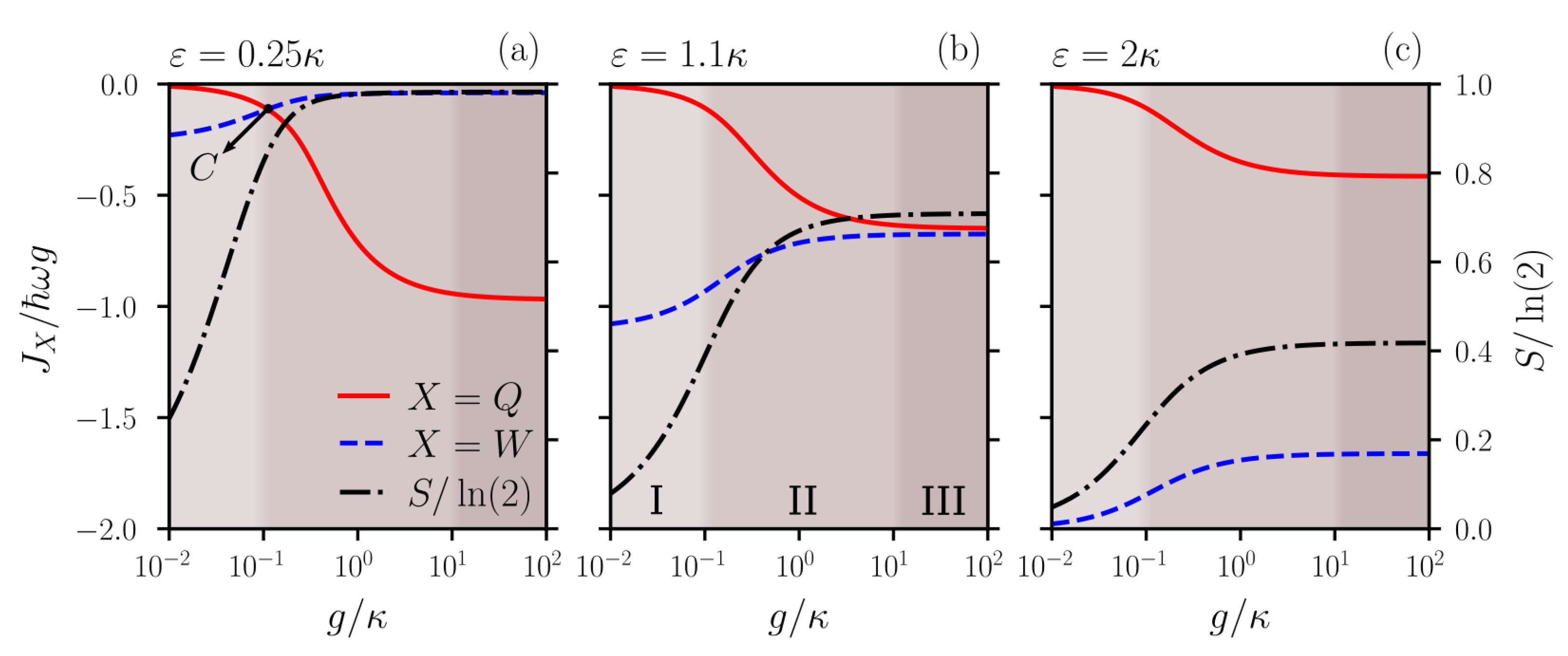
3.1. Heat and Work Fluxes in a Ramsey Zone
3.2. On the Classical Behavior of the Cavity–Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brune, M.; Schmidt-Kaler, F.; Maali, A.; Dreyer, J.; Hagley, E.; Raimond, J.M.; Haroche, S. Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity. Phys. Rev. Lett. 1996, 76, 1800–1803. [Google Scholar] [CrossRef]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565–582. [Google Scholar] [CrossRef]
- Walther, H.; Varcoe, B.T.H.; Englert, B.G.; Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 2006, 69, 1325–1382. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed.; Cambridge University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Jaynes, E.; Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Hu, D.; Niu, L.; Jin, S.; Chen, X.; Dong, G.; Schmiedmayer, J.; Zhou, X. Ramsey interferometry with trapped motional quantum states. Commun. Phys. 2018, 1, 29. [Google Scholar] [CrossRef]
- Kaubruegger, R.; Vasilyev, D.V.; Schulte, M.; Hammerer, K.; Zoller, P. Quantum Variational Optimization of Ramsey Interferometry and Atomic Clocks. Phys. Rev. X 2021, 11, 041045. [Google Scholar] [CrossRef]
- Fink, J.M.; Steffen, L.; Studer, P.; Bishop, L.S.; Baur, M.; Bianchetti, R.; Bozyigit, D.; Lang, C.; Filipp, S.; Leek, P.J.; et al. Quantum-To-Classical Transition in Cavity Quantum Electrodynamics. Phys. Rev. Lett. 2010, 105, 163601. [Google Scholar] [CrossRef]
- Everitt, M.J.; Munro, W.J.; Spiller, T.P. Quantum-classical crossover of a field mode. Phys. Rev. A 2009, 79, 032328. [Google Scholar] [CrossRef]
- Rossatto, D.Z.; Werlang, T.; Duzzioni, E.I.; Villas-Boas, C.J. Nonclassical Behavior of an Intense Cavity Field Revealed by Quantum Discord. Phys. Rev. Lett. 2011, 107, 153601. [Google Scholar] [CrossRef]
- Kim, J.I.; Fonseca Romero, K.M.; Horiguti, A.M.; Davidovich, L.; Nemes, M.C.; de Toledo Piza, A.F.R. Classical Behavior with Small Quantum Numbers: The Physics of Ramsey Interferometry of Rydberg Atoms. Phys. Rev. Lett. 1999, 82, 4737–4740. [Google Scholar] [CrossRef]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Masanes, L.; Oppenheim, J. A general derivation and quantification of the third law of thermodynamics. Nat. Commun. 2017, 8, 14538. [Google Scholar] [CrossRef] [PubMed]
- Anders, J.; Esposito, M. Focus on quantum thermodynamics. New J. Phys. 2017, 19, 010201. [Google Scholar] [CrossRef]
- Perarnau-Llobet, M.; Wilming, H.; Riera, A.; Gallego, R.; Eisert, J. Strong Coupling Corrections in Quantum Thermodynamics. Phys. Rev. Lett. 2018, 120, 120602. [Google Scholar] [CrossRef] [PubMed]
- Dou, W.; Ochoa, M.A.; Nitzan, A.; Subotnik, J.E. Universal approach to quantum thermodynamics in the strong coupling regime. Phys. Rev. B 2018, 98, 134306. [Google Scholar] [CrossRef]
- Rivas, A. Quantum Thermodynamics in the Refined Weak Coupling Limit. Entropy 2019, 21, 725. [Google Scholar] [CrossRef]
- Deffner, S.; Campbell, S. Quantum Thermodynamics; 2053–2571; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019. [Google Scholar] [CrossRef]
- Binder, F.; Correa, L.; Gogolin, C.; Anders, J.; Adesso, G. Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Landi, G.T.; Paternostro, M. Irreversible entropy production, from quantum to classical. arXiv 2020, arXiv:2009.07668. [Google Scholar] [CrossRef]
- Elouard, C.; Herrera-Martí, D.; Esposito, M.; Auffèves, A. Thermodynamics of optical Bloch equations. New J. Phys. 2020, 22, 103039. [Google Scholar] [CrossRef]
- Rivas, A. Strong Coupling Thermodynamics of Open Quantum Systems. Phys. Rev. Lett. 2020, 124, 160601. [Google Scholar] [CrossRef]
- Strasberg, P.; Winter, A. First and Second Law of Quantum Thermodynamics: A Consistent Derivation Based on a Microscopic Definition of Entropy. PRX Quantum 2021, 2, 030202. [Google Scholar] [CrossRef]
- de Assis, R.J.; Sales, J.S.; Mendes, U.C.; de Almeida, N.G. Two-level quantum Otto heat engine operating with unit efficiency far from the quasi-static regime under a squeezed reservoir. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 095501. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A Math. Gen. 1979, 12, L103–L107. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Bernardo, B. Unraveling the role of coherence in the first law of quantum thermodynamics. Phys. Rev. E 2020, 102, 062152. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, B.; Salimi, S.; Khorashad, A.S. On the contribution of work or heat in exchanged energy via interaction in open bipartite quantum systems. Sci. Rep. 2023, 13, 160. [Google Scholar] [CrossRef]
- Dann, R.; Kosloff, R. Unification of the first law of quantum thermodynamics. New J. Phys. 2023, 25, 043019. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef]
- Binder, F.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantum thermodynamics of general quantum processes. Phys. Rev. E 2015, 91, 032119. [Google Scholar] [CrossRef]
- Huber, M.; Perarnau-Llobet, M.; Hovhannisyan, K.V.; Skrzypczyk, P.; Klöckl, C.; Brunner, N.; Acín, A. Thermodynamic cost of creating correlations. New J. Phys. 2015, 17, 065008. [Google Scholar] [CrossRef]
- Alipour, S.; Benatti, F.; Bakhshinezhad, F.; Afsary, M.; Marcantoni, S.; Rezakhani, A.T. Correlations in quantum thermodynamics: Heat, work, and entropy production. Sci. Rep. 2016, 6, 35568. [Google Scholar] [CrossRef] [PubMed]
- Bera, M.N.; Riera, A.; Lewenstein, M.; Winter, A. Generalized laws of thermodynamics in the presence of correlations. Nat. Commun. 2017, 8, 2180. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Assis, R.J.; Diniz, C.M.; de Almeida, N.G.; Villas-Bôas, C.J. Thermodynamics of the Ramsey Zone. Entropy 2023, 25, 1430. https://doi.org/10.3390/e25101430
de Assis RJ, Diniz CM, de Almeida NG, Villas-Bôas CJ. Thermodynamics of the Ramsey Zone. Entropy. 2023; 25(10):1430. https://doi.org/10.3390/e25101430
Chicago/Turabian Stylede Assis, Rogério Jorge, Ciro Micheletti Diniz, Norton Gomes de Almeida, and Celso Jorge Villas-Bôas. 2023. "Thermodynamics of the Ramsey Zone" Entropy 25, no. 10: 1430. https://doi.org/10.3390/e25101430
APA Stylede Assis, R. J., Diniz, C. M., de Almeida, N. G., & Villas-Bôas, C. J. (2023). Thermodynamics of the Ramsey Zone. Entropy, 25(10), 1430. https://doi.org/10.3390/e25101430





