Distance-Metric Learning for Personalized Survival Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Setting
2.2. Survival Prediction Based on Proportional Hazards
2.3. Survival Prediction with Kernels
2.4. Transformation of Time
3. Experiments on Simulated and Real-World Data
3.1. Description of Data and Evaluation Criteria
3.2. Description of Simulation Settings
4. Results
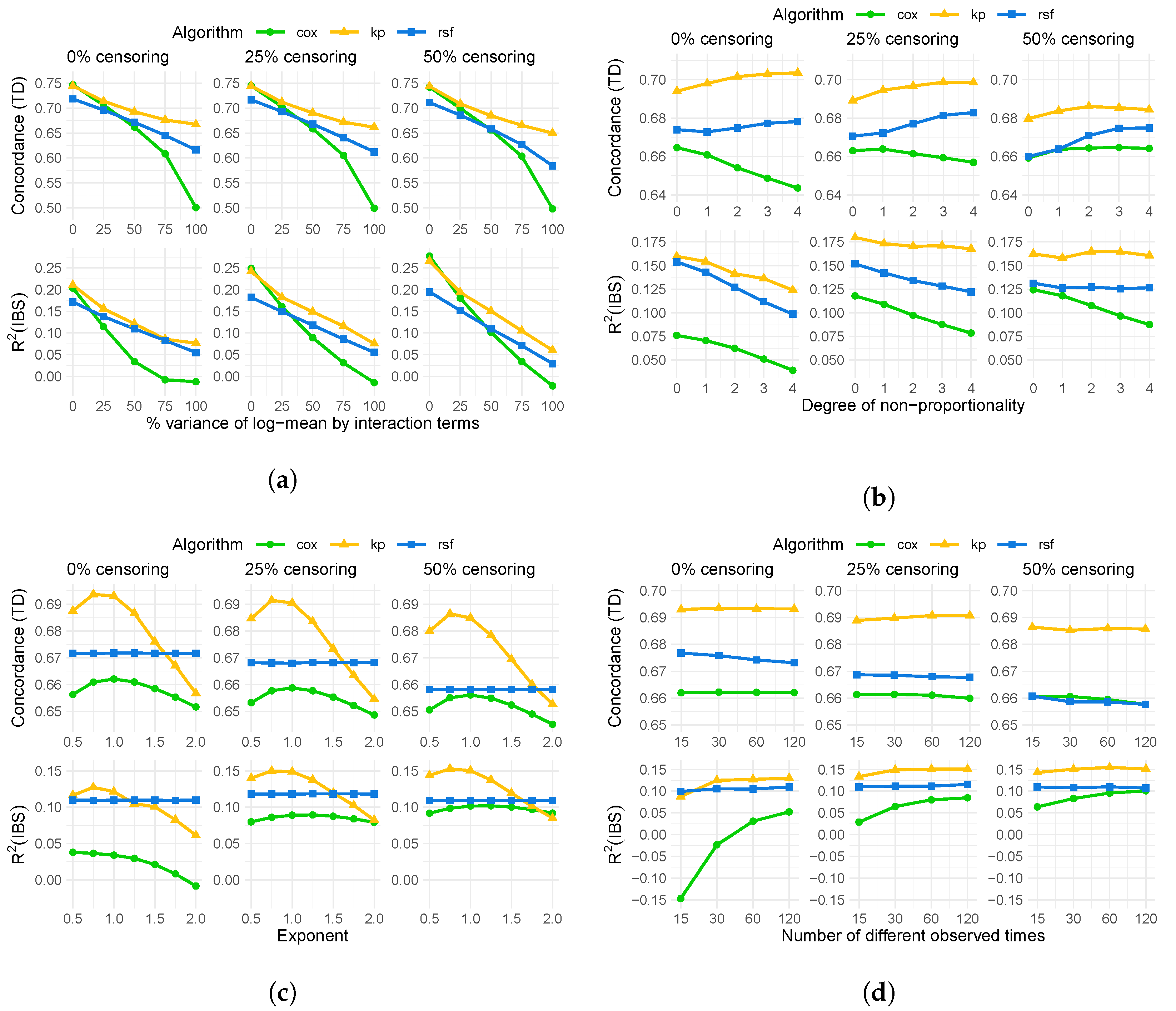
4.1. Results of Simulation
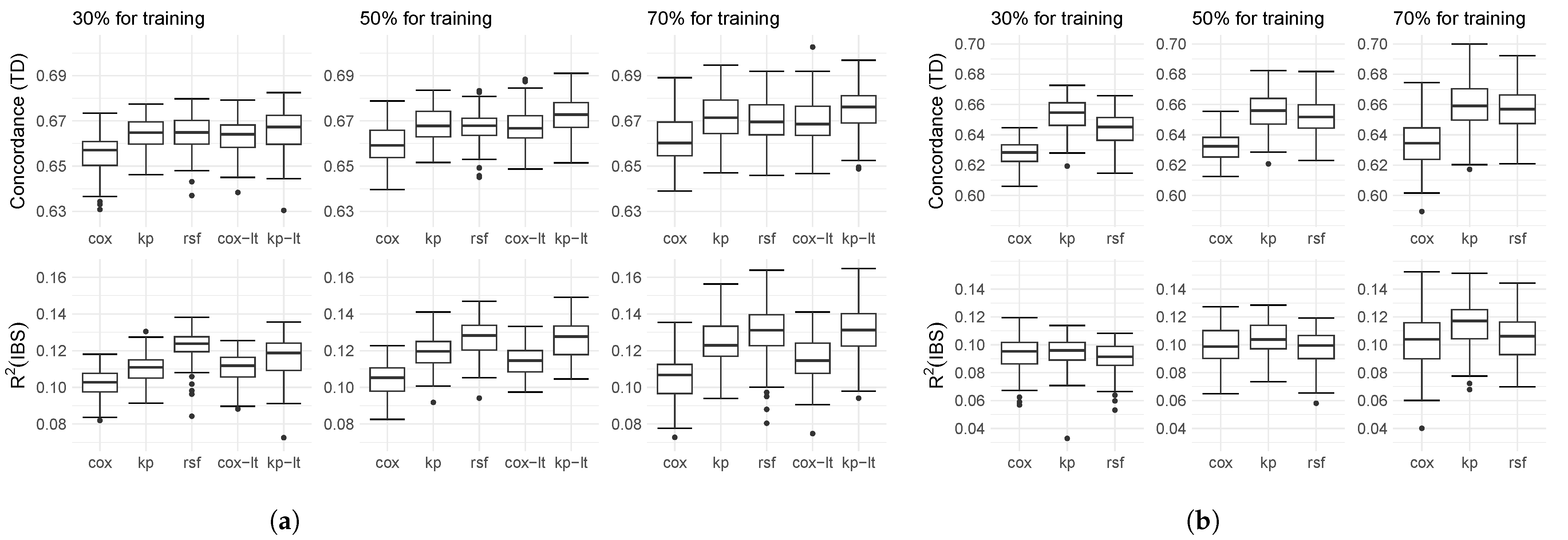
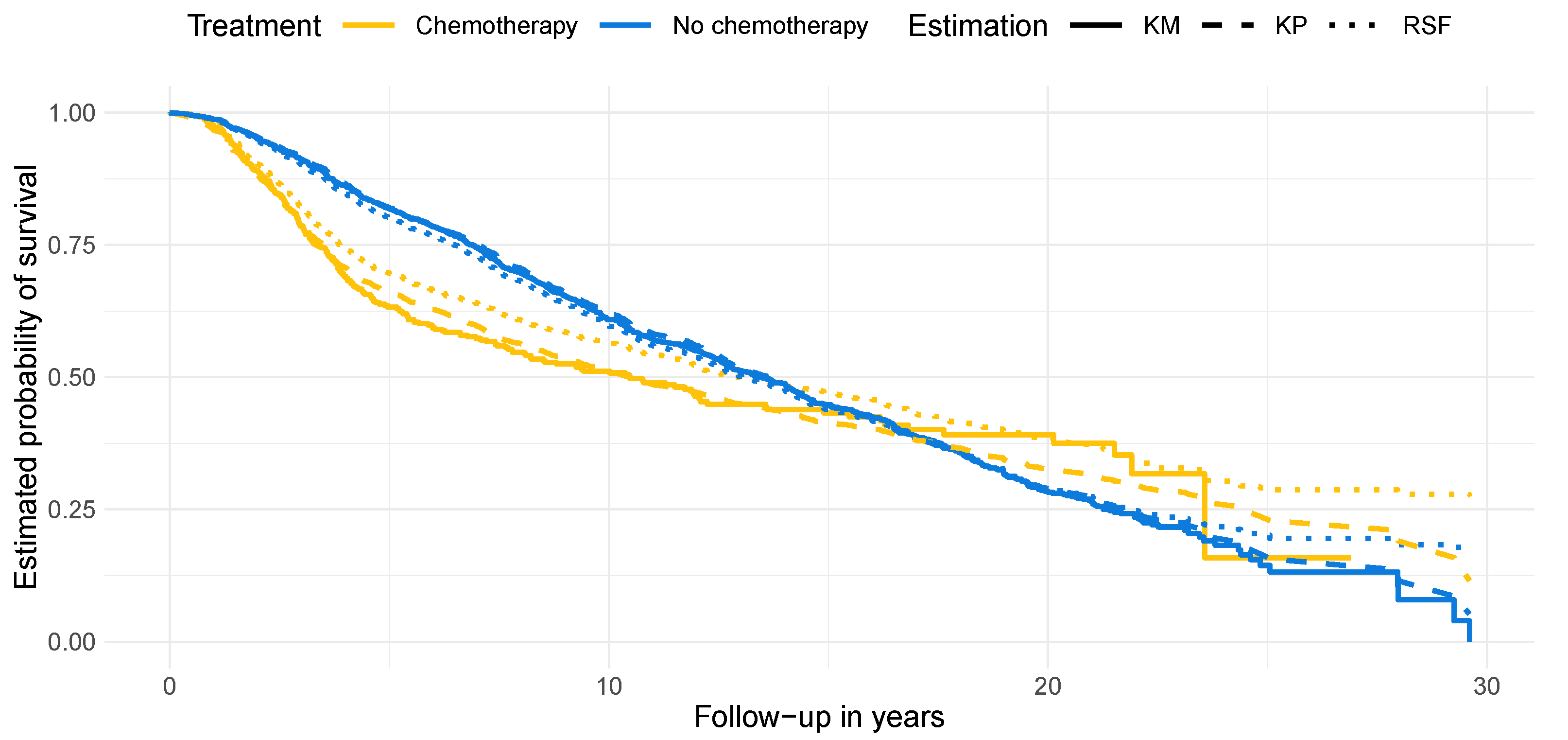
4.2. Results on Real-World Data
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Data | Number of Covariates Considered for Splits | Minimum Samples per Leaf |
|---|---|---|
| Simulation A, C | 2, 4, 6 | 5, 10, 20, 40 |
| Simulation B | 2, 4, 7 | 5, 10, 20, 40 |
| METABRIC | 3, 4, 9 | 5, 10, 20, 40 |
| Rotterdam/GBSG | 2, 3, 7 | 5, 10, 20, 40 |
Appendix C
| Degree of Non-Proportionality | |||
|---|---|---|---|
| 0 | 1.22 | 1.22 | 0 |
| 1 | 0.79 | 1.90 | 0.24 |
| 2 | 0.64 | 2.35 | 0.33 |
| 3 | 0.57 | 2.70 | 0.39 |
| 4 | 0.50 | 3.00 | 0.43 |
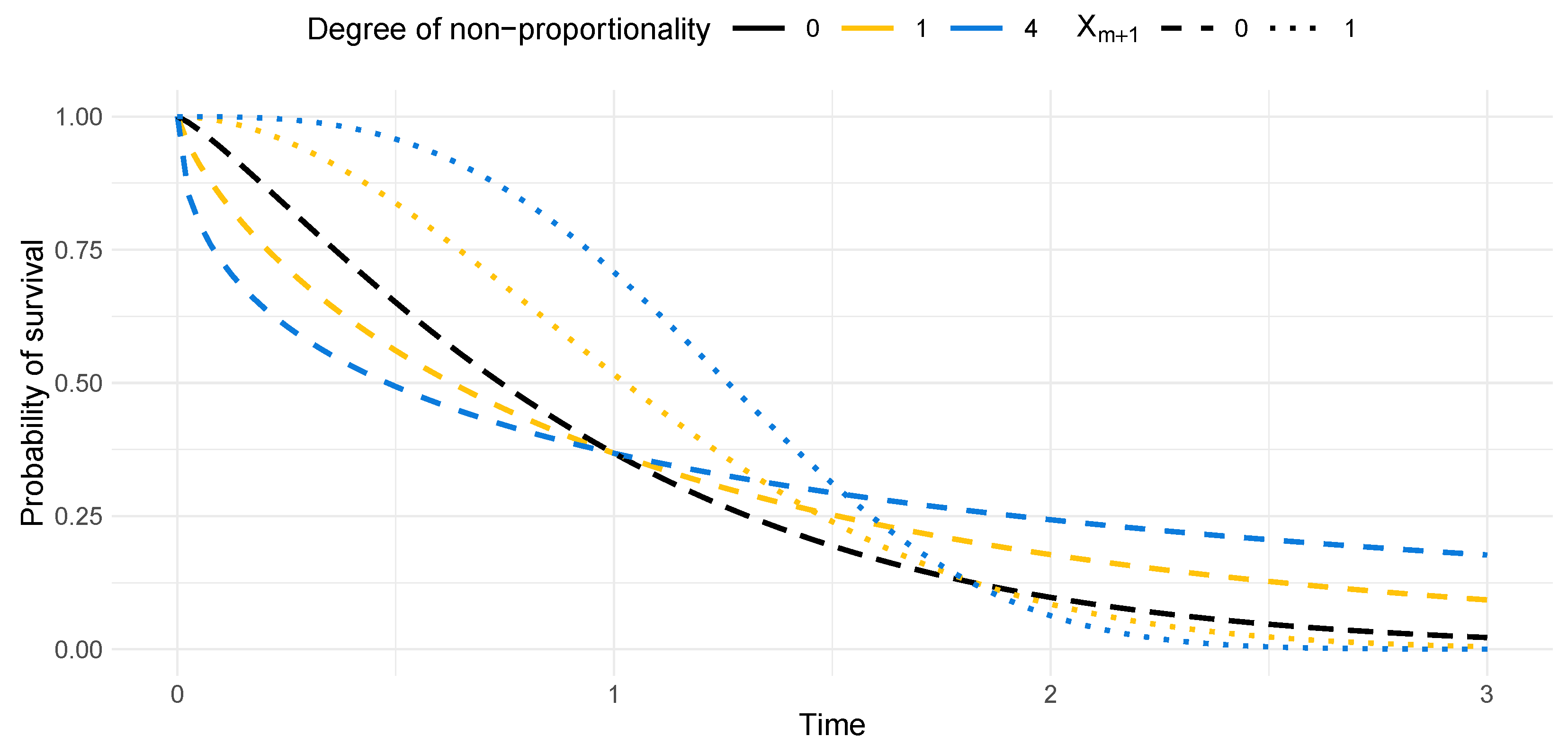
Appendix D
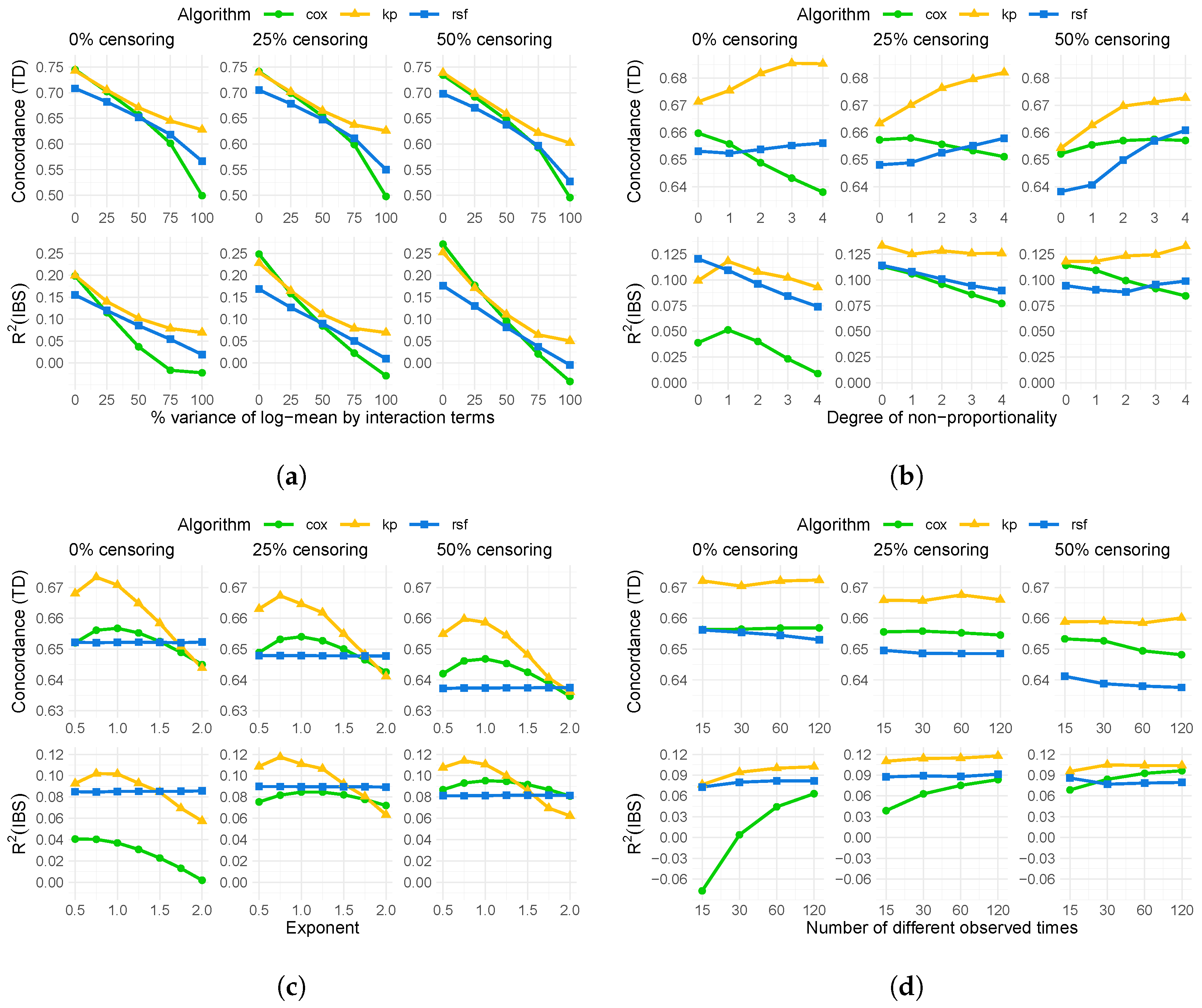
Appendix E
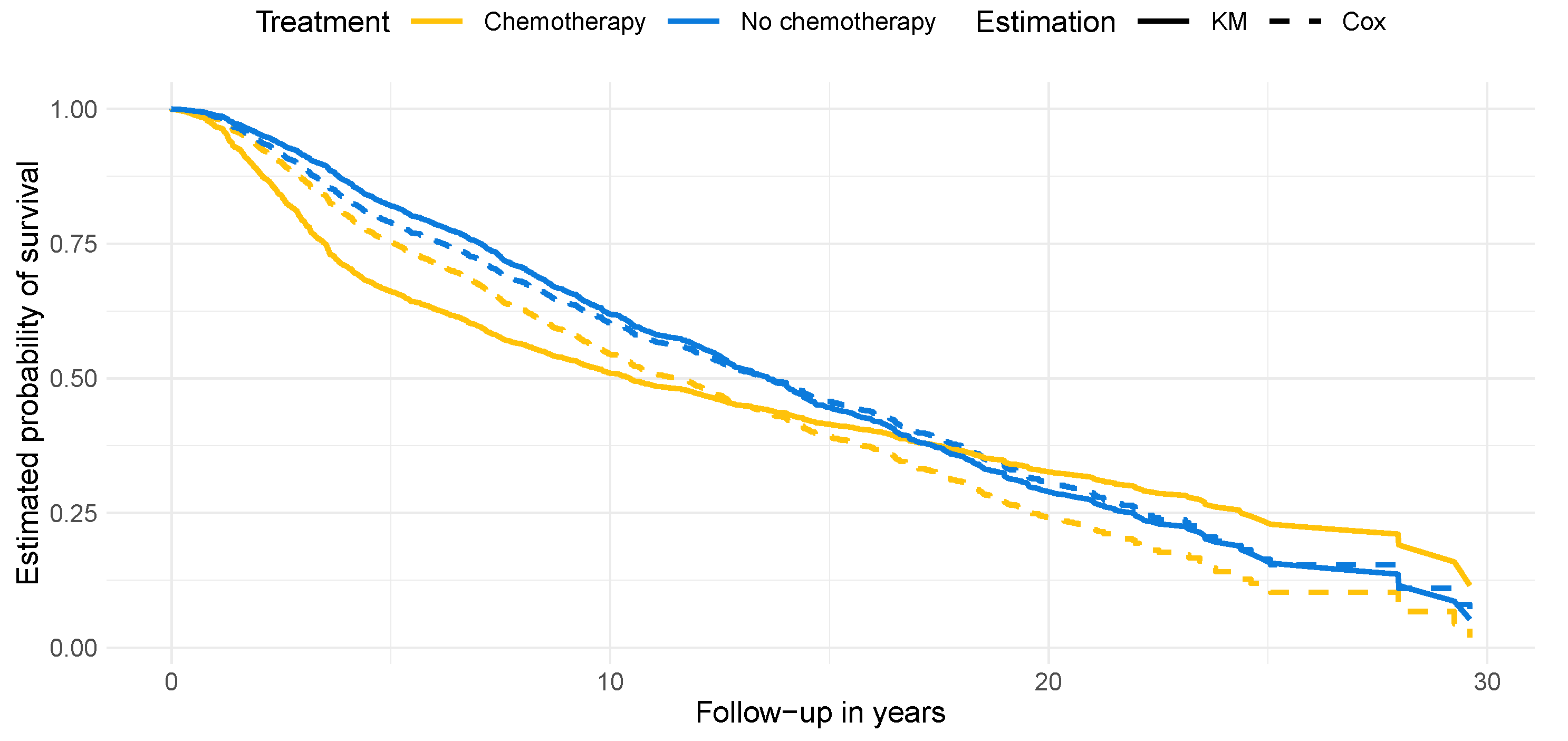
Appendix F
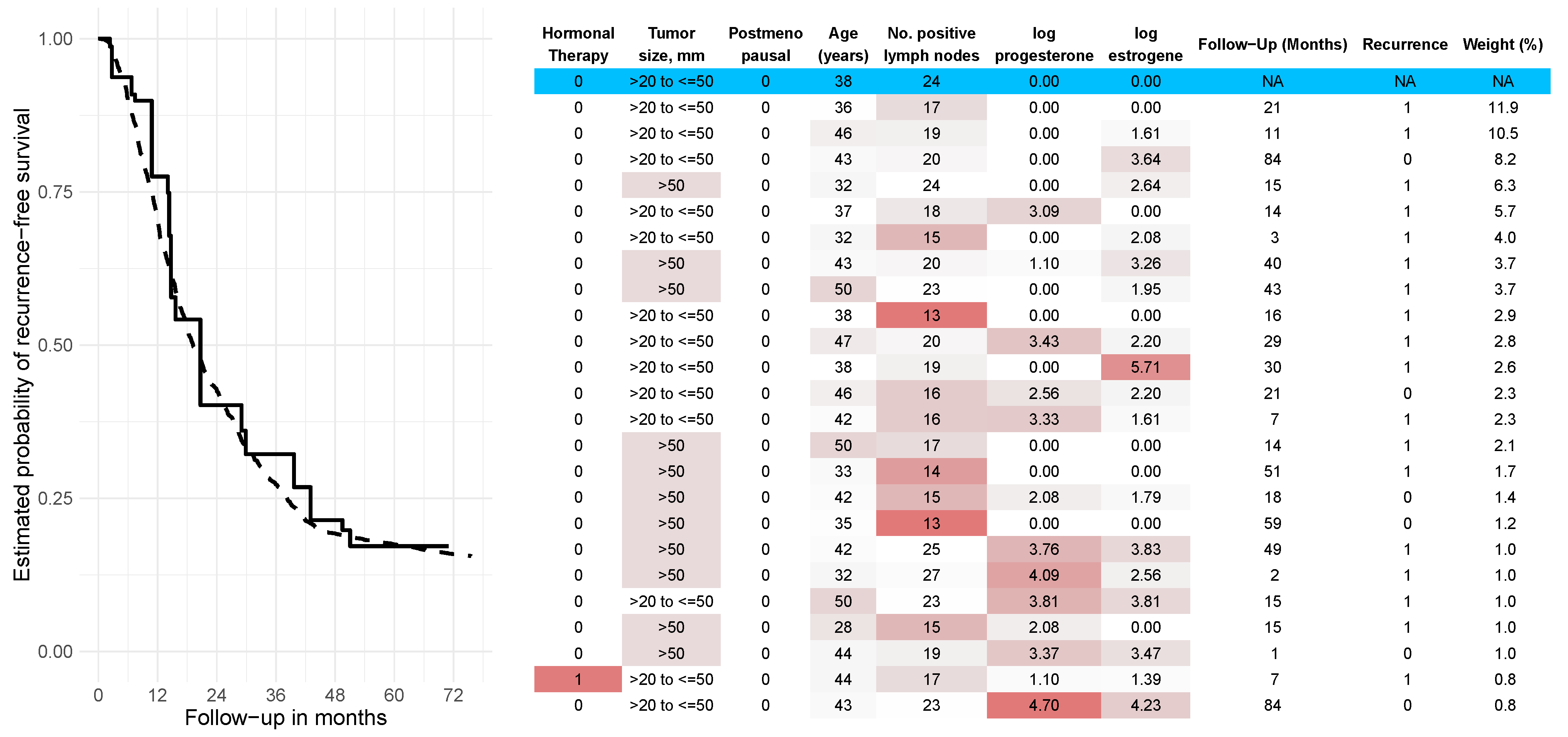
References
- Smith, M.J.; Phillips, R.V.; Luque-Fernandez, M.A.; Maringe, C. Application of targeted maximum likelihood estimation in public health and epidemiological studies: A systematic review. Ann. Epidemiol. 2023, 86, 34–48.e28. [Google Scholar] [CrossRef]
- Wager, S.; Athey, S. Estimation and Inference of Heterogeneous Treatment Effects using Random Forests. J. Am. Stat. Assoc. 2018, 113, 1228–1242. [Google Scholar] [CrossRef]
- Hu, L.; Ji, J.; Li, F. Estimating heterogeneous survival treatment effect in observational data using machine learning. Stat. Med. 2021, 40, 4691–4713. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Reddy, C.K. Machine Learning for Survival Analysis: A Survey. ACM Comput. Surv. 2019, 51, 1–36. [Google Scholar] [CrossRef]
- Pölsterl, S.; Navab, N.; Katouzian, A. Fast Training of Support Vector Machines for Survival Analysis. In Proceedings of the Machine Learning and Knowledge Discovery in Databases; Appice, A., Rodrigues, P.P., Santos Costa, V., Gama, J., Jorge, A., Soares, C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 243–259. [Google Scholar] [CrossRef]
- Segal, M.R. Regression Trees for Censored Data. Biometrics 1988, 44, 35–47. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef]
- Kvamme, H.; Borgan, Ø. Continuous and discrete-time survival prediction with neural networks. Lifetime Data Anal. 2021, 27, 710–736. [Google Scholar] [CrossRef]
- Miotto, R.; Wang, F.; Wang, S.; Jiang, X.; Dudley, J.T. Deep learning for healthcare: Review, opportunities and challenges. Briefings Bioinform. 2017, 19, 1236–1246. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning, 1st ed.; Series in Computer Science; McGraw-Hill: Chicago, IL, USA, 1997. [Google Scholar]
- Weinberger, K.Q.; Saul, L.K. Distance Metric Learning for Large Margin Nearest Neighbor Classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Li, D.; Tian, Y. Survey and experimental study on metric learning methods. Neural Netw. 2018, 105, 447–462. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Tesauro, G. Metric Learning for Kernel Regression. In Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics, San Juan, PR, USA, 21–24 March 2007; Proceedings of Machine Learning Research. Meila, M., Shen, X., Eds.; PMLR: San Juan, PR, USA, 2007; Volume 2, pp. 612–619. [Google Scholar]
- Chen, G.H. Nearest Neighbor and Kernel Survival Analysis: Nonasymptotic Error Bounds and Strong Consistency Rates. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Proceedings of Machine Learning Research (PMLR). Chaudhuri, K., Salakhutdinov, R., Eds.; PMLR: Long Beach, CA, USA, 2019; Volume 97, pp. 1001–1010. [Google Scholar]
- Lowsky, D.; Ding, Y.; Lee, D.; McCulloch, C.; Ross, L.; Thistlethwaite, J.; Zenios, S. A K-nearest neighbors survival probability prediction method. Stat. Med. 2013, 32, 2062–2069. [Google Scholar] [CrossRef]
- Chen, G.H. Deep Kernel Survival Analysis and Subject-Specific Survival Time Prediction Intervals. In Proceedings of the 5th Machine Learning for Healthcare Conference, Virtual, 7–8 August 2020; Proceedings of Machine Learning Research (PMLR). Doshi-Velez, F., Fackler, J., Jung, K., Kale, D., Ranganath, R., Wallace, B., Wiens, J., Eds.; PMLR: Virtual, 2020; Volume 126, pp. 537–565. [Google Scholar]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis, 2nd ed.; Statistics for Biology and Health; Springer: New York, NY, USA, 2003. [Google Scholar]
- Pölsterl, S. scikit-survival: A Library for Time-to-Event Analysis Built on Top of scikit-learn. J. Mach. Learn. Res. 2020, 21, 8747–8752. [Google Scholar]
- Rasmussen, C.; Williams, C. Covariance functions. In Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection Via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- LeBlanc, M.; Crowley, J. Relative Risk Trees for Censored Survival Data. Biometrics 1992, 48, 411–425. [Google Scholar] [CrossRef]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef] [PubMed]
- Foekens, J.A.; Peters, H.A.; Look, M.P.; Portengen, H.; Schmitt, M.; Kramer, M.D.; Brünner, N.; Jänicke, F.; Meijer-van Gelder, M.E.; Henzen-Logmans, S.C.; et al. The urokinase system of plasminogen activation and prognosis in 2780 breast cancer patients. Cancer Res. 2000, 60, 636–643. [Google Scholar]
- Schumacher, M.; Bastert, G.; Bojar, H.; Hübner, K.; Olschewski, M.; Sauerbrei, W.; Schmoor, C.; Beyerle, C.; Neumann, R.L.; Rauschecker, H.F. Randomized 2 × 2 trial evaluating hormonal treatment and the duration of chemotherapy in node-positive breast cancer patients. German Breast Cancer Study Group. J. Clin. Oncol. 1994, 12, 2086–2093. [Google Scholar] [CrossRef] [PubMed]
- Antolini, L.; Boracchi, P.; Biganzoli, E. A time-dependent discrimination index for survival data. Stat. Med. 2005, 24, 3927–3944. [Google Scholar] [CrossRef] [PubMed]
- Graf, E.; Schmoor, C.; Sauerbrei, W.; Schumacher, M. Assessment and comparison of prognostic classification schemes for survival data. Stat. Med. 1999, 18, 2529–2545. [Google Scholar] [CrossRef]
- Austin, P.C.; Harrell, F.E.; van Klaveren, D. Graphical calibration curves and the integrated calibration index (ICI) for survival models. Stat. Med. 2020, 39, 2714–2742. [Google Scholar] [CrossRef]
- Davidson-Pilon, C. Lifelines v0.27.7, Survival Analysis in Python. 2023. Available online: https://zenodo.org/record/7883870 (accessed on 17 May 2023).
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Schemper, M.; Wakounig, S.; Heinze, G. The estimation of average hazard ratios by weighted Cox regression. Stat. Med. 2009, 28, 2473–2489. [Google Scholar] [CrossRef] [PubMed]
- Gönen, M.; Alpaydin, E. Multiple Kernel Learning Algorithms. J. Mach. Learn. Res. 2011, 12, 2211–2268. [Google Scholar]
- Liu, F.; Huang, X.; Chen, Y.; Suykens, J.A.K. Random Features for Kernel Approximation: A Survey on Algorithms, Theory, and Beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7128–7148. [Google Scholar] [CrossRef] [PubMed]
- Yadav, M.; Sheldon, D.R.; Musco, C. Kernel Interpolation with Sparse Grids. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: New York, NY, USA, 2022; Volume 35, pp. 22883–22894. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galetzka, W.; Kowall, B.; Jusi, C.; Huessler, E.-M.; Stang, A. Distance-Metric Learning for Personalized Survival Analysis. Entropy 2023, 25, 1404. https://doi.org/10.3390/e25101404
Galetzka W, Kowall B, Jusi C, Huessler E-M, Stang A. Distance-Metric Learning for Personalized Survival Analysis. Entropy. 2023; 25(10):1404. https://doi.org/10.3390/e25101404
Chicago/Turabian StyleGaletzka, Wolfgang, Bernd Kowall, Cynthia Jusi, Eva-Maria Huessler, and Andreas Stang. 2023. "Distance-Metric Learning for Personalized Survival Analysis" Entropy 25, no. 10: 1404. https://doi.org/10.3390/e25101404
APA StyleGaletzka, W., Kowall, B., Jusi, C., Huessler, E.-M., & Stang, A. (2023). Distance-Metric Learning for Personalized Survival Analysis. Entropy, 25(10), 1404. https://doi.org/10.3390/e25101404




