On the Consensus Performance of Multi-Layered MASs with Various Graph Parameters—From the Perspective of Cardinalities of Vertex Sets
Abstract
1. Introduction
- I.
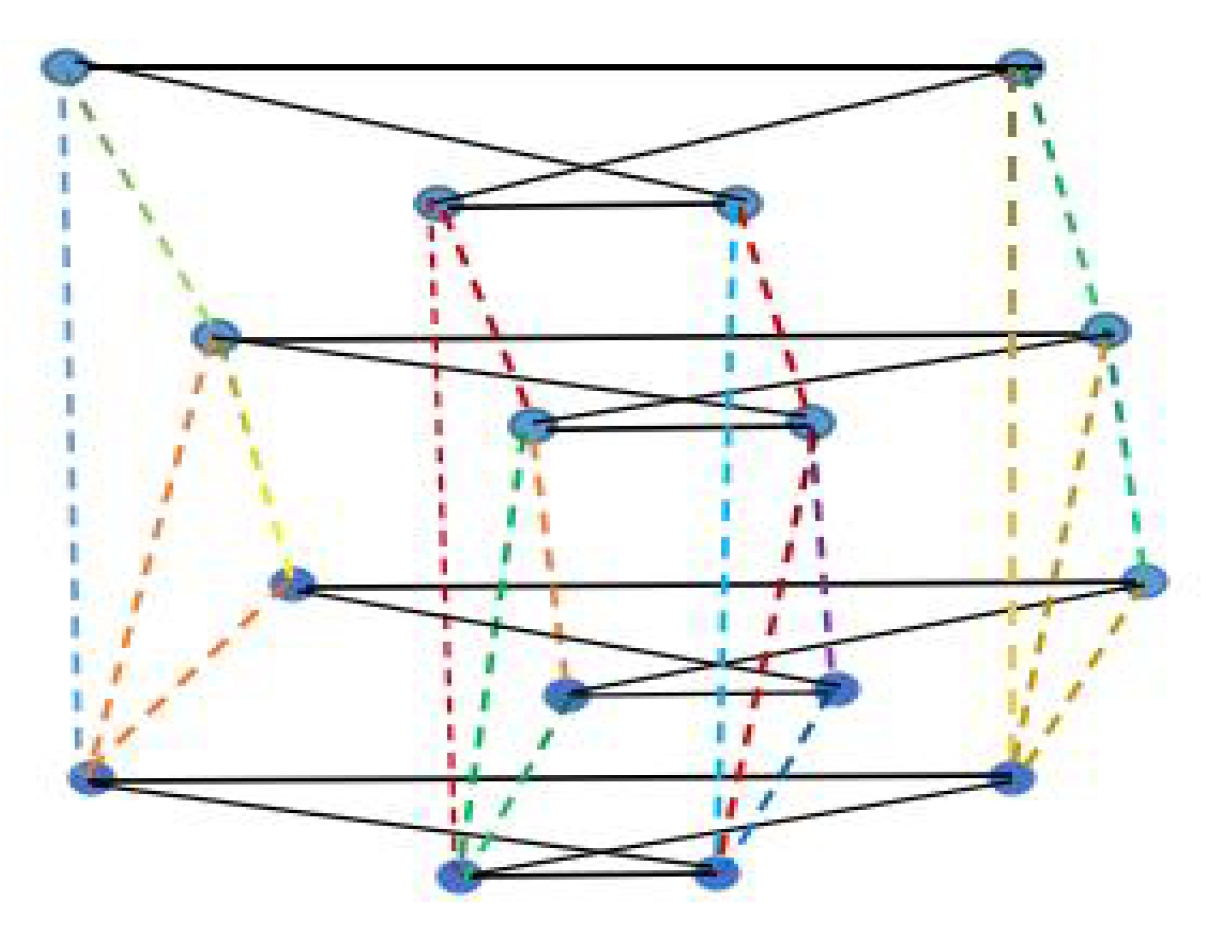
- A sort of novel multi-layered MAS with a balanced, complete, multi-partite graph has been constructed by graph operations. Different from other good research on multilayered coordination systems, the side structure in this article from the vertical view has the fan-shaped structure.
- II.
- Analysis methods with various parameters are applied for deriving the coherence, and the related asymptotic properties have been acquired.
- III.
- We found that when the vertex sets of the corresponding counterpart layers have the same cardinality, the multi-layered graph class with a complete multi-partite structure has the best robustness of all the considered layered systems if the sufficient conditions for the parameters hold.
2. Preliminaries
2.1. Graph Theory and Notations
2.2. Relations for the Coherence and Laplacian Eigenvalues
3. Main Results
3.1. The Coherence for Network Topology
- (1).
- with multiplicity 1;
- (2).
- with multiplicity ;
- (3).
- with multiplicity ;
- (4).
- with multiplicity 1;
- (5).
- with multiplicity ;
- (6).
- with multiplicity ;
- (7).
- with multiplicity 1, where ;
- (8).
- with multiplicity , ;
- (9).
- with multiplicity , .
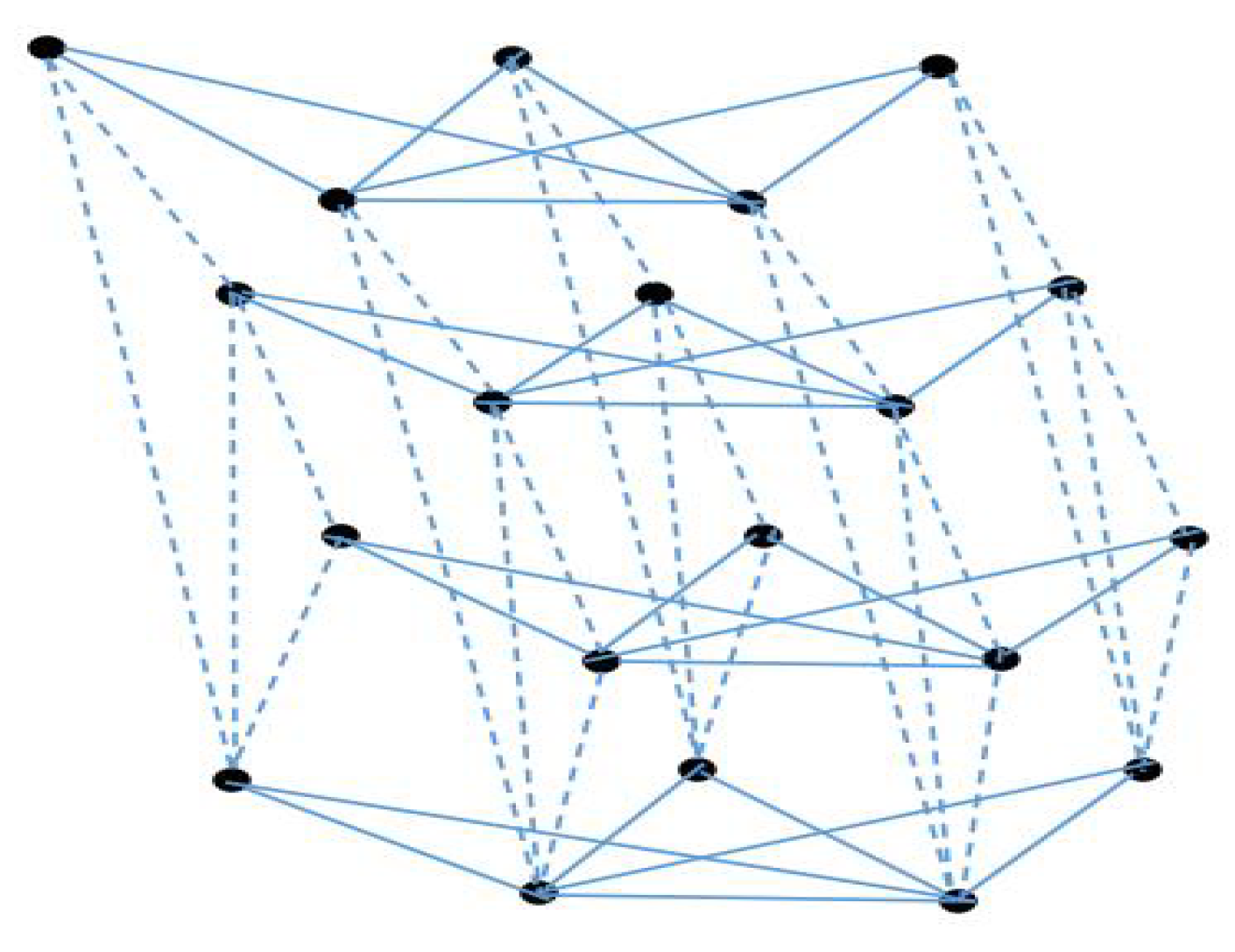
3.2. The Coherence for Network Topology
- (1).
- with multiplicity 1;
- (2).
- repeated n times;
- (3).
- repeated times;
- (4).
- with multiplicity 1;
- (5).
- with multiplicity n;
- (6).
- repeated times;
- (7).
- with multiplicity 1, ;
- (8).
- with multiplicity n, ;
- (9).
- repeated times, .
3.3. The Coherence of Structure
- (1).
- 0 and repeated once;
- (2).
- with multiplicity 1;
- (3).
- repeated once, where .
- (4).
- repeated times;
- (5).
- repeated times;
- (6).
- repeated times, where .
- (7).
- repeated times.
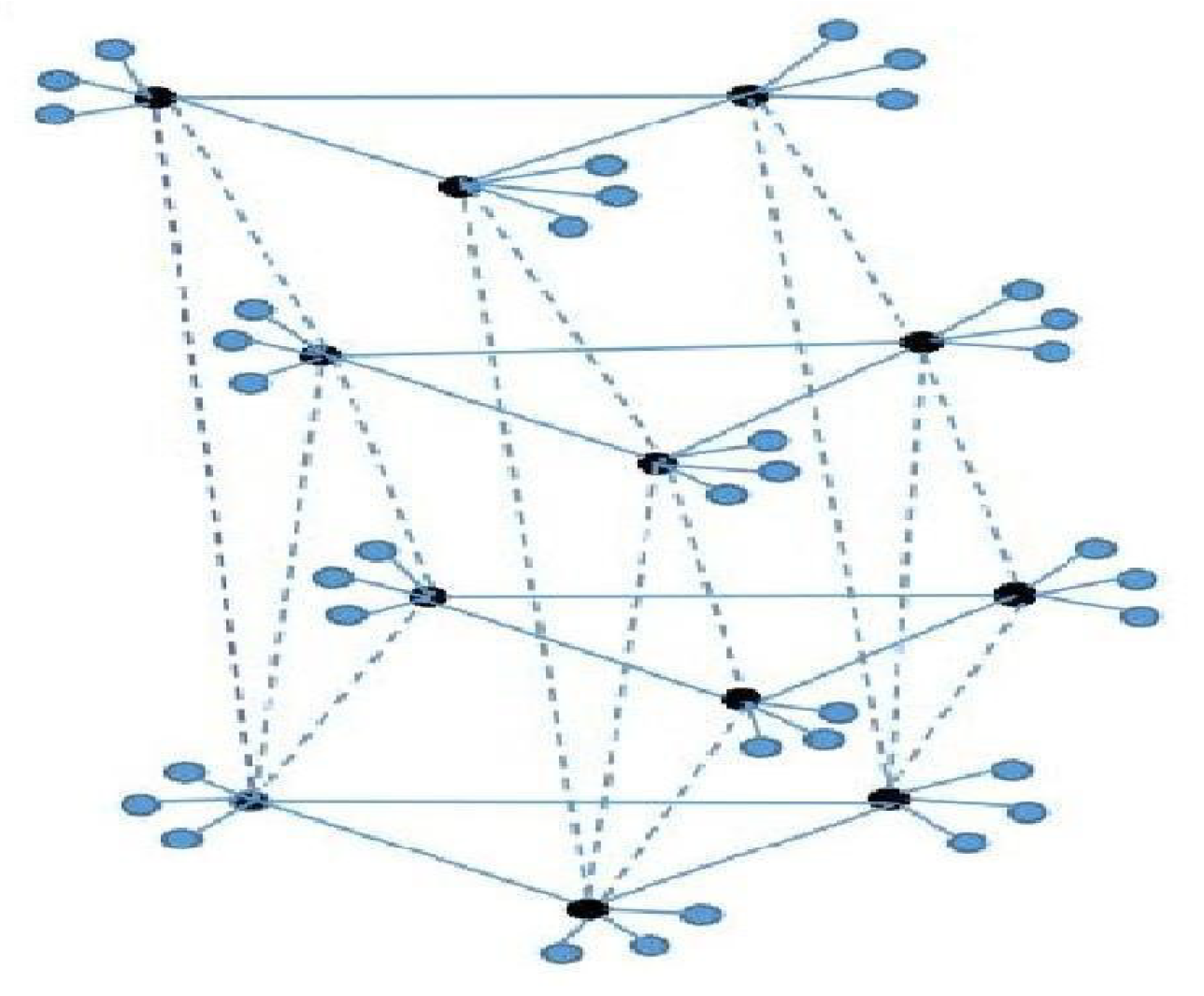
3.4. The Coherence for Special Cases
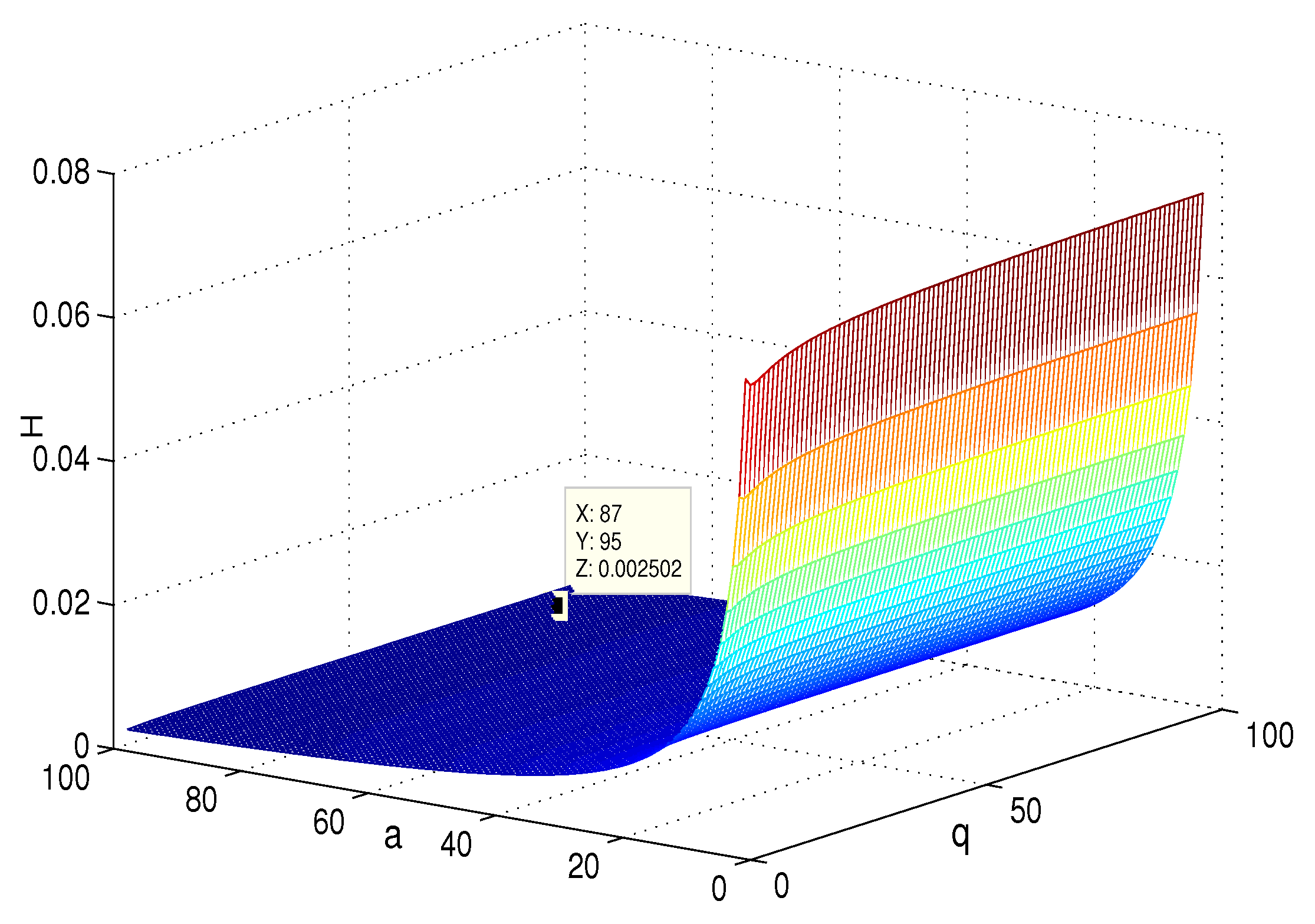
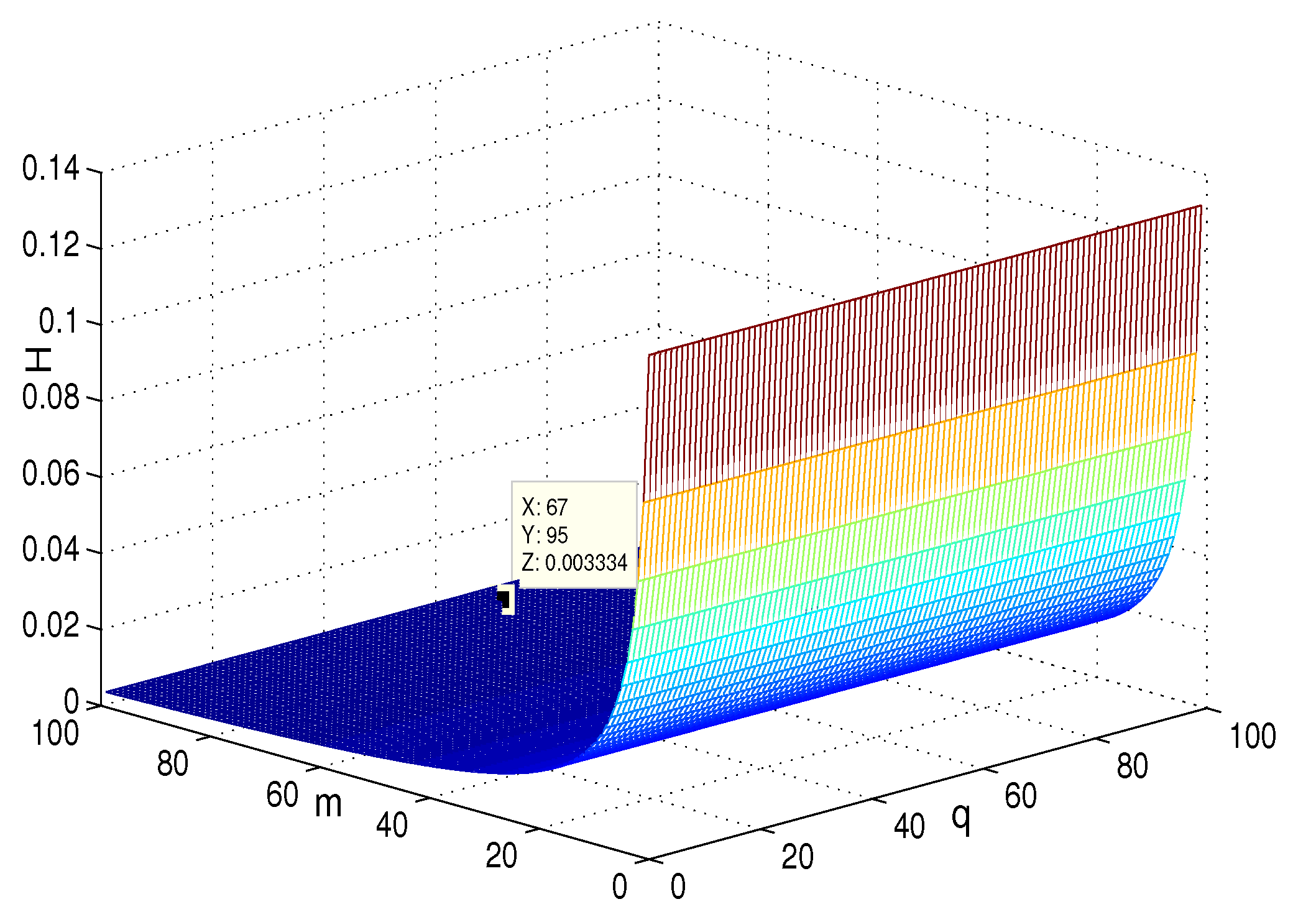
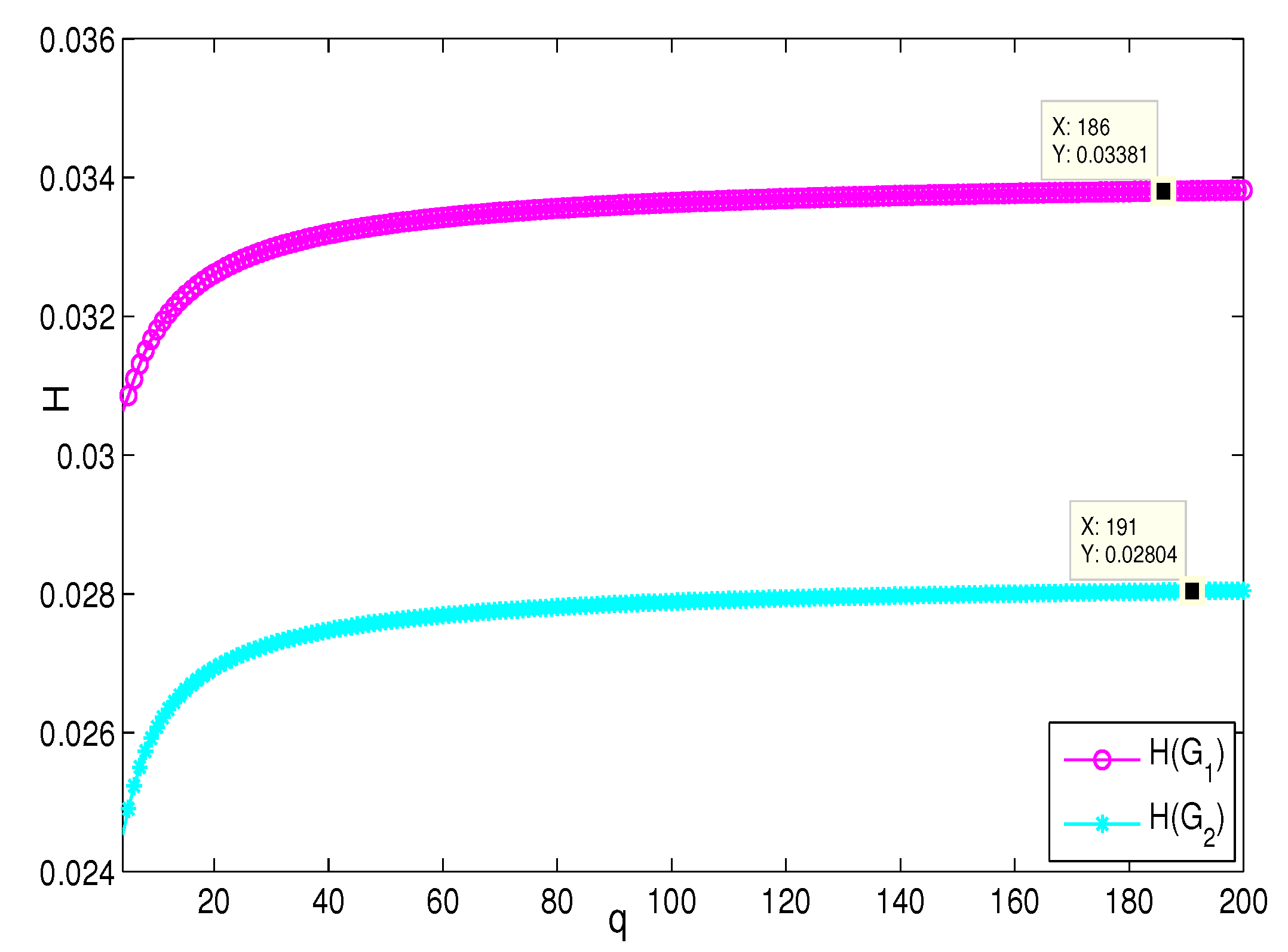
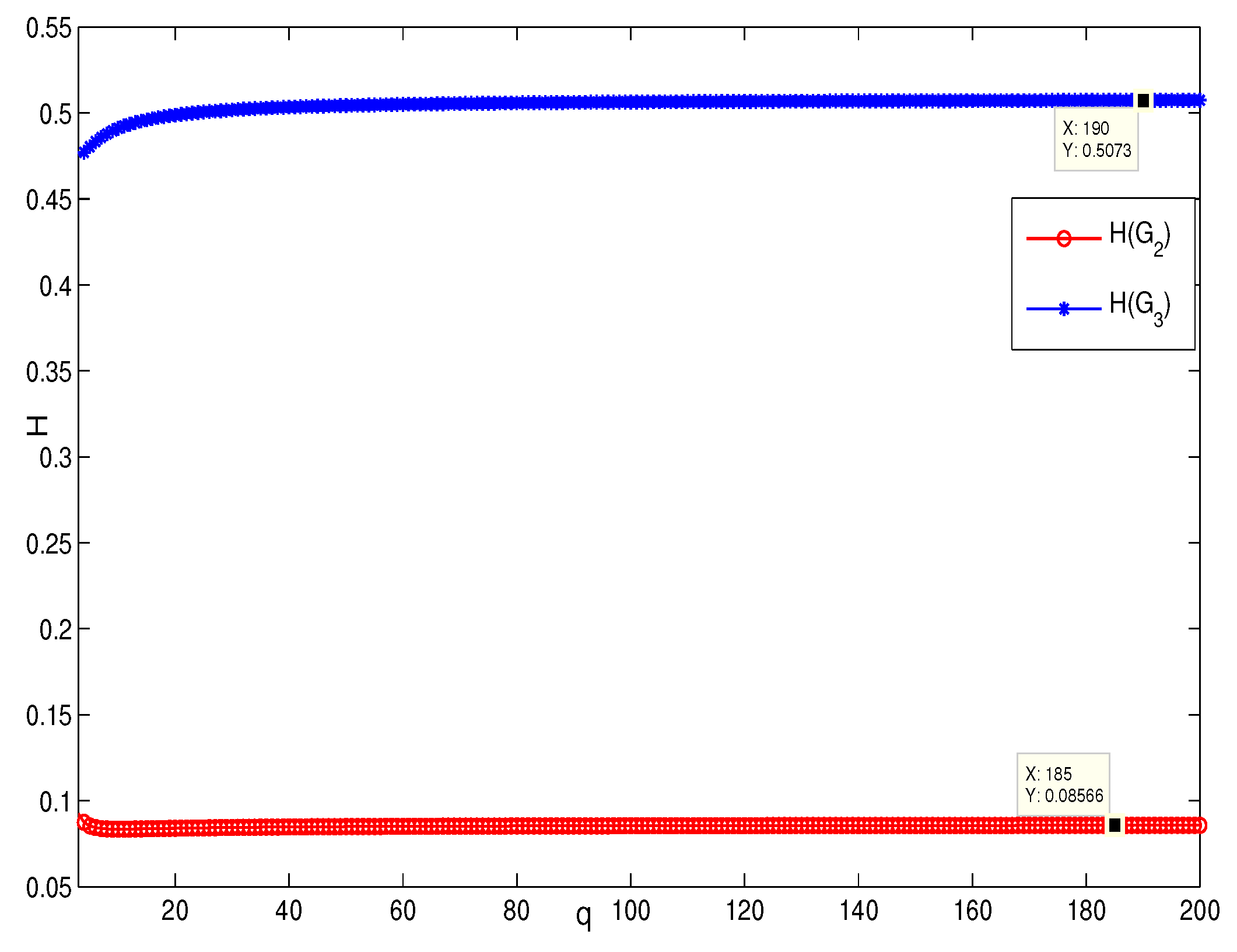
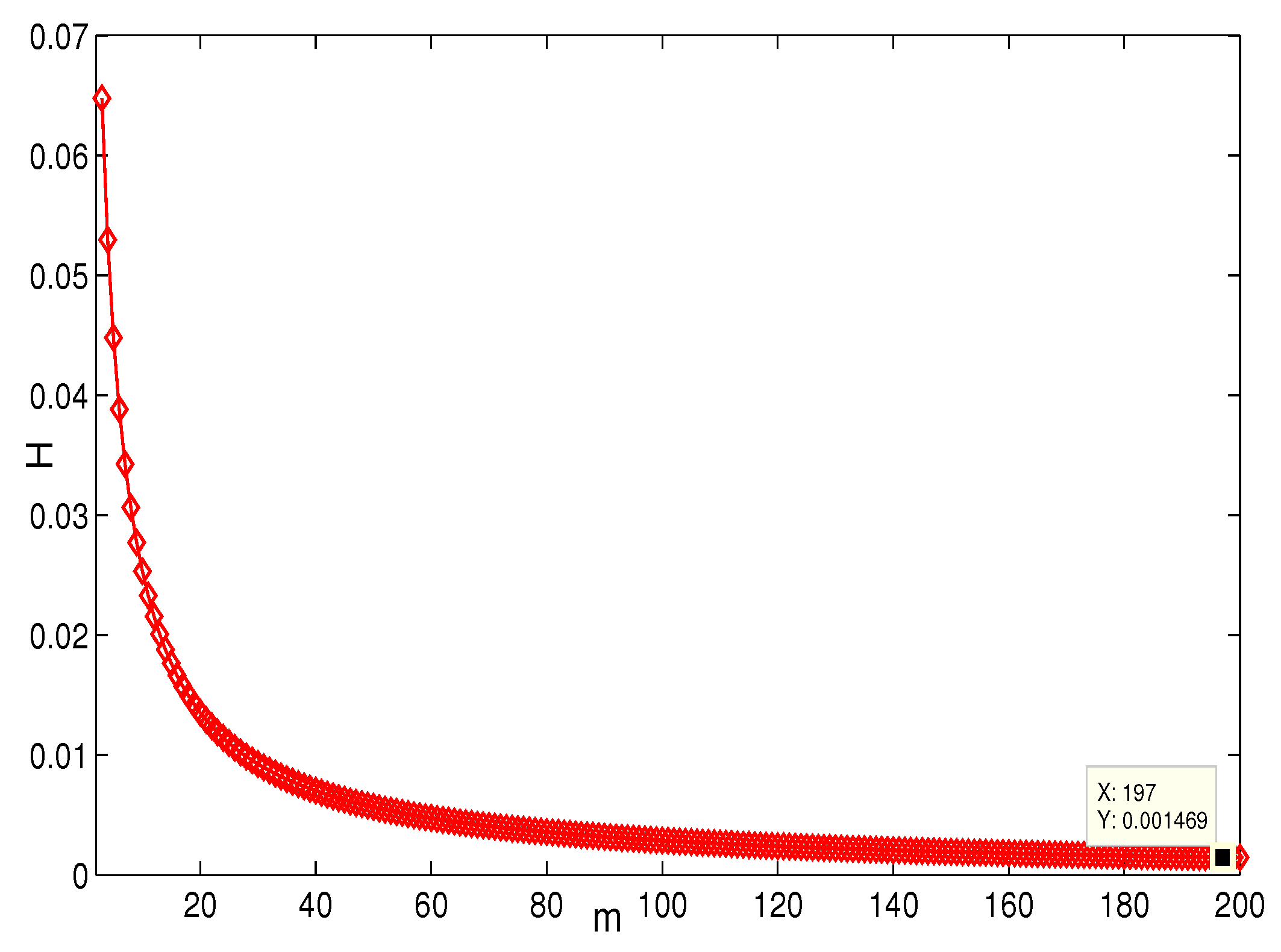
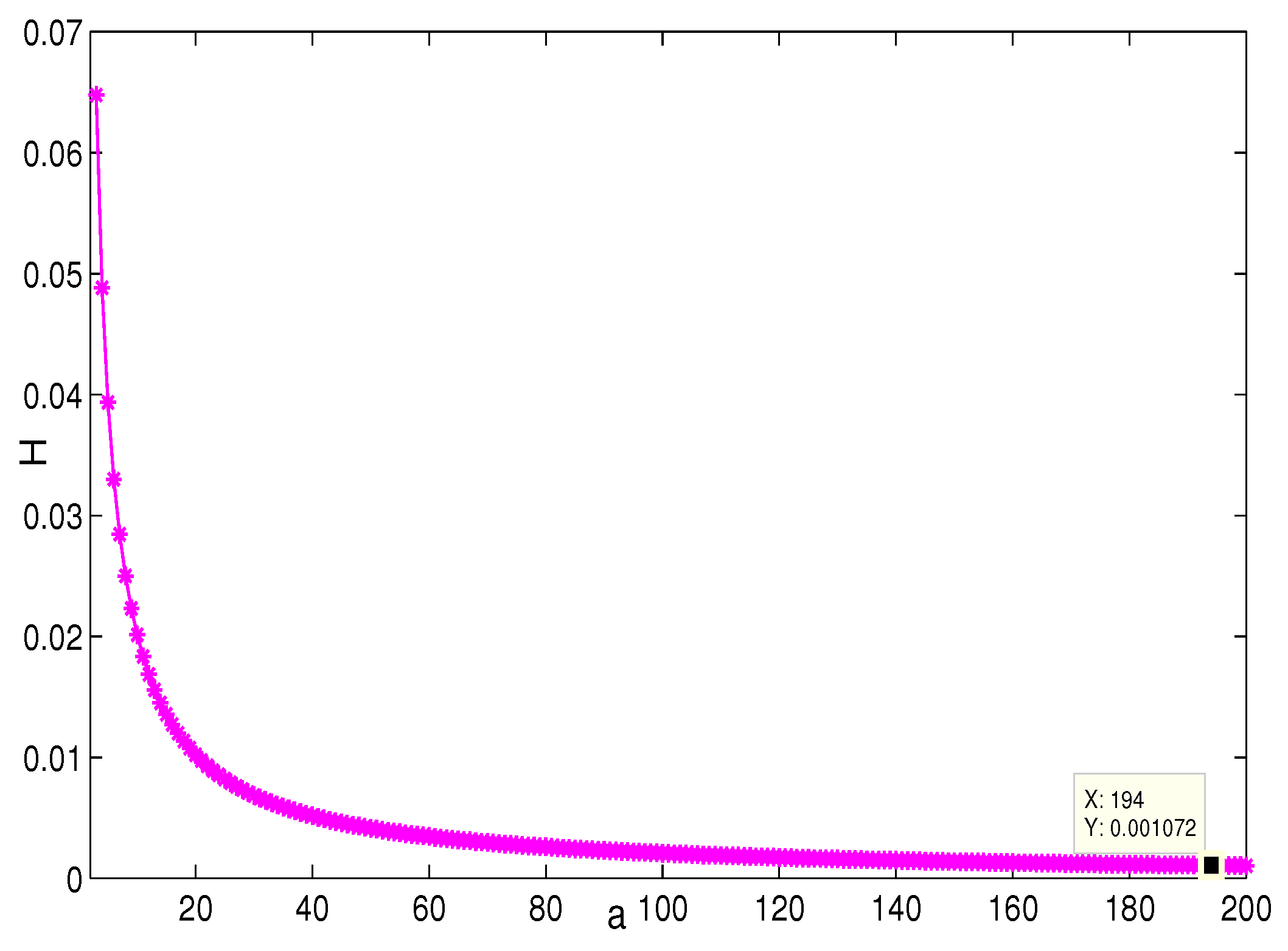
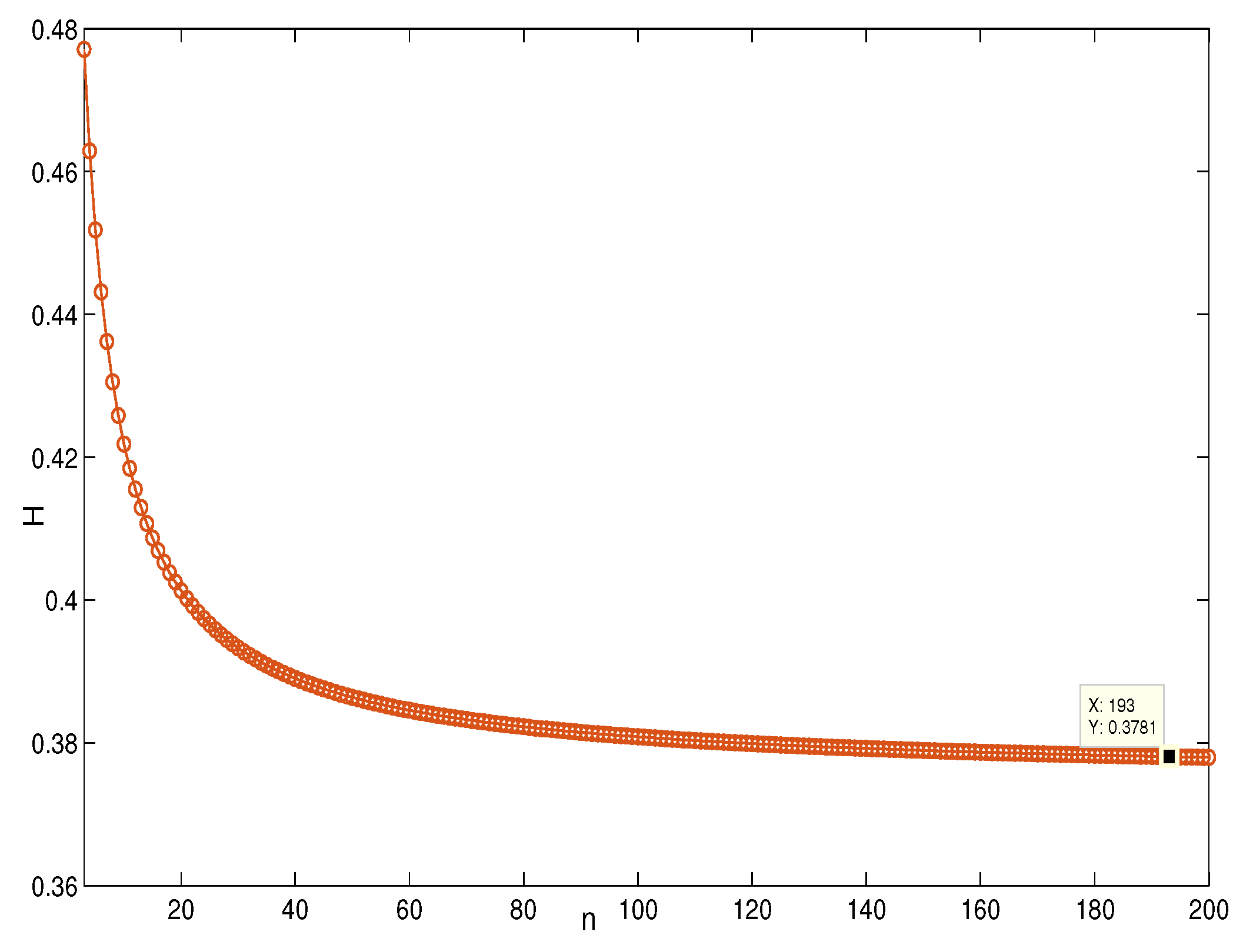
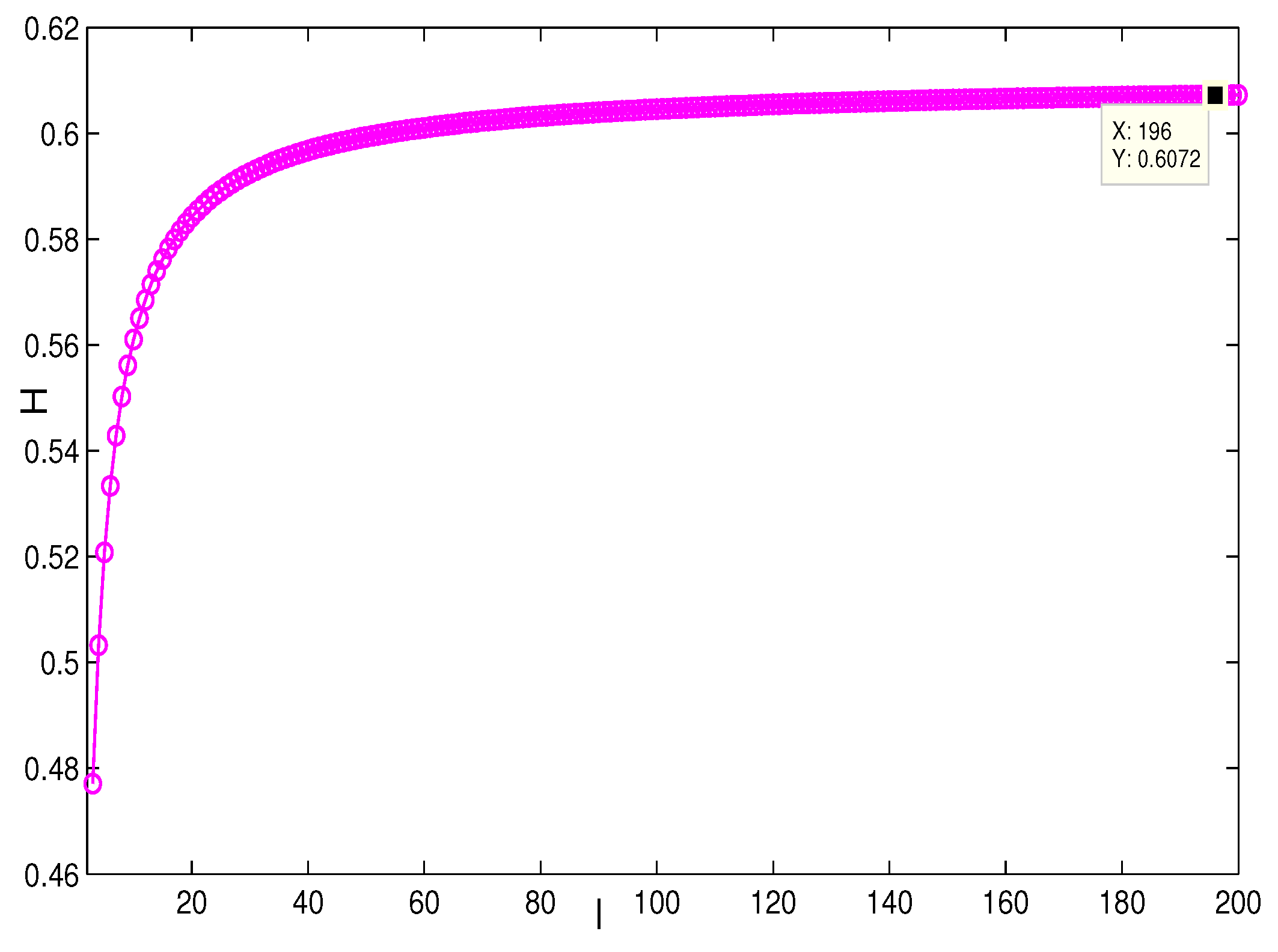
4. Simulation and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saber, O.; Murray, R. Consensus problems in Networks of Agents With Switching Topology and Time-Delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ren, W. On consensus algorithms for double-integrator dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern.-Part Cybern. 2010, 40, 881–891. [Google Scholar]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications. Int. J. Control 2013, 86, 322–331. [Google Scholar] [CrossRef]
- Shang, Y. Finite-time Consensus for Multi-Agent Systems with Fixed Topologies. Int. J. Syst. Sci. 2012, 43, 499–506. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, D.; Jiang, H.; Hu, C.; Yu, W. Distributed consensus for multiagent systems via directed spanning tree based adaptive control. Siam Control. Optim. 2018, 56, 2189–2217. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, H.; Hu, C.; Yu, J. Leader-following consensus of fractional-order multi-agent systems via adaptive pinning control. Int. J. Control 2015, 88, 1746–1756. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, G.; Rahmani, A.; Peng, Z.; Hu, W. Cluster consensus of multi-agent systems with general linear and nonlinear dynamics via intermittent adaptive pinning control. Trans. Inst. Meas. Control 2020, 43, 014233122097525. [Google Scholar] [CrossRef]
- Huang, D.; Jiang, H.; Yu, Z.; Hu, C.; Fan, X. Cluster-delay consensus in MASs with layered intermittent communication: A multi-tracking approach. Nonlinear Dyn. 2019, 95, 1713–1730. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, J.; Yu, S.; Jiang, H. Fixed-time consensus for multi-agent systems with objective optimization on directed detail-balanced networks. Inf. Sci. 2022, 607, 1583–1599. [Google Scholar] [CrossRef]
- Sun, Y.; Li, W.; Zhao, D. Convergence time and speed of multi-agent systems in noisy environments. Chaos 2012, 22, 43126. [Google Scholar] [CrossRef] [PubMed]
- Young, G.; Scardovi, L.; Leonard, N. Robustness of Noisy Consensus Dynamics with Directed Communication. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6312–6317. [Google Scholar]
- Bamieh, B.; Jovanovi, M.R.; Mitra, P.; Patterson, S. Coherence in large-scale networks: Dimension-dependent limitations of local feedback. IEEE Trans. Autom. Control 2012, 57, 2235–2249. [Google Scholar] [CrossRef]
- Patterson, S.; Bamieh, B. Consensus and Coherence in Fractal Networks. IEEE Trans. Control Netw. Syst. 2014, 1, 338–348. [Google Scholar] [CrossRef]
- Patterson, S.; Yi, Y.; Zhang, Z. A Resistance-Distance-Based Approach for Optimal Leader Selection in Noisy Consensus Networks. IEEE Trans. Control Netw. Syst. 2018, 6, 191–201. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Shan, L.; Chen, G. Robustness of First-And Second-Order Consensus Algorithms for a Noisy Scale-free Small-World Koch Network. IEEE Trans. Control Syst. Technol. 2016, 25, 342–350. [Google Scholar] [CrossRef]
- Sun, W. Coherence in a family of tree networks with an application of Laplacian spectrum. Chaos 2014, 24, 043112. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Li, Y.; Liu, S. Noisy consensus dynamics in windmill-type graphs. Chaos 2020, 30, 123131. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Hong, M.; Liu, S.; Fan, K. Leader-follower coherence in noisy ring-trees networks. Nonlinear Dyn. 2020, 102, 1–9. [Google Scholar] [CrossRef]
- Wang, X.; Xu, H.; Dai, M. First-order network coherence in 5-rose graphs. Physic A 2019, 527, 121129. [Google Scholar] [CrossRef]
- Huang, D.; Zhu, J.; Yu, Z.; Jiang, H. On Consensus Index of Triplex Star-Like Networks: A Graph Spectra Approach. Symmetry 2021, 13, 1248. [Google Scholar] [CrossRef]
- Wan, Y.; Namuduri, K.; Akula, S.; Varanasi, M. The impact of multi-group multi-layer network structure on the performance of distributed consensus building strategies. Int. J. Robust. Nonlinear Control 2012, 23, 653–662. [Google Scholar] [CrossRef]
- Wang, X.F. Complex netwroks, topology, dynamics and synchronization. Int. J. Bifurc. Chaos 2002, 12, 885–916. [Google Scholar] [CrossRef]
- Chen, G.; Duan, Z. Network synchronization analysis: A graph-theoreic approach. Chaos 2008, 18, 037102. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Chen, G.; Han, Q.-L.; Du, W.; Cao, J.; Qian, F. Multiagent Systems on Multilayer Networks: Synchronization Analysis and Network Design. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1655–1667. [Google Scholar] [CrossRef]
- Kivela, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer Networks. J. Complex Netw. 2014, 2, 203. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, C.; Chen, Z.; Chen, G. Epidemic Propagation With Positive and Negative Preventive Information in Multiplex Networks. IEEE Trans. Cybern. 2021, 51, 1454–1462. [Google Scholar] [CrossRef] [PubMed]
- Lahby, M.; Essouiri, A.; Sekkaki, A. A novel modeling approach for vertical handover based on dynamic k-partite graph in heterogeneous networks. Digit. Commun. Netw. 2019, 5, 297–307. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, B.; Zhong, F.; Zilles, S. The Fast Search Number of a Complete k-Partite Graph. Algorithmica 2018, 80, 3959–3981. [Google Scholar] [CrossRef]
- Li, Z. Exact Recovery of Community Detection in k-Partite Graph Models with Applications to Learning Electric Potentials in Electric Networks. J. Stat. Phys. 2021, 182, 6. [Google Scholar] [CrossRef]
- Yang, F.; Jia, Z.; Deng, Y. Eigenvalue Spectrum and Synchronizability of Two Types of Double-Layer Star-Ring Networks with Hybrid Directional Coupling. Discret. Dyn. Nat. Soc. 2021, 2021, 6623648. [Google Scholar] [CrossRef]
- Wang, L.; Jia, X.; Pan, X.; Xia, C. Extension of synchronizability analysis based on vital factors: Extending validity to multilayer fully coupled networks, Chaos. Solitons Fractals 2021, 142, 110484. [Google Scholar] [CrossRef]
- Xu, M.M.; Lu, J.A.; Zhou, J. Synchronizability and eigenvalues of two-layer star networks. Acta Phys. Sin. 2016, 65, 028902. [Google Scholar]
- Cvetkovic, D.; Rowlinson, P.; Simic, S. An Introduction to the Theory of Graph Spectra; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Khalifeh, M.H.; Yousefi-Azari, H.; Ashrafi, A.R. The hyper-Wiener index of graph operations. Comput. Math. Appl. 2008, 56, 1402–1407. [Google Scholar]
- Zhang, Z.; Zhu, Y. Cyclic arc-connectivity in a Cartesian product digraph. Appl. Math. Lett. 2010, 23, 796–800. [Google Scholar] [CrossRef]
- Barik, S.; Pati, S.; Sarma, B. The Spectrum of The Corona of Two Graphs. SIAM J. Discret. Math. 2007, 21, 47–56. [Google Scholar] [CrossRef]
- Liu, Q. The Laplacian spectrum of corona of two graphs. Kragujev. J. Math. 2014, 38, 163–170. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y. Resistance Distances and Kirchhoff index in circulant graphs. Int. J. Quantum Chem. 2007, 107, 330–339. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, Y. Resistance Distances and Kirchhoff indices under graph operations. IEEE Access 2020, 8, 95650–95656. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Cao, J. The Laplacian polynomial and Kirchhoff index of graphs based on R-graphs. Neurocomputing 2016, 177, 441–446. [Google Scholar] [CrossRef]
- Liu, J.; Pan, X. A unified approach to the asymptotic topological indices of various lattices. Appl. Math. Comput. 2015, 270, 62–73. [Google Scholar] [CrossRef]
- Li, X.; Peng, D. Extremal problems for graphical function-indices and f-weighted adjacency matrix. Discrete Math. Lett. 2022, 9, 57–66. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Yu, Z. On the Consensus Performance of Multi-Layered MASs with Various Graph Parameters—From the Perspective of Cardinalities of Vertex Sets. Entropy 2023, 25, 40. https://doi.org/10.3390/e25010040
Huang D, Yu Z. On the Consensus Performance of Multi-Layered MASs with Various Graph Parameters—From the Perspective of Cardinalities of Vertex Sets. Entropy. 2023; 25(1):40. https://doi.org/10.3390/e25010040
Chicago/Turabian StyleHuang, Da, and Zhiyong Yu. 2023. "On the Consensus Performance of Multi-Layered MASs with Various Graph Parameters—From the Perspective of Cardinalities of Vertex Sets" Entropy 25, no. 1: 40. https://doi.org/10.3390/e25010040
APA StyleHuang, D., & Yu, Z. (2023). On the Consensus Performance of Multi-Layered MASs with Various Graph Parameters—From the Perspective of Cardinalities of Vertex Sets. Entropy, 25(1), 40. https://doi.org/10.3390/e25010040





