Analysis of Quantum Correlations Obtained Using Local Optimal Universal Asymmetric Cloners
Abstract
1. Introduction
2. The Concurrence of the States Obtained by the Local Optimal Universal Asymmetric Cloning Machines
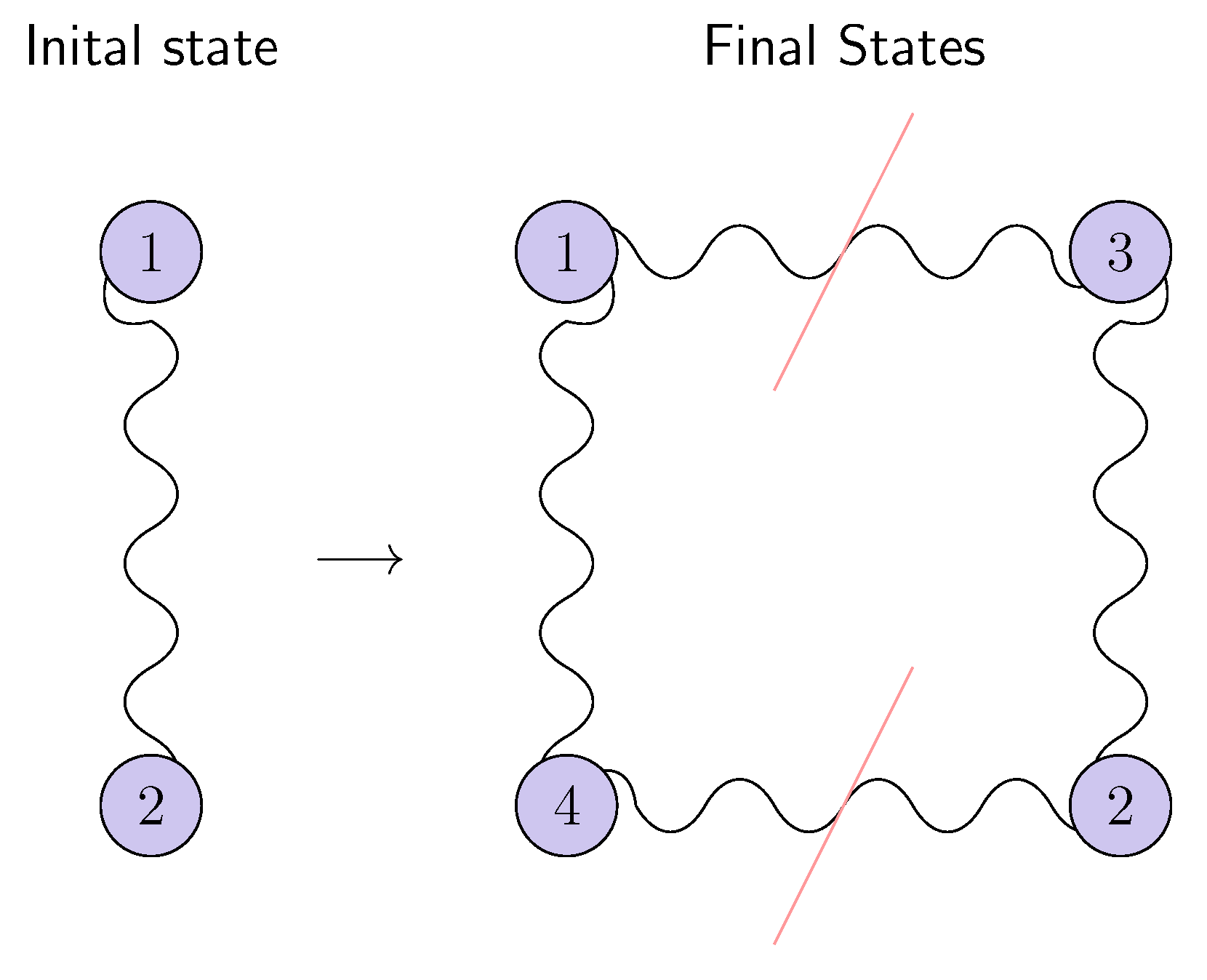
- The local reduced density operators and are separable;
- The nonlocal states and are inseparable.
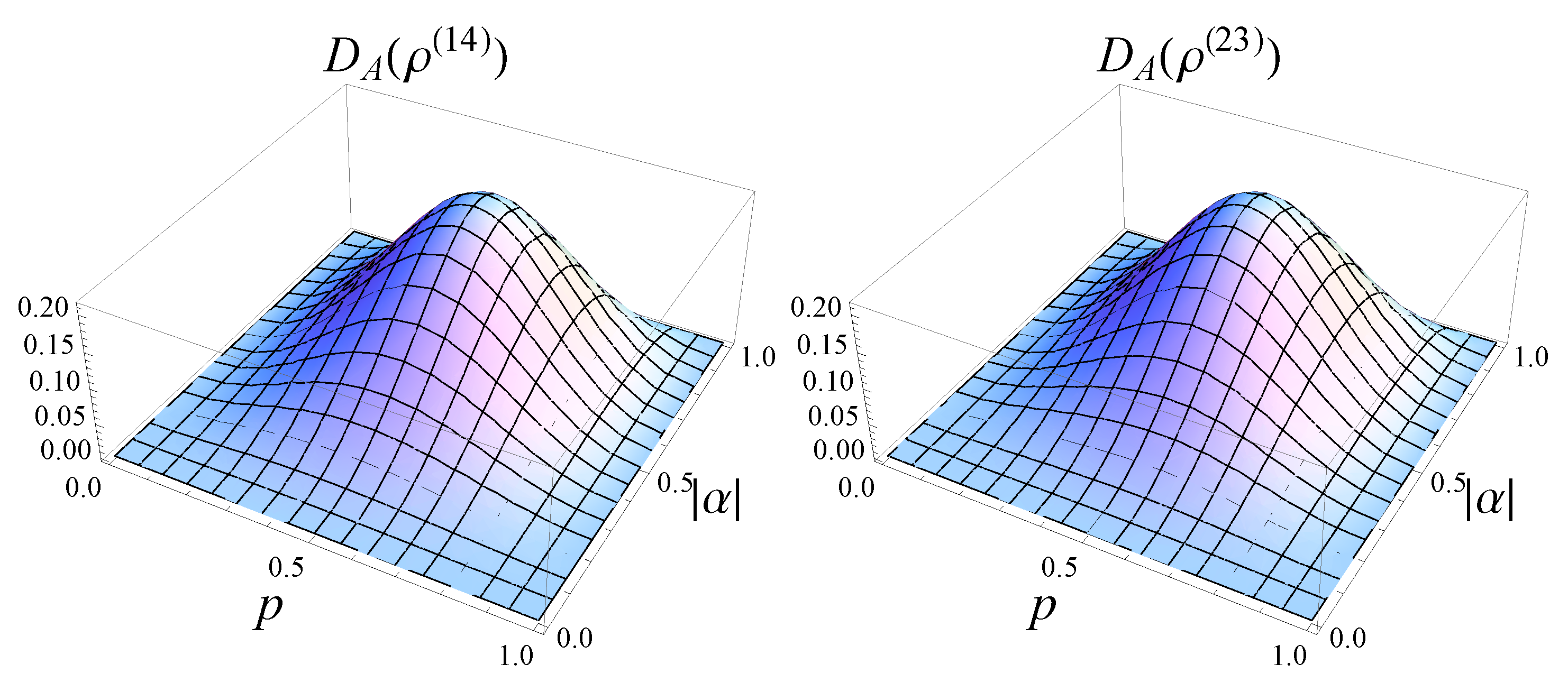
3. The Quantum Discord of the States Obtained by the Local Optimal Universal Asymmetric Cloning Machines
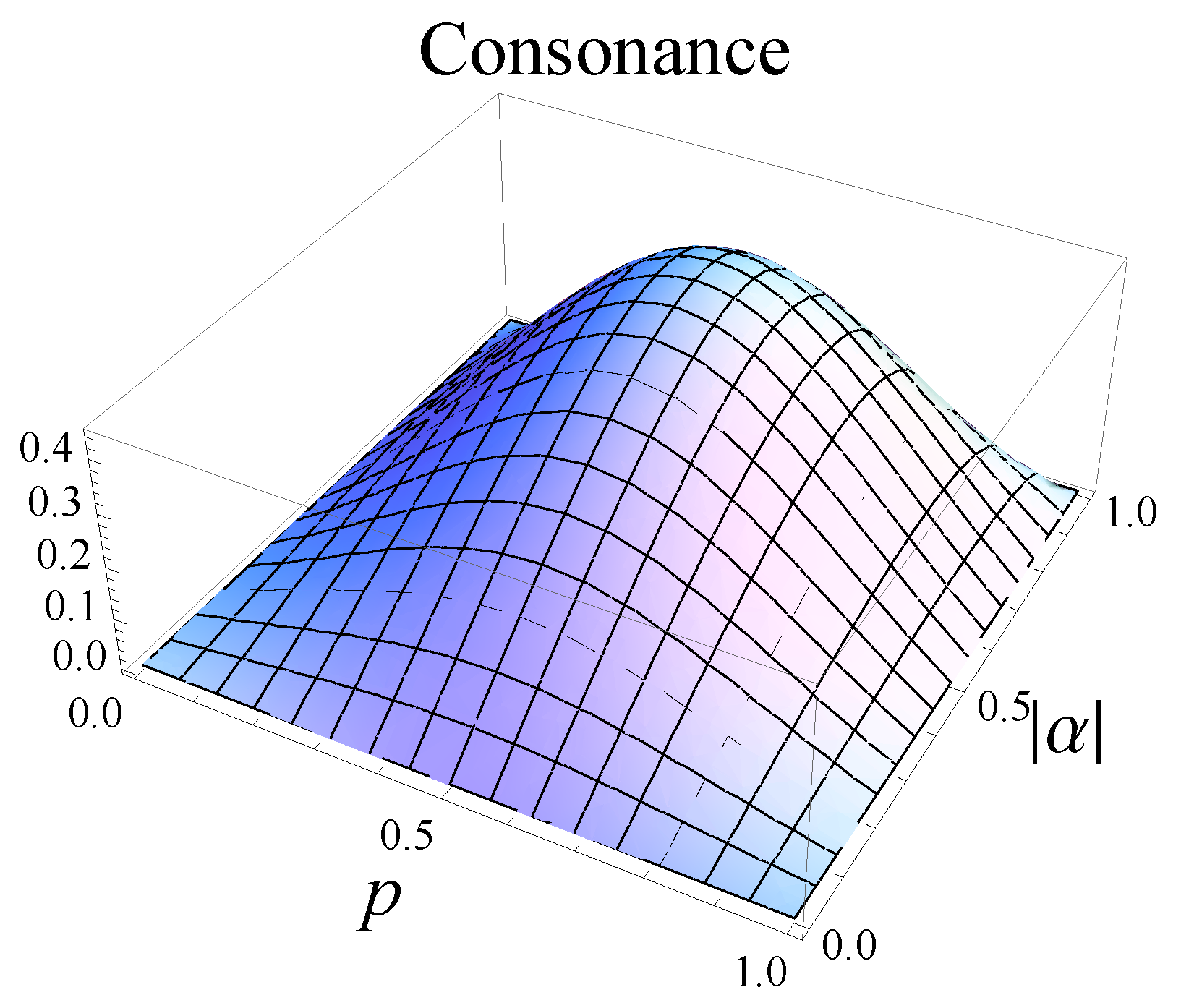
4. Consonance
5. A Comparison between the Concurrence, the Quantum -Discord, and Consonance of the Output States
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Evaluation of Quantum Discord for Two Qubits Found in the Canonical Form of the X State
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Horodecki, P.; Ekert, A. Method for Direct Detection of Quantum Entanglement. Phys. Rev. Lett. 2002, 89, 127902. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Murao, M.; Plenio, M.B.; Vedral, V. Quantum-information distribution via entanglement. Phys. Rev. A 2000, 61, 032311. [Google Scholar] [CrossRef]
- Sen, A. Quantum entanglement and its applications. Curr. Sci. 2017, 112, 1361. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef]
- Zippilli, S.; Paternostro, M.; Adesso, G.; Illuminati, F. Entanglement Replication in Driven Dissipative Many-Body systems. Phys. Rev. Lett. 2013, 110, 040503. [Google Scholar] [CrossRef]
- Ghiu, I.; Bourennane, M.; Karlsson, A. Entanglement-assisted local transformations between inequivalent classes of three-particle entangled states. Phys. Lett. A 2001, 287, 12. [Google Scholar] [CrossRef]
- Zippilli, S.; Illuminati, F. Non-Markovian dynamics and steady-state entanglement of cavity arrays in finite-bandwidth squeezed reservoirs. Phys. Rev. A 2014, 89, 033803. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, Z.Y.; Liu, Z.H.; Sun, K.; Xu, J.S.; Li, C.F.; Guo, G.C.; Castellini, A.; Bellomo, B.; Compagno, G.; et al. Remote entanglement distribution in a quantum network via multinode indistinguishability of photons. Phys. Rev. A 2022, 106, 032609. [Google Scholar] [CrossRef]
- Piccolini, M.; Nosrati, F.; Morandotti, R.; Franco, R.L. Indistinguishability-Enhanced Entanglement Recovery by Spatially Localized Operations and Classical Communication. Open Syst. Inf. Dyn. 2021, 28, 2150020. [Google Scholar] [CrossRef]
- Piccolini, M.; Nosrati, F.; Compagno, G.; Livreri, P.; Morandotti, R.; Lo Franco, R. Entanglement Robustness via Spatial Deformation of Identical Particle Wave Functions. Entropy 2021, 23, 708. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; Lo Franco, R.; Maniscalco, S.; Compagno, G. Entanglement trapping in structured environments. Phys. Rev. A 2008, 78, 060302. [Google Scholar] [CrossRef]
- Adam, P.; Andreev, V.A.; Ghiu, I.; Isar, A.; Man’ko, M.A.; Man’ko, V.I. Finite phase space, Wigner functions, and tomography for two-qubit states. J. Russ. Laser Res. 2014, 35, 427. [Google Scholar] [CrossRef]
- Eberly, J.H.; Yu, T. The End of an Entanglement. Science 2007, 316, 555. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Eberly, J.H. Sudden Death of Entanglement. Science 2009, 323, 598. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Andersson, E.; Cresser, J.D.; Compagno, G. Dynamics of correlations due to a phase-noisy laser. Phys. Scr. 2012, 2012, 014004. [Google Scholar] [CrossRef]
- Nosrati, F.; Castellini, A.; Compagno, G.; Lo Franco, R. Dynamics of spatially indistinguishable particles and quantum entanglement protection. Phys. Rev. A 2020, 102, 062429. [Google Scholar] [CrossRef]
- Nosrati, F.; Castellini, A.; Compagno, G.; Franco, R.L. Robust entanglement preparation against noise by controlling spatial indistinguishability. npj Quantum Inf. 2020, 6, 39. [Google Scholar] [CrossRef]
- Aolita, L.; de Melo, F.; Davidovich, L. Open-system dynamics of entanglement: A key issues review. Rep. Prog. Phys. 2015, 78, 042001. [Google Scholar] [CrossRef]
- Mortezapour, A.; Borji, M.A.; Franco, R.L. Protecting entanglement by adjusting the velocities of moving qubits inside non-Markovian environments. Laser Phys. Lett. 2017, 14, 055201. [Google Scholar] [CrossRef]
- Franco, R.L. Nonlocality threshold for entanglement under general dephasing evolutions: A case study. Quantum Inform. Process. 2016, 15, 2393. [Google Scholar] [CrossRef]
- Aaronson, B.; Franco, R.L.; Adesso, G. Comparative investigation of the freezing phenomena for quantum correlations under nondissipative decoherence. Phys. Rev. A 2013, 88, 012120. [Google Scholar] [CrossRef]
- Jahromi, H.R. Relation between quantum probe and entanglement in n-qubit systems within Markovian and non-Markovian environments. J. Mod. Opt. 2017, 64, 1377. [Google Scholar] [CrossRef]
- Hillery, M. Conservation laws and nonclassical states in nonlinear optical systems. Phys. Rev. A 1985, 31, 338. [Google Scholar] [CrossRef] [PubMed]
- Hillery, M. Nonclassical distance in quantum optics. Phys. Rev. A 1987, 35, 725. [Google Scholar] [CrossRef]
- Hillery, M. Total noise and nonclassical states. Phys. Rev. A 1989, 39, 2994. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, O.V.; Man’ko, V.I.; Wunsche, A. Energy-sensitive and “Classical-like” Distances between Quantum States. Phys. Scr. 1999, 59, 81. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, O.V.; Man’ko, V.I.; Wunsche, A. Hilbert-Schmidt distance and non-classicality of states in quantum optics. J. Mod. Opt. 2000, 47, 633. [Google Scholar] [CrossRef]
- Boca, M.; Ghiu, I.; Marian, P.; Marian, T.A. Quantum Chernoff bound as a measure of nonclassicality for one-mode Gaussian states. Phys. Rev. A 2009, 79, 014302. [Google Scholar] [CrossRef]
- Genoni, M.G.; Paris, M.G.A.; Banaszek, K. Measure of the non-Gaussian character of a quantum state. Phys. Rev. A 2007, 76, 042327. [Google Scholar] [CrossRef]
- Genoni, M.G.; Paris, M.G.A.; Banaszek, K. Quantifying the non-Gaussian character of a quantum state by quantum relative entropy. Phys. Rev. A 2008, 78, 060303. [Google Scholar] [CrossRef]
- Ghiu, I.; Marian, P.; Marian, T.A. Loss of non-Gaussianity for damped photon-subtracted thermal states. Phys. Scr. 2014, T160, 014014. [Google Scholar] [CrossRef]
- Ghiu, I.; Marian, P.; Marian, T.A. Modification of polarization through de-Gaussification. Phys. Rev. A 2018, 98, 033826. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A Math. Gen. 2001, 34, 6899. [Google Scholar] [CrossRef]
- Adesso, G.; Ragy, S.; Lee, A.R. Continuous Variable Quantum Information: Gaussian States and Beyond. Open Syst. Inf. Dyn. 2014, 21, 1440001. [Google Scholar] [CrossRef]
- Ciccarello, F.; Giovannetti, V. Local-channel-induced rise of quantum correlations in continuous-variable systems. Phys. Rev. A 2012, 85, 022108. [Google Scholar] [CrossRef]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Modi, K. A Pedagogical Overview of Quantum Discord. Open Syst. Inf. Dyn. 2014, 21, 1440006. [Google Scholar] [CrossRef]
- Marian, P.; Ghiu, I.; Marian, T.A. Decay of Gaussian correlations in local thermal reservoirs. Phys. Scr. 2015, 90, 074041. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.Y.; Wang, J.C.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762–764, 1. [Google Scholar] [CrossRef]
- Ma, J.; Yadin, B.; Girolami, D.; Vedral, V.; Gu, M. Converting Coherence to Quantum Correlations. Phys. Rev. Lett. 2016, 116, 160407. [Google Scholar] [CrossRef]
- Hu, M.L.; Fan, H. Relative quantum coherence, incompatibility, and quantum correlations of states. Phys. Rev. A 2017, 95, 052106. [Google Scholar] [CrossRef]
- Xu, X.X.; Hu, M.L. Maximal Steered Coherence and Its Conversion to Entanglement in Multiple Bosonic Reservoirs. Ann. Phys. 2022, 534, 2100412. [Google Scholar] [CrossRef]
- Sun, K.; Liu, Z.H.; Wang, Y.; Hao, Z.Y.; Xu, X.Y.; Xu, J.S.; Li, C.F.; Guo, G.C.; Castellini, A.; Lami, L.; et al. Activation of indistinguishability-based quantum coherence for enhanced metrological applications with particle statistics imprint. Proc. Natl. Acad. Sci. 2022, 119, e2119765119. [Google Scholar] [CrossRef] [PubMed]
- Cakmak, B.; Pezzutto, M.; Paternostro, M.; Mustecaplıoglu, O.E. Non-Markovianity, coherence, and system-environment correlations in a long-range collision model. Phys. Rev. A 2017, 96, 022109. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J.; Lo Franco, R. Cavity-based architecture to preserve quantum coherence and entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef]
- Bruss, D.; DiVincenzo, D.P.; Ekert, A.; Fuchs, C.A.; Macchiavello, C.; Smolin, J.A. Optimal universal and state-dependent quantum cloning. Phys. Rev. A 1998, 57, 2368. [Google Scholar] [CrossRef]
- Buzek, V.; Vedral, V.; Plenio, M.B.; Knight, P.L.; Hillery, M. Broadcasting of entanglement via local copying. Phys. Rev. A 1997, 55, 3327. [Google Scholar] [CrossRef]
- Cerf, N.J. Pauli cloning of a quantum bit. Phys. Rev. Lett. 2000, 84, 4497. [Google Scholar] [CrossRef]
- Cerf, N.J. Asymmetric quantum cloning in any dimension. J. Mod. Opt. 2000, 47, 187. [Google Scholar] [CrossRef]
- Cerf, N.J.; Bourennane, M.; Karlsson, A.; Gisin, N. Optimal Eavesdropping in Cryptography with Three-Dimensional Quantum States. Phys. Rev. Lett. 2002, 88, 127901. [Google Scholar]
- Bourennane, M.; Karlsson, A.; Bjork, G.; Gisin, N.; Cerf, N.J. Quantum key distribution using multilevel encoding: Security analysis. J. Phys. A 2002, 35, 10065. [Google Scholar] [CrossRef]
- Fan, H.; Wang, Y.-N.; Jing, L.; Yue, J.-D.; Shi, H.-D.; Zhang, Y.-L.; Mu, L.-Z. Quantum cloning machines and the applications. Phys. Rep. 2014, 544, 241. [Google Scholar] [CrossRef]
- Ghiu, I. Asymmetric quantum telecloning of d-level systems and broadcasting of entanglement to different locations using the “many-to-many” communication protocol. Phys. Rev. A 2003, 67, 012323. [Google Scholar] [CrossRef]
- Ghiu, I.; Karlsson, A. Broadcasting of entanglement at a distance using linear optics and telecloning of entanglement. Phys. Rev. A 2005, 72, 032331. [Google Scholar] [CrossRef]
- Jain, A.; Chakrabarty, I.; Chatterjee, S. Asymmetric broadcasting of quantum correlations. Phys. Rev. A 2019, 99, 022315. [Google Scholar] [CrossRef]
- Peres, A. Separability criterion for density matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1. [Google Scholar] [CrossRef]
- Li, B.; Wang, Z.X.; Fei, S.M. Quantum discord and geometry for a class of two-qubit states. Phys. Rev. A 2011, 83, 022321. [Google Scholar] [CrossRef]
- Rau, A.R.P. Algebraic characterization of X-states in quantum information. J. Phys. A Math. Theor. 2009, 42, 412002. [Google Scholar] [CrossRef]
- Grimaudo, R.; Isar, A.; Mihaescu, T.; Ghiu, I.; Messina, A. Dynamics of quantum discord of two coupled spin-1/2’s subjected to time-dependent magnetic fields. Results Phys. 2019, 13, 102147. [Google Scholar] [CrossRef]
- Ghiu, I.; Grimaudo, R.; Mihaescu, T.; Isar, A.; Messina, A. Quantum correlation dynamics in controlled two-coupled-qubit systems. Entropy 2020, 22, 785. [Google Scholar] [CrossRef] [PubMed]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum Inf. Comput. 2001, 1, 27. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Evolution from Entanglement to Decoherence of Bipartite Mixed X States. Quantum Inf. Comput. 2007, 7, 459. [Google Scholar]
- Sabapathy, K.K.; Simon, R. Quantum discord for two-qubit X-states: A comprehensive approach inspired by classical polarization optics. arXiv 2013, arXiv:1311.0210. [Google Scholar]
- Huang, Y. Quantum discord for two-qubit X states: Analytical formula with very small worst-case error. Phys. Rev. A 2013, 88, 014302. [Google Scholar] [CrossRef]
- Yurischev, M.A. On the quantum discord of general X states. Quantum Inf. Process. 2015, 14, 3399. [Google Scholar] [CrossRef]
- Celeri, L.C.; Maziero, J. The Sudden Change Phenomenon of Quantum Discord. In Lectures on General Quantum Correlations and Their Applications; Fanchini, F.F., Soares Pinto, D.O., Adesso, G., Eds.; Springer: Cham, Switzerland, 2017; pp. 309–337. [Google Scholar]
- Pei, P.; Wang, W.; Li, C.; Song, H.-S. Using Nonlocal Coherence to Quantify Quantum Correlation. Int. J. Theor. Phys. 2012, 51, 3350. [Google Scholar] [CrossRef]
- Fano, U. Description of States in Quantum Mechanics by Density Matrix and Operator Techniques. Rev. Mod. Phys. 1957, 29, 74. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cîrneci, C.; Ghiu, I. Analysis of Quantum Correlations Obtained Using Local Optimal Universal Asymmetric Cloners. Entropy 2023, 25, 29. https://doi.org/10.3390/e25010029
Cîrneci C, Ghiu I. Analysis of Quantum Correlations Obtained Using Local Optimal Universal Asymmetric Cloners. Entropy. 2023; 25(1):29. https://doi.org/10.3390/e25010029
Chicago/Turabian StyleCîrneci, Cătălina, and Iulia Ghiu. 2023. "Analysis of Quantum Correlations Obtained Using Local Optimal Universal Asymmetric Cloners" Entropy 25, no. 1: 29. https://doi.org/10.3390/e25010029
APA StyleCîrneci, C., & Ghiu, I. (2023). Analysis of Quantum Correlations Obtained Using Local Optimal Universal Asymmetric Cloners. Entropy, 25(1), 29. https://doi.org/10.3390/e25010029






