ImputeGAN: Generative Adversarial Network for Multivariate Time Series Imputation
Abstract
1. Introduction
- We propose a GAN-based neural network for complementation that uses a generative approach to generate complementary data and judge them with a discriminator that can handle continuously missing data more effectively.
- In contrast to other GAN-based methods of complementation, imputeGAN ensures that the complementation values are reasonable through an iterative strategy.
- The generalizability of the model is ensured with a carefully designed training framework.
2. Related Work
3. Preliminary
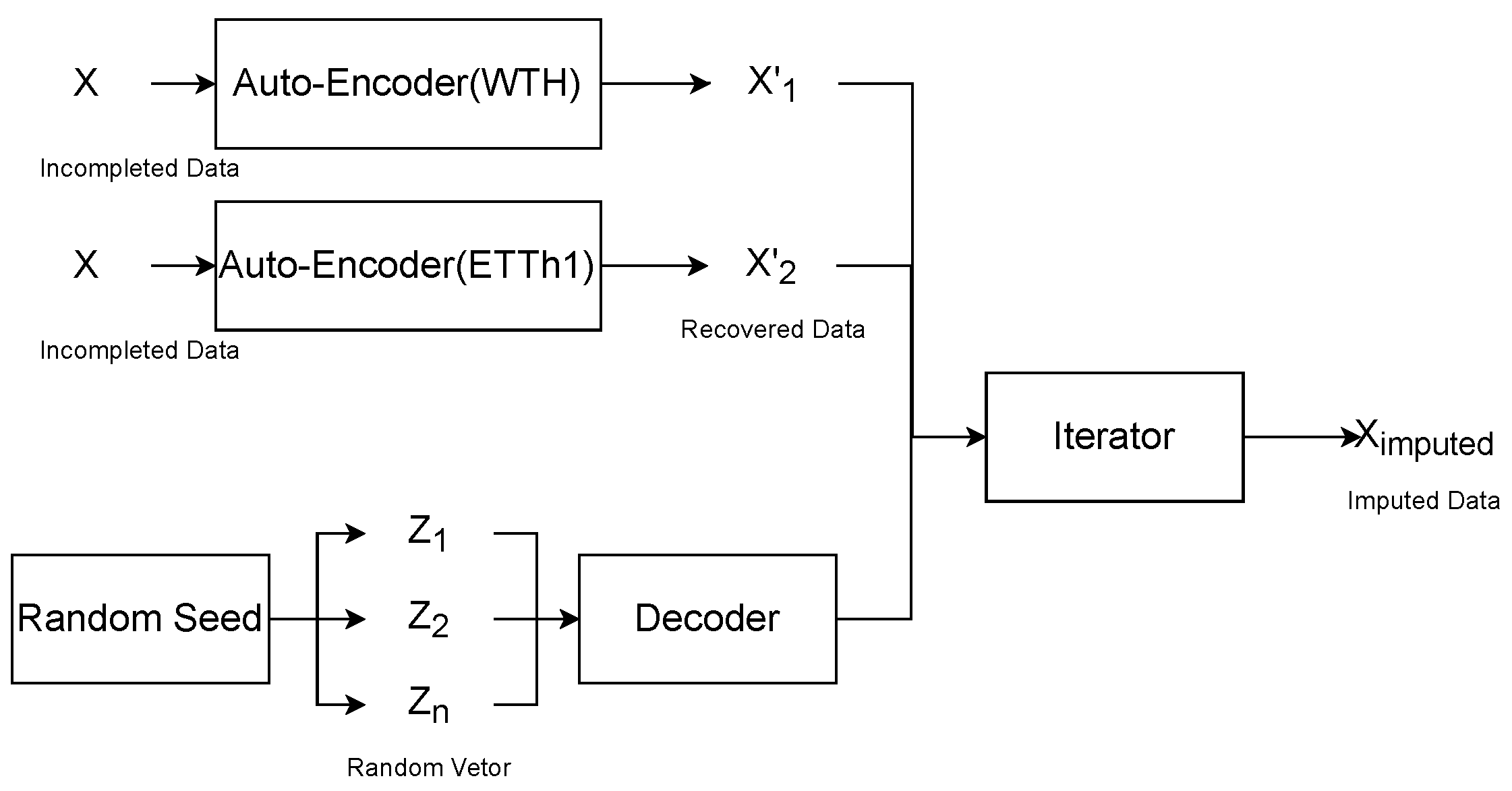
4. Proposed Method
4.1. Encoder Network Architecture
4.2. Decoder Network Architecture
4.3. Iteration Strategy
4.4. Imputation Results
4.5. Discussion
5. Experimental Evaluation
5.1. Datasets, Tasks, and Baseline
- LSTnet [36]: uses a CNN and an RNN to predict time series data.
- LSTMa [37]: adds an automatic search strategy to the encoder–decoder architecture.
- Reformer [38]: improves transformer efficiency by locally sensitive hashing self-attention.
- LogTrans [39]: the LogSparse transformer improves transformer efficiency by using a heuristic method.
- Informer [23]: improves transformer efficiency with ProbSparse self-attention.
5.2. Implementation Details
5.3. Performance Comparison of Downstream Task
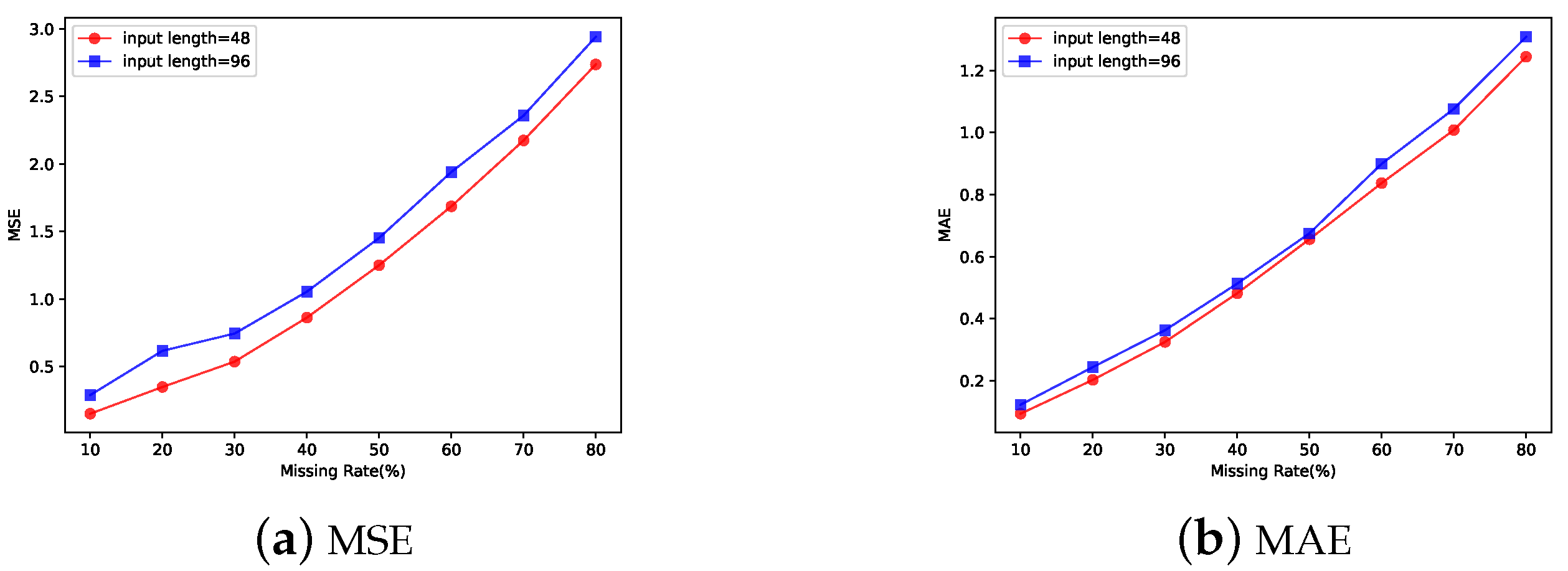
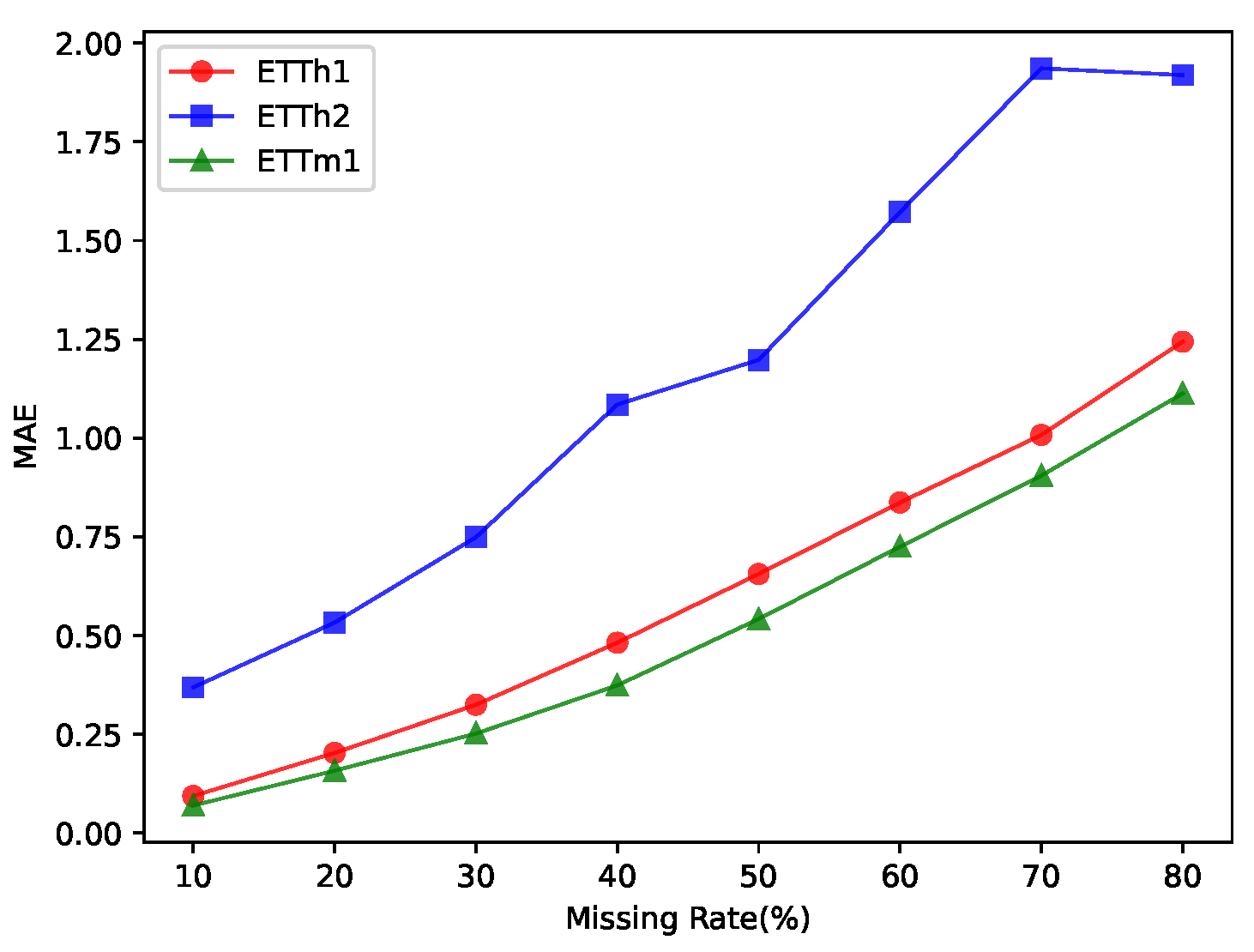
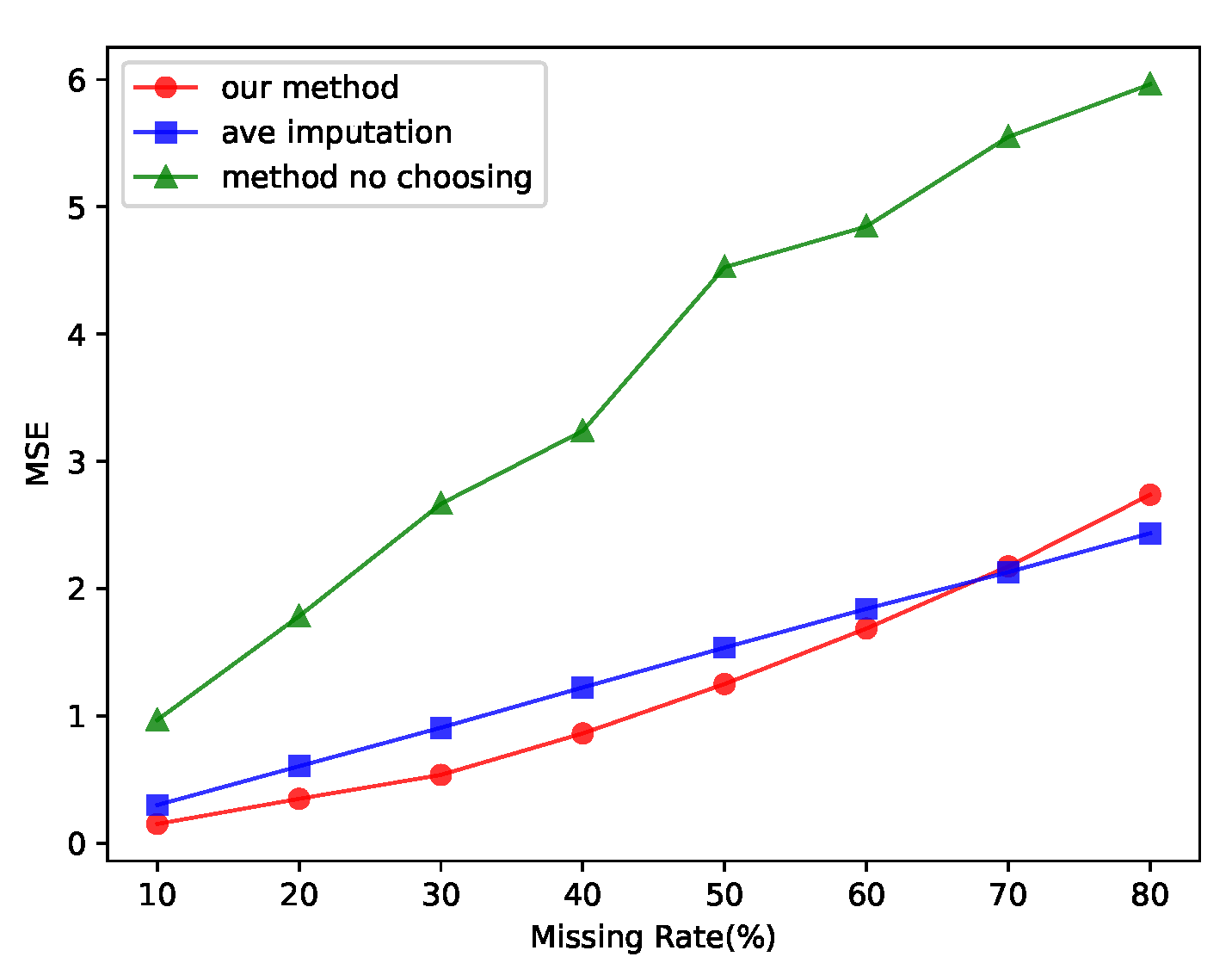
5.4. Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- de Jong, J.; Emon, M.A.; Wu, P.; Karki, R.; Sood, M.; Godard, P.; Ahmad, A.; Vrooman, H.; Hofmann-Apitius, M.; Fröhlich, H. Deep learning for clustering of multivariate clinical patient trajectories with missing values. GigaScience 2019, 8, giz134. [Google Scholar] [CrossRef] [PubMed]
- Azoff, E.M. Neural Network Time Series Forecasting of Financial Markets; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic Flow Prediction With Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Berglund, M.; Raiko, T.; Honkala, M.; Kärkkäinen, L.; Vetek, A.; Karhunen, J.T. Bidirectional Recurrent Neural Networks as Generative Models. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28. [Google Scholar]
- Gill, M.K.; Asefa, T.; Kaheil, Y.; McKee, M. Effect of missing data on performance of learning algorithms for hydrologic predictions: Implications to an imputation technique. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Kantardzic, M. Data Mining: Concepts, Models, Methods, and Algorithms; John Wiley & Sons: New York, NY, USA, 2011; Chapter 5; pp. 140–168. [Google Scholar]
- Amiri, M.; Jensen, R. Missing data imputation using fuzzy-rough methods. Neurocomputing 2016, 205, 152–164. [Google Scholar] [CrossRef]
- Purwar, A.; Singh, S.K. Hybrid prediction model with missing value imputation for medical data. Expert Syst. Appl. 2015, 42, 5621–5631. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote. Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
- Acar, E.; Dunlavy, D.M.; Kolda, T.G.; Mørup, M. Scalable Tensor Factorizations with Missing Data. In Proceedings of the SDM10: 2010 SIAM International Conference on Data Mining, Columbus, Ohio, USA, 29 April–1 May 2010; pp. 701–712. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Jiang, S.H.; Zhou, C.; Huang, J.; Guo, Z. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 2020, 17, 2919–2930. [Google Scholar] [CrossRef]
- Song, S.; Sun, Y.; Zhang, A.; Chen, L.; Wang, J. Enriching Data Imputation under Similarity Rule Constraints. IEEE Trans. Knowl. Data Eng. 2020, 32, 275–287. [Google Scholar] [CrossRef]
- Breve, B.; Caruccio, L.; Deufemia, V.; Polese, G. RENUVER: A Missing Value Imputation Algorithm based on Relaxed Functional Dependencies. In Proceedings of the EDBT, Edinburgh, UK, 29 March–1 April 2022. [Google Scholar]
- Rekatsinas, T.; Chu, X.; Ilyas, I.F.; Ré, C. HoloClean: Holistic Data Repairs with Probabilistic Inference. Proc. VLDB Endow. 2017, 10, 1190–1201. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.A.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Wang, D.; Li, J.; Zhou, H.; Li, L.; Li, Y. BRITS: Bidirectional Recurrent Imputation for Time Series. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Yoon, J.; Zame, W.R.; van der Schaar, M. Estimating Missing Data in Temporal Data Streams Using Multi-Directional Recurrent Neural Networks. IEEE Trans. Biomed. Eng. 2019, 66, 1477–1490. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Cai, X.; ZHANG, Y.; Xu, J.; xiaojie, Y. Multivariate Time Series Imputation with Generative Adversarial Networks. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Luo, Y.; Zhang, Y.; Cai, X.; Yuan, X. E2GAN: End-to-End Generative Adversarial Network for Multivariate Time Series Imputation. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, Macao, China, 10–16 August 2019; pp. 3094–3100. [Google Scholar] [CrossRef]
- Yoon, J.; Jordon, J.; van der Schaar, M. GAIN: Missing Data Imputation using Generative Adversarial Nets. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5689–5698. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.u.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Schafer, J.; Graham, J. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef] [PubMed]
- Torgo, L. Data Mining with R: Learning with Case Studies, 2nd ed.; Chapman and Hall/CRC: London, UK, 2017. [Google Scholar]
- Chen, C.W.S.; Chiu, L.M. Ordinal Time Series Forecasting of the Air Quality Index. Entropy 2021, 23, 1167. [Google Scholar] [CrossRef] [PubMed]
- Sportisse, A.; Boyer, C.; Josse, J. Imputation and low-rank estimation with Missing Non At Random data. Stat. Comput. 2018, 30, 1629–1643. [Google Scholar] [CrossRef]
- Tang, F.; Ishwaran, H. Random forest missing data algorithms. Stat. Anal. Data Min. ASA Data Sci. J. 2017, 10, 363–377. [Google Scholar] [CrossRef] [PubMed]
- Suo, Q.; Yao, L.; Xun, G.; Sun, J.; Zhang, A. Recurrent Imputation for Multivariate Time Series with Missing Values. In Proceedings of the 2019 IEEE International Conference on Healthcare Informatics (ICHI), Xi’an, China, 10–13 June 2019; pp. 1–3. [Google Scholar]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock Price Prediction Using the ARIMA Model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 106–112. [Google Scholar]
- Kalekar, P.S. Time series forecasting using holt-winters exponential smoothing. Kanwal Rekhi Sch. Inf. Technol. 2004, 4329008, 1–13. [Google Scholar]
- Samal, K.K.R.; Babu, K.S.; Das, S.K.; Acharaya, A. Time series based air pollution forecasting using SARIMA and prophet model. In Proceedings of the 2019 International Conference on Information Technology and Computer Communications, Singapore, 16–18 August 2019; pp. 80–85. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the International Conference on Learning Representations (ICLR ’18), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated Residual Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 636–644. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. arXiv 2018, arXiv:1703.07015. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. In Proceedings of the 33rd International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]


| MCAR | MAR | MNAR | Generative | Iterative | |
|---|---|---|---|---|---|
| Mean/last/mode imputation | ✓ | ✓ | ✕ | ✕ | ✕ |
| KNN | ✓ | ✓ | ✕ | ✕ | ✕ |
| Matrix factorization | ✓ | ✓ | ✕ | ✕ | ✕ |
| BRITS | ✓ | ✓ | ✓ | ✕ | ✕ |
| M-RNN | ✓ | ✓ | ✓ | ✕ | ✕ |
| GAIN | ✓ | ✓ | ✓ | ✓ | ✕ |
| GAN-2-stage | ✓ | ✓ | ✓ | ✓ | ✕ |
| GAN | ✓ | ✓ | ✓ | ✓ | ✕ |
| imputeGAN | ✓ | ✓ | ✓ | ✓ | ✓ |
| Dataset | Features | Samples | Missing Rate | Interval Time |
|---|---|---|---|---|
| ETTh1 | 7 | 17,420 | 1% | 1 h |
| ETTh2 | 7 | 17,420 | 10% | 1 h |
| ETTm1 | 7 | 69,680 | 1% | 15 min |
| ECL | 321 | 26,280 | 1% | 1 h |
| Weather | 12 | 35,040 | 5% | 1 h |
| Methods | Informer | LogTrans | Reformer | LSTMa | LSTnet | Our Method | Average | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| ETTh1 | 24 | 0.577 | 0.549 | 0.686 | 0.604 | 0.991 | 0.754 | 0.650 | 0.624 | 1.293 | 0.901 | 1.250 | 0.656 | 1.536 | 0.744 |
| 48 | 0.685 | 0.625 | 0.766 | 0.757 | 1.313 | 0.906 | 0.702 | 0.675 | 1.456 | 0.960 | 1.452 | 0.675 | |||
| 168 | 0.931 | 0.752 | 1.002 | 0.846 | 1.824 | 1.138 | 1.212 | 0.867 | 1.997 | 1.214 | 1.491 | 0.636 | |||
| 336 | 1.128 | 0.873 | 1.362 | 0.952 | 2.117 | 1.280 | 1.424 | 0.994 | 2.655 | 1.369 | 1.996 | 0.659 | |||
| 720 | 1.215 | 0.896 | 1.397 | 1.291 | 2.415 | 1.520 | 1.960 | 1.322 | 2.143 | 1.380 | 2.818 | 0.769 | |||
| ETTh2 | 24 | 0.720 | 0.665 | 0.828 | 0.750 | 1.531 | 1.613 | 1.143 | 0.813 | 2.742 | 1.457 | 5.288 | 1.198 | 3.071 | 1.005 |
| 48 | 1.457 | 1.001 | 1.806 | 1.034 | 1.871 | 1.735 | 1.671 | 1.221 | 3.567 | 1.687 | 5.835 | 1.312 | |||
| 168 | 3.489 | 1.515 | 4.070 | 1.681 | 4.660 | 1.846 | 4.117 | 1.674 | 3.242 | 2.513 | 5.732 | 1.236 | |||
| 336 | 2.723 | 1.340 | 3.875 | 1.763 | 4.028 | 1.688 | 3.434 | 1.549 | 2.544 | 2.591 | 7.375 | 1.327 | |||
| 720 | 3.467 | 1.473 | 3.913 | 1.552 | 5.381 | 2.015 | 3.963 | 1.788 | 4.625 | 3.709 | 9.934 | 7.705 | |||
| ETTm1 | 24 | 0.323 | 0.369 | 0.419 | 0.412 | 0.724 | 0.607 | 0.621 | 0.629 | 1.968 | 1.170 | 0.909 | 0.542 | 1.527 | 0.740 |
| 48 | 0.494 | 0.503 | 0.507 | 0.583 | 1.098 | 0.777 | 1.392 | 0.939 | 1.999 | 1.215 | 0.977 | 0.55 | |||
| 96 | 0.678 | 0.614 | 0.768 | 0.792 | 1.433 | 0.945 | 1.339 | 0.913 | 2.762 | 1.542 | 1.068 | 0.575 | |||
| 288 | 1.056 | 0.786 | 1.462 | 1.320 | 1.820 | 1.094 | 1.740 | 1.124 | 1.257 | 2.076 | 1.458 | 0.690 | |||
| 672 | 1.192 | 0.926 | 1.669 | 1.461 | 2.187 | 1.232 | 2.736 | 1.555 | 1.917 | 2.941 | 1.375 | 0.659 | |||
| Weather | 24 | 0.335 | 0.381 | 0.435 | 0.477 | 0.655 | 0.583 | 0.546 | 0.570 | 0.615 | 0.545 | 3.750 | 0.858 | 4.531 | 1.213 |
| 48 | 0.395 | 0.459 | 0.426 | 0.495 | 0.729 | 0.666 | 0.829 | 0.677 | 0.660 | 0.589 | 3.438 | 0.854 | |||
| 168 | 0.608 | 0.567 | 0.727 | 0.671 | 1.318 | 0.855 | 1.038 | 0.835 | 0.748 | 0.647 | 4.120 | 0.884 | |||
| 336 | 0.702 | 0.620 | 0.754 | 0.670 | 1.930 | 1.167 | 1.657 | 1.059 | 0.782 | 0.683 | 3.906 | 0.861 | |||
| 720 | 0.831 | 0.731 | 0.885 | 0.773 | 2.726 | 1.575 | 1.536 | 1.109 | 0.851 | 0.757 | 3.997 | 0.912 | |||
| ECL | 48 | 0.344 | 0.393 | 0.355 | 0.418 | 1.404 | 0.999 | 0.486 | 0.572 | 0.369 | 0.445 | 1.118 | 0.619 | 5.993 | 1.498 |
| 168 | 0.368 | 0.424 | 0.368 | 0.432 | 1.515 | 1.069 | 0.574 | 0.602 | 0.394 | 0.476 | 1.22 | 0.643 | |||
| 336 | 0.381 | 0.431 | 0.373 | 0.439 | 1.601 | 1.104 | 0.886 | 0.795 | 0.419 | 0.477 | 1.205 | 0.622 | |||
| 720 | 0.406 | 0.443 | 0.409 | 0.454 | 2.009 | 1.170 | 1.676 | 1.095 | 0.556 | 0.565 | 1.352 | 0.664 | |||
| 960 | 0.460 | 0.548 | 0.477 | 0.589 | 2.141 | 1.387 | 1.591 | 1.128 | 0.605 | 0.599 | 1.002 | 0.571 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, R.; Wang, Y. ImputeGAN: Generative Adversarial Network for Multivariate Time Series Imputation. Entropy 2023, 25, 137. https://doi.org/10.3390/e25010137
Qin R, Wang Y. ImputeGAN: Generative Adversarial Network for Multivariate Time Series Imputation. Entropy. 2023; 25(1):137. https://doi.org/10.3390/e25010137
Chicago/Turabian StyleQin, Rui, and Yong Wang. 2023. "ImputeGAN: Generative Adversarial Network for Multivariate Time Series Imputation" Entropy 25, no. 1: 137. https://doi.org/10.3390/e25010137
APA StyleQin, R., & Wang, Y. (2023). ImputeGAN: Generative Adversarial Network for Multivariate Time Series Imputation. Entropy, 25(1), 137. https://doi.org/10.3390/e25010137






