Prescribed Performance Back-Stepping Tracking Control for a Class of High-Order Nonlinear Systems via a Disturbance Observer
Abstract
1. Introduction
- (1)
- The proposed composite controller solves the output tracking problem of a class of high-order nonlinear systems, where the system states are stabilized and the tracking error converges to zero.
- (2)
- (3)
- Without the external disturbances, the nominal control performance of the proposed protocol remained.
- (4)
2. Problem Formulation and Preliminaries
2.1. Problem Formulation
- The tracking error converges to zero and achieves the prescribed performance in both transient state and steady state.
- All states in the closed-loop system are stable.
- (i)
- p is considered as
- (ii)
- satisfies: .
- (i)
- and the derivatives of are bounded, and are nonvanishing.
- (ii)
- as
2.2. Prescribed Performance
- (i)
- (ii)
2.3. Disturbance Observer
3. Main Results
3.1. Composite Controller
3.2. Stability Analysis
3.3. Prescribed Performance and Convergence Analysis
- (i)
- the disturbance estimation error asymptotically converge to zero;
- (ii)
- the tracking error satisfies
- (iii)
- the prescribed performance (3) is guaranteed.
- which implies that
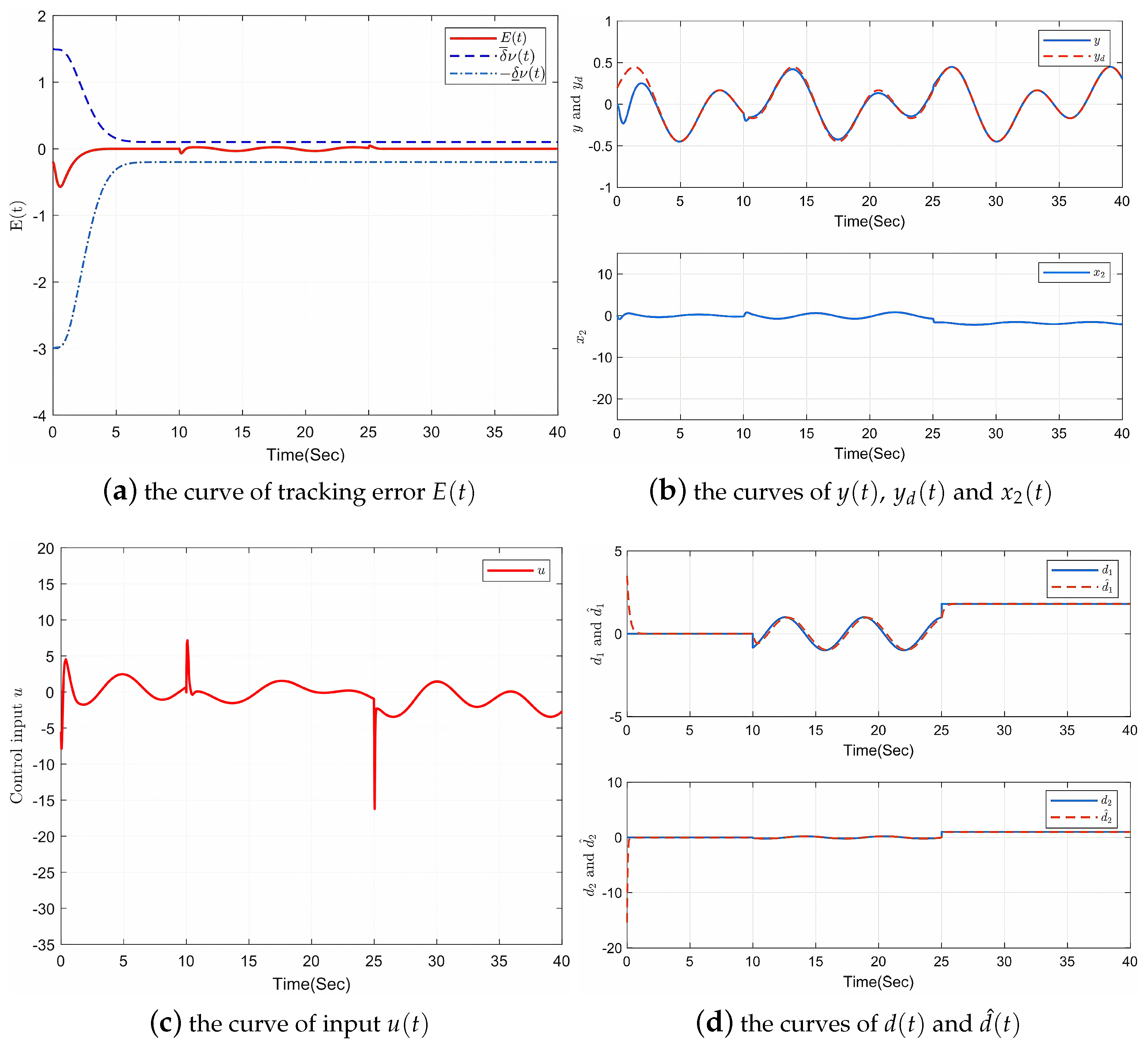
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, B.; Calise, A. Nonlinear flight control using neural networks. J. Guid. Control Dynam. 1997, 20, 26–33. [Google Scholar] [CrossRef]
- Nijmeijer, H.; Van der Schaft, A. Nonlinear Dynamical Control Systems, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Liu, C.; Liu, X.; Wang, H.; Lu, S.; Zhou, Y. Adaptive control and application for nonlinear systems with input nonlinearities and unknown virtual control coefficients. IEEE Trans. Cybern. 2022, 52, 8804–8817. [Google Scholar] [CrossRef] [PubMed]
- Oishi, Y.; Sakamoto, N. Optimal Sampled-Data Control of a Nonlinear System. arXiv 2021, arXiv:2112.145072021. [Google Scholar]
- Kawan, C.; Mironchenko, A.; Swikir, A.; Noroozi, N.; Zamani, M. A Lyapunov-based small-gain theorem for infinite networks. IEEE Trans. Autom. Control 2021, 66, 5830–5844. [Google Scholar] [CrossRef]
- Sontag, E. Stabilization implies coprime factorization. IEEE Trans. Autom. Control 1989, 34, 435–443. [Google Scholar] [CrossRef]
- Yu, P.; Qi, D.; Sun, Y.; Wan, F. Stability analysis of impulsive stochastic delayed Cohen-Grossberg neural networks driven by Levy noise. Appl. Math. Comput. 2022, 434, 127444. [Google Scholar] [CrossRef]
- He, D.; Huang, H. Input-to-state stability of efficient robust H∞ MPC scheme for nonlinear systems. Inf. Sci. 2015, 292, 111–124. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Z.; Zhang, Y.; Philip Chen, C. Adaptive neural inverse optimal tracking control for uncertain multi-agent systems. Inf. Sci. 2022, 584, 31–49. [Google Scholar] [CrossRef]
- Pu, Z.; Rao, R. LMI-based criterion on stochastic ISS property of delayed high-order neural networks with explicit gain function and simply event-triggered mechanism. Neurocomputing 2020, 377, 57–63. [Google Scholar] [CrossRef]
- Nekhoroshikh, A.; Eflmov, D.; Fridman, E.; Perruquetti, W.; Furtat, L.; Polyakov, A. Practical fixed-time ISS of neutral time-delay systems with application to stabilization by using delays. Automatica 2022, 143, 110455. [Google Scholar] [CrossRef]
- Mancilla-Aguilar, J.; Haimovich, H. (Integral-)ISS of switched and time-varying impulsive systems based on global state weak linearization. IEEE Trans. Autom. Control 2021, 67, 6918–6925. [Google Scholar] [CrossRef]
- Gao, L.; Liu, Z.; Wang, S.; Qu, M.; Zhang, M. Input-to-state stability for discrete hybrid time-delay systems with admissible edge-dependent average dwell time. J. Franklin Inst. 2021. [Google Scholar] [CrossRef]
- Gong, Y.; Guo, Y.; Ma, G.; Ran, G.; Li, D. Predefined-time tracking control for high-order nonlinear systems with control saturation. Int. J. Robust Nonlinear Control 2022, 32, 6218–6235. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Cheng, D. Output tracking of Boolean control networks. IEEE Trans. Autom. Control 2019, 65, 2730–2735. [Google Scholar] [CrossRef]
- Wu, C.; Pan, W.; Sun, G.; Liu, J.; Wu, L. Learning tracking control for cyber-physical systems. IEEE Internet Things J. 2021, 8, 9151–9163. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, S.; Jiang, H.; Hu, C. Distributed consensus for multi-agent systems via adaptive sliding mode control. Int. J. Robust Nonlinear Control 2021, 31, 7125–7151. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Ma, D. Output regulation for switched systems with multiple disturbances. IEEE Trans. Circuits Syst. Regul. Pap. 2020, 67, 5326–5335. [Google Scholar] [CrossRef]
- Liu, S.; Feng, J.; Wang, Q.; Song, W. Adaptive consensus control for a class of nonlinear multi-agent systems with unknown time delays and external disturbances. Trans. Inst. Meas. Control 2022, 44, 2063–2075. [Google Scholar] [CrossRef]
- Huang, J.; Chen, Z. A general framework for tackling the output regulation problem. IEEE Trans. Autom. Control 2004, 49, 2203–2218. [Google Scholar] [CrossRef]
- Back, J.; Shim, H. Adding robustness to nominal output-feedback controllers for uncertain nonlinear systems: A nonlinear version of disturbance observer. Automatica 2008, 44, 2528–2537. [Google Scholar] [CrossRef]
- Wang, W.; Guo, P.; Hu, C.; Zhu, L. High-performance control of fast tool servos with robust disturbance observer and modified H∞ control. Mechatronics 2022, 84, 102781. [Google Scholar]
- Santina, C.; Turby, R.; Rus, D. Data-driven disturbance observers for estimating external forces on soft robots. IEEE Robot. Autom. Lett. 2020, 5, 5717–5724. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Shen, G.; Sun, Z.; Xia, Y. Disturbance observer based adaptive fuzzy sliding mode control: A dynamic sliding surface approach. Automatica 2021, 129, 109606. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, W. Disturbance-observer-based finite-time adaptive fuzzy control for non-triangular switched nonlinear systems with input saturation. Inf. Sci. 2021, 561, 152–167. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.; Kanellakopoulos, I. Nonlinear and Adaptive Control Design; John Wiley & Sons, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Wang, J.; Rong, J.; Lu, L. Reduced-order extended state observer based event-triggered sliding mode control for DC-DC buck converter system with parameter perturbation. Asian J. Control 2020, 23, 1591–1601. [Google Scholar] [CrossRef]
- Bechlioulis, C.; Rovithakis, G. Prescribed performance adaptive control of SISO feedback linearizable systems with disturbances. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008. [Google Scholar]
- Bechlioulis, C.; Rovithakis, G. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Fu, D.; Yin, H.; Huang, J. Controlling an uncertain mobile robot with prescribed performance. Nonlinear Dyn. 2021, 5, 2347–2362. [Google Scholar] [CrossRef]
- Bai, W.; Wang, H. Robust adaptive fault-tolerant tracking control for a class of high-order nonlinear system with finite-time prescribed performance. Int. J. Robust Nonlinear Control 2020, 30, 4708–4725. [Google Scholar] [CrossRef]
- Chen, L.; Yang, H. Adaptive neural prescribed performance output feedback control of pure feedback nonlinear systems using disturbance observer. Int. J. Adapt. Control 2020, 34, 520–542. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, S.; Liu, X. H∞ synchronization and robust H∞ synchronization of coupled neural networks with non-identical nodes. Neural Process. Lett. 2021, 53, 3467–3496. [Google Scholar] [CrossRef]
- Gao, F.; Chen, W. Disturbance rejection in singular time-delay systems with external disturbances. Int. J. Control Autom. 2022, 20, 1841–1848. [Google Scholar] [CrossRef]
- Chen, F.; Dimarogonas, D. Leader-follower formation control with prescribed performance guarantees. IEEE Trans. Control Netw. 2020, 8, 450–461. [Google Scholar] [CrossRef]
- Vidyasagar, M. Nonlinear Systems Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Yang, B.; Lin, W. Homogeneous observers, iterative design and global stabilization of high-order nonlinear systems by smooth output feedback. IEEE Trans. Autom. Control 2004, 49, 1069–1080. [Google Scholar] [CrossRef]
- Qian, C.; Lin, W. Non-lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization. Syst. Control Lett. 2001, 42, 185–200. [Google Scholar] [CrossRef]
- Ho, H.; Wong, Y.; Rad, A. Adaptive fuzzy approach for a class of uncertain nonlinear systems in strict-feedback form. ISA Trans. 2008, 47, 286–299. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Jiang, H. Prescribed Performance Back-Stepping Tracking Control for a Class of High-Order Nonlinear Systems via a Disturbance Observer. Entropy 2023, 25, 103. https://doi.org/10.3390/e25010103
Tang X, Jiang H. Prescribed Performance Back-Stepping Tracking Control for a Class of High-Order Nonlinear Systems via a Disturbance Observer. Entropy. 2023; 25(1):103. https://doi.org/10.3390/e25010103
Chicago/Turabian StyleTang, Xinrui, and Haijun Jiang. 2023. "Prescribed Performance Back-Stepping Tracking Control for a Class of High-Order Nonlinear Systems via a Disturbance Observer" Entropy 25, no. 1: 103. https://doi.org/10.3390/e25010103
APA StyleTang, X., & Jiang, H. (2023). Prescribed Performance Back-Stepping Tracking Control for a Class of High-Order Nonlinear Systems via a Disturbance Observer. Entropy, 25(1), 103. https://doi.org/10.3390/e25010103




