The Cryptocurrency Market in Transition before and after COVID-19: An Opportunity for Investors?
Abstract
1. Introduction
- RQ1. Is there evidence of the existence of noise and trend effects in the cryptocurrency market? If yes, how do noise and trend effects influence the interactions between cryptocurrencies? What does the network structure of these cryptocurrencies look like after removing noise and trend effects?
- RQ2. Does the network structure change when the level of granularity changes? If this is the case, what level of granularity should we use to obtain the true network structure?
- RQ3. Is there evidence that historical events such as the COVID-19 pandemic and the global downturn in 2020 changed the overall cryptocurrency network structure? If this is the case, how did they change it? Moreover, is there any possibility that this change was caused by a change in investors’ investment strategy? In other words, does the way investors react to a downturn change the interactions between cryptocurrencies?
2. Related Works
2.1. Correlation-Based Analysis in the Financial Markets
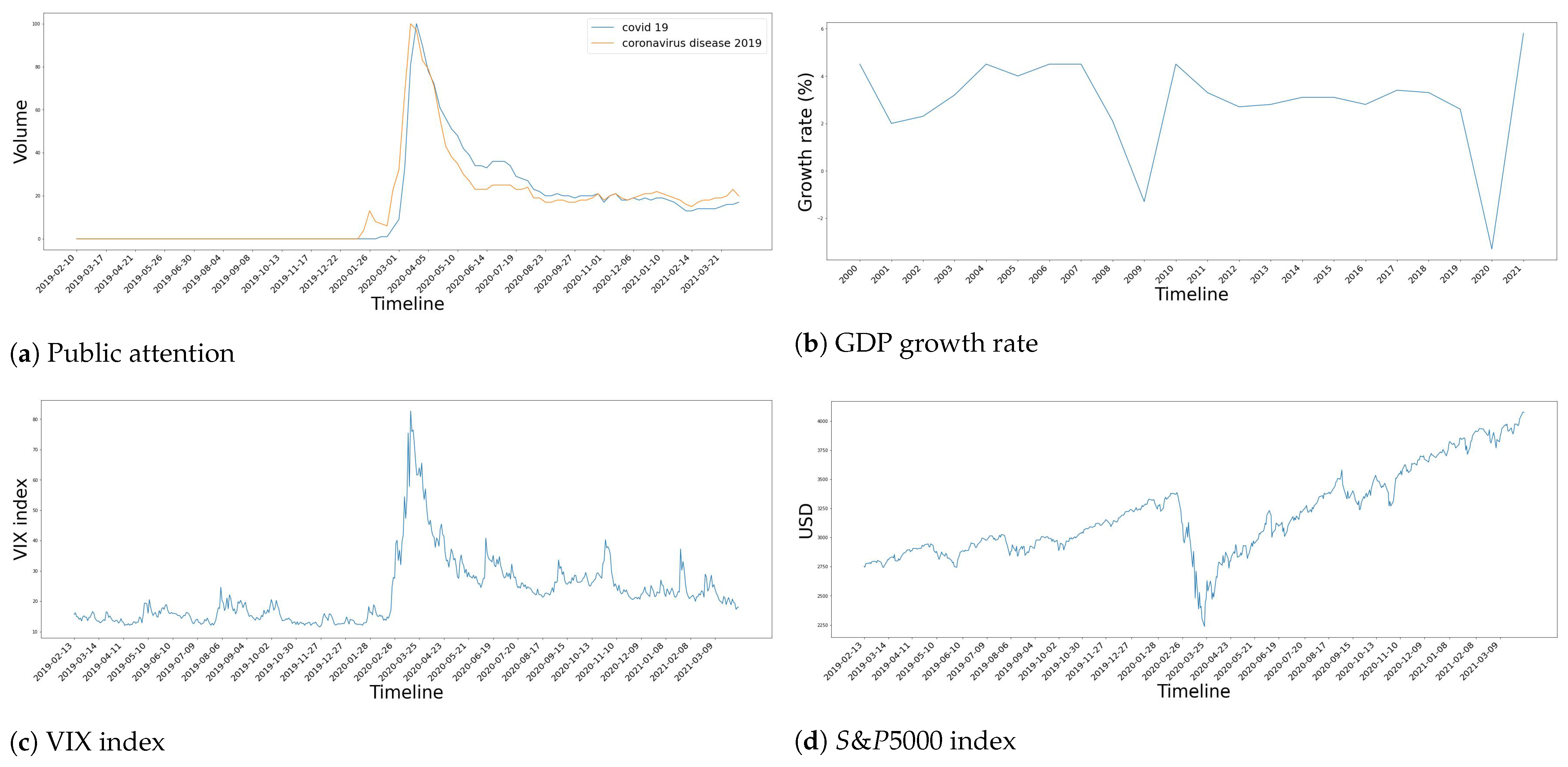
2.2. How the COVID-19 Pandemic Intervened on the Economy Worldwide
3. Data Description
3.1. A Note on Data Sampling and Missing Data
3.2. Aggregational Gaussianity
4. Research Methodology
4.1. Correlation Matrix Based on Pearson Coefficients and Random Matrix Theory
- Firstly, we make use of cryptocurrency returns in order to retain the statistical nature of the associated time series. While some authors have proposed addressing the nonlinearity problem (e.g., Spearman [59] and Kendall [53]), these have the disadvantage of converting rational numbers into integer rankings, with the potential to lose out on critical information from financial time series [60]. Moreover, it has been shown that rank correlation metrics also suffer from the nonlinearity issue in some cases [58].
- Thirdly, rank-based correlation metrics require independent observations. This is a known weakness of non-linear correlation methods such as Spearman and Kendall [60]. On the other hand, Pearson works well for time series with duplicate observations (because there is no requirement for independent observations), as is the case in financial time series. For example, the price of a cryptocurrency can be unchanged for a period of time.
4.2. Cleaning Trend and Noise Effects in the Cryptocurrency Market
4.2.1. Noise and Trend
4.2.2. Cleaning Method
4.3. Distance Matrix and Its Minimum Spanning Tree
4.4. Community Detection in the Cryptocurrency Market
4.5. Time Window Division
5. Experimental Results and Discussion
5.1. The Response of Network Structures to Noise and Trend Effects
- Residuality Coefficient [93]: This compares the relative strength of the connections above and below a threshold distance value. In this experiment, we use the highest distance value ensuring connectivity of the MST as the threshold, denoted L:
- MST-based mean distance [111]: this calculates the average distance of the MST:
5.2. Real Network Structures in Different Levels of Granularity: An Experiment on Cleaned Data
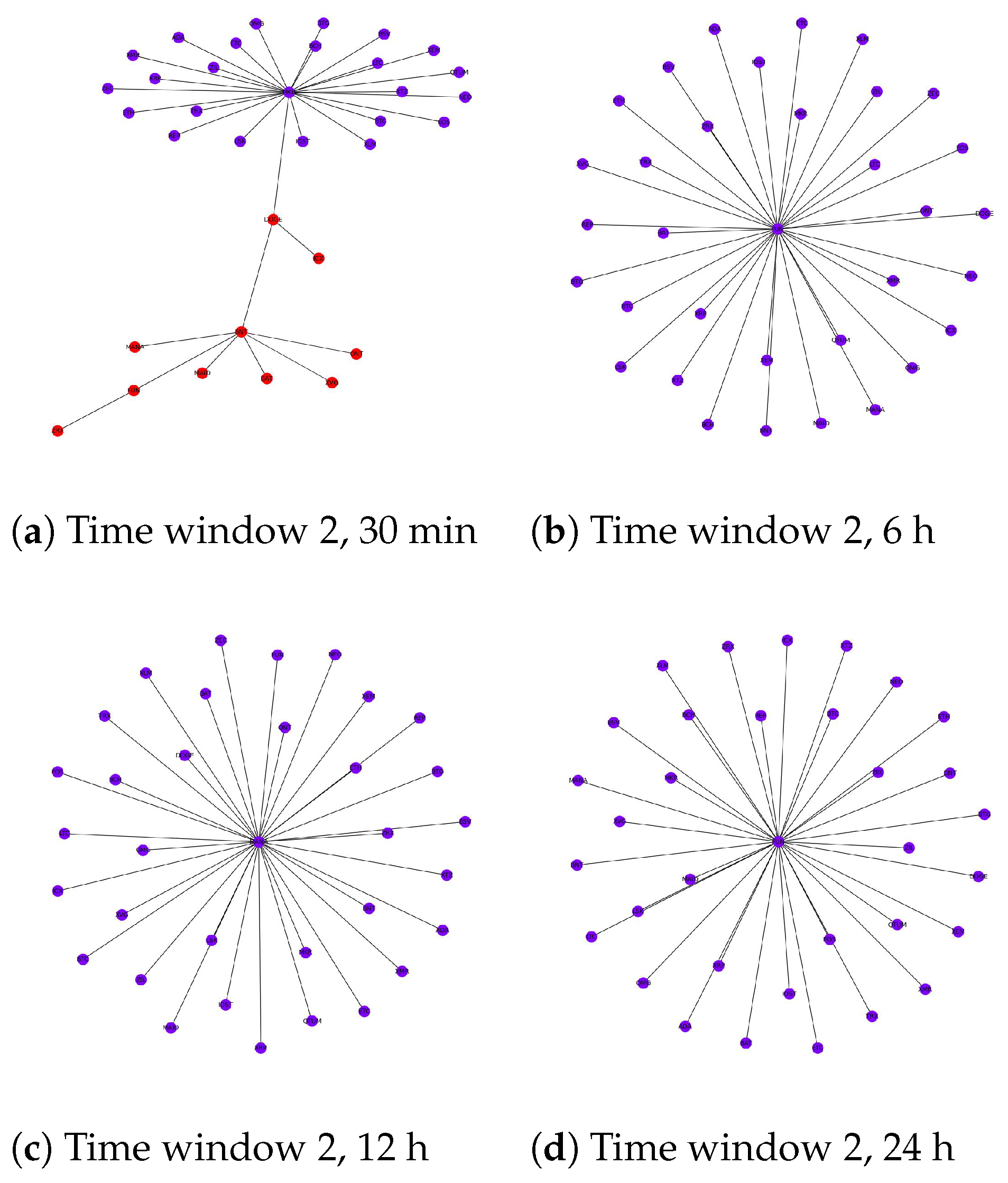
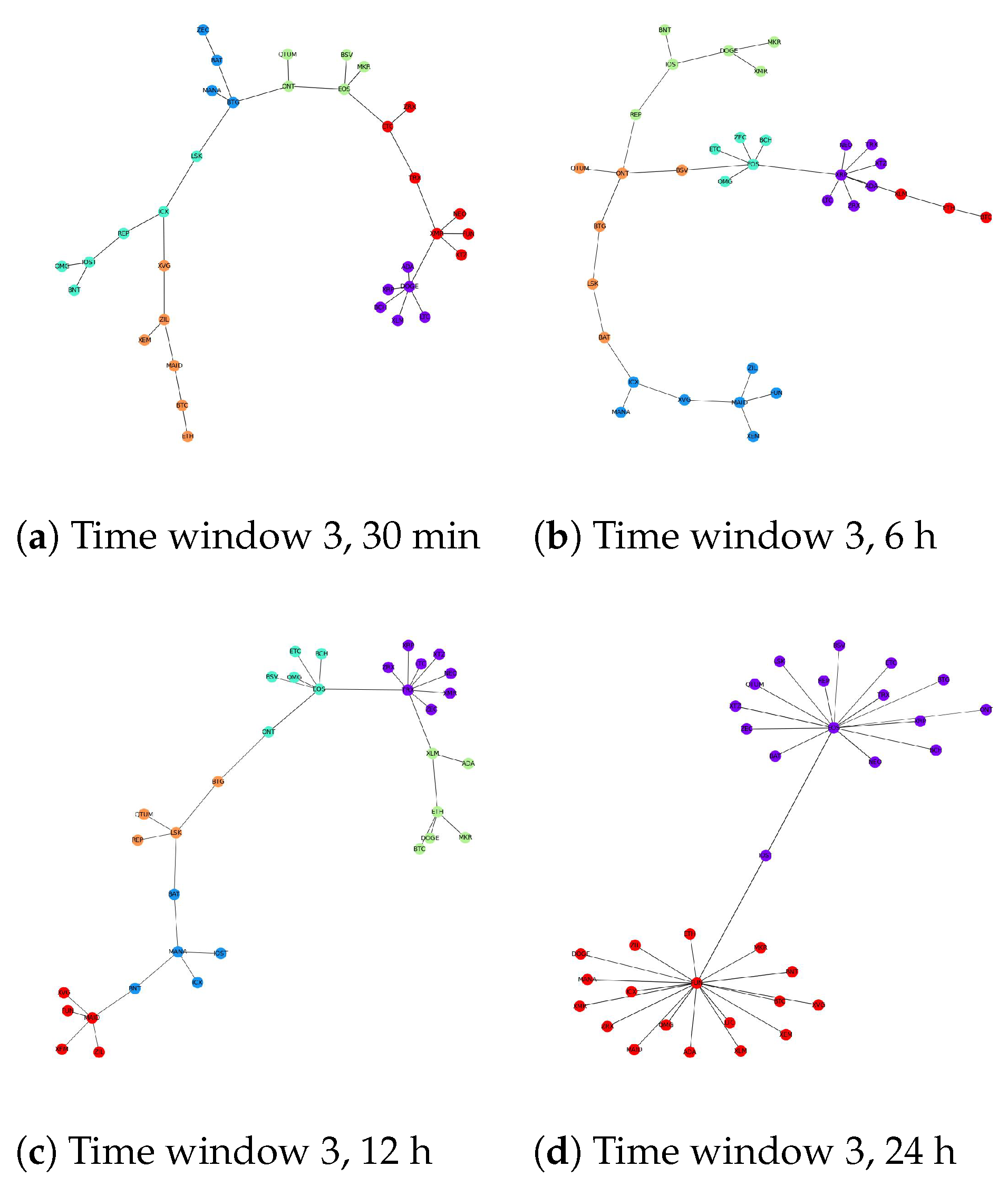
5.2.1. The Evolution of the Cryptocurrency Network According to Timescales
5.2.2. Louvain vs. Girvan–Newman for Community Structure Detection
5.3. Analysis of Investors’ Investment Decisions Based on the Time-Varying Network Structure
5.3.1. The Changes in Crypto Network Structure during Times of Crisis
5.3.2. Learning the Investment Decision of Crypto Traders Based on Ranking Distribution
6. Limitations and Future Works
6.1. Limitations
6.2. Future Works
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Jiang, X.F.; Tian, Y.; Li, S.P.; Zheng, B. Portfolio optimization based on network topology. Physica A 2019, 515, 671–681. [Google Scholar] [CrossRef]
- Zhao, L.; Li, W.; Cai, X. Structure and dynamics of stock market in times of crisis. Phys. Lett. A 2016, 380, 654–666. [Google Scholar] [CrossRef]
- Balcilar, M.; Ozdemir, H.; Agan, B. Effects of COVID-19 on cryptocurrency and emerging market connectedness: Empirical evidence from quantile, frequency, and lasso networks. Physica A 2022, 604, 127885. [Google Scholar] [CrossRef]
- Chaudhari, H.; Crane, M. Cross-correlation dynamics and community structures of cryptocurrencies. J. Comput. Sci. 2020, 44, 101130. [Google Scholar] [CrossRef]
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale characteristics of the emerging global cryptocurrency market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- Nie, C.X. A network-based method for detecting critical events of correlation dynamics in financial markets. Europhys. Lett. 2020, 131, 50001. [Google Scholar] [CrossRef]
- Papadimitriou, T.; Gogas, P.; Gkatzoglou, F. The evolution of the cryptocurrencies market: A complex networks approach. J. Comput. Appl. Math. 2020, 376, 112831. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Conlon, T.; Ruskin, H.J.; Crane, M. Cross-correlation dynamics in financial time series. Physica A 2009, 388, 705–714. [Google Scholar] [CrossRef]
- Matos, J.; Gama, S.; Ruskin, H.; Sharkasi, A.; Crane, M. Correlation of worldwide markets’ entropies. Centro 2006. Available online: https://citeseerx.ist.psu.edu/messages/downloadsexceeded.html (accessed on 18 August 2022).
- Goodell, J.W.; Goutte, S. Diversifying equity with cryptocurrencies during COVID-19. Int. Rev. Financ. Anal. 2021, 76, 101781. [Google Scholar] [CrossRef]
- Mallinger-Dogan, M.; Szigety, M.C. Higher-Frequency Analysis of Low-Frequency Data. J. Portf. Manag. 2014, 41, 121–138. [Google Scholar] [CrossRef]
- Brauneis, A.; Mestel, R. Price discovery of cryptocurrencies: Bitcoin and beyond. Econ. Lett. 2018, 165, 58–61. [Google Scholar] [CrossRef]
- Caferra, R.; Vidal-Tomás, D. Who raised from the abyss? A comparison between cryptocurrency and stock market dynamics during the COVID-19 pandemic. Financ. Res. Lett. 2021, 43, 101954. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T. The volatility of Bitcoin and its role as a medium of exchange and a store of value. Empir. Econ. 2021, 61, 2663–2683. [Google Scholar] [CrossRef]
- Barua, S. Understanding Coronanomics: The Economic Implications of the Coronavirus (COVID-19) Pandemic. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3566477 (accessed on 17 July 2022).
- Padhan, R.; Prabheesh, K. The economics of COVID-19 pandemic: A survey. Econ. Anal. Policy 2021, 70, 220–237. [Google Scholar] [CrossRef]
- Yousfi, M.; Zaied, Y.B.; Cheikh, N.B.; Lahouel, B.B.; Bouzgarrou, H. Effects of the COVID-19 pandemic on the US stock market and uncertainty: A comparative assessment between the first and second waves. Technol. Forecast. Soc. Chang. 2021, 167, 120710. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. The impact of COVID-19 pandemic upon stability and sequential irregularity of equity and cryptocurrency markets. Chaos Solit. Fractals 2020, 138, 109936. [Google Scholar] [CrossRef]
- Kwapień, J.; Wątorek, M.; Drożdż, S. Cryptocurrency Market Consolidation in 2020 & 2021. Entropy 2021, 23, 1674. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Oświęcimka, P.; Stanisz, T.; Wątorek, M. Complexity in economic and social systems: Cryptocurrency market at around COVID-19. Entropy 2020, 22, 1043. [Google Scholar] [CrossRef]
- Nie, C.X. Analysis of critical events in the correlation dynamics of cryptocurrency market. Phys. A Stat. Mech. Its Appl. 2022, 586, 126462. [Google Scholar] [CrossRef]
- Miceli, M.A.; Susinno, G. Ultrametricity in fund of funds diversification. Physica A 2004, 344, 95–99. [Google Scholar] [CrossRef]
- Onnela, J.P.; Chakraborti, A.; Kaski, K.; Kertesz, J. Dynamic asset trees and Black Monday. Physica A 2003, 324, 247–252. [Google Scholar] [CrossRef]
- Liu, H.; Zou, J.; Ravishanker, N. Clustering high-frequency financial time series based on information theory. Appl. Stoch. Model. Bus. Ind. 2022, 38, 4–26. [Google Scholar] [CrossRef]
- Durcheva, M.; Tsankov, P. Analysis of similarities between stock and cryptocurrency series by using graphs and spanning trees. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2172, p. 090004. [Google Scholar]
- Katsiampa, P.; Yarovaya, L.; Zięba, D. High-Frequency connectedness between bitcoin and other top-traded crypto assets during the COVID-19 crisis. J. Int. Financ. Mark. Inst Money 2022, 79, 101578. [Google Scholar] [CrossRef]
- Francés, C.J.; Carles, P.; Arellano, D.J. The cryptocurrency market: A network analysis. Esic Mark. Econ. Bus. J. 2018, 49, 569–583. [Google Scholar] [CrossRef]
- Briola, A.; Aste, T. Dependency structures in cryptocurrency market from high to low frequency. arXiv 2022, arXiv:2206.03386. [Google Scholar]
- Gavin, J.; Crane, M. Community Detection in Cryptocurrencies with Potential Applications to Portfolio Diversification. arXiv 2021, arXiv:2108.09756. [Google Scholar]
- Yu, A.; Bünz, B. Community Detection and Analysis in the Bitcoin Network, CS 224W Final Report; Stanford University: Stanford, CA, USA, 2015. [Google Scholar]
- Atiya, H.R.; Nawaf, H.N. Prediction of Link Weight of bitcoin Network by Leveraging the Community Structure. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristiol, UK, 2020; Volume 928, p. 032080. [Google Scholar]
- Jin, D.; Yu, Z.; Jiao, P.; Pan, S.; He, D.; Wu, J.; Yu, P.; Zhang, W. A survey of community detection approaches: From statistical modeling to deep learning. IEEE Trans. Knowl. Data. Eng 2021. [Google Scholar] [CrossRef]
- Cao, K.H.; Li, Q.; Liu, Y.; Woo, C.K. COVID-19’s adverse effects on a stock market index. Appl. Econ. Lett. 2021, 28, 1157–1161. [Google Scholar] [CrossRef]
- Ali, M.; Alam, N.; Rizvi, S.A.R. Coronavirus (COVID-19)—An epidemic or pandemic for financial markets. J. Behav. Exp. Financ. 2020, 27, 100341. [Google Scholar] [CrossRef]
- De Luca, G.; Loperfido, N. A skew-in-mean GARCH model. In Skew-Elliptical Distributions and Their Applications: A Journey beyond Normality; Genton, M.G., Ed.; Chapman and Hall/CRC: London, UK, 2004; pp. 233–252. [Google Scholar]
- Karamti, C.; Belhassine, O. COVID-19 pandemic waves and global financial markets: Evidence from wavelet coherence analysis. Financ. Res. Lett. 2022, 45, 102136. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Hamori, S. Crude oil market and stock markets during the COVID-19 pandemic: Evidence from the US, Japan, and Germany. Int. Rev. Financ. Anal. 2021, 74, 101702. [Google Scholar] [CrossRef]
- Adekoya, O.B.; Oliyide, J.A. How COVID-19 drives connectedness among commodity and financial markets: Evidence from TVP-VAR and causality-in-quantiles techniques. Resour. Policy 2021, 70, 101898. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liu, L.; Zhao, N. Fear sentiment, uncertainty, and bitcoin price dynamics: The case of COVID-19. Emerg. Mark. Financ. Trade 2020, 56, 2298–2309. [Google Scholar] [CrossRef]
- Baig, A.S.; Butt, H.A.; Haroon, O.; Rizvi, S.A.R. Deaths, panic, lockdowns and US equity markets: The case of COVID-19 pandemic. Financ. Res. Lett 2021, 38, 101701. [Google Scholar] [CrossRef]
- Sapkota, N. News-based sentiment and bitcoin volatility. Int. Rev. Financ. Anal. 2022, 82, 102183. [Google Scholar] [CrossRef]
- Bianchi, D. Cryptocurrencies as an asset class? An empirical assessment. J. Altern. Investments 2020, 23, 162–179. [Google Scholar] [CrossRef]
- Anamika, A.; Subramaniam, S. Do news headlines matter in the cryptocurrency market? Appl. Econ. 2022, 1–17. [Google Scholar] [CrossRef]
- Vidal-Tomás, D. Transitions in the cryptocurrency market during the COVID-19 pandemic: A network analysis. Financ. Res. Lett. 2021, 43, 101981. [Google Scholar] [CrossRef]
- Assaf, A.; Bhandari, A.; Charif, H.; Demir, E. Multivariate long memory structure in the cryptocurrency market: The impact of COVID-19. Int. Rev. Financ. Anal. 2022, 82, 102132. [Google Scholar] [CrossRef]
- Masconi, K.L.; Matsha, T.E.; Erasmus, R.T.; Kengne, A.P. Effects of different missing data imputation techniques on the performance of undiagnosed diabetes risk prediction models in a mixed-ancestry population of South Africa. PLoS ONE 2015, 10, e0139210. [Google Scholar] [CrossRef] [PubMed]
- Van der Heijden, G.J.; Donders, A.R.T.; Stijnen, T.; Moons, K.G. Imputation of missing values is superior to complete case analysis and the missing-indicator method in multivariable diagnostic research: A clinical example. J. Clin. Epidemiol. 2006, 59, 1102–1109. [Google Scholar] [CrossRef] [PubMed]
- Genolini, C.; Jacqmin-Gadda, H. Copy mean: A new method to impute intermittent missing values in longitudinal studies. Open J. Stat. 2013, 3, 26. [Google Scholar] [CrossRef]
- Rydberg, T.H. Realistic statistical modelling of financial data. Int. Stat. Rev. 2000, 68, 233–258. [Google Scholar] [CrossRef]
- Amien, I.; Rajaratnam, K.; Kruger, R. Inference of aggregational gaussianity in asset returns exhibiting a paretian-distribution. Procedia Econ. Financ. 2015, 25, 400–407. [Google Scholar] [CrossRef]
- Kratz, M.; Resnick, S.I. The QQ-estimator and heavy tails. Stoch. Model. 1996, 12, 699–724. [Google Scholar] [CrossRef]
- Abdi, H.; Molin, P. Lilliefors/Van Soest’s test of normality. In Encyclopedia of Measurement and Statistics; SAGE Publications: Thousand Oaks, OK, USA, 2007; pp. 540–544. [Google Scholar]
- Takaishi, T. Time-varying properties of asymmetric volatility and multifractality in Bitcoin. PLoS ONE 2021, 16, e0246209. [Google Scholar] [CrossRef]
- Kulyatin, I. Stylized Facts for Cryptocurrencies: A Sectoral Analysis; Medium: New York, NY, USA, 2015. [Google Scholar]
- Tsay, R.S. Analysis of Financial Time Series; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Schäfer, R.; Guhr, T. Local normalization: Uncovering correlations in non-stationary financial time series. Physica A 2010, 389, 3856–3865. [Google Scholar] [CrossRef]
- Tjøstheim, D.; Otneim, H.; Støve, B. Statistical Dependence: Beyond Pearson’s ρ. Stat. Sci. 2022, 37, 90–109. [Google Scholar] [CrossRef]
- Wissler, C. The Spearman correlation formula. Science 1905, 22, 309–311. [Google Scholar] [CrossRef]
- Lieberson, S. Limitations in the application of non-parametric coefficients of correlation. Am. Sociol. Rev. 1964, 29, 744–746. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.N.; Stanley, H.E. A random matrix theory approach to financial cross-correlations. Physica A 2000, 287, 374–382. [Google Scholar] [CrossRef]
- Cacciapuoti, C.; Maltsev, A.; Schlein, B. Local Marchenko-Pastur law at the hard edge of sample covariance matrices. J. Math. Phys. 2013, 54, 043302. [Google Scholar] [CrossRef]
- Laloux, L.; Cizeau, P.; Potters, M.; Bouchaud, J.P. Random matrix theory and financial correlations. Int. J. Theor. Appl. Financ. 2000, 3, 391–397. [Google Scholar] [CrossRef]
- Mai, T.; Martin, C.; Marija, B. Student behaviours in using learning resources in higher education: How do behaviours reflect success in programming education? In Proceedings of the 7th International Conference on Higher Education Advances, Torino, Italy, 22–23 June 2021; pp. 47–55. [Google Scholar]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.A.N.; Guhr, T.; Stanley, H.E. Random matrix approach to cross correlations in financial data. Phys. Rev. E 2002, 65, 066126. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. Nothing but noise? Price discovery across cryptocurrency exchanges. J. Financ. Mark. 2021, 54, 100584. [Google Scholar] [CrossRef]
- Sarr, A.; Lybek, T. Measuring Liquidity in Financial Markets. 2002. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=880932 (accessed on 27 July 2022).
- Li, T.; Shin, D.; Wang, B. Cryptocurrency Pump-and-Dump Schemes. 2021. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3267041 (accessed on 5 August 2022).
- Auer, R.; Claessens, S. Regulating cryptocurrencies: Assessing market reactions. BIS Q. Rev. Sept. 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3288097 (accessed on 8 August 2022).
- Mai, T.T.; Bezbradica, M.; Crane, M. Learning behaviours data in programming education: Community analysis and outcome prediction with cleaned data. Future Gener. Comput. Syst. 2022, 127, 42–55. [Google Scholar] [CrossRef]
- Zhang, S.; Lee, J.H. Analysis of the main consensus protocols of blockchain. ICT Express 2020, 6, 93–97. [Google Scholar] [CrossRef]
- Da Gama Silva, P.V.J.; Klotzle, M.C.; Pinto, A.C.F.; Gomes, L.L. Herding behavior and contagion in the cryptocurrency market. J. Behav. Exp. Financ. 2019, 22, 41–50. [Google Scholar] [CrossRef]
- Burda, Z.; Jarosz, A. Cleaning large-dimensional covariance matrices for correlated samples. Phys. Rev. E 2022, 105, 034136. [Google Scholar] [CrossRef] [PubMed]
- Bouchaud, J.P.; Potters, M. Financial applications of random matrix theory: A short review. arXiv 2009, arXiv:0910.1205. [Google Scholar]
- Ledoit, O.; Wolf, M. Nonlinear shrinkage estimation of large-dimensional covariance matrices. Ann. Stat. 2012, 40, 1024–1060. [Google Scholar] [CrossRef]
- Bun, J.; Allez, R.; Bouchaud, J.P.; Potters, M. Rotational invariant estimator for general noisy matrices. IEEE Trans. Inf. Theory 2016, 62, 7475–7490. [Google Scholar] [CrossRef]
- Ledoit, O.; Wolf, M. A well-conditioned estimator for large-dimensional covariance matrices. J. Multivar. Anal. 2004, 88, 365–411. [Google Scholar] [CrossRef]
- Bun, J.; Knowles, A. An optimal rotational invariant estimator for general covariance matrices: The outliers. Preprint 2018. Available online: https://www.researchgate.net/profile/Joel-Bun/publication/323255675_An_Optimal_Rotational_Invariant_Estimator_for_General_Covariance_Matrices_the_outliers/links/5a89e7fba6fdcc6b1a424f88/An-Optimal-Rotational-Invariant-Estimator-for-General-Covariance-Matrices-the-outliers.pdf (accessed on 8 August 2022).
- Shcherbakov, M.V.; Brebels, A.; Shcherbakova, N.L.; Tyukov, A.P.; Janovsky, T.A.; Kamaev, V.A. A survey of forecast error measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar]
- Markowitz, R. Cleaning Correlation Matrices. 2016. Available online: https://www.cfm.fr/assets/ResearchPapers/2016-Cleaning-Correlation-Matrices.pdf (accessed on 8 August 2022).
- Conlon, T.; Ruskin, H.J.; Crane, M. Random matrix theory and fund of funds portfolio optimisation. Physica A 2007, 382, 565–576. [Google Scholar] [CrossRef][Green Version]
- Yang, L.; McKay, M.R.; Couillet, R. High-dimensional MVDR beamforming: Optimized solutions based on spiked random matrix models. IEEE Trans. Signal Process 2018, 66, 1933–1947. [Google Scholar] [CrossRef]
- Heimo, T.; Kaski, K.; Saramäki, J. Maximal spanning trees, asset graphs and random matrix denoising in the analysis of dynamics of financial networks. Physica A 2009, 388, 145–156. [Google Scholar] [CrossRef]
- de Prado, M.M.L. Machine Learning for Asset Managers; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- O’Searcoid, M. Metric Spaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Graham, R.L.; Hell, P. On the history of the minimum spanning tree problem. IEEE Ann. Hist. Comput. 1985, 7, 43–57. [Google Scholar] [CrossRef]
- Ghosh, B.; Motagh, M.; Haghighi, M.H.; Vassileva, M.S.; Walter, T.R.; Maghsudi, S. Automatic detection of volcanic unrest using blind source separation with a minimum spanning tree based stability analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7771–7787. [Google Scholar] [CrossRef]
- Denkowska, A.; Wanat, S. Linkages and systemic risk in the European insurance sector. New evidence based on Minimum Spanning Trees. Risk Manag. 2022, 24, 123–136. [Google Scholar] [CrossRef]
- Coelho, R.; Gilmore, C.G.; Lucey, B.; Richmond, P.; Hutzler, S. The evolution of interdependence in world equity markets—Evidence from minimum spanning trees. Physica A 2007, 376, 455–466. [Google Scholar] [CrossRef]
- Kazemilari, M.; Mohamadi, A.; Mardani, A.; Streimikis, J. Network topology of renewable energy companies: Minimal spanning tree and sub-dominant ultrametric for the American stock. Technol. Econ. Dev. Econ. 2019, 25, 168–187. [Google Scholar] [CrossRef]
- Nguyen, Q.; Nguyen, N.; Nguyen, L. Dynamic topology and allometric scaling behavior on the Vietnamese stock market. Physica A 2019, 514, 235–243. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, X.; Su, R.; Yang, X.; Yang, X. Dynamic network topology and market performance: A case of the Chinese stock market. Int. J. Financ. Econ. 2022, 27, 1962–1978. [Google Scholar] [CrossRef]
- Giudici, P.; Pagnottoni, P.; Polinesi, G. Network models to enhance automated cryptocurrency portfolio management. Front. Artif. Intell. 2020, 3, 22. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Huang, F.; Gao, P.; Wang, Y. Comparison of Prim and Kruskal on Shanghai and Shenzhen 300 Index hierarchical structure tree. In Proceedings of the 2009 International Conference on Web Information Systems and Mining, Shanghai, China, 7–8 November 2009; pp. 237–241. [Google Scholar]
- Mantegna, R.N. Hierarchical structure in financial markets. Eur. Phys. J. B 1999, 11, 193–197. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, W.; Wen, J.; Zhang, W. The Financial Market in China under the COVID-19. Emerg. Mark. Financ. Trade 2022, 1–13. [Google Scholar] [CrossRef]
- Brida, J.G.; Risso, W.A. Hierarchical structure of the German stock market. Expert Syst. Appl. 2010, 37, 3846–3852. [Google Scholar] [CrossRef]
- MacMahon, M.; Garlaschelli, D. Community detection for correlation matrices. arXiv 2013, arXiv:1311.1924. [Google Scholar] [CrossRef]
- Chakrabarti, P.; Jawed, M.S.; Sarkhel, M. COVID-19 pandemic and global financial market interlinkages: A dynamic temporal network analysis. Appl. Econ. 2021, 53, 2930–2945. [Google Scholar] [CrossRef]
- Bazzi, M.; Porter, M.A.; Williams, S.; McDonald, M.; Fenn, D.J.; Howison, S.D. Community detection in temporal multilayer networks, with an application to correlation networks. Multiscale Model. Simul. 2016, 14, 1–41. [Google Scholar] [CrossRef]
- Anghinoni, L.; Vega-Oliveros, D.A.; Silva, T.C.; Zhao, L. Time series pattern identification by hierarchical community detection. Eur. Phys. J. Spec. Top. 2021, 230, 2775–2782. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef]
- Pujol, J.M.; Erramilli, V.; Rodriguez, P. Divide and conquer: Partitioning online social networks. arXiv 2009, arXiv:0905.4918. [Google Scholar]
- Roma, G.; Herrera, P. Community structure in audio clip sharing. In Proceedings of the 2010 INCoS, Thessaloniki, Greece, 24–26 November 2010; pp. 200–205. [Google Scholar]
- Wang, C.; Wang, F. GIS-automated delineation of hospital service areas in Florida: From Dartmouth method to network community detection methods. Ann. GIS 2022, 28, 93–109. [Google Scholar] [CrossRef]
- Raeder, T.; Chawla, N.V. Market basket analysis with networks. Soc. Netw. Anal. Min. 2011, 1, 97–113. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Boyle, M.; Bellucco-Chatham, A. 2008 Recession: What the Great Recession Was and What Caused It; Investopedia: New York, NY, USA, 2022. [Google Scholar]
- Liang, J.; Li, L.; Zeng, D.; Zhao, Y. Correlation-based dynamics and systemic risk measures in the cryptocurrency market. In Proceedings of the IEEE 2018 ISI, Miami, FL, USA, 9–11 November 2018; pp. 43–48. [Google Scholar]
- Spelta, A.; Araújo, T. The topology of cross-border exposures: Beyond the minimal spanning tree approach. Physica A 2012, 391, 5572–5583. [Google Scholar] [CrossRef][Green Version]
- Feng, W.; Wang, Y.; Zhang, Z. Can cryptocurrencies be a safe haven: A tail risk perspective analysis. Appl. Econ. 2018, 50, 4745–4762. [Google Scholar] [CrossRef]
- Corbet, S.; Lucey, B.; Urquhart, A.; Yarovaya, L. Cryptocurrencies as a financial asset: A systematic analysis. Int. Rev. Financ. Anal 2019, 62, 182–199. [Google Scholar] [CrossRef]
- Ammous, S. Can cryptocurrencies fulfil the functions of money? Q. Rev. Econ. Financ. 2018, 70, 38–51. [Google Scholar] [CrossRef]
- Klein, T.; Thu, H.P.; Walther, T. Bitcoin is not the New Gold–A comparison of volatility, correlation, and portfolio performance. Int. Rev. Financ. Anal. 2018, 59, 105–116. [Google Scholar] [CrossRef]
- Su, F.; Wang, X.; Yuan, Y. The intraday dynamics and intraday price discovery of bitcoin. Res. Int. Bus. Financ. 2022, 60, 101625. [Google Scholar] [CrossRef]
- Megaritis, A.; Vlastakis, N.; Triantafyllou, A. Stock market volatility and jumps in times of uncertainty. J. Int. Money Financ. 2021, 113, 102355. [Google Scholar] [CrossRef]
- Aslam, F.; Ferreira, P.; Mughal, K.S.; Bashir, B. Intraday volatility spillovers among European financial markets during COVID-19. Int. J. Financ. Stud. 2021, 9, 5. [Google Scholar] [CrossRef]
- Jarosław, K.; Marcin, W.; Marija, B.; Martin, C.; Mai, T.; Stanisław, D. Analysis of inter-transaction time fluctuations in the cryptocurrency market. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 083142. [Google Scholar]
- Rosenberg, A.; Hirschberg, J. V-measure: A conditional entropy-based external cluster evaluation measure. In Proceedings of the 2007 EMNLP-CoNLL, Prague, Czech Republic, 28–30 June 2007; pp. 410–420. [Google Scholar]
- Liang, J.; Li, L.; Zeng, D. Evolutionary dynamics of cryptocurrency transaction networks: An empirical study. PLoS ONE 2018, 13, e0202202. [Google Scholar]
- Koutra, D.; Parikh, A.; Ramdas, A.; Xiang, J. Algorithms for Graph Similarity and Subgraph Matching. 2011, Volume 17. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.377.4291&rep=rep1&type=pdf (accessed on 8 August 2022).
- Gera, R.; Alonso, L.; Crawford, B.; House, J.; Mendez-Bermudez, J.; Knuth, T.; Miller, R. Identifying network structure similarity using spectral graph theory. Appl. Netw. Sci. 2018, 3, 2. [Google Scholar] [CrossRef]
- Yarovaya, L.; Matkovskyy, R.; Jalan, A. The effects of a’Black Swan’event (COVID-19) on herding behavior in cryptocurrency markets: Evidence from cryptocurrency USD, EUR, JPY and KRW Markets. J. Int. Financ. Mark. Inst. Money 2021, 75, 101321. [Google Scholar] [CrossRef]
- Youssef, M.; Waked, S.S. Herding behavior in the cryptocurrency market during COVID-19 pandemic: The role of media coverage. N. Am. J. Econ. Financ. 2022, 62, 101752. [Google Scholar] [CrossRef]
- Susana, D.; Kavisanmathi, J.; Sreejith, S. Does herding behaviour among traders increase during COVID 19 pandemic? Evidence from the cryptocurrency market. In Proceedings of the International Working Conference on Transfer and Diffusion of IT, Tiruchirappalli, India, 18–19 December 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 178–189. [Google Scholar]
- Kaiser, L.; Stöckl, S. Cryptocurrencies: Herding and the transfer currency. Financ. Res. Lett 2020, 33, 101214. [Google Scholar] [CrossRef]
- Mnif, E.; Salhi, B.; Mouakha, K.; Jarboui, A. Investor behavior and cryptocurrency market bubbles during the COVID-19 pandemic. Rev. Behav. Financ. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Corbet, S.; Larkin, C.; Lucey, B.; Yarovaya, L. KODAKCoin: A blockchain revolution or exploiting a potential cryptocurrency bubble? Appl. Econ. Lett 2020, 27, 518–524. [Google Scholar] [CrossRef]
- Huber, C.; Huber, J.; Kirchler, M. Market shocks and professionals’ investment behavior—Evidence from the COVID-19 crash. J. Bank. Financ. 2021, 133, 106247. [Google Scholar] [CrossRef]



| Cryptocurrencies | |||||
|---|---|---|---|---|---|
| Argur (REP) | Bitcoin SV (BSV) | Ethereum Classic (ETC) | MaidSafeCoin (MAID) | Ontology (ONT) | Tron (TRX) |
| Bancor (BNT) | Cardano (ADA) | FunToken (FUN) | Maker (MKR) | Ox (ZRX) | Verge (XVG) |
| Basic Attention Token(BAT) | Decentraland (MANA) | ICON (ICX) | Monero (XMR) | QTUM | Zcash (ZEC) |
| Bitcoin (BTC) | Dogecoin (DOGE) | IOST | Nem (XEM) | Ripple (XRP) | Zilliqa (ZIL) |
| Bitcoin Cash (BCH) | EOS | Lisk (LSK) | NEO | Stellar (XLM) | |
| Bitcoin Gold (BTG) | Ethereum (ETH) | Litecoin (LTC) | OMG Network (OMG) | Tezos (XTZ) | |
| Level of Granularity | # Data Points | # Missing Values |
|---|---|---|
| 30 min | 37,632 | 289 (0.8%) |
| 6 h | 3136 | 24 (0.8%) |
| 12 h | 1568 | 12 (0.8%) |
| 24 h | 784 | 0 (0%) |
| Time Window | Stage | Time Span | # Days |
|---|---|---|---|
| 1 | Normal time | 13 February 2019–31 December 2019 | 322 days |
| 2 | Downturn time | 1 January 2020–30 June 2020 | 182 days |
| 3 | Recovery time | 1 July 2020–6 April 2021 | 280 days |
| Metric | Data Type | Time Window | Granularity | |||
|---|---|---|---|---|---|---|
| 30 min | 6 h | 12 h | 24 h | |||
| Residuality Coefficient | Original Data | 1 | 0.41 | 0.11 | 0.16 | 0.08 |
| 2 | 0.28 | 0.111 | 0.06 | 0.05 | ||
| 3 | 0.14 | 0.05 | 0.07 | 0.34 | ||
| Cleaned data | 1 | 1.69 | 6.66 | 14.82 | 14.40 | |
| 2 | 5.98 | 8.90 | 14.41 | 15.34 | ||
| 3 | 2.32 | 2.99 | 1.88 | 1.05 | ||
| Mean distance | Original Data | 1 | 1.08 | 0.82 | 0.80 | 0.76 |
| 2 | 0.99 | 0.71 | 0.65 | 0.56 | ||
| 3 | 0.98 | 0.57 | 0.46 | 0.45 | ||
| Cleaned data | 1 | 1.29 | 1.38 | 1.42 | 1.42 | |
| 2 | 1.40 | 1.42 | 1.42 | 1.42 | ||
| 3 | 1.29 | 1.12 | 1.01 | 1.22 | ||
| Granularity | ||||
|---|---|---|---|---|
| 30 min | 6 h | 12 h | 24 h | |
| Time window 1 | 0.88 | 1.00 | 1.00 | 1.00 |
| Time window 2 | 1.00 | 1.00 | 1.00 | 1.00 |
| Time window 3 | 0.87 | 0.82 | 0.91 | 1.00 |
| Metrics | Time Window 1 | Time Window 2 | Time Window 3 |
|---|---|---|---|
| Betweenness centrality | 0.15 | 0.05 | 0.16 |
| Degree Assortativity | −0.49 | −0.72 | −0.51 |
| Time Window | 1 vs. 2 | 1 vs. 3 | 2 vs. 3 | |
|---|---|---|---|---|
| Metrics | ||||
| Degree centrality | 0.5 | 0.09 | 0.42 | |
| Eigenvalue method | 844.45 | 4.59 | 759.16 | |
| v-measure | 0.04 | 0.32 | 0.02 | |
| 1l | Group | Cryptocurrencies | Rankings |
|---|---|---|---|
| Normal time | 1 | ADA, XLM, BAT, ZIL | 10, 13, 32, 99 |
| 2 | BTG, IOST, XTZ, ZRX, ETC | 12, 21, 45, 57, 83 | |
| 3 | LSK, OMG, REP, FUN, MKR | 26,54, 58, 70, 168 | |
| 4 | NEO, MANA, BNT, XVG, XEM, QTUM | 19, 31, 41, 86, 117, 184 | |
| 5 | ONT, ZEC, XMR, XRP, EOS, TRX, LTC | 3, 6, 7, 11, 16, 29, 35 | |
| 6 | ICX, MAID, DOGE, BTC, BSV, ETH, BCH | 1, 2, 5, 9, 34, 84, 130 | |
| Downturn time | 1 | DOGE, ICX, BNT, MANA, ZRX, FUN, MAID, BAT, XVG, ONT | 32, 33, 40, 45, 60, 81, 105, 124, 139, 196 |
| 2 | ADA, BCH, BSV, BTC, BTG, EOS, ETH, ETC, IOST, LSK, LTC, MKR, NEO, OMG, QTUM, REP, TRX, XEM, XLM, XMR, XRP, XTZ, ZEC, ZIL | 1, 2, 4, 5, 6, 7, 9, 11, 12, 15, 17, 18, 21, 22, 27, 30, 34, 48, 51, 53, 54, 62, 65, 91 | |
| Recovery time | 1 | BTG, MANA, BAT, ZEC | 56, 62, 67, 107 |
| 2 | ONT, QTUM, EOS, BSV, MKR | 24, 31, 53, 75, 88 | |
| 3 | XVG, ZIL, XEM, MAID, BTC, ETH | 1, 2, 38, 48, 109, 136 | |
| 4 | ADA, DOGE, XRP, BCH, XLM, LTC | 6, 7, 9, 15, 16, 20 | |
| 5 | OMG, BNT, IOST, REP, ICX, LSK | 68, 78, 85, 100, 101, 140 | |
| 6 | ETC, ZRX, TRX, NEO, XMR, FUN, XTZ | 17, 27, 33, 35, 64, 76, 129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, A.P.N.; Mai, T.T.; Bezbradica, M.; Crane, M. The Cryptocurrency Market in Transition before and after COVID-19: An Opportunity for Investors? Entropy 2022, 24, 1317. https://doi.org/10.3390/e24091317
Nguyen APN, Mai TT, Bezbradica M, Crane M. The Cryptocurrency Market in Transition before and after COVID-19: An Opportunity for Investors? Entropy. 2022; 24(9):1317. https://doi.org/10.3390/e24091317
Chicago/Turabian StyleNguyen, An Pham Ngoc, Tai Tan Mai, Marija Bezbradica, and Martin Crane. 2022. "The Cryptocurrency Market in Transition before and after COVID-19: An Opportunity for Investors?" Entropy 24, no. 9: 1317. https://doi.org/10.3390/e24091317
APA StyleNguyen, A. P. N., Mai, T. T., Bezbradica, M., & Crane, M. (2022). The Cryptocurrency Market in Transition before and after COVID-19: An Opportunity for Investors? Entropy, 24(9), 1317. https://doi.org/10.3390/e24091317







