Evaluation of Geometric Attractor Structure and Recurrence Analysis in Professional Dancers
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants and Data Collection
2.2. Phases of Pirouettes and Parameters
2.3. Phase Space Reconstruction
2.3.1. New Time Series Reconstruction
- (1)
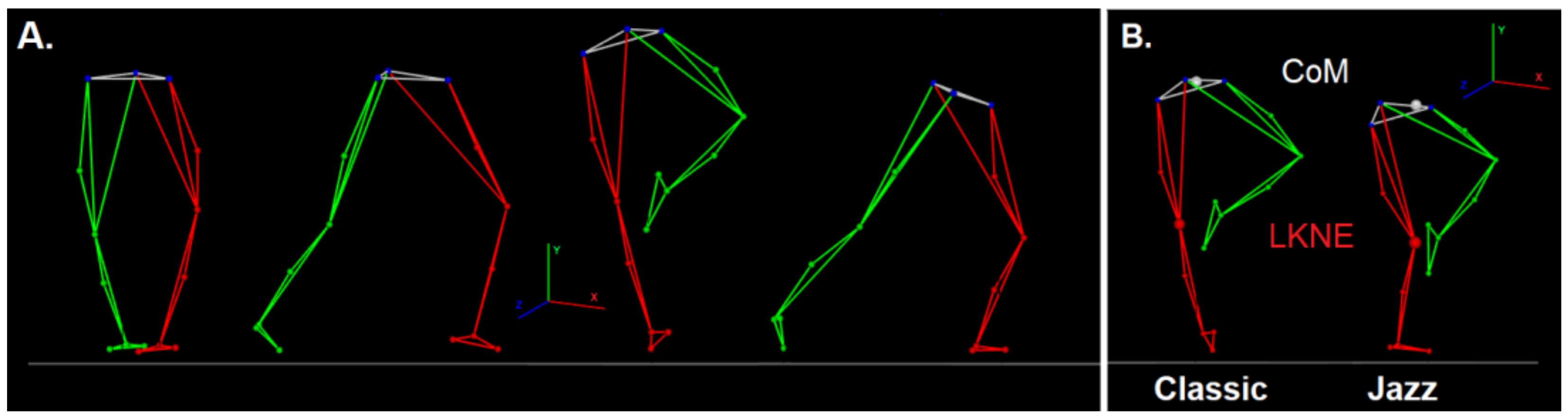
- The where —is the matrix of LKNE or CoM coordinates for the analyzed pirouettes of the i-th person (i = 1, …, 15); n—is the length of the recorded time series. The n values were in the range of 101 to 250 frames. The x-coordinate describes motion in the anterior-posterior direction, y—along a vertical axis (inferior-superior), and z—in the mediolateral direction.
- (2)
- The signals from each matrix Pi were resampled to obtain 300 samples. Its new length was longer than the maximum length of the recorded time series (250). The new signals were normalized by their maximal value.where —matrix of LKNE or CoM after transformation, for the analyzed pirouettes of the i-th person (i =1, …, 15).
- (3)
- Next, the new time series for LKNE and CoM for the x, y, and z coordinates were created. Individuals in the new time series have been shuffled to avoid bias based on their order.
2.3.2. Hurst Exponent
2.3.3. Test of Non-Stationarity
2.3.4. Nonlinearity of Time Series
2.3.5. Detection of Chaos Based on Largest Lyapunov Exponent
2.3.6. Embedding Dimension, Time Delay, and Phase Space Reconstruction
2.4. Recurrence Quantification Analysis (RQA)
3. Results
3.1. New Time Series Reconstruction
3.2. Hurst Exponent Analysis and the Largest Lyapunov Exponent
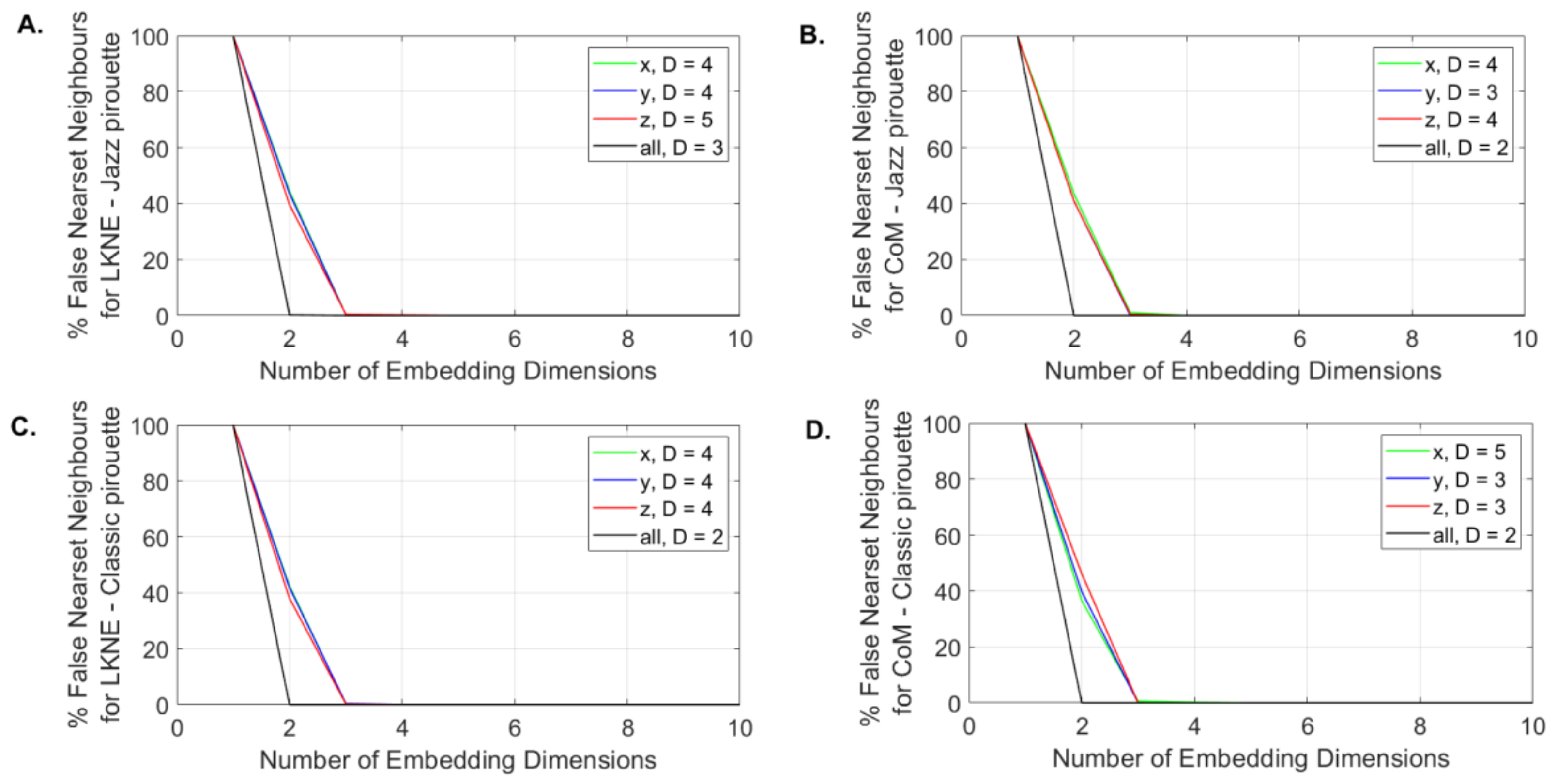
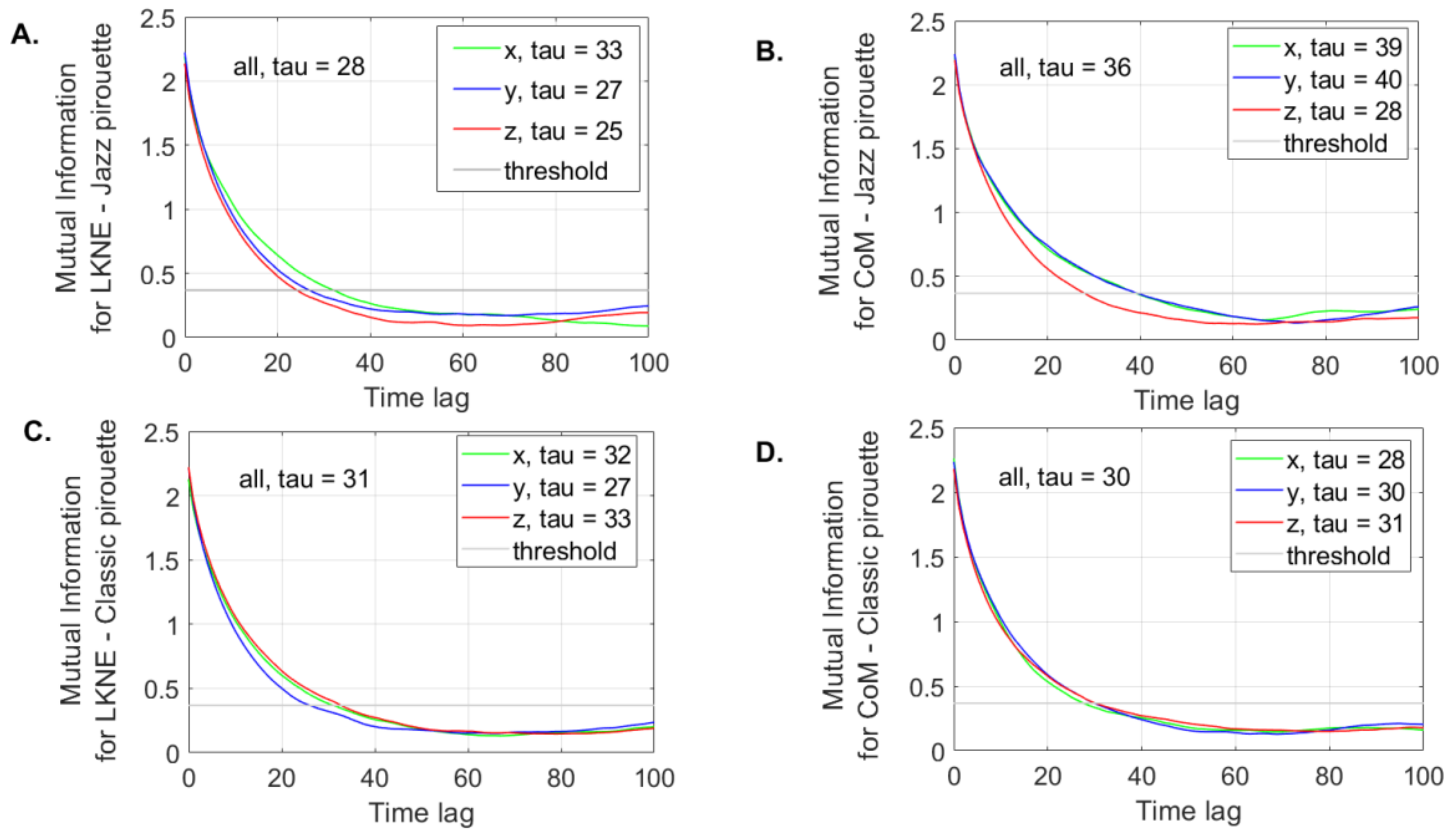
3.3. Determination of the Embedding Dimension and Time Delay
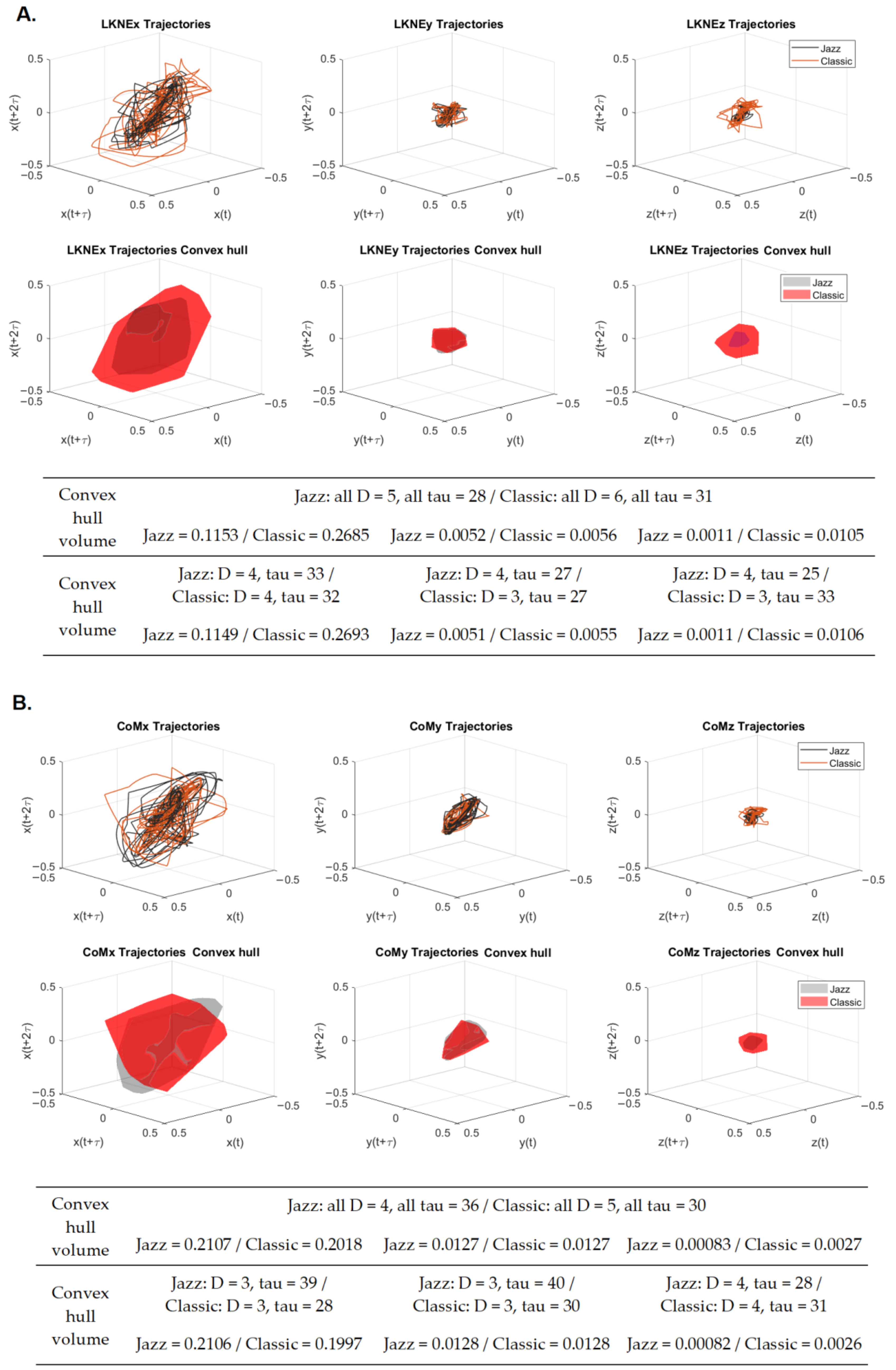
3.4. Phases Space Reconstruction and Convex Hull Calculation
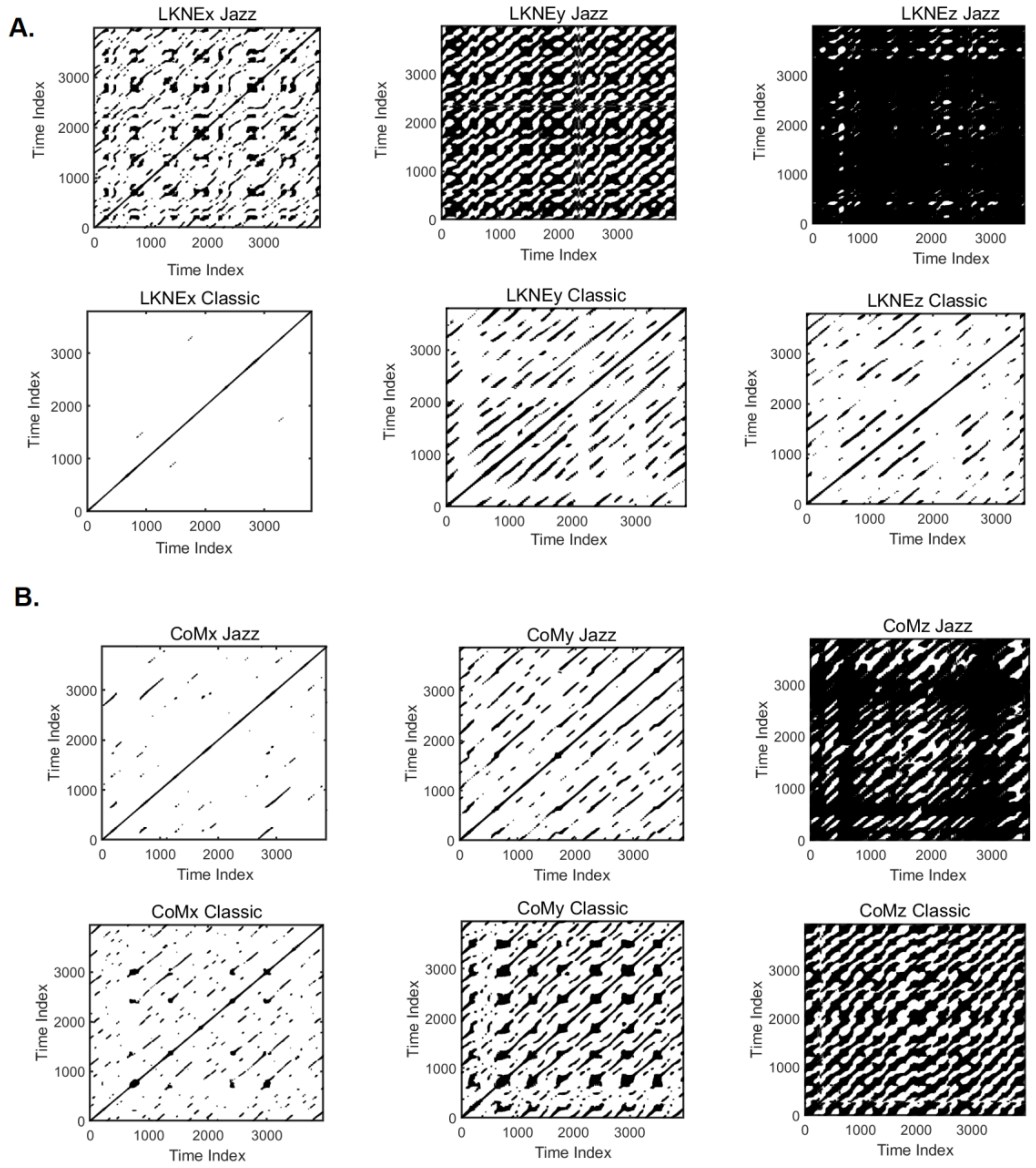
3.5. Recurrence Quantification Analysis
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stergiou, N.; Decker, L.M. Human movement variability, nonlinear dynamics, and pathology: Is there a connection? Hum. Mov. Sci. 2011, 30, 869–888. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, N. Nonlinear Analysis for Human Movement Variability; CRC Press: Boca Raton, FL, USA, 2016; 388p. [Google Scholar]
- Bernstein, N. A new method of mirror cyclographie and its application towards the study of labor movements during work on a workbench. Hyg. Saf. Pathol. Labor 1930, 5, 3–9. [Google Scholar]
- Riley, M.A.; Turvey, M.T. Variability and Determinism in Motor Behavior. J. Mot. Behav. 2002, 34, 99–125. [Google Scholar] [CrossRef] [PubMed]
- van Emmerik, R.E.A.; Ducharme, S.W.; Amado, A.C.; Hamill, J. Comparing dynamical systems concepts and techniques for biomechanical analysis. J. Sport Health Sci. 2016, 5, 3–13. [Google Scholar] [CrossRef]
- van Mourik, A.M.; Daffertshofer, A.; Beek, P.J. Deterministic and stochastic features of rhythmic human movement. Biol. Cybern. 2006, 94, 233–244. [Google Scholar] [CrossRef]
- Weber, I.; Oehrn, C.R. NoLiTiA: An Open-Source Toolbox for Non-linear Time Series Analysis. Front. Neuroinform. 2022, 16, 876012. [Google Scholar] [CrossRef]
- Donker, S.F.; Roerdink, M.; Greven, A.J.; Beek, P.J. Regularity of center-of-pressure trajectories depends on the amount of attention invested in postural control. Exp. Brain Res. 2007, 181, 1–11. [Google Scholar] [CrossRef]
- Roerdink, M.; Hlavackova, P.; Vuillerme, N. Center-of-pressure regularity as a marker for attentional investment in postural control: A comparison between sitting and standing postures. Hum. Mov. Sci. 2011, 30, 203–212. [Google Scholar] [CrossRef]
- Ramdani, S.; Tallon, G.; Bernard, P.L.; Blain, H. Recurrence quantification analysis of human postural fluctuations in older fallers and non-fallers. Ann. Biomed. Eng. 2013, 41, 1713–1725. [Google Scholar] [CrossRef]
- Bradley, E.; Kantz, H. Nonlinear time-series analysis revisited. Chaos 2015, 25, 097610. [Google Scholar] [CrossRef]
- Webber, C.; Zbilut, J. Recurrence quantification analysis of nonlinear dynamical systems. Tutor. Contemp. Nonlinear Methods Behav. Sci. 2005, 94, 26–94. [Google Scholar]
- Kędziorek, J.; Błażkiewicz, M. Nonlinear Measures to Evaluate Upright Postural Stability: A Systematic Review. Entropy 2020, 22, 1357. [Google Scholar] [CrossRef]
- Khayat, O.; Nowshiravan-Rahatabad, F. Complex feature analysis of center of pressure signal for age-related subject classification. Ann. Mil. Health Sci. Res. 2014, 12, e63518. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Liu, H.-F.; Dai, Z.-H.; Li, W.-F.; Gong, X.; Yu, Z.-H. Noise robust estimates of the largest Lyapunov exponent. Phys. Lett. A 2005, 341, 119–127. [Google Scholar] [CrossRef]
- Kantz, H. A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 1994, 185, 77–87. [Google Scholar] [CrossRef]
- Rispens, S.M.; Pijnappels, M.; van Dieën, J.H.; van Schooten, K.S.; Beek, P.J.; Daffertshofer, A. A benchmark test of accuracy and precision in estimating dynamical systems characteristics from a time series. J. Biomech. 2014, 47, 470–475. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Tarnopolski, M. On the relationship between the Hurst exponent, the ratio of the mean square successive difference to the variance, and the number of turning points. Phys. A Stat. Mech. Its Appl. 2016, 461, 662–673. [Google Scholar] [CrossRef]
- Devaney, R. An Introduction to Chaotic Dynamical Systems; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Proceedings of the Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- de Pedro-Carracedo, J.; Fuentes-Jimenez, D.; Ugena, A.M.; Gonzalez-Marcos, A.P. Phase Space Reconstruction from a Biological Time Series: A Photoplethysmographic Signal Case Study. Appl. Sci. 2020, 10, 1430. [Google Scholar] [CrossRef]
- Brick, T.R.; Gray, A.L.; Staples, A.D. Recurrence Quantification for the Analysis of Coupled Processes in Aging. J. Gerontol. Ser. B 2018, 73, 134–147. [Google Scholar] [CrossRef]
- Harbourne, R.T.; Stergiou, N. Movement variability and the use of nonlinear tools: Principles to guide physical therapist practice. Phys. Ther. 2009, 89, 267–282. [Google Scholar] [CrossRef]
- Pellecchia, G.L.; Shockley, K. Application of recurrence quantification analysis: Influence of cognitive activity on postural fluctuations. In Tutorials in Contemporary Nonlinear Methods for the Behavioral Sciences; National Science Foundation: Alexandria, VA, USA, 2005; pp. 95–141. [Google Scholar]
- Som, A.; Krishnamurthi, N.; Venkataraman, V.; Turaga, P. Attractor-shape descriptors for balance impairment assessment in Parkinson’s disease. IEEE Eng. Med. Biol. Soc. Annu. Int. Conf. 2016, 2016, 3096–3100. [Google Scholar] [CrossRef]
- Gates, D.H.; Dingwell, J.B. Comparison of different state space definitions for local dynamic stability analyses. J. Biomech. 2009, 42, 1345–1349. [Google Scholar] [CrossRef]
- Bradley, E.; Stuart, J. Using chaos to generate variations on movement sequences. Chaos 1998, 8, 800–807. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Peppoloni, L.; Lawrence, E.L.; Ruffaldi, E.; Valero-Cuevas, F.J. Characterization of the disruption of neural control strategies for dynamic fingertip forces from attractor reconstruction. PLoS ONE 2017, 12, e0172025. [Google Scholar] [CrossRef] [PubMed]
- Aston, P.J.; Nandi, M.; Christie, M.I.; Huang, Y.H. Comparison of Attractor Reconstruction and HRV Methods for Analysing Blood Pressure Data. Comput. Cardiol. 2014, 41, 437–440. [Google Scholar] [CrossRef]
- Lyle, J.; Charlton, P.; Bonet-Luz, E.; Chaffey, G.; Christie, M.; Nandi, M.; Aston, P. Beyond HRV: Analysis of ECG Signals Using Attractor Reconstruction. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017. [Google Scholar]
- Thanaj, M.; Chipperfield, A.J.; Clough, G.F. Attractor Reconstruction Analysis for Blood Flow Signals. IEEE Eng. Med. Biol. Soc. Annu. Int. Conf. 2019, 2019, 2281–2284. [Google Scholar] [CrossRef]
- van den Hoorn, W.; Hodges, P.W.; van Dieën, J.H.; Kerr, G.K. Reliability of recurrence quantification analysis of postural sway data. A comparison of two methods to determine recurrence thresholds. J. Biomech. 2020, 107, 109793. [Google Scholar] [CrossRef] [PubMed]
- Labini, F.S.; Meli, A.; Ivanenko, Y.P.; Tufarelli, D. Recurrence quantification analysis of gait in normal and hypovestibular subjects. Gait Posture 2012, 35, 48–55. [Google Scholar] [CrossRef]
- Riley, M.A.; Clark, S. Recurrence analysis of human postural sway during the sensory organization test. Neurosci. Lett. 2003, 342, 45–48. [Google Scholar] [CrossRef]
- Zimatore, G.; Gallotta, M.C.; Innocenti, L.; Bonavolontà, V.; Ciasca, G.; De Spirito, M.; Guidetti, L.; Baldari, C. Recurrence quantification analysis of heart rate variability during continuous incremental exercise test in obese subjects. Chaos 2020, 30, 033135. [Google Scholar] [CrossRef]
- Dimitriev, D.; Saperova, E.V.; Dimitriev, A.; Karpenko, Y. Recurrence Quantification Analysis of Heart Rate During Mental Arithmetic Stress in Young Females. Front. Physiol. 2020, 11, 40. [Google Scholar] [CrossRef]
- Billeci, L.; Marino, D.; Insana, L.; Vatti, G.; Varanini, M. Patient-specific seizure prediction based on heart rate variability and recurrence quantification analysis. PLoS ONE 2018, 13, e0204339. [Google Scholar] [CrossRef]
- Błażkiewicz, M. Joint loads and muscle force distribution during classical and jazz pirouettes. Acta Bioeng. Biomech. 2021, 23, 3–13. [Google Scholar] [CrossRef]
- Bläsing, B.; Schack, T. Mental Representation of Spatial Movement Parameters in Dance. Spat. Cogn. Comput. 2012, 12, 111–132. [Google Scholar] [CrossRef]
- Vaganova, A. Grundlagen des Klassischen Tanzes [Basic Principles of Classical Ballet]; Henschel: Berlin, Germany, 2002. [Google Scholar]
- Kleinow, T. Testing Continuous Time Models in Financial Markets. Ph.D Thesis, Humboldt-Universität zu Berlin, Wirtschaftswissenschaftliche Fakultät, Berlin, Germany, 2002. [Google Scholar]
- Kugiumtzis, D.; Tsimpiris, A. Measures of Analysis of Time Series (MATS): A MATLAB Toolkit for Computation of Multiple Measures on Time Series Data Bases. J. Stat. Softw. 2010, 33, 1–30. [Google Scholar] [CrossRef][Green Version]
- Zhivomirov, H.; Nedelchev, I. A Method for Signal Stationarity Estimation. Rom. J. Acoust. Vib. 2020, 17, 149–155. [Google Scholar]
- Mallika, M.C.; Suriya Prabhaa, S.; Asokan, K.; Anil Kumar, K.S.; Ramamohan, T.R.; Kumar, K.S. Testing for nonlinearity in nonstationary time series: A network-based surrogate data test. Phys. Rev. E 2021, 104, 054217. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Coloma, W.A.; Costa, A.L.; Pereira, C.; da Silva, C.A.M. Time Series Analysis for BWR Stability Studies. Nucl. Technol. 2020, 206, 554–564. [Google Scholar] [CrossRef]
- Wallot, S.; Mønster, D. Calculation of Average Mutual Information (AMI) and False-Nearest Neighbors (FNN) for the Estimation of Embedding Parameters of Multidimensional Time Series in Matlab. Front. Psychol. 2018, 9, 1679. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Baíllo, A.; Chacón, J.E. Chapter 1—Statistical outline of animal home ranges: An application of set estimation. In Handbook of Statistics; Srinivasa Rao, A.S.R., Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 44, pp. 3–37. [Google Scholar]
- Zhao, F. Extracting and representing qualitative behaviors of complex systems in phase space. Artif. Intell. 1994, 69, 51–92. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Jackson, E.S.; Tiede, M.; Riley, M.A.; Whalen, D.H. Recurrence Quantification Analysis of Sentence-Level Speech Kinematics. J. Speech Lang. Hear. Res. JSLHR 2016, 59, 1315–1326. [Google Scholar] [CrossRef]
- Yang, H. Tool Box of Recurrence Plot and Recurrence Quantification Analysis. Available online: https://www.mathworks.com/matlabcentral/fileexchange/58246-tool-box-of-recurrence-plot-and-recurrence-quantification-analysis (accessed on 2 June 2022).
- Yang, H. Multiscale recurrence quantification analysis of spatial cardiac vectorcardiogram signals. IEEE Trans. Biomed. Eng. 2011, 58, 339–347. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, H. Multiscale recurrence analysis of long-term nonlinear and nonstationary time series. Chaos Solitons Fractals 2012, 45, 978–987. [Google Scholar] [CrossRef]
- Nayak, S.K.; Bit, A.; Dey, A.; Mohapatra, B.; Pal, K. A Review on the Nonlinear Dynamical System Analysis of Electrocardiogram Signal. J. Healthc. Eng. 2018, 2018, 6920420. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Zaldivar-Comenges, J.-M.; Strozzi, F. Recurrence quantification based Liapunov exponents for monitoring divergence in experimental data. Phys. Lett. A 2002, 297, 173–181. [Google Scholar] [CrossRef]
- Riley, M.A.; Balasubramaniam, R.; Turvey, M.T. Recurrence quantification analysis of postural fluctuations. Gait Posture 1999, 9, 65–78. [Google Scholar] [CrossRef]
- Biringen, E.K. Analysis of pirouette execution for improved performance. Med. Probl. Perform. Artist. 2010, 25, 136–137. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zbilut, J.P.; Giuliani, A.; Webber, C.L. Detecting deterministic signals in exceptionally noisy environments using cross-recurrence quantification. Phys. Lett. A 1998, 246, 122–128. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Giuliani, A.; Webber, C.L. Recurrence quantification analysis and principal components in the detection of short complex signals. Phys. Lett. A 1998, 237, 131–135. [Google Scholar] [CrossRef]
- Webber, C.L.; Marwan, N.; Facchini, A.; Giuliani, A. Simpler methods do it better: Success of Recurrence Quantification Analysis as a general purpose data analysis tool. Phys. Lett. A 2009, 373, 3753–3756. [Google Scholar] [CrossRef]
- Mehdizadeh, S. The largest Lyapunov exponent of gait in young and elderly individuals: A systematic review. Gait Posture 2018, 60, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Newell, K.; Vaillancourt, D. Dimensional change in motor learning. Hum. Mov. Sci. 2001, 20, 695–715. [Google Scholar] [CrossRef]
- Stergiou, N.; Harbourne, R.T.; Cavanaugh, J.T. Optimal Movement Variability: A New Theoretical Perspective for Neurologic Physical Therapy. J. Neurol. Phys. Ther. 2006, 30, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Curtin, P.; Curtin, A.; Austin, C.; Gennings, C.; Tammimies, K.; Bölte, S.; Arora, M. Recurrence quantification analysis to characterize cyclical components of environmental elemental exposures during fetal and postnatal development. PLoS ONE 2017, 12, e0187049. [Google Scholar] [CrossRef] [PubMed]
- Burton, S.; Vicinanza, D.; Exell, T.; Newell, K.M.; Irwin, G.; Williams, G.K.R. Attractor dynamics of elite performance: The high bar longswing. Sports Biomech. 2021, 1–14. [Google Scholar] [CrossRef]

| Phase Space Reconstruction State Vector: y(t) = (x(t), x(t + τ), x(t + 2τ), …, x(t + (D − 1)τ)) from Original Time Series Data x(t) by Using Time Delay (τ) and Dimension of the Attractor D | |
|---|---|
| Possible ways of τ selection [24]: (1) Autocorrelation function (2) Mutual information | Possible ways of D selection: (1) Principal Component Analysis (PCA) [25] (2) Correlation dimension [26] (3) Box-counting [27] (4) False Nearest Neighbor (FNN) [28] |
| Group | Age [Years] | Body Mass [kg] | Body Height [m] | Training Period [Years] |
|---|---|---|---|---|
| N = 15 | 22.13 ± 2.73 | 57.56 ± 6.76 | 1.68 ± 0.62 | 12.19 ± 3.04 |
| LKNEx | LKNEy | LKNEz | CoMx | CoMy | CoMz | |
|---|---|---|---|---|---|---|
| Classic | 0.75 | 0.71 | 0.71 | 0.75 | 0.72 | 0.70 |
| Jazz | 0.76 | 0.66 | 0.70 | 0.73 | 0.69 | 0.75 |
| LKNEx | LKNEy | LKNEz | CoMx | CoMy | CoMz | |
|---|---|---|---|---|---|---|
| Classic | 1.53 | 1.43 | 2.05 | 2.11 | 1.44 | 1.3 |
| Jazz | 1.43 | 1.13 | 2.57 | 2.04 | 1.79 | 1.69 |
| allREC | dREC | allDET | dDET | allLMAX | dLMAX | allENT | dENT | allLAM | dLAM | allTT | dTT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LKNEx_J | 8.61 | 8.08 | 99.59 | 99.60 | 1018 | 1019 | 5.75 | 5.83 | 99.74 | 99.77 | 16.54 | 19.95 |
| LKNEy_J | 43.34 | 41.2 | 99.8 | 99.85 | 2212 | 2243 | 6.9 | 7.1 | 99.9 | 99.93 | 54.08 | 65.31 |
| LKNEz_J | 90.41 | 82.46 | 99.93 | 99.96 | 3935 | 3972 | 7.54 | 8.17 | 99.97 | 99.98 | 163.39 | 223.12 |
| LKNEx_C | 1.6 | 1.62 | 99.6 | 99.61 | 1246 | 1305 | 5.69 | 5.75 | 98.33 | 99.65 | 9.7 | 15.36 |
| LKNEy_C | 16.3 | 20.1 | 99.72 | 99.86 | 2109 | 2210 | 6.46 | 7.05 | 99.87 | 99.94 | 43.45 | 77.38 |
| LKNEz_C | 10.5 | 18.51 | 99.81 | 99.92 | 2425 | 2514 | 6.44 | 7.23 | 99.9 | 99.97 | 36.36 | 67.22 |
| CoMx_J | 2 | 2.87 | 99.73 | 99.76 | 915 | 945 | 6.29 | 6.30 | 99.74 | 99.85 | 16.2 | 20.82 |
| CoMy_J | 11.97 | 18.16 | 99.91 | 99.93 | 3939 | 3967 | 7.23 | 7.37 | 99.95 | 99.97 | 37.3 | 46.92 |
| CoMz_J | 86.35 | 86.52 | 99.98 | 99.98 | 3939 | 3963 | 8.23 | 8.26 | 99.99 | 99.99 | 261.59 | 262 |
| CoMx_C | 1.12 | 1.63 | 99.65 | 99.74 | 1536 | 1600 | 6.25 | 6.32 | 99.64 | 99.85 | 12.36 | 20.96 |
| CoMy_C | 9.84 | 12.74 | 99.87 | 99.93 | 3927 | 3987 | 6.83 | 7.14 | 99.95 | 99.98 | 38.04 | 55.04 |
| CoMz_C | 32.59 | 42.18 | 99.93 | 99.94 | 3927 | 3954 | 7.15 | 7.32 | 99.97 | 99.98 | 76.2 | 89.77 |
| REC | DET | LMAX | ENT | LAM | TT | |
|---|---|---|---|---|---|---|
| Jazz | 19.47 | 0.02 | 1.17 | 2.52 | 0.03 | 22.07 |
| Classic | 34.22 | 0.07 | 3.27 | 5.08 | 0.29 | 58.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Błażkiewicz, M. Evaluation of Geometric Attractor Structure and Recurrence Analysis in Professional Dancers. Entropy 2022, 24, 1310. https://doi.org/10.3390/e24091310
Błażkiewicz M. Evaluation of Geometric Attractor Structure and Recurrence Analysis in Professional Dancers. Entropy. 2022; 24(9):1310. https://doi.org/10.3390/e24091310
Chicago/Turabian StyleBłażkiewicz, Michalina. 2022. "Evaluation of Geometric Attractor Structure and Recurrence Analysis in Professional Dancers" Entropy 24, no. 9: 1310. https://doi.org/10.3390/e24091310
APA StyleBłażkiewicz, M. (2022). Evaluation of Geometric Attractor Structure and Recurrence Analysis in Professional Dancers. Entropy, 24(9), 1310. https://doi.org/10.3390/e24091310









