Opinion Dynamics with Higher-Order Bounded Confidence
Abstract
:1. Introduction
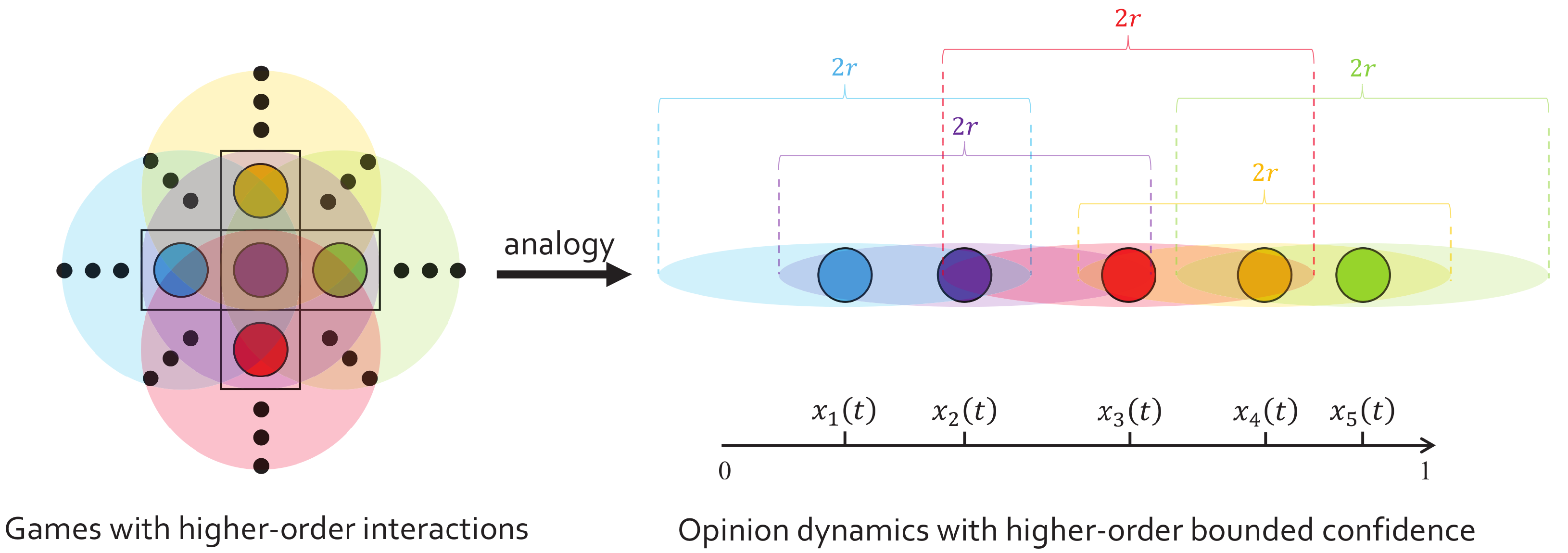
2. Model
3. Numerical Simulation
3.1. Experiment Design
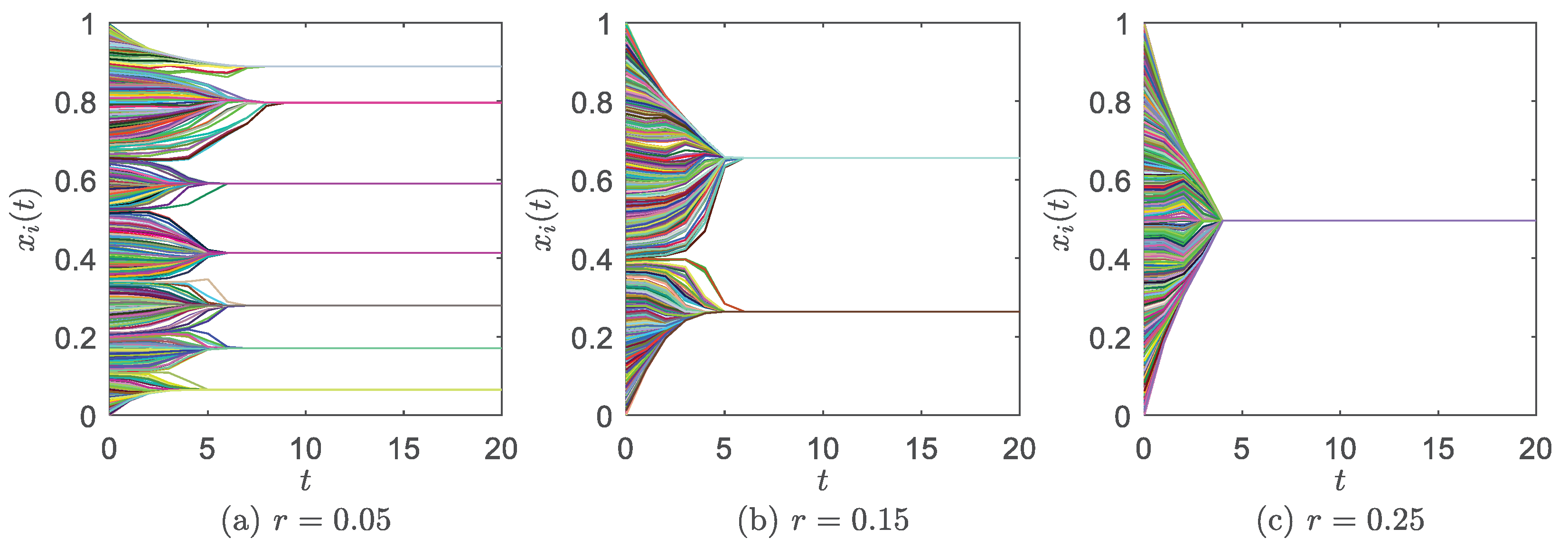
- , the frequency of consensus in multiple runs (). In a run, if there is only one opinion cluster left in the system (e.g., Figure 2c), we say the system achieves consensus;
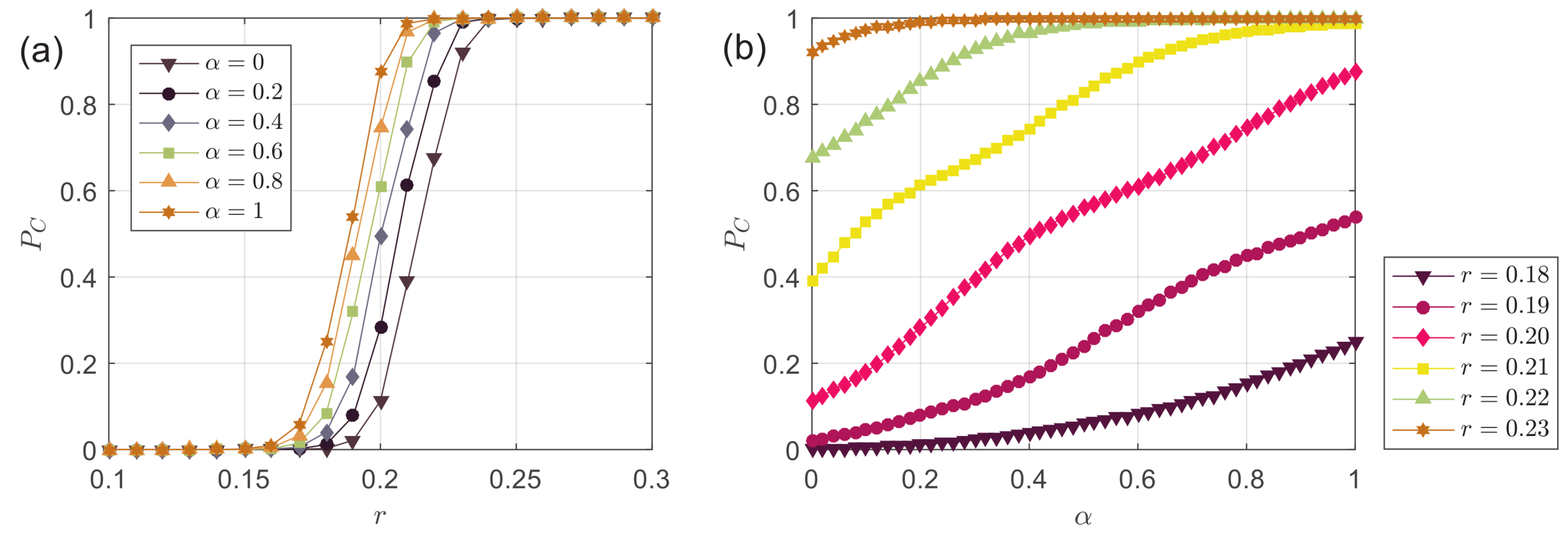
- , the lower bounded confidence above which the system may consistently achieve consensus (i.e., , , and , ). Similarly, , the upper bounded confidence below which the system cannot achieve consensus (i.e., , , and , );
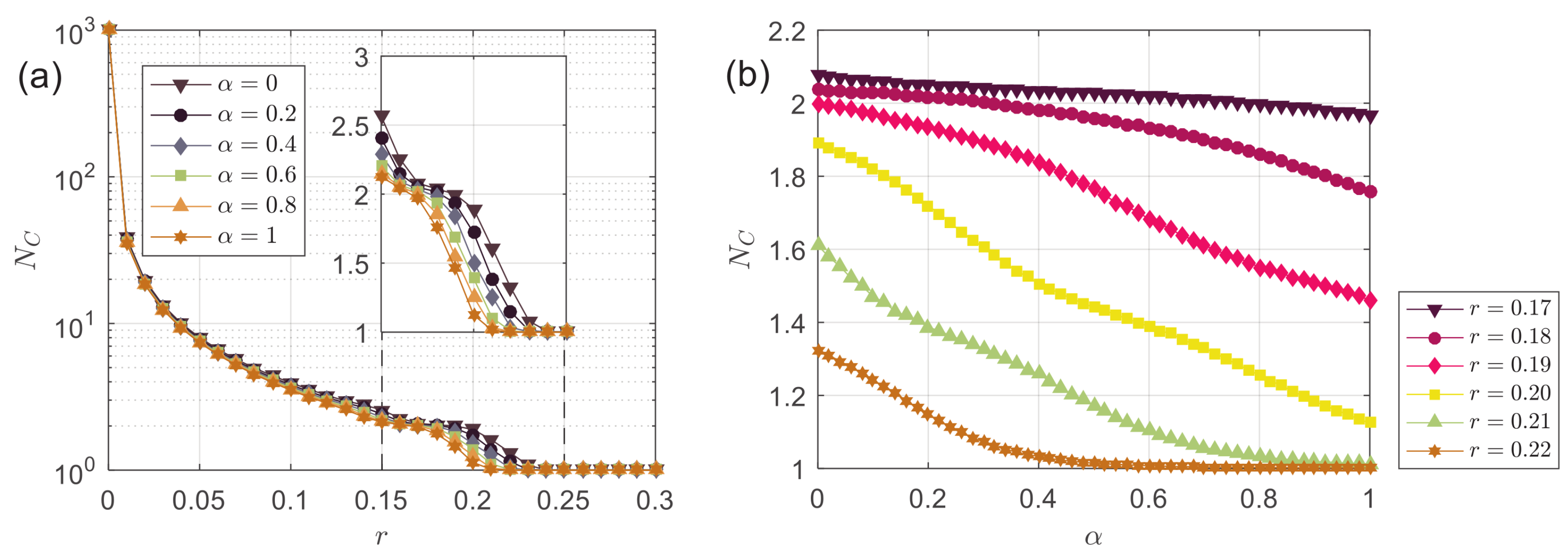
- , the number of opinion clusters. For example, in Figure 2a–c, we have , and , respectively. means the system achieves consensus;
- , the relative size of the largest opinion cluster. We find the opinion cluster with the highest number of agents and divide it by N. Obviously, this quantity yields ;
- , the distribution of stability opinions. We divide the range between 0 and 1 into 100 equal parts, and denote . If , we add 1 to the distribution function at the nth part (). After going through , we divide the result in each part by N, and acquire the normalized opinion distribution;
- , the convergence time. If , , then, we denote .
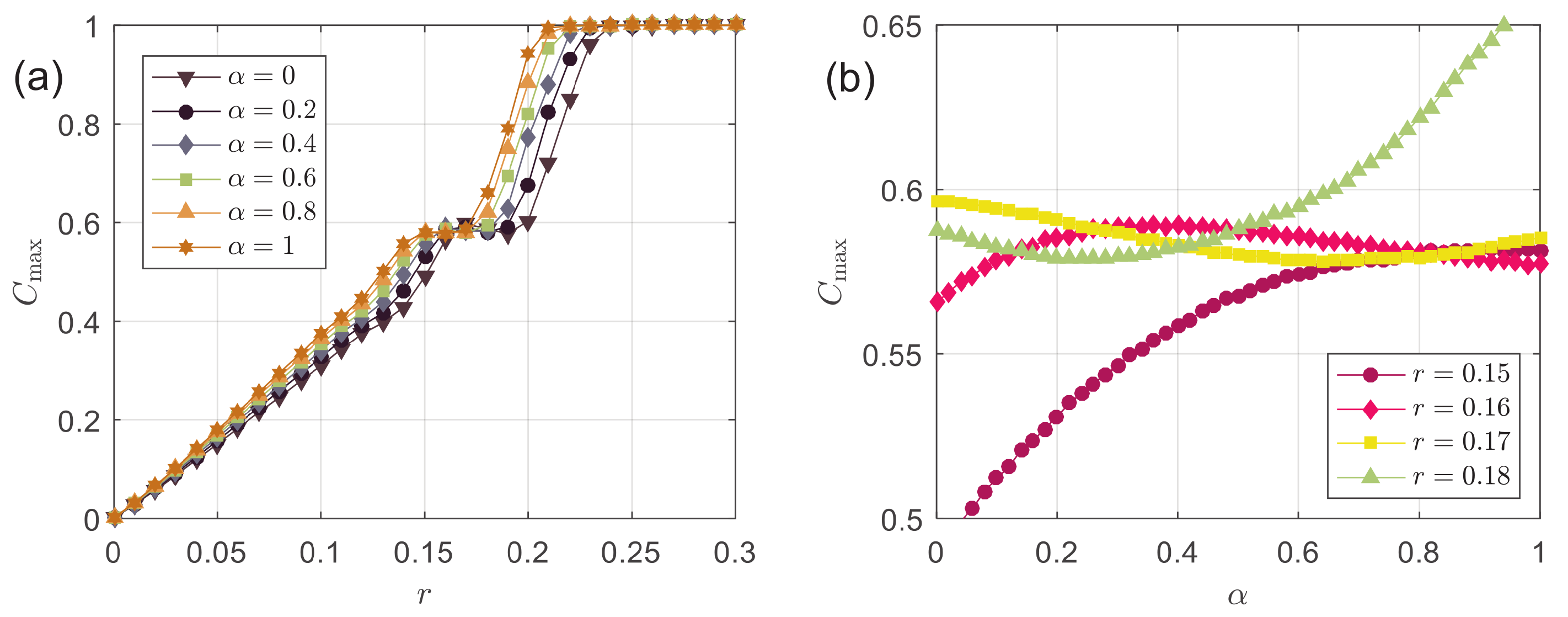
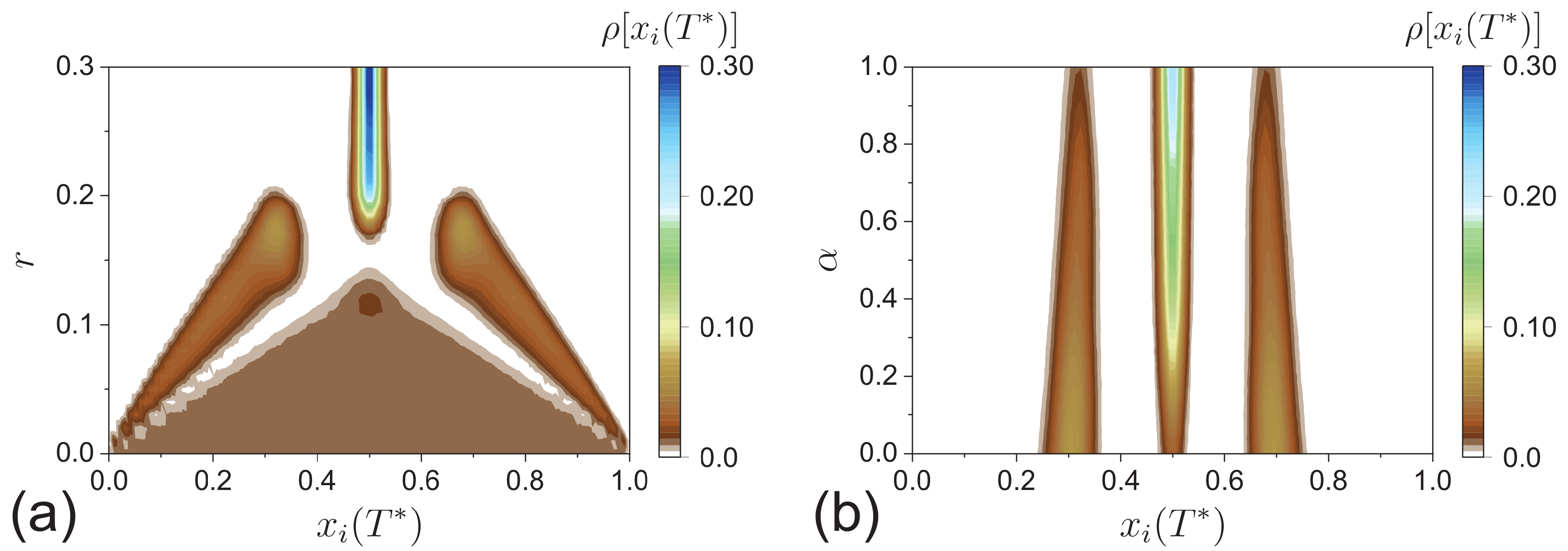
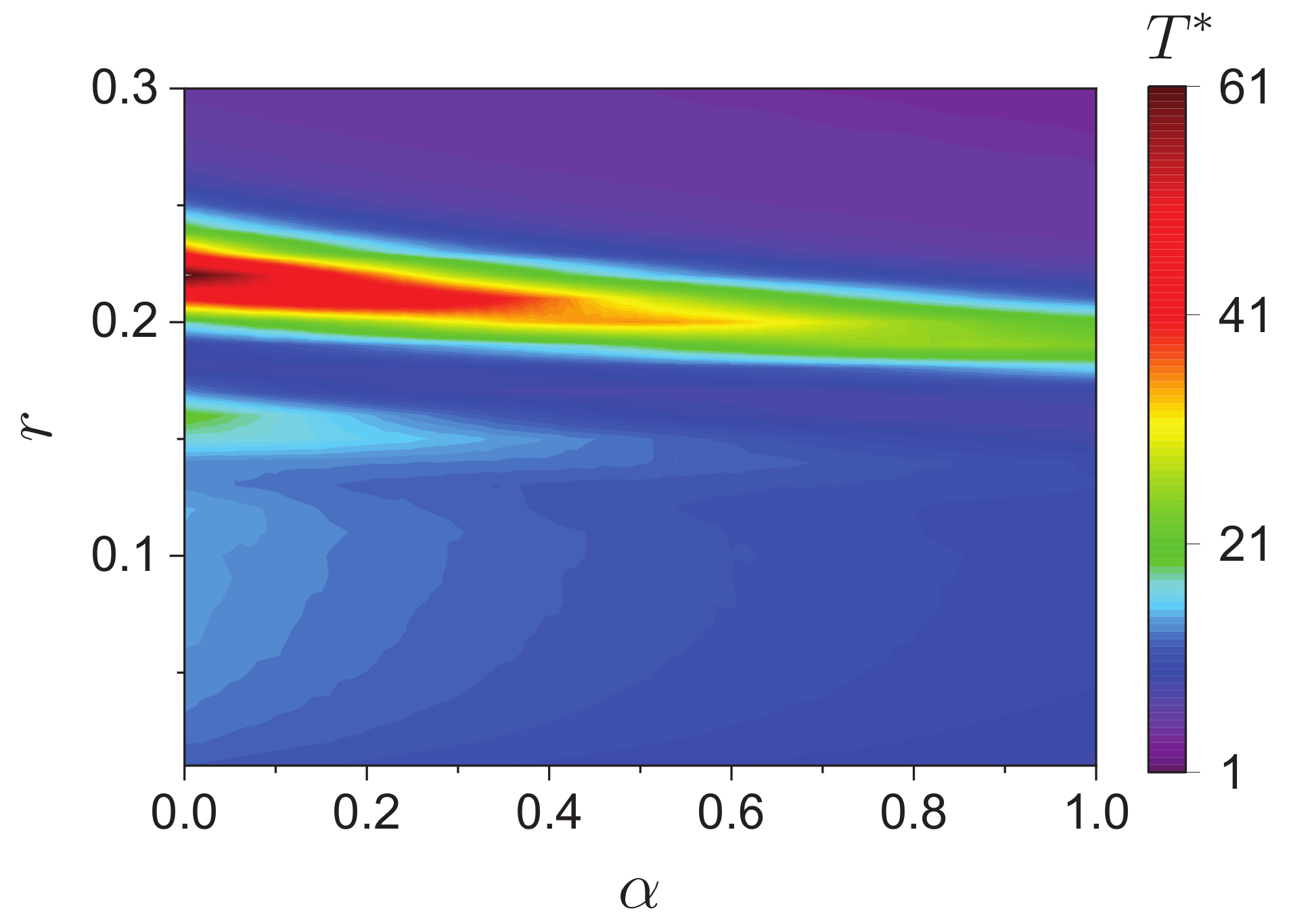
3.2. Results
3.3. Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Section Baumann, F.; Lorenz-Spreen, P.; Sokolov, I.M.; Starnini, M. Modeling echo chambers and polarization dynamics in social networks. Phys. Rev. Lett. 2020, 124, 048301. [Google Scholar] [CrossRef] [PubMed]
- Noorazar, H. Recent advances in opinion propagation dynamics: A 2020 survey. Eur. Phys. J. Plus 2020, 135, 521. [Google Scholar] [CrossRef]
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrika 1973, 60, 581–588. [Google Scholar] [CrossRef]
- Fernández-Gracia, J.; Suchecki, K.; Ramasco, J.J.; San Miguel, M.; Eguíluz, V.M. Is the voter model a model for voters? Phys. Rev. Lett. 2014, 112, 158701. [Google Scholar] [CrossRef]
- Jo, H.H.; Masuda, N. Finite-size effects on the convergence time in continuous-opinion dynamics. Phys. Rev. E 2021, 104, 014309. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Sznajd, J. Opinion evolution in closed community. Int. J. Mod. Phys. C 2000, 11, 1157–1165. [Google Scholar] [CrossRef]
- Pan, Q.; Qin, Y.; Xu, Y.; Tong, M.; He, M. Opinion evolution in open community. Int. J. Mod. Phys. C 2017, 28, 1750003. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Sznajd, J.; Weron, T. A review on the Sznajd model—20 years after. Phys. A Stat. Mech. Its Appl. 2021, 565, 125537. [Google Scholar] [CrossRef]
- Cheon, T.; Galam, S. Dynamical Galam model. Phys. Lett. A 2018, 382, 1509–1515. [Google Scholar] [CrossRef]
- Galam, S. The Trump phenomenon: An explanation from sociophysics. Int. J. Mod. Phys. B 2017, 31, 1742015. [Google Scholar] [CrossRef] [Green Version]
- Galam, S. Will Trump win again in the 2020 election? An answer from a sociophysics model. Phys. A Stat. Mech. Its Appl. 2021, 570, 125835. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Johnsen, E.C. Social influence and opinions. J. Math. Sociol. 1990, 15, 193–206. [Google Scholar] [CrossRef]
- Xu, H.Y.; Luo, Y.P.; Wu, J.W.; Huang, M.C. Hierarchical centralities of information transmissions in reaching a consensus. Phys. Lett. A 2019, 383, 432–439. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics and bounded confidence: Models, analysis, and simulation. J. Artif. Soc. Soc. Simul. 2002, 5, 1–33. [Google Scholar]
- Sunstein, C.R. Infotopia: How Many Minds Produce Knowledge; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Bhattacharyya, A.; Braverman, M.; Chazelle, B.; Nguyen, H.L. On the convergence of the Hegselmann–Krause system. In Proceedings of the 4th Conference on Innovations in Theoretical Computer Science, Berkeley, CA, USA, 9–12 January 2013; pp. 61–66. [Google Scholar]
- Chen, G.; Su, W.; Mei, W.; Bullo, F. Convergence properties of the heterogeneous Deffuant–Weisbuch model. Automatica 2020, 114, 108825. [Google Scholar] [CrossRef]
- Holzer, M.; Khatri, R. Pattern formation, traveling fronts and consensus versus fragmentation in a model of opinion dynamics. Phys. Lett. A 2017, 381, 3197–3202. [Google Scholar] [CrossRef]
- Han, W.; Feng, Y.; Qian, X.; Yang, Q.; Huang, C. Clusters and the entropy in opinion dynamics on complex networks. Phys. A Stat. Mech. Its Appl. 2020, 559, 125033. [Google Scholar] [CrossRef]
- Shang, L.; Chen, S. Opinion dynamics with decentralized proportional–integral control strategy. Phys. A Stat. Mech. Its Appl. 2019, 533, 121916. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Tang, M.; Kou, G. Bounded confidence opinion dynamics with opinion leaders and environmental noises. Comput. Oper. Res. 2016, 74, 205–213. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, S.; Li, W. Opinion dynamics model based on cognitive styles: Field-dependence and field-independence. Complexity 2019, 2019, 2864124. [Google Scholar] [CrossRef]
- Hou, J.; Li, W.; Jiang, M. Opinion dynamics in modified expressed and private model with bounded confidence. Phys. A Stat. Mech. Its Appl. 2021, 574, 125968. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, M.; Dong, Y.; Peng, Y. Fuzzy inference based Hegselmann–Krause opinion dynamics for group decision-making under ambiguity. Inf. Process. Manag. 2021, 58, 102671. [Google Scholar] [CrossRef]
- Han, W.; Huang, C.; Yang, J. Opinion clusters in a modified Hegselmann–Krause model with heterogeneous bounded confidences and stubbornness. Phys. A Stat. Mech. Its Appl. 2019, 531, 121791. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics under the influence of radical groups, charismatic leaders, and other constant signals: A simple unifying model. Netw. Heterog. Media 2015, 10, 477. [Google Scholar] [CrossRef]
- Brooks, H.Z.; Porter, M.A. A model for the influence of media on the ideology of content in online social networks. Phys. Rev. Res. 2020, 2, 023041. [Google Scholar] [CrossRef]
- Pineda, M.; Toral, R.; Hernández-García, E. The noisy Hegselmann-Krause model for opinion dynamics. Eur. Phys. J. B 2013, 86, 490. [Google Scholar] [CrossRef]
- Chazelle, B.; Jiu, Q.; Li, Q.; Wang, C. Well-posedness of the limiting equation of a noisy consensus model in opinion dynamics. J. Differ. Equations 2017, 263, 365–397. [Google Scholar] [CrossRef]
- Su, W.; Chen, G.; Hong, Y. Noise leads to quasi-consensus of Hegselmann–Krause opinion dynamics. Automatica 2017, 85, 448–454. [Google Scholar] [CrossRef]
- Chen, G.; Su, W.; Ding, S.; Hong, Y. Heterogeneous Hegselmann–Krause dynamics with environment and communication noise. IEEE Trans. Autom. Control 2019, 65, 3409–3424. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Dai, Q.; Han, W.; Feng, Y.; Cheng, H.; Li, H. Effects of heterogeneous convergence rate on consensus in opinion dynamics. Phys. A Stat. Mech. Its Appl. 2018, 499, 428–435. [Google Scholar] [CrossRef]
- Fu, G.; Zhang, W.; Li, Z. Opinion dynamics of modified Hegselmann–Krause model in a group-based population with heterogeneous bounded confidence. Phys. A Stat. Mech. Its Appl. 2015, 419, 558–565. [Google Scholar] [CrossRef]
- Cheng, C.; Yu, C. Opinion dynamics with bounded confidence and group pressure. Phys. A Stat. Mech. Its Appl. 2019, 532, 121900. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Chen, X.; Tang, S.; Zheng, Z. Modeling confirmation bias and peer pressure in opinion dynamics. Front. Phys. 2021, 9, 120. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, H.; Huang, C.; Han, W.; Dai, Q.; Li, H.; Yang, J. Deffuant model on a ring with repelling mechanism and circular opinions. Phys. Rev. E 2017, 95, 042118. [Google Scholar] [CrossRef]
- Gao, S.; Huang, C.; Han, W.; Yang, J. General consensus with circular opinion under attractive and repulsive mechanisms. Int. J. Mod. Phys. C 2020, 31, 2050068. [Google Scholar] [CrossRef]
- Dittmer, J.C. Consensus formation under bounded confidence. Nonlinear Anal. Theory, Methods Appl. 2001, 47, 4615–4621. [Google Scholar] [CrossRef]
- Vasca, F.; Bernardo, C.; Iervolino, R. Practical consensus in bounded confidence opinion dynamics. Automatica 2021, 129, 109683. [Google Scholar] [CrossRef]
- Bernardo, C.; Vasca, F.; Iervolino, R. Heterogeneous Opinion Dynamics with Confidence Thresholds Adaptation. IEEE Trans. Control. Netw. Syst. 2021. [Google Scholar] [CrossRef]
- Bernardo, C.; Altafini, C.; Vasca, F. Finite-time convergence of opinion dynamics in homogeneous asymmetric bounded confidence models. Eur. J. Control. 2022, 100674. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, F.; Zhu, J.; Zhang, Y. External activation promoting consensus formation in the opinion model with interest decay. Phys. Lett. A 2013, 377, 362–366. [Google Scholar] [CrossRef]
- Liu, X.; Huang, C.; Li, H.; Dai, Q.; Yang, J. The Combination of Pairwise and Group Interactions Promotes Consensus in Opinion Dynamics. Complexity 2021, 2021, 4382836. [Google Scholar] [CrossRef]
- Battiston, F.; Cencetti, G.; Iacopini, I.; Latora, V.; Lucas, M.; Patania, A.; Young, J.G.; Petri, G. Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 2020, 874, 1–92. [Google Scholar] [CrossRef]
- Battiston, F.; Amico, E.; Barrat, A.; Bianconi, G.; Ferraz de Arruda, G.; Franceschiello, B.; Iacopini, I.; Kéfi, S.; Latora, V.; Moreno, Y.; et al. The physics of higher-order interactions in complex systems. Nat. Phys. 2021, 17, 1093–1098. [Google Scholar] [CrossRef]
- Majhi, S.; Perc, M.; Ghosh, D. Dynamics on higher-order networks: A review. J. R. Soc. Interface 2022, 19, 20220043. [Google Scholar] [CrossRef]
- Iacopini, I.; Petri, G.; Barrat, A.; Latora, V. Simplicial models of social contagion. Nat. Commun. 2019, 10, 2485. [Google Scholar] [CrossRef]
- de Arruda, G.F.; Petri, G.; Moreno, Y. Social contagion models on hypergraphs. Phys. Rev. Res. 2020, 2, 023032. [Google Scholar] [CrossRef]
- Landry, N.W.; Restrepo, J.G. The effect of heterogeneity on hypergraph contagion models. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 103117. [Google Scholar] [CrossRef]
- Burgio, G.; Matamalas, J.T.; Gómez, S.; Arenas, A. Evolution of cooperation in the presence of higher-order interactions: From networks to hypergraphs. Entropy 2020, 22, 744. [Google Scholar] [CrossRef]
- Alvarez-Rodriguez, U.; Battiston, F.; de Arruda, G.F.; Moreno, Y.; Perc, M.; Latora, V. Evolutionary dynamics of higher-order interactions in social networks. Nat. Hum. Behav. 2021, 5, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Jia, D.; Sendiña-Nadal, I.; Zhang, M.; Wang, Z.; Li, X.; Alfaro-Bittner, K.; Moreno, Y.; Boccaletti, S. Evolutionary games on simplicial complexes. Chaos Solitons Fractals 2021, 150, 111103. [Google Scholar] [CrossRef]
- Neuhäuser, L.; Mellor, A.; Lambiotte, R. Multibody interactions and nonlinear consensus dynamics on networked systems. Phys. Rev. E 2020, 101, 032310. [Google Scholar] [CrossRef]
- Sahasrabuddhe, R.; Neuhäuser, L.; Lambiotte, R. Modelling nonlinear consensus dynamics on hypergraphs. J. Physics: Complex. 2021, 2, 025006. [Google Scholar]
- Hickok, A.; Kureh, Y.; Brooks, H.Z.; Feng, M.; Porter, M.A. A bounded-confidence model of opinion dynamics on hypergraphs. SIAM J. Appl. Dyn. Syst. 2022, 21, 1–32. [Google Scholar] [CrossRef]
- Horstmeyer, L.; Kuehn, C. Adaptive voter model on simplicial complexes. Phys. Rev. E 2020, 101, 022305. [Google Scholar] [CrossRef] [PubMed]
- Perc, M.; Gómez-Gardenes, J.; Szolnoki, A.; Floría, L.M.; Moreno, Y. Evolutionary dynamics of group interactions on structured populations: A review. J. R. Soc. Interface 2013, 10, 20120997. [Google Scholar] [CrossRef]
- Su, Q.; Li, A.; Wang, L.; Eugene Stanley, H. Spatial reciprocity in the evolution of cooperation. Proc. R. Soc. B 2019, 286, 20190041. [Google Scholar] [CrossRef]
- Chen, W.; Gracia-Lázaro, C.; Li, Z.; Wang, L.; Moreno, Y. Evolutionary dynamics of N-person Hawk–Dove games. Sci. Rep. 2017, 7, 4800. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C. Opinion Dynamics with Higher-Order Bounded Confidence. Entropy 2022, 24, 1300. https://doi.org/10.3390/e24091300
Wang C. Opinion Dynamics with Higher-Order Bounded Confidence. Entropy. 2022; 24(9):1300. https://doi.org/10.3390/e24091300
Chicago/Turabian StyleWang, Chaoqian. 2022. "Opinion Dynamics with Higher-Order Bounded Confidence" Entropy 24, no. 9: 1300. https://doi.org/10.3390/e24091300
APA StyleWang, C. (2022). Opinion Dynamics with Higher-Order Bounded Confidence. Entropy, 24(9), 1300. https://doi.org/10.3390/e24091300





