Consensus-Related Performance of Triplex MASs Based on Partial Complete Graph Structure
Abstract
:1. Introduction
- 1.
- Several novel triplex networks with partial complete graph structures are constructed by graph operations, and the related three-layered networks are also proposed;
- 2.
- Theory on graph spectra is applied to obtain the Laplacian spectrums. Methods on analysis are applied for the calculation of network coherence, and new results on the asymptotic behaviour are acquired;
- 3.
- We find that, under the condition that the number of nodes in partial complete substructures n tends to infinity, the coherence asymptotic behaviour of the considered non-isomorphic three-layered networks will increased by , which is irrelevant to the peripheral vertices parameter p. When p tends to infinity, the adding star copies operation will reverse the original size relationship of the coherence under the consideration of the novel triplex networks.
2. Preliminaries
2.1. Graph Theory and Notations
2.2. Relations for the Coherence and Laplacian Eigenvalues
3. Main Results
3.1. The Coherence for the Triplex Networks with
- (i).
- If , then it can be obtained that ;
- (ii).
- If , then .
- (1).
- repeated only once’
- (2).
- repeated n times;
- (3).
- repeated times;
- (4).
- with multiplicity 1;
- (5).
- repeated n times;
- (6).
- repeated times;
- (7).
- repeated 1 time;
- (8).
- repeated n times;
- (9).
- repeated times;
- (10).
- repeated times.
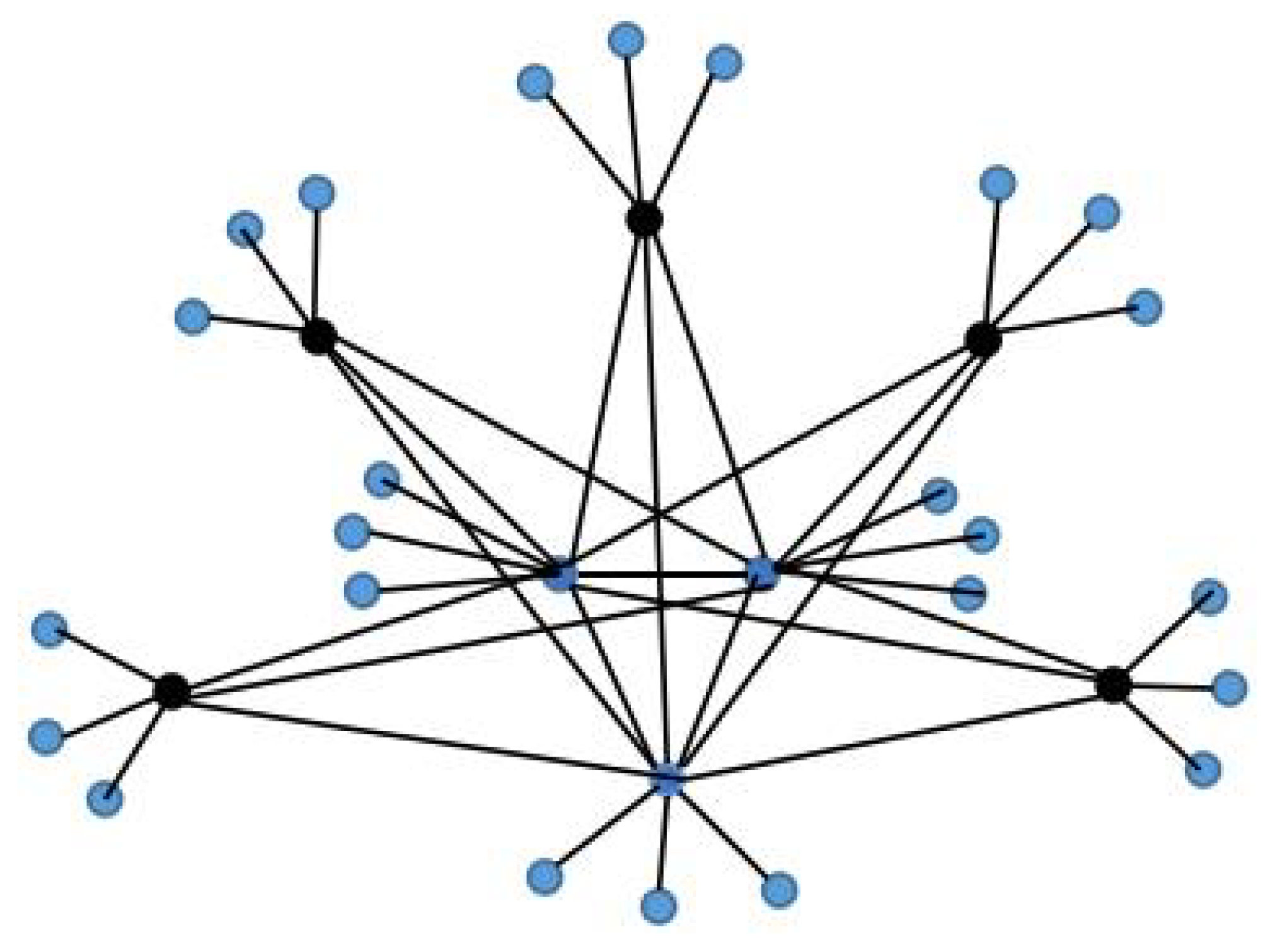
- (i).
- When n and r are fixed, as , and it is irrelevant to n;
- (ii).
- Let ; then, , it is irrelevant to p;
- (iii).
- If , then
- (i).
- Let n be fixed and ; then, it can be obtained that:
- (ii).
- If p is fixed, let ; then, ;

- (i).
- When n and r are fixed,
- (ii).
- Let , holds;
- (iii).
- If ,
3.2. Coherence for the Special Cases: Triplex Star/ Wheel/ Fan Graph
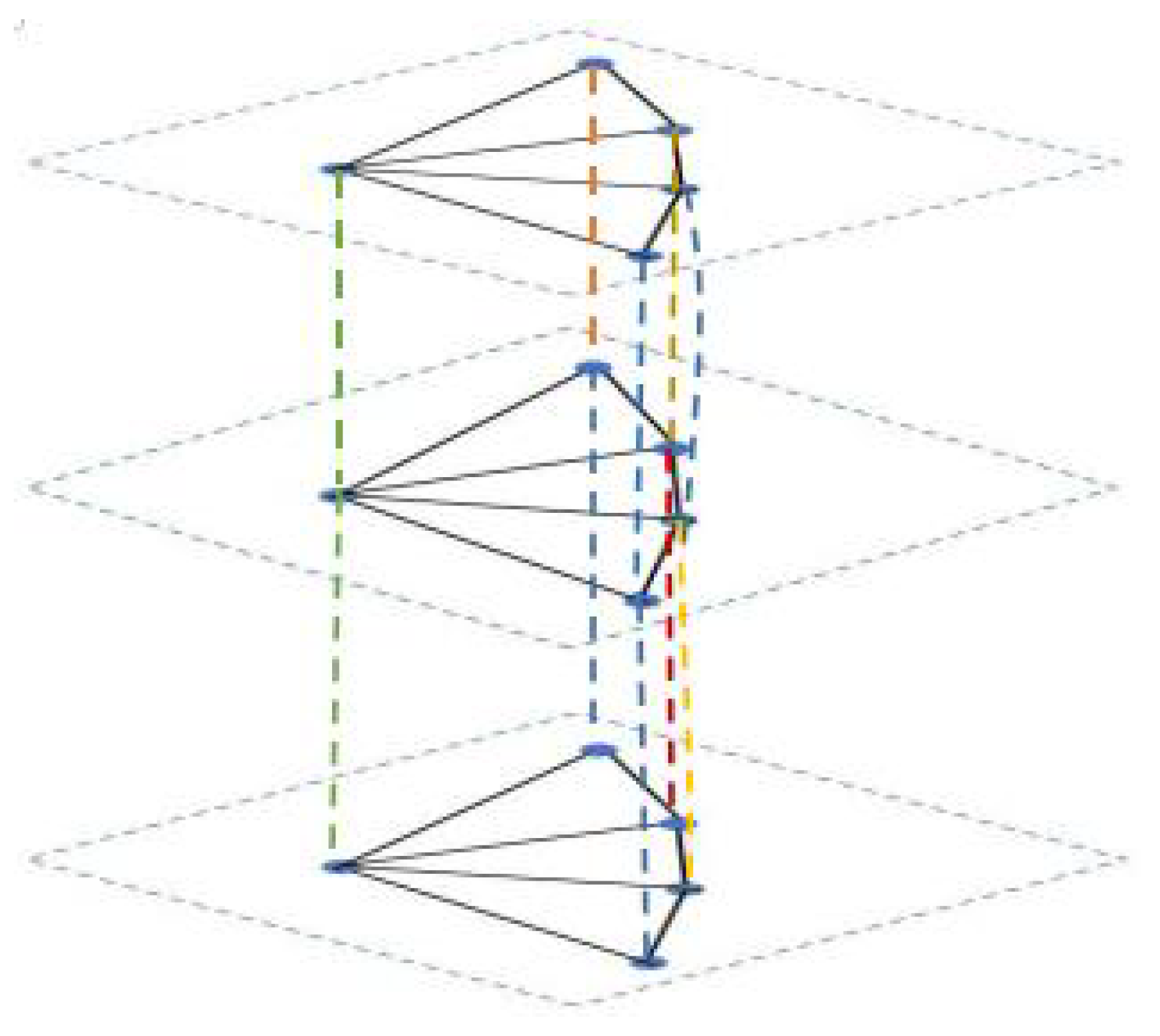
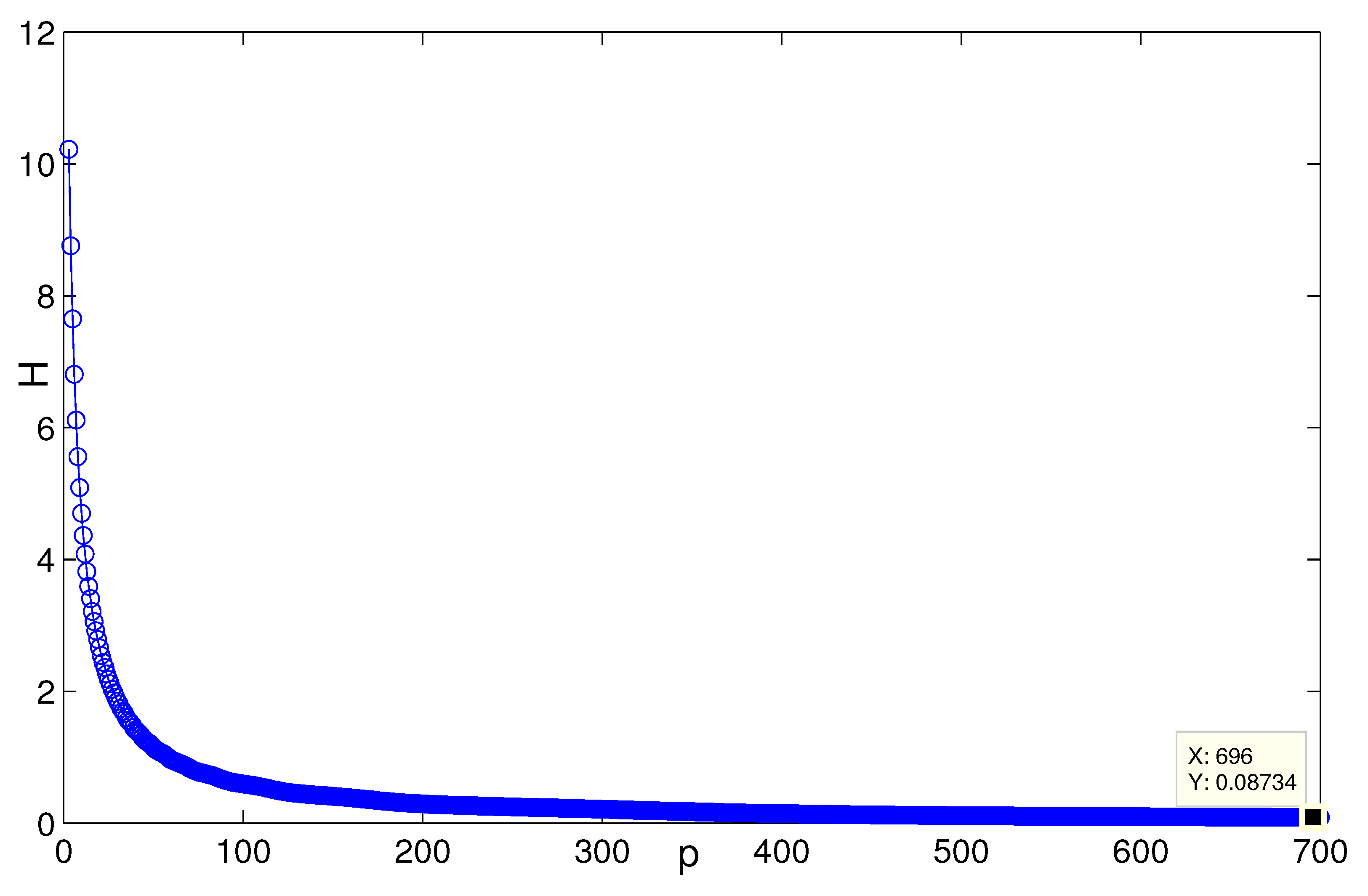
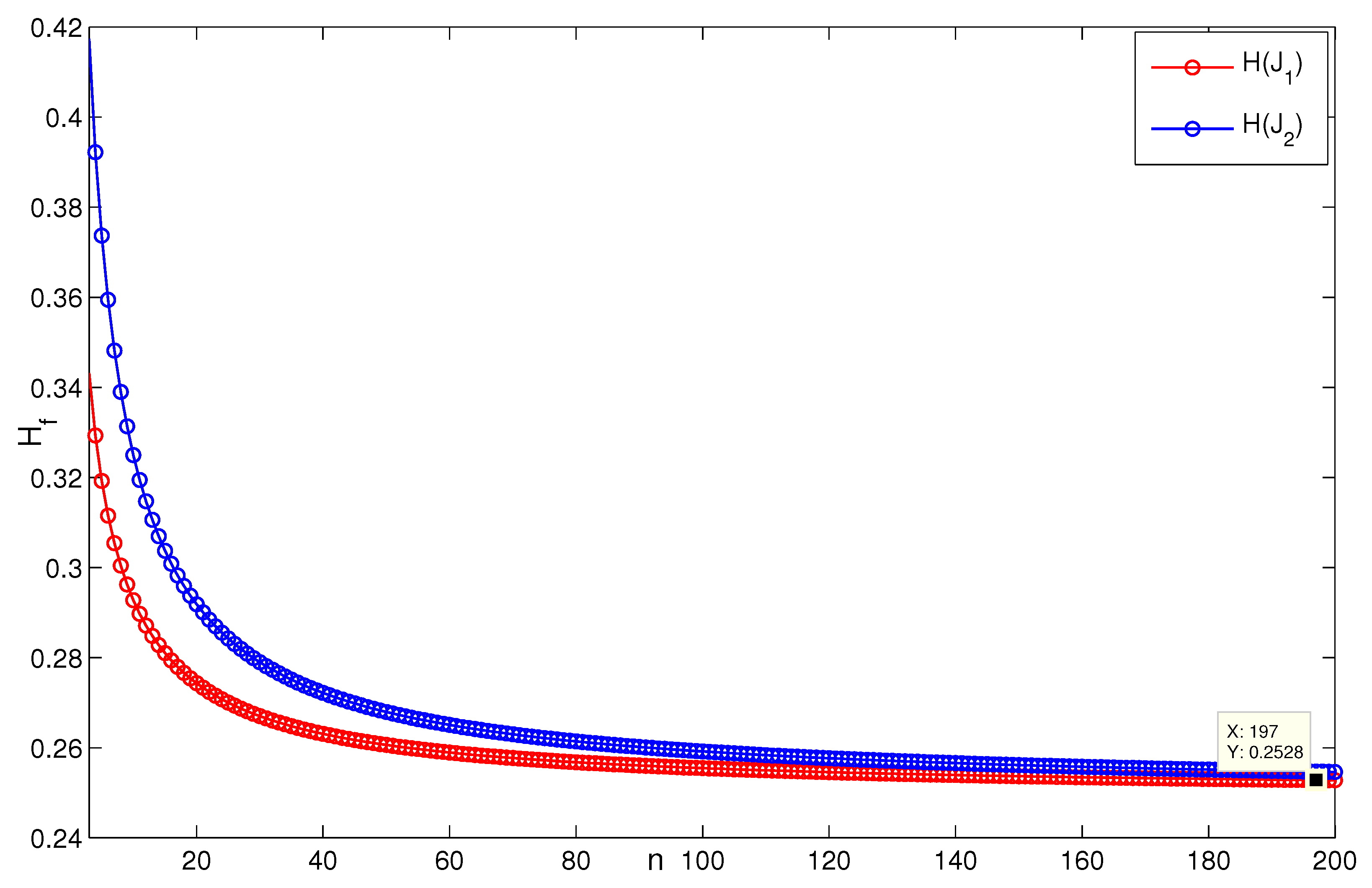
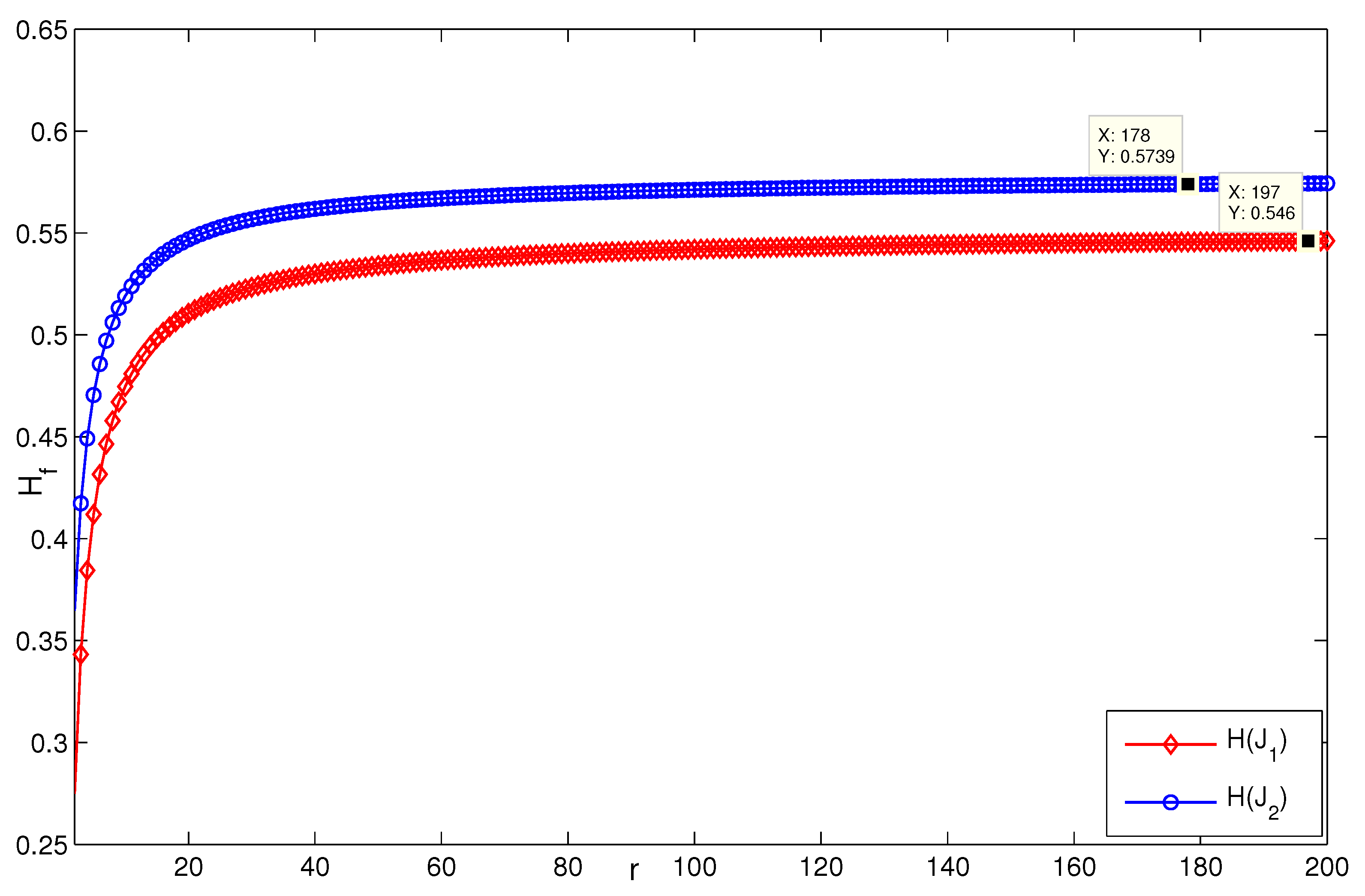
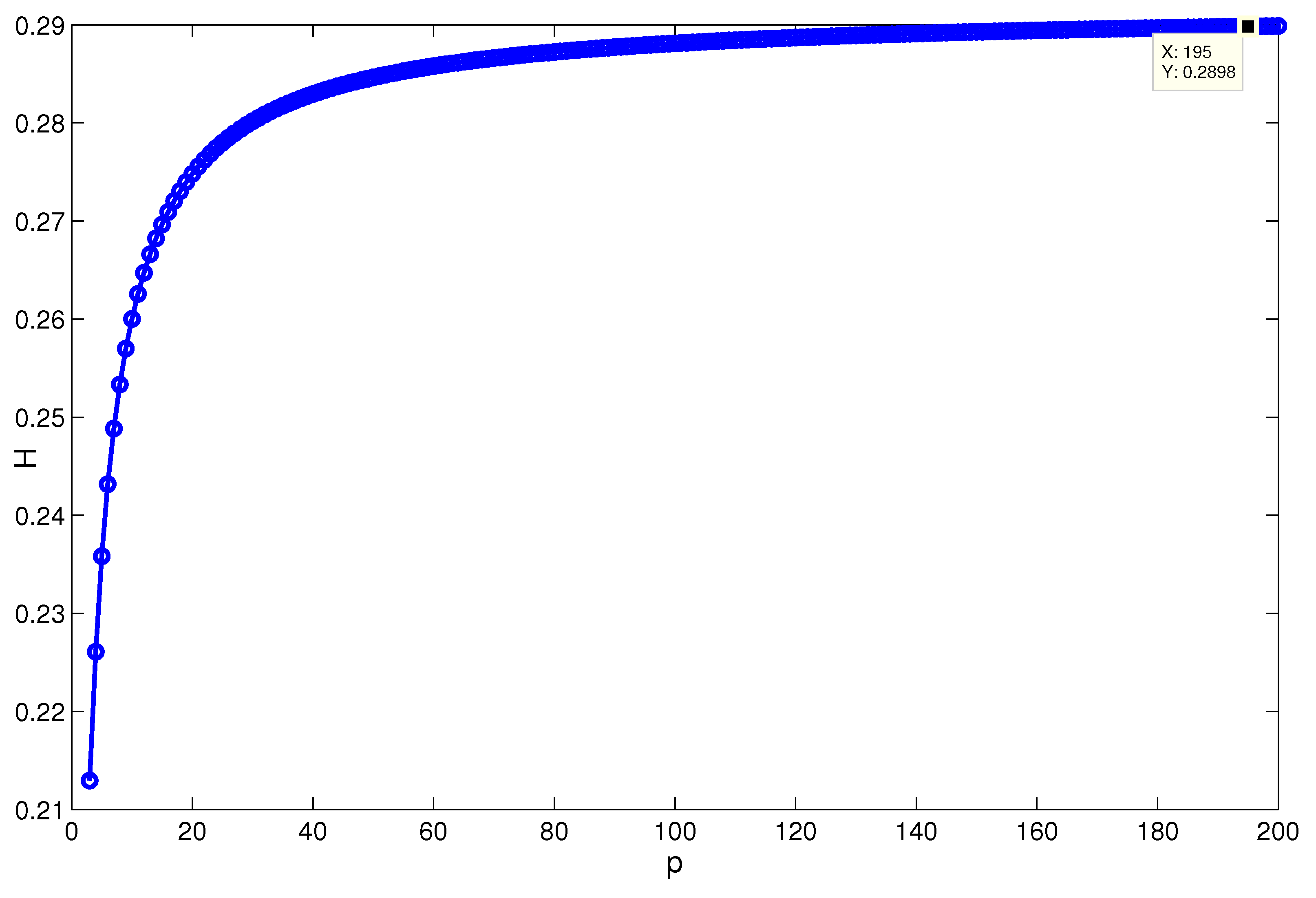
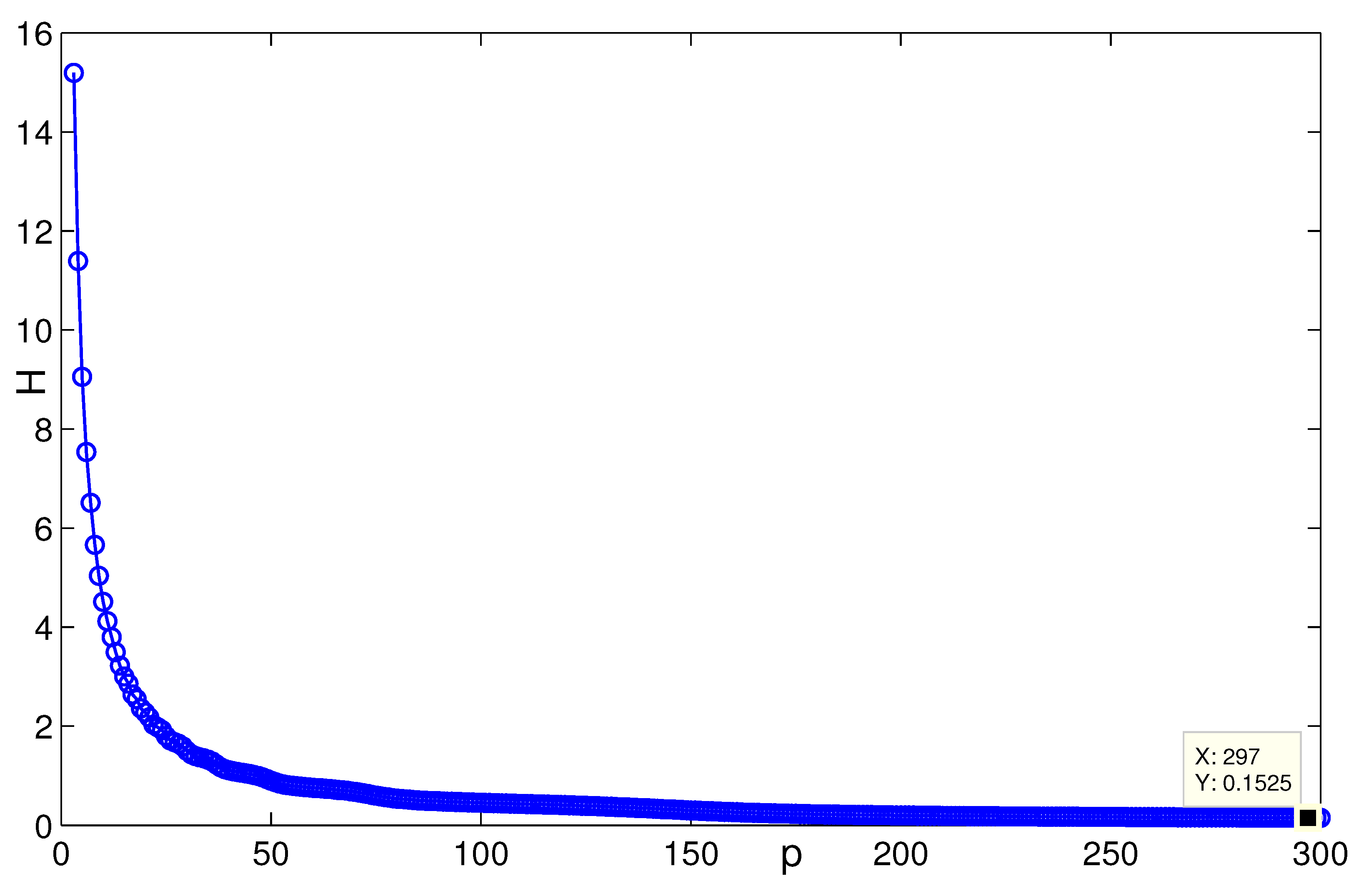
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saber, O.; Murray, R. Consensus problems in Networks of Agents With Switching Topology and Time-Delays. IEEE Trans. Autom. Control. 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ren, W. On consensus algorithms for double-integrator dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern.-Part Cybern. 2010, 40, 881–891. [Google Scholar]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications. Int. J. Control 2013, 86, 322–331. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, D.; Jiang, H.; Hu, C.; Yu, W. Distributed consensus for multiagent systems via directed spanning tree based adaptive control. Siam J. Control Optim. 2018, 56, 2189–2217. [Google Scholar] [CrossRef]
- Zhao, M.; Gu, C.; Zhao, L.; Liu, Y. Fixed-Time Leader-Following Consensus Tracking Control for Nonliear Multi-Agent Systems under Jointly Connected Graph. Entropy 2022, 24, 1130. [Google Scholar] [CrossRef]
- Huang, D.; Jiang, H.; Yu, Z.; Hu, C.; Fan, X. Cluster-delay consensus in MASs with layered intermittent communication: A multi-tracking approach. Nonlinear Dyn. 2019, 95, 1713–1730. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, S.; Jiang, H.; Mei, X. Distributed fixed-time optimization for multi-agent systems over a directed network. Nonlinear Dyn. 2021, 10, 1–15. [Google Scholar] [CrossRef]
- Sun, Y.; Li, W.; Zhao, D. Convergence time and speed of multi-agent systems in noisy environments. Chaos 2012, 22, 43126. [Google Scholar] [CrossRef]
- Young, G.; Scardovi, L.; Leonard, N. Robustness of Noisy Consensus Dynamics with Directed Communication. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6312–6317. [Google Scholar]
- Bamieh, B.; Jovanovi, M.R.; Mitra, P.; Patterson, S. Coherence in large-scale networks: Dimension-dependent limitations of local feedback. IEEE Trans. Autom. Control 2012, 57, 2235–2249. [Google Scholar] [CrossRef]
- Patterson, S.; Bamieh, B. Consensus and Coherence in Fractal Networks. IEEE Trans. Control. Netw. Syst. 2014, 1, 338–348. [Google Scholar] [CrossRef] [Green Version]
- Yi, Y.; Zhang, Z.; Shan, L.; Chen, G. Robustness of First-and Second-Order Consensus Algorithms for a Noisy Scale-Free Small-World Koch Network. IEEE Trans. Control. Syst. Technol. 2017, 25, 342–350. [Google Scholar] [CrossRef]
- Sun, W.; Hong, M.; Liu, S.; Fan, K. Leader-follower coherence in noisy ring-trees networks. Nonlinear Dyn. 2020, 102, 1–9. [Google Scholar] [CrossRef]
- Sun, W.; Li, L.; Zheng, S. Leader selection for coherence in symmetric and asymmetric trees. J. Stat. Mech. Theory Exp. 2021, 2021, 073401. [Google Scholar] [CrossRef]
- Huang, D.; Bian, J.; Jiang, H.; Yu, Z. Consensus indices of two-layered multi-star networks: An application of Laplacian spectrum. Front. Phys. 2021, 9, 803941. [Google Scholar] [CrossRef]
- Wan, Y.; Namuduri, K.; Akula, S.; Varanasi, M. The impact of multi-group multi-layer network structure on the performance of distributed consensus building strategies. Int. J. Robust. Nonlinear Control 2012, 23, 653–662. [Google Scholar] [CrossRef]
- Luo, H.; Wang, Y.; Zhan, R.; Zhang, X.; Wen, H.; Yang, S. Cluster-delay mean square consensus of stochastic multi-agent systems with impulse time windows. Entropy 2021, 23, 1033. [Google Scholar] [CrossRef]
- Li, X.; Yu, Z.; Jiang, H. Event-triggered fixed-time integral sliding mode control for nonlinear multi-agent systems with disturbances. Entropy 2021, 23, 1412. [Google Scholar] [CrossRef]
- Drauschke, F.; Sawicki, J.; Berner, R.; Omelchenko, I.; Sch<i>o</i>¨ll, E. Effect of topology upon relay synchronization in triplex neuronal networks. Chaos 2020, 30, 051104. [Google Scholar] [CrossRef]
- Gu, Y.; Shao, C.; Fu, X. Complete synchronization and stability of star-shaped complex networks. Chaos Solitons Fractals 2006, 28, 480–488. [Google Scholar] [CrossRef]
- Xu, M.M.; Lu, J.A.; Zhou, J. Synchronizability and eigenvalues of two-layer star networks. Acta Phys. Sin. 2016, 65, 028902. [Google Scholar]
- Hu, C.; He, H.; Jiang, H. Synchronization of complex-valued dynamic networks with intermittently adaptive coupling: A direct error method. Automatica 2020, 112, 108675. [Google Scholar] [CrossRef]
- Yang, F.; Jia, Z.; Deng, Y. Eigenvalue spectrum and synchronizability of two types of double-layer star-ring networks with hybrid directional coupling. Discret. Dyn. Nat. Soc. 2021, 2021, 6623648. [Google Scholar] [CrossRef]
- He, W.; Chen, G.; Han, Q.-L.; Du, W.; Cao, J.; Qian, F. Multiagent systems on multilayer networks: Synchronization analysis and network design. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1655–1667. [Google Scholar] [CrossRef]
- Kivela, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer, Networks, J. Complex Netw. 2014, 2, 203. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, C.; Chen, Z.; Chen, G. Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Trans. Cybern. 2021, 51, 1454–1462. [Google Scholar] [CrossRef]
- Rescigno, A. Optimally balanced spanning tree of the star network. IEEE Trans. Comput. 2001, 50, 88–91. [Google Scholar] [CrossRef]
- Cvetkovic, D.; Rowlinson, P.; Simic, S. An introduction to the Theory of Graph Spectra; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Barik, S.; Pati, S.; Sarma, B. The spectrum of the corona of two graphs. SIAM J. Discret. Math. 2007, 21, 47–56. [Google Scholar] [CrossRef]
- Liu, Q. The laplacian spectrum of corona of two graphs. Kragujev. J. Math. 2014, 38, 163–170. [Google Scholar] [CrossRef]
- Douglas, B. West, Introduction to Graph Theory, 2nd ed.; Pearson Education: Hong Kong, China, 2004. [Google Scholar]
- Zhang, Z.; Zhu, Y. Cyclic arc-connectivity in a Cartesian product digraph. Appl. Math. Lett. 2010, 23, 796–800. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Meng, J. The restricted arc connectivity of Cartesian product digraphs. Inf. Process. Lett. 2009, 109, 1202–1205. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, J.; Huang, D.; Xu, J.; Yu, Z. Consensus-Related Performance of Triplex MASs Based on Partial Complete Graph Structure. Entropy 2022, 24, 1296. https://doi.org/10.3390/e24091296
Bian J, Huang D, Xu J, Yu Z. Consensus-Related Performance of Triplex MASs Based on Partial Complete Graph Structure. Entropy. 2022; 24(9):1296. https://doi.org/10.3390/e24091296
Chicago/Turabian StyleBian, Jicheng, Da Huang, Jiabo Xu, and Zhiyong Yu. 2022. "Consensus-Related Performance of Triplex MASs Based on Partial Complete Graph Structure" Entropy 24, no. 9: 1296. https://doi.org/10.3390/e24091296
APA StyleBian, J., Huang, D., Xu, J., & Yu, Z. (2022). Consensus-Related Performance of Triplex MASs Based on Partial Complete Graph Structure. Entropy, 24(9), 1296. https://doi.org/10.3390/e24091296




