Discovering Noncritical Organization: Statistical Mechanical, Information Theoretic, and Computational Views of Patterns in One-Dimensional Spin Systems
Abstract
:1. Introduction
1.1. Historical Context
1.2. Focus
1.3. Applications
1.4. Overview
2. Statistical Mechanics
2.1. Spin Systems: Notation and Definitions
2.2. Statistical Mechanical Measures of Structure
2.2.1. Correlation Function and Correlation Length
2.2.2. Susceptibility and Structure Factors
2.2.3. Specific Heat
2.3. Other Statistical Mechanical Approaches to Structure
3. Information Theory
3.1. Shannon Entropy: Its Forms and Uses
3.2. Entropy Growth
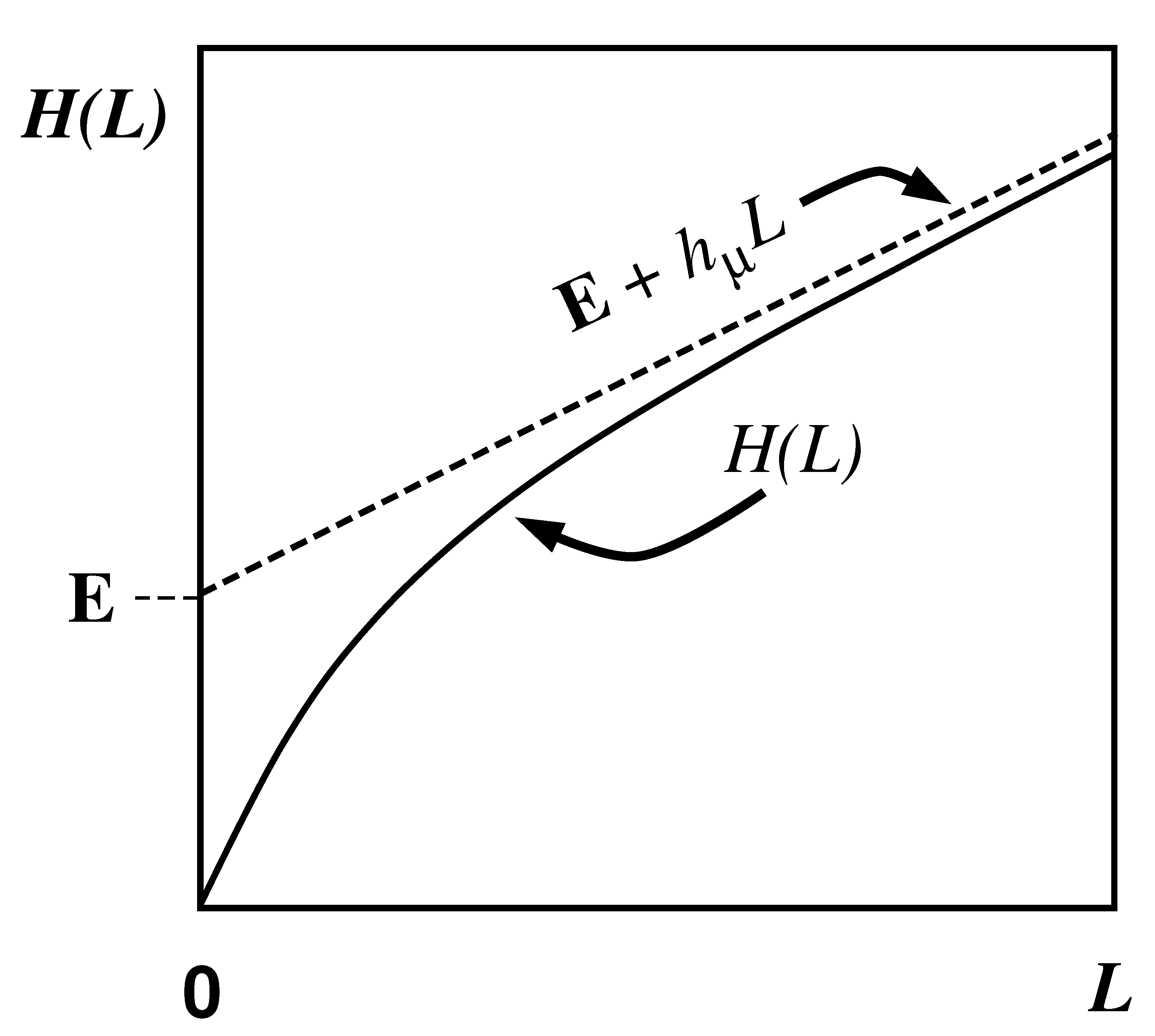
3.3. Entropy Density and Convergence to It
3.4. Density, Rate, and Algorithmic Complexity
3.5. Redundancy
3.6. Shannon’s Coding Theorems
3.7. Two-Spin Mutual Information
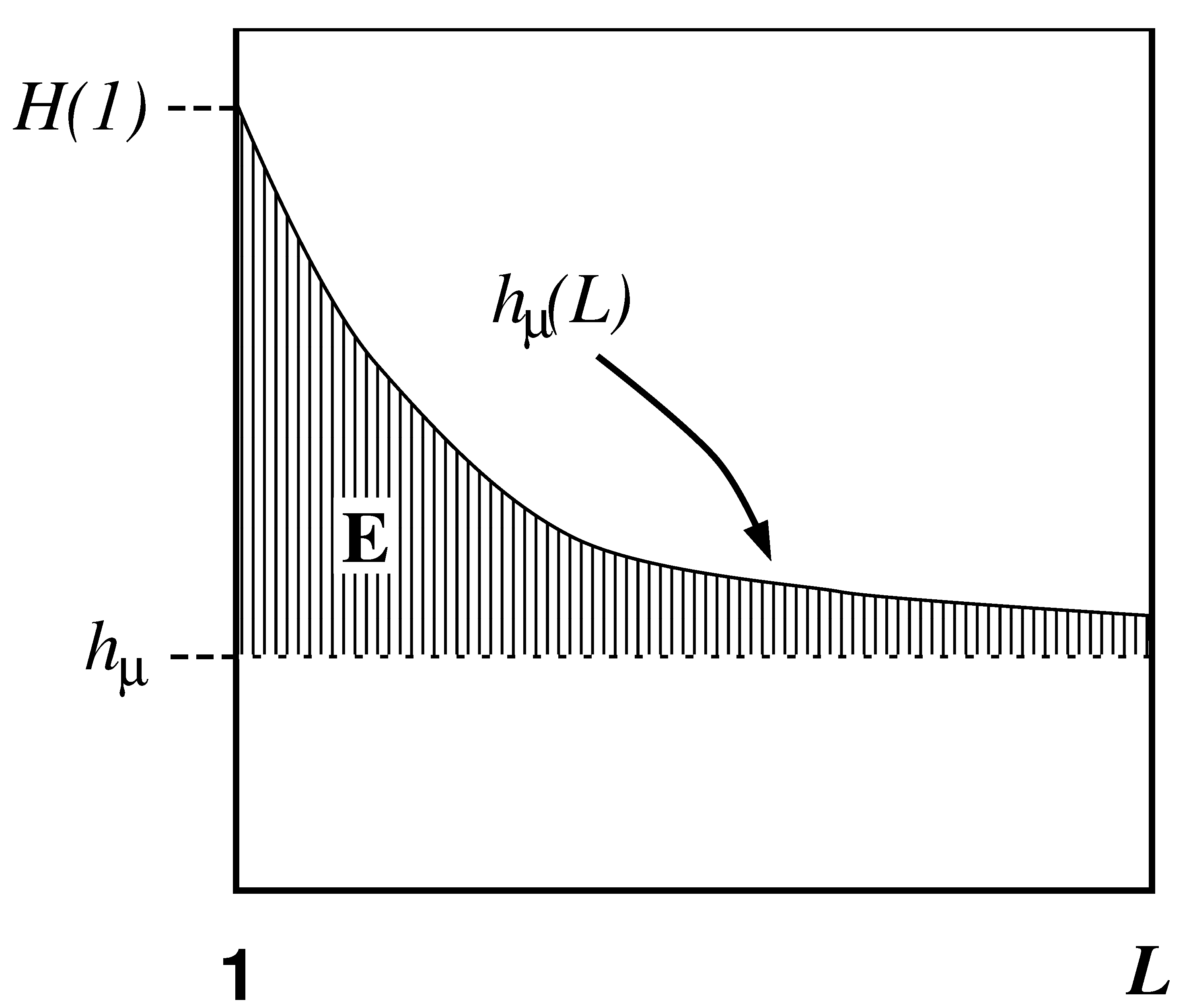
3.8. Excess Entropy
3.9. Correlation Information
3.10. Information Theoretic Approaches to Structure in Dynamics, Statistical Physics, and Elsewhere
4. Computational Mechanics
4.1. Effective States: Preliminary Examples
4.1.1. Fair Coin Configuration
4.1.2. Period-1 Configuration
4.1.3. Period-2 Configuration
4.1.4. Noisy Period-2 Configuration
4.1.5. Summary of Examples
4.2. Causal States and -Machines
4.3. Related Computational and Statistical Model Classes
4.4. What Do -Machines Represent?
4.5. Global Spatial Properties from -Machines
4.5.1. Statistical Complexity
4.5.2. Block Distributions and Entropies
4.5.3. Two-Spin Mutual Information and Correlation Function
4.5.4. -Machine Entropy Rate
4.5.5. -Machine Excess Entropy
4.5.6. Relationships between Measures of Memory
4.5.7. The examples Analyzed Quantitatively
4.5.8. Scan-Direction Invariance
4.5.9. Related, or Not, “Complexity” Measures
4.5.10. -Machine Thermodynamics
4.6. Summary and a Look Ahead
5. Computational Mechanics of One-Dimensional Spin Systems
5.1. Calculational Methods
5.1.1. Determination of Recurrent Causal States
5.1.2. Causal State Transitions
5.1.3. Spin System Statistical Complexity
5.1.4. Spin System Entropy Density
5.1.5. Spin System Excess Entropy
5.1.6. Relationships between Spin System Memory Measures
5.2. Spin-1/2 Nearest-Neighbor Systems
5.2.1. -Machines for the Spin-, Nearest-Neighbor Ising Model
5.2.2. Paramagnet
5.2.3. Ferromagnetic Coupling
5.2.4. Antiferromagnetic Coupling
5.2.5. General Remarks
5.3. Spin- Next-Nearest Neighbor Ising System
6. Excess Entropy Is a Wavelength-Independent Measure of Periodic Structure
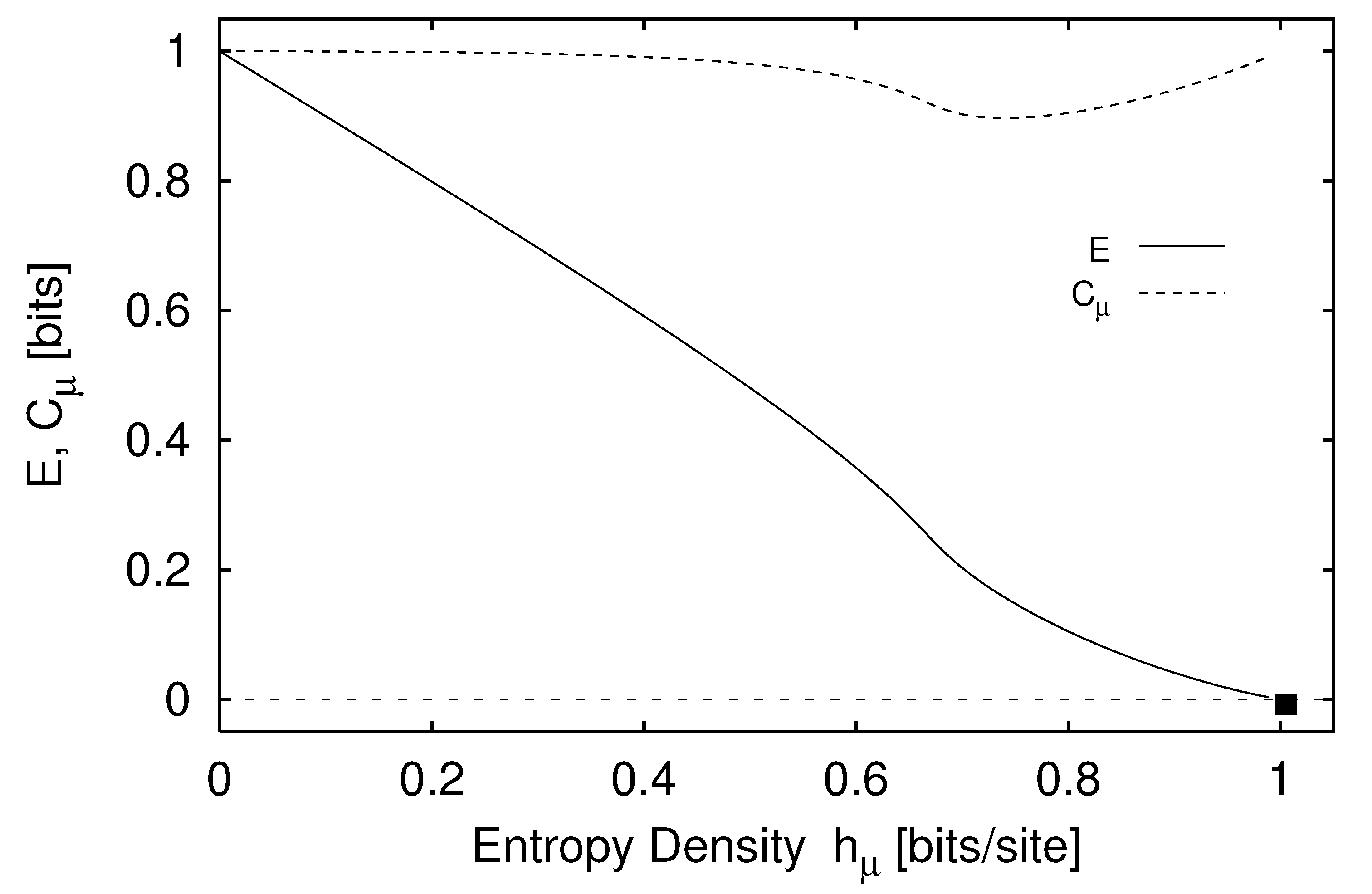
7. -Machines Reveal Structural Features in Entropic Processes
7.1. Discovering and Describing Entropic Patterns
7.2. Detecting Entropic Patterns
8. Phenomenological Comparison of Excess Entropy and Statistical Mechanical Quantities
8.1. Excess Entropy versus Correlation Length
8.2. Excess Entropy versus Specific Heat
8.3. Excess Entropy versus Particular Structure Factors
8.4. Excess Entropy versus (1)
8.5. Phenomenological Observations
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. On the Equivalence Relation∼that Induces Causal States
- reflexive: ;
- symmetric: ; and
- transitive: .
- .
- .
- .
- If , either
- (a)
- or
- (b)
- .
- The causal states are a partition of . That is,
- (a)
- for each ,
- (b)
- , and
- (c)
- for all .
- The index —the state’s “name”.
- The set of left-half configurations, of various lengths, comprising the equivalence class: .
- A conditional distribution over right-half configurations: . We denote this distribution more concisely by .
Appendix B. Transient Structure from the Recurrent ϵ-Machine
- Initialize: Given a recurrent -machine determine the asymptotic probability of the recurrent causal states via Equation (63). This distribution is the starting node for the tree and is indicated in Figure A1 by the node with the double oval. At this stage is a leaf, since we have not yet determined all the links (transitions) that leave it. Thus, and .
- Build Transient Tree: While is nonempty:
- (a)
- Determine Links: For each leaf draw a link (an outgoing transition) for each spin value s. Label the link with the transition probability that starting in node n spin value s is seen:If the transition has zero probability, ignore .
- (b)
- Form Node Distributions: For each link determine the probability distribution to which it leads using:Note that the term in the denominator is simply a normalization. The quantity gives the updated distribution over recurrent causal states after having observed the particular spin sequence . Recall that, since the -machine is deterministic, if the transition is allowed and 0 otherwise.
- (c)
- Merge Duplicate Nodes: Now consider, in turn, the probability distributions just formed: . Is n identical to another node distribution ?
- If yes, then connect to node .
- If no, add n to the set of tree leaves.
- Minimize: The resulting machine has a recurrent part that is identical to , but it may not be minimal. Merge nodes pairwise under the equivalence relation ∼ of Equation (53). The result is the complete -machine, with all transient and recurrent states.




Appendix C. ϵ-Machine Entropy Density
References
- Feldman, D.P. Computational Mechanics of Classical Spin Systems. Ph.D. Thesis, University of California, Davis, CA, USA, 1998. [Google Scholar]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos 2003, 13, 25–54. [Google Scholar] [CrossRef] [PubMed]
- Feldman, D.P.; Crutchfield, J.P. Structural information in two-dimensional patterns: Entropy convergence and excess entropy. Phys. Rev. E 2003, 67, 051104. [Google Scholar] [CrossRef] [PubMed]
- Feldman, D.P.; McTague, C.S.; Crutchfield, J.P. The organization of intrinsic computation: Complexity-entropy diagrams and the diversity of natural information processing. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 043106. [Google Scholar] [CrossRef] [PubMed]
- Robinson, M.D.; Feldman, D.P.; McKay, S.R. Local entropy and structure in a two-dimensional frustrated system. Chaos 2011, 21, 037114. [Google Scholar] [CrossRef] [PubMed]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037109. [Google Scholar] [CrossRef]
- Riechers, P.; Crutchfield, J.P. Spectral simplicity of apparent complexity, Part I: The nondiagonalizable metadynamics of prediction. Chaos 2018, 28, 033115. [Google Scholar] [CrossRef]
- Riechers, P.M.; Crutchfield, J.P. Beyond the spectral theorem: Decomposing arbitrary functions of nondiagonalizable operators. AIP Adv. 2018, 8, 065305. [Google Scholar] [CrossRef]
- Riechers, P.; Crutchfield, J.P. Spectral simplicity of apparent complexity, Part II: Exact complexities and complexity spectra. Chaos 2018, 28, 033116. [Google Scholar] [CrossRef]
- Vijayaraghavan, V.S.; James, R.G.; Crutchfield, J.P. Anatomy of a spin: The information-theoretic structure of classical spin systems. Entropy 2017, 19, 214. [Google Scholar] [CrossRef]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. “dit“: A Python package for discrete information theory. J. Open Source Softw. 2018, 3, 738. [Google Scholar] [CrossRef]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural Comput. 2001, 13, 2409–2463. [Google Scholar] [CrossRef] [PubMed]
- Prokopenko, M.; Boschetti, F.; Ryan, A.J. An information-theoretic primer on complexity, self-organization, and emergence. Complexity 2009, 15, 11–28. [Google Scholar] [CrossRef]
- Crutchfield, J.P. Between order and chaos. Nat. Phys. 2012, 8, 17–24. [Google Scholar] [CrossRef]
- Crutchfield, J.P. Is anything ever new? Considering emergence. In Complexity: Metaphors, Models, and Reality, Volume XIX of Santa Fe Institute Studies in the Sciences of Complexity; Cowan, G., Pines, D., Melzner, D., Eds.; Addison-Wesley: Reading, MA, USA, 1994; pp. 479–497. [Google Scholar]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics, and induction. Phys. D 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, reprinted in The Mathematical Theory of Communication; Shannon, C.E.,Weaver, W., Eds.; University of Illinois Press: Champaign, IL, USA, 1963.. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Kolmogorov, A.N. A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl. Akad. Nauk. SSSR 1958, 119, 861–864. (In Russian) Math. Rev. vol. 21, no. 2035a [Google Scholar]
- Sinai, J.G. On the concept of entropy of a dynamical system. Dokl. Akad. Nauk. SSSR 1959, 124, 768–771. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Beck, C.; Schlögl, F. Thermodynamics of Chaotic Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Huberman, B.A.; Hogg, T. Complexity and adaptation. Phys. D 1986, 22, 376–384. [Google Scholar] [CrossRef]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Intl. J. Theo. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Packard, N.H. Symbolic dynamics of noisy chaos. Phys. D 1983, 7, 201–223. [Google Scholar] [CrossRef]
- Szépfalusy, P.; Györgyi, G. Entropy decay as a measure of stochasticity in chaotic systems. Phys. Rev. A 1986, 33, 2852–2855. [Google Scholar] [CrossRef] [PubMed]
- Wolfram, S. Universality and complexity in cellular automata. Physica 1984, 10D, 1–35. [Google Scholar]
- Shaw, R. The Dripping Faucet as a Model Chaotic System; Aerial Press: Santa Cruz, CA, USA, 1984. [Google Scholar]
- Bennett, C.H. On the nature and origin of complexity in discrete, homogeneous locally-interacting systems. Found. Phys. 1986, 16, 585–592. [Google Scholar] [CrossRef]
- Lindgren, K.; Norhdal, M.G. Complexity measures and cellular automata. Complex Syst. 1988, 2, 409–440. [Google Scholar]
- Li, W. On the relationship between complexity and entropy for Markov chains and regular languages. Complex Syst. 1991, 5, 381–399. [Google Scholar]
- Wackerbauer, B.; Witt, A.; Atmanspacher, H.; Kurths, J.; Scheingraber, H. A comparative classification of complexity measures. Chaos Solitons Fractals 1994, 4, 133–173. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Badii, R.; Politi, A. Complexity: Hierarchical Structures and Scaling in Physics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Li, M.; Vitanyi, P.M.B. An Introduction to Kolmogorov Complexity and its Applications; Springer: New York, NY, USA, 1993. [Google Scholar]
- Papadimitriou, C.H. Computational Complexity; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Freund, J.; Ebeling, W.; Rateitschak, K. Self-similar sequences and universal scaling of dynamical entropies. Phys. Rev. E 1996, 54, 5561–5566. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Statistical complexity of simple one-dimensional spin systems. Phys. Rev. E 1997, 55, 1239R–1243R. [Google Scholar] [CrossRef]
- Arnold, D. Information-theoretic analysis of phase transitions. Complex Syst. 1996, 10, 143–155. [Google Scholar]
- Upper, D.R. Theory and Algorithms for Hidden Markov Models and Generalized Hidden Markov Models. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1997. [Google Scholar]
- Crutchfield, J.P. Semantics and thermodynamics. In Nonlinear Modeling and Forecasting, Volume XII of Santa Fe Institute Studies in the Sciences of Complexity; Casdagli, M., Eubank, S., Eds.; Addison-Wesley: Reading, MA, USA, 1992; pp. 317–359. [Google Scholar]
- Crutchfield, J.P.; Young, K. Computation at the onset of chaos. In Complexity, Entropy and the Physics of Information, Volume VIII of Santa Fe Institute Studies in the Sciences of Compexity; Zurek, W.H., Ed.; Addison-Wesley: Reading, MA, USA, 1990; pp. 223–269. [Google Scholar]
- Goncalves, W.M.; Pinto, R.D.; Sartorelli, J.C.; de Oliveira, M.J. Inferring statistical complexity in the dripping faucet experiment. Physica A 1998, 257, 385–389. [Google Scholar] [CrossRef]
- Hanson, J.E.; Crutchfield, J.P. The attractor-basin portrait of a cellular automaton. J. Stat. Phys. 1992, 66, 1415–1462. [Google Scholar] [CrossRef]
- Hanson, J.E.; Crutchfield, J.P. Computational mechanics of cellular automata: An example. Phys. D 1997, 103, 169–189. [Google Scholar] [CrossRef]
- Delgado, J.; Solé, R.V. Collective-induced computation. Phys. Rev. E 1997, 55, 2338–2344. [Google Scholar] [CrossRef]
- Witt, A.; Neiman, A.; Kurths, J. Characterizing the dynamics of stochastic bistable systems by measures of complexity. Phys. Rev. 1997, E55, 5050–5059. [Google Scholar] [CrossRef] [Green Version]
- Raijmakers, M. Epigensis in Neural Network Models of Cognitive Development: Bifurcations, More Powerful Structures, and Cognitive Concepts. Ph.D. Thesis, Universiteit van Amsterdam, Amsterdam, The Netherlands, 1996. [Google Scholar]
- Drexler, K.E. Nanosystems: Molecular Machinery, Manufacturing, and Computation; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Coppersmith, S.N.; Jones, T.C.; Kadanoff, L.P.; Levine, A.; McCarten, J.P.; Nagel, S.R.; Venkataramani, S.C.; Wu, X. Self-organized short-term memories. Phys. Rev. Lett. 1997, 78, 3983–3986. [Google Scholar] [CrossRef]
- Fischer, K.H.; Hertz, J.A. Spin Glasses; Cambridge Studies in Magnetism; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Bak, P.; Tang, C.; Weisenfield, K. Self-organized criticality: An explanation of 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- van Nimwegen, E.; Crutchfield, J.P.; Mitchell, M. Finite populations induce metastability in evolutionary search. Phys. Lett. A 1997, 229, 144–150. [Google Scholar] [CrossRef]
- van Nimwegen, E.; Crutchfield, J.P.; Mitchell, M. Statistical dynamics of the Royal Road genetic algorithm. Theoret. Comp. Sci. 1998, in press. [Google Scholar] [CrossRef]
- Nagel, K.; Paczuski, M. Emergent traffic jams. Phys. Rev. E 1995, 51, 2909–2918. [Google Scholar] [CrossRef] [PubMed]
- Nagel, K. Particle hopping models and traffic flow theory. Phys. Rev. E 1996, 53, 4655–4672. [Google Scholar] [CrossRef] [PubMed]
- Saad, D.; Solla, S.A. On-line learning in soft committee machines. Phys. Rev. E 1995, 52, 4225–4243. [Google Scholar] [CrossRef] [PubMed]
- Watkin, T.L.H.; Rau, A.; Biehl, M. The statistical mechanics of learning a rule. Rev. Mod. Phys. 1993, 65, 499–556. [Google Scholar] [CrossRef]
- Binney, J.J.; Dowrick, N.J.; Fisher, A.J.; Newman, M.E.J. The Theory of Critical Phenomena: An Introduction to the Renormalization Group; Oxford Science Publications: Oxford, UK, 1992. [Google Scholar]
- Schultz, T.D.; Mattis, D.C.; Lieb, E.H. Two-dimensional Ising model as a soluble problem of many fermions. Rev. Mod. Phys. 1964, 36, 856–871. [Google Scholar] [CrossRef]
- Parisi, G. Statistical Field Theory, Volume 66 of Frontiers in Physics; Addison-Wesley: Reading, MA, USA, 1988. [Google Scholar]
- Cvitanović, P. Invariant measurement of strange sets in terms of cycles. Phys. Rev. Lett. 1988, 61, 2729–2732. [Google Scholar] [CrossRef] [Green Version]
- Mainieri, R. Thermodynamic Zeta functions for Ising models with long-range interactions. Phys. Rev. A 1992, 45, 3580–3591. [Google Scholar] [CrossRef]
- Mainieri, R. Cycle expansion for the Lyapunov exponent of a product of random matrices. Chaos 1992, 2, 91–97. [Google Scholar] [CrossRef]
- Hartley, R.V.L. Transmission of information. Bell. Sys. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Boltzmann, L. Lectures on Gas Theory; University of California Press: Berkeley, CA, USA, 1964. [Google Scholar]
- McMillan, B. The basic theorems of information theory. Ann. Math. Stat. 1953, 24, 196–219. [Google Scholar] [CrossRef]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1957. [Google Scholar]
- Jaynes, E.T. Essays on Probability, Statistics, and Statistical Physics; Reidel: London, UK, 1983. [Google Scholar]
- Cox, R.T. Probability, frequency, and reasonable expectation. Am. J. Phys. 1946, 14, 1–13. [Google Scholar] [CrossRef]
- Baierlein, R. Atoms and Information Theory; An Introduction to Statistical Mechanics; W. H. Freeman: San Francisco, CA, USA, 1971. [Google Scholar]
- Grandy, W.T. Foundations of Statistical Mechanics; Fundamental Theories of Physics; D. Reidel: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Gray, R.M. Entropy and Information Theory; Springer: New York, NY, USA, 1990. [Google Scholar]
- Li, W. Mutual information functions versus correlation functions. J. Stat. Phys. 1990, 60, 823–837. [Google Scholar] [CrossRef]
- Lindgren, K. Microscopic and macroscopic entropy. Phys. Rev. A 1988, 38, 4794–4798. [Google Scholar] [CrossRef]
- del Junco, A.; Rahe, M. Finitary codings and weak Bernoulli partitions. Proc. AMS 1979, 75, 259. [Google Scholar] [CrossRef]
- Lindgren, K. Entropy and correlations in dynamical lattice systems. In Cellular Automata and Modeling of Complex Systems, Volume 46 of Springer Proceedings in Physics; Manneville, P., Boccara, N., Vichniac, G.Y., Bidaux, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 27–40. [Google Scholar]
- Crutchfield, J.P.; Packard, N.H. Symbolic dynamics of one-dimensional maps: Entropies, finite precision, and noise. Int. J. Theo. Phys. 1982, 21, 433–466. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Packard, N.H. Noise scaling of symbolic dynamics entropies. In Evolution of Order and Chaos; Haken, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 215–227. [Google Scholar]
- Packard, N.H. Measurements of Chaos in the Presence of Noise. Ph.D. Thesis, University of California, Santa Cruz, CA, USA, 1982. [Google Scholar]
- Csordás, A. Szépfalusy, P. Singularities in Rényi information as phase transitions in chaotic states. Phys. Rev. A. 1989, 39, 4767–4777. [Google Scholar] [CrossRef]
- Kaufmann, Z. Characteristic quantities of multifractals—Application to the Feigenbaum attractor. J. Phys. D 1991, 54, 75–84. [Google Scholar] [CrossRef]
- Rothstein, J. Generalized entropy, boundary conditions, and biology. In The Maximum Entropy Formalism; Levine, R.D., Tribus, M., Eds.; MIT Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Chaitin, G. Information, Randomness and Incompleteness; World Scientific: Singapore, 1987. [Google Scholar]
- van Emden, M.H. An Analysis of Complexity, Volume 35 of Mathematical Centre Tracts; Mathematisch Centrum: Amsterdam, The Netherlands, 1971. [Google Scholar]
- Watanabe, S. Knowing and Guessing; Mathematisch Centrum; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Kolmogorov, A.N. Combinatorial foundations of information theory and the calculus of probabilities. Russ. Math. Surv. 1983, 38, 29. [Google Scholar] [CrossRef]
- Wallace, C.S.; Boulton, D.M. An information measure for classification. Comput. J. 1968, 11, 185. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Bialek, W.; Callan, C.G.; Strong, S.P. Field theories for learning probability distributions. Phys. Rev. Lett. 1996, 77, 4693–4697. [Google Scholar] [CrossRef] [PubMed]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Brookshear, J.G. Theory of Computation: Formal Languages, Automata, and Complexity; Benjamin/Cummings: Redwood City, CA, USA, 1989. [Google Scholar]
- Hopcroft, J.E.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation; Addison-Wesley: Reading, NJ, USA, 1979. [Google Scholar]
- Crutchfield, J.P. Critical computation, phase transitions, and hierarchical learning. In Towards the Harnessing of Chaos; Yamaguti, M., Ed.; Elsevier Science: Amsterdam, The Netherlands, 1994; pp. 29–46. [Google Scholar]
- Knorr, W.R. The Ancient Tradition of Geometric Problems; Birkhauser: Boston, MA, USA, 1986. [Google Scholar]
- Hero of Alexandria (Ed.) Volume III: Metrica. In Opera; B. G. Teubner: Leipzig, Germany, 1903. [Google Scholar]
- Michie, D.; Spiegelhalter, D.; Taylor, C.C. Machine Learning, Neural and Statistical Classification; Series in Artificial Intelligence; E. Horwood: New York, NY, USA, 1994. [Google Scholar]
- Schurmann, J. Pattern Classification: A Unified View of Statistical and Neural Approaches; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan Kaufmann: New York, NY, USA, 1988. [Google Scholar]
- Lauritzen, S.L. Graphical Models; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Crutchfield, J.P.; Shalizi, C.R. Thermodynamic depth of causal states: Objective complexity via minimal representations. Phys. Rev. E 1999, 59, 275–283. [Google Scholar] [CrossRef]
- Blackwell, D.; Koopmans, L. On the identifiability problem for functions of Markov chains. Ann. Math. Statist. 1957, 28, 1011–1015. [Google Scholar] [CrossRef]
- Paz, A. Introduction to Probabilistic Automata; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Elliot, R.J.; Aggoun, L.; Moore, J.B. Hidden Markov Models: Estimation and Control, Volume 29 of Applications of Mathematics; Springer: New York, NY, USA, 1995. [Google Scholar]
- Kitchens, B.; Tuncel, S. Finitary measures for subshifts of finite type and sofic systems. Mem. AMS 1985, 58, 1–68. [Google Scholar] [CrossRef]
- Young, K. The Grammar and Statistical Mechanics of Complex Physical Systems. Ph.D. Thesis, University of California, Santa Cruz, CA, USA, 1991. [Google Scholar]
- Wolfram, S. Computation theory of cellular automata. Comm. Math. Phys. 1984, 96, 15. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Crutchfield, J.P. Computational mechanics: Pattern and prediction, structure and simplicity. J. Stat. Phys. 2001, 104, 817–879. [Google Scholar] [CrossRef]
- Brudno, A.A. Entropy and the complexity of the trajectories of a dynamical system. Trans. Mosc. Math. Soc. 1983, 44, 127. [Google Scholar]
- Koppel, M. Complexity, depth, and sophistication. Complex Syst. 1987, 1, 1087–1091. [Google Scholar]
- Rhodes, J. Applications of Automata Theory and Algebraic via the Mathematical Theory of Complexity to Biology, Physics, Psychology, Philosophy, Games, and Codes; University of California: Berkeley, CA, USA, 1971. [Google Scholar]
- Nehaniv, C.L.; Rhodes, J.L. Krohn-Rhodes theory, hierarchies, and evolution. In Mathematical Hierarchies and Biology; DIMACS Series in Discrete Mathematics and Theoretical Computer Science; America Mathematical Society: Providence, RI, USA, 1997; pp. 29–42. [Google Scholar]
- Lloyd, S.; Pagels, H. Complexity as thermodynamic depth. Ann. Phys. 1988, 188, 186–213. [Google Scholar] [CrossRef]
- Landauer, R. A simple measure of complexity. Nature 1988, 336, 306–307. [Google Scholar] [CrossRef]
- Young, K.; Crutchfield, J.P. Fluctuation spectroscopy. Chaos Solitons Fractals 1993, 4, 5–39. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Bucklew, J.A. Large Deviation Techniques in Decision, Simulation, and Estimation; Wiley-Interscience: New York, NY, USA, 1990. [Google Scholar]
- Oono, Y. Large deviation and statistical physics. Prog. Theo. Phys. 1989, 99, 165–205. [Google Scholar] [CrossRef]
- Renyi, A. On the dimension and entropy of probability distributions. Acta Math. Hung. 1959, 10, 193. [Google Scholar] [CrossRef]
- H A Kramers, G.H.W. Statistics of the two-dimensional ferromagnet: Part I. Phys. Rev. 1941, 60, 252–263. [Google Scholar] [CrossRef]
- Yeomans, J.M. Statistical Mechanics of Phase Transitions; Clarendon Press: Oxford, UK, 1992. [Google Scholar]
- Dobson, J.F. Many-neighbored Ising chain. J. Math. Phys. 1969, 10, 40–45. [Google Scholar] [CrossRef]
- Lind, D.; Marcus, B. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press,: New York, NY, USA, 1995. [Google Scholar]
- Baker, G.A. Markov-property Monte Carlo method: One-dimensional Ising model. J. Stat. Phys. 1993, 72, 621–640. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Hanson, J.E. Turbulent pattern bases for cellular automata. Phys. D 1993, 69, 279–301. [Google Scholar] [CrossRef]
- Lindgren, K.; Moore, C.; Nordahl, M. Complexity of Two-Dimensional Patterns. J. Stat. Phys. 1998, 91, 909–951. [Google Scholar] [CrossRef]
- Badii, R.; Politi, A. Thermodynamics and complexity of cellular automata. Phys. Rev. Lett. 1997, 78, 444–447. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Räth, C.; Weidenmann, G. Statistics and meta-statistics in the concept of complexity. Physica 1997, 243, 819–829. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. Compression of two dimensional data. IEEE Trans. Inf. Theory 1986, 32, 1–8. [Google Scholar] [CrossRef]
- Packard, N.H.; Wolfram, S. Two-dimensional cellular automata. J. Stat. Phys. 1985, 38, 901–946. [Google Scholar] [CrossRef]
- Solé, R.V.; Manrubia, S.C.; Luque, B.; Delgado, J.; Bascompte, J. Phase transitions and complex systems. Complexity 1996, 1, 13–26. [Google Scholar] [CrossRef]
- Matsuda, H.; Kudo, K.; Nakamura, R.; Yamakawa, O.; Murata, T. Mutual information of Ising systems. Int. J. Theo. Phys. 1985, 35, 839–845. [Google Scholar] [CrossRef]
- Lidl, R.; Pilz, G. Applied Abstract Algebra; Springer: New York, NY, USA, 1984. [Google Scholar]
- Trakhtenbrot, B.A.; Barzdin, Y.M. Finite Automata; North-Holland: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Rissanen, J. Universal coding, information, prediction, and estimation. IEEE Trans. Inf. Theory 1984, 30, 629–636. [Google Scholar] [CrossRef] [Green Version]
























| Process | E | ||
|---|---|---|---|
| Fair Coin | 1 | 0 | 0 |
| Period 1 | 0 | 0 | 0 |
| Period 2 | 0 | 1 | 1 |
| Noisy Period 2 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feldman, D.P.; Crutchfield, J.P. Discovering Noncritical Organization: Statistical Mechanical, Information Theoretic, and Computational Views of Patterns in One-Dimensional Spin Systems. Entropy 2022, 24, 1282. https://doi.org/10.3390/e24091282
Feldman DP, Crutchfield JP. Discovering Noncritical Organization: Statistical Mechanical, Information Theoretic, and Computational Views of Patterns in One-Dimensional Spin Systems. Entropy. 2022; 24(9):1282. https://doi.org/10.3390/e24091282
Chicago/Turabian StyleFeldman, David P., and James P. Crutchfield. 2022. "Discovering Noncritical Organization: Statistical Mechanical, Information Theoretic, and Computational Views of Patterns in One-Dimensional Spin Systems" Entropy 24, no. 9: 1282. https://doi.org/10.3390/e24091282
APA StyleFeldman, D. P., & Crutchfield, J. P. (2022). Discovering Noncritical Organization: Statistical Mechanical, Information Theoretic, and Computational Views of Patterns in One-Dimensional Spin Systems. Entropy, 24(9), 1282. https://doi.org/10.3390/e24091282






