Dynamics and Entropy Analysis of a Frictionally Loaded Pendulum
Abstract
:1. Introduction
2. Physical and Mathematical Models
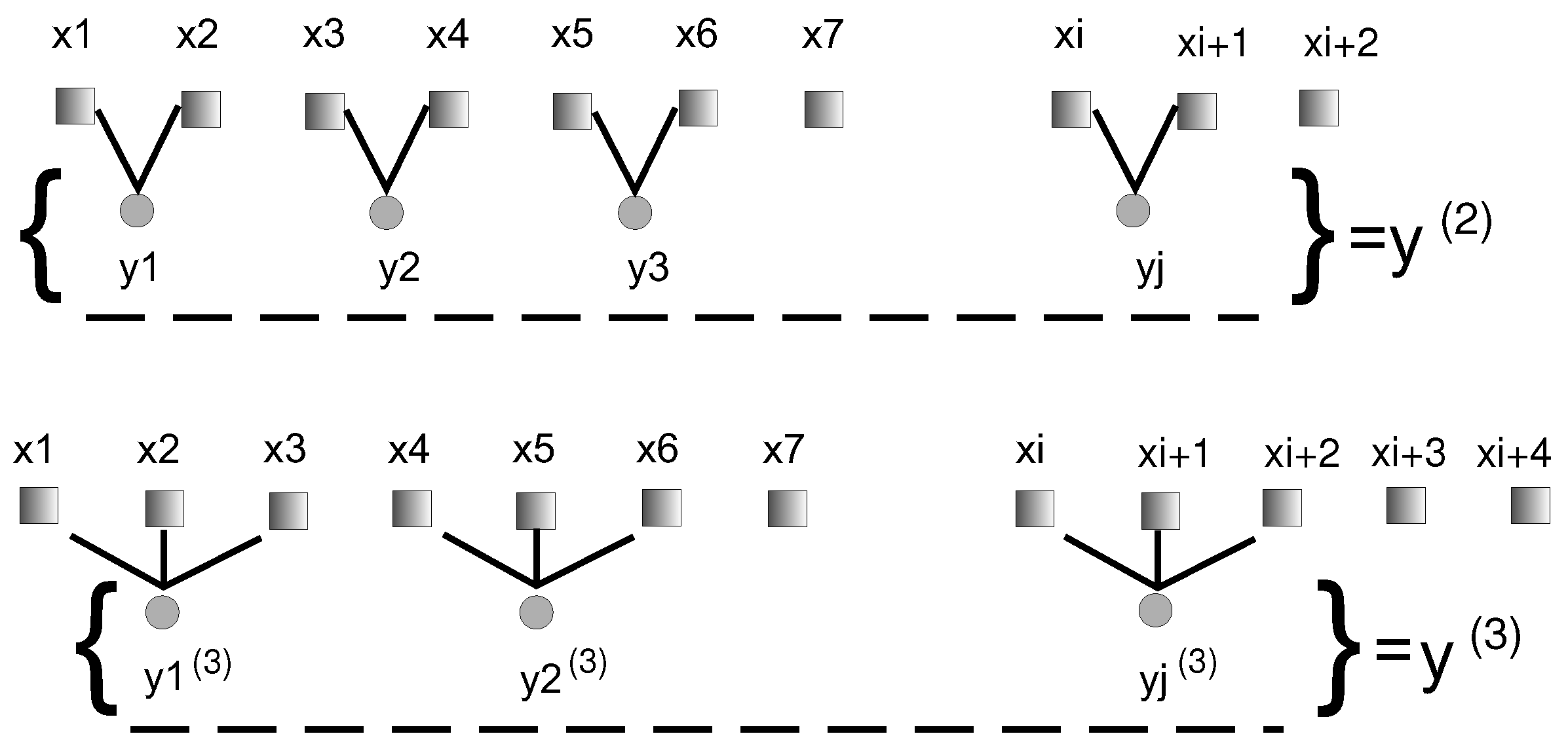
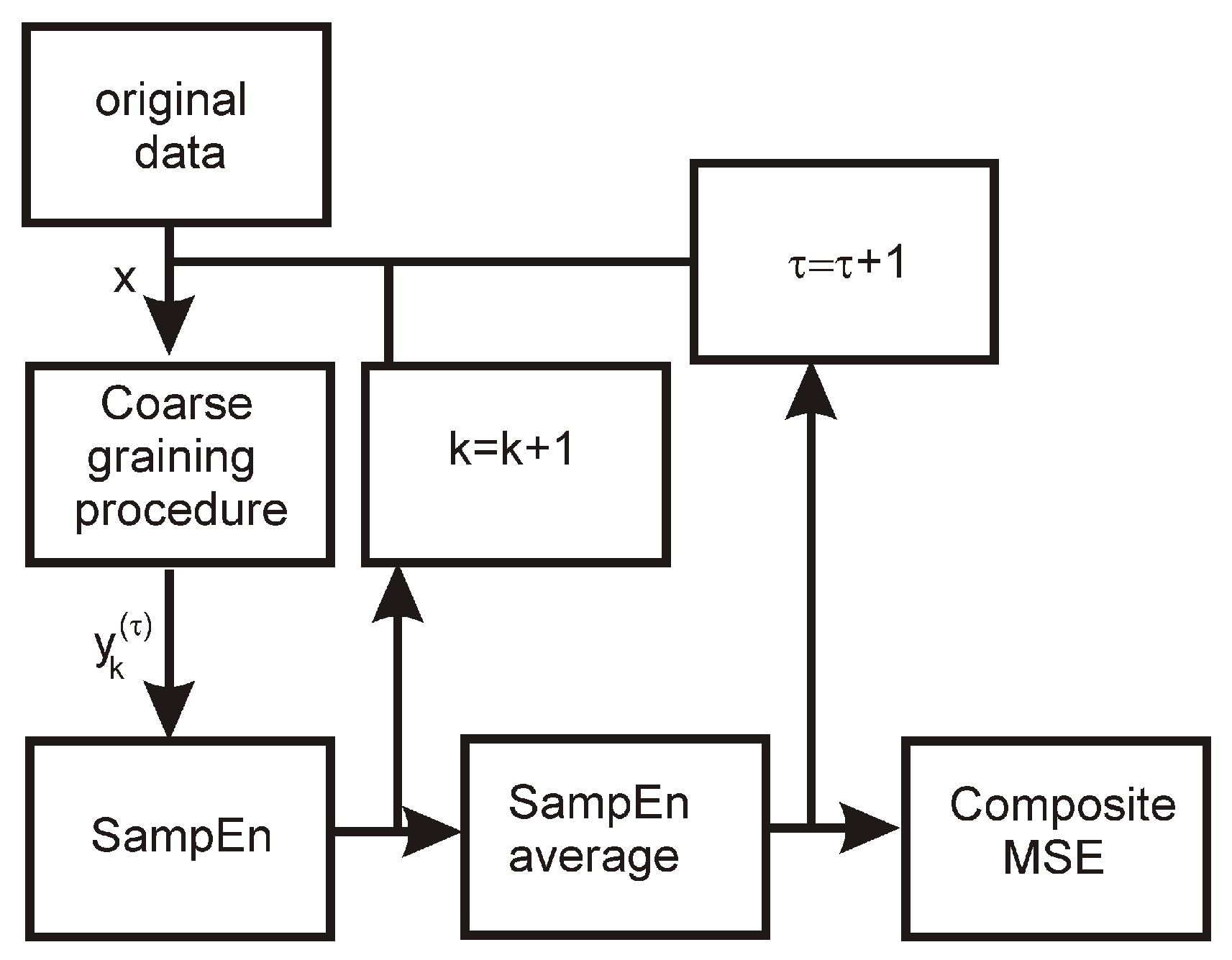
3. Multiscaled Entropy
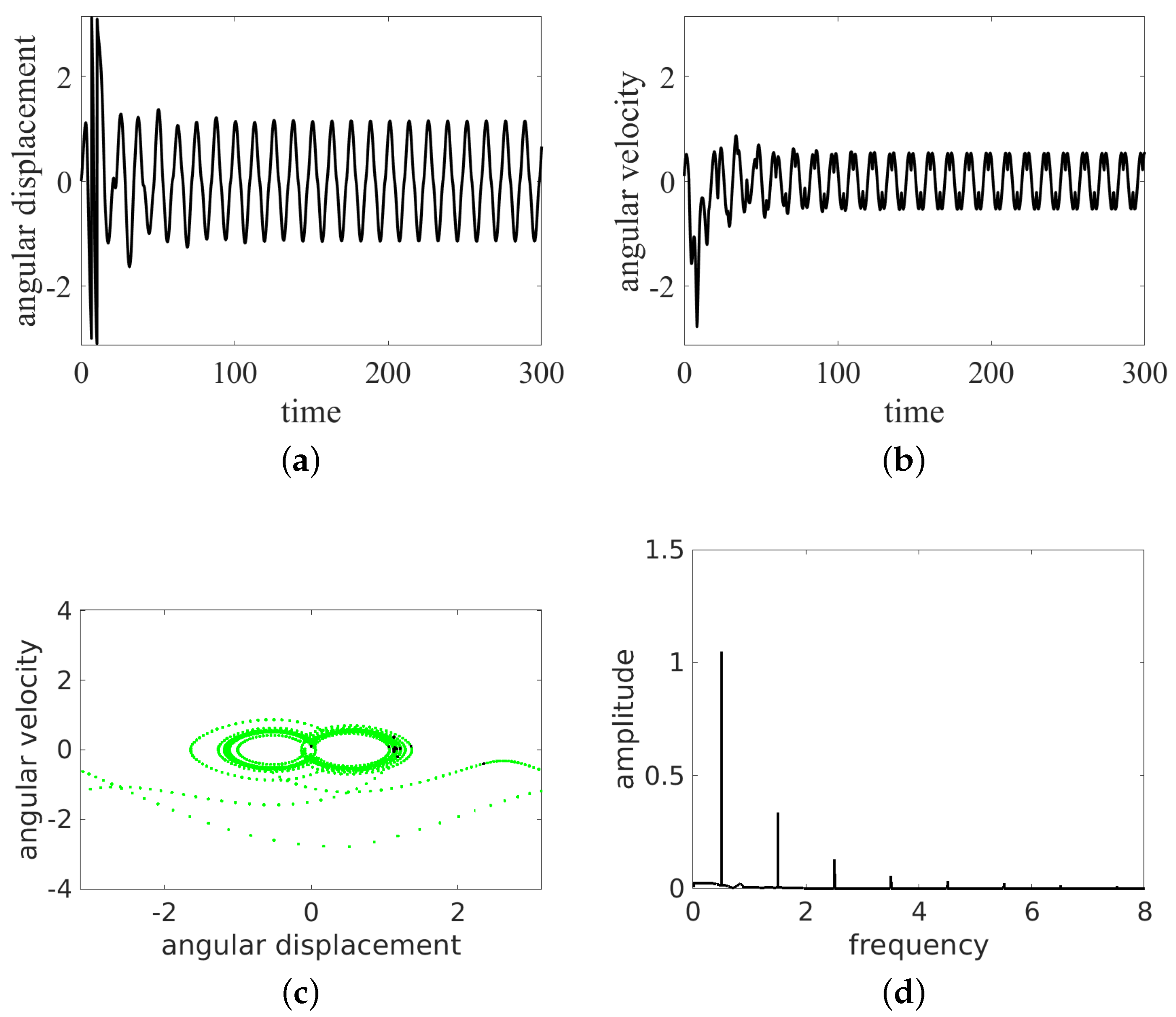
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Litak, G.; Margielewicz, J.; Gaska, D.; Yurchenko, D.; Dabek, K. Dynamic response of the spherical pendulum subjected to horizontal Lissajous excitation. Nonl. Dyn. 2020, 102, 2125–2142. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P.; Zhou, S.; Wang, J.; Litak, G.; Gaidai, O.; Ye, R. Nonlinear vibration mitigation of a crane’s payload using pendulum absorber. Mech. Syst. Sig. Process. 2021, 156, 107558. [Google Scholar] [CrossRef]
- Kudra, G.; Balthazar, J.M.; Tusset, A.M.; Wasilewski, G.; Stańczyk, B.; Awrejcewicz, J. Dynamics analysis and control of a pendulum driven by a DC motor via a slider-crank mechanism. Mech. Syst. Sig. Process. 2022, 166, 108415. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Zhou, H. Investigation of the frictional damping in friction induced vibration. J. Vibr. Cont. 2022. [Google Scholar] [CrossRef]
- Strelkov, S.P. The Froude pendulum. Zh. Tekh. Fiz. 1933, 3, 563–573. [Google Scholar]
- Tabueva, V.A. On circular motions of the froude pendulum. J. Appl. Mathem. Mech. 1961, 25, 854–858. [Google Scholar] [CrossRef]
- Litak, G.; Spuz-Szpos, G.; Szabelski, K.; Warminski, J. Vibration of externally-forced Froude pendulum. Int. J. Bifur. Chaos 1999, 9, 561–570. [Google Scholar] [CrossRef]
- Cao, H.; Chi, X.; Chen, G. Suppressing or inducing chaos by weak resonant excitations in an externally-forced Froude pendulum. Int. J. Bifur. Chaos 2004, 14, 1115–1120. [Google Scholar] [CrossRef]
- Borowiec, M.; Litak, G.; Troger, H. Vibrations of a pendulum with oscillating support and extra torque. Proc. App. Math. Mech. 2006, 6, 291–292. [Google Scholar] [CrossRef]
- Kuznetsov, S.P.; Sedova, Y.V. Robust hyperbolic chaos in Froude pendulum with delayed feedback and periodic braking. Int. J. Bifur. Chaos 2019, 29, 1930035. [Google Scholar] [CrossRef]
- Kuznetsov, S.P.; Kruglov, V.P. Hyperbolic chaos in a system of two Froude pendulums with alternating periodic braking. Commun. Nonl. Scien. Numer. Simul. 2019, 67, 152–161. [Google Scholar] [CrossRef]
- Kuznetsov, S.P.; Kruglov, V.P.; Sedova, Y.V. Mechanical systems with hyperbolic chaotic attractors based on froude pendulums. Russ. J. Nonl. Dynam. 2020, 16, 51–58. [Google Scholar] [CrossRef]
- Borowiec, M.; Sen, A.K.; Litak, G.; Hunicz, J.; Koszalka, G.; Niewczas, A. Vibrations of a vehicle excited by real road profiles. Forsch. Ingenieurw. 2010, 74, 99–109. [Google Scholar] [CrossRef]
- Borowiec, M.; Rysak, A.; Betts, D.N.; Bowen, R.C.; Kim, A.H.; Litak, G. Complex response of a bistable laminated plate: Multiscale entropy analysis. Eur. Phys. J. Plus 2014, 129, 211. [Google Scholar] [CrossRef]
- Hunicz, J.; Medina, A.; Litak, G.; Curto-Risso, P.L.; Guzmán-Vargas, L. Effects of direct fuel injection strategies on cycle-by-cycle variability in a gasoline homogeneous charge compression ignition engine: Sample entropy analysis. Entropy 2015, 17, 539–559. [Google Scholar] [CrossRef]
- Cao, J.; Syta, A.; Litak, G.; Zhou, S.; Inman, D.I.; Chen, Y. Regular and chaotic vibration in a piezoelectric energy harvester with fractional damping. Eur. Phys. J. Plus 2015, 130, 103. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Warminski, J.; Latalski, J.; Rusinek, R.; Mitura, A.; Borowiec, M. Numerical Modelling of Mechanica Systems; Lublin University of Technology: Lublin, Poland, 2015. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis (MSE); Beth Israel Deaconess Medical Center: Boston, MA, USA, 2002. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of physiologic time series. Phys. Rev. Lett. 2002, 89, 062102. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circul. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P. Information and complexity measures in dynamical systems. In Information Dynamics; Atmanspacher, H., Scheingraber, H., Eds.; Plenum Press: New York, NY, USA, 1991; pp. 15–33. [Google Scholar]
- Pan, Y.-H.; Lin, W.-Y.; Wang, Y.-H.; Lee, K.-T. Computing multiscale entropy with orthogonal range search. J. Mar. Sci. Technol. 2011, 19, 107–113. [Google Scholar] [CrossRef]
- Lake, D.E.; Richmann, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Heart Circul. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef]
- Nikulin, V.V.; Brismar, T. Comment on “Multiscale entropy analysis of complex physiological time series”. Phys. Rev. Lett. 2004, 92, 089803. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Phys. A 2003, 330, 53–60. [Google Scholar] [CrossRef]
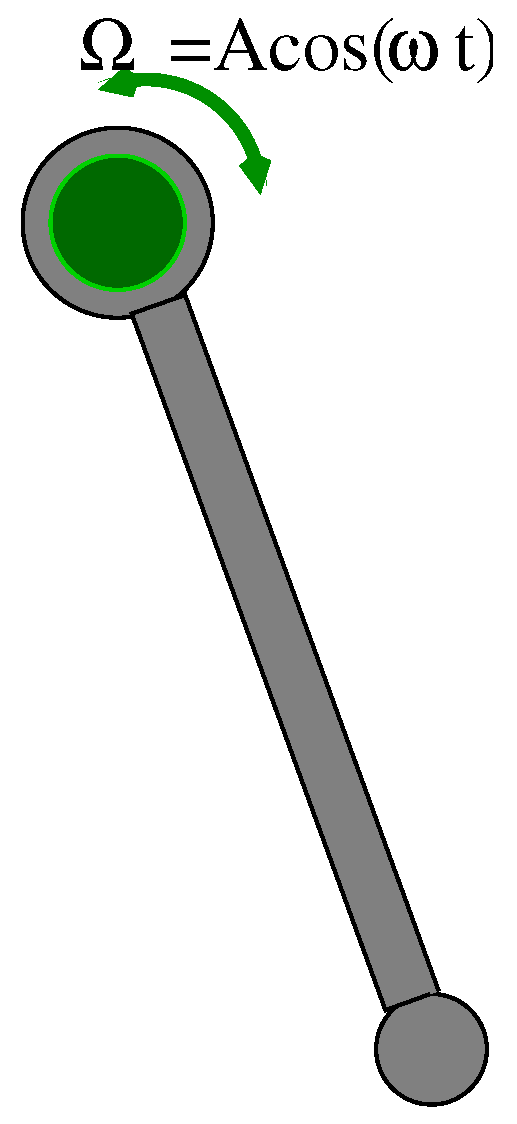

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litak, G.; Borowiec, M.; Da̧bek, K. Dynamics and Entropy Analysis of a Frictionally Loaded Pendulum. Entropy 2022, 24, 1269. https://doi.org/10.3390/e24091269
Litak G, Borowiec M, Da̧bek K. Dynamics and Entropy Analysis of a Frictionally Loaded Pendulum. Entropy. 2022; 24(9):1269. https://doi.org/10.3390/e24091269
Chicago/Turabian StyleLitak, Grzegorz, Marek Borowiec, and Krzysztof Da̧bek. 2022. "Dynamics and Entropy Analysis of a Frictionally Loaded Pendulum" Entropy 24, no. 9: 1269. https://doi.org/10.3390/e24091269
APA StyleLitak, G., Borowiec, M., & Da̧bek, K. (2022). Dynamics and Entropy Analysis of a Frictionally Loaded Pendulum. Entropy, 24(9), 1269. https://doi.org/10.3390/e24091269








