Abstract
In this paper, a novel image encryption algorithm is proposed based on hyperchaotic two-dimensional sin-fractional-cos-fractional (2D-SFCF), called sin-fractional-cos-fractional image-encryption (SFCF-IE). The 2D-SFCF is constructed from two one-dimensional cosine fractional (1-DCFs), and it has a more complex chaotic behavior with a larger parameter space than one-dimensional chaotic systems. Compared with the two-dimensional (2D) chaotic system, the 2D-SFCF has a simple structure, and the parameter space in the chaotic state is continuous, which is beneficial to generating the keystream in the cryptosystem. Therefore, in the novel image encryption algorithm, we use the 2D-SFCF to generate the keystream of the cryptosystem. The encryption algorithm is a process of scrambling and diffusion. Different from common diffusion methods, the diffusion starting position of the SFCF-IE is randomly generated, enhancing the algorithm’s security. Simulation experiments show that the image encrypted by this algorithm has better distribution characteristics and can resist common attack methods.
1. Introduction
Images are the basis of human vision. Since digital images are vivid and intuitive, the most important means for people to obtain information is to obtain information from images in daily life [1,2]. With the accelerated development of the Internet, the study of ensuring the secure transmission of images in the network has become one of the hot issues [3,4,5]. Compared with text information, the image has a two-dimensional structure and the adjacent pixels have a strong correlation. Therefore, text information encryption algorithms are unsuitable for image encryption, such as 3DES and AES [6].
Many image protection methods have been proposed, such as image hiding technology, image watermarking technology, and image encryption technology [7,8,9,10,11]. Among these image protection techniques, image encryption is the most direct way, which converts the original plaintext information into a noisy image. The image encryption algorithm consists of two steps, scrambling and diffusion. The scrambling part is to change the position of the original plaintext pixel value, and the diffusion algorithm is to change the value of the original plaintext pixel [12,13].
Because the chaotic system is highly sensitive to the change of the initial value, a large number of excellent pseudorandom sequences can be generated by the chaotic system, which is consistent with the keystream required for scrambling and diffusion of image encryption. Therefore, the image encryption algorithm combined with chaos theory has gradually become the main research method for image encryption algorithms [14,15,16,17,18,19,20]. In Ding’s algorithm, two chaotic systems are used to generate the keystream, fractional-order Henon is used for shuffling, and the keystream generated by the 4D hyperchaotic system is used in the diffusion stage [15]. Li et al. proposed a fractional-order chaotic system and simulated it on the DSP platform, then proposed a new image encryption algorithm using this fractional-order chaotic system [17]. Chai et al. used a Four-wing hyperchaotic system to generate a keystream and used DNA technology in image encryption. The experimental results verified that the algorithm has good performance. However, the efficiency of DNA decoding and encoding operations in computer simulations is slow [20].
For the chaotic image encryption algorithm, the security is mainly related to the performance of the chaotic system. Chaotic systems are divided into low-dimensional and high-dimensional chaotic systems [21,22,23]. The structure of low-dimensional chaotic systems is simple and easy to generate, and many image encryption methods based on low-dimensional chaos have been proposed [24,25,26]. However, low-dimensional systems have the disadvantages of small parameter space and no complex dynamic behavior, and their trajectories are easily estimated on computer platforms with limited precision [27,28]. Compared with low-dimensional chaotic systems, high-dimensional chaotic systems have larger parameter spaces, more complex structures, and better dynamic behavior. Many high-dimensional chaos-based image encryption methods have been proposed today [29,30,31]. However, due to the complex structure of the high-dimensional mixed-degree system, the efficiency of generating the keystream is slow, and it is difficult to achieve in industrial production.
To balance the disadvantages and advantages of high-dimensional chaotic systems and low-dimensional chaotic systems. We propose a new two-dimensional chaotic system called 2D-SFCF. The 2D-SFCF evolved from two 1-DCFs [32]. The 2D-SFCF has a larger parameter space and better dynamic behavior than one-dimensional chaotic systems. The 2D-SFCF is a hyperchaotic system. Compared with chaotic behavior, hyperchaotic behavior is a more complex state. Compared with high-dimensional chaotic systems, the 2D-SFCF has a simpler structure, and this simple structure can also evolve complex dynamic behavior, and the speed of the 2D-SFCF generating keystream is fast.
Based on the excellent performance of the 2D-SFCF, we designed a new image encryption algorithm called SFCF-IE. The SFCF-IE is a scramble-to-diffusion process. A hash function generates the key of the SFCF-IE, which is converted into the initial value and parameters of the 2D-SFCF to generate the keystream required for scrambling and diffusion. The scrambling adopts a random scrambling method. In the diffusion algorithm, the starting position of the diffusion is randomly generated, not the starting position of the image pixel value. This diffusion method enhances the security of the encryption algorithm. In addition, the SFCF-IE only needs one round of encryption to achieve the security required by the cryptosystem, and the image encrypted by the SFCF-IE has good distribution characteristics.
2. 2D-SFCF
In this paper, a new 2D-SFCF is proposed, mathematical expression of the 2D-SFCF is shown in Equation (1),
There are two inputs and two outputs in the 2D-SFCF. and are the control parameters of the 2D-SFCF, and . and are the iterative sequence, and .
2D-SFCF is evolved from 1-DCF [32], and its expression is shown in Equation (2),
Compared with the 1-DCF, the dynamic behavior of the 2D-SFCF is more complex and the parameter space in chaotic state is larger.
2.1. Attractor
The attractor indicates the ergodicity of the system. If the nonlinear dynamical system has good ergodicity, its attractor distribution will fill the entire phase space. The nonlinear dynamic system with strong ergodicity is more suitable for the cryptographic system. The cryptographic system requires random keys and this is not easy to predict. The attractors of the 2D-SFCF are shown in Figure 1 in different parameter. The initial value is set to and .
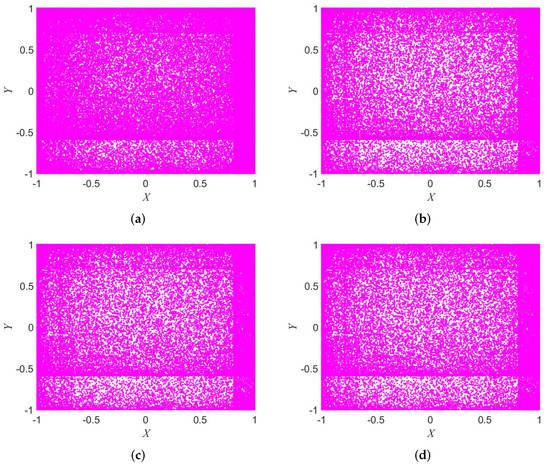
Figure 1.
Attractor of 2D-SFCF. (a) . (b) . (c) . (d) .
It can be seen from Figure 1 that the 2D-SFCF has good ergodicity, and its attractors are evenly distributed in the phase space, so it can be shown that the chaotic sequence generated by the 2D-SFCF has good randomness.
2.2. NIST Statistical Test Suite
The National Institute of Standards and Technology (NIST) is an important tool for counting the randomness of a sequence. Given the significance level, when the test value is greater than the significance level, it indicates that the sequence passes the test and is random. In this section, given the significance level , the NIST test results of the 2D-SFCF are shown in Table 1, where the initial values of the 2D-SFCF are and . The NIST test results show that the sequences generated by the 2D-SFCF have a high degree of randomness. The 2D-SFCF is suitable for cryptosystem to generate keystream.

Table 1.
NISTtest of plaintext and ciphertext.
2.3. Lyapunov Exponents
The Lyapunov exponent is recognized as one of the most effective means of judging whether a nonlinear dynamical system is chaotic. The calculation formula of Lyapunov exponents is shown in Equation (3),
When the nonlinear dynamical system has more than one positive Lyapunov exponent, it indicates that the system is in a hyperchaotic state. A hyperchaotic state is a more complex dynamical behavior than a chaotic state. The Lyapunov exponents of the 2D-SFCF are shown in Figure 2a–f. Furthermore, it is compared with the Lyapunov exponents of the 1-DCF [32] and the 2D-SCMCI [33], which are shown in Figure 2g–i.
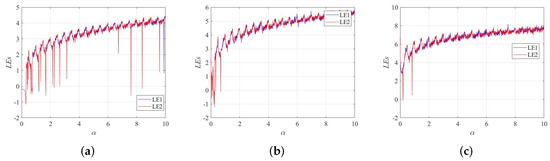
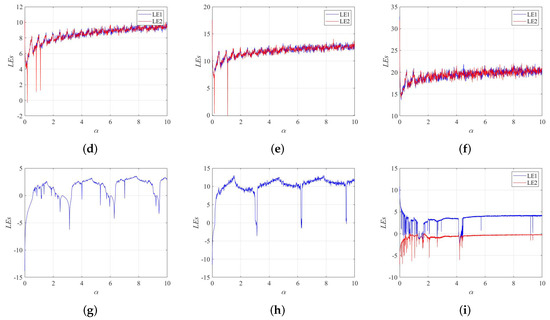
Figure 2.
Lyapunov exponents. (a) LEs of 2D-SFCF with . (b) LEs of 2D-SFCF with . (c) LEs of 2D-SFCF with . (d) LEs of 2D-SFCF with . (e) LEs of 2D-SFCF with . (f) LEs of 2D-SFCF with . (g) LEs of 1-DCF with . (h) LEs of 1-DCF with . (i) LEs of 2D-SCMCI.
Compared with the 1-DCF, the 2D-SFCF has a larger parameter space in the chaotic state. In the same parameter space, the 2D-SFCF exhibits a hyperchaotic state, while the 1-DCF is in a chaotic state or even a periodic state. Compared with the 2D-SCMCI, the parameter space of 2D-SFCF in the chaotic state is continuous, which is beneficial to generating the secret key of the cryptosystem. The comparison results show that the 2D-SFCF has good kinetic behavior. Furthermore, we verify the accuracy of Lyapunov exponents using bifurcation diagrams, the bifurcation diagrams of the 2D-SFCF are shown in Figure 3a–d. The bifurcation diagrams of the 1-DCF are shown in Figure 3e,f. The bifurcation diagrams of the 2D-SCMCI are shown in Figure 3g,h.
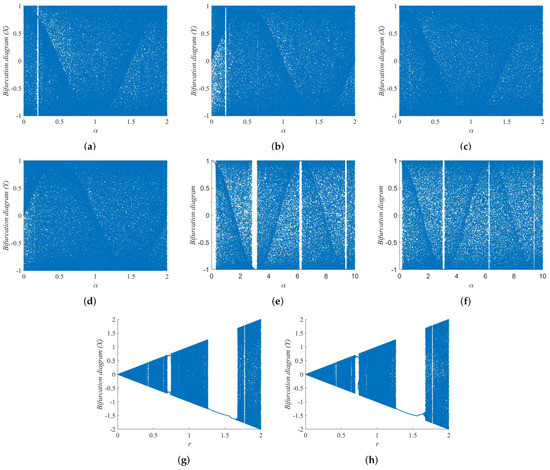
Figure 3.
Bifurcation diagram (BD). (a) BD of 2D-SFCF with (X). (b) BD of 2D-SFCF with (Y). (c) BD of 2D-SFCF with (X). (d) BD of 2D-SFCF with (Y). (e) BD of 1-DCF with . (f) BD of 1-DCF with . (g) BD of 2D-SCMCI (X). (h) BD of 2D-SCMCI (Y).
3. SFCF-IE Algorithm
The SFCF-IE is divided into three parts, key generation, scrambling, and diffusion. The SFCF-IE is a symmetric cryptosystem, and the decryption process is the reverse process of encryption. The structure of the SFCF-IE is shown in Figure 4.
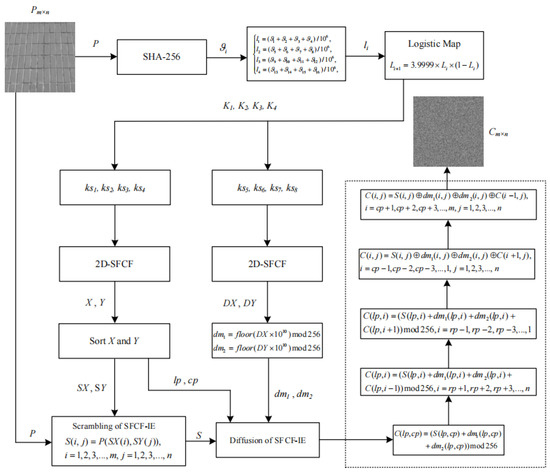
Figure 4.
Schematic diagram of SFCF-IE.
3.1. Function Declaration
- (1)
- (2)
- Set to a keystream generation function , where a is the parameter of the 2D-SFCF, b is the parameter of the 2D-SFCF, c is the initial value of the 2D-SFCF, d is the initial value of the 2D-SFCF, and N is the number of iterations. Output sequences are and . Note that when generating a chaotic sequence, some initial values of iterations need to be discarded, so that the generated sequence is sufficiently chaotic. Here, the first 100 iteration values are set to be discarded.
- (3)
- Set a sorting function , which can sort the one-dimensional vector a and find the position of the sorted vector in the vector a, and the return value is B. An example of a sorting function. If , and then .
3.2. Key Generation of SFCF-IE
The key of the SFCF-IE is generated by a hash function. The initial key is a 256-bit binary stream. The initial key is processed so that the initial key becomes the initial value and parameter of the 2D-SFCF. The key generation process is described as follows.
Input: P ()
Step 1: Use SHA-256 to generate the initial key , which is a 256-bit key, and the input to the hash function is a plaintext image.
Step 2: Every 16 bits in is converted into a new key , which is a decimal, , .
Step 3: Processing , so that can become the initial value of Logistic,
Step 4: are the initial value of Logistic, iterate 30 times by Equation (6),
Step 5: The new keys are set to , , , and .
Output: and
3.3. Scrambling of SFCF-IE
The scrambling algorithm is described as follows.
Step 1: Process the generated secret key , and , . Get the initial values and parameters of the 2D-SFCF.
Step 2: Generate a key stream by 2D-SFCF, , and output two sequences, and .
Step 3: Sort X and Y, generate a row scrambled matrix and a column scrambled matrix , where and .
3.4. Diffusion of SFCF-IE
Different from the common diffusion algorithm that starts from position , the starting position of the SFCF-IE diffusion algorithm is determined by the secret key. This design method increases the diversity of the algorithm and increases the difficulty of cracking. The diffusion algorithm is described as follow.
Input: S ()
Step 1: The starting positions and of the diffusion is generated by the sequence X and Y,
Step 2: The matrixs required for diffusion are generated by Equation (9),
Convert to two matrixs, and .
Step 3: The diffusion process is described as
(1) .
(2) .
(3) .
(4) .
(5) .
Output: C ()
4. Performance Analysis
To evaluate the performance of the SFCF-IE algorithm, in this paper, we will analyze the encryption effect and security of the algorithm from the visualization, key space analysis, histogram analysis, key sensitivity, information entropy, correlation, and NIST.
4.1. Visualization
Images are selected from the USC-SIPI Image Database for visualization analysis. The visual analysis of the SFCF-IE are shown in Figure 5, Figure 6 and Figure 7, including the encryption and decryption results of the image. The visualization results show that the ciphertext image obtained by the SFCF-IE is a noise image, and the attacker cannot obtain any information from the ciphertext image.

Figure 5.
Visualization of SFCF-IE for image ‘1.5.01’ (512 × 512). (a) plaintext of ‘1.5.01’. (b) ciphertext of ‘1.5.01’. (c) decrypted ‘1.5.01’.

Figure 6.
Visualization of SFCF-IE for image ‘1.5.03’ (512 × 512). (a) plaintext of ‘1.5.03’. (b) ciphertext of ‘1.5.03’. (c) decrypted ‘1.5.03’.

Figure 7.
Visualization of SFCF-IE for image Black (512 × 512). (a) plaintext of Black. (b) ciphertext of Black. (c) decrypted Black.
4.2. Key Analysis
The original key of SFCF-IE is generated by a hash function, and the rest of the keys are converted from the original key, so the key space of the SFCF-IE is . The key space of the SFCF-IE is much larger than , so the algorithm in this paper is sufficient to resist external exhaustive attacks.
In addition to being large, the key of a cryptographic system also needs to be sensitive enough. A good cryptographic algorithm must be highly sensitive to small changes in the key. Figure 8 analyzes the key sensitivity of the SFCF-IE. The original key is K, and the slightly changed keys are . Decrypt with the correct key and the wrong key, respectively.

Figure 8.
Key sensitivity analysis of SFCF-IE. (a) decrypted by K. (b) decrypted by . (c) decrypted by . (d) decrypted by . (e) decrypted by . (f) decrypted by . (g) decrypted by . (h) decrypted by .
4.3. Histogram Analysis
The histogram analysis can intuitively reflect the distribution characteristics of pixels. If the ciphertext cannot cover up the statistical characteristics of the image, the attacker will infer the information distribution of the plaintext according to the ciphertext to crack the algorithm. The histogram analysis of the SFCF-IE is shown in Figure 9 and Figure 10.
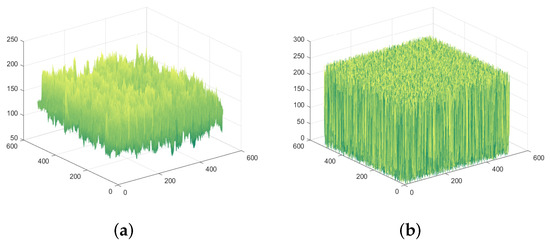
Figure 9.
Spatiotemporal histogram of ‘1.5.01’. (a) Plaintext spatiotemporal histogram of ‘1.5.01’. (b) Ciphertext spatiotemporal histogram of ‘1.5.01’.
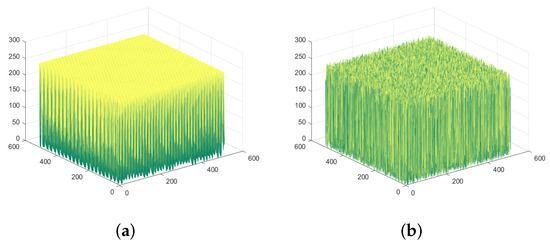
Figure 10.
Spatiotemporal histogram of ‘1.5.02’. (a) Plaintext spatiotemporal histogram of ‘1.5.02’. (b) Ciphertext spatiotemporal histogram of ‘1.5.02’.
Experimental results show that the algorithm can well mask the statistical properties of plaintext images. After encryption, the gray value appears with approximately equal probability.
4.4. Information Entropy Analysis
Shannon’s theorem states that when the degree of disorder of information increases, its entropy value will increase, and when the probability of occurrence of each element in the information is equal, its entropy value will reach its maximum value. The calculation formula of information entropy is
The information entropy of the SFCF-IE is shown in Table 2. In addition, the comparison with the average information entropy of some classical algorithms [34,35,36,37,38] are shown in Table 3.

Table 2.
Information entropy of SFCF-IE.

Table 3.
Information entropy comparison.
The experimental results show that the ciphertext information entropy of the SFCF-IE is close to 8. Compared with other algorithms, the information entropy of the SFCF-IE is closer to the theoretical value, so it can be shown that the SFCF-IE has better encryption effect.
4.5. Correlation Analysis
The attacker can attack an image by analyzing the correlation between adjacent pixels of the image, so the encryption algorithm should eliminate this correlation. The adjacent pixel correlation is defined as,
Figure 11 is the result of the SFCF-IE adjacent pixel correlation analysis. When the correlation between adjacent pixels is strong, the image presents a state of aggregation, and when the correlation between adjacent pixels is weak, the image presents a state of divergence.
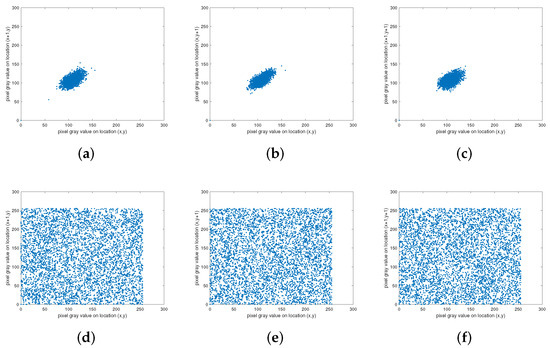
Figure 11.
Correlation analysis of ‘1.5.06’. (a) Horizontal of plaintext. (b) Vertical of plaintext. (c) Diagonal of plaintext. (d) Horizontal of ciphertext. (e) Vertical of ciphertext. (f) Diagonal of ciphertext.
Table 4 shows the quantitative analysis results of the correlation between adjacent pixels of the SFCF-IE, and the comparison results with some classical algorithms (Refs. [34,35,36,37,38]) are shown in Table 5.

Table 4.
Correlation coefficients of SFCF-IE.

Table 5.
Correlation coefficients of SFCF-IE.
4.6. NIST for Ciphertexts
Use the NIST to test whether the ciphertext image obtained by the SFCF-IE is random. The NIST test results are shown in Table 6. The plaintext image fails in 14 tests, and one test is successful. The plaintext image does not have randomness, and the distribution of pixel values has certain regularity. The ciphertext passed 15 tests, indicating that the ciphertext image has good randomness, and the attacker cannot find information related to the plaintext from the ciphertext image. Therefore, the SFCF-IE has strong security.

Table 6.
NISTtest of SFCF-IE.
5. Conclusions
In this work, a 2D-SFCF hyperchaotic system is proposed. Through Attractor, Lyapunov exponent, and bifurcation graph, NIST verified that the 2D-SFCF has better dynamic behavior and larger parameter space than low-dimensional chaotic systems. In addition, the parameter space of the 2D-SFCF in a hyperchaotic state is continuous. Based on the 2D-SFCF, we propose a new image encryption algorithm called SFCF-IE. Through key analysis, information entropy analysis, correlation analysis, NIST, and other methods, it is verified that THE 2D-SFCF has high security and high practical value and is widely used in secure real-time communication of images and other occasions.
Author Contributions
Conceptualization, Y.H. and H.W.; validation, Y.H., H.W. and L.Z.; writing—original draft preparation, Y.H.; writing—review and editing, H.W. and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable for studies not involving humans or animals.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, G.; Yu, S.; Wang, Q. Security Analysis of the Image Encryption Algorithm Based on a Two-Dimensional Infinite Collapse Map. Entropy 2022, 24, 1023. [Google Scholar] [CrossRef] [PubMed]
- Hua, Z.; Yi, S.; Zhou, Y. Medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process. 2018, 144, 134–144. [Google Scholar] [CrossRef]
- Chai, X.; Wu, H.; Gan, Z.; Han, D.; Zhang, Y.; Chen, Y. An efficient approach for encrypting double color images into a visually meaningful cipher image using 2D compressive sensing. Inf. Sci. 2021, 556, 305–340. [Google Scholar] [CrossRef]
- Toktas, A.; Erkan, U.; Toktas, F.; Yetgın, Z. Chaotic map optimization for image encryption using triple objective differential evolution algorithm. IEEE Access 2021, 9, 127814–127832. [Google Scholar] [CrossRef]
- Fu, X.Q.; Liu, B.C.; Xie, Y.Y.; Li, W.; Liu, Y. Image encryption-then-transmission using DNA encryption algorithm and the double chaos. IEEE Photonics J. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Hsiao, F.H. Applying 3DES to Chaotic Synchronization Cryptosystems. IEEE Access 2021, 10, 1036–1050. [Google Scholar] [CrossRef]
- Wang, C.; Ma, B.; Xia, Z.; Li, J.; Li, Q.; Shi, Y.Q. Stereoscopic image description with trinion fractional-order continuous orthogonal moments. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 1998–2012. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Ma, B.; Li, Q.; Shi, Y.-Q. High precision error prediction algorithm based on ridge regression predictor for reversible data hiding. IEEE Signal Process. Lett. 2021, 28, 1125–1129. [Google Scholar] [CrossRef]
- Ma, B.; Shi, Y.Q. A reversible data hiding scheme based on code division multiplexing. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1914–1927. [Google Scholar] [CrossRef]
- Li, Q.; Wang, X.; Ma, B.; Wang, X.; Wang, C.; Gao, S.; Shi, Y. Concealed attack for robust watermarking based on generative model and perceptual loss. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 5695–5706. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Toktas, F.; Alenezi, F. 2D epimap for image encryption. Inf. Sci. 2022, 589, 770–789. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S. A chaotic image encryption algorithm based on a counting system and the semi-tensor product. Multimed. Tools Appl. 2021, 80, 10301–10322. [Google Scholar] [CrossRef]
- Li, T.; Shi, J.; Li, X.; Wu, J.; Pan, F. Image encryption based on pixel-level diffusion with dynamic filtering and DNA-level permutation with 3D Latin cubes. Entropy 2019, 21, 319. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Luo, C.; Cao, Y. An improved color image encryption scheme and cryptanalysis based on a hyperchaotic sequence. Phys. Scr. 2019, 94, 085206. [Google Scholar] [CrossRef]
- Ding, L.; Ding, Q. A novel image encryption scheme based on 2D fractional chaotic map, DWT and 4D hyper-chaos. Electronics 2020, 9, 1280. [Google Scholar] [CrossRef]
- Masood, F.; Ahmad, J.; Shah, S.A.; Jamal, S.S.; Hussain, I. A novel hybrid secure image encryption based on julia set of fractals and 3D Lorenz chaotic map. Entropy 2020, 22, 274. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Mou, J.; Xiong, L.; Wang, Z.; Xu, J. Fractional-order double-ring erbium-doped fiber laser chaotic system and its application on image encryption. Opt. Laser Technol. 2021, 140, 107074. [Google Scholar] [CrossRef]
- Wang, T.; Ge, B.; Xia, C.; Dai, G. Multi-Image Encryption Algorithm Based on Cascaded Modulation Chaotic System and Block-Scrambling-Diffusion. Entropy 2022, 24, 1053. [Google Scholar] [CrossRef]
- Gao, S.; Wu, R.; Wang, X.; Wang, J.; Li, Q.; Wang, C.; Tang, X. A 3D model encryption scheme based on a cascaded chaotic system. Signal Process. 2022, 202, 108745. [Google Scholar] [CrossRef]
- Chai, X.; Wu, H.; Gan, Z.; Zhang, Y.; Chen, Y.; Nixon, K.W. An efficient visually meaningful image compression and encryption scheme based on compressive sensing and dynamic LSB embedding. Opt. Lasers Eng. 2020, 124, 105837. [Google Scholar] [CrossRef]
- Hua, Z.; Zhu, Z.; Yi, S.; Zhang, Z.; Huang, H. Cross-plane colour image encryption using a two-dimensional logistic tent modular map. Inf. Sci. 2021, 546, 1063–1083. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S.; Yu, L.; Sun, Y.; Sun, H. Chaotic image encryption algorithm based on bit-combination scrambling in decimal system and dynamic diffusion. IEEE Access 2019, 7, 103662–103677. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, G.; Zhu, C. A secure and fast image encryption scheme based on double chaotic S-boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef] [PubMed]
- Pak, C.; An, K.; Jang, P.; Kim, J.; Kim, S. A novel bit-level color image encryption using improved 1D chaotic map. Multimed. Tools Appl. 2019, 78, 12027–12042. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Improved cryptanalysis and enhancements of an image encryption scheme using combined 1D chaotic maps. Entropy 2018, 20, 843. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Yuan, Y.; Iu, H.H.-C.; Fernando, T. Parameter identification of chaotic and hyper-chaotic systems using synchronization-based parameter observer. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1464–1475. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine-transform-based chaotic system with FPGA implementation. IEEE Trans. Ind. Electron. 2017, 65, 2557–2566. [Google Scholar] [CrossRef]
- Al-Hazaimeh, O.M.; Al-Jamal, M.F.; Alhindawi, N.; Omari, A. Image encryption algorithm based on Lorenz chaotic map with dynamic secret keys. Neural Comput. Appl. 2019, 31, 2395–2405. [Google Scholar] [CrossRef]
- Pourasad, Y.; Ranjbarzadeh, R.; Mardani, A. A new algorithm for digital image encryption based on chaos theory. Entropy 2021, 23, 341. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S.; Ye, X.; Shuang, Z.; Mingxu, W. A new image encryption algorithm with cantor diagonal scrambling based on the PUMCML system. Int. J. Bifurc. Chaos 2021, 31, 2150003. [Google Scholar]
- Talhaoui, M.Z.; Wang, X.; Talhaoui, A. A new one-dimensional chaotic map and its application in a novel permutation-less image encryption scheme. Vis. Comput. 2021, 37, 1757–1768. [Google Scholar] [CrossRef]
- Sun, J. 2D-SCMCI hyperchaotic map for image encryption algorithm. IEEE Access 2021, 9, 59313–59327. [Google Scholar] [CrossRef]
- Ibrahim, S.; Abbas, A.M. Efficient key-dependent dynamic S-boxes based on permutated elliptic curves. Inf. Sci. 2021, 558, 246–264. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.M.; Hirota, K.; Abd EL-Latif, A.A. Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf. Sci. 2020, 515, 191–217. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Inf. Sci. 2019, 486, 340–358. [Google Scholar] [CrossRef]
- Ravichandran, D.; Praveenkumar, P.; Rayappan, J.B.B.; Amirtharajan, R. Chaos based crossover and mutation for securing DICOM image. Comput. Biol. Med. 2016, 72, 170–184. [Google Scholar] [CrossRef]
- Ravichandran, D.; Praveenkumar, P.; Rayappan, J.B.B.; Amirtharajan, R. DNA chaos blend to secure medical privacy. IEEE Trans. Nanobioscience 2017, 16, 850–858. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).