Analysis of Energy Loss Characteristics of Vertical Axial Flow Pump Based on Entropy Production Method under Partial Conditions
Abstract
:1. Introduction
2. Mathematical Model and Numerical Simulation Method
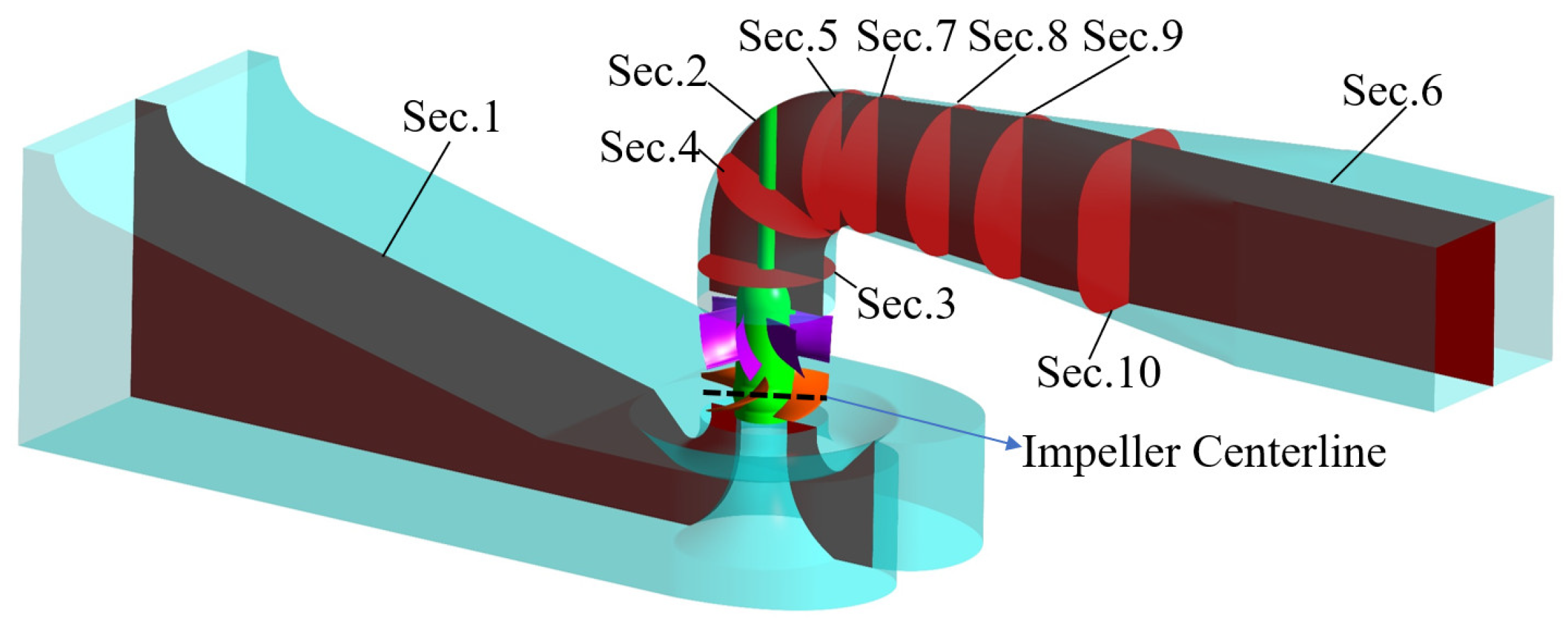
2.1. Numerical Calculation Model
2.2. Numerical Method
2.3. Grid Reliability Analysis
2.4. Entropy Production Method
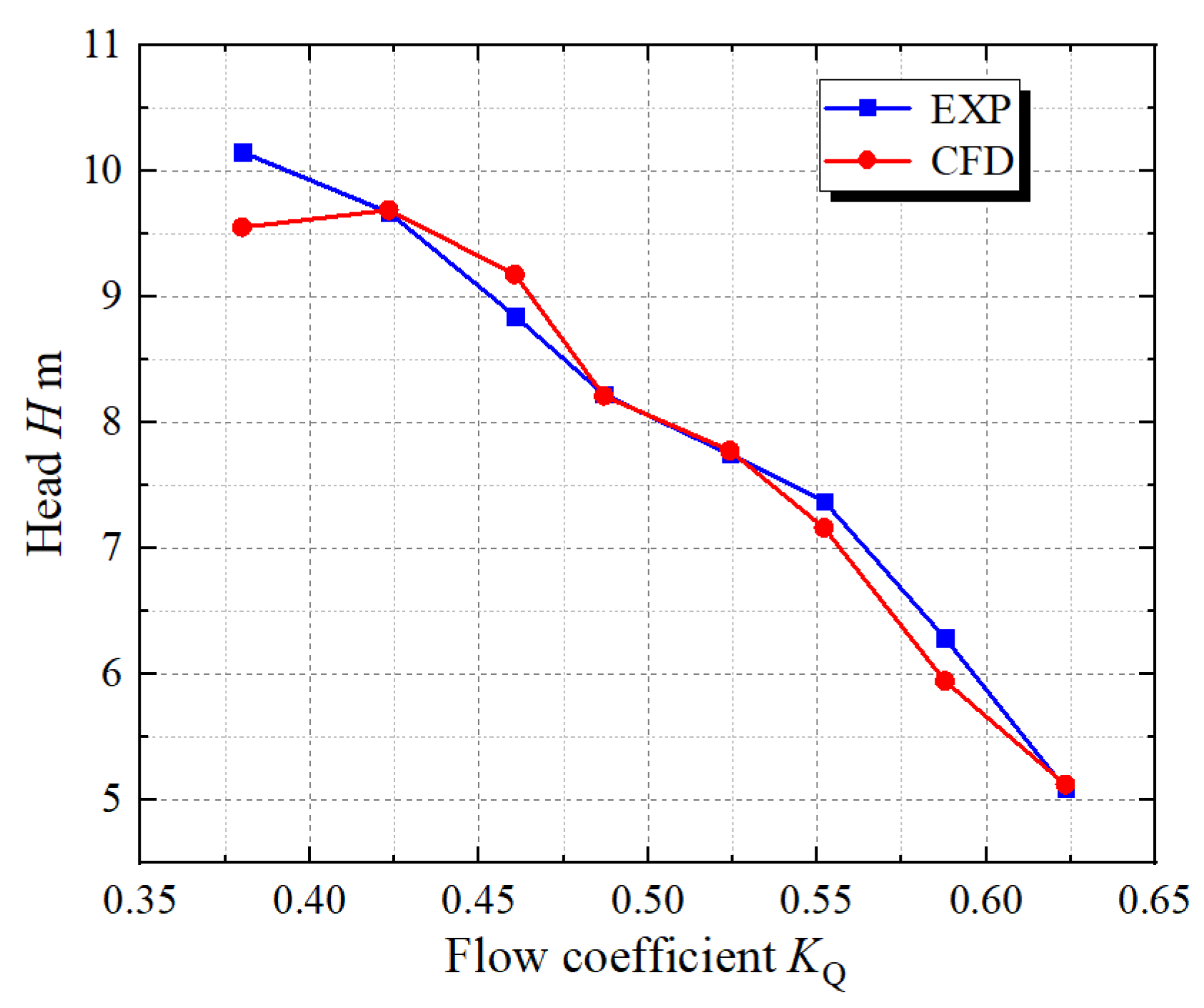
2.5. Reliability Verification of Numerical Calculation and Entropy Production Calculation
3. Results and Analysis
4. Conclusions
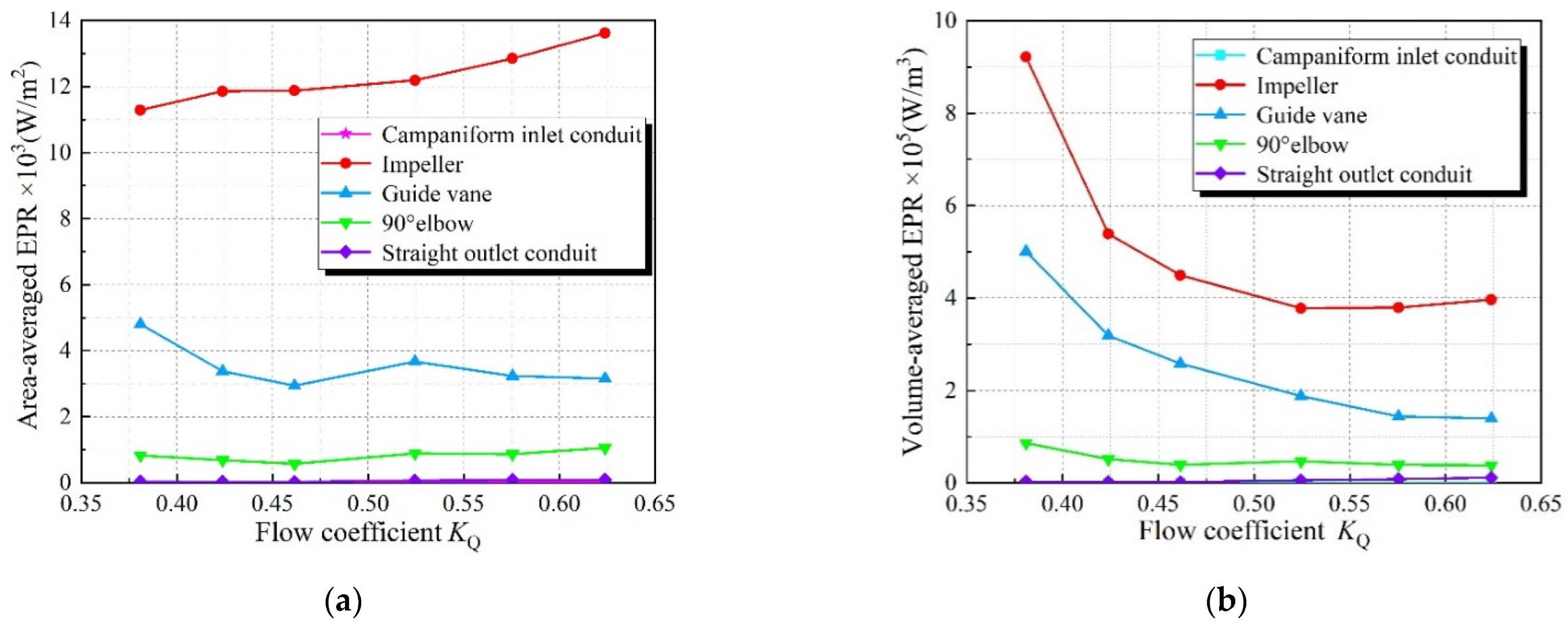
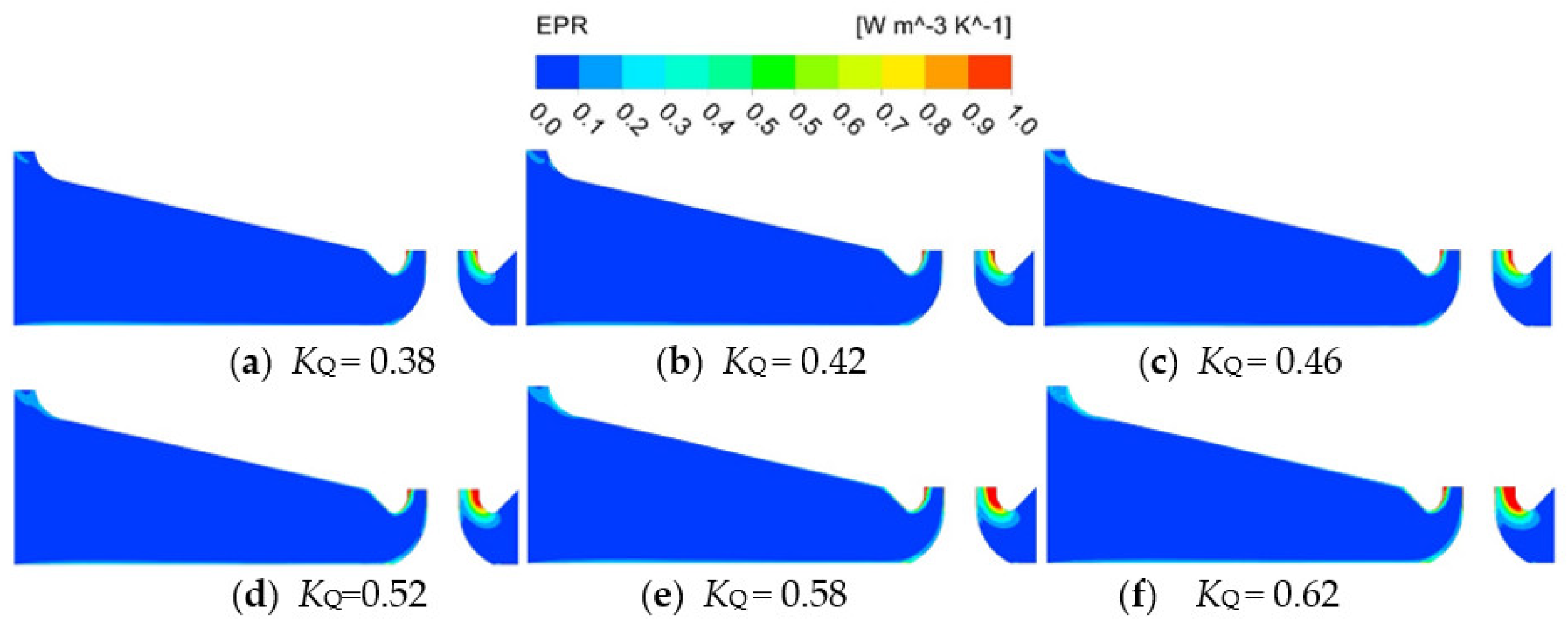
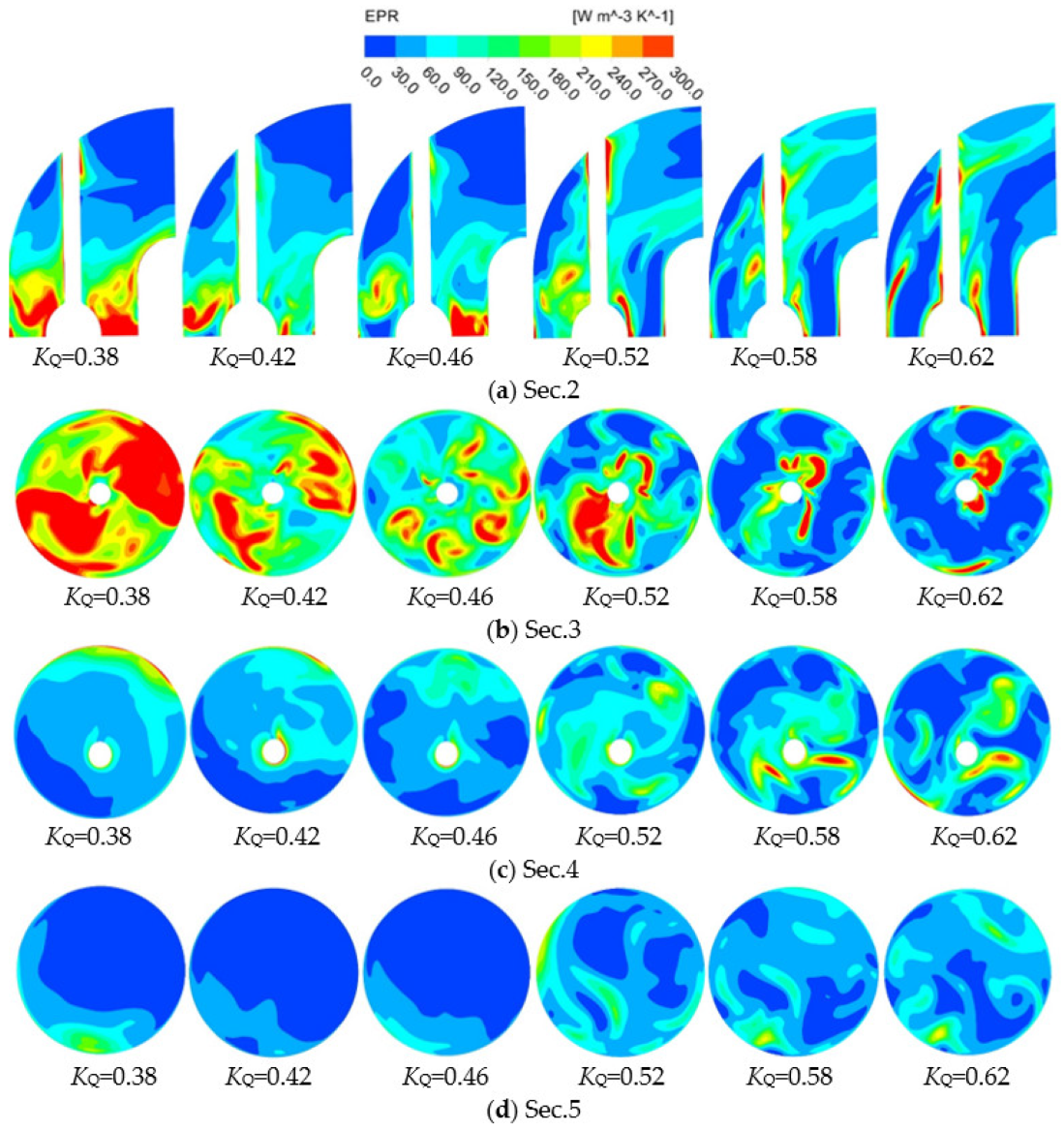
- The energy loss of the impeller is the largest in the vertical axial flow pump device. From KQ = 0.38 to KQ = 0.62, the energy loss of the impeller reduces first and then increases, and the volume average EPR is consistent with the energy loss. The area average EPR is minimum at KQ = 0.38 and maximum at KQ = 0.62. The high EPR of the impeller is mainly focused on the rim, which is influenced by the tip clearance leakage. The energy loss of the guide vane reduces as the KQ increases. The high EPR of the guide vane is mainly distributed on the backside and trailing edge of the vane;
- The energy loss of the campaniform inlet conduit is the smallest, and the ratio of energy loss to total energy loss is less than 1% under various KQ. The high EPR distribution area is mainly concentrated in the outlet area. The volume average EPR and area average EPR of campaniform inlet conduit increase with the increase of KQ. The energy loss trend of the elbow is similar to that of the guide vane, which reduces with the increase of KQ. From KQ = 0.38 to KQ = 0.62, the high EPR area develops from the inlet guide cap to the elbow outlet. When KQ = 0.62, the maximum energy loss of the straight outlet conduit is 1707 W, and when KQ = 0.42, the minimum is 281 W. The energy loss, volume average EPR and area average EPR all decrease first and then increase with the increase of KQ. The main loss is distributed in the linear shrinking section of the conduit;
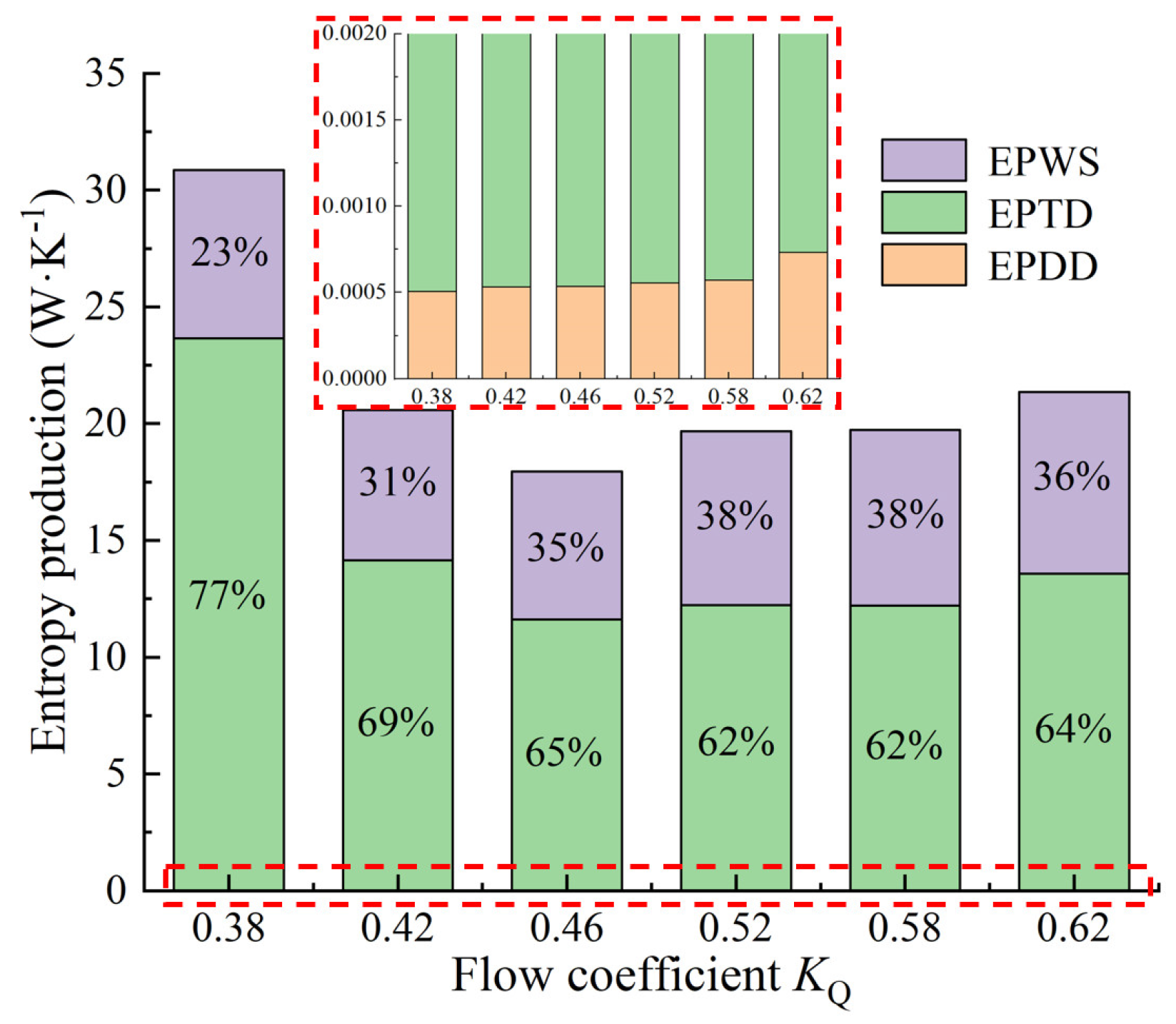
- The energy dissipation of the flow in the pump device is mainly turbulent dissipation. Under various flow rates, the EPTD accounts for the largest proportion, up to 77%. The EPDD accounted for less than 1%, and the EPWS increased by 15% when KQ = 0.52 and KQ = 0.58. With the increase of KQ, the EPWS decreased first and then increased.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C. Researches and Development of Axial Flow Pump System. Trans. Chin. Soc. Agric. Mach. 2015, 46, 49–59. [Google Scholar]
- Yang, F.; Li, Z.; Fu, J.; Lv, Y.; Ji, Q.; Jian, H. Numerical and Experimental Analysis of Transient Flow Field and Pressure Pulsations of an Axial-Flow Pump Considering the Pump–Pipeline Interaction. J. Mar. Sci. Eng. 2022, 10, 258. [Google Scholar] [CrossRef]
- Gong, R.; Wang, H.; Chen, L.; Li, D.; Zhang, H.; Wei, X. Application of entropy production theory to hydro-turbine hydraulic analysis. Sci. China Technol. Sci. 2013, 56, 1636–1643. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Y.; Tang, Q.; Cai, J.; Zhao, L.; Ge, X. Energy analysis of Francis turbine for various mass flow rate conditions based on entropy production theory. Renew. Energy 2022, 183, 447–458. [Google Scholar] [CrossRef]
- Huang, P.; Appiah, D.; Chen, K.; Zhang, F.; Cao, P.; Hong, Q. Energy dissipation mechanism of a centrifugal pump with entropy generation theory. AIP Adv. 2021, 11, 045208. [Google Scholar] [CrossRef]
- Li, D.; Miao, B.; Li, Y.; Gong, R.; Wang, H. Numerical study of the hydrofoil cavitation flow with thermodynamic effects. Renew. Energy 2021, 169, 894–904. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Tian, F.; Agarwal, R. Effect of blade thickness on rotating stall of mixed-flow pump using entropy generation analysis. Energy 2021, 236, 121381. [Google Scholar] [CrossRef]
- Hongyu, G.; Wei, J.; Yuchuan, W.; Hui, T.; Ting, L.; Diyi, C. Numerical simulation and experimental investigation on the influence of the clocking effect on the hydraulic performance of the centrifugal pump as turbine. Renew. Energy 2021, 168, 21–30. [Google Scholar] [CrossRef]
- Ghorani, M.M.; Haghighi, M.H.S.; Maleki, A.; Riasi, A. A numerical study on mechanisms of energy dissipation in a pump as turbine (PAT) using entropy generation theory. Renew. Energy 2020, 162, 1036–1053. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Zhu, Z.; Si, Q.; Li, Y. Entropy generation analysis for the cavitating head-drop characteristic of a centrifugal pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4637–4646. [Google Scholar] [CrossRef]
- Lai, F.; Huang, M.; Wu, X.; Nie, C.; Li, G. Local Entropy Generation Analysis for Cavitation Flow Within a Centrifugal Pump. J. Fluids Eng. 2022, 144, 101206. [Google Scholar] [CrossRef]
- Riaz, A.; Zeeshan, A.; Bhatti, M.M. Entropy analysis on a three-dimensional wavy flow of eyring–powell nanofluid: A comparative study. Math. Probl. Eng. 2021, 2021, 6672158. [Google Scholar] [CrossRef]
- Riaz, A.; Abbas, T.; Zeeshan, A.; Doranehgard, M.H. Entropy generation and MHD analysis of a nanofluid with peristaltic three dimensional cylindrical enclosures. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2698–2714. [Google Scholar] [CrossRef]
- Zhao, T.; Khan, M.I.; Chu, Y. Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Shen, S.; Qian, Z.; Ji, B. Numerical analysis of mechanical energy dissipation for an axial-flow pump based on entropy generation theory. Energies 2019, 12, 4162. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, F. Energy loss evaluation of axial flow pump systems in reverse power generation operations based on entropy production theory. Sci. Rep. 2022, 12, 8667. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Hu, W.; Liu, C.; Jiang, D.; Liu, D.; Nasr, A. Analysis of flow loss characteristics of slanted axial-flow pump device based on entropy production theory. R. Soc. Open Sci. 2022, 9, 211208. [Google Scholar] [CrossRef]
- Fei, Z.; Zhang, R.; Xu, H.; Feng, J.; Mu, T.; Chen, Y. Energy performance and flow characteristics of a slanted axial-flow pump under cavitation conditions. Phys. Fluids 2022, 34, 035121. [Google Scholar] [CrossRef]
- Zhang, D.; Katayama, Y.; Watanabe, S.; Tsuda, S.I.; Furukawa, A. Numerical study on loss mechanism in rear rotor of contra-rotating axial flow pump. Int. J. Fluid Mach. Syst. 2020, 13, 241–252. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Meng, F.; Osman, M.K. The effect of root clearance on mechanical energy dissipation for axial flow pump device based on entropy production. Processes 2020, 8, 1506. [Google Scholar] [CrossRef]
- Melzer, S.; Pesch, A.; Schepeler, S.; Kalkkuhl, T.; Skoda, R. Three-dimensional simulation of highly unsteady and isothermal flow in centrifugal pumps for the local loss analysis including a wall function for entropy production. J. Fluids Eng. 2020, 142, 111209. [Google Scholar] [CrossRef]
- Wu, C.; Pu, K.; Li, C.; Wu, P.; Huang, B.; Wu, D. Blade redesign based on secondary flow suppression to improve energy efficiency of a centrifugal pump. Energy 2022, 246, 123394. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Yu, Z.; Yan, Y.; Wang, W.; Liu, X. Entropy production analysis for vortex rope of a Francis turbine using hybrid RANS/LES method. Int. Commun. Heat Mass Transf. 2021, 127, 105494. [Google Scholar] [CrossRef]
- Meng, F.; Li, Y.; Pei, J. Energy Characteristics of Full Tubular Pump Device with Different Backflow Clearances Based on Entropy Production. Appl. Sci. 2021, 11, 3376. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Q.; Meng, F.; Zheng, Y.; Xu, X. Research on the Influence of Tip Clearance of Axial-Flow Pump on Energy Characteristics under Pump and Turbine Conditions. Machines 2022, 10, 56. [Google Scholar] [CrossRef]
- Yang, F.; Chang, P.; Yuan, Y.; Li, N.; Xie, R.; Zhang, X.; Lin, Z. Analysis of Timing Effect on Flow Field and Pulsation in Vertical Axial Flow Pump. J. Mar. Sci. Eng. 2021, 9, 1429. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Yuan, J.; Yuan, S. Effects of different vortex designs on optimization results of mixed-flow pump. Eng. Appl. Comput. Fluid Mech. 2022, 16, 36–57. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Xie, L.; Wang, B.; Yao, Z.; Xiao, R. On the vortical characteristics of horn-like vortices in stator corner separation flow in an axial flow pump. J. Fluids Eng. 2021, 143, 061201. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Y.; Lin, S.; Gong, R.; Wang, H.; Luo, X. Cavitation effects on pressure fluctuation in pump-turbine hump region. J. Energy Storage 2022, 47, 103936. [Google Scholar] [CrossRef]
- Yang, W.; Lei, X.; Zhang, Z.; Li, H.; Wang, F. Hydraulic Design of Submersible Axial-flow Pump Based on Blade Loading Distributions. Trans. Chin. Soc. Agric. Mach. 2017, 48, 179–187. [Google Scholar]
- Chalghoum, I.; Elaoud, S.; Kanfoudi, H.; Akrout, M. The effects of the rotor-stator interaction on unsteady pressure pulsation and radial force in a centrifugal pump. J. Hydrodyn. 2018, 30, 672–681. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, F.; Wang, C.; Chen, W.; Yao, Z.; Shi, X.; Li, X.; Zhong, Q. Study on the characteristics of horn-like vortices in an axial flow pump impeller under off-design conditions. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1613–1628. [Google Scholar] [CrossRef]
- Liu, H.; Liu, M.; Bai, Y.; Du, H.; Dong, L. Grid convergence based on GCI for centrifugal pump. J. Jiangsu Univ. Nat. Sci. Ed. 2014, 35, 279–283. [Google Scholar]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Yang, F. Internal Flow Characteristics and Hydraulic Stability of Low-Head Pump Device; China Water & Power Press: Beijing, China, 2020. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Yang, F.; Liu, C.; Tang, F.; Zhou, J. Numerical Simulation on the Hydraulic Performance and Model Test of Slanted Axial Pumping System. J. Mech. Eng. 2012, 48, 152–159. [Google Scholar] [CrossRef]
- Kim, J.H.; Ahn, H.J.; Kim, K.Y. High-efficiency design of a mixed-flow pump. Sci. China Ser. E Technol. Sci. 2010, 53, 24–27. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Q.; Chen, H.; Zhou, D. Investigations of the thermodynamic entropy evaluation in a hydraulic turbine under various operating conditions. Renew. Energy 2021, 180, 1026–1043. [Google Scholar] [CrossRef]
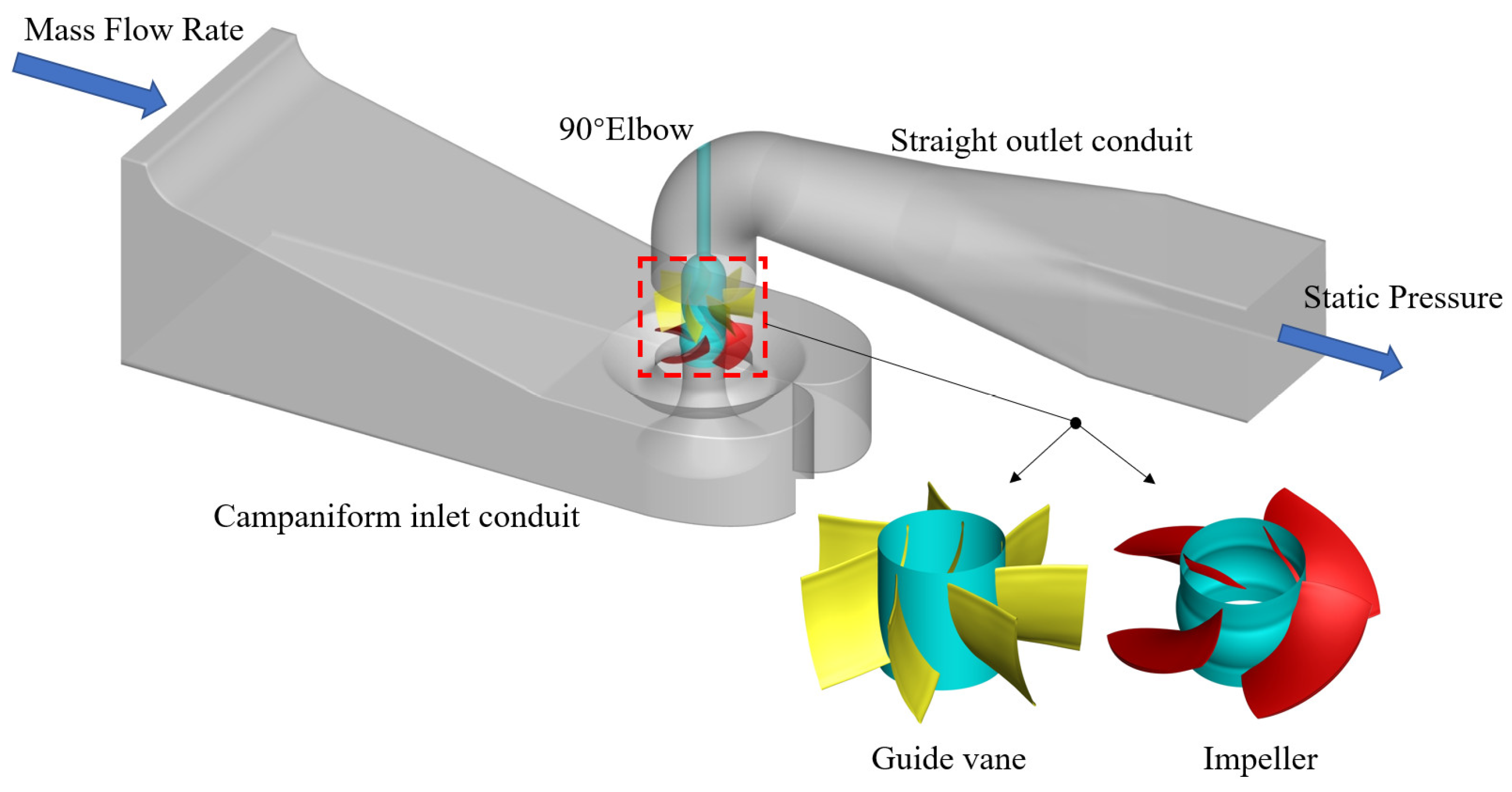
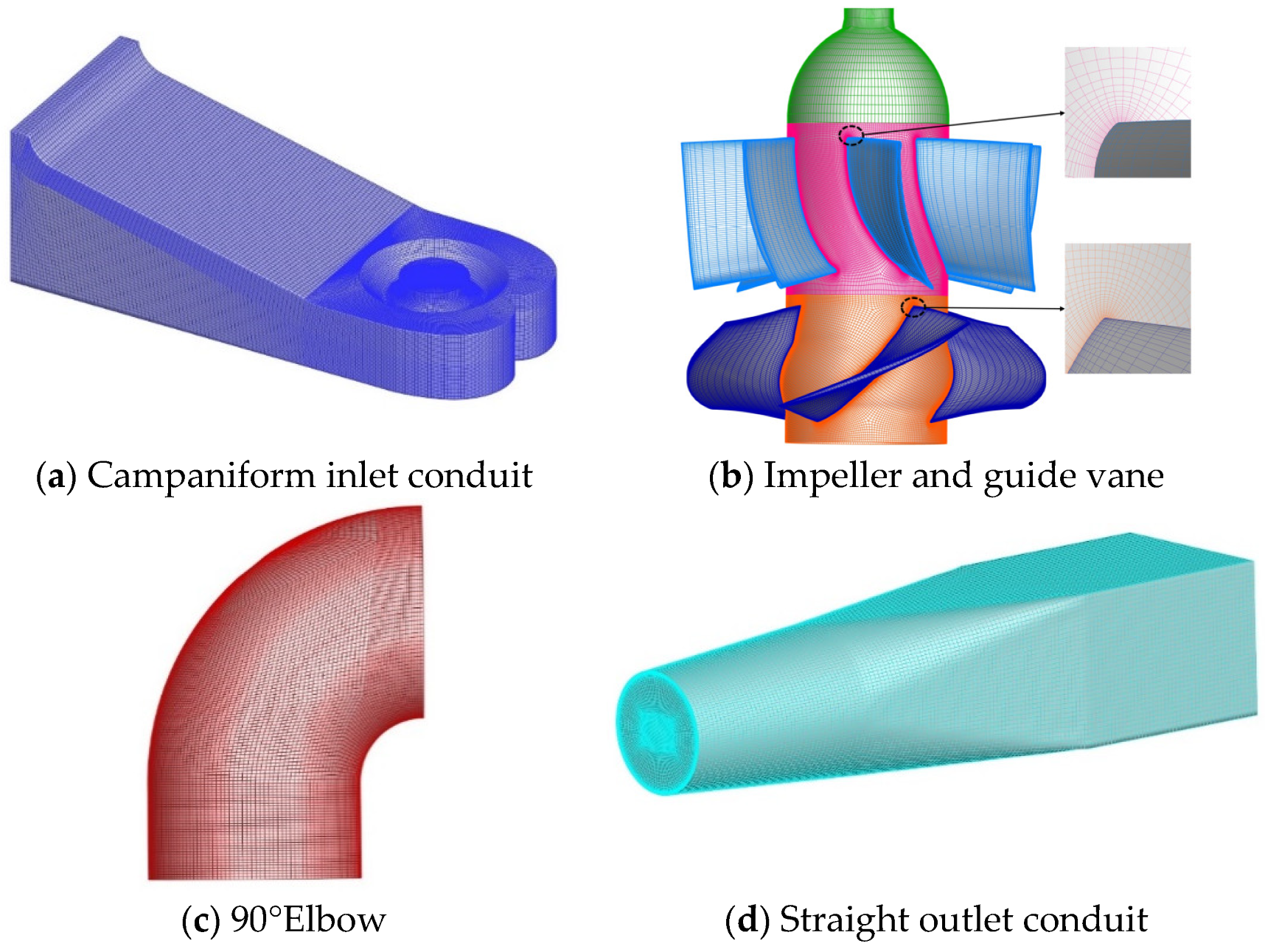

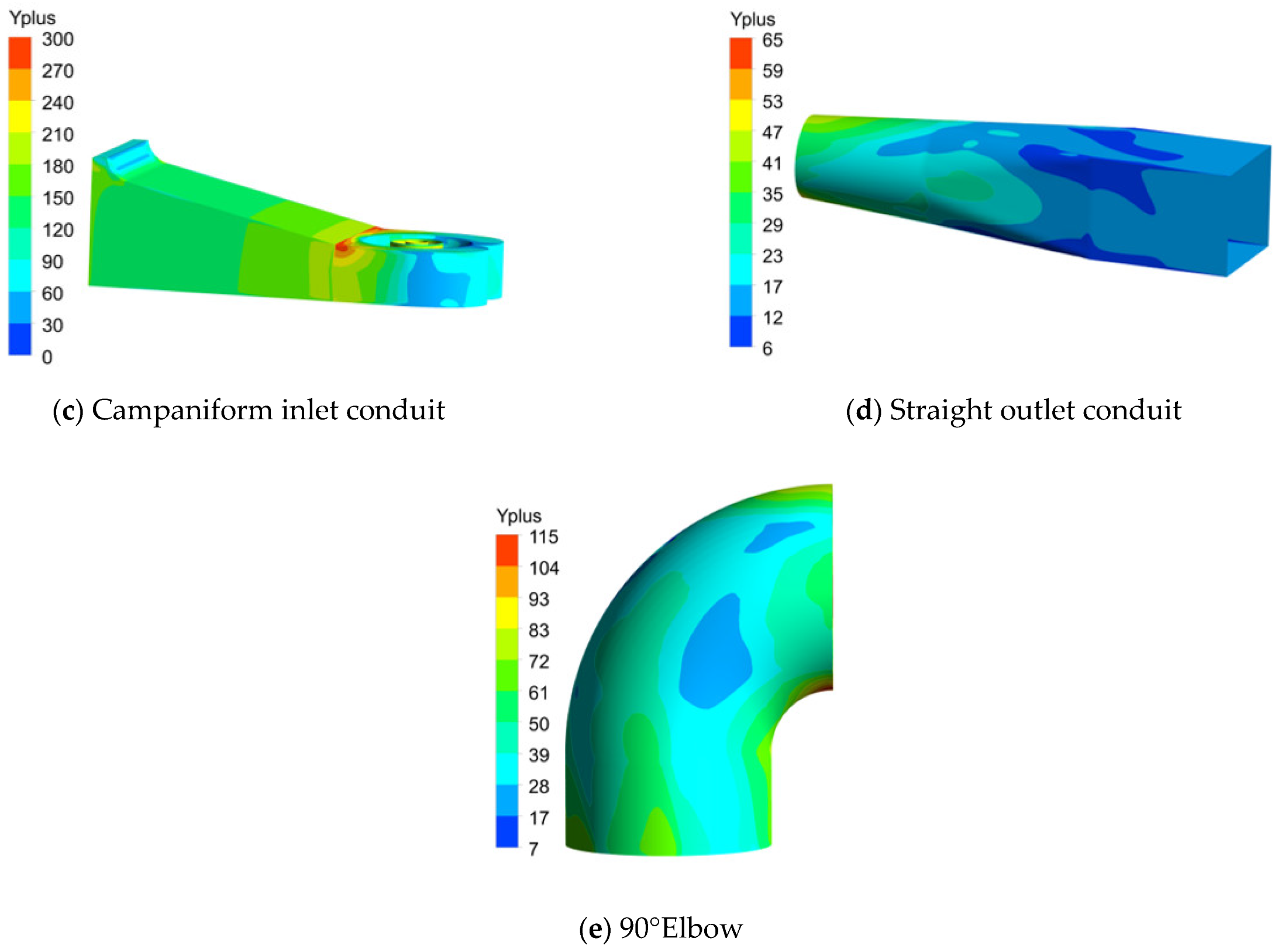






| Position | Boundary Types |
|---|---|
| Inlet surface of water inlet extension part | Mass flow rate |
| Exit surface of water outlet extension part | Standard atmospheric pressure |
| Pump device wall | No-slip wall |
| Interface on both sides of impeller | Frozen Rotor |
| Other computing domain interfaces | None |
| Convergence precision | 10−5 |
| Grid Scheme | Grid Number/104 | Efficiency/% | Relative Error/% |
|---|---|---|---|
| 1 | 220 | 85.79 | |
| 2 | 284 | 84.68 | −1.31 |
| 3 | 330 | 82.50 | −2.69 |
| 4 | 382 | 81.67 | −0.97 |
| 5 | 426 | 79.74 | −2.42 |
| 6 | 502 | 79.59 | −0.18 |
| 7 | 560 | 79.58 | −0.02 |
| Grid Number/104 | r | p * | f | ε | GCI/% |
|---|---|---|---|---|---|
| 220 | 85.789 | ||||
| 502 | 1.316519 | 3.2689 | 79.5911 | −0.07787 | GCI21 = 0.0668 |
| 560 | 1.037118 | 3.2689 | 79.5764 | −0.00018 | GCI32 = 0.0018 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Chang, P.; Cai, Y.; Lin, Z.; Tang, F.; Lv, Y. Analysis of Energy Loss Characteristics of Vertical Axial Flow Pump Based on Entropy Production Method under Partial Conditions. Entropy 2022, 24, 1200. https://doi.org/10.3390/e24091200
Yang F, Chang P, Cai Y, Lin Z, Tang F, Lv Y. Analysis of Energy Loss Characteristics of Vertical Axial Flow Pump Based on Entropy Production Method under Partial Conditions. Entropy. 2022; 24(9):1200. https://doi.org/10.3390/e24091200
Chicago/Turabian StyleYang, Fan, Pengcheng Chang, Yiping Cai, Zhikang Lin, Fangping Tang, and Yuting Lv. 2022. "Analysis of Energy Loss Characteristics of Vertical Axial Flow Pump Based on Entropy Production Method under Partial Conditions" Entropy 24, no. 9: 1200. https://doi.org/10.3390/e24091200
APA StyleYang, F., Chang, P., Cai, Y., Lin, Z., Tang, F., & Lv, Y. (2022). Analysis of Energy Loss Characteristics of Vertical Axial Flow Pump Based on Entropy Production Method under Partial Conditions. Entropy, 24(9), 1200. https://doi.org/10.3390/e24091200








