Adaptive Problem Solving Dynamics in Gate-Model Quantum Computers
Abstract
:1. Introduction
- A mathematical model of adaptive problem solving dynamics is defined for gate-model quantum computers. The proposed model characterizes the dynamical attributes of adaptive problem solving via iterative objective function maximization.
- A canonical equation of adaptive problem solving dynamics is derived for objective function maximization in a gate-model quantum computer (variational quantum algorithm).
- We define the stability of the problem solving steps to reach a maximized target value of the objective function. The stability of the objective function evaluation is associated with the gate errors in the hardware level of the gate-model quantum computer.
2. Problem Statement and System Model
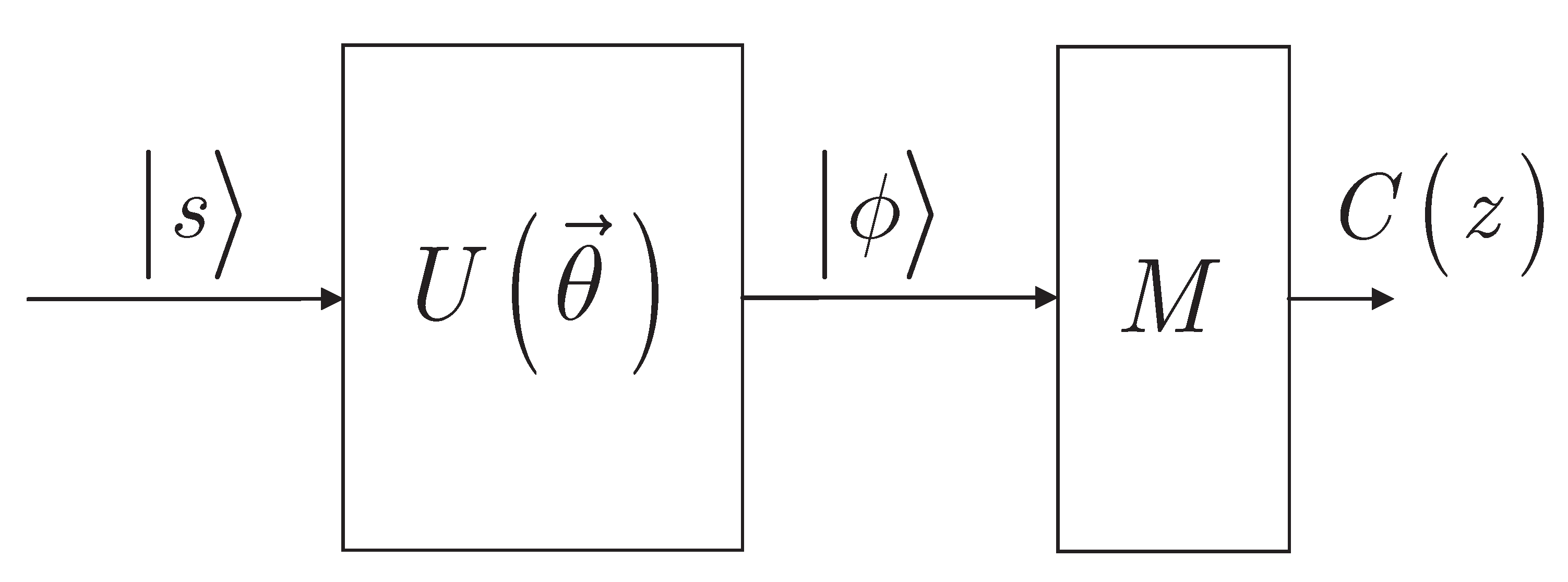
2.1. Problem Statement
2.2. System Model
2.3. Objective Function
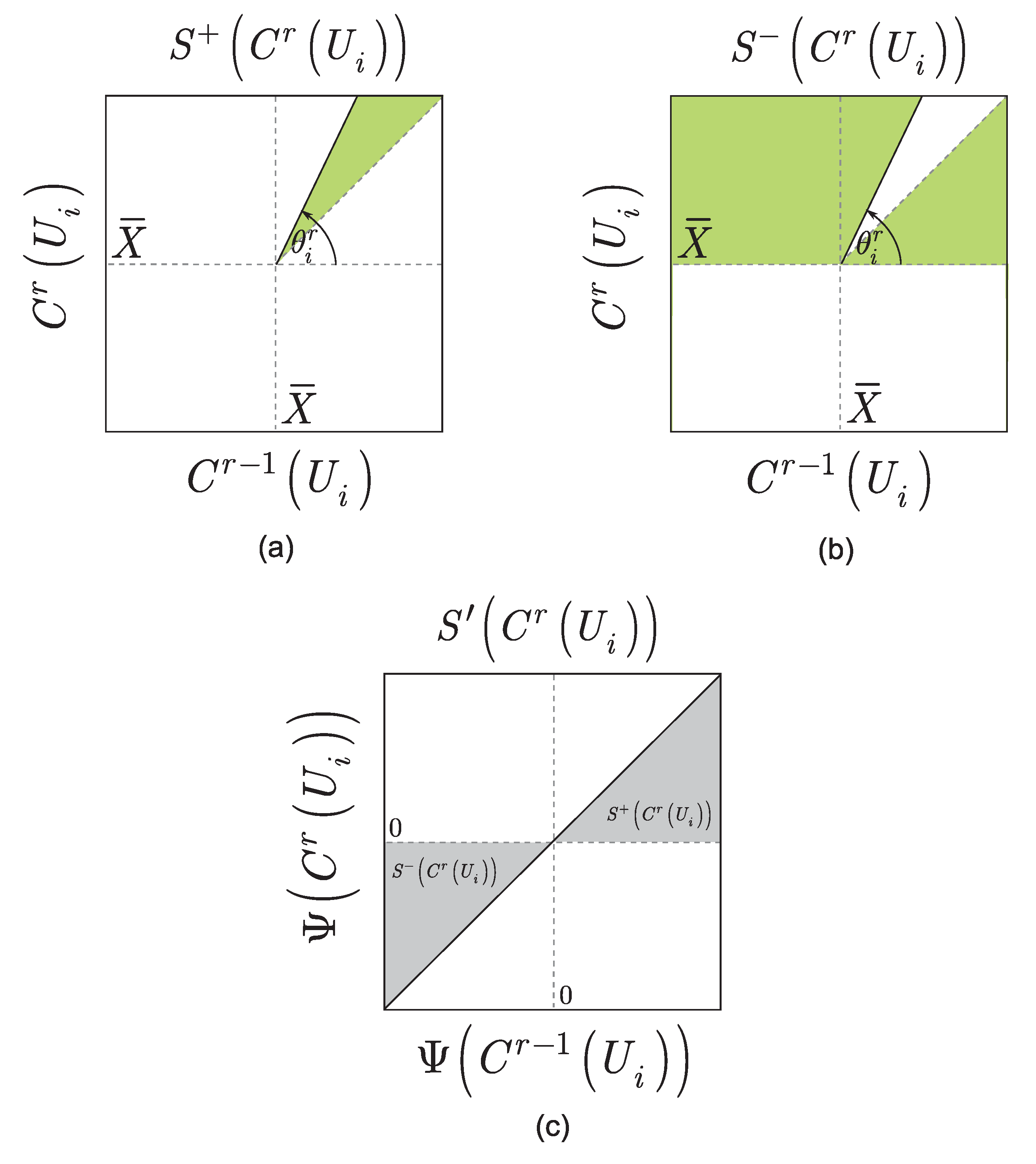
3. Stability of Objective Function Evaluation
4. Canonical Equation
5. Superposition of Stability Functions
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Abbreviations
Appendix A.2. Notations
| Notation | Description |
|---|---|
| An i-th unitary gate, , where P is a generalized Pauli operator formulated by a tensor product of Pauli operators , while is the gate parameter associated with . | |
| Gate parameter of . | |
| System state, , where identifies an i-th unitary gate. | |
| Gate parameter vector of the L unitaries, . | |
| Classical objective function of a computational problem fed into the quantum computer, , where is an objective function component evaluated between quantum qubits in the structure of the gate-model quantum computer. | |
| L | Number of unitaries of the quantum computer. |
| n | Number of qubits of input state ; bit length of string z. |
| Total number of unitary gates of the quantum computer. | |
| X | Pauli X operator. |
| Z | Pauli Z operator. |
| Y | Pauli Y operator. |
| L | Number of unitaries in a particular unitary sequence. |
| R | Number of total measurement rounds set for the optimization problem fed into the quantum computer. |
| Optimal (target) objective function value. | |
| r | An r-th measurement round, . |
| A string resulting from a measurement in an r-th measurement round, . | |
| Objective function evaluated via a string of an r-th measurement round, . | |
| Objective function component in associated with a connection between unitaries and . | |
| An i-th bit of , . | |
| Objective function component defined for in an r-th measurement round. | |
| Objective function component defined for in an r-th measurement round. | |
| Gate parameter of unitary in an r-th measurement round. | |
| Objective function component associated with in an r-th measurement round | |
| Objective function update function, where is the objective function component at , while is an updated objective function component if . | |
| A | , where and are some constants. |
| B | , where and are some constants. |
| Target objective function value subject to be reached in R measurement rounds. | |
| Target objective function component set for . | |
| A unitary sequence of an -th measurement round, . | |
| Objective function component vector at , . | |
| Objective function component vector at , . | |
| Vector of the total , objective function components at an -th measurement round, | |
| A vector in an -th measurement round, defined as . | |
| An r-th measurement round, . | |
| A Jacobian matrix at a particular and . | |
| A vector identifying at an equilibrium state. | |
| A vector referring to vector at an equilibrium state. | |
| A function evaluating the derivative of . | |
| A function evaluating the derivative of . | |
| A coefficient identifying the number of non-zero objective function components in an -th measurement round taken over unitaries . | |
| A coefficient referring to the number of zero objective function components of an -th measurement round taken over . | |
| State space, . | |
| Equilibrium state , . | |
| Jacobian matrix at the equilibrium , . | |
| An eigenvalue of , . | |
| Stability of objective function component , . | |
| A stable function. | |
| An unstable function. | |
| Evolution function (canonical equation) of an objective function component . | |
| Coefficient defined for , | |
| A ratio of probabilities. | |
| A rate function. | |
| A term in the canonical equation. | |
| A constant. | |
| A distribution family, . | |
| A probability distribution with a standard deviation , . | |
| Distance between the objective function component from a target value . | |
| A constant. | |
| Probability that the objective function component is updated from to such that the value of at an time interval is in the interval of . | |
| W | A vector referring to in an equilibrium state as . |
| Coefficient for , . | |
| Coefficient for , . | |
| Coefficient for at an equilibrium, . | |
| Coefficient for at an equilibrium, . | |
| A gate parameter value defined for a unitary in an r-th measurement round. | |
| Superposition of stability functions with respect to a particular objective function component , , where p is the probability of an unstable stability function . | |
| A function, defined for the for the unstable component, . | |
| A function, defined for the for the stable component , as . |
| Notation | Description |
|---|---|
| Gate parameter of unitary in an r-th measurement round. | |
| Objective function component associated with in an r-th measurement round | |
| Objective function update function, where is the objective function component at , while is an updated objective function component if . | |
| A | , where and are some constants. |
| B | , where and are some constants. |
| Target objective function value subject to be reached in R measurement rounds. | |
| Target objective function component set for . | |
| A unitary sequence of an -th measurement round, . | |
| Objective function component vector at , . | |
| Objective function component vector at , . | |
| Vector of the total , objective function components at an -th measurement round, | |
| A vector in an -th measurement round, defined as . | |
| An r-th measurement round, . | |
| A Jacobian matrix at a particular and . | |
| A vector, identifies at an equilibrium state. | |
| A vector referring to vector at an equilibrium state. | |
| A function evaluating the derivative of . | |
| A function evaluating the derivative of . | |
| A coefficient identifying the number of non-zero objective function components in an -th measurement round taken over unitaries . | |
| A coefficient referring to the number of zero objective function components of an -th measurement round taken over . | |
| State space, . | |
| Equilibrium state , . | |
| Jacobian matrix at the equilibrium , . | |
| An eigenvalue of , . | |
| Stability of objective function component , . | |
| A stable function. | |
| An unstable function. | |
| Evolution function (canonical equation) of an objective function component . | |
| Coefficient defined for , | |
| A ratio of probabilities. | |
| A rate function. | |
| A term in the canonical equation. | |
| A constant. | |
| A distribution family, . | |
| A probability distribution with a standard deviation , . | |
| Distance between the objective function component from a target value . | |
| A constant. | |
| Probability that the objective function component is updated from to such that the value of at an time interval is in the interval of . | |
| W | A vector referring to in an equilibrium state as . |
| Coefficient for , . | |
| Coefficient for , . | |
| Coefficient for at an equilibrium, . | |
| Coefficient for at an equilibrium, . | |
| A gate parameter value defined for a unitary in an r-th measurement round. | |
| Superposition of stability functions with respect to a particular objective function component , , where p is the probability of an unstable stability function . | |
| A function, defined for the for the unstable component, . | |
| A function, defined for the for the stable component , as . |
References
- Gyongyosi, L.; Imre, S. Problem Solving Dynamics for Gate-Model Quantum Computers. In Proceedings of the SPIE Quantum Information Science, Sensing, and Computation XIV, Orlando, FL, USA, 30 May 2022. [Google Scholar]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Harrow, A.W.; Montanaro, A. Quantum Computational Supremacy. Nature 2017, 549, 203–209. [Google Scholar] [CrossRef]
- Aaronson, S.; Chen, L. Complexity-theoretic foundations of quantum supremacy experiments. In Proceedings of the 32nd Computational Complexity Conference, CCC ’17, Riga, Latvia, 6–9 July 2017; pp. 22:1–22:67. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028v1. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Neven, H. Quantum Algorithms for Fixed Qubit Architectures. arXiv 2017, arXiv:1703.06199v1. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Zhou, L. The Quantum Approximate Optimization Algorithm and the Sherrington-Kirkpatrick Model at Infinite Size. arXiv 2019, arXiv:1910.08187. [Google Scholar] [CrossRef]
- Farhi, E.; Gamarnik, D.; Gutmann, S. The Quantum Approximate Optimization Algorithm Needs to See the Whole Graph: A Typical Case. arXiv 2020, arXiv:2004.09002v1. [Google Scholar]
- Farhi, E.; Gamarnik, D.; Gutmann, S. The Quantum Approximate Optimization Algorithm Needs to See the Whole Graph: Worst Case Examples. arXiv 2020, arXiv:2005.08747. [Google Scholar]
- Alexeev, Y.; Bacon, D.; Brown, K.R.; Calderbank, R.; Carr, L.D.; Chong, F.T.; DeMarco, B.; Englund, D.; Farhi, E.; Fefferman, B.; et al. Quantum Computer Systems for Scientific Discovery. arXiv 2019, arXiv:1912.07577. [Google Scholar] [CrossRef]
- Loncar, M.; Awschalom, D.; Berggren, K.K.; Bernien, H.; Bhave, S.; Carr, L.D.; Davids, P.; Economou, S.E.; Englund, D.; Faraon, A.; et al. Development of Quantum InterConnects for Next-Generation Information Technologies. arXiv 2019, arXiv:1912.06642. [Google Scholar]
- Foxen, B.; Neill, C.; Dunsworth, A.; Roushan, P.; Chiaro, B.; Megrant, A.; Kelly, J.; Chen, Z.; Satzinger, K.; Barends, R.; et al. Demonstrating a Continuous Set of Two-qubit Gates for Near-term Quantum Algorithms. Phys. Rev. Lett. 2020, 125, 120504. [Google Scholar] [CrossRef]
- Ajagekar, A.; Humble, T.; You, F. Quantum Computing based Hybrid Solution Strategies for Large-scale Discrete-Continuous Optimization Problems. Comput. Chem. Eng. 2020, 132, 106630. [Google Scholar] [CrossRef]
- Ajagekar, A.; You, F. Quantum computing for energy systems optimization: Challenges and opportunities. Energy 2019, 179, 76–89. [Google Scholar] [CrossRef]
- Harrigan, M.P.; Sung, K.J.; Neeley, M.; Satzinger, K.J.; Arute, F.; Arya, K.; Atalaya, J.; Bardin, J.C.; Barends, R. Quantum Approximate Optimization of Non-Planarusing eigenenergies Graph Problems on a Planar Superconducting Processor. arXiv 2020, arXiv:2004.04197. [Google Scholar]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Bengtsson, A.; Boixo, S.; Broughton, M.; Buckley, B.B.; et al. Observation of separated dynamics of charge and spin in the Fermi-Hubbard model. arXiv 2020, arXiv:2010.07965. [Google Scholar]
- Neill, C.; McCourt, T.; Mi, X.; Jiang, Z.; Niu, M.Y.; Mruczkiewicz, W.; Aleiner, I.; Arute, F.; Arya, K.; Atalaya, J.; et al. Accurately computing electronic properties of materials using eigenenergies. arXiv 2020, arXiv:2012.00921. [Google Scholar]
- Rubin, N.C.; Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Boixo, S.; Broughton, M.; Buckley, B.B.; et al. Hartree-Fock on a superconducting qubit quantum computer. Science 2020, 69, 1084–1089. [Google Scholar]
- Lloyd, S. Quantum approximate optimization is computationally universal. arXiv 2018, arXiv:1812.11075. [Google Scholar]
- Sax, I.; Feld, S.; Zielinski, S.; Gabor, T.; Linnhoff-Popien, C.; Mauerer, W. Approximate Approximation on a Quantum Annealer. arXiv 2020, arXiv:2004.09267. [Google Scholar]
- Brown, K.A.; Roser, T. Towards storage rings as quantum computers. Phys. Rev. Accel. Beams 2020, 23, 054701. [Google Scholar] [CrossRef]
- Bae, J.; Alsing, P.M.; Ahn, D.; Miller, W.A. Quantum circuit optimization using quantum Karnaugh map. Sci. Rep. 2020, 10, 15651. [Google Scholar] [CrossRef] [PubMed]
- Gill, S.S.; Kumar, A.; Singh, H.; Singh, M.; Kaur, K.; Usman, M.; Buyya, R. Quantum Computing: A Taxonomy, Systematic Review and Future Directions. ACM Comput. Surv. 2020. submitted. [Google Scholar] [CrossRef]
- Li, S.; Feng, X.; Cui, K.; Liu, F.; Zhang, W.; Huang, Y. Implementing Unitary Operators with Decomposition into Diagonal Matrices of Transform Domains. arXiv 2020, arXiv:2011.03250. [Google Scholar]
- Bugu, S.; Ozaydin, F.; Kodera, T. Surpassing the Classical Limit in Magic Square Game with Distant Quantum Dots Coupled to Optical Cavities. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef]
- Teplukhin, A.; Kendrick, B.; Babikov, D. Solving complex eigenvalue problems on a quantum annealer with applications to quantum scattering resonances. Phys. Chem. Chem. Phys. 2020, 22, 26136–26144. [Google Scholar] [CrossRef] [PubMed]
- Gyongyosi, L.; Imre, S. Advances in the Quantum Internet. Commun. ACM 2022, 65, 52–63. [Google Scholar] [CrossRef]
- Farhi, E.; Neven, H. Classification with Quantum Neural Networks on Near Term Processors. arXiv 2018, arXiv:1802.06002v1. [Google Scholar]
- Kardashin, A.; Pervishko, A.; Biamonte, J.; Biamonte, J. Benchmarking variational quantum simulation against an exact solution. arXiv 2021, arXiv:2105.06208. [Google Scholar]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.-H.; Zhou, X.-Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Wecker, D.; Hastings, M.B.; Troyer, M. Progress towards practical quantum variational algorithms. Phys. Rev. A 2015, 92, 042303. [Google Scholar] [CrossRef]
- Gyongyosi, L. Approximation Method for Optimization Problems in Gate-Model Quantum Computers. Chaos Solitons Fractals X 2021, 7, 100066. [Google Scholar] [CrossRef]
- McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. [Google Scholar] [CrossRef]
- Yuan, X.; Endo, S.; Zhao, Q.; Li, Y.; Benjamin, S. Theory of variational quantum simulation. Quantum 2019, 3, 191. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.-C.; Rahmani, A.; Shabani, A.; Neven, H.; Chamon, C. Optimizing Variational Quantum Algorithms Using Pontryagin’s Minimum Principle. Phys. Rev. X 2017, 7, 021027. [Google Scholar] [CrossRef]
- Oh, Y.-H.; Mohammadbagherpoor, H.; Dreher, P.; Singh, A.; Yu, X.; Rindos, A.J. Solving Multi-Coloring Combinatorial Optimization Problems Using Hybrid Quantum Algorithms. arXiv 2019, arXiv:1911.00595. [Google Scholar]
- Dercole, F.; Rinaldi, S. Analysis of Evolutionary Processes; Princeton University Press: Princeton, NJ, USA, 2008; ISBN 978-0-691-12006-5. [Google Scholar]
- Dercole, F.; Ferrière, R.; Gragnani, A.; Rinaldi, S. Coevolution of slow–fast populations: Evolutionary sliding, evolutionary pseudo-equilibria and complex Red Queen dynamics. Proc. R. Soc. Lond. B Biol. Sci. 2006, 273, 983–990. [Google Scholar] [CrossRef]
- Dieckmann, U.; Law, R. The dynamical theory of coevolution: A derivation from stochastic ecological processes. J. Math. Biol. 1996, 34, 579–612. [Google Scholar] [CrossRef]
- James, C. Introduction to Stochastics Search and Optimization; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Boussaid, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
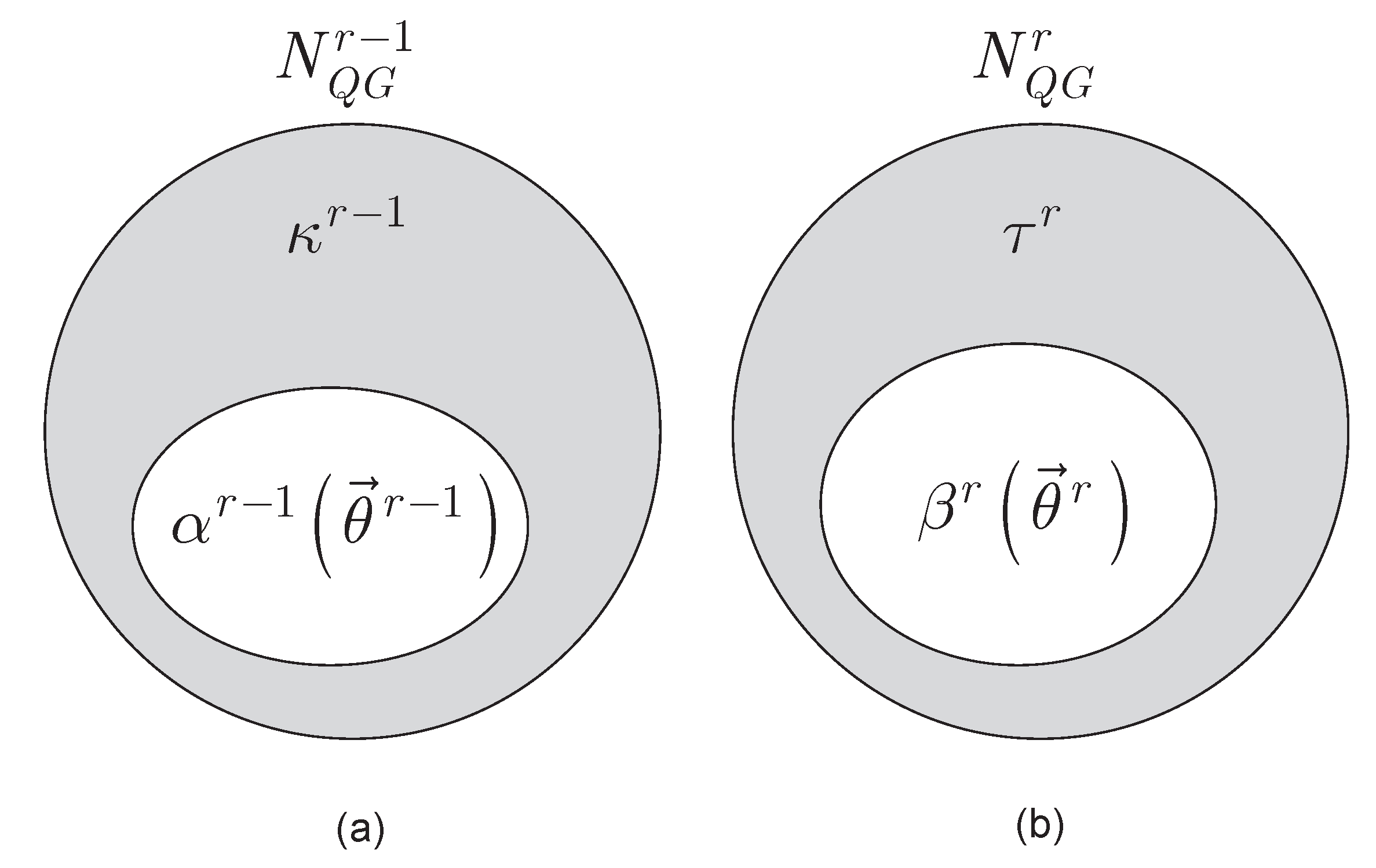
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyongyosi, L. Adaptive Problem Solving Dynamics in Gate-Model Quantum Computers. Entropy 2022, 24, 1196. https://doi.org/10.3390/e24091196
Gyongyosi L. Adaptive Problem Solving Dynamics in Gate-Model Quantum Computers. Entropy. 2022; 24(9):1196. https://doi.org/10.3390/e24091196
Chicago/Turabian StyleGyongyosi, Laszlo. 2022. "Adaptive Problem Solving Dynamics in Gate-Model Quantum Computers" Entropy 24, no. 9: 1196. https://doi.org/10.3390/e24091196
APA StyleGyongyosi, L. (2022). Adaptive Problem Solving Dynamics in Gate-Model Quantum Computers. Entropy, 24(9), 1196. https://doi.org/10.3390/e24091196





