Rate-Distortion-Based Stego: A Large-Capacity Secure Steganography Scheme for Hiding Digital Images
Abstract
:1. Introduction
- Providing an informational-theoretic-based high capacity steganographic algorithm to hide multiple security-sensitive messages, such as multiple RGB images and QR-coded images;
- Using rate-distortion theory to ensure better fidelity of the stego-image and increase the compressibility of the embedded secret images (the information embedding capacity is higher than those within the existing competing works, with better or similar PSNR ratios);
- Enhancing the system’s security with appropriate machine learning techniques. The proposed RD-Stego can survive the chosen cover attacks, which is another strong point compared to previous works;
- Deriving maximized MI lower bounds for the cover vs. the stego and the embedded secret vs. the reconstructed secret during network training, which provides reasonable regulations for the training process and enhances the stability of the trained model;
- Justifying the claimed ability to embed and reconstruct many payloads, such as multiple full-color images and QR-coded images, through a series of concrete experiments.
2. Related Works
2.1. Steganography Based on GANs
- , where Emb(.) denotes a data-embedding method based on a specific carrier c or a set of carriers C. The sender needs to design a scheme to construct stego media with an embedding key kemb.
- , where Ext(.) denotes a message extraction operation, which needs the inputs and the extraction key kext. The receiver can recover a secret message by using kext and the message extraction operation.
- , where and represent the cover set and the stego set, respectively, and stands for a quantifiable level of security for indistinguishability, the so-called -security.
2.2. The Limitations of the Current Steganography Works
3. The Proposed Approach
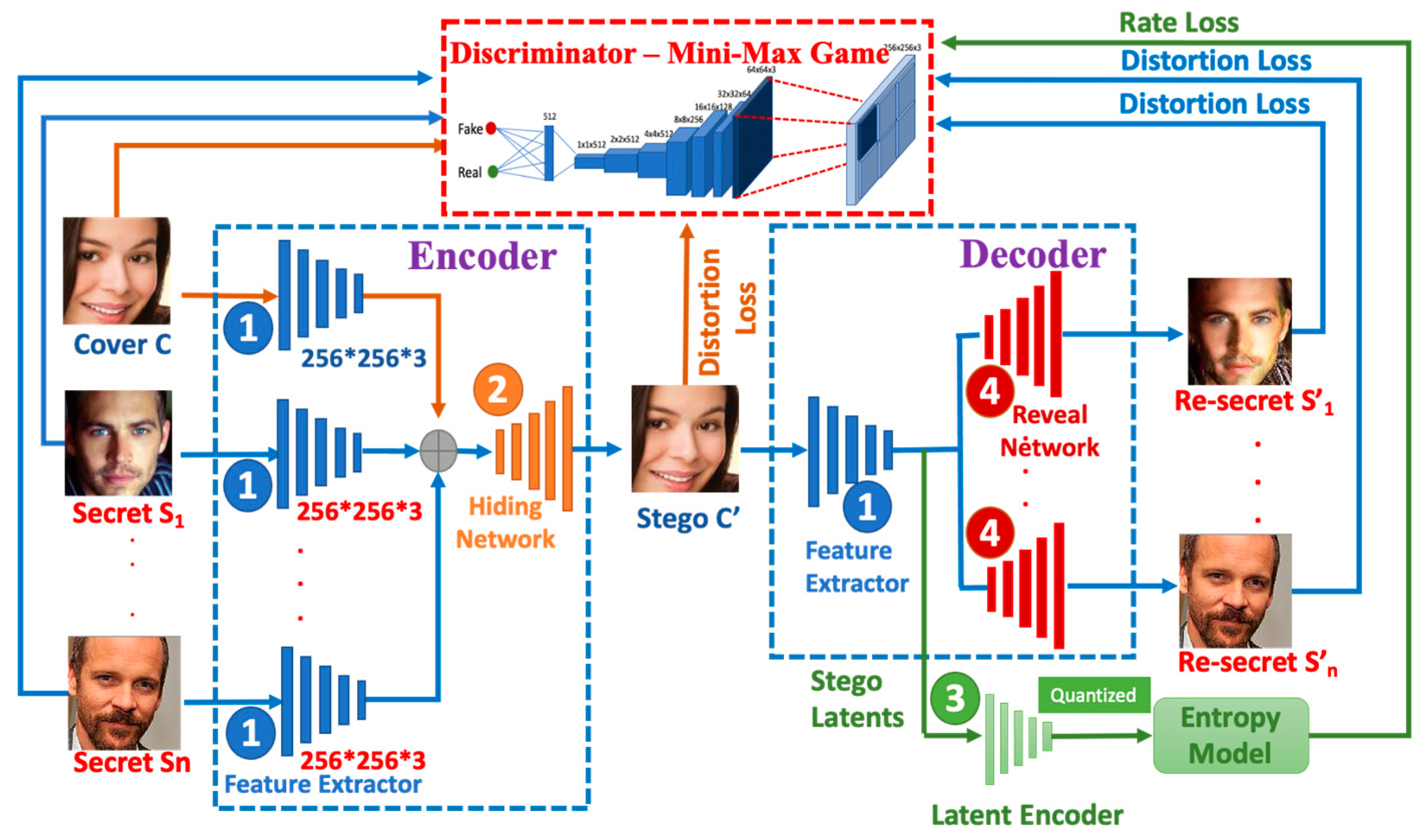
3.1. The RD-Stego Network Architecture
- 1.
- An encoder uses a three-channel color cover image, multiple three-channel color secret images, and even a QR code as inputs to generate a stego-image;
- 2.
- A decoder takes the stego-image as the input and reconstructs the secret-related messages and the QR-coded messages as well;
- 3.
- A latent encoder takes the stego latents as the input and quantizes these stego latents to the nearest integer. Then, the entropy model proceeds to calculate the entropy between the stego latents and quantized stego latents;
- 4.
- A Discriminator uses PatchGAN-D [29] to judge whether the cover and the stego-images, the secret and the reconstructed secret photos, or the embedded QR-coded and the reconstructed QR-coded messages are similar.
3.2. The Disentangle Efficacy of the Designed Loss Functions
3.2.1. Rate-Distortion Loss Functions
3.2.2. The Overall Loss Function and the Discriminator
- . This loss guarantees D will accurately classify the cover image to the stego-image associated with the label information and correct for the bias of the encoder.
- . This loss guarantees D will accurately classify the first secret image to the first reconstructed secret image associated with the first secret label information , and correct for the bias of the decoder.
- . This loss guarantees D will accurately classify the second secret image to the second reconstructed secret image associated with the second secret label information and correct for the bias of the decoder.
- . This loss guarantees D will accurately classify the nth secret image to the nth reconstructed secret image associated with the nth secret label information , and correct for the bias of the decoder.
- . This loss guarantees that D will accurately correct its bias with the aid of the cover image label information .
- . This loss guarantees that D will accurately correct its bias with the aid of the secret label information .
- . This loss guarantees that D will accurately correct its bias with the aid of the second secret image label information .
- . This loss guarantees that D will accurately correct its bias with the aid of the nth secret image label information .
3.3. The Information-Theoretic Based Analyses—Cost Functions
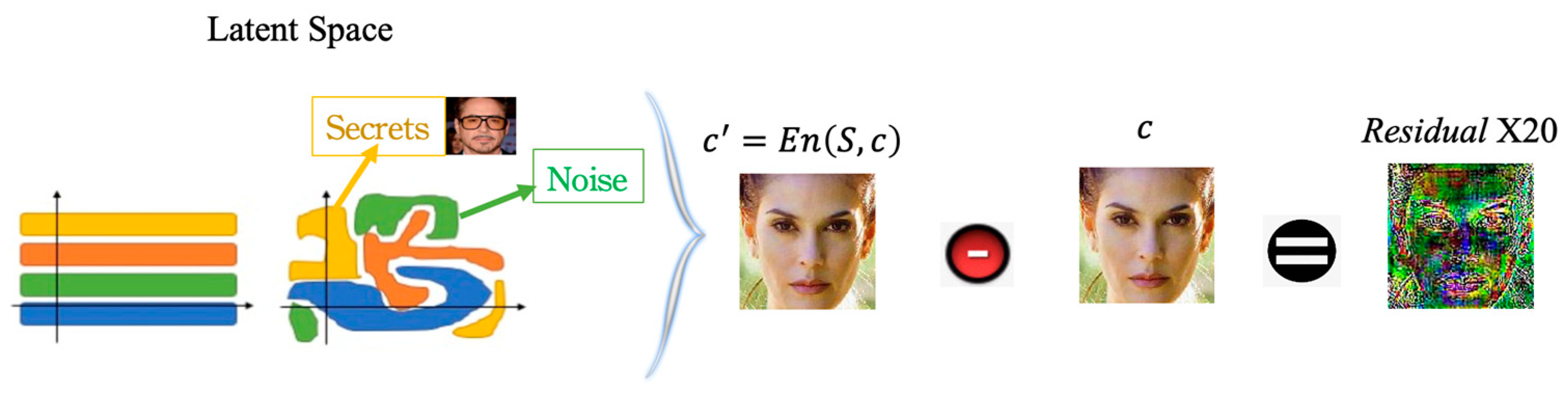
3.3.1. Visual Acceptability
3.3.2. Recovery Fidelity
4. Experimental Materials and the Related Benchmarking Methods
4.1. Experimental Environments and Testing Datasets
4.2. Evaluation Metrics
4.3. The Related Benchmarking Methods
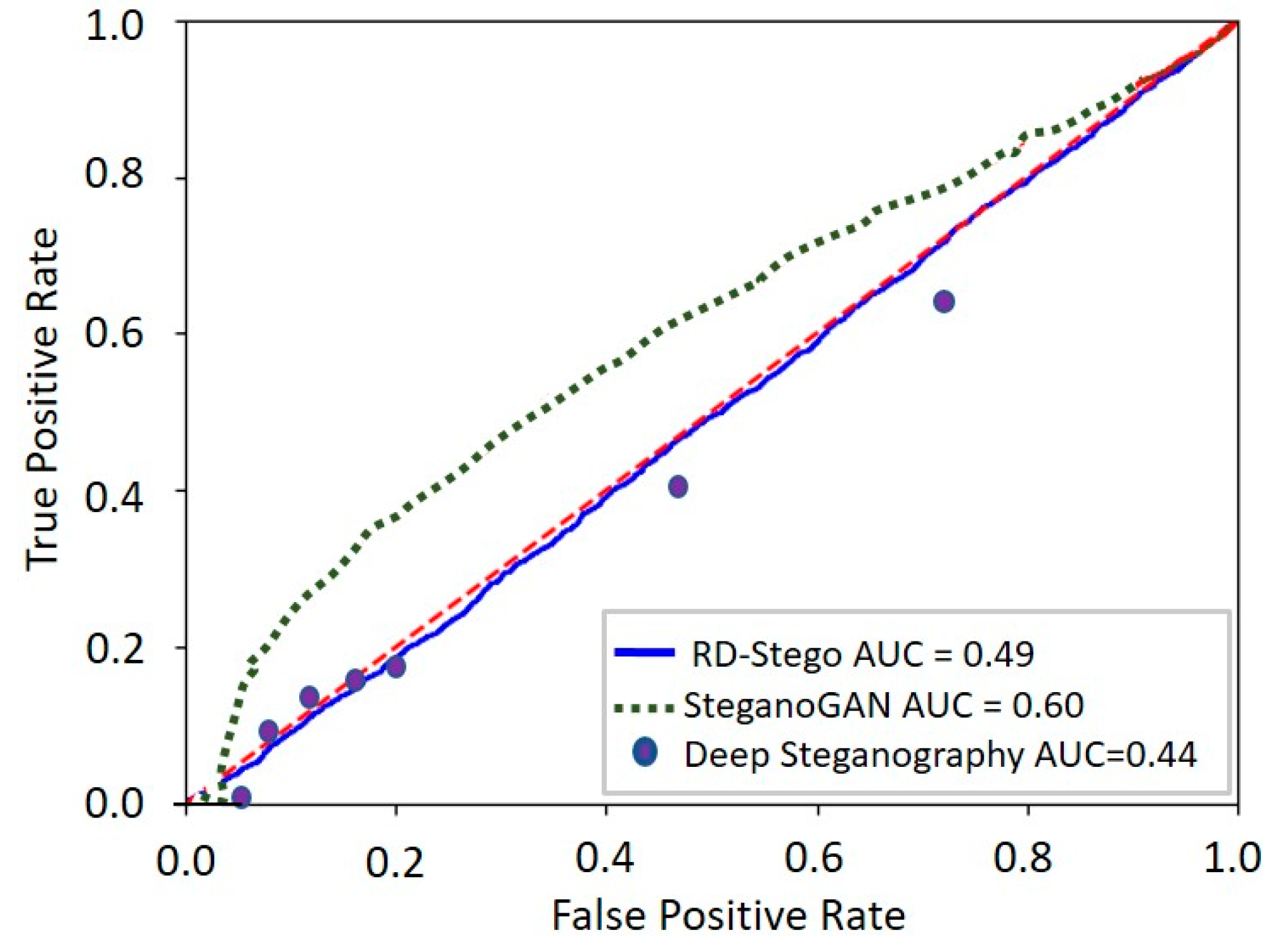
5. Experimental Results and Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Appendix A. The Computing Power Limitation of the Proposed RD-Stego

Appendix B. The Performances of RD-Stego under Some Preliminary Attacks
- a.
- Gaussian Noise Attack

- b.
- JPEG Compression Attack


References
- Petitcolas, F.; Anderson, R.; Kuhn, M. Information Hiding-A Survey. Proc. IEEE 1999, 87, 1062–1078. [Google Scholar] [CrossRef] [Green Version]
- Pevný, T.; Filler, T.; Bas, P. Using High-Dimensional Image Models to Perform Highly Undetectable Steganography. In Lecture Notes in Computer Science; Springer Science + Business Media: Berlin, Germany, 2010; Volume 6387, p. 161. [Google Scholar] [CrossRef] [Green Version]
- Hayes, J.; Danezis, G. Generating Steganographic Images via Adversarial Training. arXiv 2017, arXiv:stat.ML/1703.00371. [Google Scholar]
- Ke, Y.; Zhang, M.; Liu, J.; Su, T.; Yang, X. Generative Steganography with Kerckhoffs’ Principle. arXiv 2021, arXiv:cs.MM/1711.04916. [Google Scholar] [CrossRef]
- Shi, H.; Dong, J.; Wang, W.; Qian, Y.; Zhang, X. SSGAN: Secure Steganography Based on Generative Adversarial Networks. arXiv 2018, arXiv:cs.CV/1707.01613. [Google Scholar]
- Baluja, S. Hiding Images in Plain Sight: Deep Steganography. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Zhang, K.A.; Cuesta-Infante, A.; Xu, L.; Veeramachaneni, K. SteganoGAN: High Capacity Image Steganography with GANs. arXiv 2019, arXiv:cs.CV/1901.03892. [Google Scholar]
- Fu, Z.; Wang, F.; Xu, C. The Secure Steganography for Hiding Images via GAN. EURASIP J. Image Video Processing 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Ballé, J.; Minnen, D.; Singh, S.; Hwang, S.J.; Johnston, N. Variational Image Compression with a Scale Hyperprior. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lu, S.P.; Wang, R.; Zhong, T.; Rosin, P.L. Large-capacity Image Steganography Based on Invertible Neural Networks. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10811–10820. [Google Scholar]
- Liu, J.; Ke, Y.; Zhang, Z.; Lei, Y.; Li, J.; Zhang, M.; Yang, X. Recent Advances of Image Steganography With Generative Adversarial Networks. IEEE Access 2020, 8, 60575–60597. [Google Scholar] [CrossRef]
- Duan, X.; Jia, K.; Li, B.; Guo, D.; Zhang, E.; Qin, C. Reversible Image Steganography Scheme Based on a U-Net Structure. IEEE Access 2019, 7, 9314–9323. [Google Scholar] [CrossRef]
- Duan, X.; Liu, N.; Gou, M.; Wang, W.; Qin, C. SteganoCNN: Image Steganography with Generalization Ability Based on Convolutional Neural Network. Entropy 2020, 22, 1140. [Google Scholar] [CrossRef] [PubMed]
- Ng, H.W.; Winkler, S. A Data-driven Approach to Cleaning Large Face Datasets. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 343–347. [Google Scholar]
- Yi, D.; Lei, Z.; Liao, S.; Li, S.Z. Learning Face Representation from Scratch. arXiv 2014, arXiv:1411.7923. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep Learning Face Attributes in the Wild. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A Large-scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Abadi, M.; Andersen, D.G. Learning to Protect Communications with Adversarial Neural Cryptography. arXiv 2016, arXiv:cs.CR/1610.06918. [Google Scholar]
- Zhu, J.; Kaplan, R.; Johnson, J.; Fei-Fei, L. HiDDeN: Hiding Data With Deep Networks. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Tancik, M.; Mildenhall, B.; Ng, R. StegaStamp: Invisible Hyperlinks in Physical Photographs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Hu, D.; Wang, L.; Jiang, W.; Zheng, S.; Li, B. A Novel Image Steganography Method via Deep Convolutional Generative Adversarial Networks. IEEE Access 2018, 6, 38303–38314. [Google Scholar] [CrossRef]
- Liu, M.m.; Zhang, M.q.; Liu, J.; Zhang, Y.n.; Ke, Y. Coverless Information Hiding Based on Generative adversarial networks. arXiv 2017, arXiv:cs.CR/1712.06951. [Google Scholar]
- Fridrich, J. Steganography in Digital Media: Principles, Algorithms, and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; He, J.; Huang, J.; Shi, Y.Q. A Survey on Image Steganography and Steganalysis. J. Inf. Hiding Multim. Signal Process. 2011, 2, 142–172. [Google Scholar]
- Rehman, A.u.; Rahim, R.; Nadeem, M.S.; Hussain, S.u. End-to-End Trained CNN Encoder-Decoder Networks for Image Steganography. In Proceedings of the Computer Vision—ECCV 2018 Workshops—Munich, Germany, 8–14 September 2018, Proceedings, Part IV; Leal-Taixé, L., Roth, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2018; Volume 11132, pp. 723–729. [Google Scholar] [CrossRef]
- Dong, S.; Zhang, R.; Liu, J. Invisible Steganography via Generative Adversarial Network. arXiv 2018, arXiv:abs/1807.08571. [Google Scholar]
- Tang, W.; Li, B.; Tan, S.; Barni, M.; Huang, J. CNN-Based Adversarial Embedding for Image Steganography. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2074–2087. [Google Scholar] [CrossRef] [Green Version]
- Barber, D.; Agakov, F.V. The IM Algorithm: A Variational Approach to Information Maximization. In Proceedings of the NIPS, Vancouver, BC, Canada, 8–13 December 2003; pp. 201–208. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Prashnani, E.; Cai, H.; Mostofi, Y.; Sen, P. PieAPP: Perceptual Image-Error Assessment Through Pairwise Preference. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Boehm, B. StegExpose—A Tool for Detecting LSB Steganography. arXiv 2014, arXiv:cs.MM/1410.6656. [Google Scholar]










| Methodology | Payload Capacity | Advantages | Info. Theoretic Based Analyses | Limitations |
|---|---|---|---|---|
| Deep Stegano. [6], 2017. | Larger than 0.4 bpp |
| -N/A |
|
| Duant et al. [12], 2019 | 8 bpp |
| -N/A |
|
| SteganoGAN [7], 2019. | 4.4 bpp |
| -N/A |
|
| HIGAN [8], 2020. | 24 bpp |
| -N/A |
|
| SteganoCNN [13], 2020. | 48 bpp |
| -N/A |
|
| ISN [10], 2021 | 24∼120 bpp |
| -N/A |
|
| RD-Stego | 192 + bpp |
| -Yes |
|
| CPU Model | CPU Memory | Frequency | # of CPU Cores | GPU Model | # of GPU |
|---|---|---|---|---|---|
| Intel(R) Xeon(R) Gold 6128 CPU | 192 GB | 3.4 GHz | 24 | Tesla V100 | 2 |
| Operation System | Docker | # of GPUs in Docker | GPU Memory in Docker | CUDA Version | Language |
| Ubuntu 20.04 | 20.10.13 | 1 | 12GB | 11.4 | Python 3.7.10 Pytorch 1.9.0 |
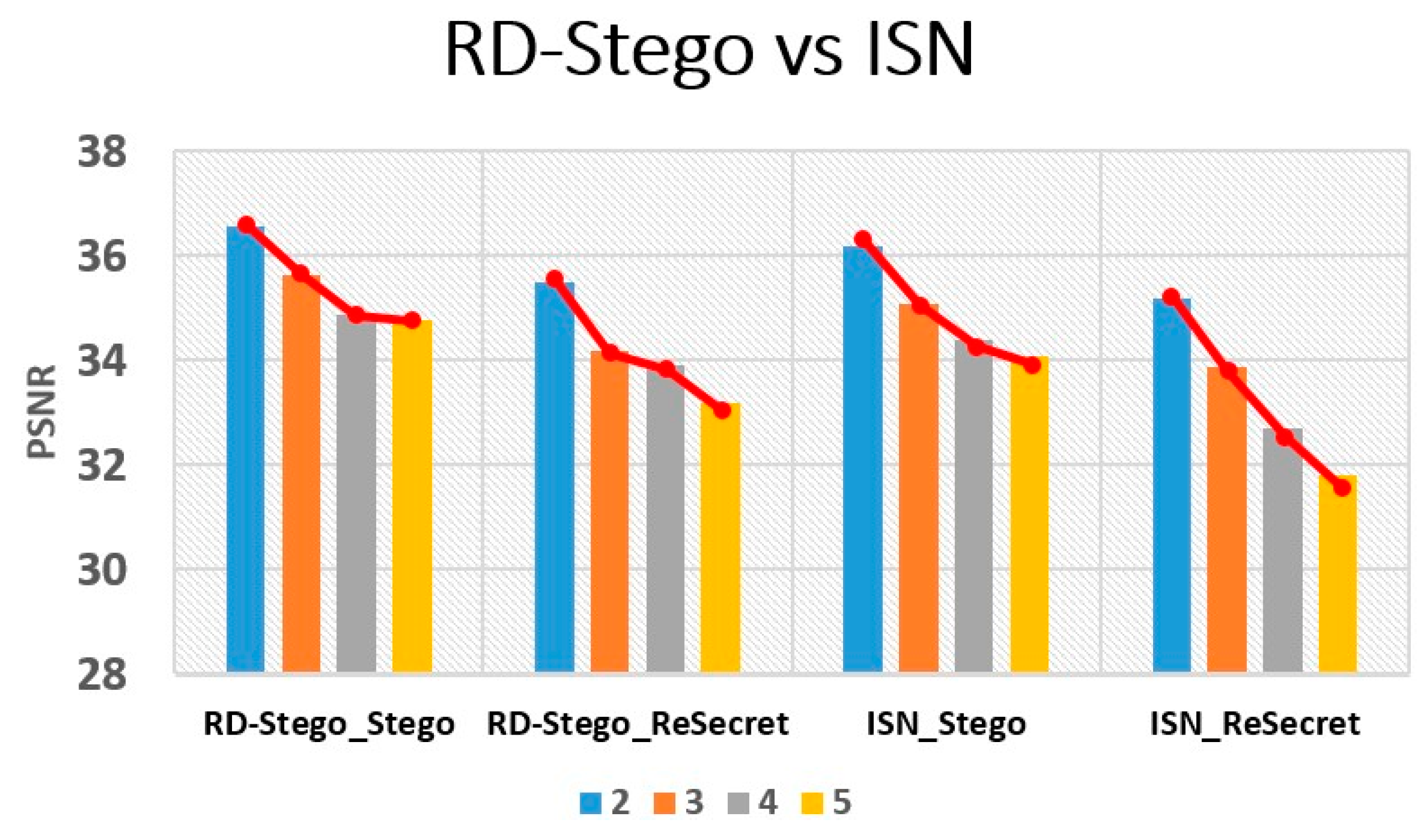
| Method | Hiding Images | Stego (SSIM) | Stego (PSNR) | Re-Constructed Secret (SSIM) | Re-Constructed Secret PNSR) |
|---|---|---|---|---|---|
| DeepStegano. [6] | 1 | 0.92 | 28.41 | 0.92 | 28.06 |
| Duan [12] | 1 | 0.95 | 36.71 | 0.96 | 36.97 |
| HIGAN [8] | 1 | 0.94 | 30.95 | 0.94 | 29.67 |
| Ours | 1 | 0.965 | 36.8 | 0.94 | 36.81 |
| ISN [10] | 2 | 0.94 | 36.2 | 0.92 | 35.2 |
| Ours | 2 | 0.96 | 36.58 | 0.94 | 35.5 |
| Dataset | CelebA | FaceScrub | ImageNet | |||
|---|---|---|---|---|---|---|
| PSNR/SSIM | PSNR/SSIM | PSNR/SSIM | ||||
| Stego | Secret | Stego | Secret | Stego | Secret | |
| 2 Secret | 36.58/0.960 | 35.50/0.931 | 36.27/0.952 | 34.86/0.925 | 34.80/0.932 | 32.87/0.917 |
| 3 Secret | 35.64/0.951 | 34.19/0.925 | 35.04/0.941 | 34.05/0.921 | 34.30/0.923 | 31.65/0.907 |
| 4 Secret | 34.86/0.939 | 33.905/0.913 | 34.25/0.923 | 33.75/0.911 | 33.98/0.914 | 30.52/0.898 |
| 5 Secret | 34.76/0.921 | 33.176/0.906 | 34.1/0.916 | 32.15/0.905 | 33.39/0.901 | 29.92/0.891 |
| 6 Secret | 34.5/0.909 | 31.905/0.901 | 33.92/0.902 | 31.02/0.891 | 32.18/0.896 | 28.87/0.885 |
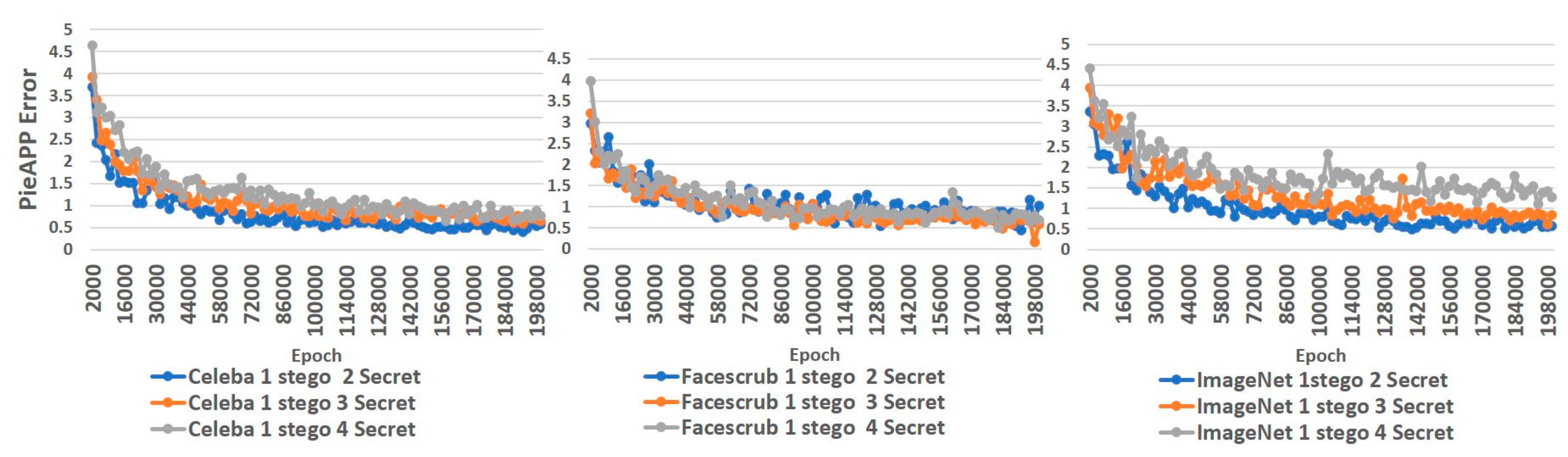
| Dataset | CelebA | FaceScrub | ImageNet | |||
|---|---|---|---|---|---|---|
| PieAPP | PieAPP | PieAPP | ||||
| Stego | Secret | Stego | Secret | Stego | Secret | |
| 2 Secret | 0.110 | 0.396 | 0.133 | 0.385 | 0.262 | 0.447 |
| 3 Secret | 0.131 | 0.329 | 0.152 | 0.392 | 0.265 | 0.597 |
| 4 Secret | 0.169 | 0.387 | 0.157 | 0.450 | 0.230 | 0.618 |
| 5 Secret | 0.163 | 0.419 | 0.162 | 0.475 | 0.322 | 0.621 |
| 6 Secret | 0.215 | 0.481 | 0.138 | 0.562 | 0.421 | 0.751 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.-L.; Wu, J.-L. Rate-Distortion-Based Stego: A Large-Capacity Secure Steganography Scheme for Hiding Digital Images. Entropy 2022, 24, 982. https://doi.org/10.3390/e24070982
Pan Y-L, Wu J-L. Rate-Distortion-Based Stego: A Large-Capacity Secure Steganography Scheme for Hiding Digital Images. Entropy. 2022; 24(7):982. https://doi.org/10.3390/e24070982
Chicago/Turabian StylePan, Yi-Lun, and Ja-Ling Wu. 2022. "Rate-Distortion-Based Stego: A Large-Capacity Secure Steganography Scheme for Hiding Digital Images" Entropy 24, no. 7: 982. https://doi.org/10.3390/e24070982
APA StylePan, Y.-L., & Wu, J.-L. (2022). Rate-Distortion-Based Stego: A Large-Capacity Secure Steganography Scheme for Hiding Digital Images. Entropy, 24(7), 982. https://doi.org/10.3390/e24070982







