Low Entropy Future Boundary Conditions
Abstract
1. Introduction
2. Various Indicators
3. Black Holes?
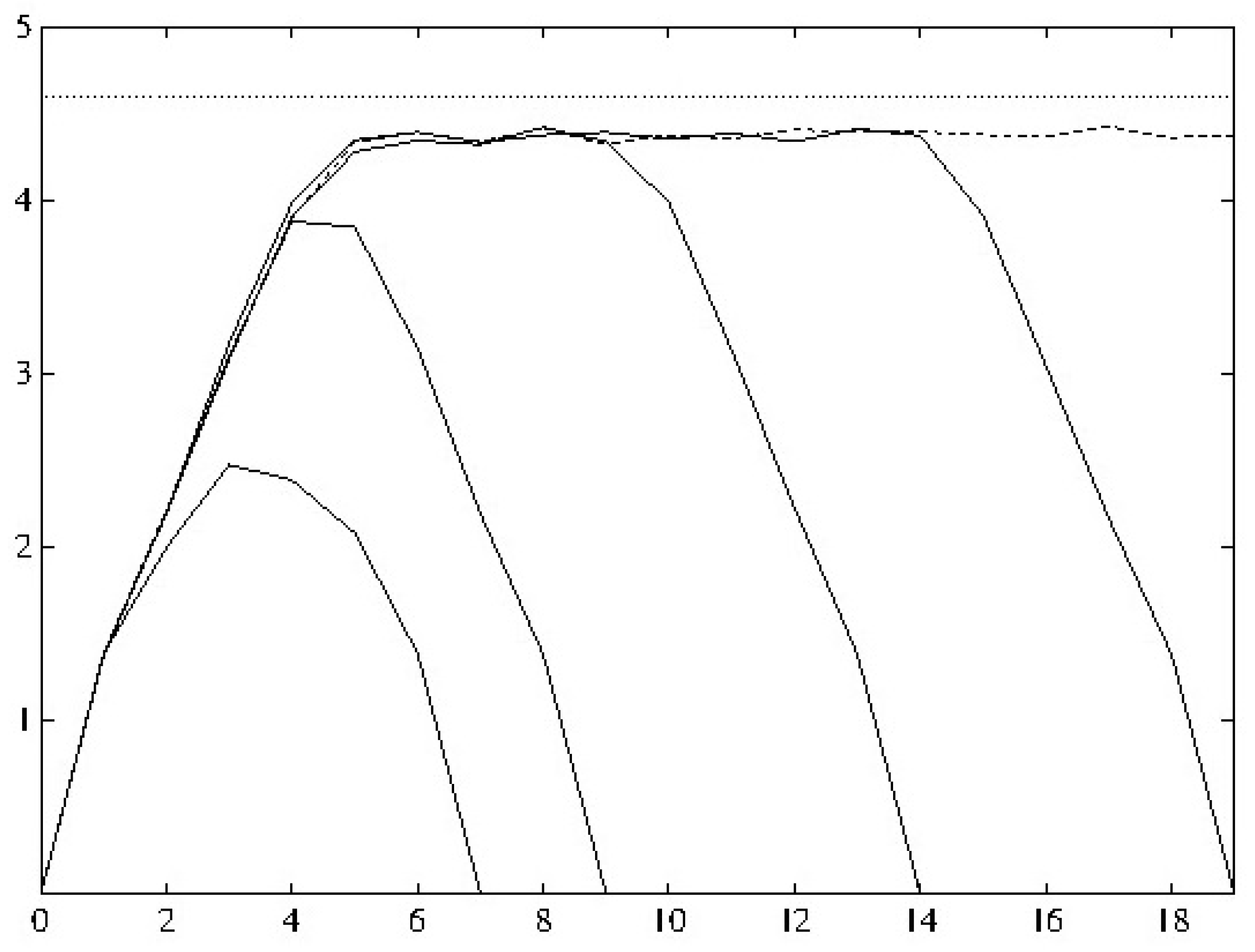
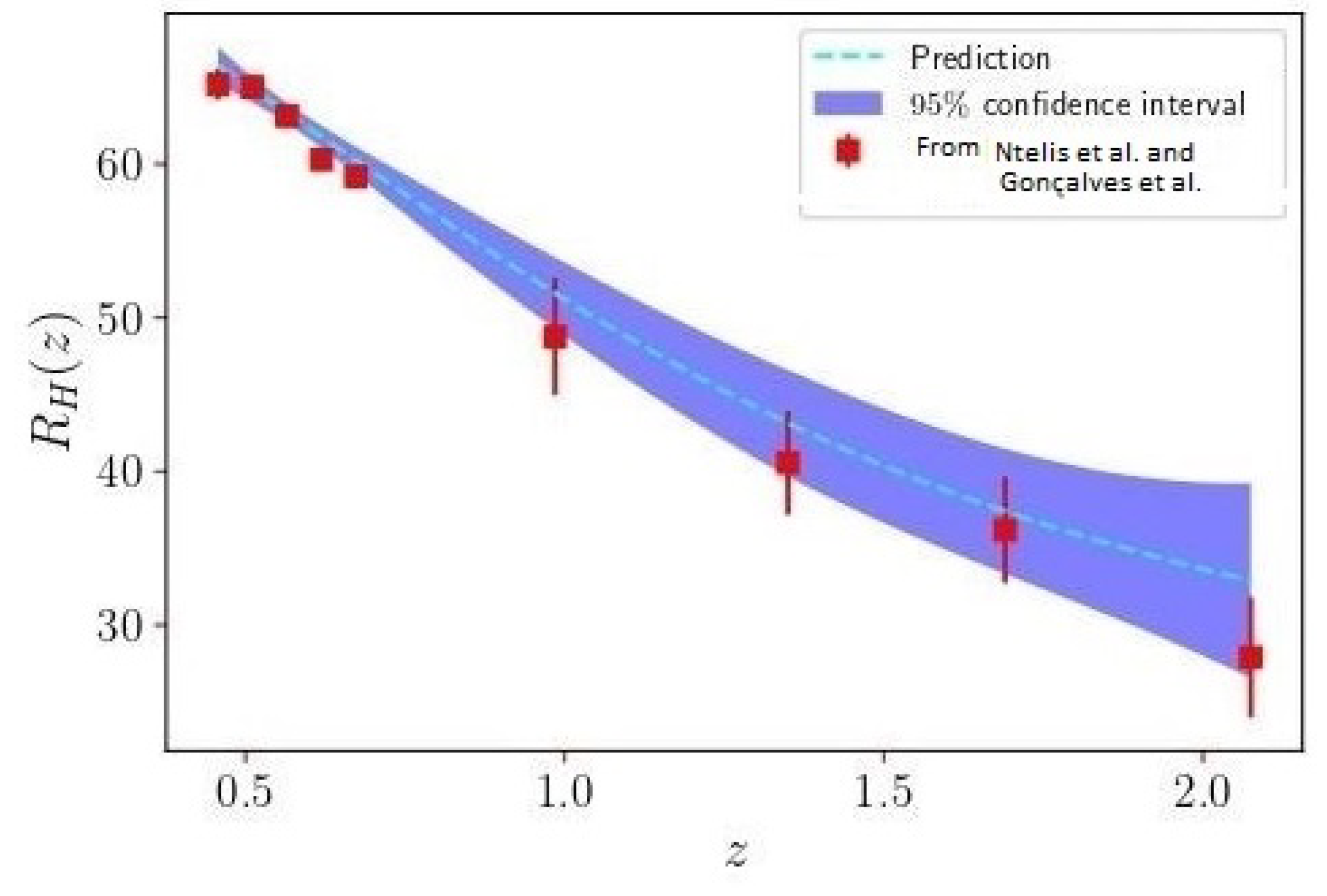
4. Doubts about Conventional Cosmology
5. Conclusions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Schulman, L.S. Time’s Arrows and Quantum Measurement; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Schulman, L.S. Special states demand a force for the observer. Found. Phys. 2016, 46, 1471–1494. [Google Scholar] [CrossRef]
- Schulman, L.S. Program for the special state theory of quantum measurement. Entropy 2017, 19, 343. [Google Scholar] [CrossRef]
- Schulman, L.S.; da Luz, M.G.E. Looking for the source of change. Found. Phys. 2016, 46, 1495–1501. [Google Scholar] [CrossRef]
- Wheeler, J.A. At some point in the 1970s this was mentioned by Wheeler. I do not have a reference and I asked Wheeler, but he did not recall. I am nevertheless sure that this should be attributed to him. The closest I could come was J. A. Wheeler. In General Relativity and Gravitation (GR7); Shaviv, G., Rosen, J., Eds.; Wiley: New York, NY, USA; Israel University Press: Israel, 1975. [Google Scholar]
- Schulman, L.S. Illustration of reversed causality with remarks on experiment. J. Stat. Phys. 1977, 16, 217–231. [Google Scholar] [CrossRef]
- Buchert, T. Toward physical cosmology: Focus on inhomogeneous geometry and its non-perturbative effects. Class. Quant. Grav. 2011, 28, 164007. [Google Scholar] [CrossRef]
- Khoury, J.; Steinhardt, P.J.; Turok, N. Designing cyclic universe models. Phys. Rev. Lett. 2004, 92, 31302. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Lynden-Bell, D. Statistical mechanics of violent relaxation in stellar systems. Mont. Not. R. Astronom. Soc. 1977, 136, 101–121. [Google Scholar] [CrossRef]
- Yadav, J.K.; Bagla, J.S.; Khandai, N. Fractal dimension as a measure of the scale of homogeneity. Mont. Not. R. Astronom. Soc. 2010, 405, 2009–2015. [Google Scholar] [CrossRef]
- Cosmai, L.; Fanizza, G.; Labini, F.S.; Pietronero, L.; Tedesco, L. Fractal universe and cosmic acceleration in a Lemaître–Tolman–Bondi scenario. Class. Quant. Grav. 2019, 36, 45007. [Google Scholar]
- Hogg, D.W.; Eisenstein, D.J.; Blanton, M.R.; Bahcall, N.A.; Brinkmann, J.; Gunn, J.E.; Schneider, D.P. Cosmic homogeneity demonstrated with luminous red galaxies. Astrophys. J. 2005, 624, 54–58. [Google Scholar] [CrossRef]
- Avila, F.; Bernui, A.; Nunes, R.C.; de Carvalho, E.; Novaes, C.P. The homogeneity scale and the growth rate of cosmic structures. Mon. Not. R. Astron. Soc. 2022, 509, 2994–3003. [Google Scholar] [CrossRef]
- Gonçalves, R.S.; Carvalho, G.C.; Andrade, U.; Bengaly, C.A.P.; Carvalho, J.C.; Alcaniz, J. Measuring the cosmic homogeneity scale with SDSS-IV DR16 quasars. J. Cosmo. Astropart. Phys. 2021, 3, 29. [Google Scholar] [CrossRef]
- Ntelis, P.; Hamilton, J.; Goff, J.L.; Burtin, E.; Laurent, P.; Rich, J.; Busca, N.G.; Tinker, J.; Aubourg, E.; de Bourboux, H.M.; et al. Exploring cosmic homogeneity with the BOSS DR12 galaxy sample. J. Cosmo. Astropart. Phys. 2017, 6, 19. [Google Scholar] [CrossRef]
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 25, 6587138. [Google Scholar] [CrossRef]
- Heinesen, A. Cosmological homogeneity scale estimates are dressed. J. Cosmol. Astropart. Phys. 2020, 2020, 52. [Google Scholar] [CrossRef]
- Li, M.; Lin, H. Testing the homogeneity of the universe using gamma-ray bursts. Astronom. Astrophys. 2015, 582, A111. [Google Scholar] [CrossRef][Green Version]
- Dirac, P.A.M. Classical theory of radiating electrons. Proc. R. Soc. Lond. 1938, 167, 148–169. [Google Scholar]
- Volta, G. This was reported in a talk by G. Volta at Univ. of Zurich. In Proceedings of the Swiss Physics Society Annual Meeting, Zurich, Switzerland, 26–30 August 2019. [Google Scholar]
- XENON Collaboration. Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532–535. [Google Scholar] [CrossRef]
- Alibés, A.; Labay, J.; Canal, R. Galactic chemical abundance evolution in the solar neighborhood up to the iron peak. Astronom. Astrophys. 2001, 370, 1103–1121. [Google Scholar] [CrossRef]
- Bisterzo, S.; Gallino, C.T.a.R.; Wiescher, M.; Käppeler, F. Galactic chemical evolution and solar s-process abundances: Dependence on the 13C-pocket structure. Astrophys. J. 2014, 787, 10–14. [Google Scholar] [CrossRef]
- Cook, D.L.; Smith, T.; Leya, I.; Hilton, C.D.; Walker, R.J.; Schönbächler, M. Excess 180W in IIAB iron meteorites: Identification of cosmogenic, radiogenic, and nucleosynthetic components. Earth Planet. Sci. Lett. 2018, 503, 29–36. [Google Scholar] [CrossRef]
- Den Hartog, E.A.; Lawler, J.E.; Sneden, C.; Cowan, J.J. Improved laboratory transition probabilities for Nd II and application to the neodymium abundances of the sun and three metal-poor stars. Astrophys. J. Suppl. 2003, 148, 543–566. [Google Scholar] [CrossRef]
- Peek, K.M.G. A new technique for determining europium abundances in solar-metallicity stars. Pub. Astron. Soc. Pacific 2009, 121, 755–766. [Google Scholar] [CrossRef]
- Roederer, I.U.; Lawler, J.E.; Cowan, J.J.; Beers, T.C.; Frebel, A.; Ivans, I.I.; Schatz, H.; Sobeck, J.S.; Sneden, C. Detection of the second r-process peak element tellurium in metal-poor stars. Astrophys. J. Lett. 2012, 747, 5. [Google Scholar] [CrossRef]
- Travaglio, C.; Gallino, R.; Arnone, E.; Cowan, J.; Jordan, F.; Sneden, C. Galactic evolution of Sr, Y, and Zr: A multiplicity of nucleosynthetic processes. Astrophys. J. 2004, 601, 864–884. [Google Scholar] [CrossRef]
- Srinivasan, B.; Anders, E. Noble gases in the Murchison meteorite: Possible relics of s-process nucleosynthesis. Science 1978, 201, 51–60. [Google Scholar] [CrossRef]
- Schulman, L.S. Normal and reversed causality in a model system. Phys. Lett. A 1976, 57, 305–306. [Google Scholar] [CrossRef]
- Lazicki, A.; McGonegle, D.; Rygg, J.R.; Braun, D.G.; Swift, D.C.; Gorman, M.G.; Smith, R.F.; Heighway, P.G.; Higginbotham, A.; Suggit, M.J.; et al. Metastability of diamond ramp-compressed to 2 terapascals. Nature 2021, 589, 532–535, Erratum in Nature 2022, 605, 1. [Google Scholar] [CrossRef]
- Wikipedia. Accelerated Expansion. Available online: https://en.wikipedia.org/wiki/Accelerating_expansion_of_the_universe. (accessed on 30 May 2022).
- Blanchard, A.; Douspis, M.; Rowan-Robinson, M.; Sarkar, S. An alternative to the cosmological “concordance model”. Astronom. Astrophys. 2003, 412, 35–44. [Google Scholar] [CrossRef]
- Bolejko, K.; Krasiǹski, A.; Hellaby, C.; Calerier, M. Structures in the Universe by Exact Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Clarkson, C.; Cortês, M.; Bassett, B. Dynamical dark energy or simply cosmic curvature? J. Cosmol. Astropart. Phys. 2007, 8, 11. [Google Scholar] [CrossRef]
- Ellis, G. Patchy solutions. Nature 2008, 452, 158–161. [Google Scholar] [CrossRef] [PubMed]
- Leith, B.M.; Ng, S.C.C.; Wiltshire, D.L. Gravitational energy as dark energy: Concordance of cosmological tests. Astrophys. J. 2008, 672, L91–L94. [Google Scholar] [CrossRef]
- Maartens, R. Is the universe homogeneous? Phil. Trans. Roy. Soc. A 2011, 389, 1957. [Google Scholar] [CrossRef]
- Mertens, J.B.; Giblin, J.T., Jr.; Starkman, G.D. Integration of inhomogeneous cosmological spacetimes in the BSSN formalism. Phys. Rev. D 2016, 93, 124059. [Google Scholar] [CrossRef]
- Rácz, G.; Dobos, L.; Beck, R.; Szapudi, I.; Csabai, I. Concordance cosmology without dark energy. Mont. Not. R. Astronom. Soc. 2017, 469, L1–L5. [Google Scholar] [CrossRef]
- Boudewijn, F.; Roukema, P.M.; Buchert, T.; Ostrowski, J.J. The background Friedmannian Hubble constant in relativistic inhomogeneous cosmology and the age of the universe. Astronom. Astrophys. 2017, 591, A111. [Google Scholar]
- Vigneron, Q.; Buchert, T. Dark matter from backreaction? Collapse models on galaxy cluster scales. Class. Quant. Grav. 2019, 36, 175006. [Google Scholar] [CrossRef]
| Isotope | Half-Life (years) | Isotope | Half-Life (years) |
|---|---|---|---|
| hafnium-174 | 2.002 | zirconium-96 | 20 |
| osmium-186 | 2.002 | bismuth-209 | 20.1 |
| neodymium-144 | 2.292 | calcium-48 | 23.01 |
| samarium-148 | 7.005 | cadmium-116 | 31.02 |
| cadmium-113 | 7.7 | selenium-82 | 110 |
| vanadium-50 | 140 | barium-130 | 1.2 |
| tungsten-180 | 1.801 | germanium-76 | 1.8 |
| europium-151 | 5.004 | xenon-136 | 2.165 |
| molybdenum-100 | 7.804 | krypton-78 | 9.2 |
| neodymium-150 | 7.905 | xenon-124 | 18 |
| tellurium-130 | 8.806 | tellurium-128 | 2.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulman, L.S. Low Entropy Future Boundary Conditions. Entropy 2022, 24, 976. https://doi.org/10.3390/e24070976
Schulman LS. Low Entropy Future Boundary Conditions. Entropy. 2022; 24(7):976. https://doi.org/10.3390/e24070976
Chicago/Turabian StyleSchulman, Lawrence S. 2022. "Low Entropy Future Boundary Conditions" Entropy 24, no. 7: 976. https://doi.org/10.3390/e24070976
APA StyleSchulman, L. S. (2022). Low Entropy Future Boundary Conditions. Entropy, 24(7), 976. https://doi.org/10.3390/e24070976






