Scalably Using Node Attributes and Graph Structure for Node Classification †
Abstract
:1. Introduction
1.1. Previous Work
1.2. Our Contribution
- We define a generative model that formally captures a diverse set of relationships between graph structure, node attributes, and node labels.
- We describe a general algorithm to compute a good initial estimate of and a training algorithm called JANE for node classification. We also design batching and minibatching variants of JANE that scale well to large graphs.
- From our experimental results, we present three findings. First, we demonstrate the shortcomings of existing approaches and versatility of JANE on synthetic datasets. Second, we empirically validate the performance of four variants of JANE on seven real-world datasets and compare to five standard baselines. Thirdly, we conduct an extensive empirical analysis characterizing the usefulness of a good initial node embedding, the importance of updates to the embedding during training, and the trade-off between preserving adjacency and label information on classification accuracy.
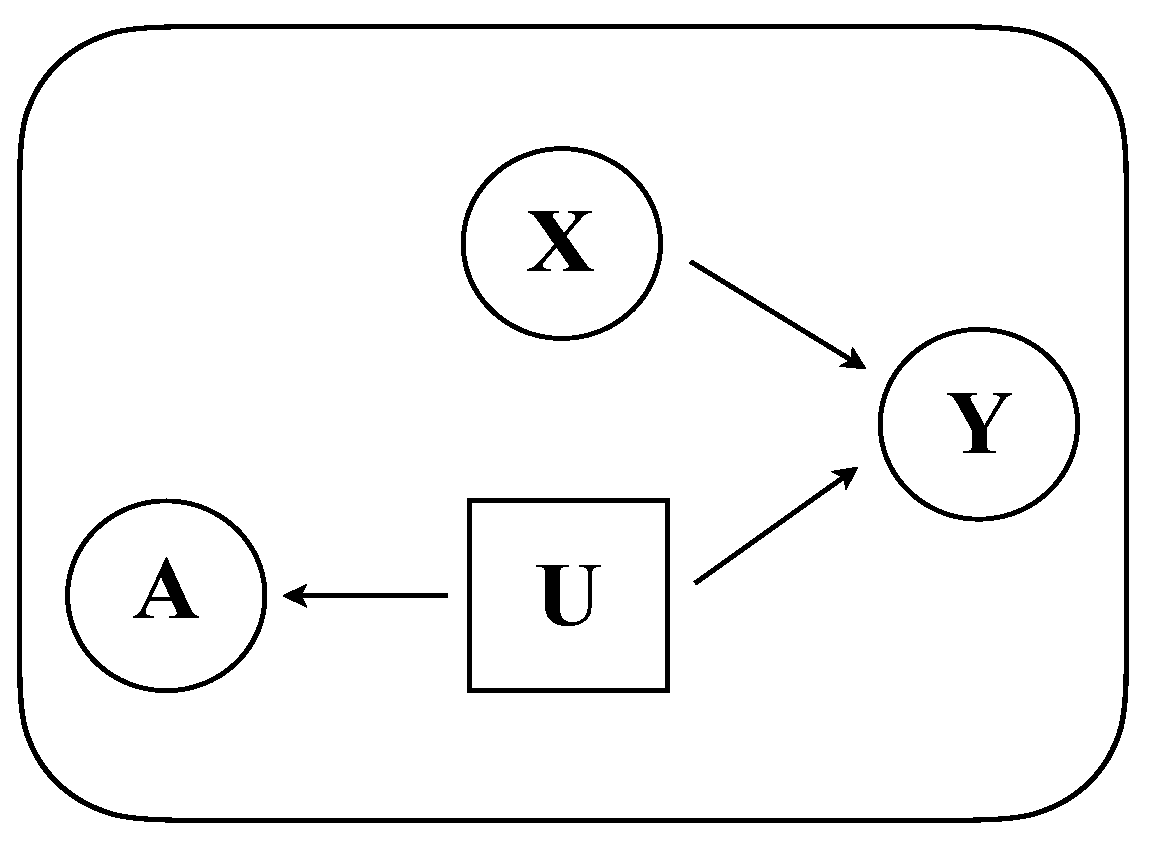
2. Problem Setting
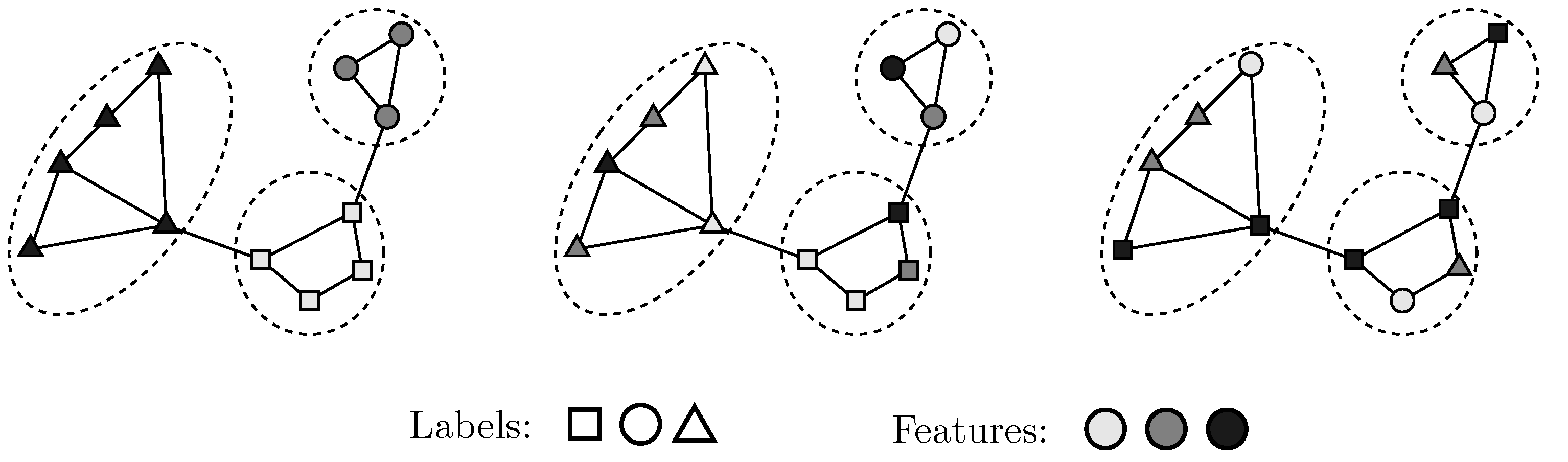
3. Our Approach
3.1. Model
3.2. Algorithms
3.2.1. Training
| Algorithm 1: INITIALIZE. |
| 1 Input: Adjacency Matrix ; Embedding method EMBEDDING∈ {Laplacian, Gosh}, embedding dimensionality k; |
| 2 Output: Latent attributes , Scale s; |
| 3 |
| 4 |
| 5 // ((cf. Equation (7)) |
| 6 , // Rescale |
| return |
| Algorithm 2: JANE-U (Batching). |
 |
3.2.2. Prediction
3.2.3. Complexity Analysis
| Algorithm 3: JANE-U-M (Mini-Batching). |
 |
4. Experiments
4.1. Algorithms
- JANE-R: This chooses a random matrix of appropriate dimensions () as and trains according to Algorithm 2 in a batched manner.
- JANE-U-M: This is similar to JANE-U, except that it trains in a minibatched fashion (cf. Algorithm 3).
- Graph-structure agnostic algorithms: Random Forest (RF) [18] trains a random forest on the attribute matrix and does not incorporate adjacency information.
- Node-attribute agnostic algorithms: Label Propagation (LP) [8] chooses labels for nodes based on the community label of its r-hop neighbors. DeepWalk (DW) [12] encodes neighbourhood information via truncated random walks and uses a Random Forest Classifier for label prediction. These do not incorporate node attributes.
- Graph-convolution based algorithms: GCN [31] and GraphSAGE (mean aggregator) [3] convolve over node attributes using the adjacency matrix. We acknowledge that this is extremely active area of research today and there exist several advancements that demonstrate improved performance in terms of training efficiency [32,33] and low homophily datasets [34,35]. However, GCN and GraphSAGE continue to prove to be strong benchmarks, and so we empirically compare with them to demonstrate our central point: JANE is a simple algorithm that efficiently scales and is competitive with the state-of-the-art on a variety of datasets.
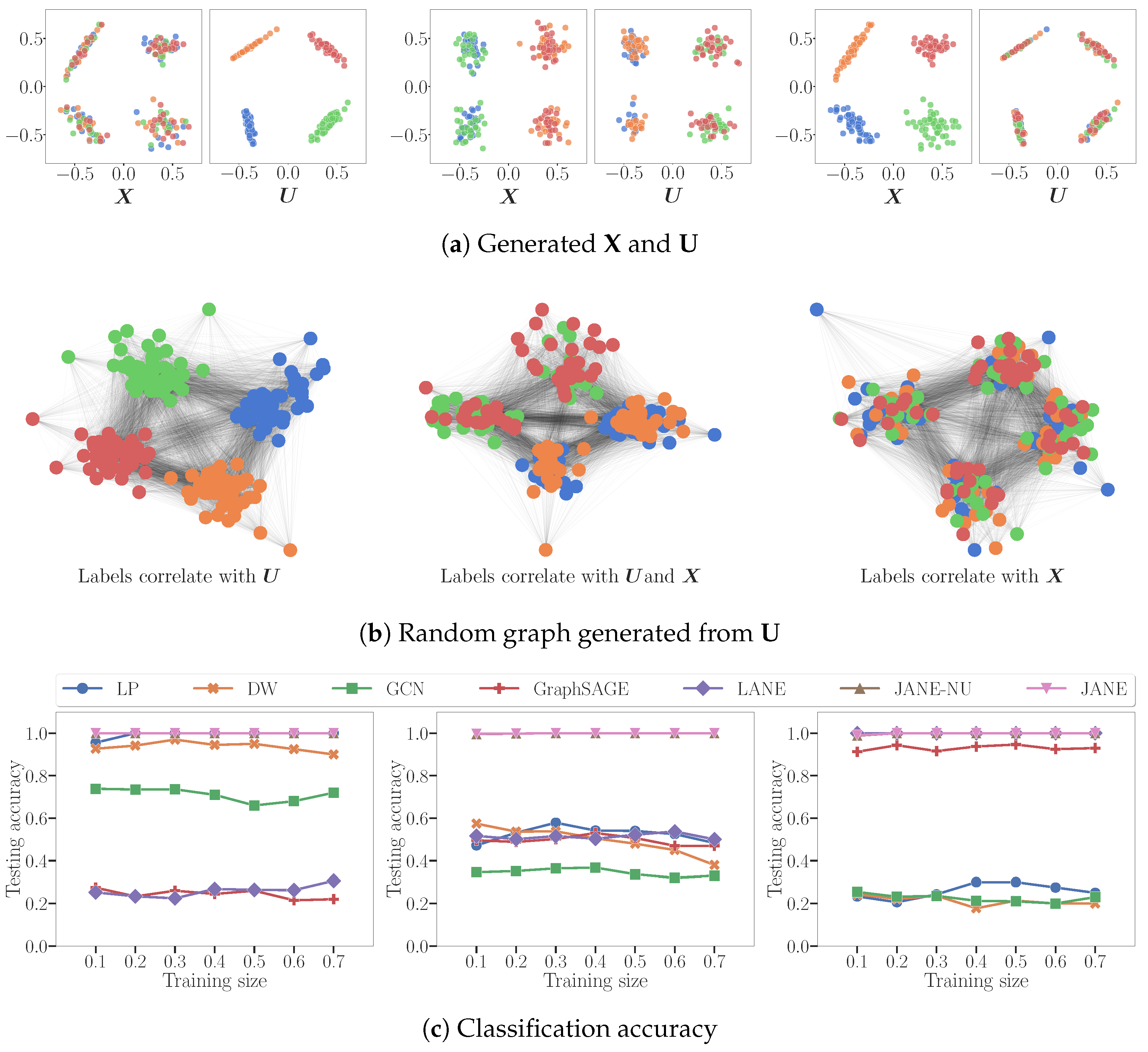
4.2. Node Classification on Synthetic Data
- : LP and DW infer that labels derive from (indirectly). GCN converges attribute values of nodes in the same cluster but is not perfectly accurate because does not correlate with . LANE forces the proximity representation to be similar to the attribute representation, and then smoothens it using the labels. It does not perform well, since there is no correlation between them.
- : LP, DW are able to correctly classify nodes belonging to 2 out of 4 classes, i.e. precisely those nodes whose labels are influenced by . Conversely, LANE is able to classify those nodes belonging to two classes of nodes that correlate with . GCN smoothens the attribute values of adjacent nodes, and thus can correctly infer labels correlated with .
- LP and DW reduce to random classifiers since adjacent nodes do not have similar labels. GCN reduces to a nearly random classifier because, by forcing adjacent nodes with different attribute values to become similar, it destroys the correlation between and the labels.
4.3. Node Classification on Real-World Data
4.3.1. Datasets
- Citation Networks: Cora, Citeseer, PubMed [1] represent academic papers as nodes, edges denote a citation between two nodes, node features are 0/1-valued sparse bag-of-words vectors and class labels denote the subfield of research to which the papers belong.
- Social Networks: Flickr denotes users of the social media site that post images as nodes, edges represent follower relationships, and features are specified by a list of tags reflecting the interests of the users [39]. The labels used to predict are pre-defined categories of images.
- Squirrel: This is a Wikipedia dataset [40] where nodes are web pages, edges are mutual links between pages, features correspond to informative nouns in the pages, and labels are categories based on the average number of monthly views of the page.
4.3.2. Experimental Setup
4.3.3. Performance Analysis
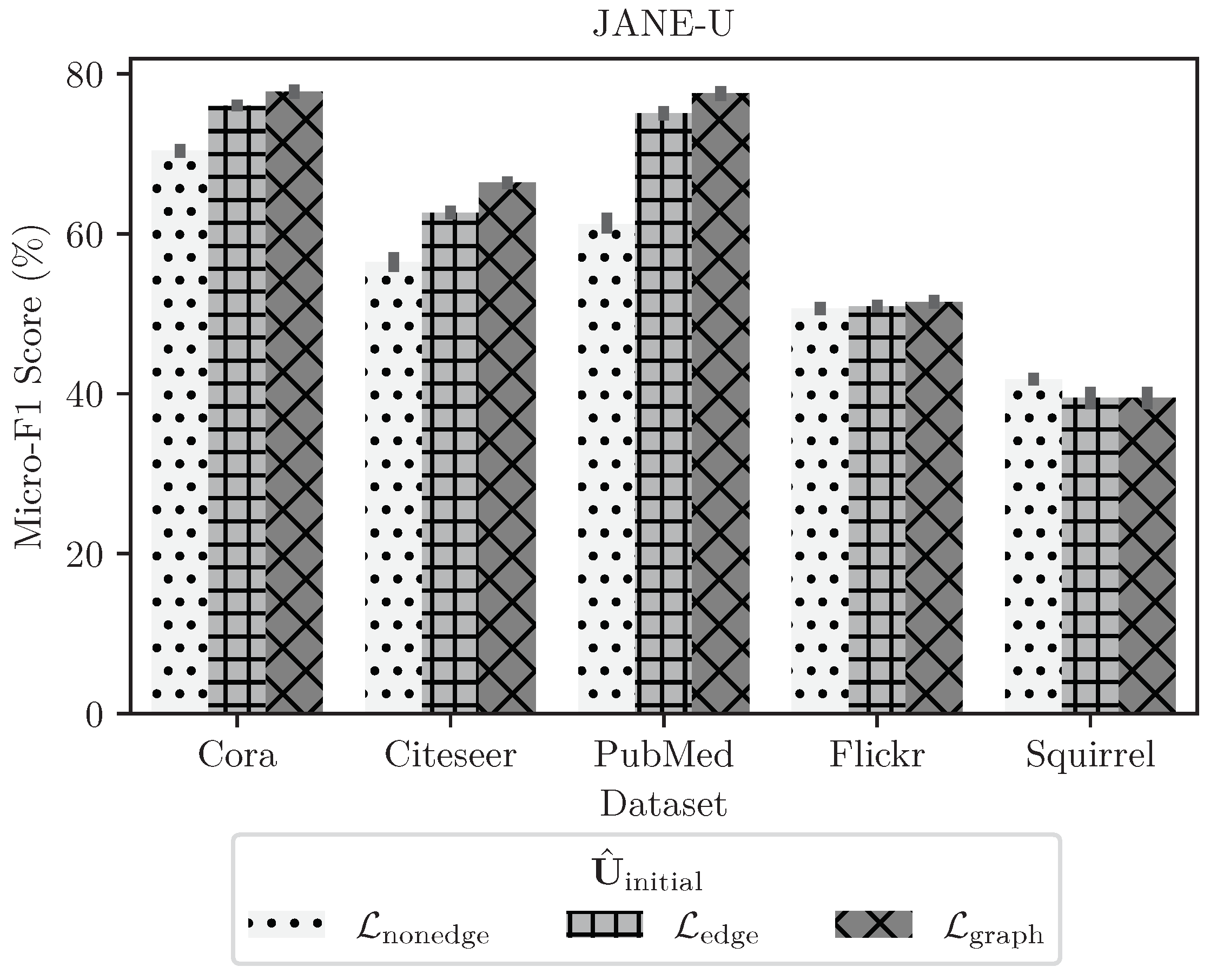
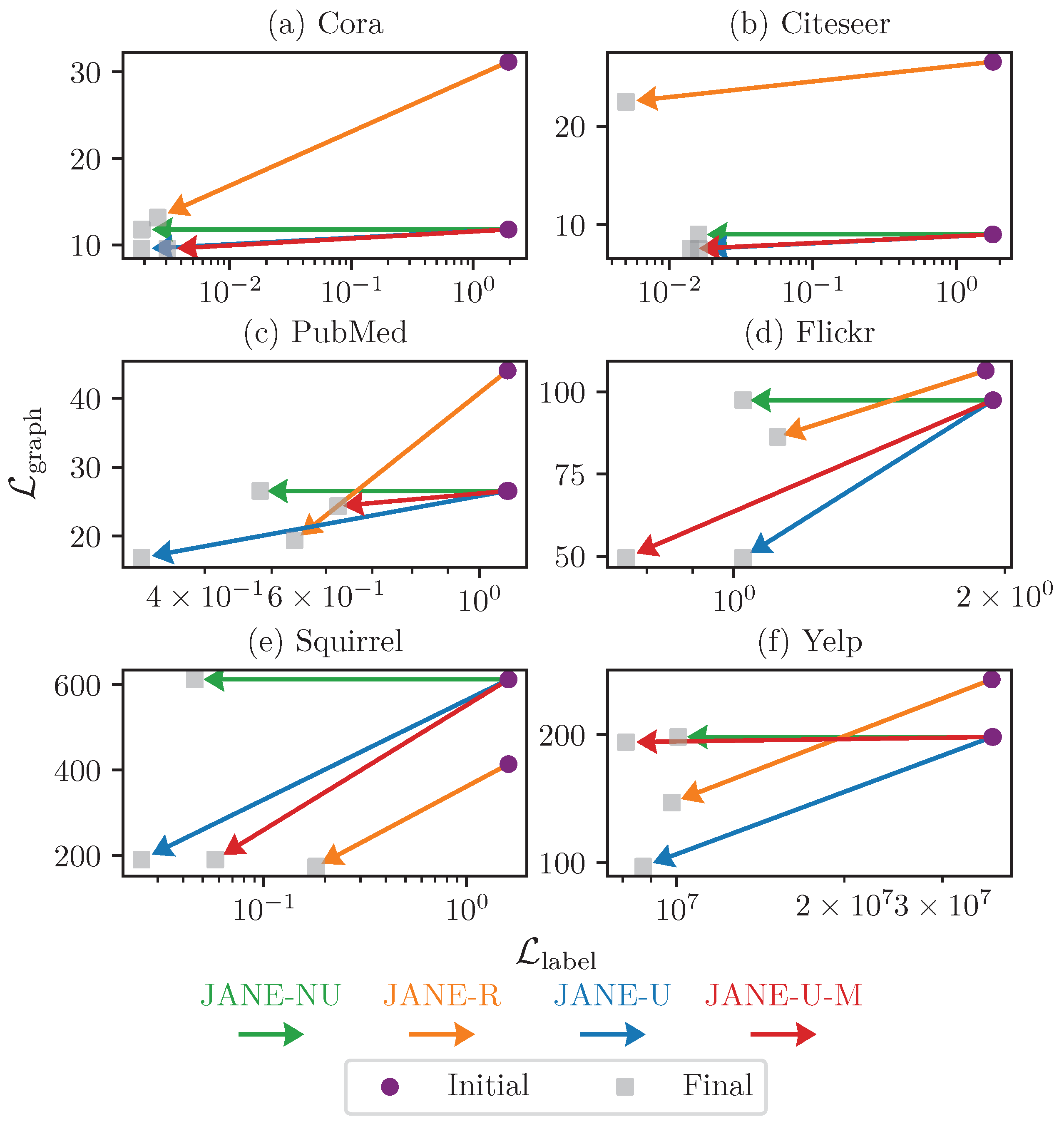
4.3.4. Ablation Study on Choosing
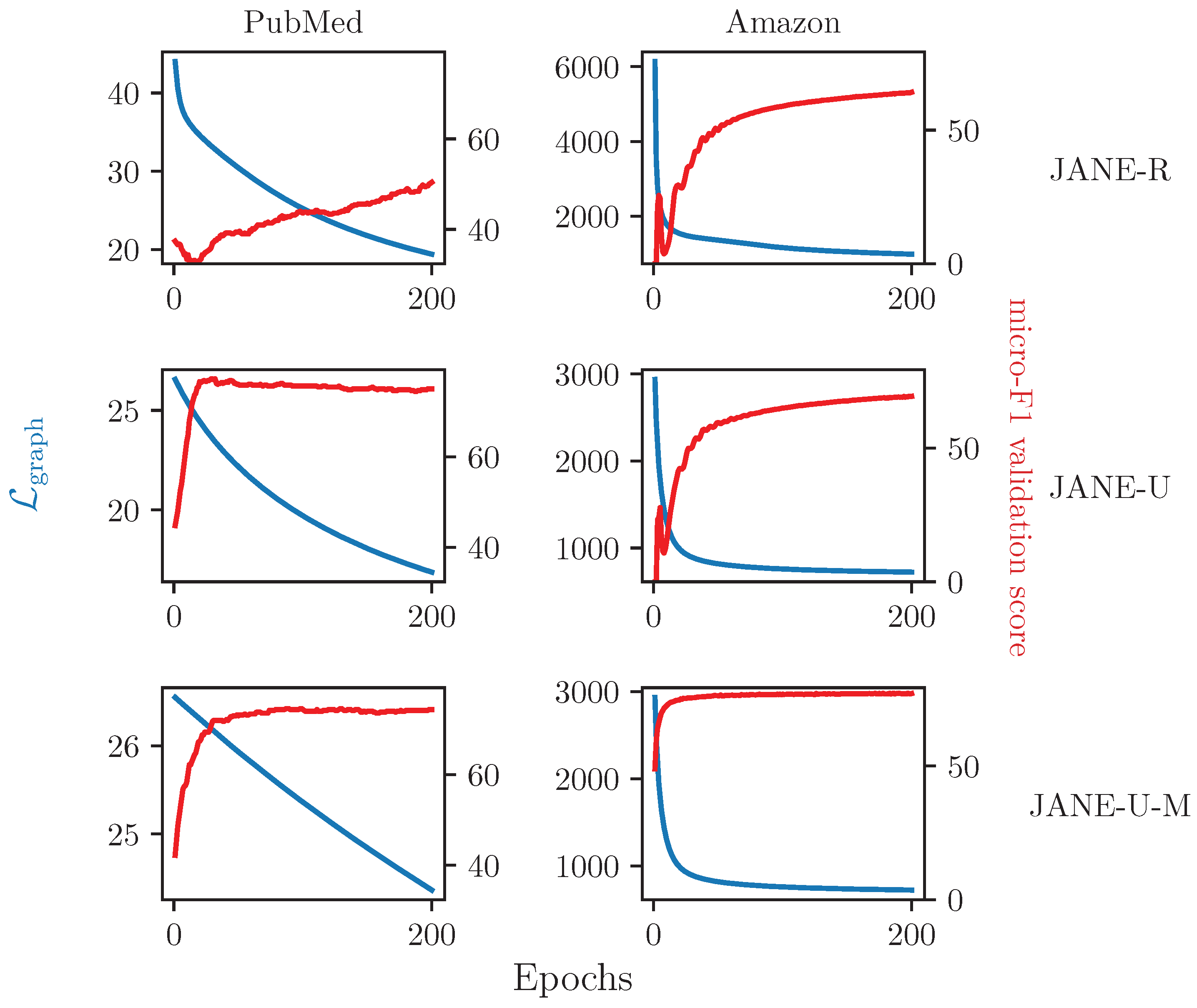
4.3.5. Ablation Study on Updating
4.3.6. Relationship between and Accuracy
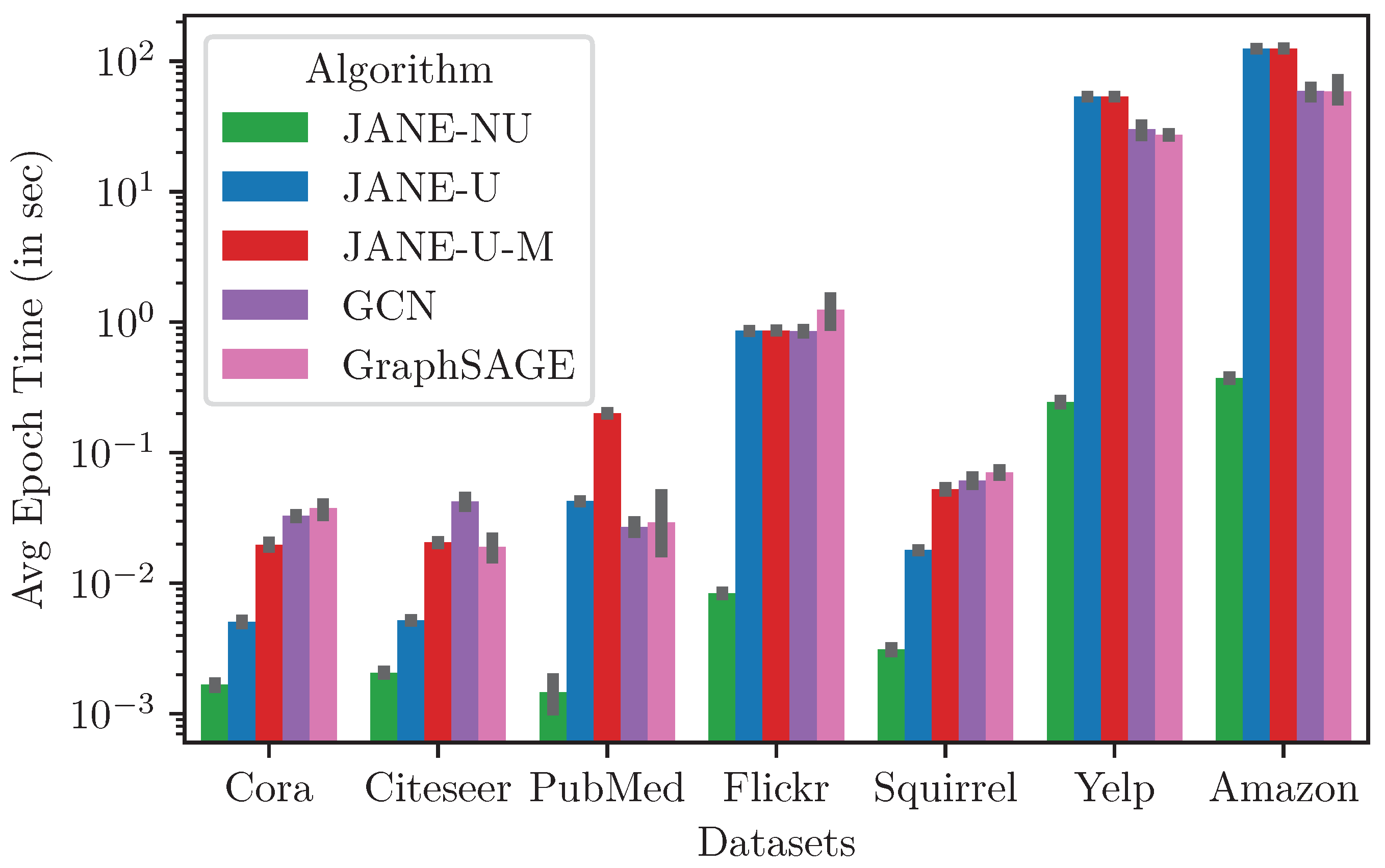
4.3.7. Runtime and Memory
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Goldberg, A.B. Introduction to semi-supervised learning. Synth. Lect. Artif. Intell. Mach. Learn. 2009, 3, 1–130. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Yue, X.; Wang, Z.; Huang, J.; Parthasarathy, S.; Moosavinasab, S.; Huang, Y.; Lin, S.M.; Zhang, W.; Zhang, P.; Sun, H. Graph embedding on biomedical networks: Methods, applications and evaluations. Bioinformatics 2019, 36, 1241–1251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parisot, S.; Ktena, S.I.; Ferrante, E.; Lee, M.; Guerrero, R.; Glocker, B.; Rueckert, D. Disease prediction using graph convolutional networks: Application to Autism Spectrum Disorder and Alzheimer’s disease. Med. Image Anal. 2018, 48, 117–130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McPherson, M.; Smith-Lovin, L.; Cook, J.M. Birds of a feather: Homophily in social networks. Annu. Rev. Sociol. 2001, 27, 415–444. [Google Scholar] [CrossRef] [Green Version]
- Marsden, P.V.; Friedkin, N.E. Network studies of social influence. Sociol. Methods Res. 1993, 22, 127–151. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, J.; Schölkopf, B. Learning from labeled and unlabeled data on a directed graph. In Proceedings of the 22nd International Conference on Machine Learning—ICML ’05, Bonn, Germany, 7–11 August 2005; ACM Press: New York, NY, USA, 2005; pp. 1036–1043. [Google Scholar] [CrossRef] [Green Version]
- Blum, A.; Lafferty, J.; Rwebangira, M.R.; Reddy, R. Semi-supervised learning using randomized mincuts. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; ACM: New York, NY, USA, 2004; p. 13. [Google Scholar]
- Joachims, T. Transductive learning via spectral graph partitioning. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 290–297. [Google Scholar]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Qiu, J.; Dong, Y.; Ma, H.; Li, J.; Wang, K.; Tang, J. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Los Angeles, CA, USA, 5–9 February 2018; pp. 459–467. [Google Scholar]
- Lorrain, F.; White, H.C. Structural equivalence of individuals in social networks. J. Math. Sociol. 1971, 1, 49–80. [Google Scholar] [CrossRef]
- Sailer, L.D. Structural equivalence: Meaning and definition, computation and application. Soc. Netw. 1978, 1, 73–90. [Google Scholar] [CrossRef]
- Huang, X.; Li, J.; Hu, X. Accelerated attributed network embedding. In Proceedings of the 2017 SIAM International Conference on data mining, Houston, TX, USA, 27–29 April 2017; pp. 633–641. [Google Scholar]
- Gao, H.; Huang, H. Deep Attributed Network Embedding. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Huang, X.; Li, J.; Hu, X. Label informed attributed network embedding. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; pp. 731–739. [Google Scholar]
- Wu, J.; He, J.; Xu, J. Net: Degree-specific graph neural networks for node and graph classification. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 406–415. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Li, Q.; Han, Z.; Wu, X.M. Deeper insights into graph convolutional networks for semi-supervised learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Ying, Z.; You, J.; Morris, C.; Ren, X.; Hamilton, W.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. In Proceedings of the 2018 Conference on Neural Information Processing Systems NeurIPS 2018, Montreal, QC, Canada, 3–8 December 2018; pp. 4800–4810. [Google Scholar]
- Wang, X.; Zhu, M.; Bo, D.; Cui, P.; Shi, C.; Pei, J. Am-gcn: Adaptive multi-channel graph convolutional networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1243–1253. [Google Scholar]
- Xiao, S.; Wang, S.; Dai, Y.; Guo, W. Graph neural networks in node classification: Survey and evaluation. Mach. Vis. Appl. 2022, 33, 1–19. [Google Scholar] [CrossRef]
- Merchant, A.; Mathioudakis, M. Joint Use of Node Attributes and Proximity for Node Classification. In Proceedings of the International Conference on Complex Networks and Their Applications; Springer: Cham, Switzerland, 2021; pp. 511–522. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1998; Number 92. [Google Scholar]
- Akyildiz, T.A.; Alabsi Aljundi, A.; Kaya, K. Gosh: Embedding big graphs on small hardware. In Proceedings of the 49th International Conference on Parallel Processing, Edmonton, AB, Canada, 17–20 August 2020; pp. 1–11. [Google Scholar]
- Tsitsulin, A.; Mottin, D.; Karras, P.; Müller, E. Verse: Versatile graph embeddings from similarity measures. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 539–548. [Google Scholar]
- Rahman, M.K.; Sujon, M.H.; Azad, A. Force2Vec: Parallel force-directed graph embedding. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 442–451. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Cong, W.; Forsati, R.; Kandemir, M.; Mahdavi, M. Minimal Variance Sampling with Provable Guarantees for Fast Training of Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1393–1403. [Google Scholar]
- Hu, W.; Fey, M.; Zitnik, M.; Dong, Y.; Ren, H.; Liu, B.; Catasta, M.; Leskovec, J. Open graph benchmark: Datasets for machine learning on graphs. arXiv 2020, arXiv:2005.00687. [Google Scholar]
- Pei, H.; Wei, B.; Chang, K.C.C.; Lei, Y.; Yang, B. Geom-gcn: Geometric graph convolutional networks. arXiv 2020, arXiv:2002.05287. [Google Scholar]
- Zhu, J.; Yan, Y.; Zhao, L.; Heimann, M.; Akoglu, L.; Koutra, D. Generalizing graph neural networks beyond homophily. arXiv 2020, arXiv:2006.11468. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast graph representation learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Zeng, H.; Zhou, H.; Srivastava, A.; Kannan, R.; Prasanna, V. GraphSAINT: Graph Sampling Based Inductive Learning Method. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 26–30 April 2020. [Google Scholar]
- Li, J.; Hu, X.; Tang, J.; Liu, H. Unsupervised streaming feature selection in social media. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015. [Google Scholar]
- Rozemberczki, B.; Allen, C.; Sarkar, R. Multi-scale attributed node embedding. J. Complex Netw. 2021, 9, cnab014. [Google Scholar] [CrossRef]
- Shchur, O.; Mumme, M.; Bojchevski, A.; Günnemann, S. Pitfalls of graph neural network evaluation. arXiv 2018, arXiv:1811.05868. [Google Scholar]
- Yang, Z.; Cohen, W.; Salakhudinov, R. Revisiting semi-supervised learning with graph embeddings. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 40–48. [Google Scholar]
- Zeng, H.; Zhang, M.; Xia, Y.; Srivastava, A.; Malevich, A.; Kannan, R.; Prasanna, V.; Jin, L.; Chen, R. Decoupling the Depth and Scope of Graph Neural Networks. Adv. Neural Inf. Process. Syst. 2021, 34, 19665–19679. [Google Scholar]
| Graph | Size | Properties | |||
|---|---|---|---|---|---|
| Number of Classes | Number of Features | Edge Homophily | |||
| Cora | 2485 | 5069 | 7 | 1428 | 0.86 |
| Citeseer | 2110 | 3668 | 6 | 3669 | 0.80 |
| PubMed | 19,717 | 44324 | 3 | 500 | 0.86 |
| Squirrel | 5201 | 401,907 | 5 | 2089 | 0.29 |
| Flickr | 89,250 | 989,006 | 7 | 500 | 0.41 |
| Yelp | 703,655 | 13,927,667 | 100 | 300 | NA |
| Amazon | 1,066,627 | 263,793,649 | 107 | 200 | NA |
| Algorithm | Cora | Citeseer | Squirrel | PubMed | Flickr | Yelp | Amazon |
|---|---|---|---|---|---|---|---|
| RandomForest | |||||||
| LabelPropagation | |||||||
| DeepWalk | NA | NA | |||||
| GCN | |||||||
| GraphSAGE | |||||||
| JANE-R | |||||||
| JANE-NU | |||||||
| JANE-U | |||||||
| JANE-U-M |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merchant, A.; Mahadevan, A.; Mathioudakis, M. Scalably Using Node Attributes and Graph Structure for Node Classification. Entropy 2022, 24, 906. https://doi.org/10.3390/e24070906
Merchant A, Mahadevan A, Mathioudakis M. Scalably Using Node Attributes and Graph Structure for Node Classification. Entropy. 2022; 24(7):906. https://doi.org/10.3390/e24070906
Chicago/Turabian StyleMerchant, Arpit, Ananth Mahadevan, and Michael Mathioudakis. 2022. "Scalably Using Node Attributes and Graph Structure for Node Classification" Entropy 24, no. 7: 906. https://doi.org/10.3390/e24070906
APA StyleMerchant, A., Mahadevan, A., & Mathioudakis, M. (2022). Scalably Using Node Attributes and Graph Structure for Node Classification. Entropy, 24(7), 906. https://doi.org/10.3390/e24070906






