Modelling Foreign Exchange Interventions under Rayleigh Process: Applications to Swiss Franc Exchange Rate Dynamics
Abstract
1. Introduction
2. Methods
2.1. Basic Exchange Rate Model and Boundary Conditions
2.2. Fundamental Dynamics Incorporated with Intervention Policy
3. Results
3.1. Exchange Rate Solution
3.2. Interest Rate Differential at ZLB
3.3. Exchange Rate Distribution
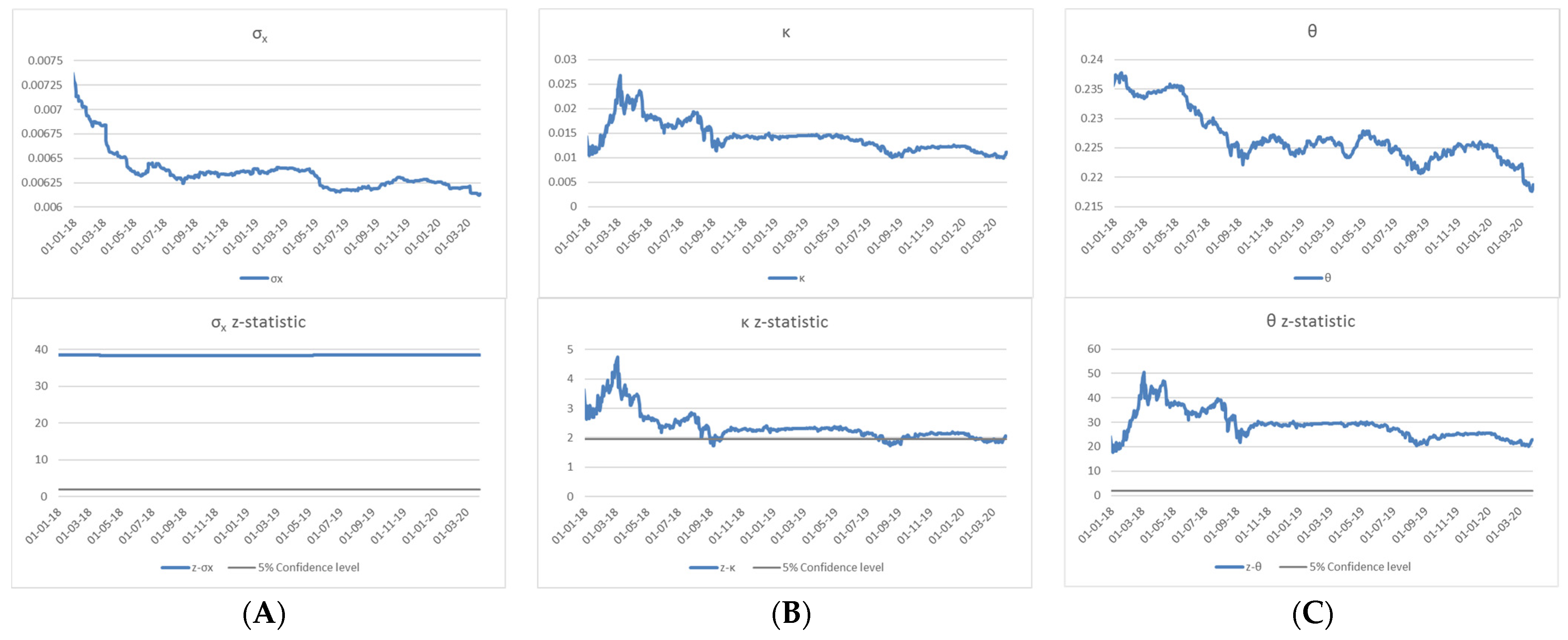
3.4. Model Calibrations for Swiss Franc
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blanchard, O.; Adler, G.; Filho, I.C. Can foreign exchange intervention stem exchange rate pressures from global capital flow shocks? In IMF Working Paper 15/159; International Monetary Fund: Washington, DC, USA, 2015. [Google Scholar]
- Amador, M.; Bianchi, J.; Bocola, L.; Perri, F. Exchange rate policies at the zero lower bound. In NBER Working Paper 23266; National Bureau of Economic Research: Cambridge, MA, USA, 2018. [Google Scholar]
- Dominguez, K.; Frankel, J. Does foreign exchange intervention matter? The portfolio effect. Am. Econ. Rev. 1993, 83, 1356–1369. [Google Scholar]
- Sarno, L.; Taylor, M.P. Official Intervention in the Foreign Exchange Market: Is It Effective and, If So, How Does It Work? J. Econ. Lit. 2001, 39, 839–868. [Google Scholar] [CrossRef]
- Dominguez, K. The market microstructure of central bank intervention. J. Int. Econ. 2003, 59, 25–45. [Google Scholar] [CrossRef]
- Dominguez, K. When do central bank interventions influence intra-daily and longer-term exchange rate movements? J. Int. Money Financ. 2006, 25, 1051–1071. [Google Scholar] [CrossRef][Green Version]
- Hoshikawa, T. The effect of intervention frequency on the foreign exchange market: The Japanese experience. J. Int. Money Financ. 2008, 27, 547–559. [Google Scholar] [CrossRef]
- Menkhoff, L. High-frequency analysis of foreign exchange interventions: What do we learn? J. Econ. Surv. 2010, 24, 85–112. [Google Scholar] [CrossRef]
- Adler, G.; Tovar Mora, C.E. Foreign exchange intervention: A shield against appreciation winds? In IMF Working Paper 11/165; International Monetary Fund: Washington, DC, USA, 2011. [Google Scholar]
- Engel, C. Exchange rates and interest parity. In Handbook of International Economics; Gopinath, G., Helpman, E., Rogoff, K., Eds.; Elsevier: Amsterdam, The Netherland, 2014; Volume 4. [Google Scholar]
- Pasquariello, P. Government intervention and arbitrage. Rev. Financ. Stud. 2018, 31, 3344–3408. [Google Scholar] [CrossRef]
- Hertrich, M. Foreign exchange interventions under a minimum exchange rate regime and the Swiss franc. Rev. Int. Econ. 2022, 30, 450–489. [Google Scholar] [CrossRef]
- Ranaldo, A.; Söderlind, P. Safe haven currencies. Rev. Financ. 2010, 14, 385–407. [Google Scholar] [CrossRef]
- Auer, R.A. A Safe Haven: International Demand for Swiss Francs during the Euro Area Debt Crisis, Quarterly Bulletin 2015/Q2; Swiss National Bank: Berne, Switzerland, 2015. [Google Scholar]
- Gourinchas, P.-O.; Rey, H. Real Interest rates, imbalances and the curse of regional safe asset providers at the zero lower bound. In NBER Working Paper 22618; National Bureau of Economic Research: Cambridge, MA, USA, 2016. [Google Scholar]
- Baltensperger, E.; Kugler, P. The historical origins of the safe haven status of the Swiss franc. Aussenwirtschaft 2016, 67, 1–30. [Google Scholar]
- Lo, C.F.; Hui, C.H.; Fong, T.; Chu, S.W. A quasi-bounded target zone model—Theory and application to Hong Kong dollar. Int. Rev. Econ. Financ. 2015, 37, 1–17. [Google Scholar] [CrossRef]
- Hui, C.H.; Lo, C.F.; Fong, T. Swiss franc’s one-sided target zone during 2011–2015. Int. Rev. Econ. Financ. 2016, 44, 54–67. [Google Scholar] [CrossRef]
- Hui, C.H.; Lo, C.F.; Ip, H.Y. Modelling asymmetric unemployment dynamics: The logarithmic-harmonic potential approach. Entropy 2022, 24, 400. [Google Scholar] [CrossRef] [PubMed]
- Giorno, V.; Nobile, A.G.; Ricciardi, L.M.; Sacerdote, L. Some remarks on the Rayleigh process. J. Appl. Probab. 1986, 23, 398–408. [Google Scholar] [CrossRef]
- Guarnieri, F.; Moon, W.; Wettlaufer, J.S. Solution of the Fokker-Planck equation with a logarithmic potential and mixed eigenvalue spectrum. J. Math. Phys. 2017, 58, 093301. [Google Scholar] [CrossRef]
- Schädler, T.; Grabinski, M. Income from speculative financial transactions will always lead to macro-economic instability. Int. J. Financ. Insur. Risk Manag. 2015, 5, 922. Available online: https://www.journalfirm.com/journal/128# (accessed on 20 May 2022).
- Klinkova, G.; Grabinski, M. Due to instability gambling is the best model for most financial products. Arch. Bus. Res. 2017, 5, 255–261. [Google Scholar] [CrossRef]
- Gutiérrez-Jáimez, R.; Gutierrez-Sanchez, R.; Nafidi, A. The Stochastic Rayleigh diffusion model: Statistical inference and computational aspects. Applications to modelling of real cases. Appl. Math. Comput. 2006, 175, 628–644. [Google Scholar]
- Ferrante, L.; Bompadre, S.; Possati, L.; Leone, L. Parameter estimation in a Gompertzian stochastic model for tumor growth. Biometrics 2000, 56, 1076–1081. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Nafidi, A.; Gutiérrez-Sánchez, R. Forecasting total natural-gas consumption in Spain by using the stochastic Gompertz innovation diffusion model. Appl. Energy 2005, 80, 115–124. [Google Scholar] [CrossRef]
- Davidov, D.; Linetsky, V. Pricing and hedging path-dependent options under CEV processes. Manag. Sci. 2001, 47, 949–965. [Google Scholar] [CrossRef]
- Appel, D.; Grabinski, M. The origin of financial crisis: A wrong definition of value. PJQM 2011, 3, 33. [Google Scholar]
- Dyer, D.D.; Whisenand, C.W. Best Linear Unbiased estimator of the parameter of the Rayleigh distribution: Part-II optimum theory for selected order statistics. IEEE Trans. Reliab. 1973, R-22, 229–231. [Google Scholar] [CrossRef]
- Wu, S.J.; Huang, S.R. Optimal warranty length for a Rayleigh distributed product with progressive censoring. IEEE Trans. 2010, 59, 661–666. [Google Scholar] [CrossRef]
- Kotb, M.S.; Mohie El-Din, M.M. Parametric inference for step-stress accelerated life testing from Rayleigh distribution under ordered ranked set sampling. IEEE Trans. Reliab. 2022, 71, 16–27. [Google Scholar] [CrossRef]
- Kundu, D.; Raqab, M.Z. Generalized Rayleigh distribution: Different methods of estimations. Comput. Stat. Data Anal. 2005, 49, 187–200. [Google Scholar] [CrossRef]
- Voda, V.G. A new generalization of Rayleigh distribution. Reliab. Theory Appl. 2007, 2, 47–56. [Google Scholar]
- Merovci, F. Transmuted generalized Rayleigh distribution. J. Stat. Appl. Probab. 2014, 3, 9–20. [Google Scholar] [CrossRef]
- Sebastian, N.; Mathai, A.; Haubold, H. Entropy Optimization, Maxwell–Boltzmann, and Rayleigh Distributions. Entropy 2021, 23, 754. [Google Scholar] [CrossRef]
- Krugman, P. It’s Baaack: Japan’s slump and the return of the liquidity trap. Brook. Pap. Econ. Act. 1998, 1998, 137–205. [Google Scholar] [CrossRef]
- Cook, D.; Devereux, M.B. Sharing the burden: Monetary and fiscal responses to a world liquidity trap. Am. Econ. J. Macroecon. 2013, 5, 190–228. [Google Scholar] [CrossRef][Green Version]
- Svensson, L.E.O. Escaping from a liquidity trap and deflation: The Foolproof Way and others. J. Econ. Perspect. 2003, 17, 145–166. [Google Scholar] [CrossRef]
- Benigno, P.; Romei, F. Debt deleveraging and the exchange rate. J. Int. Econ. 2014, 93, 1–16. [Google Scholar] [CrossRef]
- Acharya, S.; Bengui, J. Liquidity traps, capital flows. In CIREQ Working Paper 14-2015; Journal of International Economics: The Netherland, 2015. [Google Scholar]
- Caballero, R.J.; Farhi, E.; Gourinchas, P.-O. Global imbalances and currency wars at the ZLB. In NBER Working Paper 21670; National Bureau of Economic Research: Cambridge, MA, USA, 2015. [Google Scholar]
- Corsetti, G.; Kuester, K.; Müller, G. The Case for Flexible Exchange Rates in a Great Recession; Mimeo: Cambridge, UK, 2016. [Google Scholar]
- Eggertsson, G.B.; Mehrotra, N.R.; Singh, S.R.; Summers, L.H. A Contagious Malady? Open Economy Dimensions of Secular Stagnation. IMF Econ. Rev. 2016, 64, 581–634. [Google Scholar] [CrossRef]
- Fornaro, L. International debt deleveraging. J. Eur. Econ. Assoc. 2018, 16, 1394–1432. [Google Scholar] [CrossRef]
- Krugman, P. Target zones and exchange rate dynamics. Q. J. Econ. 1991, 106, 669–682. [Google Scholar] [CrossRef]
- Krugman, P.; Rotemberg, J. Target zones with limited reserves. In NBER Working Paper 3418; National Bureau of Economic Research: Cambridge, MA, USA, 1990. [Google Scholar]
- Hui, C.H.; Lo, C.F.; Liu, C.H. Exchange rate dynamics with crash risk and interventions. Int. Rev. Econ. Financ. 2022, 79, 18–37. [Google Scholar] [CrossRef]
- Ritschel, S.; Cherstvy, A.G.; Metzler, R. Universality of delay-time averages for financial time series: Analytical results, computer simulations, and analysis of historical stock-market prices. J. Phys. Complex. 2021, 4, 045003. [Google Scholar] [CrossRef]
- Backus, D.K.; Foresi, S.; Telmer, C.I. Affine Term Structure Models and the Forward Premium Anomaly. J. Financ. 2001, 56, 279–304. [Google Scholar] [CrossRef]
- Bakshi, G.; Carr, P.; Wu, L. Stochastic risk premiums, stochastic skewness in currency options, and stochastic discount factors in international economies. J. Financ. Econ. 2007, 87, 132–156. [Google Scholar] [CrossRef]
- Jurek, J.W.; Xu, Z. Option-Implied Currency Risk Premia; Working Paper; University of Pennsylvania: Philadelphia, PA, USA, 2014. [Google Scholar]
- Hoffmann, M.; Suter, R. The Swiss Franc exchange rate and deviations from uncovered interest parity: Global vs domestic factors. Swiss J. Econ. Stat. 2010, 146, 349–371. [Google Scholar] [CrossRef][Green Version]
- Grisse, C.; Nitschka, T. On financial risk and the safe haven characteristics of Swiss franc exchange rates. J. Empir. Financ. 2015, 32, 153–164. [Google Scholar] [CrossRef]
- Froot, K.; Obstfeld, M. Exchange rate dynamics under stochastic regime shifts: A unified approach. J. Int. Econ. 1991, 31, 203–229. [Google Scholar] [CrossRef]
- Delgado, F.; Dumas, B. Target zones, broad and narrow. In Exchange Rate Targets and Currency Bands; Krugman, P., Miller, M., Eds.; Cambridge University Press: Cambridge, UK, 1992; pp. 35–56. [Google Scholar]
- Karlin, S.; Taylor, H.M. A Second Course in Stochastic Processes; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Svensson, L.E.O. The term structure of interest rate differentials in a target zone: Theory and Swedish data. J. Monet. Econ. 1991, 28, 87–116. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t–distribution. J. Roy. Statist. Soc. Ser. B 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Cook, D.; Yetman, J. Currency boards when interest rates are zero. Pac. Econ. Rev. 2014, 19, 135–151. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Co-integration and error correction: Representation, estimation and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- MacKinnon, J.G. Numerical distribution functions for unit root and cointegration test. J. Appl. Econom. 1996, 11, 601–618. [Google Scholar] [CrossRef]
| ln(σx) | ln(ΔθS) | ln(Reserves) | ||||
|---|---|---|---|---|---|---|
| Monthly Last | Monthly Last | Monthly | ||||
| Level | Change | Level | Change | Level | Change | |
| Mean | −5.06 | 0.00 | −1.50 | 0.00 | 13.53 | 0.002 |
| Median | −5.06 | 0.00 | −1.50 | 0.00 | 13.53 | 0.003 |
| Maximum | −4.98 | 0.01 | −1.47 | 0.02 | 13.57 | 0.026 |
| Minimum | −5.09 | −0.05 | −1.54 | −0.01 | 13.50 | −0.027 |
| Std. Dev. | 0.03 | 0.01 | 0.02 | 0.01 | 0.02 | 0.015 |
| Skewness | 1.79 | −1.73 | −0.03 | 0.33 | 0.05 | −0.402 |
| Kurtosis | 6.19 | 6.37 | 2.61 | 2.27 | 1.82 | 2.349 |
| ADF test statistics | 1.67 | −3.394 *** | −0.28 | −4.550 *** | −3.21 | −6.017 *** |
| Phillips–Perron test statistics | 1.67 | −3.216 *** | −0.27 | −4.551 *** | −3.19 | −6.570 *** |
| Correlation (between ln(Reserves) and y) | −0.652 | - | 0.605 | - | - | - |
| Observations | 26 | 25 | 26 | 25 | 26 | 25 |
| Dependent Variable | ln(σx) | ln(ΔθS) |
|---|---|---|
| Monthly | Monthly | |
| ADF test statistic | −3.64 *** | −2.09 ** |
| Phillips–Perron test statistic | −3.66 *** | −2.26 ** |
| Dependent Variable | ln(σx) | ln(ΔθS) |
|---|---|---|
| Monthly | Monthly | |
| ln(Reserves) | −0.83 *** | 0.49 *** |
| Constant | 6.17 * | −8.11 *** |
| Dependent Variable | ln(σx) | ln(ΔθS) |
|---|---|---|
| Monthly | Monthly | |
| ln(Reserves) | ||
| Speed of adjustment | −0.34 * | −0.55 ** |
| Lag length | 4 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, C.-H.; Lo, C.-F.; Liu, C.-H. Modelling Foreign Exchange Interventions under Rayleigh Process: Applications to Swiss Franc Exchange Rate Dynamics. Entropy 2022, 24, 888. https://doi.org/10.3390/e24070888
Hui C-H, Lo C-F, Liu C-H. Modelling Foreign Exchange Interventions under Rayleigh Process: Applications to Swiss Franc Exchange Rate Dynamics. Entropy. 2022; 24(7):888. https://doi.org/10.3390/e24070888
Chicago/Turabian StyleHui, Cho-Hoi, Chi-Fai Lo, and Chi-Hei Liu. 2022. "Modelling Foreign Exchange Interventions under Rayleigh Process: Applications to Swiss Franc Exchange Rate Dynamics" Entropy 24, no. 7: 888. https://doi.org/10.3390/e24070888
APA StyleHui, C.-H., Lo, C.-F., & Liu, C.-H. (2022). Modelling Foreign Exchange Interventions under Rayleigh Process: Applications to Swiss Franc Exchange Rate Dynamics. Entropy, 24(7), 888. https://doi.org/10.3390/e24070888






