Effective Field Theory of Random Quantum Circuits
Abstract
1. Introduction
2. Diagnostic of Spectral Statistics of Time-Periodic Systems
3. Replica Sigma Model for Generic Floquet Systems
3.1. Generating Function for Level Correlation Function
3.2. Replica Sigma Model for Level Correlation Function
3.3. Ensemble-Averaged Effective Theory
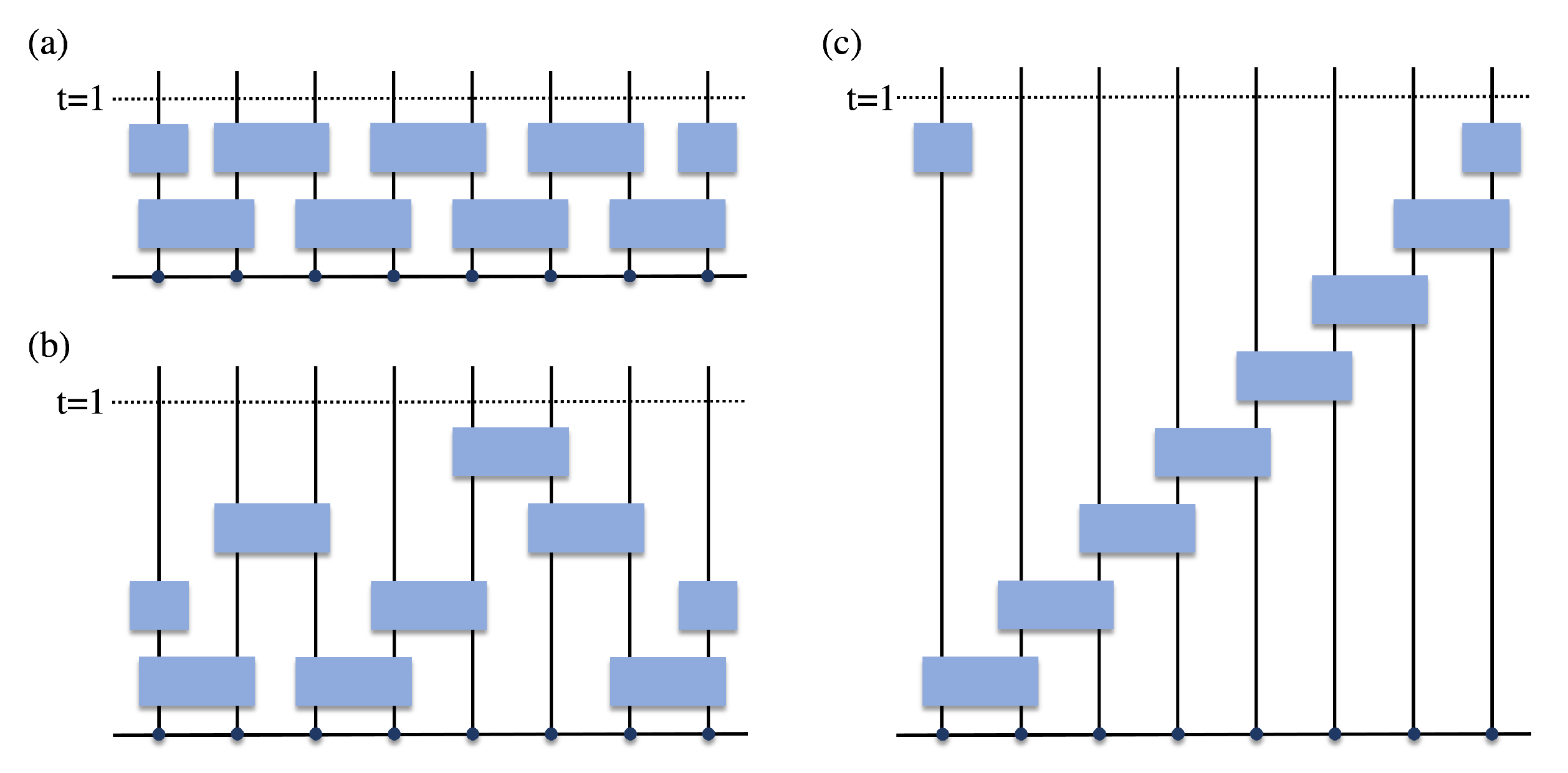
4. Application to Floquet Random Quantum Circuits
4.1. Floquet Random Quantum Circuits
4.2. Quadratic Fluctuations
4.3. Quartic Fluctuations
4.4. Two-Level Correlation Function
5. Weingarten Calculus
5.1. Sigma Model Derivation for the Weingarten Calculus
5.2. General Properties of the Weingarten Function
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of the Moments of Floquet Operator
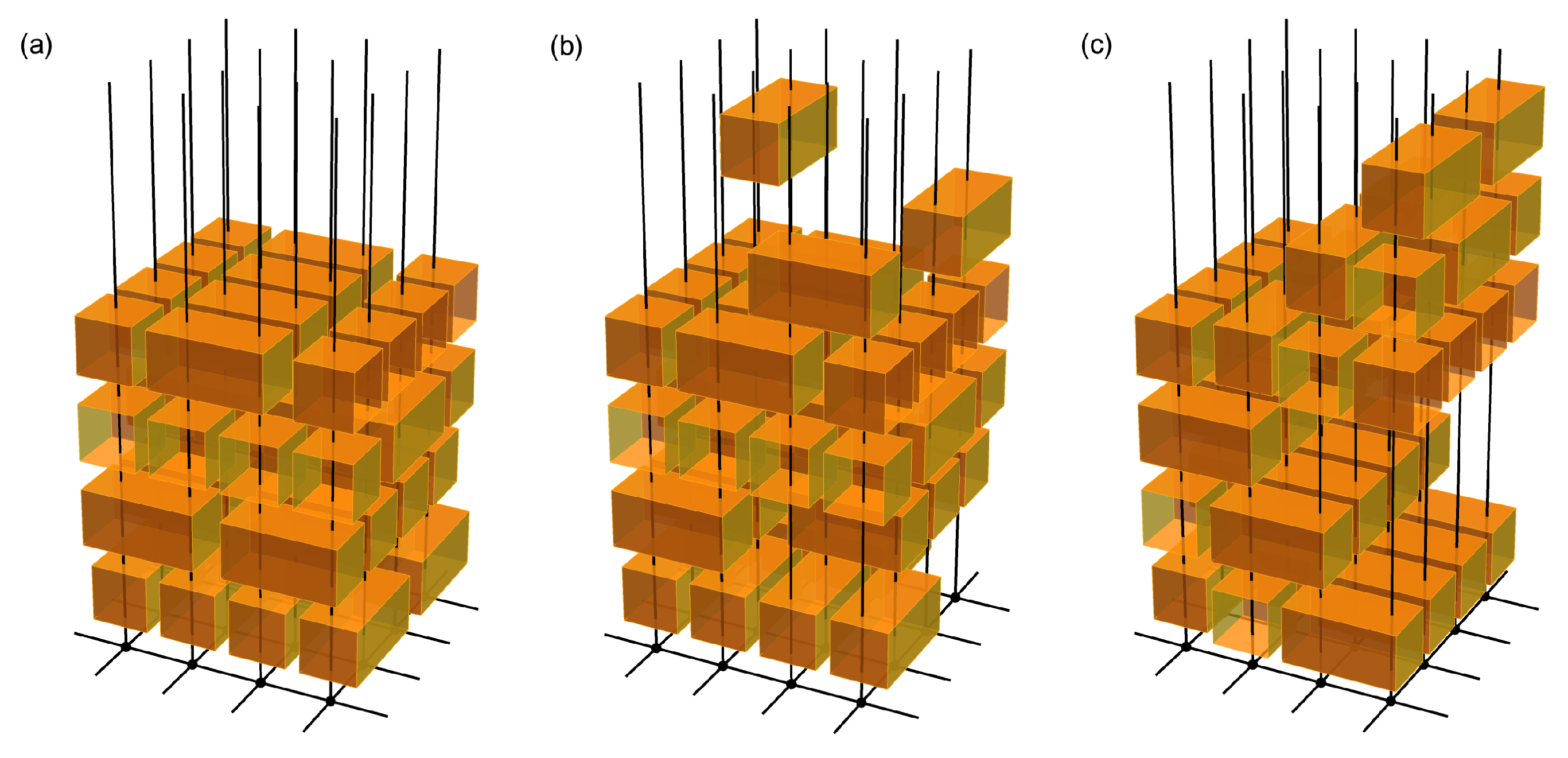
Appendix B. Generalization to Higher-Dimensional Floquet Quantum Circuits
Appendix C. Effective Field Theory of a Non-interacting Floquet Model
Appendix D. Large q Expansion of the Weingarten Function
Appendix E. Recursion Relation for the Weingarten Function
References
- Emerson, J.; Weinstein, Y.S.; Saraceno, M.; Lloyd, S.; Cory, D.G. Pseudo-random unitary operators for quantum information processing. Science 2003, 302, 2098–2100. [Google Scholar] [CrossRef] [PubMed]
- Emerson, J.; Livine, E.; Lloyd, S. Convergence conditions for random quantum circuits. Phys. Rev. A 2005, 72, 060302. [Google Scholar] [CrossRef]
- Oliveira, R.; Dahlsten, O.C.O.; Plenio, M.B. Generic Entanglement Can Be Generated Efficiently. Phys. Rev. Lett. 2007, 98, 130502. [Google Scholar] [CrossRef] [PubMed]
- Harrow, A.W.; Low, R.A. Random Quantum Circuits are Approximate 2-designs. Commun. Math. Phys. 2009, 291, 257–302. [Google Scholar] [CrossRef]
- Brandao, F.G.; Harrow, A.W.; Horodecki, M. Local Random Quantum Circuits are Approximate Polynomial-Designs. Commun. Math. Phys. 2016, 346, 397–434. [Google Scholar] [CrossRef]
- Žnidarič, M. Optimal two-qubit gate for generation of random bipartite entanglement. Phys. Rev. A 2007, 76, 012318. [Google Scholar] [CrossRef]
- Žnidarič, M. Exact convergence times for generation of random bipartite entanglement. Phys. Rev. A 2008, 78, 032324. [Google Scholar] [CrossRef]
- Arnaud, L.; Braun, D. Efficiency of producing random unitary matrices with quantum circuits. Phys. Rev. A 2008, 78, 062329. [Google Scholar] [CrossRef]
- Brown, W.G.; Viola, L. Convergence Rates for Arbitrary Statistical Moments of Random Quantum Circuits. Phys. Rev. Lett. 2010, 104, 250501. [Google Scholar] [CrossRef]
- Nakata, Y.; Hirche, C.; Koashi, M.; Winter, A. Efficient Quantum Pseudorandomness with Nearly Time-Independent Hamiltonian Dynamics. Phys. Rev. X 2017, 7, 021006. [Google Scholar] [CrossRef]
- Diniz, I.T.; Jonathan, D. Comment on “Random Quantum Circuits are Approximate 2-designs” by A.W. Harrow and R.A. Low (Commun. Math. Phys. 291, 257–302 (2009)). Commun. Math. Phys. 2011, 304, 281–293. [Google Scholar] [CrossRef]
- Gross, D.; Audenaert, K.; Eisert, J. Evenly distributed unitaries: On the structure of unitary designs. J. Math. Phys. 2007, 48, 052104. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Solution of a Minimal Model for Many-Body Quantum Chaos. Phys. Rev. X 2018, 8, 041019. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Spectral Statistics in Spatially Extended Chaotic Quantum Many-Body Systems. Phys. Rev. Lett. 2018, 121, 060601. [Google Scholar] [CrossRef]
- Friedman, A.J.; Chan, A.; De Luca, A.; Chalker, J.T. Spectral Statistics and Many-Body Quantum Chaos with Conserved Charge. Phys. Rev. Lett. 2019, 123, 210603. [Google Scholar] [CrossRef]
- Garratt, S.J.; Chalker, J.T. Local Pairing of Feynman Histories in Many-Body Floquet Models. Phys. Rev. X 2021, 11, 021051. [Google Scholar] [CrossRef]
- Garratt, S.J.; Chalker, J.T. Many-Body Delocalization as Symmetry Breaking. Phys. Rev. Lett. 2021, 127, 026802. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Spectral Lyapunov exponents in chaotic and localized many-body quantum systems. Phys. Rev. Res. 2021, 3, 023118. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Random Matrix Spectral Form Factor of Dual-Unitary Quantum Circuits. Commun. Math. Phys. 2021, 387, 597–620. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Exact Spectral Form Factor in a Minimal Model of Many-Body Quantum Chaos. Phys. Rev. Lett. 2018, 121, 264101. [Google Scholar] [CrossRef]
- Kos, P.; Bertini, B.; Prosen, T. Chaos and Ergodicity in Extended Quantum Systems with Noisy Driving. Phys. Rev. Lett. 2021, 126, 190601. [Google Scholar] [CrossRef] [PubMed]
- Moudgalya, S.; Prem, A.; Huse, D.A.; Chan, A. Spectral statistics in constrained many-body quantum chaotic systems. Phys. Rev. Res. 2021, 3, 023176. [Google Scholar] [CrossRef]
- Chan, A.; Shivam, S.; Huse, D.A.; De Luca, A. Many-Body Quantum Chaos and Space-time Translational Invariance. arXiv 2021, arXiv:2109.04475. [Google Scholar]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of chaotic quantum spectra and universality of level fluctuation laws. Phys. Rev. Lett. 1984, 52, 1. [Google Scholar] [CrossRef]
- Kos, P.; Ljubotina, M.; Prosen, T. Many-Body Quantum Chaos: Analytic Connection to Random Matrix Theory. Phys. Rev. X 2018, 8, 021062. [Google Scholar] [CrossRef]
- Roy, D.; Prosen, T. Random matrix spectral form factor in kicked interacting fermionic chains. Phys. Rev. E 2020, 102, 060202. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Mishra, D.; Prosen, T. Spectral form factor in a minimal bosonic model of many-body quantum chaos. arXiv 2022, arXiv:2203.05439. [Google Scholar]
- Flack, A.; Bertini, B.; Prosen, T. Statistics of the spectral form factor in the self-dual kicked Ising model. Phys. Rev. Res. 2020, 2, 043403. [Google Scholar] [CrossRef]
- Berry, M.V. Semiclassical theory of spectral rigidity. Proc. R. Soc. Lond. Ser. A 1985, 400, 229–251. [Google Scholar]
- Sieber, M.; Richter, K. Correlations between Periodic Orbits and their Role in Spectral Statistics. Phys. Scr. 2001, T90, 128. [Google Scholar] [CrossRef]
- Müller, S.; Heusler, S.; Braun, P.; Haake, F.; Altland, A. Periodic-orbit theory of universality in quantum chaos. Phys. Rev. E 2005, 72, 046207. [Google Scholar] [CrossRef]
- Altland, A.; Bagrets, D. Quantum ergodicity in the SYK model. Nucl. Phys. B 2018, 930, 45–68. [Google Scholar] [CrossRef]
- Saad, P.; Shenker, S.H.; Stanford, D. A semiclassical ramp in SYK and in gravity. arXiv 2018, arXiv:1806.06840. [Google Scholar]
- Liao, Y.; Galitski, V. Emergence of many-body quantum chaos via spontaneous breaking of unitarity. Phys. Rev. B 2022, 105, L140202. [Google Scholar] [CrossRef]
- Liao, Y.; Galitski, V. Universal dephasing mechanism of many-body quantum chaos. Phys. Rev. Res. 2022, 4, L012037. [Google Scholar] [CrossRef]
- Liao, Y.; Vikram, A.; Galitski, V. Many-Body Level Statistics of Single-Particle Quantum Chaos. Phys. Rev. Lett. 2020, 125, 250601. [Google Scholar] [CrossRef] [PubMed]
- Bertini, B.; Kos, P.; Prosen, T. Exact Correlation Functions for Dual-Unitary Lattice Models in 1+1 Dimensions. Phys. Rev. Lett. 2019, 123, 210601. [Google Scholar] [CrossRef] [PubMed]
- Piroli, L.; Bertini, B.; Cirac, J.I.; Prosen, T. Exact dynamics in dual-unitary quantum circuits. Phys. Rev. B 2020, 101, 094304. [Google Scholar] [CrossRef]
- Nahum, A.; Vijay, S.; Haah, J. Operator Spreading in Random Unitary Circuits. Phys. Rev. X 2018, 8, 021014. [Google Scholar] [CrossRef]
- Von Keyserlingk, C.W.; Rakovszky, T.; Pollmann, F.; Sondhi, S.L. Operator Hydrodynamics, OTOCs, and Entanglement Growth in Systems without Conservation Laws. Phys. Rev. X 2018, 8, 021013. [Google Scholar] [CrossRef]
- Rakovszky, T.; Pollmann, F.; von Keyserlingk, C.W. Diffusive Hydrodynamics of Out-of-Time-Ordered Correlators with Charge Conservation. Phys. Rev. X 2018, 8, 031058. [Google Scholar]
- Khemani, V.; Vishwanath, A.; Huse, D.A. Operator Spreading and the Emergence of Dissipative Hydrodynamics under Unitary Evolution with Conservation Laws. Phys. Rev. X 2018, 8, 031057. [Google Scholar]
- Hunter-Jones, N. Operator growth in random quantum circuits with symmetry. arXiv 2018, arXiv:1812.08219. [Google Scholar]
- Bertini, B.; Piroli, L. Scrambling in random unitary circuits: Exact results. Phys. Rev. B 2020, 102, 064305. [Google Scholar] [CrossRef]
- Nahum, A.; Ruhman, J.; Vijay, S.; Haah, J. Quantum Entanglement Growth under Random Unitary Dynamics. Phys. Rev. X 2017, 7, 031016. [Google Scholar] [CrossRef]
- Jonay, C.; Huse, D.A.; Nahum, A. Coarse-grained dynamics of operator and state entanglement. arXiv 2018, arXiv:1803.00089. [Google Scholar]
- Bertini, B.; Kos, P.; Prosen, T. Entanglement Spreading in a Minimal Model of Maximal Many-Body Quantum Chaos. Phys. Rev. X 2019, 9, 021033. [Google Scholar]
- Bertini, B.; Kos, P.; Prosen, T. Operator Entanglement in Local Quantum Circuits I: Chaotic Dual-Unitary Circuits. SciPost Phys. 2020, 8, 67. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Operator Entanglement in Local Quantum Circuits II: Solitons in Chains of Qubits. SciPost Phys. 2020, 8, 68. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Lamacraft, A. Unitary circuits of finite depth and infinite width from quantum channels. Phys. Rev. B 2019, 100, 064309. [Google Scholar] [CrossRef]
- Rakovszky, T.; Pollmann, F.; von Keyserlingk, C.W. Sub-ballistic Growth of Rényi Entropies due to Diffusion. Phys. Rev. Lett. 2019, 122, 250602. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. The approach to thermal equilibrium in quantized chaotic systems. J. Phys. A 1999, 32, 1163. [Google Scholar] [CrossRef]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Eigenstate Correlations, Thermalization, and the Butterfly Effect. Phys. Rev. Lett. 2019, 122, 220601. [Google Scholar] [CrossRef]
- Fritzsch, F.; Prosen, T. Eigenstate thermalization in dual-unitary quantum circuits: Asymptotics of spectral functions. Phys. Rev. E 2021, 103, 062133. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Kjaergaard, M.; Schwartz, M.E.; Braumüller, J.; Krantz, P.; Wang, J.I.J.; Gustavsson, S.; Oliver, W.D. Superconducting Qubits: Current State of Play. Annu. Rev. Condens. Matter Phys. 2020, 11, 369–395. [Google Scholar] [CrossRef]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef]
- Monroe, C.; Campbell, W.C.; Duan, L.M.; Gong, Z.X.; Gorshkov, A.V.; Hess, P.W.; Islam, R.; Kim, K.; Linke, N.M.; Pagano, G.; et al. Programmable quantum simulations of spin systems with trapped ions. Rev. Mod. Phys. 2021, 93, 025001. [Google Scholar] [CrossRef]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Mi, X.; Roushan, P.; Quintana, C.; Mandrà, S.; Marshall, J.; Neill, C.; Arute, F.; Arya, K.; Atalaya, J.; Babbush, R.; et al. Information scrambling in quantum circuits. Science 2021, 374, 1479–1483. [Google Scholar] [CrossRef] [PubMed]
- Zirnbauer, M.R. Supersymmetry for systems with unitary disorder: Circular ensembles. J. Phys. A 1996, 29, 7113–7136. [Google Scholar] [CrossRef]
- Zirnbauer, M.R. The color-flavor transformation and a new approach to quantum chaotic maps. In Proceedings of the 12th International Congress of Mathematical Physics (ICMP 97), Brisbane, Australia, 13–19 July 1997; pp. 290–297. [Google Scholar]
- Zirnbauer, M.R. Pair correlations of quantum chaotic maps from supersymmetry. In Supersymmetry and Trace Formulae: Chaos and Disorder; Kluwer Academic/Plenum: New York, NY, USA, 1999; pp. 153–172. [Google Scholar]
- Altland, A.; Zirnbauer, M.R. Field Theory of the Quantum Kicked Rotor. Phys. Rev. Lett. 1996, 77, 4536–4539. [Google Scholar] [CrossRef]
- Zirnbauer, M.R. Color-Flavor Transformation Revisited. arXiv 2021, arXiv:2109.10272. [Google Scholar]
- Wegner, F. The mobility edge problem: Continuous symmetry and a conjecture. Z. Phys. B 1979, 35, 207–210. [Google Scholar] [CrossRef]
- Efetov, K.B. Supersymmetry in Disorder and Chaos; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Tian, C.; Altland, A. Theory of localization and resonance phenomena in the quantum kicked rotor. New J. Phys. 2010, 12, 043043. [Google Scholar] [CrossRef]
- Tian, C.; Altland, A.; Garst, M. Theory of the Anderson Transition in the Quasiperiodic Kicked Rotor. Phys. Rev. Lett. 2011, 107, 074101. [Google Scholar] [CrossRef]
- Tian, C.; Altland, A. Field theory of Anderson transition of the kicked rotor. Phys. Scr. 2012, T151, 014049. [Google Scholar] [CrossRef]
- Gnutzmann, S.; Altland, A. Universal Spectral Statistics in Quantum Graphs. Phys. Rev. Lett. 2004, 93, 194101. [Google Scholar] [CrossRef] [PubMed]
- Gnutzmann, S.; Altland, A. Spectral correlations of individual quantum graphs. Phys. Rev. E 2005, 72, 056215. [Google Scholar] [CrossRef] [PubMed]
- Gnutzmann, S.; Keating, J.P.; Piotet, F. Quantum Ergodicity on Graphs. Phys. Rev. Lett. 2008, 101, 264102. [Google Scholar] [CrossRef] [PubMed]
- Gnutzmann, S.; Keating, J.; Piotet, F. Eigenfunction statistics on quantum graphs. Ann. Phys. 2010, 325, 2595–2640. [Google Scholar] [CrossRef]
- Zirnbauer, M.R. Toward a theory of the integer quantum Hall transition: Continuum limit of the Chalker–Coddington model. J. Math. Phys. 1997, 38, 2007–2036. [Google Scholar] [CrossRef]
- Janssen, M.; Metzler, M.; Zirnbauer, M.R. Point-contact conductances at the quantum Hall transition. Phys. Rev. B 1999, 59, 15836–15853. [Google Scholar] [CrossRef]
- Altland, A.; Gnutzmann, S.; Haake, F.; Micklitz, T. A review of sigma models for quantum chaotic dynamics. Rep. Prog. Phys. 2015, 78, 086001. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Brouwer, P.; Beenakker, C. Diagrammatic method of integration over the unitary group, with applications to quantum transport in mesoscopic systems. J. Math. Phys. 1996, 37, 4904–4934. [Google Scholar] [CrossRef]
- Samuel, S. U(N) Integrals, 1/N, and the De Wit-’t Hooft anomalies. J. Math. Phys. 1980, 21, 2695–2703. [Google Scholar] [CrossRef]
- Weingarten, D. Asymptotic behavior of group integrals in the limit of infinite rank. J. Math. Phys. 1978, 19, 999–1001. [Google Scholar] [CrossRef]
- Collins, B. Moments and cumulants of polynomial random variables on unitary groups, the itzykson-zuber integral, and free probability. Int. Math. Res. Not. 2003, 2003, 953–982. [Google Scholar] [CrossRef]
- Collins, B.; Śniady, P. Integration with respect to the Haar measure on unitary, orthogonal and symplectic group. Commun. Math. Phys. 2006, 264, 773–795. [Google Scholar] [CrossRef]
- Collins, B.; Matsumoto, S.; Novak, J. The weingarten calculus. arXiv 2021, arXiv:2109.14890. [Google Scholar] [CrossRef]
- Köstenberger, G. Weingarten Calculus. arXiv 2021, arXiv:2101.00921. [Google Scholar]
- Argaman, N.; Zee, A. Diagrammatic theory of random scattering matrices for normal-metal–superconducting mesoscopic junctions. Phys. Rev. B 1996, 54, 7406–7420. [Google Scholar] [CrossRef] [PubMed]
- Sünderhauf, C.; Pérez-García, D.; Huse, D.A.; Schuch, N.; Cirac, J.I. Localization with random time-periodic quantum circuits. Phys. Rev. B 2018, 98, 134204. [Google Scholar] [CrossRef]
- Li, Y.; Vasseur, R.; Fisher, M.; Ludwig, A.W. Statistical Mechanics Model for Clifford Random Tensor Networks and Monitored Quantum Circuits. arXiv 2021, arXiv:2110.02988. [Google Scholar]
- Collins, B.; Matsumoto, S. On some properties of orthogonal Weingarten functions. J. Math. Phys. 2009, 50, 113516. [Google Scholar] [CrossRef]
- Matsumoto, S. General moments of matrix elements from circular orthogonal ensembles. Random Matrices Theory Appl. 2012, 1, 1250005. [Google Scholar] [CrossRef]
- Matsumoto, S. Weingarten calculus for matrix ensembles associated with compact symmetric spaces. Random Matrices Theory Appl. 2013, 2, 1350001. [Google Scholar] [CrossRef]
- Andreev, A.V.; Agam, O.; Simons, B.D.; Altshuler, B.L. Quantum Chaos, Irreversible Classical Dynamics, and Random Matrix Theory. Phys. Rev. Lett. 1996, 76, 3947–3950. [Google Scholar] [CrossRef] [PubMed]
- Andreev, A.; Simons, B.; Agam, O.; Altshuler, B. Semiclassical field theory approach to quantum chaos. Nucl. Phys. B 1996, 482, 536–566. [Google Scholar] [CrossRef][Green Version]
- Joshi, L.K.; Elben, A.; Vikram, A.; Vermersch, B.; Galitski, V.; Zoller, P. Probing Many-Body Quantum Chaos with Quantum Simulators. Phys. Rev. X 2022, 12, 011018. [Google Scholar] [CrossRef]
- Dyson, F.J. Statistical Theory of the Energy Levels of Complex Systems. J. Math. Phys. 1962, 3, 140–156. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Kamenev, A. Field Theory of Non-Equilibrium Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Winer, M.; Jian, S.K.; Swingle, B. Exponential Ramp in the Quadratic Sachdev-Ye-Kitaev Model. Phys. Rev. Lett. 2020, 125, 250602. [Google Scholar] [CrossRef]
- Andreev, A.V.; Altshuler, B.L. Spectral Statistics beyond Random Matrix Theory. Phys. Rev. Lett. 1995, 75, 902–905. [Google Scholar] [CrossRef]
- Kamenev, A.; Mézard, M. Wigner-Dyson statistics from the replica method. J. Phys. A 1999, 32, 4373. [Google Scholar] [CrossRef]
- Kamenev, A.; Mézard, M. Level correlations in disordered metals: The replica σ model. Phys. Rev. B 1999, 60, 3944. [Google Scholar] [CrossRef]
- Altland, A.; Kamenev, A. Wigner-Dyson statistics from the Keldysh σ-model. Phys. Rev. Lett. 2000, 85, 5615. [Google Scholar] [CrossRef]
- Skinner, B.; Ruhman, J.; Nahum, A. Measurement-Induced Phase Transitions in the Dynamics of Entanglement. Phys. Rev. X 2019, 9, 031009. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Fisher, M.P.A. Quantum Zeno effect and the many-body entanglement transition. Phys. Rev. B 2018, 98, 205136. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Fisher, M.P.A. Measurement-driven entanglement transition in hybrid quantum circuits. Phys. Rev. B 2019, 100, 134306. [Google Scholar] [CrossRef]
- Potter, A.C.; Vasseur, R. Entanglement dynamics in hybrid quantum circuits. arXiv 2021, arXiv:2111.08018. [Google Scholar]
- Morningstar, A.; Colmenarez, L.; Khemani, V.; Luitz, D.J.; Huse, D.A. Avalanches and many-body resonances in many-body localized systems. arXiv 2021, arXiv:2107.05642. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Exact Spectral Statistics in Strongly Localising Circuits. arXiv 2021, arXiv:2110.15938. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Galitski, V. Effective Field Theory of Random Quantum Circuits. Entropy 2022, 24, 823. https://doi.org/10.3390/e24060823
Liao Y, Galitski V. Effective Field Theory of Random Quantum Circuits. Entropy. 2022; 24(6):823. https://doi.org/10.3390/e24060823
Chicago/Turabian StyleLiao, Yunxiang, and Victor Galitski. 2022. "Effective Field Theory of Random Quantum Circuits" Entropy 24, no. 6: 823. https://doi.org/10.3390/e24060823
APA StyleLiao, Y., & Galitski, V. (2022). Effective Field Theory of Random Quantum Circuits. Entropy, 24(6), 823. https://doi.org/10.3390/e24060823





