Pareto-Optimal Clustering with the Primal Deterministic Information Bottleneck
Abstract
:1. Introduction
| Algorithm 1 Pareto Mapper: -greedy agglomerative search |
Input: Joint distribution , and search parameter Output: Approximate Pareto frontier P
|
1.1. Objectives and Relation to Prior Work
1.1.1. The Deterministic Information Bottleneck
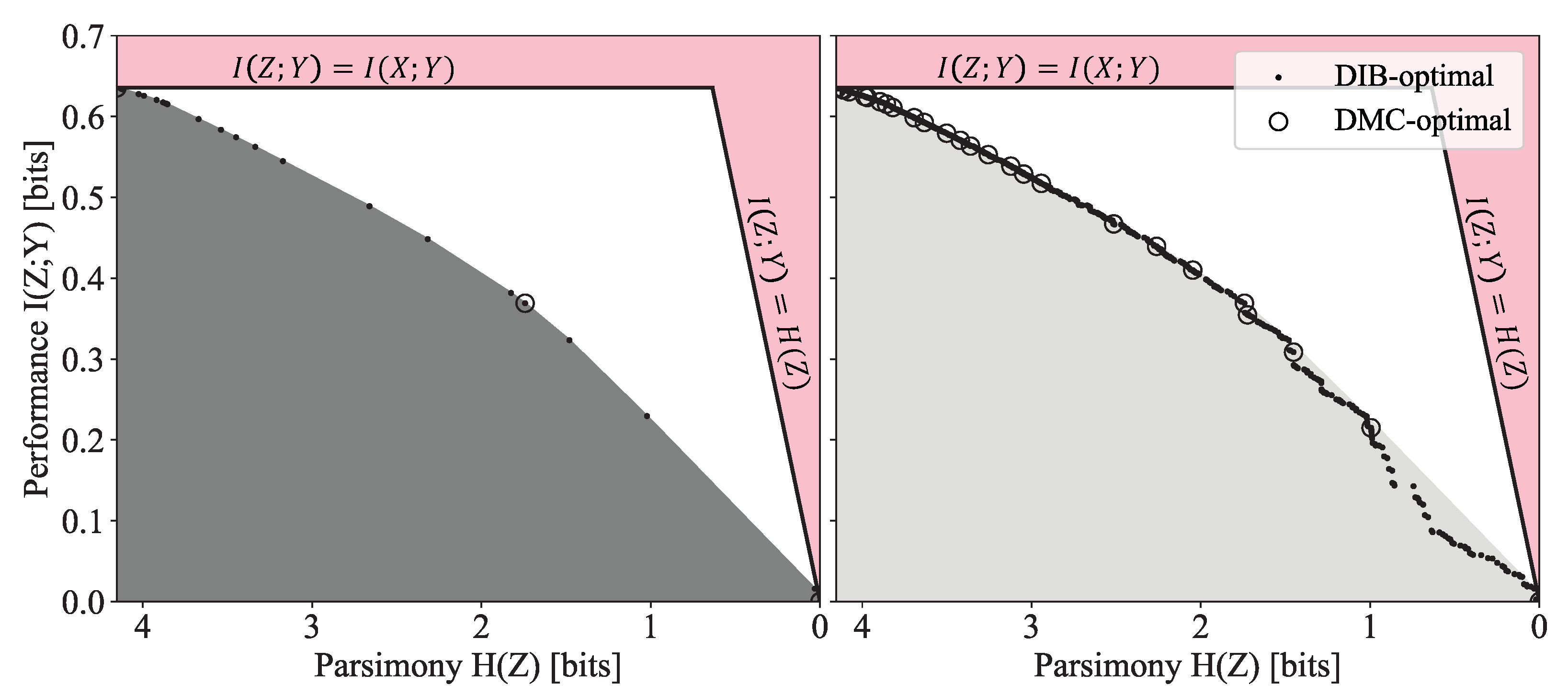
1.1.2. Discrete Memoryless Channels
1.1.3. Pareto Front Learning
1.1.4. Motivation and Objectives
1.2. Roadmap
2. Methods
2.1. The Pareto Mapper
2.2. Robust Pareto Mapper
| Algorithm 2 Robust Pareto Mapper: dealing with finite data |
Input: Empirical joint distribution , search parameter , and sample size S Output: Approximate Pareto frontier P with uncertainties
return |
3. Results
3.1. General Properties of Pareto Frontiers
3.1.1. Argument for the Sparsity of the Pareto Frontier
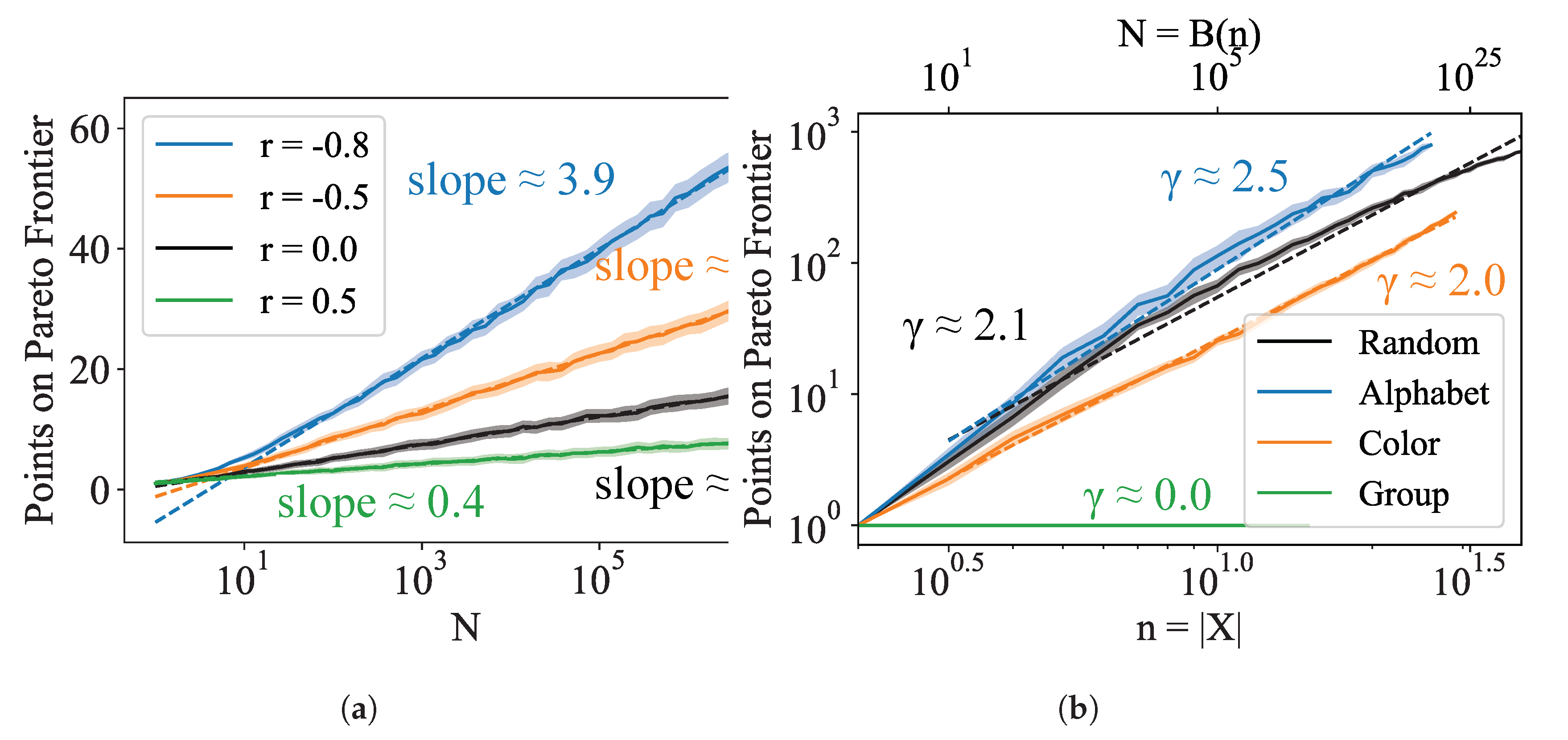
3.1.2. Dependence on Number of Items
3.2. At the Pareto Frontier: Three Vignettes
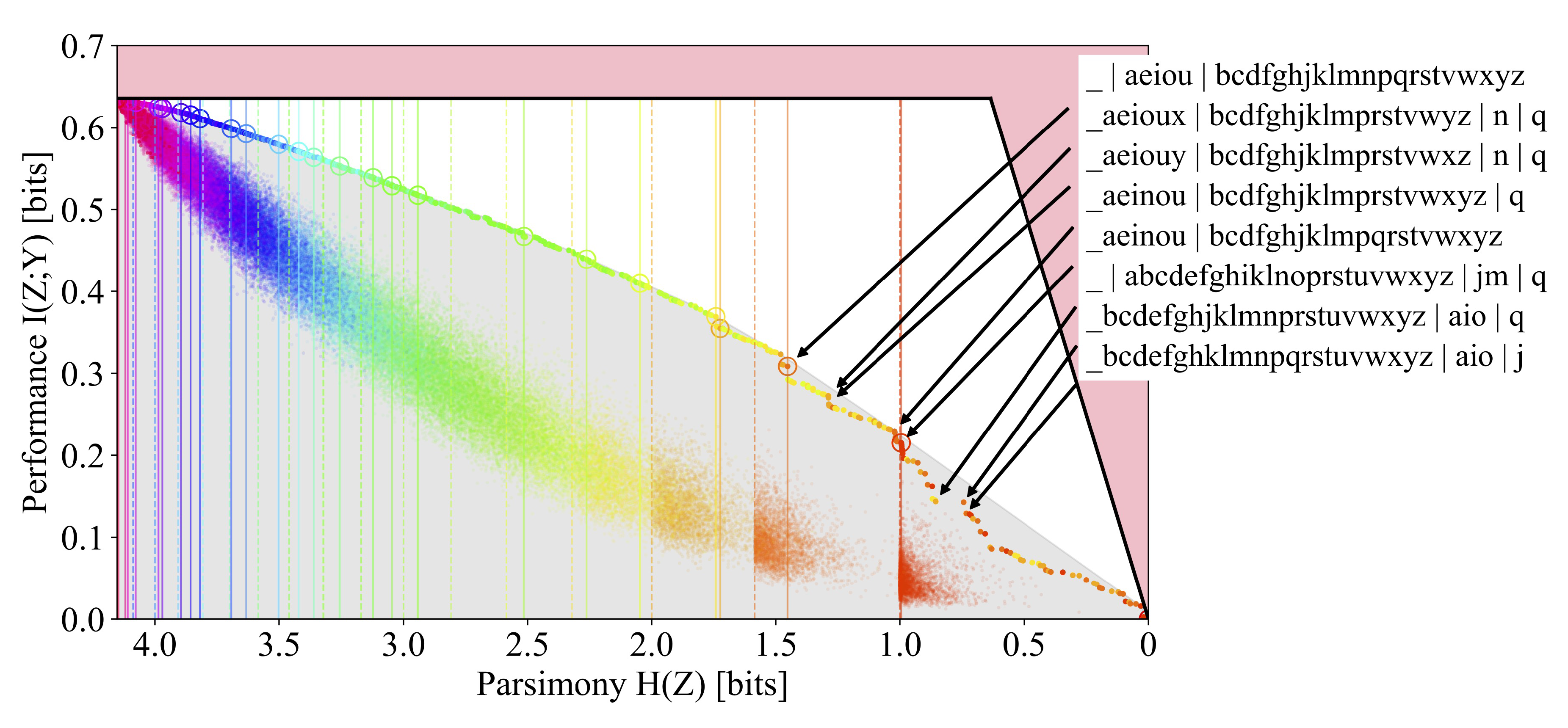
3.2.1. Compressing the English Alphabet
3.2.2. Naming the Colors of the Rainbow
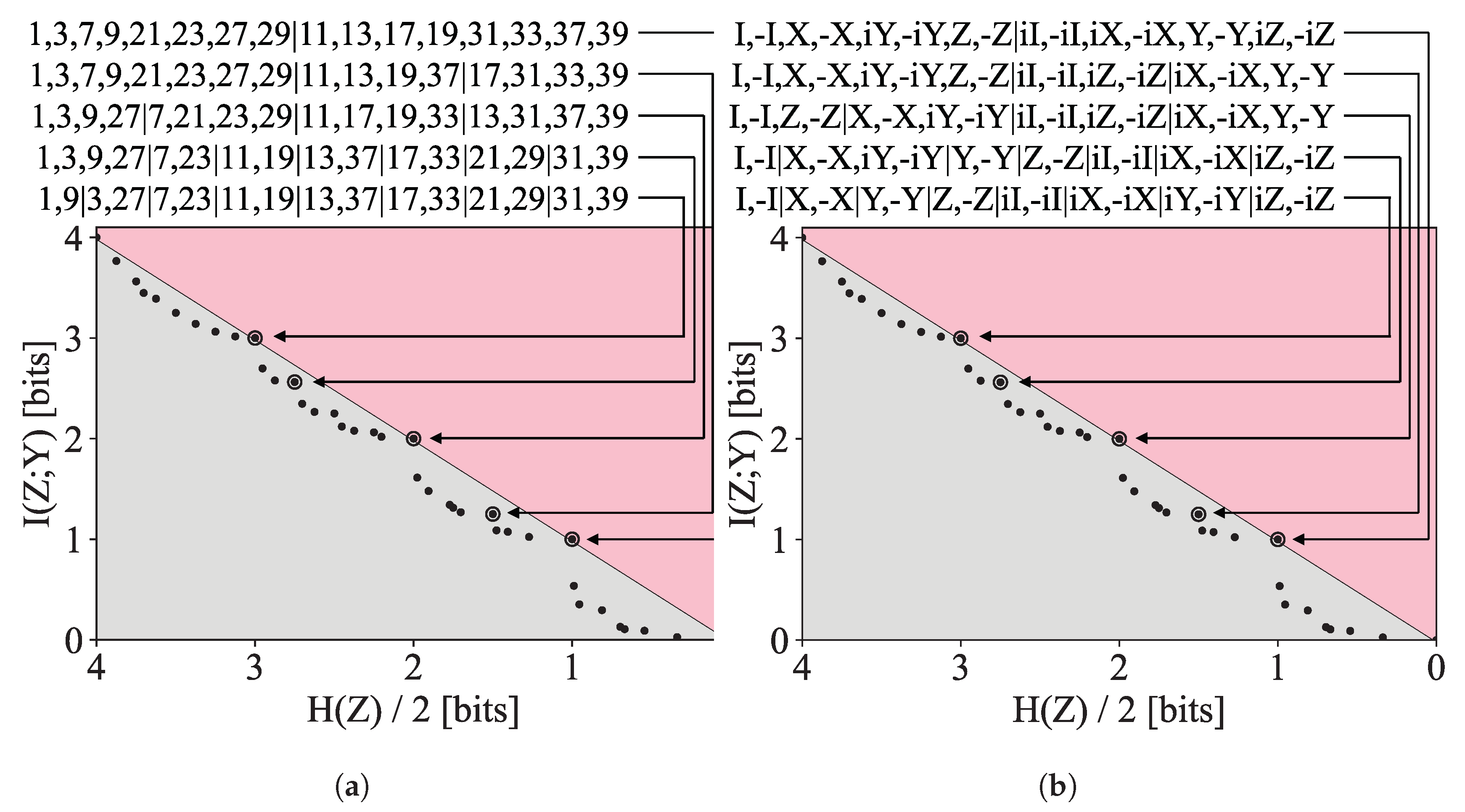
3.2.3. Symmetric Compression of Groups
4. Discussion
Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Pareto Set Scaling Theorem
Appendix B. Auxiliary Functions
| Algorithm A1 Check if a point is Pareto optimal |
Input: Point on objective plane p, and Pareto Set P Output: true if and only if p is Pareto optimal in P
|
| Algorithm A2 Add point to Pareto Set |
Input: Point on objective plane p, and Pareto Set P Output: Updated Pareto Set P
return P |
| Algorithm A3 Calculate distance to Pareto frontier |
Input: Point on objective plane p, and Pareto Set P Output: Distance to Pareto frontier (defined to be zero if Pareto optimal)
return d |
Appendix C. The Symmetric Pareto Mapper
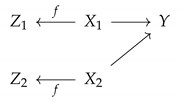

| Algorithm A4 Symmetric Pareto Mapper |
Input: Joint distribution , and search parameter Output: Approximate Pareto frontier P
|
References
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar]
- Strouse, D.; Schwab, D.J. The deterministic information bottleneck. Neural Comput. 2017, 29, 1611–1630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alemi, A.A.; Fischer, I. TherML: Thermodynamics of machine learning. arXiv 2018, arXiv:1807.04162. [Google Scholar]
- Fischer, I. The conditional entropy bottleneck. Entropy 2020, 22, 999. [Google Scholar] [CrossRef] [PubMed]
- Hassanpour, S.; Wuebben, D.; Dekorsy, A. Overview and investigation of algorithms for the information bottleneck method. In Proceedings of the SCC 2017, 11th International ITG Conference on Systems, Communications and Coding, Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Pereira, F.; Tishby, N.; Lee, L. Distributional clustering of English words. In Proceedings of the 31st Annual Meeting on Association for Computational Linguistics, Columbus, OH, USA, 22–26 June 1993; pp. 183–190. [Google Scholar]
- Slonim, N.; Tishby, N. Agglomerative information bottleneck. In Advances in Neural Information Processing Systems 12, Proceedings of the NIPS Conference, Denver, CO, USA, 29 November–4 December 1999; Solla, S.A., Leen, T.K., Müller, K., Eds.; The MIT Press: Cambridge, MA, USA, 1999; pp. 617–623. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J.; Lafferty, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep variational information bottleneck. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017 (Conference Track Proceedings, OpenReview.net), Toulon, France, 24–26 April 2017. [Google Scholar]
- Andritsos, P.; Tsaparas, P.; Miller, R.J.; Sevcik, K.C. LIMBO: Scalable clustering of categorical data. In Proceedings of the Advances in Database Technology—EDBT 2004, 9th International Conference on Extending Database Technology, Crete, Greece, 14–18 March 2004; pp. 123–146. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D.; Van Kuyk, S. Caveats for information bottleneck in deterministic scenarios. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Tegmark, M.; Wu, T. Pareto-optimal data compression for binary classification tasks. Entropy 2019, 22, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurkoski, B.M.; Yagi, H. Quantization of binary-input discrete memoryless channels. IEEE Trans. Inf. Theory 2014, 60, 4544–4552. [Google Scholar] [CrossRef]
- Zhang, J.A.; Kurkoski, B.M. Low-complexity quantization of discrete memoryless channels. In Proceedings of the 2016 International Symposium on Information Theory and Its Applications (ISITA), Monterey, CA, USA, 30 October–2 November 2016; pp. 448–452. [Google Scholar]
- Navon, A.; Shamsian, A.; Fetaya, E.; Chechik, G. Learning the Pareto Front with Hypernetworks. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 36–30 April 2020. [Google Scholar]
- Lin, X.; Yang, Z.; Zhang, Q.; Kwong, S. Controllable pareto multi-task learning. arXiv 2020, arXiv:2010.06313. [Google Scholar]
- Strouse, D.; Schwab, D.J. The information bottleneck and geometric clustering. Neural Comput. 2019, 31, 596–612. [Google Scholar] [CrossRef] [PubMed]
- Still, S.; Bialek, W. How many clusters? An information-theoretic perspective. Neural Comput. 2004, 16, 2483–2506. [Google Scholar] [CrossRef] [PubMed]
- Awasthi, P.; Charikar, M.; Krishnaswamy, R.; Sinop, A.K. The hardness of approximation of euclidean k-Means. In Proceedings of the 31st International Symposium on Computational Geometry (SoCG 2015), Eindhoven, The Netherlands, 22–25 June 2015. [Google Scholar]
- Nemenman, I.; Shafee, F.; Bialek, W. Entropy and Inference, Revisited. In Advances in Neural Information Processing Systems; Dietterich, T., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2002; Volume 14, pp. 471–478. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef] [Green Version]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nemenman, I.; Bialek, W.; de Ruyter van Steveninck, R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, 056111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poole, B.; Ozair, S.; Van Den Oord, A.; Alemi, A.; Tucker, G. On variational bounds of mutual information. In Proceedings of the International Conference on Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; pp. 5171–5180. [Google Scholar]
- Twomey, C.R.; Roberts, G.; Brainard, D.H.; Plotkin, J.B. What we talk about when we talk about colors. Proc. Natl. Acad. Sci. USA 2021, 118, e2109237118. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common objects in context. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 740–755. [Google Scholar]
- Achille, A.; Soatto, S. Emergence of invariance and disentanglement in deep representations. J. Mach. Learn. Res. 2018, 19, 1947–1980. [Google Scholar]
- Wu, T.; Fischer, I.S. Phase Transitions for the Information Bottleneck in Representation Learning. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020 (OpenReview.net), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Wu, T.; Fischer, I.; Chuang, I.L.; Tegmark, M. Learnability for the information bottleneck. In Uncertainty in Artificial Intelligence, Proceedings of the PMLR, Cambridge, MA, USA, 16–18 November 2020; AUAI Press: Corvallis, OR, USA, 2020; pp. 1050–1060. [Google Scholar]
- Ngampruetikorn, V.; Schwab, D.J. Perturbation theory for the information bottleneck. In Advances in Neural Information Processing Systems; Springer: Berlin, Germany, 2021; Volume 34. [Google Scholar]
- Rezende, D.J.; Viola, F. Taming VAEs. arXiv 2018, arXiv:1810.00597. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jeju Island, Korea, 11–15 October 2015; pp. 1–5. [Google Scholar]
- Chaudhari, P.; Soatto, S. Stochastic gradient descent performs variational inference, converges to limit cycles for deep networks. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–10. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. J. Stat. Mech. Theory Exp. 2019, 2019, 124020. [Google Scholar] [CrossRef]
- Still, S. Thermodynamic cost and benefit of memory. Phys. Rev. Lett. 2020, 124, 050601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buesing, L.; Maass, W. A spiking neuron as information bottleneck. Neural Comput. 2010, 22, 1961–1992. [Google Scholar] [CrossRef] [PubMed]


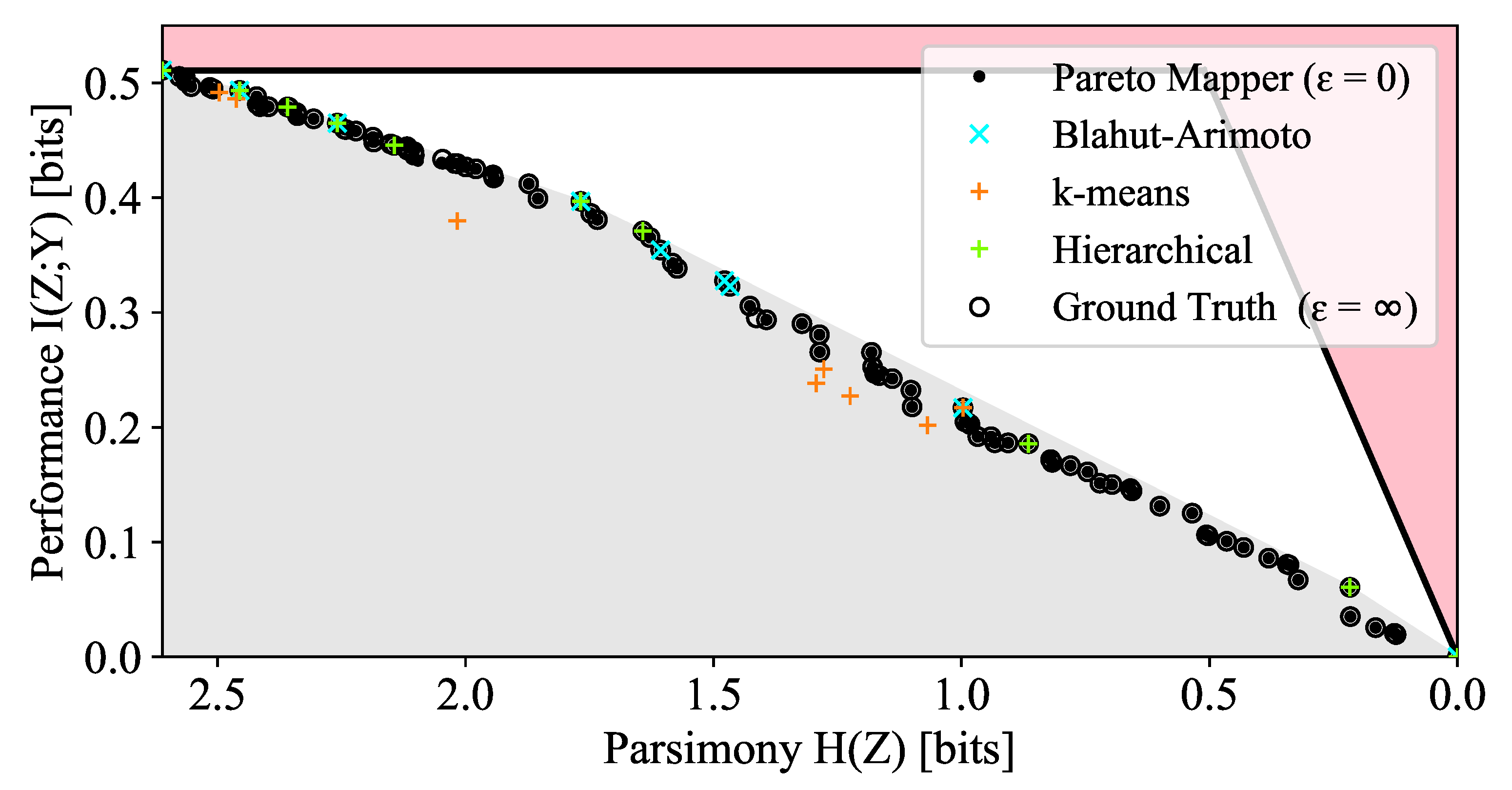
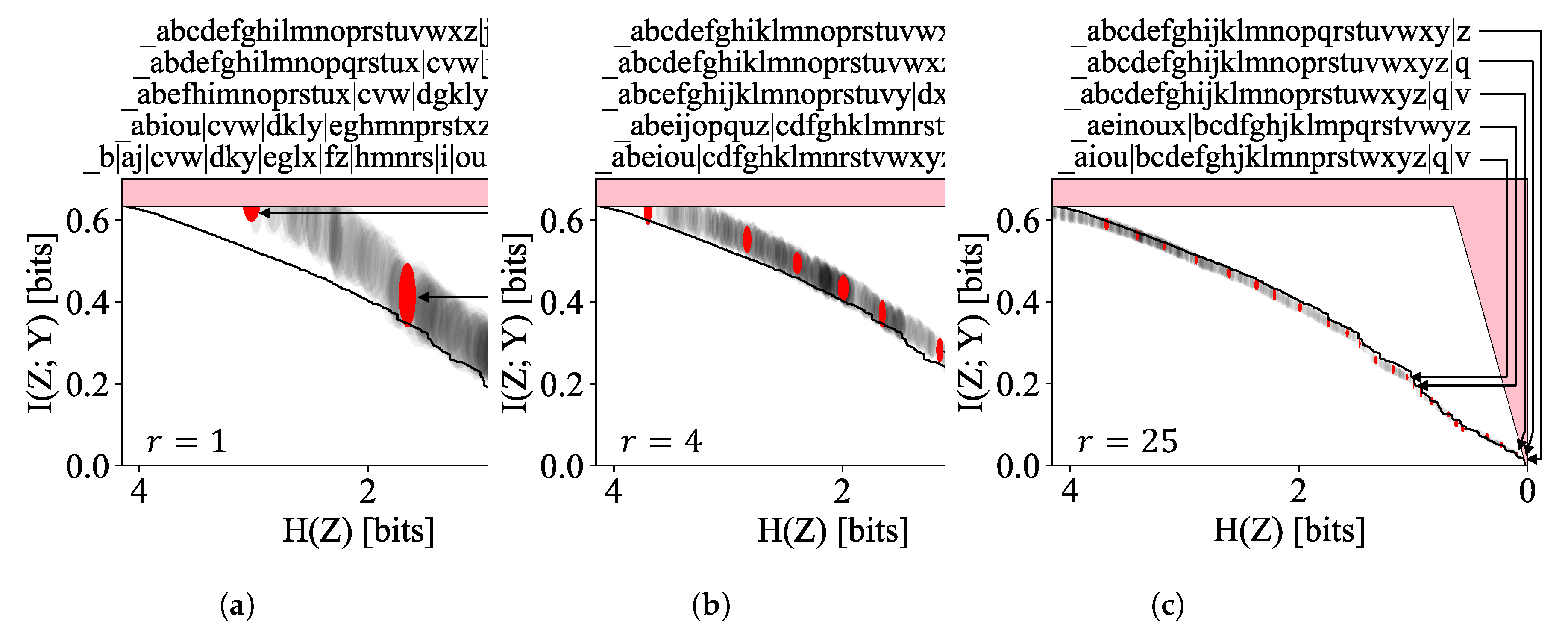
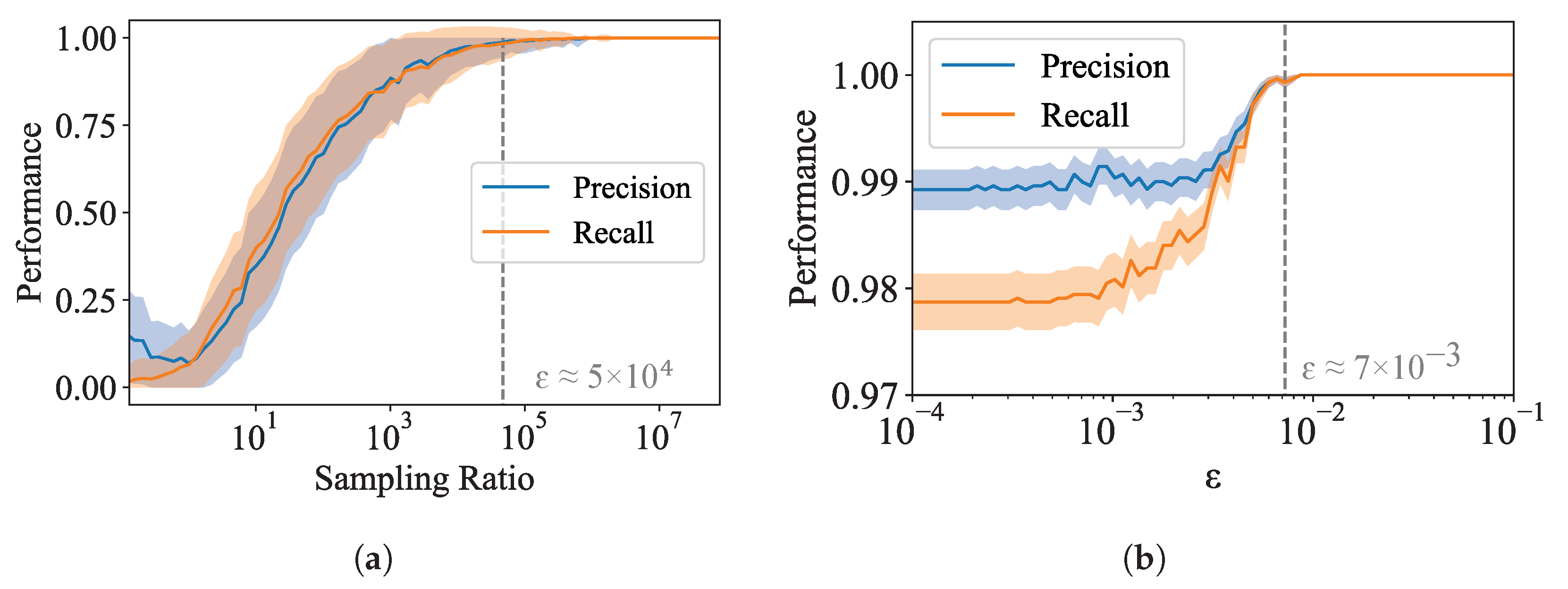
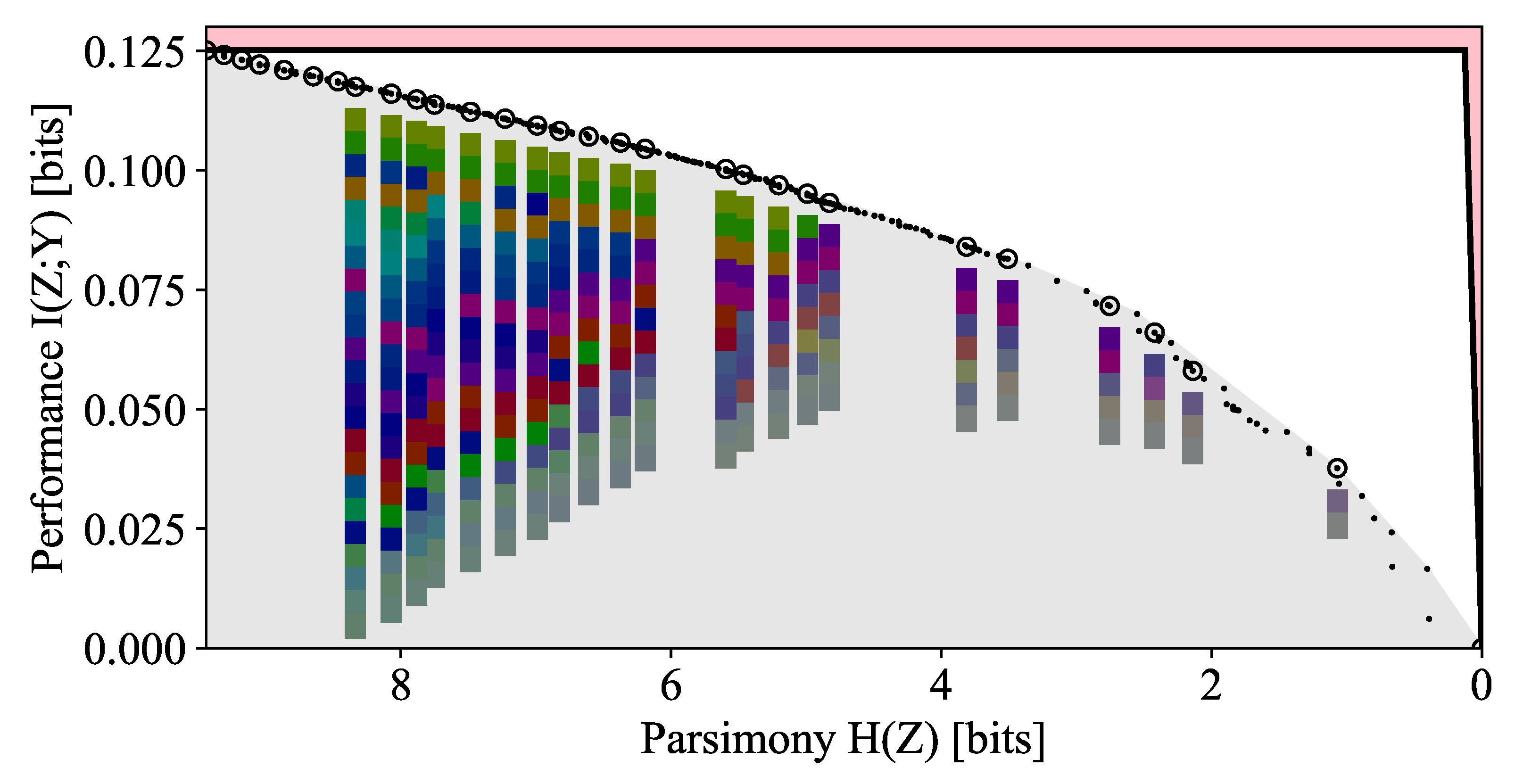

| Method | Points | TP | FP | FN | Precision | Recall |
|---|---|---|---|---|---|---|
| Ground truth () | 94 | 94 | 0 | 0 | 1.00 | 1.00 |
| Pareto Mapper () | 94 | 94 | 0 | 0 | 1.00 | 1.00 |
| Pareto Mapper () | 91 | 88 | 3 | 6 | 0.97 | 0.94 |
| Hierarchical (average) | 10 | 7 | 3 | 87 | 0.70 | 0.07 |
| Hierarchical (single) | 10 | 10 | 0 | 84 | 1.00 | 0.11 |
| Hierarchical (Ward) | 10 | 7 | 3 | 87 | 0.70 | 0.07 |
| k-means (JSD) | 10 | 3 | 7 | 91 | 0.30 | 0.02 |
| k-means (wJSD) | 10 | 2 | 8 | 92 | 0.20 | 0.10 |
| Blahut Arimoto | 9 | 9 | 0 | 85 | 1.00 | 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, A.K.; Tegmark, M.; Chuang, I.L. Pareto-Optimal Clustering with the Primal Deterministic Information Bottleneck. Entropy 2022, 24, 771. https://doi.org/10.3390/e24060771
Tan AK, Tegmark M, Chuang IL. Pareto-Optimal Clustering with the Primal Deterministic Information Bottleneck. Entropy. 2022; 24(6):771. https://doi.org/10.3390/e24060771
Chicago/Turabian StyleTan, Andrew K., Max Tegmark, and Isaac L. Chuang. 2022. "Pareto-Optimal Clustering with the Primal Deterministic Information Bottleneck" Entropy 24, no. 6: 771. https://doi.org/10.3390/e24060771
APA StyleTan, A. K., Tegmark, M., & Chuang, I. L. (2022). Pareto-Optimal Clustering with the Primal Deterministic Information Bottleneck. Entropy, 24(6), 771. https://doi.org/10.3390/e24060771






