Predicting Box-Office Markets with Machine Learning Methods
Abstract
:1. Introduction
- We propose an SVM-based method to predict the global box-office market of a country by its economic factor of GDP.
- We implemented four machine learning methods and four econometric methods with diverse combinations of economic factors as prediction variables. The comparison results in both the US and China box-office markets highlight the selected prediction strategy according to prediction performances.
- The time-series cross-validation and the mimicked prediction of the box-office market in real application scenarios prove the effectiveness and efficiency of our proposed method of predicting nationwide box-offices. The easy availability of economic factors also implies its flexibility.
- The empirical experiments with different combinations of economic factors indicate their diverse effects on box-office prediction. The selected prediction variable of GDP proves its interpretable close relationship with box-office revenues.
2. Materials and Methods
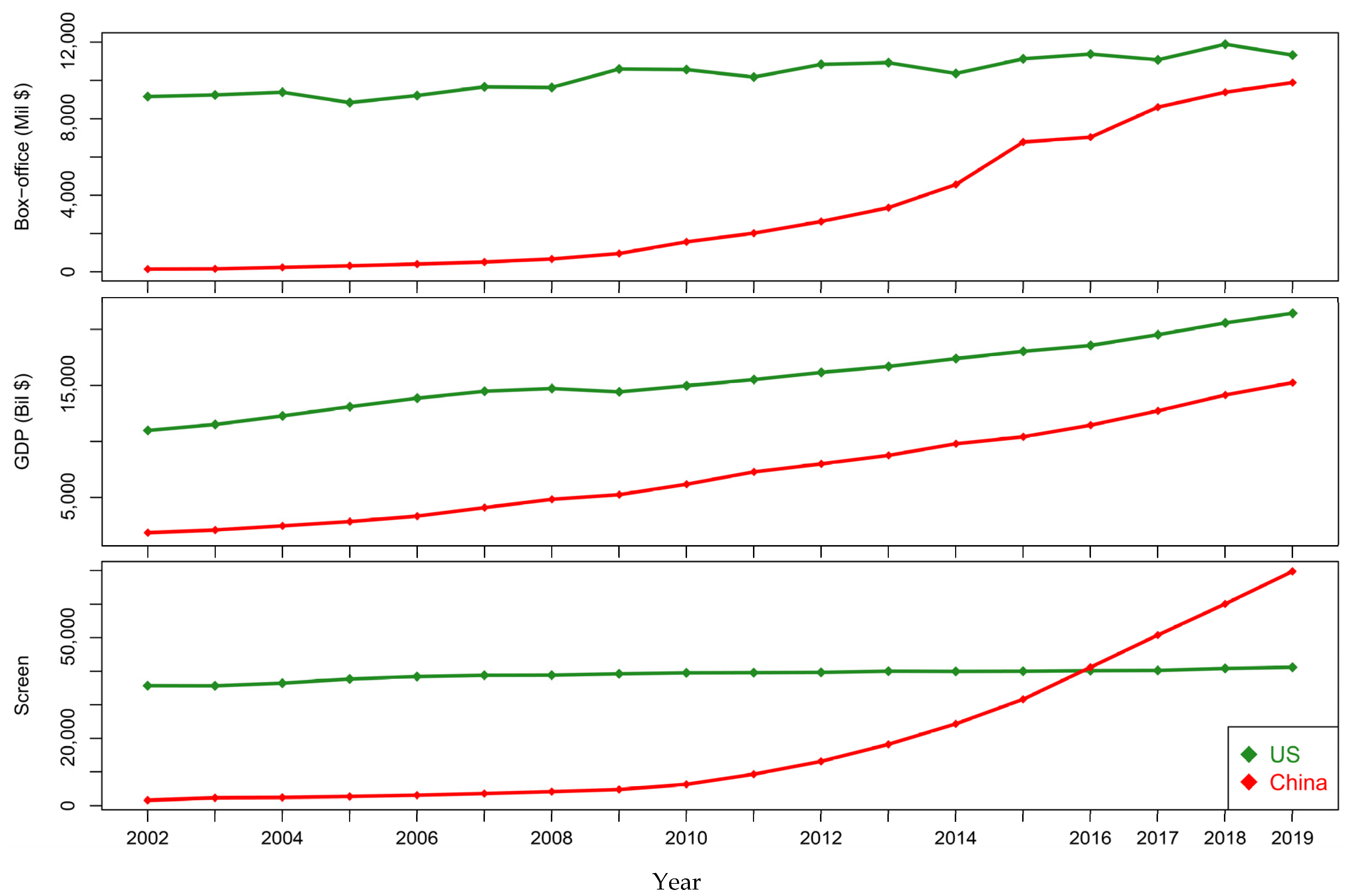
2.1. Data
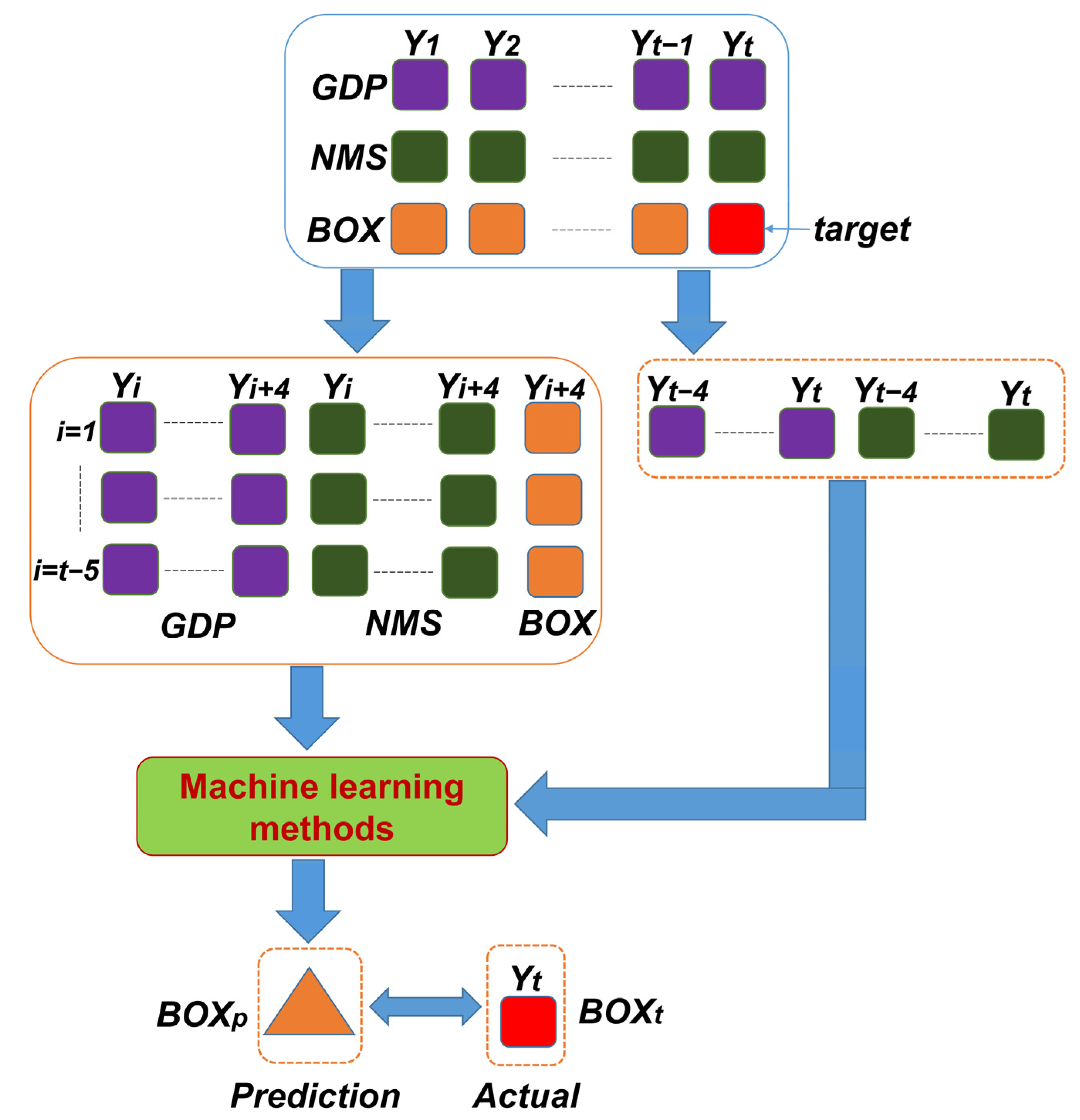
2.2. Framework of Prediction
2.3. Machine Learning Methods
2.3.1. Support Vector Machine
2.3.2. Random Forest
2.3.3. Neural Network and Deep Neural Network
2.4. Econometric Methods
2.4.1. Linear Regression, Log-Linear Regression and Ridge Regression
2.4.2. ARIMA
2.5. Prediction Performance Evaluation
3. Results and Discussion
3.1. Predictions by Different Methods
3.2. Selection of Prediction Variables
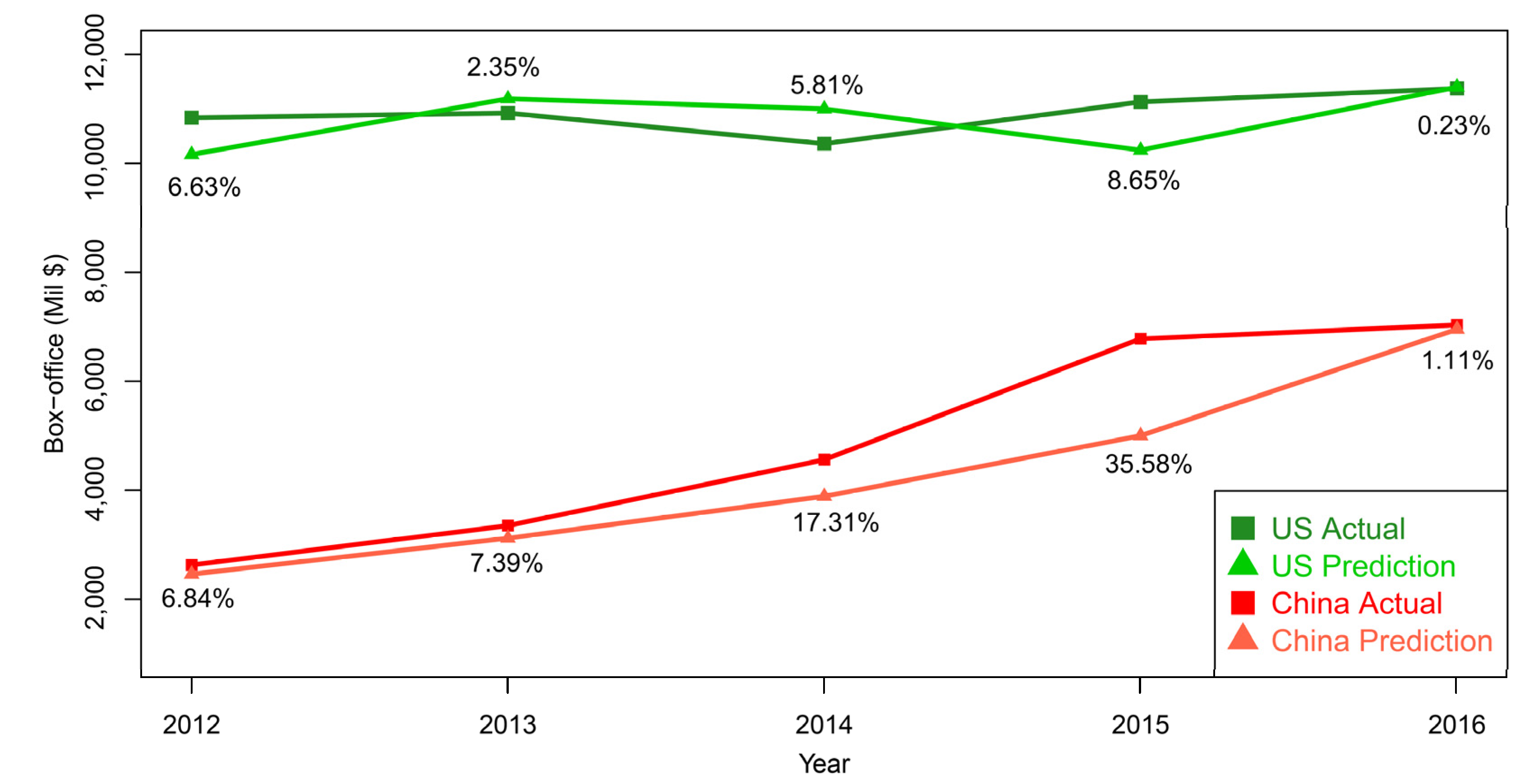
3.3. Predictions for the US and China Markets
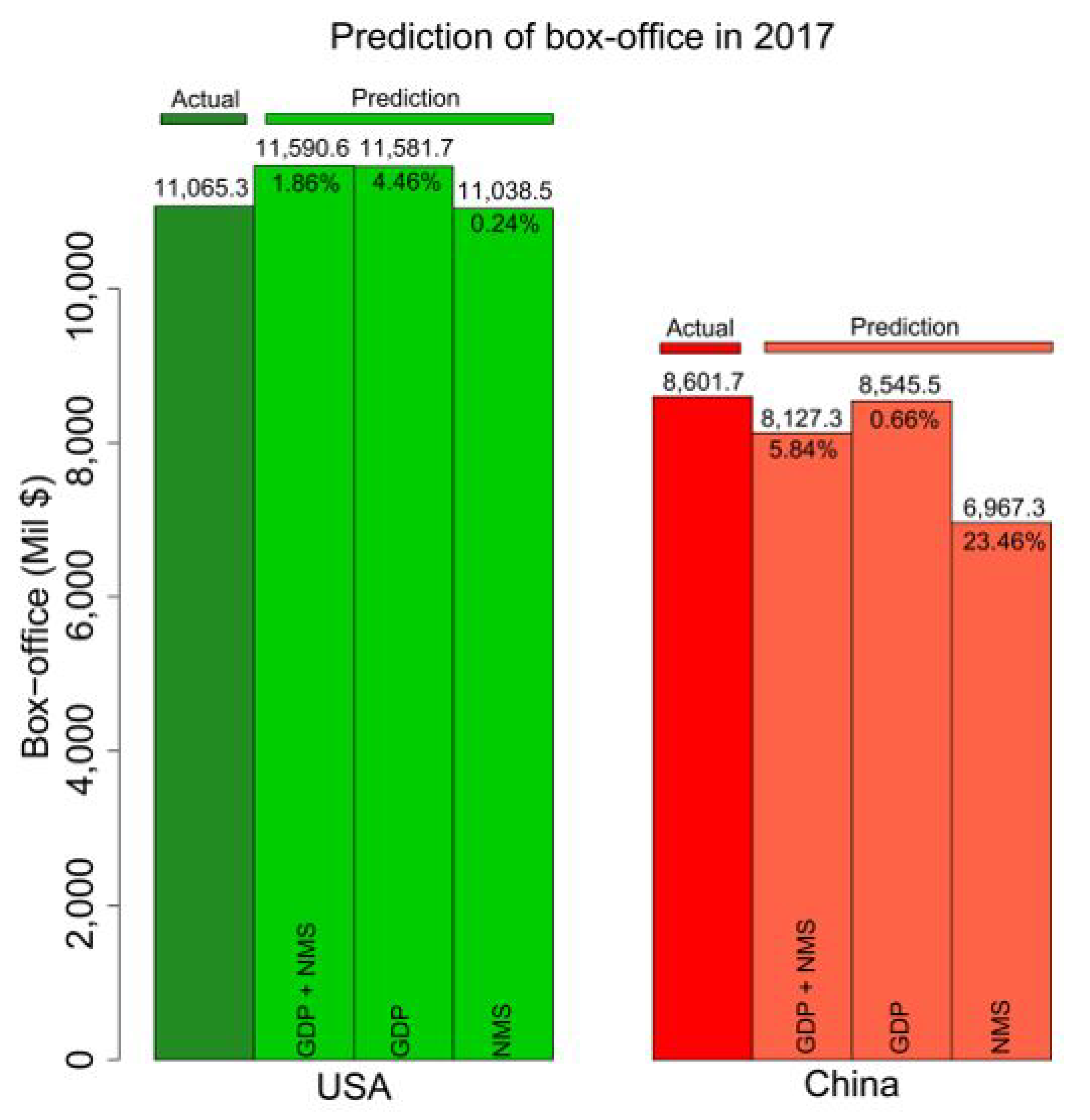
3.4. Predictions in 2017
3.5. Consecutive Predictions in 2018 and 2019
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peltoniemi, M. Cultural Industries: Product–Market Characteristics, Management Challenges and Industry Dynamics. Int. J. Manag. Rev. 2015, 17, 41–68. [Google Scholar] [CrossRef] [Green Version]
- McKenzie, J. The Economics of Movies: A Literature Survey. J. Econ. Surv. 2010, 26, 42–70. [Google Scholar] [CrossRef]
- Zhou, R.; Cai, R.; Tong, G. Applications of Entropy in Finance: A Review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
- Jamin, A.; Humeau-Heurtier, A. (Multiscale) Cross-Entropy Methods: A Review. Entropy 2019, 22, 45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef] [Green Version]
- Litman, B.R. Predicting Success of Theatrical Movies: An Empirical Study. J. Popul. Cult. 1983, 16, 159–175. [Google Scholar] [CrossRef]
- Mbunge, E.; Fashoto, S.G.; Bimha, H. Prediction of box-office success: A review of trends and machine learning computational models. Int. J. Bus. Intell. Data Min. 2022, 20, 192. [Google Scholar] [CrossRef]
- Sharda, R.; Delen, D. Predicting box-office success of motion pictures with neural networks. Expert Syst. Appl. 2006, 30, 243–254. [Google Scholar] [CrossRef]
- Ghiassi, M.; Lio, D.; Moon, B. Pre-production forecasting of movie revenues with a dynamic artificial neural network. Expert Syst. Appl. 2015, 42, 3176–3193. [Google Scholar] [CrossRef]
- Elberse, A.; Eliashberg, J. Demand and Supply Dynamics for Sequentially Released Products in International Markets: The Case of Motion Pictures. Mark. Sci. 2003, 22, 329–354. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Luo, J.; Yang, S. Forecasting box office revenue of movies with BP neural network. Expert Syst. Appl. 2009, 36, 6580–6587. [Google Scholar] [CrossRef]
- Ahmed, U.; Waqas, H.; Afzal, M.T. Pre-production box-office success quotient forecasting. Soft Comput. 2019, 24, 6635–6653. [Google Scholar] [CrossRef]
- Kim, T.; Hong, J.; Kang, P. Box office forecasting using machine learning algorithms based on SNS data. Int. J. Forecast. 2015, 31, 364–390. [Google Scholar] [CrossRef]
- Panaligan, R.; Chen, A. Quantifying Movie Magic with Google Search. Google Whitepaper—Industry Perspectives+ User Insights. 2013. Available online: https://docplayer.net/90506950-Quantifying-movie-magic-with-google-search.html (accessed on 31 January 2019).
- Mestyán, M.; Yasseri, T.; Kertész, J. Early Prediction of Movie Box Office Success Based on Wikipedia Activity Big Data. PLoS ONE 2013, 8, e71226. [Google Scholar]
- Chen, X.; Chen, Y.; Weinberg, C.B. Learning about movies: The impact of movie release types on the nationwide box office. J. Cult. Econ. 2012, 37, 359–386. [Google Scholar] [CrossRef]
- Sochay, S. Predicting the Performance of Motion Pictures. J. Media Econ. 1994, 7, 1–20. [Google Scholar] [CrossRef]
- Sawhney, M.S.; Eliashberg, J. A Parsimonious Model for Forecasting Gross Box-Office Revenues of Motion Pictures. Mark. Sci. 1996, 15, 113–131. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hill, T.; O’Connor, M.; Remus, W. Neural Network Models for Time Series Forecasts. Manag. Sci. 1996, 42, 1082–1092. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Seal, H.L. Studies in the History of Probability and Statistics. XV The historical development of the Gauss linear model. Biometrika 1967, 54, 1–24. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Hastie, T. Ridge Regularization: An Essential Concept in Data Science. Technometrics 2020, 62, 1–8. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Emsia, E.; Coskuner, C. Economic Growth Prediction Using Optimized Support Vector Machines. Comput. Econ. 2015, 48, 453–462. [Google Scholar] [CrossRef]
- Marshall, P.; Dockendorff, M.; Ibáñez, S. A forecasting system for movie attendance. J. Bus. Res. 2013, 66, 1800–1806. [Google Scholar] [CrossRef]
- Krzywanski, J.; Sztekler, K.; Szubel, M.; Siwek, T.; Nowak, W.; Mika, Ł. A comprehensive three-dimensional analysis of a large-scale multi-fuel cfb boiler burning coal and syngas. Part 1. The CFD model of a large-scale multi-fuel CFB combustion. Entropy 2020, 22, 964. [Google Scholar] [CrossRef] [PubMed]
- Krzywanski, J.; Sztekler, K.; Szubel, M.; Siwek, T.; Nowak, W.; Mika, Ł. A Comprehensive, Three-Dimensional Analysis of a Large-Scale, Multi-Fuel, CFB Boiler Burning Coal and Syngas. Part 2. Numerical Simulations of Coal and Syngas Co-Combustion. Entropy 2020, 22, 856. [Google Scholar] [CrossRef] [PubMed]
- Krzywanski, J. Heat Transfer Performance in a Superheater of an Industrial CFBC Using Fuzzy Logic-Based Methods. Entropy 2019, 21, 919. [Google Scholar] [CrossRef] [Green Version]

| Method | Predictor Variable | Country | RAPE | RMSE | ||||
|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2015 | 2016 | ||||
| SVM | GDP | US | 0.066 | 0.024 | 0.058 | 0.086 | 0.002 | 0.056 |
| China | 0.068 | 0.074 | 0.173 | 0.356 | 0.011 | 0.183 | ||
| NMS | US | 0.052 | 0.026 | 0.026 | 0.037 | 0.002 | 0.033 | |
| China | 0.058 | 0.075 | 0.008 | 0.117 | 0.225 | 0.121 | ||
| GDP + NMS | US | 0.092 | 0.041 | 0.059 | 0.083 | 0.019 | 0.065 | |
| China | 0.063 | 0.069 | 0.085 | 0.175 | 0.219 | 0.137 | ||
| RF | GDP | US | 0.042 | 0.035 | 0.035 | 0.048 | 0.043 | 0.041 |
| China | 0.537 | 0.509 | 0.586 | 0.761 | 0.235 | 0.552 | ||
| NMS | US | 0.039 | 0.030 | 0.043 | 0.045 | 0.045 | 0.041 | |
| China | 0.532 | 0.529 | 0.599 | 0.718 | 0.234 | 0.546 | ||
| GDP + NMS | US | 0.04 | 0.034 | 0.035 | 0.044 | 0.046 | 0.040 | |
| China | 0.539 | 0.509 | 0.613 | 0.753 | 0.226 | 0.555 | ||
| NN | GDP | US | 0.084 | 0.092 | 0.036 | 0.113 | 0.138 | 0.098 |
| China | 0.021 | 0.079 | 0.252 | 0.554 | 0.199 | 0.289 | ||
| NMS | US | 0.078 | 0.087 | 0.031 | 0.107 | 0.132 | 0.093 | |
| China | 0.262 | 0.228 | 0.081 | 0.046 | 0.239 | 0.193 | ||
| GDP + NMS | US | 0.079 | 0.088 | 0.032 | 0.108 | 0.133 | 0.094 | |
| China | 0.153 | 0.018 | 0.034 | 0.321 | 0.139 | 0.172 | ||
| DNN | GDP | US | 0.104 | 0.141 | 0.043 | 0.182 | 0.140 | 0.131 |
| China | 0.415 | 0.213 | 0.064 | 0.361 | 0.243 | 0.287 | ||
| NMS | US | 0.089 | 0.110 | 0.135 | 0.153 | 0.130 | 0.125 | |
| China | 0.403 | 0.274 | 0.089 | 0.351 | 0.240 | 0.292 | ||
| GDP + NMS | US | 0.129 | 0.159 | 0.061 | 0.136 | 0.208 | 0.147 | |
| China | 0.491 | 0.271 | 0.062 | 0.196 | 0.198 | 0.281 | ||
| LR | GDP | US | 0.490 | 1.176 | 0.099 | 0.111 | 0.038 | 0.574 |
| China | 0.292 | 0.398 | 0.105 | 0.369 | 0.189 | 0.292 | ||
| NMS | US | 0.174 | 0.041 | 0.034 | 0.024 | 0.028 | 0.083 | |
| China | 4.617 | 0.497 | 0.953 | 0.039 | 0.220 | 2.122 | ||
| GDP + NMS | US | 0.49 | 1.176 | 0.099 | 0.111 | 0.038 | 0.574 | |
| China | 0.292 | 0.398 | 0.105 | 0.369 | 0.189 | 0.292 | ||
| LLR | GDP | US | 0.607 | 0.662 | 0.100 | 0.108 | 0.040 | 0.408 |
| China | 0.221 | 0.519 | 0.133 | 0.232 | 0.215 | 0.295 | ||
| NMS | US | 0.166 | 0.045 | 0.034 | 0.023 | 0.027 | 0.080 | |
| China | 2.433 | 0.838 | 0.998 | 0.171 | 0.158 | 1.239 | ||
| GDP + NMS | US | 0.607 | 0.662 | 0.100 | 0.108 | 0.040 | 0.408 | |
| China | 0.221 | 0.519 | 0.133 | 0.232 | 0.215 | 0.295 | ||
| RR | GDP | US | 0.176 | 0.054 | 0.02 | 0.113 | 0.049 | 0.100 |
| China | 0.181 | 0.047 | 0.254 | 0.405 | 0.047 | 0.231 | ||
| NMS | US | 0.057 | 0.004 | 0.067 | 0.041 | 0.017 | 0.044 | |
| China | 0.586 | 0.507 | 0.111 | 0.018 | 0.268 | 0.370 | ||
| GDP + NMS | US | 0.104 | 0.050 | 0.054 | 0.090 | 0.055 | 0.074 | |
| China | 0.086 | 0.134 | 0.016 | 0.063 | 0.281 | 0.147 | ||
| ARIMA | BOX | US | 0.665 | 0.509 | 0.382 | 0.287 | 0.176 | 0.438 |
| China | 0.063 | 0.035 | 0.120 | 0.175 | 0.252 | 0.151 | ||
| Predictor Variable | RAPE | RMSE | ||||
|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2015 | 2016 | ||
| BOX | 0.577 | 0.361 | 0.495 | 0.740 | 0.326 | 0.494 |
| GDP + BOX | 0.044 | 0.015 | 0.093 | 0.187 | 0.149 | 0.117 |
| NOS + BOX | 0.056 | 0.045 | 0.027 | 0.153 | 0.190 | 0.114 |
| GDP + NOS + BOX | 0.021 | 0.010 | 0.086 | 0.255 | 0.029 | 0.121 |
| Country | Variable | 2018 | 2019 | ||||
|---|---|---|---|---|---|---|---|
| Predicted | Actual | RAPE | Predicted | Actual | RAPE | ||
| US | Box office (Mil $) | 11,147.17 | 11,889.3 | 6.24% | 11,542.76 | 11,320.9 | 1.96% |
| Projected GDP (Bil $) | 20,351.8 | 20,580.2 | 1.11% | 21,239.30 | 21,433.2 | 0.91% | |
| China | Box office (Mil $) | 9890.37 | 9380.92 | 5.43% | 10,030.98 | 9887.08 | 1.46% |
| Projected GDP (Bil $) | 13,552.08 | 14,142.78 | 4.18% | 14,432.96 | 15,244.08 | 5.32% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Liu, Z.-P. Predicting Box-Office Markets with Machine Learning Methods. Entropy 2022, 24, 711. https://doi.org/10.3390/e24050711
Li D, Liu Z-P. Predicting Box-Office Markets with Machine Learning Methods. Entropy. 2022; 24(5):711. https://doi.org/10.3390/e24050711
Chicago/Turabian StyleLi, Dawei, and Zhi-Ping Liu. 2022. "Predicting Box-Office Markets with Machine Learning Methods" Entropy 24, no. 5: 711. https://doi.org/10.3390/e24050711
APA StyleLi, D., & Liu, Z.-P. (2022). Predicting Box-Office Markets with Machine Learning Methods. Entropy, 24(5), 711. https://doi.org/10.3390/e24050711






