Heuristic Optimization of Deep and Shallow Classifiers: An Application for Electroencephalogram Cyclic Alternating Pattern Detection
Abstract
:1. Introduction
- Presentation of a novel algorithm for optimizing the structure of deep learning models (code is publicly available). The optimization of deep learning models’ structure is a challenging task. As a result, there is a need for simple algorithms that can allow users to develop new models without requiring a detailed optimization procedure;
- Proposal for a fully automatic sleep stability analysis based on CAP, which provides the A phase, CAP cycle, and CAP rate assessments. To the authors’ best knowledge, this is the first time a single algorithm provides all these metrics with such high accuracy;
- For CAP analysis, the performance of the machine learning models, using features, and deep learning models, with automatic feature extraction, was compared. To the authors’ best knowledge, this is the first time this examination was carried out.
2. State-of-the-Art
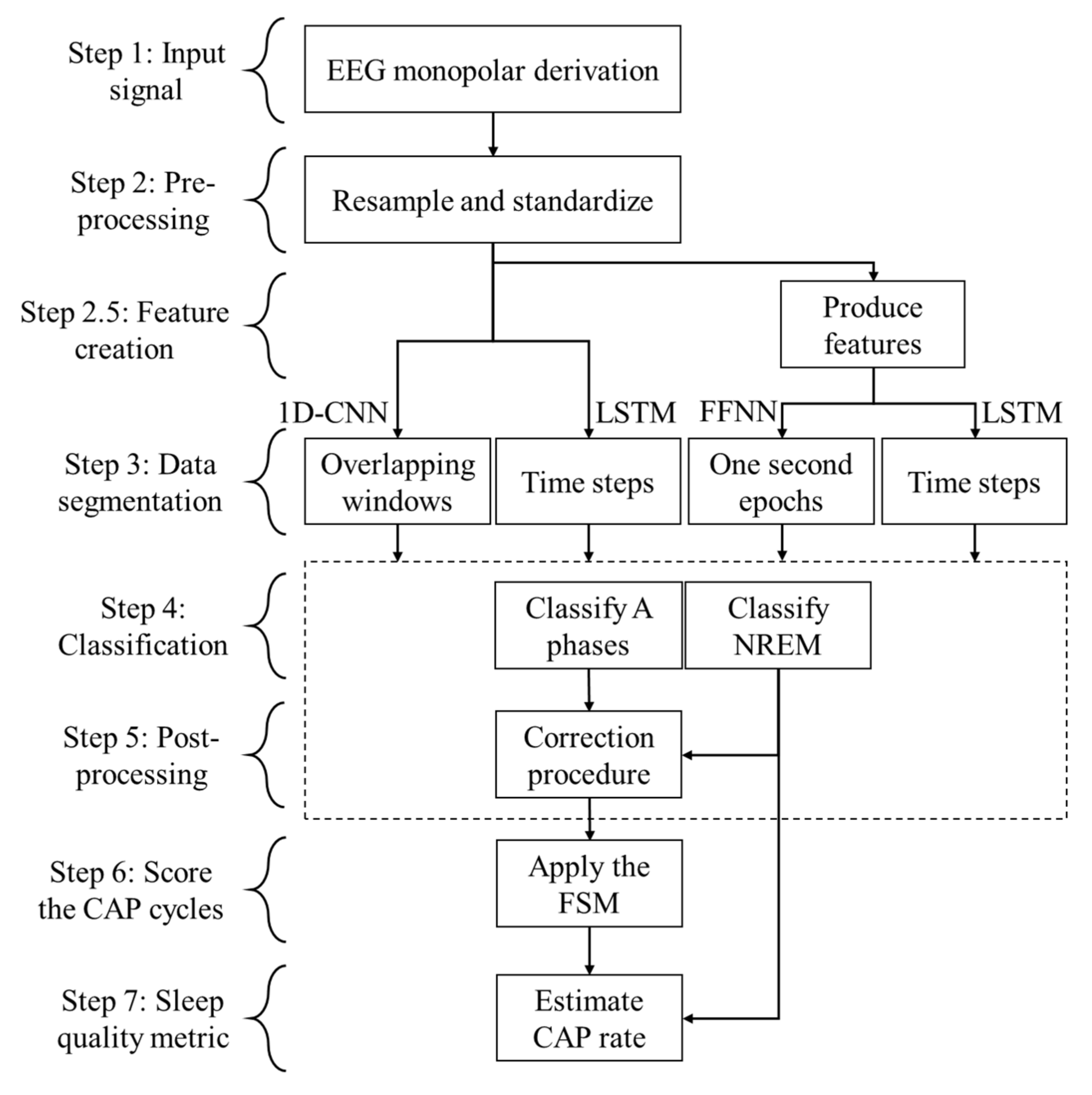
3. Materials and Methods
3.1. Studied Population
3.2. Pre-Processing Resampling Procedure
3.3. Pre-Processing Segmentation Procedure
3.4. Feature Creation
3.5. Classification
3.6. Post-Processing Procedure and CAP Assessment
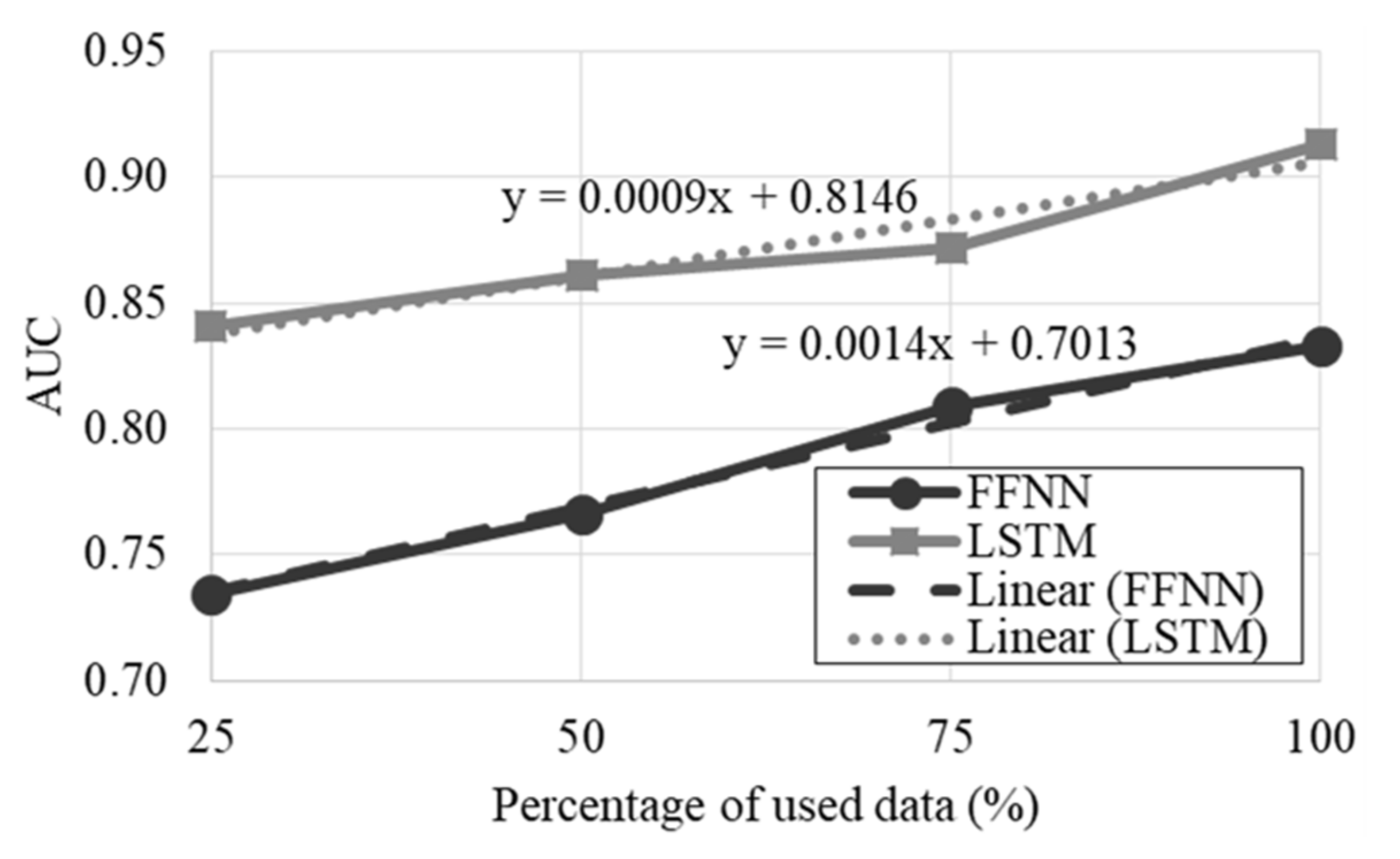
3.7. Performance Assessment and Optimization of the Classifiers
4. Experimental Evaluation
4.1. Development of the AFC Classifiers
4.2. Development of the Feature-Based Classifiers
4.3. Performance Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| A Phase | NREM | CAP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) |
| 1 | 82.37 | 84.61 | 82.07 | 0.911 | 86.11 | 92.52 | 66.13 | 0.927 | 73.40 | 70.49 | 74.98 |
| 2 | 77.16 | 75.76 | 77.32 | 0.842 | 79.04 | 88.79 | 55.54 | 0.880 | 70.82 | 64.21 | 73.08 |
| 3 | 79.87 | 73.94 | 80.37 | 0.851 | 80.01 | 83.24 | 73.22 | 0.886 | 73.34 | 40.14 | 83.77 |
| 4 | 79.41 | 85.77 | 78.91 | 0.900 | 85.46 | 87.57 | 82.63 | 0.933 | 77.46 | 76.08 | 77.82 |
| 5 | 82.25 | 84.92 | 81.93 | 0.912 | 85.57 | 82.36 | 94.79 | 0.926 | 80.09 | 77.11 | 81.87 |
| 6 | 83.53 | 81.49 | 83.86 | 0.900 | 80.12 | 71.98 | 98.22 | 0.937 | 75.29 | 49.47 | 91.34 |
| 7 | 80.45 | 93.37 | 79.17 | 0.938 | 80.91 | 75.42 | 92.76 | 0.922 | 72.93 | 47.87 | 83.42 |
| 8 | 76.58 | 83.62 | 75.72 | 0.872 | 81.64 | 86.83 | 70.80 | 0.896 | 72.41 | 64.33 | 76.00 |
| 9 | 84.16 | 83.60 | 84.20 | 0.910 | 70.77 | 62.87 | 86.52 | 0.884 | 81.18 | 37.26 | 92.29 |
| 10 | 79.44 | 57.92 | 82.01 | 0.818 | 77.72 | 74.70 | 83.84 | 0.864 | 77.37 | 24.44 | 90.11 |
| 11 | 80.62 | 72.01 | 81.56 | 0.858 | 68.94 | 68.94 | 68.93 | 0.769 | 80.20 | 48.96 | 91.76 |
| 12 | 84.08 | 82.75 | 84.27 | 0.903 | 85.33 | 96.74 | 67.36 | 0.955 | 86.41 | 82.12 | 88.53 |
| 13 | 85.77 | 76.31 | 87.06 | 0.889 | 76.14 | 96.23 | 35.76 | 0.903 | 73.05 | 66.55 | 75.33 |
| 14 | 83.56 | 87.82 | 82.94 | 0.924 | 85.23 | 86.48 | 81.31 | 0.920 | 78.65 | 74.28 | 80.94 |
| 15 | 84.44 | 73.36 | 86.24 | 0.872 | 74.71 | 97.03 | 17.20 | 0.842 | 81.10 | 70.71 | 88.22 |
| 16 | 77.57 | 60.76 | 79.08 | 0.782 | 74.63 | 83.08 | 63.25 | 0.823 | 76.14 | 22.09 | 94.02 |
| 17 | 78.07 | 61.17 | 84.09 | 0.824 | 73.71 | 73.54 | 74.47 | 0.822 | 44.42 | 10.07 | 99.59 |
| 18 | 72.37 | 58.75 | 78.74 | 0.758 | 85.63 | 90.96 | 72.43 | 0.915 | 61.91 | 49.21 | 76.12 |
| 19 | 74.57 | 55.71 | 83.52 | 0.789 | 53.62 | 48.47 | 78.53 | 0.707 | 43.90 | 25.59 | 87.96 |
| Mean | 80.33 | 75.45 | 81.74 | 0.866 | 78.17 | 81.46 | 71.77 | 0.880 | 72.63 | 52.68 | 84.59 |
| Standard deviation | 3.55 | 11.22 | 2.94 | 0.050 | 7.77 | 12.32 | 19.15 | 0.062 | 10.98 | 20.92 | 7.49 |
| A Phase | NREM | CAP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) |
| 1 | 79.96 | 75.25 | 80.60 | 0.852 | 85.79 | 92.52 | 64.79 | 0.924 | 73.61 | 79.65 | 70.31 |
| 2 | 83.00 | 73.15 | 84.44 | 0.863 | 88.22 | 94.31 | 78.61 | 0.957 | 83.53 | 84.52 | 83.04 |
| 3 | 83.17 | 72.39 | 84.74 | 0.862 | 88.52 | 94.11 | 79.71 | 0.957 | 83.16 | 84.55 | 82.48 |
| 4 | 82.41 | 72.01 | 83.93 | 0.853 | 88.24 | 93.73 | 79.58 | 0.953 | 82.57 | 81.09 | 83.31 |
| 5 | 85.40 | 61.16 | 89.08 | 0.856 | 87.16 | 88.06 | 84.30 | 0.927 | 81.73 | 67.49 | 90.60 |
| 6 | 83.07 | 66.37 | 85.72 | 0.830 | 87.81 | 91.27 | 80.11 | 0.941 | 80.61 | 77.67 | 82.44 |
| 7 | 81.68 | 84.94 | 81.35 | 0.897 | 89.57 | 92.76 | 82.69 | 0.950 | 76.35 | 75.98 | 76.50 |
| 8 | 82.37 | 72.00 | 83.89 | 0.854 | 88.30 | 93.13 | 80.69 | 0.953 | 82.73 | 82.91 | 82.64 |
| 9 | 91.14 | 61.44 | 93.30 | 0.877 | 91.31 | 91.01 | 91.91 | 0.949 | 83.84 | 48.36 | 92.82 |
| 10 | 82.41 | 73.19 | 83.76 | 0.859 | 88.56 | 93.99 | 79.99 | 0.958 | 82.43 | 83.81 | 81.75 |
| 11 | 84.03 | 55.87 | 87.10 | 0.812 | 80.02 | 76.26 | 85.33 | 0.881 | 81.90 | 59.89 | 90.05 |
| 12 | 83.91 | 78.84 | 84.65 | 0.888 | 89.56 | 94.00 | 82.56 | 0.960 | 84.96 | 87.57 | 83.67 |
| 13 | 80.39 | 73.14 | 81.38 | 0.843 | 82.85 | 93.42 | 61.59 | 0.899 | 71.61 | 80.68 | 68.42 |
| 14 | 85.64 | 74.86 | 87.21 | 0.885 | 90.42 | 96.12 | 72.57 | 0.958 | 82.62 | 81.89 | 83.01 |
| 15 | 77.31 | 61.99 | 79.79 | 0.785 | 81.46 | 95.80 | 44.47 | 0.905 | 73.16 | 72.59 | 73.55 |
| 16 | 78.81 | 52.75 | 81.16 | 0.749 | 72.46 | 81.56 | 60.20 | 0.825 | 73.07 | 45.64 | 82.14 |
| 17 | 77.76 | 52.90 | 86.63 | 0.775 | 73.54 | 71.19 | 83.55 | 0.841 | 60.86 | 41.45 | 92.03 |
| 18 | 62.02 | 51.49 | 66.94 | 0.628 | 78.41 | 86.46 | 58.43 | 0.839 | 67.94 | 71.68 | 63.74 |
| 19 | 69.23 | 57.01 | 75.04 | 0.703 | 79.60 | 86.38 | 46.75 | 0.763 | 69.43 | 70.16 | 67.65 |
| Mean | 80.72 | 66.88 | 83.19 | 0.825 | 84.83 | 89.79 | 73.57 | 0.913 | 77.69 | 72.51 | 80.53 |
| Standard deviation | 6.11 | 9.57 | 5.40 | 0.068 | 5.54 | 6.62 | 13.14 | 0.056 | 6.64 | 13.63 | 8.22 |
| A Phase | NREM | CAP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) |
| 1 | 81.96 | 76.33 | 82.72 | 0.866 | 79.01 | 77.85 | 82.63 | 0.842 | 75.33 | 51.72 | 88.20 |
| 2 | 45.50 | 91.34 | 40.19 | 0.757 | 72.28 | 67.82 | 83.01 | 0.802 | 67.87 | 65.70 | 68.61 |
| 3 | 76.09 | 59.01 | 77.53 | 0.750 | 70.74 | 62.91 | 87.15 | 0.799 | 69.35 | 27.51 | 82.49 |
| 4 | 64.14 | 85.15 | 62.47 | 0.813 | 81.54 | 73.37 | 92.49 | 0.877 | 80.29 | 68.81 | 83.22 |
| 5 | 85.23 | 76.47 | 86.56 | 0.886 | 74.47 | 68.42 | 93.61 | 0.845 | 81.46 | 58.82 | 95.55 |
| 6 | 81.56 | 73.53 | 82.83 | 0.853 | 74.58 | 66.45 | 92.64 | 0.849 | 76.49 | 50.60 | 92.57 |
| 7 | 80.98 | 84.16 | 80.67 | 0.890 | 76.20 | 67.39 | 95.16 | 0.871 | 73.32 | 47.36 | 84.18 |
| 8 | 37.51 | 92.57 | 30.75 | 0.752 | 77.92 | 77.00 | 79.85 | 0.846 | 62.00 | 65.15 | 60.58 |
| 9 | 91.57 | 51.69 | 94.47 | 0.887 | 67.29 | 52.40 | 96.90 | 0.846 | 82.17 | 24.41 | 96.78 |
| 10 | 79.35 | 46.64 | 83.25 | 0.768 | 80.56 | 76.09 | 89.61 | 0.877 | 74.29 | 40.10 | 82.51 |
| 11 | 82.56 | 59.90 | 85.03 | 0.820 | 75.35 | 75.52 | 75.10 | 0.811 | 79.77 | 47.98 | 91.53 |
| 12 | 78.32 | 78.50 | 78.29 | 0.846 | 82.55 | 83.13 | 81.64 | 0.878 | 82.94 | 67.01 | 90.81 |
| 13 | 76.16 | 71.82 | 76.75 | 0.801 | 82.56 | 84.85 | 77.95 | 0.867 | 69.84 | 62.84 | 72.30 |
| 14 | 85.21 | 69.26 | 87.54 | 0.886 | 73.76 | 73.37 | 74.99 | 0.820 | 76.36 | 45.76 | 92.35 |
| 15 | 49.03 | 92.14 | 42.07 | 0.795 | 76.26 | 85.43 | 52.64 | 0.769 | 71.24 | 85.84 | 61.24 |
| 16 | 65.68 | 74.02 | 64.93 | 0.753 | 77.06 | 67.15 | 90.37 | 0.832 | 74.55 | 53.99 | 81.35 |
| 17 | 74.43 | 54.69 | 81.47 | 0.762 | 54.37 | 44.46 | 96.32 | 0.788 | 41.45 | 5.75 | 98.68 |
| 18 | 59.01 | 52.42 | 62.09 | 0.614 | 70.78 | 62.19 | 92.03 | 0.832 | 52.15 | 27.95 | 79.15 |
| 19 | 57.16 | 89.38 | 41.89 | 0.727 | 49.70 | 41.64 | 88.56 | 0.702 | 39.15 | 22.14 | 80.00 |
| Mean | 71.13 | 72.58 | 70.60 | 0.801 | 73.53 | 68.81 | 85.40 | 0.829 | 70.00 | 48.39 | 83.27 |
| Standard deviation | 14.77 | 14.45 | 18.44 | 0.069 | 8.43 | 11.96 | 10.31 | 0.043 | 12.49 | 19.36 | 10.90 |
| A Phase | NREM | CAP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) | AUC | Acc (%) | Sen (%) | Spe (%) |
| 1 | 85.22 | 79.66 | 85.97 | 0.907 | 89.84 | 88.64 | 93.59 | 0.956 | 79.83 | 69.60 | 85.41 |
| 2 | 85.67 | 81.82 | 86.24 | 0.906 | 93.73 | 94.75 | 92.11 | 0.979 | 84.75 | 81.87 | 86.17 |
| 3 | 85.17 | 61.87 | 87.14 | 0.823 | 82.36 | 77.93 | 91.67 | 0.925 | 78.34 | 40.26 | 90.31 |
| 4 | 84.90 | 82.67 | 85.22 | 0.898 | 91.71 | 94.55 | 87.22 | 0.975 | 84.47 | 85.50 | 83.96 |
| 5 | 88.07 | 76.81 | 89.77 | 0.923 | 89.24 | 86.89 | 96.70 | 0.964 | 85.88 | 72.02 | 94.52 |
| 6 | 83.51 | 79.76 | 84.11 | 0.886 | 89.93 | 88.53 | 93.05 | 0.956 | 82.25 | 76.57 | 85.78 |
| 7 | 84.01 | 91.77 | 83.24 | 0.946 | 95.53 | 96.17 | 94.16 | 0.984 | 78.99 | 81.96 | 77.74 |
| 8 | 73.23 | 90.40 | 71.12 | 0.898 | 85.21 | 87.65 | 80.12 | 0.924 | 69.36 | 80.78 | 64.21 |
| 9 | 91.24 | 78.08 | 92.20 | 0.939 | 93.20 | 93.34 | 92.92 | 0.967 | 84.68 | 54.68 | 92.28 |
| 10 | 83.80 | 48.49 | 88.01 | 0.816 | 95.48 | 94.73 | 97.03 | 0.986 | 75.91 | 50.89 | 81.93 |
| 11 | 83.58 | 66.57 | 85.43 | 0.851 | 89.80 | 86.86 | 93.95 | 0.952 | 77.34 | 66.64 | 81.30 |
| 12 | 85.36 | 84.20 | 85.53 | 0.919 | 90.71 | 93.12 | 86.91 | 0.970 | 82.83 | 78.04 | 85.20 |
| 13 | 84.87 | 79.22 | 85.65 | 0.897 | 89.67 | 96.52 | 75.86 | 0.951 | 75.15 | 78.88 | 73.83 |
| 14 | 86.78 | 87.70 | 86.65 | 0.938 | 95.05 | 96.43 | 90.69 | 0.982 | 84.71 | 84.50 | 84.83 |
| 15 | 78.84 | 73.82 | 79.65 | 0.838 | 82.34 | 94.42 | 51.12 | 0.923 | 80.73 | 79.27 | 81.74 |
| 16 | 87.32 | 55.03 | 90.23 | 0.842 | 82.53 | 77.42 | 89.42 | 0.906 | 78.25 | 32.01 | 93.56 |
| 17 | 83.58 | 70.06 | 88.40 | 0.873 | 73.59 | 68.82 | 93.89 | 0.921 | 67.52 | 50.83 | 94.35 |
| 18 | 71.87 | 83.77 | 66.30 | 0.842 | 77.49 | 76.48 | 80.01 | 0.877 | 72.72 | 76.24 | 68.78 |
| 19 | 69.26 | 82.39 | 63.03 | 0.821 | 80.97 | 83.21 | 70.14 | 0.858 | 75.60 | 83.17 | 57.38 |
| Mean | 82.96 | 76.53 | 83.36 | 0.882 | 87.81 | 88.24 | 86.87 | 0.945 | 78.91 | 69.67 | 82.28 |
| Standard deviation | 5.54 | 11.24 | 7.75 | 0.042 | 6.18 | 7.88 | 11.04 | 0.036 | 5.17 | 15.63 | 9.91 |
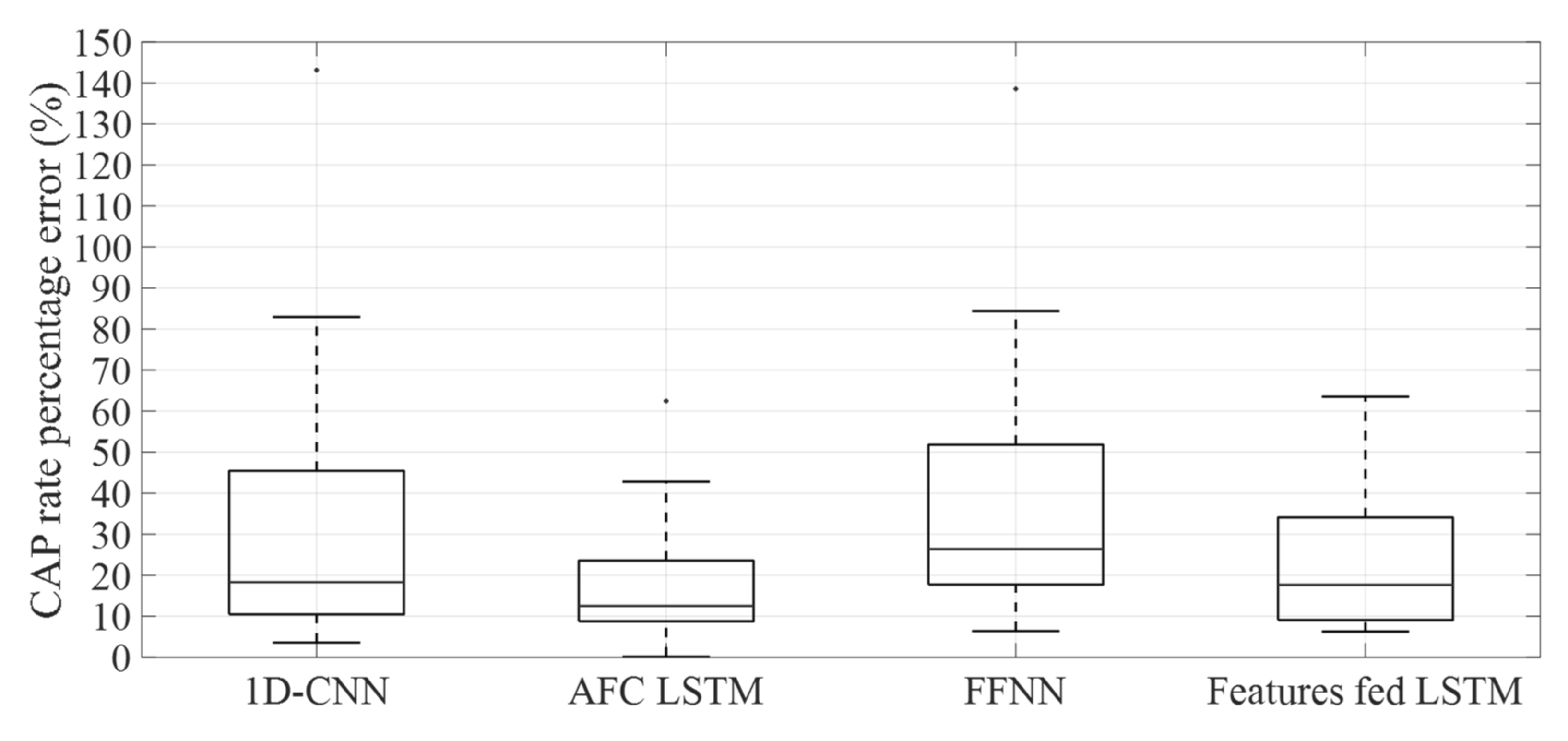
| Model Based on the 1D-CNN | Model Based on the AFC LSTM | Model Based on the FFNN | Model Based on the LSTM Fed with Features | |||||
|---|---|---|---|---|---|---|---|---|
| Subject | CAP rate error (%) | CAP rate percentage error | CAP rate error (%) | CAP rate percentage error | CAP rate error (%) | CAP rate percentage error | CAP rate error (%) | CAP rate percentage error |
| 1 | 5.94 | 12.64 | 13.60 | 28.94 | −5.59 | 11.89 | 2.93 | 6.23 |
| 2 | 12.01 | 25.55 | 5.54 | 11.79 | 39.67 | 84.40 | 5.30 | 11.28 |
| 3 | −1.68 | 3.57 | 6.60 | 14.04 | 8.08 | 17.19 | −4.56 | 9.70 |
| 4 | 22.45 | 47.77 | 4.14 | 8.81 | 25.09 | 53.38 | 8.29 | 17.64 |
| 5 | 14.82 | 31.53 | −5.60 | 11.91 | −2.99 | 6.36 | −4.14 | 8.81 |
| 6 | −7.12 | 15.15 | 3.25 | 6.91 | −4.97 | 10.57 | 4.87 | 10.36 |
| 7 | 3.50 | 7.45 | 13.39 | 28.49 | 9.91 | 21.09 | 15.82 | 33.66 |
| 8 | 7.54 | 16.04 | 6.48 | 13.79 | 34.82 | 74.09 | 29.84 | 63.49 |
| 9 | 2.16 | 4.60 | −5.87 | 12.49 | −9.11 | 19.38 | −3.67 | 7.81 |
| 10 | −4.72 | 10.04 | 7.09 | 15.09 | 11.51 | 24.49 | 8.94 | 19.02 |
| 11 | −11.86 | 25.23 | −0.06 | 0.13 | −10.94 | 23.28 | 13.00 | 27.66 |
| 12 | −5.47 | 11.64 | 8.08 | 17.19 | −4.76 | 10.13 | 3.52 | 7.49 |
| 13 | 2.35 | 5.00 | 20.13 | 42.83 | 18.42 | 39.19 | 16.09 | 34.23 |
| 14 | 8.60 | 18.30 | 4.10 | 8.72 | −12.40 | 26.38 | 6.39 | 13.60 |
| 15 | −18.04 | 38.38 | −2.98 | 6.34 | 22.13 | 47.09 | −3.93 | 8.36 |
| 16 | −26.28 | 55.91 | −4.49 | 9.55 | 20.77 | 44.19 | −17.54 | 37.32 |
| 17 | −67.26 | 143.11 | −29.35 | 62.45 | −65.13 | 138.57 | −17.61 | 37.47 |
| 18 | −22.98 | 48.89 | 0.71 | 1.51 | −21.75 | 46.28 | 17.29 | 36.79 |
| 19 | −38.97 | 82.91 | −12.07 | 25.68 | −27.92 | 59.40 | 10.94 | 23.28 |
| Mean | - | 31.77 | - | 17.19 | - | 39.86 | - | 21.80 |
| Median | −1.68 | 18.30 | 4.10 | 12.49 | −2.99 | 26.38 | 5.30 | 17.64 |
| Standard deviation | - | 33.29 | - | 14.71 | - | 31.79 | - | 14.96 |
References
- Berry, R.; Brooks, R.; Gamaldo, C.; Harding, S.; Lloyd, R.; Marcus, C.; Vaughn, B. The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specifications; American Academy of Sleep Medicine: Darien, IL, USA, 2017. [Google Scholar]
- Kubicki, S.; Herrmann, W. The Future of Computer-Assisted Investigation of the Polysomnogram: Sleep Microstructure. J. Clin. Neurophysiol. 1996, 13, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Terzano, M.; Parrino, L. Origin and Significance of the Cyclic Alternating Pattern (CAP). Sleep Med. Rev. 2000, 4, 101–123. [Google Scholar] [CrossRef] [PubMed]
- Terzano, M.; Parrino, L.; Sherieri, A.; Chervin, R.; Chokroverty, S.; Guilleminault, C.; Hirshkowitz, M.; Mahowald, M.; Moldofsky, H.; Rosa, A.; et al. Atlas, Rules, and Recording Techniques for the Scoring of Cyclic Alternating Pattern (CAP) in Human Sleep. Sleep Med. 2001, 2, 537–553. [Google Scholar] [CrossRef]
- Halász, P.; Terzano, M.; Parrino, L.; Bódizs, R. The Nature of Arousal in Sleep. J. Sleep Res. 2004, 13, 1–23. [Google Scholar] [CrossRef]
- Parrino, L.; Ferri, R.; Bruni, O.; Terzano, M. Cyclic Alternating Pattern (CAP): The Marker of Sleep Instability. Sleep Med. Rev. 2012, 16, 27–45. [Google Scholar] [CrossRef]
- Terzano, M.; Parrino, L. Clinical Applications of Cyclic Alternating Pattern. Physiol. Behav. 1993, 54, 807–813. [Google Scholar] [CrossRef]
- Parrino, L.; Milioli, G.; Melpignano, A.; Trippi, I. The Cyclic Alternating Pattern and the Brain-Body-Coupling during Sleep. Epileptologie 2016, 33, 150–160. [Google Scholar]
- Terzano, M.; Parrino, L.; Boselli, M.; Spaggiari, M.; Di Giovanni, G. Polysomnographic Analysis of Arousal Responses in Obstructive Sleep Apnea Syndrome by Means of the Cyclic Alternating Pattern. J. Clin. Neurophysiol. 1996, 13, 145–155. [Google Scholar] [CrossRef]
- Largo, R.; Lopes, M.; Spruyt, K.; Guilleminault, C.; Wang, Y.; Rosa, A. Visual and Automatic Classification of the Cyclic Alternating Pattern in Electroencephalography during Sleep. Braz. J. Med. Biol. Res. 2019, 52, e8059. [Google Scholar] [CrossRef]
- Rosa, A.; Alves, G.; Brito, M.; Lopes, M.; Tufik, S. Visual and Automatic Cyclic Alternating Pattern (CAP) Scoring: Inter-Rater Reliability Study. Arq. Neuro-Psiquiatr. 2006, 64, 578–581. [Google Scholar] [CrossRef] [Green Version]
- Mendez, M.; Alba, A.; Chouvarda, I.; Milioli, G.; Grassi, A.; Terzano, M.; Parrino, L. On separability of A-phases during the cyclic alternating pattern. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 2253–2256. [Google Scholar]
- Hartmann, S.; Baumert, M. Automatic A-Phase Detection of Cyclic Alternating Patterns in Sleep Using Dynamic Temporal Information. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1695–1703. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, S.; Mendonça, F.; Ravelo-García, A.; Juliá-Serdá, G.; Morgado-Dias, F. Multi-Objective Hyperparameter Optimization of Convolutional Neural Network for Obstructive Sleep Apnea Detection. IEEE Access 2020, 8, 129586–129599. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D. 1D Convolutional Neural Networks and Applications: A Survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Mendonça, F.; Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. A Portable Wireless Device for Cyclic Alternating Pattern Estimation from an EEG Monopolar Derivation. Entropy 2019, 21, 1203. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Obonyo, E. Convolutional Long Short-Term Memory Model for Recognizing Construction Workers’ Postures from Wearable Inertial Measurement Units. Adv. Eng. Inform. 2020, 46, 101177. [Google Scholar] [CrossRef]
- Mendonça, F.; Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. On the Use of Patterns Obtained from LSTM and Feature-Based Methods for Time Series Analysis: Application in Automatic Classification of the CAP A Phase Subtypes. J. Neural Eng. 2020, 18, 036004. [Google Scholar] [CrossRef]
- Hartmann, S.; Baumert, M. Improved A-Phase Detection of Cyclic Alternating Pattern Using Deep Learning. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23 July 2019. [Google Scholar]
- Mariani, S.; Bianchi, A.; Manfredini, E.; Rosso, V.; Mendez, M.; Parrino, L.; Matteucci, M.; Grassi, A.; Cerutti, S.; Terzano, M. Automatic Detection of A Phases of the Cyclic Alternating Pattern during Sleep. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 5085–5088. [Google Scholar]
- Barcaro, U.; Bonanni, E.; Maestri, M.; Murri, L.; Parrino, L.; Terzano, M. A General Automatic Method for the Analysis of NREM Sleep Microstructure. Sleep Med. 2004, 5, 567–576. [Google Scholar] [CrossRef]
- Largo, R.; Munteanu, C.; Rosa, A. CAP Event Detection by Wavelets and GA Tuning. In Proceedings of the IEEE International Workshop on Intelligent Signal Processing, Faro, Portugal, 1–3 September 2005; pp. 44–48. [Google Scholar]
- Niknazar, H.; Seifpour, S.; Mikaili, M.; Nasrabadi, A.; Banaraki, A. A Novel Method to Detect the A Phases of Cyclic Alternating Pattern (CAP) Using Similarity Index. In Proceedings of the 2015 23rd Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015; pp. 67–71. [Google Scholar]
- Mariani, S.; Manfredini, E.; Rosso, V.; Mendez, M.; Bianchi, A.; Matteucci, M.; Terzano, M.; Cerutti, S.; Parrino, L. Characterization of A Phases during the Cyclic Alternating Pattern of Sleep. Clin. Neurophysiol. 2011, 122, 2016–2024. [Google Scholar] [CrossRef] [Green Version]
- Mariani, S.; Grassi, A.; Mendez, M.; Parrino, L.; Terzano, M.; Bianchi, A. Automatic Detection of CAP on Central and Fronto-Central EEG Leads via Support Vector Machines. In Proceedings of the 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August 2011. [Google Scholar]
- Mariani, S.; Manfredini, E.; Rosso, V.; Grassi, A.; Mendez, M.; Alba, A.; Matteucci, M.; Parrino, L.; Terzano, M.; Cerutti, S.; et al. Efficient Automatic Classifiers for the Detection of A Phases of the Cyclic Alternating Pattern in Sleep. Med. Biol. Eng. Comput. 2012, 50, 359–372. [Google Scholar] [CrossRef]
- Mariani, S.; Grassi, A.; Mendez, M.; Milioli, G.; Parrino, L.; Terzano, M.; Bianchi, A. EEG Segmentation for Improving Automatic CAP Detection. Clin. Neurophysiol. 2013, 124, 1815–1823. [Google Scholar] [CrossRef]
- Mendonça, F.; Fred, A.; Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. Automatic Detection of Cyclic Alternating Pattern. Neural Comput. Appl. 2018, 1–11. [Google Scholar] [CrossRef]
- Mostafa, S.; Mendonça, F.; Ravelo-García, A.; Morgado-Dias, F. Combination of Deep and Shallow Networks for Cyclic Alternating Patterns Detection. In Proceedings of the 2018 13th APCA International Conference on Automatic Control and Soft Computing (CONTROLO), Ponta Delgada, Portugal, 4 June 2018. [Google Scholar]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, M.; Ivanov, P.; Mark, R.; Mietus, J.; Moody, G.; Peng, C.; Stanley, H. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Digital Signal Processing Committee, I. Programs for Digital Signal Processing; IEEE Press: New York, NY, USA, 1979. [Google Scholar]
- Phillips, C.; Parr, J.; Riskin, E. Signals, Systems, and Transforms; Pearson: London, UK, 2013. [Google Scholar]
- Muralidharan, K. A Note on Transformation, Standardization and Normalization. IUP J. Oper. Manag. 2010, 9, 116–122. [Google Scholar]
- Urigüen, J.; Zapirain, B. EEG Artifact Removal—State-of-the-Art and Guidelines. J. Neural Eng. 2015, 12, 031001. [Google Scholar] [CrossRef] [PubMed]
- Ortigueira, M. Processamento Digital de Sinais, 1st ed.; Fundação Calouste Gulbenkian: Lisboa, Portugal, 2005. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature Selection Based on Mutual Information Criteria of Max-Dependency, Max-Relevance, and Minredundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kiranyaz, S.; Ince, T.; Hamila, R.; Gabbouj, M. Convolutional Neural Networks for Patient-Specific ECG Classification. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25 August 2015. [Google Scholar]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-Time Patient-Specific ECG Classification by 1-D Convolutional Neural Networks. IEEE Trans. Biomed. Eng. 2016, 63, 664–675. [Google Scholar] [CrossRef]
- Mendonça, F.; Mostafa, S.; Morgado-Dias, F.; Juliá-Serdá, G.; Ravelo-García, A. A Method for Sleep Quality Analysis Based on CNN Ensemble With Implementation in a Portable Wireless Device. IEEE Access 2020, 8, 158523–158537. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sackett, D.; Haynes, R.; Guyatt, G.; Tugwell, P. Clinical Epidemiology: A Basic Science for Clinical Medicine, 2nd ed.; Lippincott Williams and Wilkins: Philadelphia, PL, USA, 1991. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Mostafa, S.; Baptista, D.; Ravelo-García, A.; Juliá-Serdá, G.; Morgado-Dias, F. Greedy Based Convolutional Neural Network Optimization for Detecting Apnea. Comput. Methods Programs Biomed. 2020, 197, 105640. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, R.; Nishio, M.; Do, R.; Togashi, K. Convolutional Neural Networks: An Overview and Application in Radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guidici, D.; Clark, M. One-Dimensional Convolutional Neural Network Land-Cover Classification of Multi-Seasonal Hyperspectral Imagery in the San Francisco Bay Area, California. Remote Sens. 2017, 9, 629. [Google Scholar] [CrossRef] [Green Version]
- Ng, W.; Minasny, B.; Montazerolghaem, M.; Padarian, J.; Ferguson, R.; Bailey, S.; McBratney, A. Convolutional Neural Network for Simultaneous Prediction of Several Soil Properties Using Visible/near-Infrared, Mid-Infrared, and Their Combined Spectra. Geoderma 2019, 352, 251–267. [Google Scholar] [CrossRef]
- Thai-Nghe, N.; Gantner, Z.; Schmidt-Thieme, L. Cost-Sensitive Learning Methods for Imbalanced Data. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18 July 2010. [Google Scholar]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection; ACM: Montreal, QC, Canada, 1995. [Google Scholar]
- Yadav, A.; Jha, C.; Sharan, A. Optimizing LSTM for Time Series Prediction in Indian Stock Market. Procedia Comput. Sci. 2020, 167, 2091–2100. [Google Scholar] [CrossRef]
- Shen, H.; Ran, F.; Xu, M.; Guez, A.; Li, A.; Guo, A. An Automatic Sleep Stage Classification Algorithm Using Improved Model Based Essence Features. Sensors 2020, 20, 4677. [Google Scholar] [CrossRef]


| Measure | Mean | Range |
|---|---|---|
| Age (years) | 40.58 | 23–78 |
| REM time (seconds) | 5652.63 | 480–11,430 |
| NREM time (seconds) | 20,505.79 | 13,260–27,180 |
| A phase time (seconds) | 4059.21 | 1911–10,554 |
| CAP cycles time (seconds) | 10,323.95 | 5000–23,306 |
| CAP rate (%) | 49.16 | 29–86 |
| HOSA-1D-CNN (Data, Gmax, Mmax, Mstart, MULmax, Nmax, Nstart, Nstep, Omax, tr) G = [1, 2, …, Gmax] O = [0, 1, 3, 5, …, Omax] K = 2M where Mstart ≤ M ≤ Mmax N = [Nstart, Nstart + Nstep, …, Nmax] for g = 1 to length (G) | for o = 1 to length (O) | | for k = 1 to length (K) | | | for n = 1 to length (N) | | | | if O (o) > 0 | | | | | W = [2 × O (1) + 1, 2 × O (2) + 1, …, 2 × O (length (O)) + 1] | | | | | Ap = [W (1), W (floor (W/2 + 1)), W (length (W))] | | | | else | | | | | Ap = 1 | | | | for a = 1 to length (Ap) | | | | | Net ← Ipt (Data, O (o), Ap (a)) | | | | | for z = 1 to g | | | | | if z == 1 | | | | | | mul = 1 | | | | | | Netg,o,k,n,a,z,mul:MULmax ← Net + GL (K (k)) | | | | | | kz,mul:MULmax = K (k) | | | | | else | | | | | | for mul = 1 to MULmax | | | | | | | kz,mul = mul × kz-1,mul | | | | | | | Netg,o,k,n,a,z,mul ← Netg,o,k,n,a,z-1,mul + GL (kz,mul) | | | | Netg,o,k,n,a,z,mul ← Net g,o,k,n,a,z,mul + De (N (n)) + De (2) | | | | AUCg,o,k,n,a,z,mul ← test (train (Netg,o,k,n,a,z,mul)) | AUCg,o,k,n,a,z,mul,max = max (AUCg,o,k,n,a,z,mul)|for all o,k,n,a,mul | if g > 1 | | if AUCg,o,k,n,a,z,mul,max–AUCg-1,o,k,n,a,z,mul,max ≤ tr | | | if AUCg,o,k,n,a,z,mul,max > AUCg-1,o,k,n,a,z,mul,max | | | | BestNet = Netg,o,k,n,a,z,mul|AUCg,o,k,n,a,z,mul,max | | | else | | | | BestNet = Netg−1,o,k,n,a,z,mul|AUCg-1,o,k,n,a,z,mul,max | | | break | | else | | | BestNet = Netg,o,k,n,a,z,mul|AUCg,o,k,n,a,z,mul,max | | | return BestNet | HOSA-LSTM (Data, Grmax, Nhmax, Nhstart, Nhstep, Tmax, Tstart, Tstep, tr) Gr = [1, 2, …, Grmax] T = [Tstart, Tstart + Tstep, …, Tmax] Nh = [Nhstart, Nhstart + Nhstep, …, Nhmax] L = [LSTM, BLSTM] | for t = 1 to length (T) | | for n = 1 to length (Nh) | | | for g = 1 to length (Gr) | | | | for l = 1 to length (L) | | | | | Layer = L (l) | | | | | for m = 1 to 4 | | | | | | Net0,l,t,n,0,m ← Ip (Data, T (t)) | | | | | | for z = 1 to g | | | | | | | Netz,l,t,n,0,m ← Netz-1,l,t,n,0,m + Layer (Nh (n)) | | | | | | if m == 1 | | | | | | | Nprev = floor (Nh (n)/2 + 1/2) | | | | | | | Netg,l,t,n,1,m ← Netg,l,t,n,0,m + De (Nprev) + De (2) | | | | | | else | | | | | | | if m == 2 | | | | | | | | Nprev = Nh (n) | | | | | | | | Netg,l,t,n,1,m ← Netg,l,t,n,0,m + De (Nprev) + De (2) | | | | | | | else | | | | | | | | if m == 3 | | | | | | | | | Nprev = Nh (n) × 2 | | | | | | | | | Netg,l,t,n,1,m ← Netg,l,t,n,0,m + De (Nprev) + De (2) | | | | | | | | else | | | | | | | | | Netg,l,t,n,1,m ← Netg,l,t,n,0,m + De (2) | | | | | | AUCg,l,t,n,m ← test (train (Netg,l,t,n,1,m)) | | | AUCg,l,t,n,m,max = max (AUCg,l,t,n,m)|for all l,m | | | if g > 1 | | | | if AUCg,l,t,n,m,max–AUCg-1,l,t,n,m,max ≤ tr | | | | | if AUCg,l,t,n,m,max > AUCg-1,l,t,n,m,max | | | | | | BestNett,n = Netg,l,t,n,1,m|AUCg,l,t,n,m,max | | | | | else | | | | | | BestNett,n = Netg-1,l,t,n,1,m|AUCg-1,l,t,n,m,max | | | | | break | | | | else | | | | | BestNett,n = Netg-1,l,t,n,1,m|AUCg-1,l,t,n,m,max | | | | return BestNett=1:length (T), n=1:length(Nh) |
| Estimation | Metric | FFNN | 1D-CNN | AFC LSTM | Features Fed LSTM |
|---|---|---|---|---|---|
| A phase | Acc (%) Sen (%) Spe (%) AUC | 71.13 ± 14.77 72.58 ± 14.45 70.60 ± 18.44 0.801 ± 0.069 | 80.33 ± 3.55 (0.001 *) 75.45 ± 11.22 (0.948) 81.74 ± 2.94 (<0.001 *) 0.866 ± 0.050 (0.078) | 80.72 ± 6.11 (0.004 *) 66.88 ± 9.57 (0.198) 83.19 ± 5.40 (0.018 *) 0.825 ± 0.068 (<0.001 *) | 82.96 ± 5.54 (<0.001 *) 76.53 ± 11.24 (0.098) 83.36 ± 7.75 (<0.001 *) 0.882 ± 0.042 (<0.001 *) |
| NREM | Acc (%) Sen (%) Spe (%) AUC | 73.53 ± 8.43 68.81 ± 11.96 85.40 ± 10.31 0.829 ± 0.043 | 78.17 ± 7.77 (<0.001 *) 81.46 ± 12.32 (<0.001 *) 71.77 ± 19.15 (1.000) 0.880 ± 0.062 (<0.001 *) | 84.83 ± 5.54 (0.004 *) 89.79 ± 6.62 (<0.001 *) 73.57 ± 13.14 (1.000) 0.913 ± 0.056 (<0.001 *) | 87.81 ± 6.18 (<0.001 *) 88.24 ± 7.88 (<0.001 *) 86.87 ± 11.04 (0.271) 0.945 ± 0.036 (<0.001 *) |
| CAP cycles | Acc (%) Sen (%) Spe (%) | 70.00 ± 12.49 48.39 ± 19.36 83.27 ± 10.90 | 72.63 ± 10.98 (<0.001 *) 52.68 ± 20.92 (<0.001 *) 84.59 ± 7.49 (0.948) | 77.69 ± 6.64 (0.003 *) 72.51 ± 13.63 (0.067) 80.53 ± 8.22 (0.384) | 78.91 ± 5.17 (<0.001 *) 69.67 ± 15.63 (<0.001 *) 82.28 ± 9.91 (0.779) |
| CAP rate | Percentage error(%) | 39.86 ± 31.79 | 31.77 ± 33.29 | 17.19 ± 14.71 | 21.80 ± 14.96 |
| Work | Number of Examined Subjects | Method | Acc (%) | Sen (%) | Spe (%) | Average * (%) |
|---|---|---|---|---|---|---|
| [29] | 13 | EEG signal fed a DSAE | 67 | 55 | 69 | 64 |
| [24] | 8 | Differential variance classified by a threshold | 72 | 52 | 76 | 67 |
| [16] | 15 | EEG signal fed an LSTM | 76 | 75 | 77 | 76 |
| [28] | 13 | Auto-covariance, Shannon entropy, TEO, and frequency domain features fed an FFNN | 79 | 76 | 80 | 78 |
| [22] | 12 | Moving averages classified by a threshold | 81 | 85 | 78 | 81 |
| [23] | 6 | Similarity analysis with reference windows | 81 | 76 | 81 | 79 |
| [20] | 4 | Band descriptors, Hjorth descriptors, and differential variance classified by an FFNN | 82 | 76 | 83 | 80 |
| [19] | 15 | Entropy-based features, TEO, differential variance, and frequency-based features fed an LSTM | 83 | 76 | 84 | 81 |
| [21] | 10 | Band descriptors classified by a threshold | 84 | - | - | - |
| [25] | 4 | Band descriptors, Hjorth descriptors, and differential variance classified by an SVM | 84 | 74 | 86 | 81 |
| [26] | 8 | Band descriptors, Hjorth descriptors, and differential variance classified by an LDA | 85 | 73 | 87 | 82 |
| [27] | 16 | Variable windows fed to three discriminant functions | 86 | 67 | 90 | 81 |
| Proposed work– 1D-CNN | 19 | Overlapping windows fed a 1D-CNN | 80 | 76 | 82 | 79 |
| Proposed work–AFC LSTM | 19 | Pre-processed EEG signal fed an LSTM | 81 | 67 | 83 | 77 |
| Proposed work–FFNN | 19 | Amplitude, frequency, and amplitude-frequency-based features fed an FFNN | 71 | 73 | 70 | 71 |
| Proposed work– feature-based LSTM | 19 | Amplitude, frequency, and amplitude-frequency-based features fed an LSTM | 83 | 77 | 83 | 81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendonça, F.; Mostafa, S.S.; Freitas, D.; Morgado-Dias, F.; Ravelo-García, A.G. Heuristic Optimization of Deep and Shallow Classifiers: An Application for Electroencephalogram Cyclic Alternating Pattern Detection. Entropy 2022, 24, 688. https://doi.org/10.3390/e24050688
Mendonça F, Mostafa SS, Freitas D, Morgado-Dias F, Ravelo-García AG. Heuristic Optimization of Deep and Shallow Classifiers: An Application for Electroencephalogram Cyclic Alternating Pattern Detection. Entropy. 2022; 24(5):688. https://doi.org/10.3390/e24050688
Chicago/Turabian StyleMendonça, Fábio, Sheikh Shanawaz Mostafa, Diogo Freitas, Fernando Morgado-Dias, and Antonio G. Ravelo-García. 2022. "Heuristic Optimization of Deep and Shallow Classifiers: An Application for Electroencephalogram Cyclic Alternating Pattern Detection" Entropy 24, no. 5: 688. https://doi.org/10.3390/e24050688
APA StyleMendonça, F., Mostafa, S. S., Freitas, D., Morgado-Dias, F., & Ravelo-García, A. G. (2022). Heuristic Optimization of Deep and Shallow Classifiers: An Application for Electroencephalogram Cyclic Alternating Pattern Detection. Entropy, 24(5), 688. https://doi.org/10.3390/e24050688










