Optimal Population Coding for Dynamic Input by Nonequilibrium Networks
Abstract
:1. Introduction
2. Model and Analysis
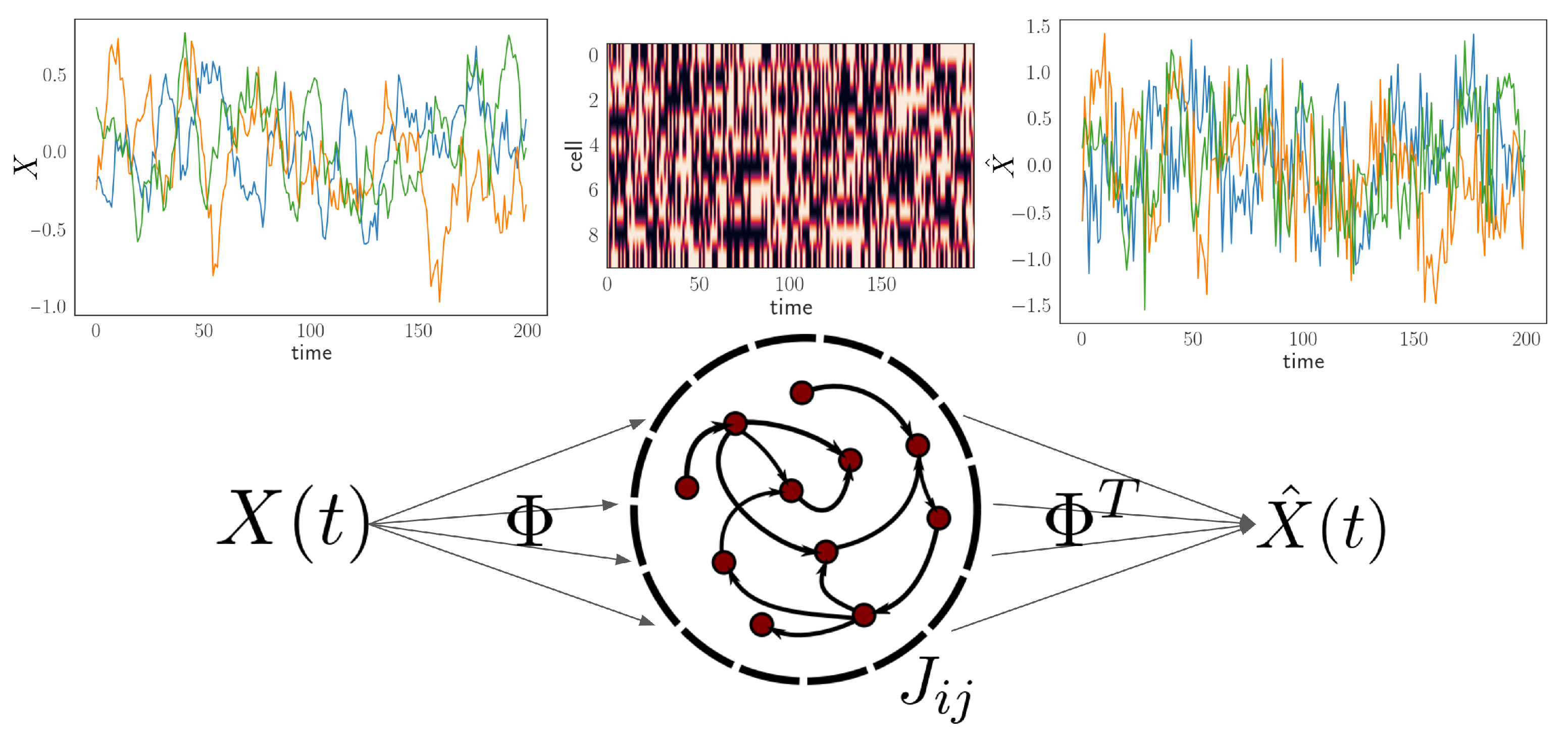
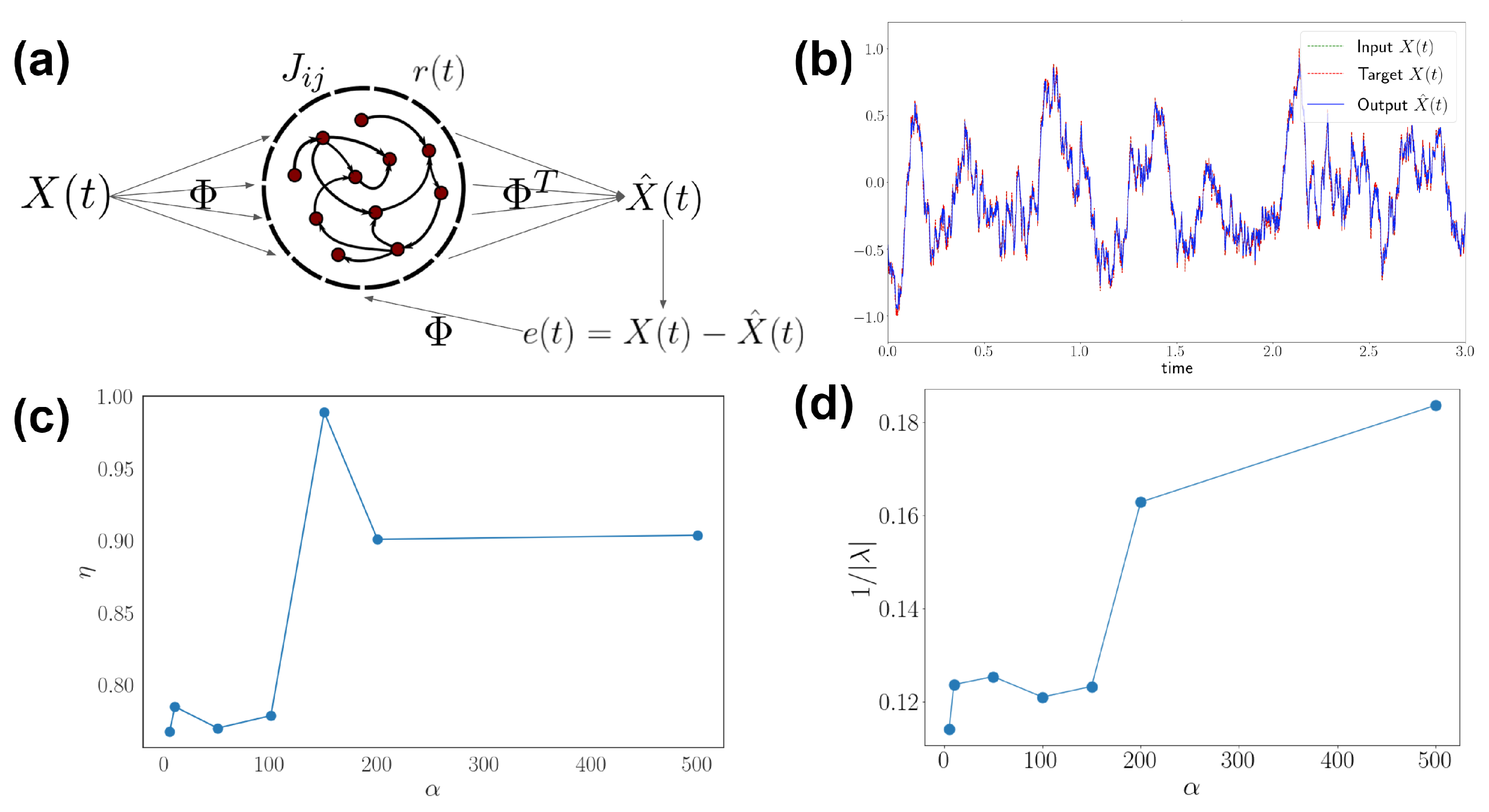
2.1. Neural Encoding and Decoding Framework
2.2. Nonequilibrium Network and Inference Methods
2.3. Protocol of Network Simulation and Training
2.4. Analysis of the Optimal Population Coding
3. Results
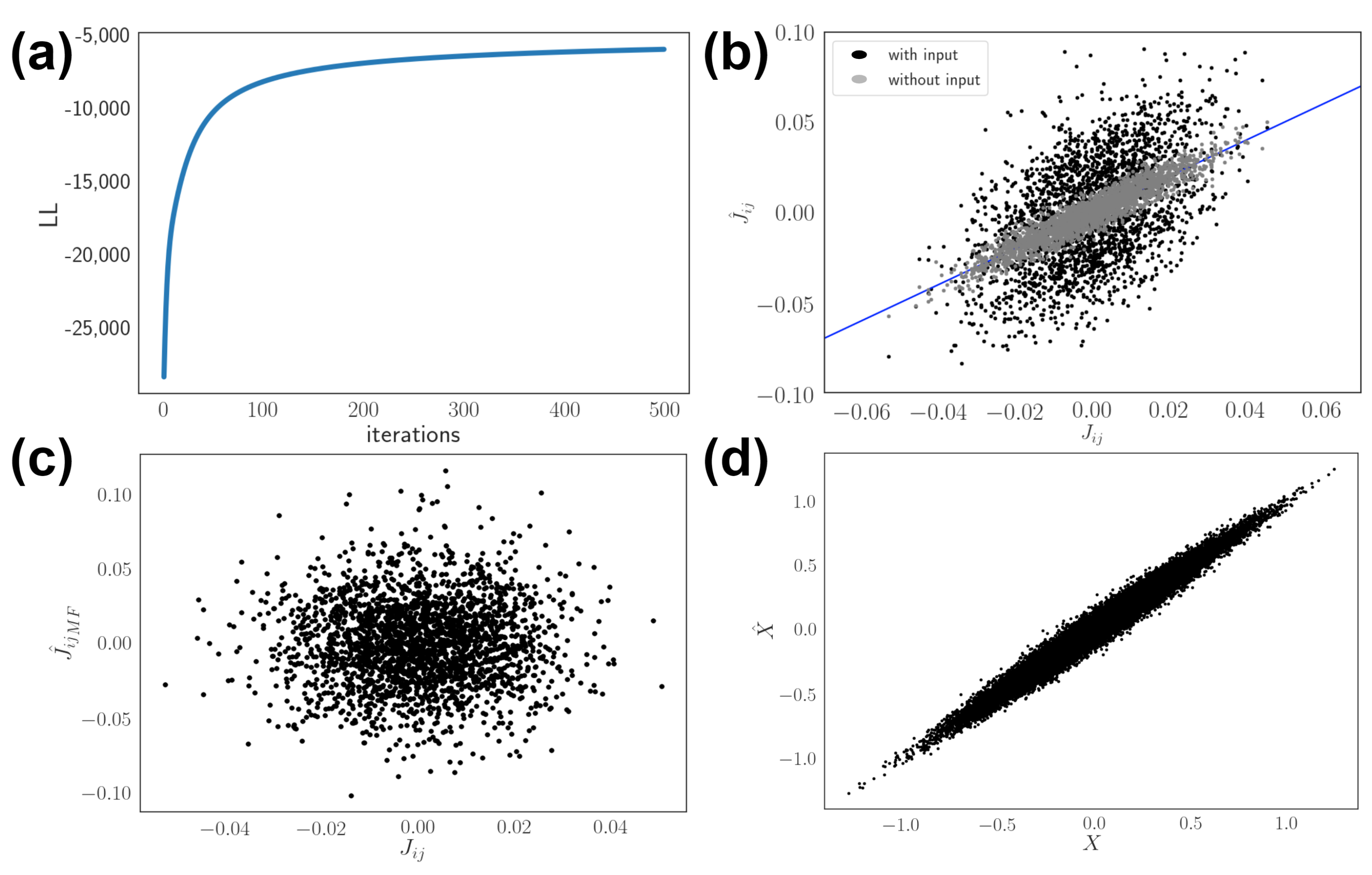
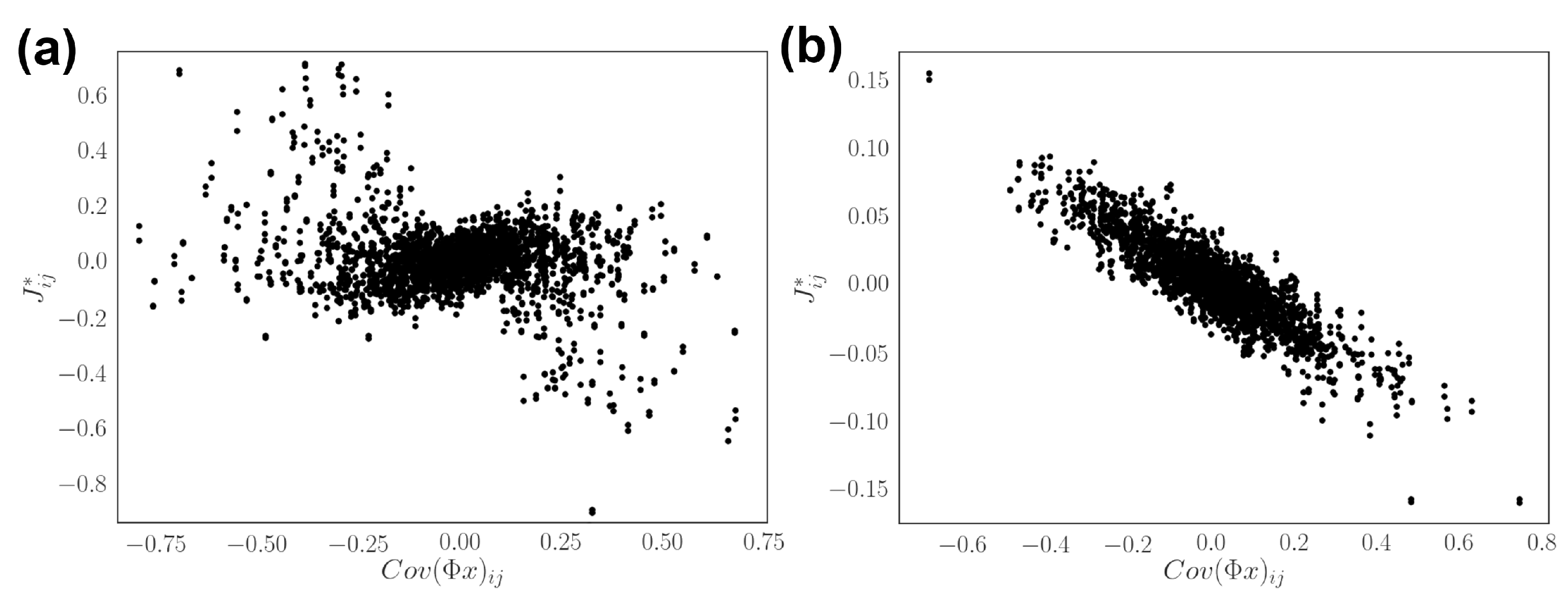
3.1. Model Setup and Network Inference
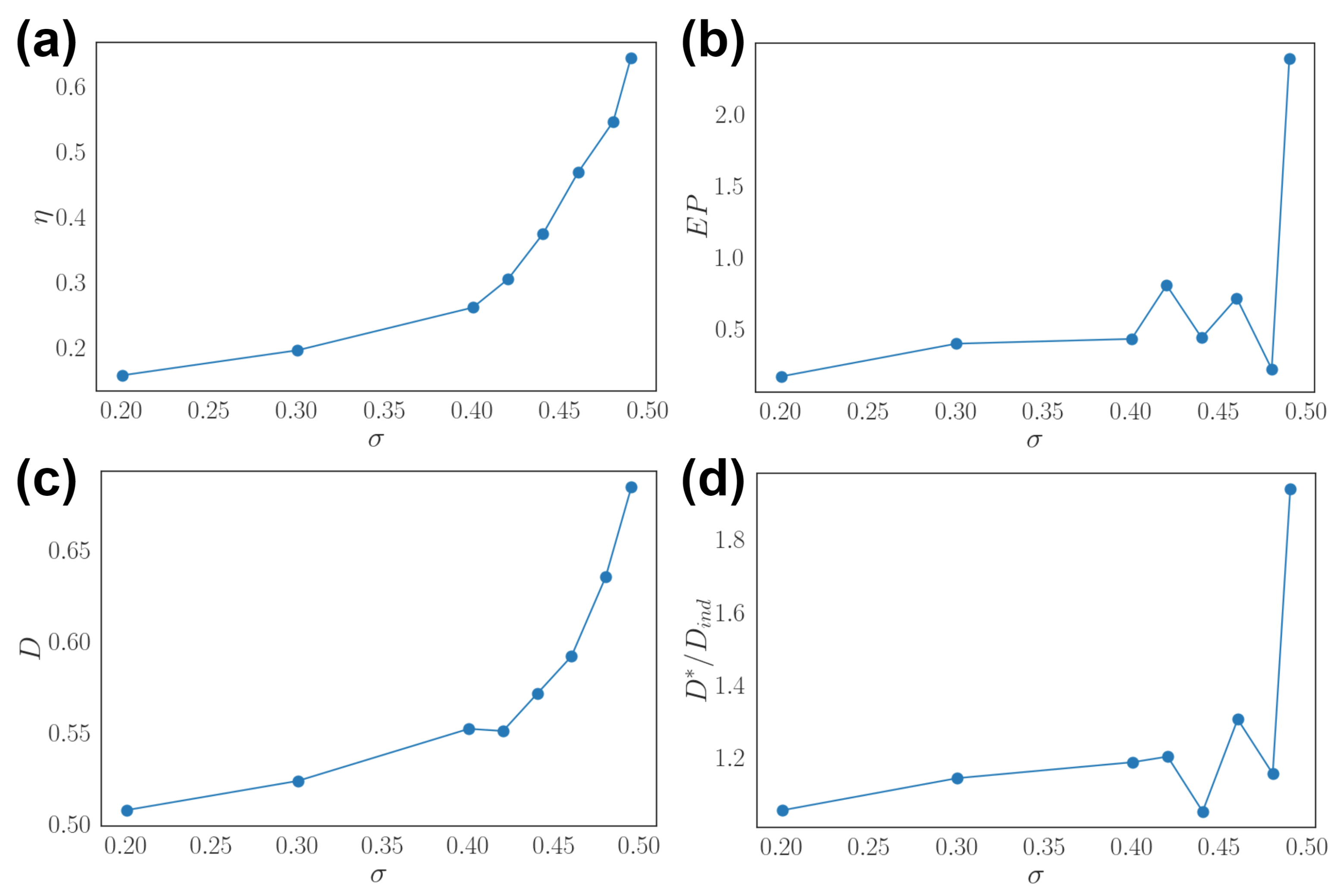
3.2. Effects of Dynamic Input
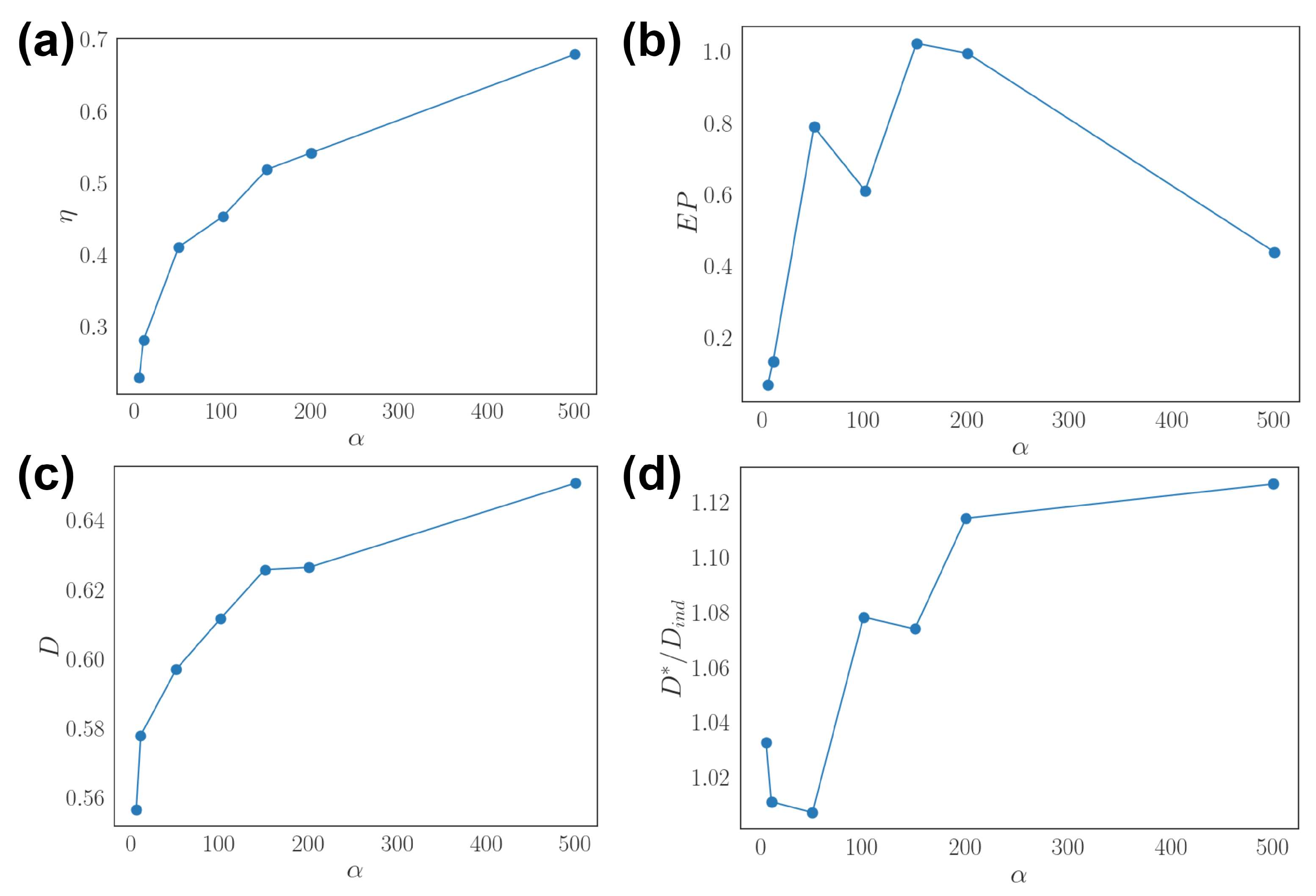
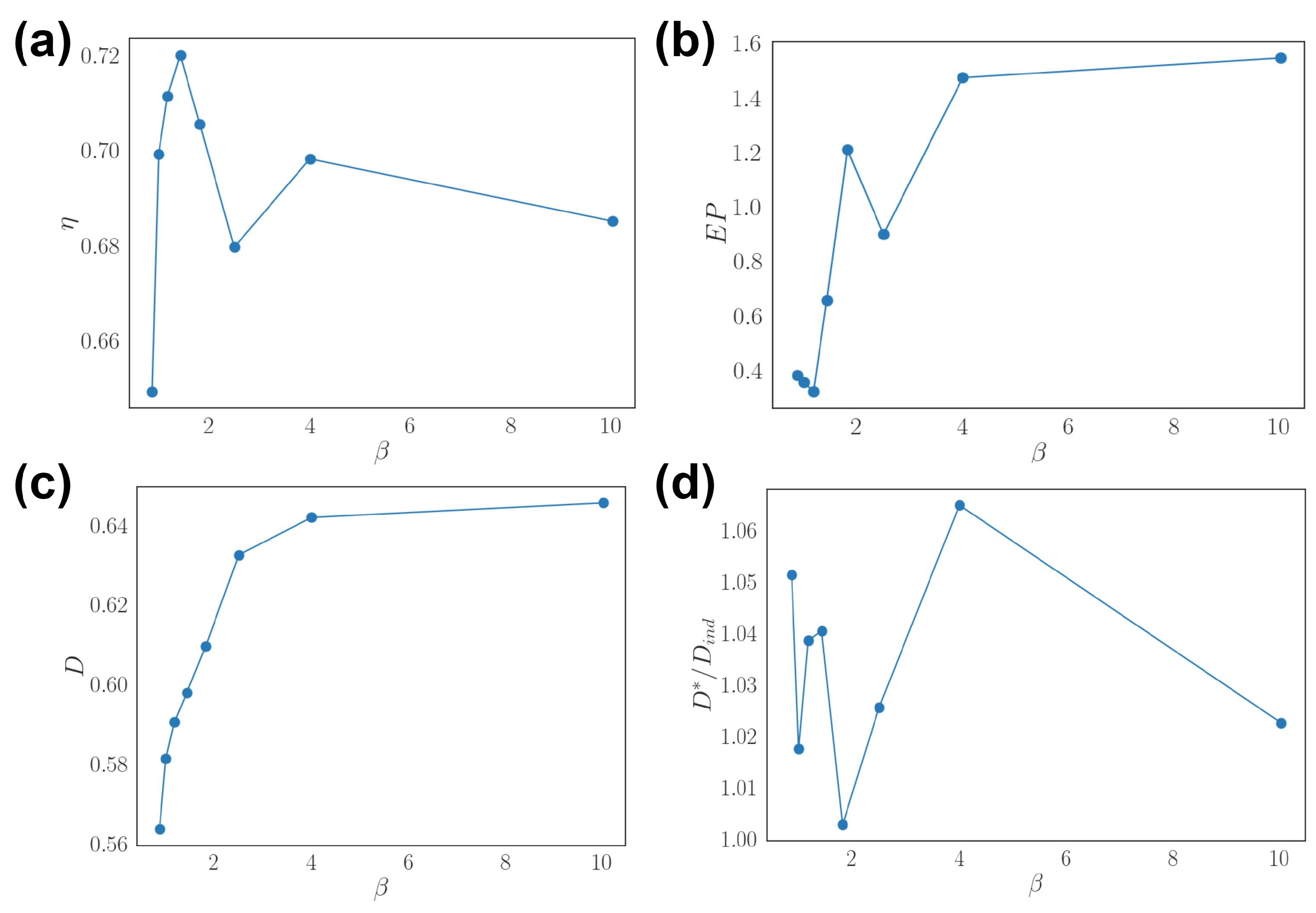
3.3. Optimal Population Coding and Network Properties
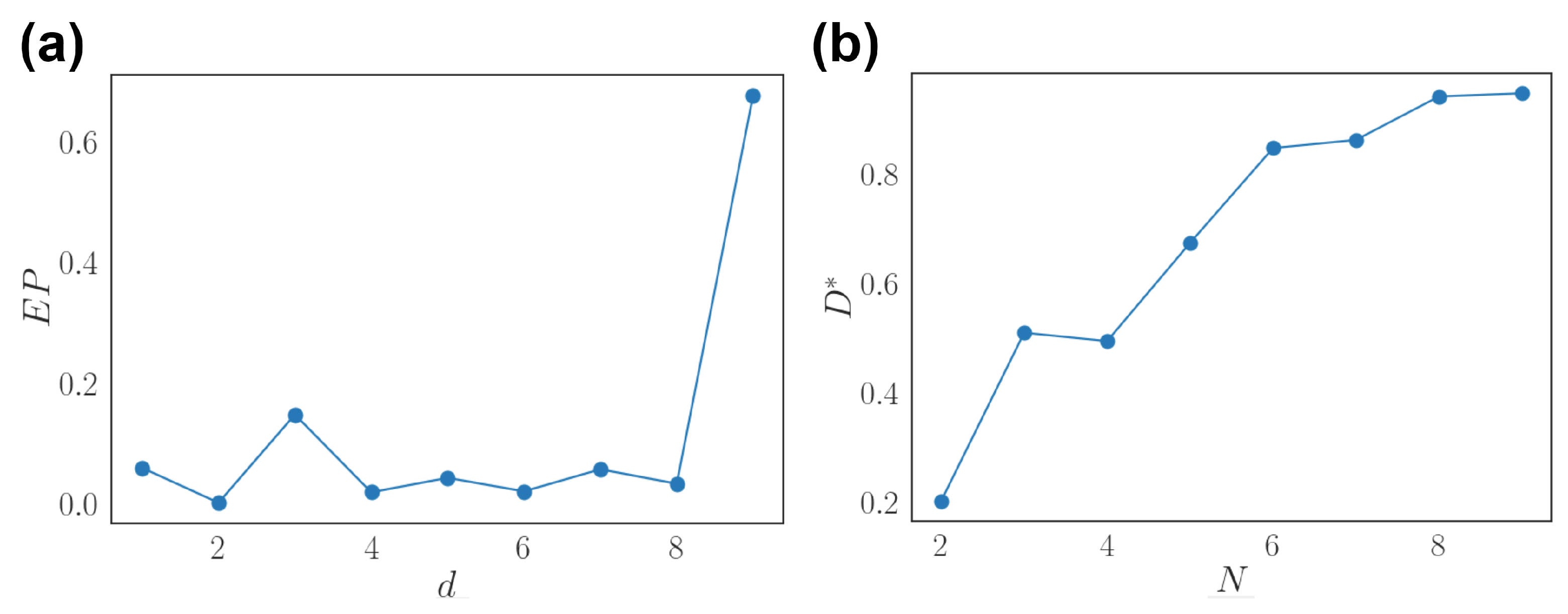
3.4. Generalization to Recurrent Networks and Nonlinear Stimuli
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barlow, H.B. Possible principles underlying the transformations of sensory messages. In Sensory Communication; The MIT Press: Cambridge, MA, USA, 2012; pp. 216–234. [Google Scholar]
- Park, I.M.; Pillow, J.W. Bayesian Efficient Coding. bioRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.J.; Beck, J.M.; Latham, P.E.; Pouget, A. Bayesian inference with probabilistic population codes. Nat. Neurosci. 2006, 9, 1432–1438. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.S.; Chen, C.C.; Chan, C.K. Characterization of Predictive Behavior of a Retina by Mutual Information. Front. Comput. Neurosci. 2017, 11, 66. [Google Scholar] [CrossRef] [PubMed]
- Palmer, S.E.; Marre, O.; Berry, M.J., 2nd; Bialek, W. Predictive information in a sensory population. Proc. Natl. Acad. Sci. USA 2015, 112, 6908–6913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seung, H.S.; Sompolinsky, H. Simple models for reading neuronal population codes. Proc. Natl. Acad. Sci. USA 1993, 90, 10749–10753. [Google Scholar] [CrossRef] [Green Version]
- Brunel, N.; Nadal, J.P. Mutual information, Fisher information, and population coding. Neural Comput. 1998, 10, 1731–1757. [Google Scholar] [CrossRef] [PubMed]
- Susemihl, A.; Meir, R.; Opper, M. Dynamic state estimation based on Poisson spike trains—Towards a theory of optimal encoding. J. Stat. Mech. Theory Exp. 2013, 2013, P03009. [Google Scholar] [CrossRef] [Green Version]
- Pillow, J.W.; Shlens, J.; Paninski, L.; Sher, A.; Litke, A.M.; Chichilnisky, E.J.; Simoncelli, E.P. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 2008, 454, 995–999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneidman, E.; Berry, M.J., II; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Granot-Atedgi, E.; Tkačik, G.; Segev, R.; Schneidman, E. Stimulus-dependent maximum entropy models of neural population codes. PLoS Comput. Biol. 2013, 9, e1002922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roudi, Y.; Aurell, E.; Hertz, J.A. Statistical physics of pairwise probability models. Front. Comput. Neurosci. 2009, 3, 22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donner, C.; Obermayer, K.; Shimazaki, H. Approximate Inference for Time-Varying Interactions and Macroscopic Dynamics of Neural Populations. PLoS Comput. Biol. 2017, 13, e1005309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tkačik, G.; Mora, T.; Marre, O.; Amodei, D.; Palmer, S.E.; Berry, M.J., 2nd; Bialek, W. Thermodynamics and signatures of criticality in a network of neurons. Proc. Natl. Acad. Sci. USA 2015, 112, 11508–11513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mora, T.; Deny, S.; Marre, O. Dynamical criticality in the collective activity of a population of retinal neurons. Phys. Rev. Lett. 2015, 114, 078105. [Google Scholar] [CrossRef] [Green Version]
- Rajan, K.; Harvey, C.D.; Tank, D.W. Recurrent Network Models of Sequence Generation and Memory. Neuron 2016, 90, 128–142. [Google Scholar] [CrossRef] [Green Version]
- De Pasquale, B.; Cueva, C.J.; Rajan, K.; Sean Escola, G.; Abbott, L.F. full-FORCE: A target-based method for training recurrent networks. PLoS ONE 2018, 13, e0191527. [Google Scholar]
- Mastrogiuseppe, F.; Ostojic, S. Linking Connectivity, Dynamics, and Computations in Low-Rank Recurrent Neural Networks. Neuron 2018, 99, 609–623.e29. [Google Scholar] [CrossRef] [Green Version]
- Rabinovich, M.I.; Varona, P.; Selverston, A.I.; Abarbanel, H.D.I. Dynamical principles in neuroscience. Rev. Mod. Phys. 2006, 78, 1213–1265. [Google Scholar] [CrossRef] [Green Version]
- Coolen, A.C.C. Statistical Mechanics of Recurrent Neural Networks II. Dynamics. arXiv 2000, arXiv:cond-mat.dis-nn/cond-mat/0006011. [Google Scholar]
- Chen, K.S. Nonequilibrium thermodynamics of input-driven networks. arXiv 2020, arXiv:q-bio.NC/2012.13252. [Google Scholar]
- Yan, H.; Zhao, L.; Hu, L.; Wang, X.; Wang, E.; Wang, J. Nonequilibrium landscape theory of neural networks. Proc. Natl. Acad. Sci. USA 2013, 110, E4185–E4194. [Google Scholar] [CrossRef] [Green Version]
- Shimazaki, H. The principles of adaptation in organisms and machines II: Thermodynamics of the Bayesian brain. arXiv 2020, arXiv:q-bio.NC/2006.13158. [Google Scholar]
- Zhong, W.; Lu, Z.; Schwab, D.J.; Murugan, A. Non-equilibrium statistical mechanics of continuous attractors. arXiv 2018, arXiv:cond-mat.dis-nn/1809.11167. [Google Scholar]
- Sigg, D.; Voelz, V.A.; Carnevale, V. Microcanonical coarse-graining of the kinetic Ising model. J. Chem. Phys. 2020, 152, 084104. [Google Scholar] [CrossRef] [PubMed]
- Agakov, F.; Barber, D. Variational Information Maximization for Neural Coding; Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2004; pp. 543–548. [Google Scholar]
- Roudi, Y.; Hertz, J. Mean field theory for nonequilibrium network reconstruction. Phys. Rev. Lett. 2011, 106, 048702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakellariou, J.; Roudi, Y.; Mezard, M.; Hertz, J. Effect of coupling asymmetry on mean-field solutions of the direct and inverse Sherrington–Kirkpatrick model. Philos. Mag. 2012, 92, 272–279. [Google Scholar] [CrossRef]
- Battistin, C.; Hertz, J.; Tyrcha, J.; Roudi, Y. Belief propagation and replicas for inference and learning in a kinetic Ising model with hidden spins. J. Stat. Mech. 2015, 2015, P05021. [Google Scholar] [CrossRef] [Green Version]
- Tkačik, G.; Prentice, J.S.; Balasubramanian, V.; Schneidman, E. Optimal population coding by noisy spiking neurons. Proc. Natl. Acad. Sci. USA 2010, 107, 14419–14424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schuessler, F.; Dubreuil, A.; Mastrogiuseppe, F.; Ostojic, S.; Barak, O. Dynamics of random recurrent networks with correlated low-rank structure. Phys. Rev. 2020, 2, 013111. [Google Scholar] [CrossRef] [Green Version]
- Schaub, M.T.; Schultz, S.R. The Ising decoder: Reading out the activity of large neural ensembles. J. Comput. Neurosci. 2012, 32, 101–118. [Google Scholar] [CrossRef] [Green Version]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. 1986, 48, 259–279. [Google Scholar] [CrossRef] [Green Version]
- Zeng, H.L.; Alava, M.; Aurell, E.; Hertz, J.; Roudi, Y. Maximum likelihood reconstruction for Ising models with asynchronous updates. Phys. Rev. Lett. 2013, 110, 210601. [Google Scholar] [CrossRef] [PubMed]
- Aguilera, M.; Amin Moosavi, S.; Shimazaki, H. A unifying framework for mean-field theories of asymmetric kinetic Ising systems. Nat. Commun. 2021, 12, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Thouless, D.J.; Anderson, P.W.; Palmer, R.G. Solution of ’Solvable model of a spin glass’. Philos. Mag. J. Theor. Exp. Appl. Phys. 1977, 35, 593–601. [Google Scholar] [CrossRef]
- Mézard, M.; Sakellariou, J. Exact mean-field inference in asymmetric kinetic Ising systems. J. Stat. Mech. 2011, 2011, L07001. [Google Scholar] [CrossRef]
- Monteforte, M.; Wolf, F. Dynamical Entropy Production in Spiking Neuron Networks in the Balanced State 2010. arXiv 2020, arXiv:cond-mat.dis-nn/1003.4410. [Google Scholar]
- Beck, J.; Bejjanki, V.R.; Pouget, A. Insights from a simple expression for linear fisher information in a recurrently connected population of spiking neurons. Neural Comput. 2011, 23, 1484–1502. [Google Scholar] [CrossRef]
- Młynarski, W.F.; Hermundstad, A.M. Efficient and adaptive sensory codes. Nat. Neurosci. 2021, 24, 998–1009. [Google Scholar] [CrossRef]
- Röth, K.; Shao, S.; Gjorgjieva, J. Efficient population coding depends on stimulus convergence and source of noise. PLoS Comput. Biol. 2021, 17, e1008897. [Google Scholar] [CrossRef]
- Berkowitz, J.A.; Sharpee, T.O. Quantifying Information Conveyed by Large Neuronal Populations. Neural Comput. 2019, 31, 1015–1047. [Google Scholar] [CrossRef]
- Chalk, M.; Marre, O.; Tkačik, G. Toward a unified theory of efficient, predictive, and sparse coding. Proc. Natl. Acad. Sci. USA 2018, 115, 186–191. [Google Scholar] [CrossRef] [Green Version]
- Cofré, R.; Maldonado, C.; Cessac, B. Thermodynamic Formalism in Neuronal Dynamics and Spike Train Statistics. Entropy 2020, 22, 1330. [Google Scholar] [CrossRef] [PubMed]
- Ngampruetikorn, V.; Schwab, D.J.; Stephens, G.J. Energy consumption and cooperation for optimal sensing. Nat. Commun. 2020, 11, 975. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salazar, D.S.P. Nonequilibrium thermodynamics of restricted Boltzmann machines. Phys. Rev. E 2017, 96, 022131. [Google Scholar] [CrossRef] [Green Version]
- Goldt, S.; Seifert, U. Stochastic Thermodynamics of Learning. Phys. Rev. Lett. 2017, 118, 010601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Denève, S.; Machens, C.K. Efficient codes and balanced networks. Nat. Neurosci. 2016, 19, 375–382. [Google Scholar] [CrossRef]
- Bellec, G.; Salaj, D.; Subramoney, A.; Legenstein, R.; Maass, W. Long short-term memory and Learning-to-learn in networks of spiking neurons. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef]
- Cofré, R.; Maldonado, C. Information Entropy Production of Maximum Entropy Markov Chains from Spike Trains. Entropy 2018, 20, 34. [Google Scholar] [CrossRef] [Green Version]
- Ladenbauer, J.; McKenzie, S.; English, D.F.; Hagens, O.; Ostojic, S. Inferring and validating mechanistic models of neural microcircuits based on spike-train data. Nat. Commun. 2019, 10, 4933. [Google Scholar] [CrossRef] [Green Version]
- Kadirvelu, B.; Hayashi, Y.; Nasuto, S.J. Inferring structural connectivity using Ising couplings in models of neuronal networks. Sci. Rep. 2017, 7, 8156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kunert-Graf, J.M.; Shlizerman, E.; Walker, A.; Kutz, J.N. Multistability and Long-Timescale Transients Encoded by Network Structure in a Model of C. elegans Connectome Dynamics. Front. Comput. Neurosci. 2017, 11, 53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campajola, C.; Lillo, F.; Mazzarisi, P.; Tantari, D. On the equivalence between the kinetic Ising model and discrete autoregressive processes. J. Stat. Mech. 2021, 2021, 033412. [Google Scholar] [CrossRef]
- Cho, M.W.; Choi, M.Y. Origin of the spike-timing–dependent plasticity rule. EPL 2016, 38001. [Google Scholar] [CrossRef]
- Rezende, D.; Wierstra, D.; Gerstner, W. Variational learning for recurrent spiking networks. Adv. Neural Inf. Process. Syst. 2011, 24. [Google Scholar]
- Ganguli, S.; Huh, D.; Sompolinsky, H. Memory traces in dynamical systems. Proc. Natl. Acad. Sci. USA 2008, 105, 18970–18975. [Google Scholar] [CrossRef] [Green Version]
- Goldman, M.S. Memory without feedback in a neural network. Neuron 2009, 61, 621–634. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.S. Optimal Population Coding for Dynamic Input by Nonequilibrium Networks. Entropy 2022, 24, 598. https://doi.org/10.3390/e24050598
Chen KS. Optimal Population Coding for Dynamic Input by Nonequilibrium Networks. Entropy. 2022; 24(5):598. https://doi.org/10.3390/e24050598
Chicago/Turabian StyleChen, Kevin S. 2022. "Optimal Population Coding for Dynamic Input by Nonequilibrium Networks" Entropy 24, no. 5: 598. https://doi.org/10.3390/e24050598
APA StyleChen, K. S. (2022). Optimal Population Coding for Dynamic Input by Nonequilibrium Networks. Entropy, 24(5), 598. https://doi.org/10.3390/e24050598





